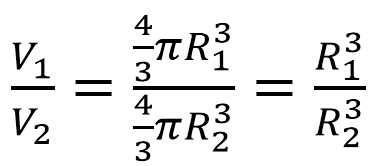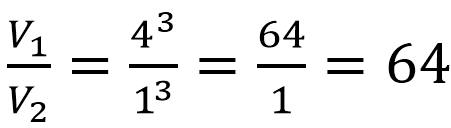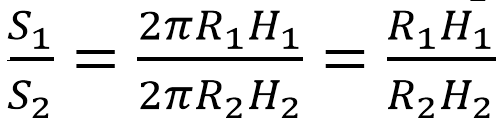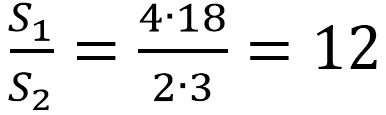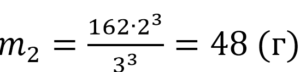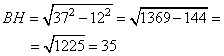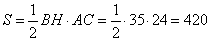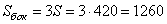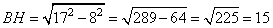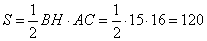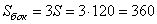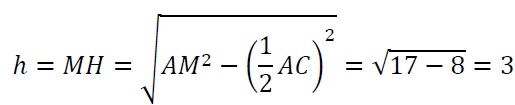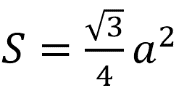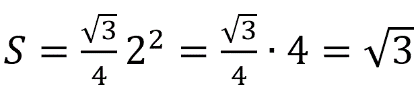Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды
2
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
3
Два ребра прямоугольного параллелепипеда равны 7 и 4, а объём параллелепипеда равен 140. Найдите площадь поверхности этого параллелепипеда.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 120914.
4
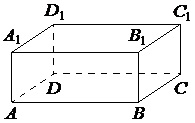
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра AB, BC и диагональ боковой грани BC1 равны соответственно 7, 3 и
Найдите объём параллелепипеда ABCDA1B1C1D1.
5
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 боковой грани равны соответственно 2, 4 и
Найдите площадь поверхности параллелепипеда ABCDA1B1C1D1.
Пройти тестирование по этим заданиям
Наглядная стереометрия
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры – например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии – они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Вариант 13МБ1
[su_note note_color=”#defae6″]
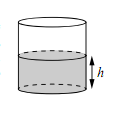
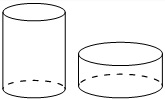
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
[/su_note]
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.
- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
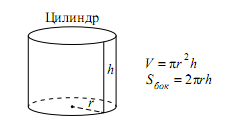
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае.
V1 = π r1 2 h1
V2 = π r2 2 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r1 2 h1 = π r2 2 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r1 2 h1)/ π r2 2
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r1 2 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r1 2 h1)/ 16 r1 2
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5.
Вариант 13МБ2
[su_note note_color=”#defae6″]
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
[/su_note]
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2.
Вариант 13МБ3
[su_note note_color=”#defae6″]
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
[/su_note]
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 1,5 c2 (первая коробка в полтора раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй.
Ответ: 6.
Вариант 13МБ4
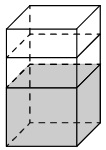
[su_note note_color=”#defae6″]
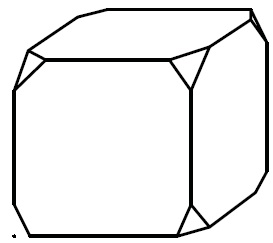
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
[/su_note]
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового “куба”. Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Вариант 13МБ5
[su_note note_color=”#defae6″]
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
[/su_note]
Алгоритм выполнения
- Записываем ф-лу для вычисления объема цилиндра.
- Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
- Формируем формулы для объема 1-го и 2-го цилиндров.
- Вычисляем отношение объемов.
Решение:
Объем цилиндра равен: V=πR2H. Обозначим радиус основания 1-го цилиндра через R1, а его высоту – через Н1. Соответственно, радиус основания 2-го цилиндра обозначим через R2, а высоту – через Н2.
Отсюда получим: V1=πR12H1, V2=πR22H2.
Запишем искомое отношение объемов:
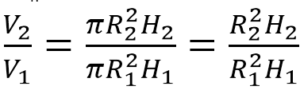
Подставляем в полученное отношение числовые данные:
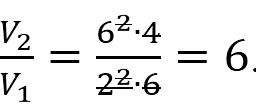
Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.
Вариант 13МБ6
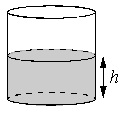
[su_note note_color=”#defae6″]
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
[/su_note]
Алгоритм выполнения
- Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
- Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
- Переводим результат, полученный в литрах, в куб.см.
Решение:
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см).
Вариант 13МБ7
[su_note note_color=”#defae6″]
Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
[/su_note]
Алгоритм выполнения
- Записываем ф-лу для расчета объема цилиндра.
- На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
- Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h2.
Решение:
Объем цилиндра равен: V=Sоснh=πR2h.
Объем воды в 1-м сосуде: V1=πR12h1.
Объем во 2-м сосуде: V2=πR22h2.
Приравниваем V1 и V2: πR12h1=πR22h2.
Сокращаем на π, выражаем h2:
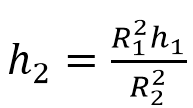
По условию R2=2R1. Отсюда:
.
Вариант 13МБ8
[su_note note_color=”#defae6″]
От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?
[/su_note]
Алгоритм выполнения
- Определяем количество вершин у треугольной призмы.
- Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.
Решение:
Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями правильной треугольной призмы являются правильные треугольники, то вершин у такой призмы 3·2=6 штук.
Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. То есть вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.
Вариант 13МБ9
[su_note note_color=”#defae6″]
Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?
[/su_note]
Алгоритм выполнения
- Вводим обозначения для линейных параметров коробок и их объемов.
- Определяем зависимость линейных параметров согласно условию.
- Записываем формулу для вычисления объема призмы.
- Адаптируем эту формулу для объемов коробок.
- Находим отношение объемов.
Решение:
Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а1, а для второй а2. Высоты коробок обозначим соответственно h1 и h2. Объемы – V1 и V2.
Согласно условию, h2=4,5h1, а1=3а2.
Объем призмы равен: V=Sоснh. Т.к. в основании коробок лежит квадрат, то Sосн=а2. Отсюда: V=a2h.
Для 1-й коробки имеем: V1=a12h1. Для 2-й коробки: V2=a22h2.
Тогда получаем отношение:
Ответ: 2
Вариант 13МБ10
[su_note note_color=”#defae6″]
В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
[/su_note]
Алгоритм выполнения
- Доказываем, что данные в условии конусы подобны.
- Определяем коэффициент подобия.
- Используя свойство для объемов подобных тел, находим объем жидкости.
Решение:
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
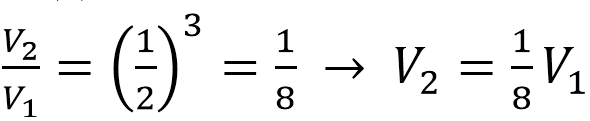
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл.
Вариант 13МБ11
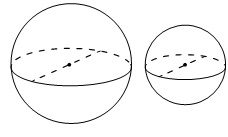
[su_note note_color=”#defae6″]
Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
[/su_note]
Алгоритм выполнения
- Записываем формулу для вычисления объема шара.
- Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
- Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Решение:
Объем шара вычисляется по ф-ле: .
Отсюда объем 1-го (большего) шара равен 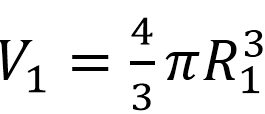
.
Составим отношение объемов:
Подставляем в полученную формулу числовые данные из условия:
Вывод: объем большего шара в 64 раза больше.
Вариант 13МБ12
[su_note note_color=”#defae6″]
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
[/su_note]
Алгоритм выполнения
- Записываем формулу для определения площади бок.поверхности цилиндра.
- Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
- Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Решение:
Площадь бок.поверхности цилиндра вычисляется так: S=2πRH.
Для 1-го цилиндра имеем: S1=2πR1H1. Для 2-го цилиндра: S2=2πR2H2.
Составим отношение этих площадей:
Найдем числовое значение полученного отношения:
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Вариант 13МБ13
[su_note note_color=”#defae6″]
Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
[/su_note]
Алгоритм выполнения
- Записываем формулу для определения массы большего шаров через плотность и объем.
- Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
- Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
- Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
Решение:
Масса большего (1-го) шара равна: m1=ρV1. Объем этого шара составляет V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13. Из этого уравнения выразим плотность: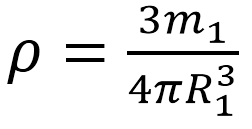
Масса меньшего (2-го) шара равна: m2=ρV2. Объем шара: V2=(4/3)πR23. В ур-ние для m2 подставим выражения для ρ и V2. Получаем:
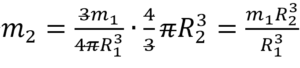
Вариант 13МБ14
[su_note note_color=”#defae6″]
В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
[/su_note]
Алгоритм выполнения
- Определяем часть призмы, соответствующую объему погруженной детали.
- Вычисляем объем детали на основании формулы для определения объема прямой призмы с квадратом в основании.
Решение:
Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь имеет объем, равный части жидкости, занимающей объем 40х40х10 (см).
Найдем этот объем:
V=40·40·10=16000 (см3).
Даниил Романович | Просмотров: 19.1k
- ЕГЭ по математике база
Подборка задач базового ЕГЭ по математике задание №13 — стереометрия
Для выполнения задания 13 необходимо уметь выполнять действия с геометрическими фигурами.
Практика ЕГЭ по базовой математике задание №13
Примеры заданий:
1. Два ребра прямоугольного параллелепипеда равны 12 и 6, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
2. В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 5 и 7. Найдите объём призмы, если её высота равна 4.
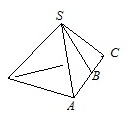
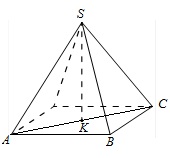
3. В треугольной пирамиде ABCD рёбра AB, AC и AD взаимно перпендикулярны. Найдите объём этой пирамиды, если AB=3, AC=18 и AD=7.
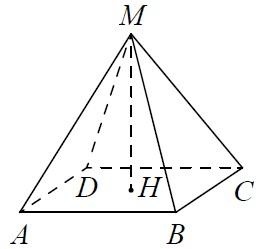
4. Стороны основания правильной треугольной пирамиды равны 14, а боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.
5. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 9 и 8, а второго – 12 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Смотрите также:
ЗАДАЧИ
ПО СТЕРЕОМЕТРИИ №16
1. Площадь
поверхности куба равна 18. Найдите его диагональ.
Пояснение.
Пусть ребро куба равно ,
тогда площадь поверхности куба ,
а диагональ куба .
Тогда

2. Если каждое
ребро куба увеличить на 1, то его площадь поверхности увеличится на 54.
Найдите ребро куба.
Пояснение.
Площадь поверхности куба выражается
через его ребро как
,
поэтому при увеличении длины ребра на площадь
увеличится на
Отсюда находим, что ребро куба
равно
.Ответ: 4.
3. Два ребра
прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4.
Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро,
выходящее из той же вершины.
Пояснение.
Обозначим известные ребра за и
,
а неизвестное за .
Площадь поверхности параллелепипеда выражается как .
Выразим :
,
откуда неизвестное ребро
.Ответ: 5.
4. Два ребра
прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь
поверхности параллелепипеда равна 16. Найдите его диагональ.
Пояснение.
Пусть длина третьего ребра, исходящего
из той же вершины, равна ,
тогда площадь поверхности параллелепипеда даётся формулой .
По условию площадь поверхности равна 16, тогда откуда
Длина диагонали прямоугольного
параллелепипеда равна квадратному корню из суммы квадратов его
измерений, поэтому .
Ответ: 3.
5. Прямоугольный
параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Пояснение.
Высота и сторона такого
параллелепипеда равны диаметру сферы, то есть это куб со стороной 2. Площадь
поверхности куба со стороной :
Ответ: 24.
6. Найдите
угол прямоугольного
параллелепипеда, для которого ,
,
. Дайте
ответ в градусах.
Пояснение.
В прямоугольнике отрезок
является
диагональю, По
теореме Пифагора
Прямоугольный
треугольник равнобедренный:
,
значит, его острые углы равны
Ответ: 45.
7. Два ребра
прямоугольного параллелепипеда равны 8 и 5, а объём параллелепипеда
равен 280. Найдите площадь поверхности этого параллелепипеда.
Пояснение.
Найдем третье ребро прямоугольного
параллелепипеда: .
Найдем площадь поверхности параллелепипеда:
Ответ: 262
8. В основании
прямой призмы лежит прямоугольный треугольник, один из катетов которого
равен 2, а гипотенуза равна Найдите
объём призмы, если её высота равна 3.
Пояснение.
Пусть второй катет — b с
помощью теоремы Пифагора найдём его:
Найдём площадь основания:
Найдём объём призмы:
Ответ: 21.
9. В бак, имеющий
форму прямой призмы, налито 5 л воды. После полного погружения в воду
детали уровень воды в баке поднялся в 1,4 раза. Найдите объём детали.
Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических
сантиметров.
Пояснение.
Найдем объём воды в баке после погружения
детали (уровень воды прямопропорционален объему): л.
Таким образом, при погружении детали в бак объём воды увеличился на л,
что и является объёмом детали. В кубических сантиметрах — Ответ: 2000.
10. Найдите объем правильной
шестиугольной призмы, стороны основания которой равны 1, а боковые ребра
равны .
Пояснение.
Объем прямой призмы равен ,
где —
площадь основания, а —
боковое ребро. Площадь правильного шестиугольника со стороной ,
лежащего в основании, задается формулой
Тогда объем призмы
равен
.Ответ: 4,5.
11. Через среднюю
линию основания треугольной призмы, площадь боковой поверхности которой равна
24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой
поверхности отсеченной треугольной призмы.
Пояснение.
Площадь боковых граней отсеченной
призмы вдвое меньше соответствующих площадей боковых граней исходной призмы.
Поэтому площадь боковой поверхности отсеченной призмы вдвое меньше площади
боковой поверхности исходной. Ответ:
12.
12. Найдите объем
правильной треугольной пирамиды, стороны основания которой равны 1, а высота
равна .
Пояснение.
Объем пирамиды равен
,
где –
площадь основания, а
– высота пирамиды. Площадь равностороннего треугольника в основании
,
Тогда объем
пирамиды равен
.Ответ: 0,25.
13. В правильной
четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое
ребро этой пирамиды.
Пояснение.
Объем пирамиды с площадью основания
и
высотой равен
,
откуда площадь основания Сторона
основания тогда ,
а диагональ .
Боковое ребро найдем по теореме Пифагора:

13.
14. Сторона основания
правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем
пирамиды.
Пояснение.
В правильном шестиугольнике сторона
равна радиусу описанной окружности, поэтому найдем высоту пирамиды по теореме
Пифагора: .
Площадь основания
.
Тогда объем
пирамиды
.Ответ: 12.
15. Найдите объем
пирамиды, изображенной на рисунке. Ее основанием является многоугольник,
соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно
плоскости основания и равно 3.
Пояснение.
Площадь лежащего в основании
пирамиды многоугольника является разностью площадей квадратов со сторонами
6 и 3 (см. рис.):
Поскольку высота пирамиды равна
3, имеем:
Ответ:
27.
16. В основании прямой
призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите
объем цилиндра, описанного около этой призмы.
Пояснение.
По теореме Пифагора длина
гипотенузы треугольника в основании .
Поскольку гипотенуза является диаметром основания описанного цилиндра, его
объем
.Ответ: 125.
17. Даны два цилиндра.
Радиус основания и высота первого равны соответственно 2 и 6, а второго
— 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?
Пояснение.
Объём цилиндра находится по формуле
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма второго
шара к первому:
Ответ:
10,5.
18. Радиус основания
цилиндра равен 15, а его образующая равна 19. Сечение, параллельное оси
цилиндра, удалено от неё на расстояния, равное 9. Найдите площадь этого
сечения.
Пояснение.
Запишем выражение для площади
сечения
AK найдём из
треугольника KOA — прямоугольного, KO = 9, AO = 15,
AKKO,
Таким образом, Ответ: 456.
19. Вода в сосуде цилиндрической
формы находится на уровне h = 80 см. На каком уровне окажется
вода, если её перелить в другой цилиндрический сосуд, у которого радиус
основания вдвое больше, чем у первого? Ответ дайтев сантиметрах.
Пояснение.
Объём воды по условию не изменен
и вычисляется по формуле: .
Таким образом, если радиус основания увеличится вдвое, то при неизменном
объёме высота уменьшится в раза
().
Ответ: 20.
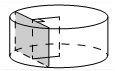
20. Найдите объем части
цилиндра, изображенной на рисунке. В ответе укажите .
Пояснение.
Объем данной части цилиндра равен
. Ответ: 144.
21. Конус получается
при вращении равнобедренного прямоугольного треугольника вокруг
катета, равного 6. Найдите его объем, деленный на .
Пояснение.
Треугольник –
так же равнобедренный, т.к. углы при основании .
Тогда радиус основания равен 6, и объем конуса, деленный на :
Ответ: 72.
22. Конус описан
около правильной четырехугольной пирамиды со стороной основания 4 и высотой
6. Найдите его объем, деленный на .
Пояснение.
Радиус основания конуса равен
половине диагонали квадрата :

Тогда объем конуса, деленный на :
Ответ: 16.
23. Площадь боковой
поверхности конуса в два раза больше площади основания. Найдите угол между образующей
конуса и плоскостью основания. Ответ дайте в градусах.
Пояснение.
Площадь основания конуса равна ,
а площадь боковой поверхности .
Из условия имеем:
Значит, в прямоугольном
треугольнике, образованном высотой, образующей и радиусом основания конуса,
катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла
30°. Следовательно, угол между образующей конуса и плоскостью основания равен
60°. Ответ: 60.
24. Найдите объем части
конуса, изображенной на рисунке. В ответе укажите .
Пояснение. Объем
данной части конуса равен
. Ответ: 87,75.
25. Конус вписан в
шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите
объем конуса.
Пояснение.
Запишем формулу для объёма шара:
Объём конуса в 4 раза меньше:
. Ответ: 7.
26. Диаметр основания
конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения
этого конуса.
Пояснение.

конуса является равнобедренный треугольник, основание
которого — диаметр основания конуса, а высота совпадает с высотой
конуса. Образующая конуса ,
его высота и
радиус основания связаны
соотношением откуда
Следовательно,
площадь осевого сечения равна
0,5 · 12 · 8 = 48. Ответ: 48.
27. В куб с ребром 3
вписан шар. Найдите объем этого шара, деленный на .
Пояснение. Радиус
вписанного в куб шара равен половине длины ребра: .
Тогда объем шара

28. Конус вписан в
шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите
объем шара.
Пояснение
. Ответ: 24.
29. Даны два шара с радиусами
4 и 1. Во сколько раз объём большего шара больше объёма другого?
Пояснение.
Найдём объём первого шара:
Найдём объём второго шара:
Найдём
отношение объёма большего шара к объёму меньшего:
Ответ: 64.
30. Даны два шара с радиусами
14 и 2. Во сколько раз площадь поверхности большего шара больше площади
поверхности другого?
Пояснение.
Найдём площадь поверхности первого
шара:
Найдём площадь поверхности второго
шара:
Найдём отношение площадей большего
шара к меньшему
Ответ: 49.
mathlesson.ru
- Обо мне
- Вопрос-Ответ
- Блог
- Отзывы
- Личный кабинет
Темы
ЕГЭ База
←
ЕГЭ (база) / Задачи по стереометрии
→
Стереометрия
В задании №16 базового уровня ЕГЭ по математике нам предстоит столкнуться со стереометрией. Как таковой «стереометрии» мы не встретим, обычно условие задания содержит объемную фигуру, в которой нам необходимо найти какое-либо расстояние. В данном задании необходимо правильно применить пространственное мышление и выбрать нужное сечение, остальные расчеты происходят в плоскости, причем по несложным формулам (теорема Пифагора и т.д.). Какой-либо конкретной теории я пока приводить не буду, а рассмотрю типовые варианты, на которых мы и рассмотрим алгоритмы решения задач данного типа.
Разбор типовых вариантов заданий №16 ЕГЭ по математике базового уровня
Вариант 16МБ1
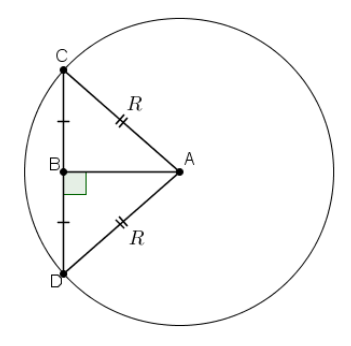
Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.
Алгоритм выполнения:
- Определить тип фигуры, образующей сечение.
- Записать формулу для нахождения площади фигуры, образующей сечение.
- Вычислить недостающие данные.
- Вычислить искомую площадь сечения.
Решение:
Из рисунка видно, что сечение является прямоугольником, одна из сторон которого образующая цилиндра.
Площадь прямоугольника равна произведению длины на ширину.
Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху:
Ширина прямоугольника – CD.
По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.
СD = СВ + ВD. СВ = ВD
Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае СА2 = СВ2 + АВ2
СВ2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
СВ2 = СА2 — АВ2
СВ = √(СА2 — АВ2)
СВ = √(132 — 122) = √(169 — 144) = √25 = 5
Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10
Вычислим искомую площадь сечения.
10 · 18 = 180
Ответ: 180.
Вариант 16МБ2
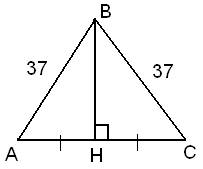
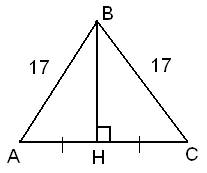
Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
Алгоритм выполнения:
- Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
- Найти площади треугольников.
- Найти площадь боковой поверхности пирамиды.
Решение:
Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=24:2=12.
Рассмотрим треугольник АВН.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае АВ2 = ВН2 + АН2
ВН2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
ВН2 = АВ2 — АН2
Следовательно, высота BH, равна:
Площадь треугольника равна половине произведения основания на высоту.
Тогда, площадь треугольника может быть вычислена как
Найдем площадь боковой поверхности пирамиды.
Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:
Ответ: 1260.
Вариант 16МБ3
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Алгоритм выполнения:
- Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
- Найти площади треугольников.
- Найти площадь боковой поверхности пирамиды.
Решение:
Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 17, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=16:2=8.
Рассмотрим треугольник АВН.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае АВ2 = ВН2 + АН2
ВН2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
ВН2 = АВ2 — АН2
Следовательно, высота BH, равна:
Площадь треугольника равна половине произведения основания на высоту.
Тогда, площадь треугольника может быть вычислена как
Найдем площадь боковой поверхности пирамиды.
Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:
Ответ: 360.
Вариант 16МБ4
Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты.
Площадь основания рассчитываем по формуле площади квадрата — квадрат стороны:
После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:
После этого легко вычисляем объем:
V = 1/3 • 16 •3 = 16
Ответ: 16
Вариант 16МБ5
В треугольной пирамиде АВСD ребра АВ, АС и АD взаимно перпендикулярны. Найдите объем этой пирамиды, если АВ=2, АС=15 и AD=11.
Алгоритм выполнения
- Записываем формулу для определения объема пирамиды.
- Находим площадь основания по формуле для площади прямоугольного треугольника.
- Показываем, что высота пирамиды совпадает с ребром AD. Вычисляем искомый объем.
Решение:
Объем пирамиды:
Т.к. в основании пирамиды лежит прямоугольный треугольник с катетами АВ и АС (по условию АВ перпендикулярно АС), то Sосн=АВ·АС/2.
Получаем:
Sосн=2·15/2=15.
Т.к. AD перпендикулярно АВ и АС и пересекается с ними в одной точке, то (по признаку перпендикулярности прямой и плоскости) AD перпендикулярно плоскости основания пирамиды.
Значит AD – высота пирамиды. Т.е. Н=AD=11.
Отсюда имеем:
Вариант 16МБ6
Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА1В1С1.
Алгоритм выполнения
- Находим площадь основы призмы через формулу для площади правильного треугольника.
- Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину.
Решение:
Площадь правильного треугольника равна:
Здесь а – сторона основания призмы.
Вычислим площадь:
Объем призмы: V=Sh, где h – высота призмы, S– площадь ее основания (в нашем случае – площадь правильного треугольника, лежащего в основании).
Вычисляем объем:
Вариант 16МБ7
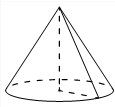
Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
Алгоритм выполнения
- Записываем формулу для объема конуса. Из нее выражаем площадь основания.
- Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса.
- Из этих двух формул выражаем искомую величину. Вычисляем ее.
Решение:
Объем конуса равен:
Отсюда:
Sосн=3V/h.
Площадь круга составляет:
S=πR2.
Поскольку в данном случае Sосн=S, то πR2=3V/h.
Получаем:
Вариант 16МБ8
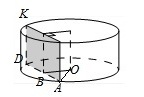
Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.
Алгоритм выполнения
- Определяем, что образующая цилиндра – это одна из сторон сечения-прямоугольника. Вводим обозначения для точек, которые необходимы для выполнения расчетов. Получаем, что образующая – это отрезок DK.
- Делаем дополнительное построение – соединяем точки О и А в основании цилиндра. Получаем прямоугольный ∆АВО.
- Из ∆АВО по т.Пифагора находим значение АВ. Этот отрезок – половина AD. Отсюда находим AD.
- Зная величину DK и AD, вычисляем площадь сечения-прямоугольника.
Решение:
Поскольку образующая цилиндра и его высота совпадают, то DK=14. Это – одна из сторон прямоугольника, форму которого и имеет сечение.
Найдем 2-ю сторону этого прямоугольника. Из прямоугольного ∆АВО по т.Пифагора АО2=АВ2+ВО2.
Отсюда
АО – радиус основания, поэтому АО=15. ВО=12, поскольку ВО – это расстояние от оси до плоскости сечения.
Тогда имеем:
AD=2AB=2·9=18.
Площадь сечения равна:
S=AD·DK=18·14=252.
Вариант 16МБ9
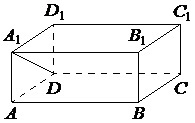
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объем параллелепипеда ABCDA1B1C1D1.
Алгоритм выполнения
- Соединяем вершины А1 и D. Получаем прямоугольный ∆А1АD. Из этого треугольника находим АА1.
- Записываем формулу для вычисления объема параллелепипеда. Находим значение для объема.
Решение:
Т.к. ABCDA1B1C1D1 параллелепипед, то угол А1АD равен 900. Поэтому ∆А1АD – прямоугольный. Тогда по т.Пифагора А1А2+AD2=A1D2. Отсюда получаем:
Объем параллелепипеда найдем по формуле:
V=AD·DC·AA1.
Тогда имеем:
V=3·5·5=75.
Вариант 16МБ10
Стороны основания правильной треугольной пирамиды равны 16, а боковые ребра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Алгоритм выполнения
- Записываем формулу для площади боковой поверхности через периметр основания и апофему.
- Находим периметр треугольника, лежащего в основании пирамиды.
- Доказываем, что апофема является не только высотой, но и медианой для боковой стороны пирамиды.
- Из прямоугольного треугольника, образованного апофемой, боковым ребром и половиной стороны основания, по т.Пифагора находим величину апофемы.
- Вычисляем площадь боковой поверхности пирамиды.
Решение:
Площадь боковой поверхности пирамиды равна:
Находим периметр основания:
Росн=3х, где х – сторона основания.
Росн=3·16=48.
Т.к. пирамида правильная, то ее боковые грани – равнобедренные треугольники. Тогда апофема, которая является высотой боковой грани, проведенной к основанию, является еще и медианой. Значит, SB – медиана и АВ=АС/2=16/2=8.
Из прямоугольного ∆ABS по т.Пифагора АВ2+SB2=AS2.
Отсюда:
Т.е. апофема а=15.
Получаем:
Вариант 16МБ11
Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.
Алгоритм выполнения
- Записываем формулу для объема пирамиды через площадь ее основания и высоту.
- Находим площадь основания, учитывая, что в основании пирамиды лежит квадрат.
- Находим диагональ квадрата, лежащего в основании, как гипотенузу из ∆АВС. Используем для этого т.Пифагора Делим полученную величину пополам.
- Из треугольника, построенного на половине диагонали основания, высоте пирамиды и ее боковом ребре, по т.Пифагора определяем высоту.
- Вычисляем объем.
Решение:
Объем пирамиды:
Т.к. пирамида правильная, то четырехугольник в ее основании – это квадрат. Поэтому Sосн=а2, где а – сторона основания.
Имеем:
Sосн=82=64.
Из прямоугольного ∆АВС по т.Пифагора АС2=АВ2+ВС2.
Отсюда:
Тогда АК=АС/2=4√2.
Из прямоугольного ∆АКS по т.Пифагора AS2=AK2+SK2.
Получаем:
Т.е. Н=3.
Значит, объем пирамиды составляет:
Вариант 16МБ12
Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
Алгоритм выполнения
- Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра.
- Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение.
Решение:
Объем прямоугольного параллелепипеда равен:
V=abc, где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно.
Тогда из этой формулы:
с=V/(ab).
Получаем:
с=280/(8·5)=7.
Площадь поверхности прямоугольного параллелепипеда вычисляется так:
S=2(ab+bc+ac).
Отсюда имеем:
S=2(8·5+5·7+8·7)=2(40+35+56)=2·131=262.
Вариант 16МБ13
Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.
Алгоритм выполнения
- Записываем формулу для объема конуса. Из нее выражаем высоту.
- Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь.
- Подставляем числовые данные в формулу для объема, вычисляем искомую величину.
Решение:
Объем конуса составляет:
.
Отсюда:
Площадь основания (как площадь круга) равна:
Sосн=πR2.
Вычисляем площадь:
Sосн=π·22=4π.
Тогда высота конуса:
Вариант 16МБ14
Основанием четырехугольной пирамиды является прямоугольник со сторонами 3 и 12. Найдите высоту этой пирамиды, если ее объем равен 60.
Алгоритм выполнения
- Записываем формулу для объема пирамиды через площадь ее основания и высоту. Из нее выражаем высоту.
- Находим площадь основы-прямоугольника.
- Подставляем числовые данные в формулу для высоты, вычисляем искомую величину.
Решение:
Объем пирамиды вычисляется так:
Отсюда:
Sосн=ab, a и b – стороны прямоугольника, лежащего в основе пирамиды.
Следовательно:
Sосн=3·12=36.
Тогда получаем:
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по стереометрии формата ЕГЭ
Задание
1
#3868
Уровень задания: Равен ЕГЭ
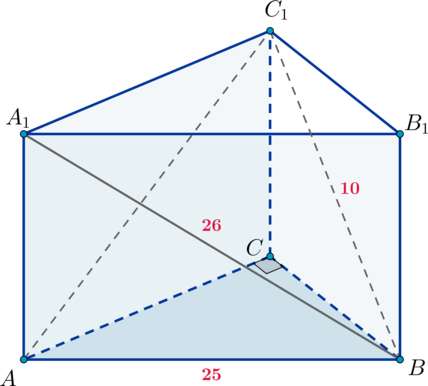
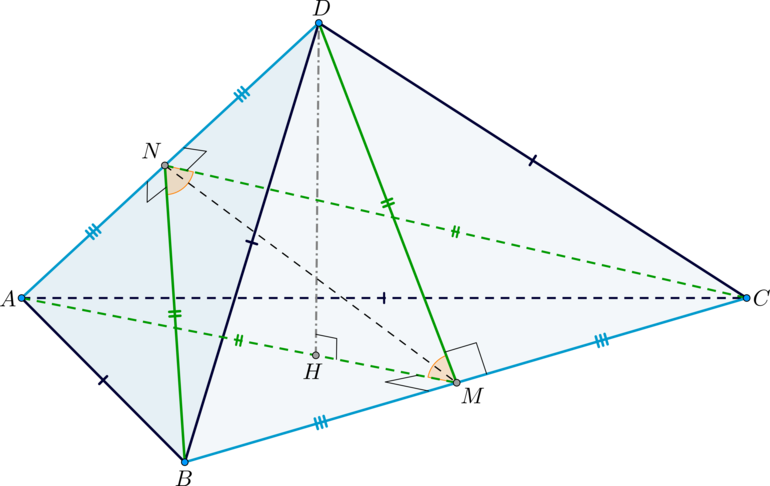
Основанием прямой треугольной призмы (ABCA_1B_1C_1) является прямоугольный треугольник (ABC), причем (angle C=90^circ). Диагонали боковых граней (AA_1B_1B) и (BB_1C_1C) равны соответственно (26) и (10), (AB=25).
а) Докажите, что (triangle BA_1C_1) – прямоугольный.
б) Найдите объем пирамиды (AA_1C_1B).
а) Так как (BB_1perp (A_1B_1C_1)), (B_1C_1perp A_1C_1), то по теореме о трех перпендикулярах (BC_1perp A_1C_1) (как наклонная). Следовательно, (triangle A_1C_1B) – прямоугольный.
б) Заметим, что (BCperp AC) и (BCperp CC_1), следовательно, по признаку (BCperp (AA_1C_1)). Следовательно, (BC) – высота пирамиды (BAA_1C_1) с основанием (AA_1C_1).
Так как (triangle AA_1C_1) прямоугольный, то [V_{BAA_1C_1}=dfrac{frac12cdot AA_1cdot A_1C_1cdot BC}3] По теореме Пифагора [begin{aligned}
&A_1C_1=sqrt{26^2-10^2}=sqrt{16cdot 36}=24\[1ex]
&AA_1=sqrt{26^2-25^2}=sqrt{1cdot 51}=sqrt{51}\[1ex]
&BC=sqrt{10^2-51}=sqrt{49}=7 end{aligned}] Тогда [V_{BAA_1C_1}=dfrac{frac12cdot 24cdot sqrt{51}cdot 7}3=28sqrt{51}]
Ответ:
б) (28sqrt{51})
Задание
2
#6924
Уровень задания: Равен ЕГЭ
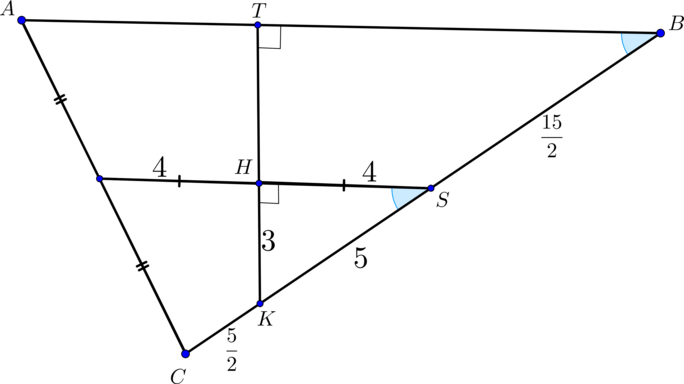
(ABCA_1B_1C_1) — прямая треугольная призма, (AB=16, BC=15,
AA_1=8), (cosangle ABC=0,8). (M, N) – середины ребер (AC) и (B_1C_1) соответственно. (K,P) – такие точки на ребрах (BC) и (B_1C_1) соответственно, что (CK=B_1P=dfrac{1}{6}BC).
а) Построить сечение призмы плоскостью (alpha), параллельной прямой (MN) и проходящей через точки (K) и (P).
б) Найти площадь сечения призмы плоскостью (alpha).
а) 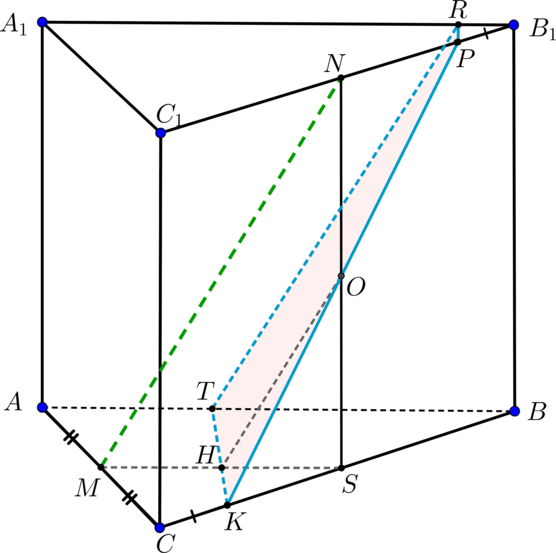
Если прямая (MNparallel alpha Rightarrow MN) параллельна некоторой прямой, лежащей в (alpha). Проведем (NSperp BC, NScap
KP=O). В плоскости (MNS) проведем (OHparallel MN Rightarrow
MH=HS). Тогда прямая (KHcap AB=T). Так как плоскости (ABC) и (A_1B_1C_1) параллельны, то (alpha) пересечет плоскость (A_1B_1C_1) по прямой, параллельной (KT). Следовательно, проведем (PRparallel
KT). Таким образом, (TRPK) – искомое сечение (трапеция).
б) Заметим, что (CK=dfrac{1}{6} cdot 15=dfrac{5}{2} Rightarrow
KS=5). Т.к. (MS) – средняя линия треугольника (ABC Rightarrow MS=8
Rightarrow HS=4). Так как (angle HSK=angle ABC), то по теореме косинусов (HK=sqrt{16+25-2cdot 4cdot 5cdot frac45}=3). Таким образом, по обратной теореме Пифагора треугольник (HKS) – прямоугольный, следовательно, (angle H =90^circ). Таким образом, по теореме о трех перпендикулярах, из того, что (NSperp (ABC),
HSperp KT Rightarrow
OHperp KT).
Проведем (PH_1 perp KT). Из подобия треугольников (HOK) и (H_1PK) следует, что (PH_1=2OH). Т.к. (OS=dfrac{1}{2}NS=4, HS=4 Rightarrow
OH=4sqrt2). Таким образом найдена высота трапеции (PH_1=8sqrt2).
Найдем основания трапеции (KT) и (PR).
(sin angle KSH = dfrac{3}{5}=sin angle B=dfrac{KT}{KB}
Rightarrow KT=dfrac{15}{2}).
(bigtriangleup PRB_1 sim bigtriangleup KTB Rightarrow
PR=dfrac{3}{2}).
Таким образом, (S_{TRPK} = dfrac{1}{2}cdot
left(dfrac{15}{2}+dfrac{3}{2}right)cdot 8sqrt2 = 36sqrt2)
Ответ:
б) (36sqrt2)
Задание
3
#2300
Уровень задания: Равен ЕГЭ
В треугольной пирамиде (DABC) двугранные углы при ребрах (AD) и (BC) равны. Известно также, что (AB=BD=DC=AC=sqrt{15}).
а) Докажите, что (AD=BC).
б) Найдите объем пирамиды, если двугранные углы при (AD) и (BC) равны по (60^circ).
а) Рассмотрим пирамиду (DABC), (AB=BD=DC=CA), (angle
(BAD,CAD)=angle (BAC,BDC)).
Т.к. (triangle ABD) и (triangle ACD) – равнобедренные, причем (AD) – общее основание, то высоты к основаниями попадут в одну точку – в середину стороны (AD), точку (N). То есть (BNperp AD), (CNperp AD). Таким образом, (angle BNC) – линейный угол двугранного угла (angle(BAD,CAD)).
Аналогичным образом строится угол (angle AMD) – линейный угол двугранного угла (angle (BAC,BDC)), где (M) – середина (BC). Таким образом, (angle BNC=angle AMD).
Т.к. (triangle ABD=triangle ACD) по трем сторонам, то (BN=CN). Аналогично (AM=DM). Значит, (triangle AMD) и (triangle BNC) – равнобедренные и подобные (по двум пропорциональным сторонам и углу между ними).
Заметим, что плоскости ((AMD)) и ((BNC)) имеют две общие точки – это точки (N) и (M). Следовательно, они пересекаются по прямой (MN). Отрезок (NM) – это высота в (triangle AMD) и (triangle BNC) к основаниям (AD) и (BC) соответственно. Следовательно, эти треугольники равны. Следовательно, (AD=BC), чтд.
б) Из пункта а) также следует, что (AM=DM=BN=CN). Т.к. двугранные углы равны (60^circ), то (triangle AMD) и (triangle BNC) – равносторонние.
Пусть (AM=DM=BN=CN=AD=BC=x).
Проведем высоту пирамиды (DH). Т.к. (DMperp BC), то по теореме о трех перпендикулярах (HMperp BC). Таким образом, точка (H) должна лежать на (AM), причем на середине, т.к. (triangle AMD) – равносторонний.
(DH=frac{sqrt3}2cdot AD=frac{sqrt3}2x). Найдем по теореме Пифагора (x) из (triangle ABM):
(AM=x), (BM=frac x2), (AB=sqrt{15}), следовательно, (x=2sqrt3).
Таким образом, [V_{DABC}=frac13cdot DHcdot S_{ABC}=dfrac13cdot
frac{sqrt3}2xcdot frac12x^2=6]
Ответ:
б) (6)
Задание
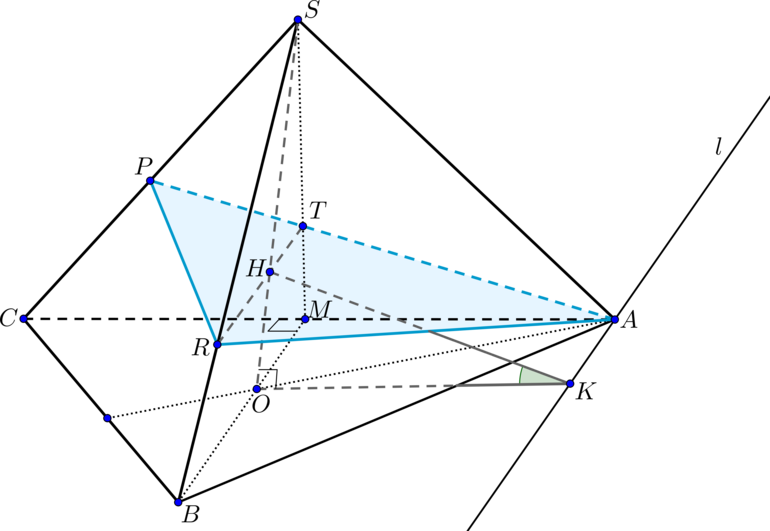
4
#1265
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC), (H) – такая точка на высоте (SO), что (OH:HS=1:3). Плоскость (alpha) проходит через точки (A) и (H) параллельно медиане (BM) треугольника (ABC) и пересекает ребро (CS) в точке (P).
а) Докажите, что (CP:PS=2:3).
б) Найдите угол между плоскостями (alpha) и (ABC).
а)
Правильный тетраэдр — это правильная треугольная пирамида, у которой все ребра равны. Пусть ребро пирамиды равно (a).
Т.к. пирамида правильная, то высота (SO) падает в точку пересечения медиан (bigtriangleup ABC). Рассмотрим плоскость (BSM), точка (H) лежит в этой плоскости. Т.к. плоскость (alpha) параллельна (BM), то она пересекает плоскость (BSM) по прямой, параллельной (BM).
Проведем (RTparallel BM, Hin RT). Тогда по теореме Фалеса (dfrac{SH}{HO}=dfrac{ST}{TM}=dfrac{3}{1}).
Прямая (AT) пересечет (CS) в точке (P). (bigtriangleup APR) – сечение пирамиды плоскостью (alpha).
Напишем теорему Менелая для (bigtriangleup CSM) и прямой (AP):
[dfrac{CP}{PS}cdot dfrac{ST}{TM}cdot dfrac{MA}{AC}=1] Из этого равенства находим, что (dfrac{CP}{PS}=dfrac{2}{3})
б) Докажем, что линия пересечения плоскостей (alpha) и (ABC) параллельна прямой (BM). Пусть это не так: пусть (l) – линия пересечения (alpha) и (ABC) и (lcap BM=Z). Тога прямая (BMcap
alpha=Z), следовательно, не может быть параллельна (alpha). Получили противоречие, следовательно, (lparallel BM). Заметим, что прямая (l) проходит через точку (A).
Построим линейный угол двугранного угла между (alpha) и (ABC). Т.к. (HOperp ABC), проведем (OKperp l), следовательно, по теореме о трех перпендикулярах (HKperp l). Таким образом, (angle HKO) – искомый угол.
1) Найдем (HO).
(BO=dfrac{2}{3}cdot BM=dfrac{2}{3}cdot
dfrac{sqrt3}{2}a=dfrac{a}{sqrt3})
Тогда (SO=sqrt{a^2 -dfrac{a^2}{3}}=sqrt{dfrac{2}{3}}a
Rightarrow HO=dfrac{1}{4}SO=dfrac{sqrt2a}{4sqrt3})
2) Найдем (OK).
(BMperp AC, BMparallel l Rightarrow ACperp l). Т.к. (OKperp l
Rightarrow OKparallel AC). Таким образом, (OMAK) – параллелограмм, следовательно, (OK=MA=dfrac{1}{2}a).
Треугольник (HOK) – прямоугольный, следовательно, (mathrm{ctg},angle
HKO=dfrac{OK}{HO}=sqrt6)
Тогда (angle HKO= mathrm{arcctg},sqrt6).
Ответ:
б) (mathrm{arcctg},sqrt6)
Задание
5
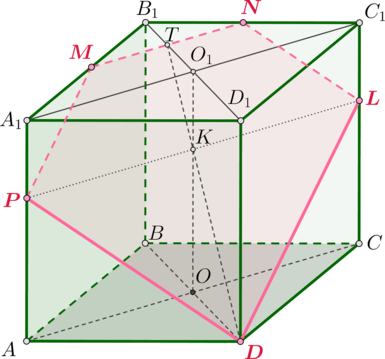
#3059
Уровень задания: Равен ЕГЭ
Дана правильная четырехугольная призма (ABCDA_1B_1C_1D_1), стороны основания которой равна (4), а боковые ребра равны (5).
а) Постройте сечение призмы плоскостью (DMN), где (M) и (N) – середины отрезков (A_1B_1) и (B_1C_1).
б) Найдите угол между данным сечением и плоскостью (ABC).
(Задача от подписчиков)
а) Из условия следует, что призма прямая и основаниями являются квадраты.
(MN) – средняя линия в (triangle A_1B_1C_1), следовательно, (MNparallel A_1C_1). Тогда плоскость (DMN) пересечет плоскость (A_1C_1CA) по прямой (l), параллельной (A_1C_1) (в противном случае (l) пересечет (A_1C_1) в некоторой точке (K), которая будет лежать и на (A_1C_1), и в плоскости (DMN), следовательно, должна будет лежать и на (MN), что невозможно, так как (MN) не пересекает (A_1C_1)).
Таким образом, найдем точку, в которой плоскость (DMN) пересекает плоскость (A_1C_1CA).
Пусть плоскость (B_1D_1DB) пересекает (MN) в точке (T). Тогда (DTin
(DMN)). Если (O) и (O_1) – точки пересечения диагоналей оснований, то прямые (DT) и (OO_1) лежат в плоскости (B_1D_1DB). Пусть точка их пересечения – точка (K). Тогда (K) – искомая точка пересечения плоскости (DMN) и плоскости (A_1C_1CA).
Проведем через точку (K) прямую (l) параллельно (A_1C_1). Пусть она пересекла (AA_1) в точке (P), (CC_1) в точке (L). Таким образом, получили сечение (DPMNL) призмы плоскостью (DMN).
б) Заметим, что (KOperp (ABC)), следовательно, так как (ODperp
AC), то и (KDperp AC) по теореме о трех перпендикулярах. Значит, (angle KDO) равен углу между плоскостями (DMN) и (ABC).
По теореме Фалеса [dfrac{A_1M}{MB_1}=dfrac11=dfrac{O_1T}{TB_1}
quadRightarrowquad O_1T=TB_1.] (triangle TO_1Ksim triangle DOK), следовательно, [dfrac{O_1T}{OD}=dfrac12=dfrac{O_1K}{OK}] Следовательно, (OK=frac23OO_1=frac23AA_1=frac23cdot
5=frac{10}3).
(OD=frac12 BD=frac12cdot sqrt2AB=2sqrt2.)
Тогда [mathrm{tg},angle KDO=dfrac{OK}{OD}=dfrac56sqrt2
quadRightarrowquad
angle KDO=mathrm{arctg},dfrac56sqrt2.]
Ответ:
б) (mathrm{arctg},dfrac56sqrt2)
Задание
6
#3064
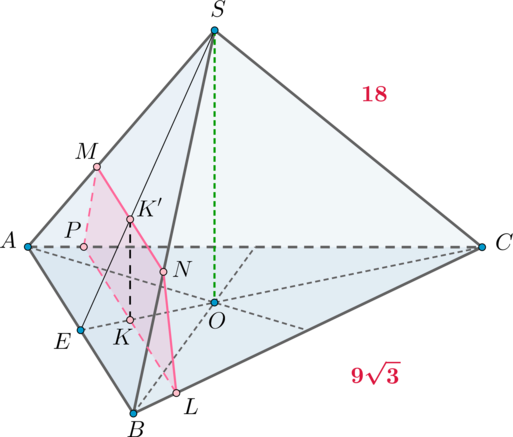
Уровень задания: Равен ЕГЭ
В правильной треугольной пирамиде (SABC) с основанием (ABC) на медиане основания (CE) взята точка (K) так, что (CK:KE=8:1). Через точку (K) проведена плоскость (alpha), которая перпендикулярна прямой (CE) и пересекает боковые ребра (SA) и (SB) в точках (M) и (N) соответственно.
а) Докажите, что (MN:AB=2:3).
б) Найдите объем пирамиды, вершиной которой является точка (C), а основанием – сечение пирамиды (SABC) плоскостью (alpha), если известно, что (AB=9sqrt3), (SA=18).
(Задача от подписчиков)
а) Пусть (SO) – высота пирамиды, (O) – точка пересечения медиан. Следовательно, [dfrac{CO}{OE}=dfrac21] Так как по условию (CK:KE=8:1), то можно обозначить (CK=8x), (KE=x). Тогда (CE=9x). Следовательно, (CO=frac23CE=6x), (OE=3x), (OK=2x).
Так как (CE) перпендикулярна плоскости (alpha), то нужно построить две пересекающиеся прямые в плоскости (alpha), которым (CE) будет перпендикулярна.
Первая прямая: так как (CEperp AB), то проведем через точку (K) прямую (PLparallel AB). Тогда (CEperp PL) ((Pin AC, Lin BC)).
Вторая прямая: так как (SOperp (ABC)), то (SOperp CE). Следовательно, проведем (KK’parallel SO), тогда (KK’perp CE) ((K’in SE)).
Следовательно, (alpha) проходит через точки (P, L, K’).
Заметим, что (alpha) пересечет плоскость (ASB) по прямой, параллельной (AB) (в противном случае (alpha) будет иметь общую точку с (AB), что невозможно, так как (ABparallel PL
quadRightarrowquad ABparallel alpha)).
Следовательно, (MNparallel AB) и проходит через (K’).
Из подобия (triangle K’EKsim triangle SEO): [dfrac{SE}{K’E}=dfrac{OE}{KE}=dfrac31 quadRightarrowquad K’E=
dfrac13SE
quadRightarrowquad SK’=dfrac23SE.] Из подобия (triangle
MSNsim triangle ASB): [dfrac{MN}{AB}=dfrac{SK’}{SE}=dfrac23.]
б) Рассмотрим пирамиду (CPMNL). (CK) – высота этой пирамиды, (PMNL) – трапеция ((MNparallel ABparallel PL)).
Следовательно, [V=dfrac13cdot CKcdot dfrac{MN+PL}2cdot KK’] Так как (BC=9sqrt3), то (CE=sqrt{BC^2-EB^2}=frac{27}2). Следовательно, [CK=dfrac89CE=12.] Из подобия (triangle PCLsim triangle ACB): [dfrac{PL}{AB}=dfrac{CK}{CE}=dfrac89quadRightarrowquad PL=
8sqrt3.] Из пункта а) [MN=dfrac23AB=6sqrt3.] Из подобия (triangle
EK’Ksim triangle ESO): [KK’=dfrac13SO=dfrac13sqrt{SC^2-CO^2}=dfrac13sqrt{18^2-9^2}=
3sqrt3.] Следовательно, [V=dfrac13cdot 12cdot dfrac{6sqrt3+8sqrt3}2cdot 3sqrt3=252.]
Ответ:
б) 252
Задание
7
#3063
Уровень задания: Равен ЕГЭ
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S), стороны основания которой равны (6sqrt2), а боковые ребра равны (21).
а) Постройте сечение пирамиды плоскостью, проходящей через точку (A) и середину ребра (SC) параллельно прямой (BD).
б) Найдите площадь построенного сечения.
(Задача от подписчиков)
а) Пусть (N) – середина ребра (SC), (SH) – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную (BD). Рассмотрим плоскость (ASC). Прямая (AN) пересекает (SH) в точке (O). Теперь рассмотрим (BSD). Проведем в этой плоскости через точку (O) прямую, параллельную (BD). Пусть она пересечет ребра (SB) и (SD) в точках (M) и (K) соответственно. Таким образом, (AMNK) – искомое сечение.
б) Заметим, что по теореме о трех перпендикулярах (так как (OHperp
(ABC), AHperp BD)) (AOperp BD). Так как (BDparallel MK), то (AOperp MK), следовательно, (ANperp MK). Следовательно, у четырехугольника (AMNK) диагонали взаимно перпендикулярны. Значит, его площадь можно найти как [S=dfrac12 ANcdot MK.]
Заметим сразу, что (BD=AC=ABsqrt2=12).
Рассмотрим плоскость (ASC).
По теореме Менелая: [dfrac{SN}
{NC}cdot dfrac{CA}{AH}cdot dfrac{HO}{OS}=1 quadRightarrow
quad dfrac{HO}{OS}=dfrac12 quadRightarrowquad OS=2OH
quadRightarrowquad dfrac{SO}{SH}=dfrac23.] (это нам понадобится позже для поиска (MK))
Проведем (NQperp AC). Тогда из подобия (triangle SHC) и (triangle
NQC): [dfrac{SH}{NQ}=dfrac{SC}{NC}=2 quadRightarrowquad
NQ=dfrac12SH=dfrac12sqrt{SC^2-HC^2}=dfrac12sqrt{21^2-6^2}=
dfrac12sqrt{81cdot 5}] (Q) – середина (HC), следовательно, (AQ=frac34AC=frac34cdot 12=9). Тогда по теореме Пифагора [AN=sqrt{AQ^2+NQ^2}=sqrt{dfrac{81cdot 5}4+81}=dfrac{27}2.]
Рассмотрим (BSD). Так как (triangle MSKsim triangle BSD), то [dfrac{MK}{BD}=dfrac{SO}{SH}=dfrac23 quadRightarrowquad
MK=dfrac23BD=dfrac23cdot 12=8.] Следовательно, площадь сечения равна [S=dfrac12cdot 8cdot dfrac{27}2=54.]
Ответ:
б) 54

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ