Задачи по стереометрии егэ с решениями профильный уровень - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

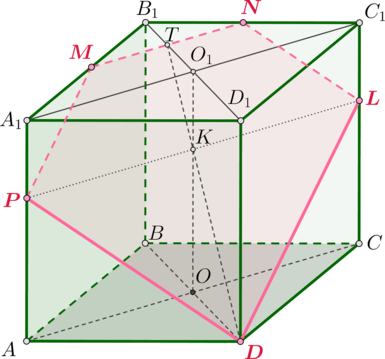
На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по стереометрии формата ЕГЭ

Задание
1

#3868

Уровень задания: Равен ЕГЭ

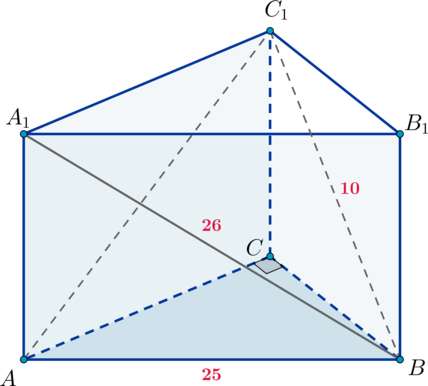
Основанием прямой треугольной призмы (ABCA_1B_1C_1) является прямоугольный треугольник (ABC), причем (angle C=90^circ). Диагонали боковых граней (AA_1B_1B) и (BB_1C_1C) равны соответственно (26) и (10), (AB=25).

а) Докажите, что (triangle BA_1C_1) – прямоугольный.

б) Найдите объем пирамиды (AA_1C_1B).

а) Так как (BB_1perp (A_1B_1C_1)), (B_1C_1perp A_1C_1), то по теореме о трех перпендикулярах (BC_1perp A_1C_1) (как наклонная). Следовательно, (triangle A_1C_1B) – прямоугольный.

б) Заметим, что (BCperp AC) и (BCperp CC_1), следовательно, по признаку (BCperp (AA_1C_1)). Следовательно, (BC) – высота пирамиды (BAA_1C_1) с основанием (AA_1C_1).
Так как (triangle AA_1C_1) прямоугольный, то [V_{BAA_1C_1}=dfrac{frac12cdot AA_1cdot A_1C_1cdot BC}3] По теореме Пифагора [begin{aligned}
&A_1C_1=sqrt{26^2-10^2}=sqrt{16cdot 36}=24\[1ex]
&AA_1=sqrt{26^2-25^2}=sqrt{1cdot 51}=sqrt{51}\[1ex]
&BC=sqrt{10^2-51}=sqrt{49}=7 end{aligned}] Тогда [V_{BAA_1C_1}=dfrac{frac12cdot 24cdot sqrt{51}cdot 7}3=28sqrt{51}]

Ответ:

б) (28sqrt{51})

Задание
2

#6924

Уровень задания: Равен ЕГЭ

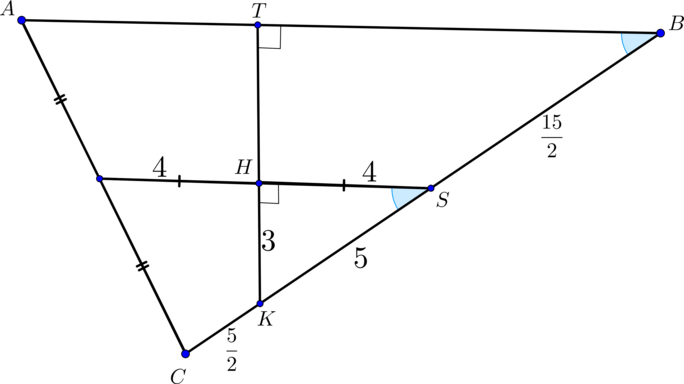
(ABCA_1B_1C_1) — прямая треугольная призма, (AB=16, BC=15,
AA_1=8), (cosangle ABC=0,8). (M, N) – середины ребер (AC) и (B_1C_1) соответственно. (K,P) – такие точки на ребрах (BC) и (B_1C_1) соответственно, что (CK=B_1P=dfrac{1}{6}BC).

а) Построить сечение призмы плоскостью (alpha), параллельной прямой (MN) и проходящей через точки (K) и (P).

б) Найти площадь сечения призмы плоскостью (alpha).

а)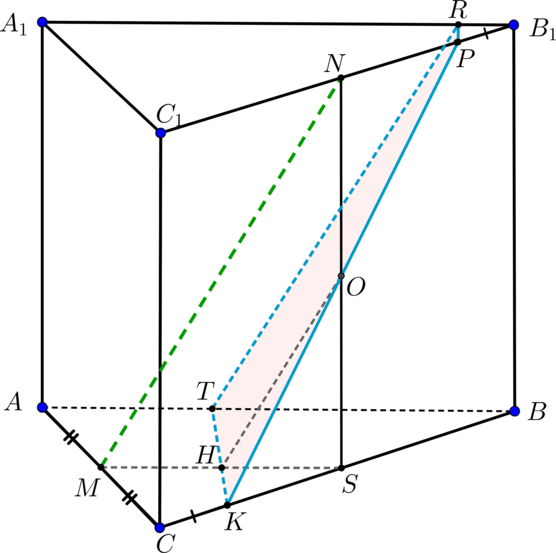

Если прямая (MNparallel alpha Rightarrow MN) параллельна некоторой прямой, лежащей в (alpha). Проведем (NSperp BC, NScap
KP=O). В плоскости (MNS) проведем (OHparallel MN Rightarrow
MH=HS). Тогда прямая (KHcap AB=T). Так как плоскости (ABC) и (A_1B_1C_1) параллельны, то (alpha) пересечет плоскость (A_1B_1C_1) по прямой, параллельной (KT). Следовательно, проведем (PRparallel
KT). Таким образом, (TRPK) – искомое сечение (трапеция).

б) Заметим, что (CK=dfrac{1}{6} cdot 15=dfrac{5}{2} Rightarrow
KS=5). Т.к. (MS) – средняя линия треугольника (ABC Rightarrow MS=8
Rightarrow HS=4). Так как (angle HSK=angle ABC), то по теореме косинусов (HK=sqrt{16+25-2cdot 4cdot 5cdot frac45}=3). Таким образом, по обратной теореме Пифагора треугольник (HKS) – прямоугольный, следовательно, (angle H =90^circ). Таким образом, по теореме о трех перпендикулярах, из того, что (NSperp (ABC),
HSperp KT Rightarrow
OHperp KT).

Проведем (PH_1 perp KT). Из подобия треугольников (HOK) и (H_1PK) следует, что (PH_1=2OH). Т.к. (OS=dfrac{1}{2}NS=4, HS=4 Rightarrow
OH=4sqrt2). Таким образом найдена высота трапеции (PH_1=8sqrt2).

Найдем основания трапеции (KT) и (PR).

(sin angle KSH = dfrac{3}{5}=sin angle B=dfrac{KT}{KB}
Rightarrow KT=dfrac{15}{2}).

(bigtriangleup PRB_1 sim bigtriangleup KTB Rightarrow
PR=dfrac{3}{2}).

Таким образом, (S_{TRPK} = dfrac{1}{2}cdot
left(dfrac{15}{2}+dfrac{3}{2}right)cdot 8sqrt2 = 36sqrt2)

Ответ:

б) (36sqrt2)

Задание
3

#2300

Уровень задания: Равен ЕГЭ

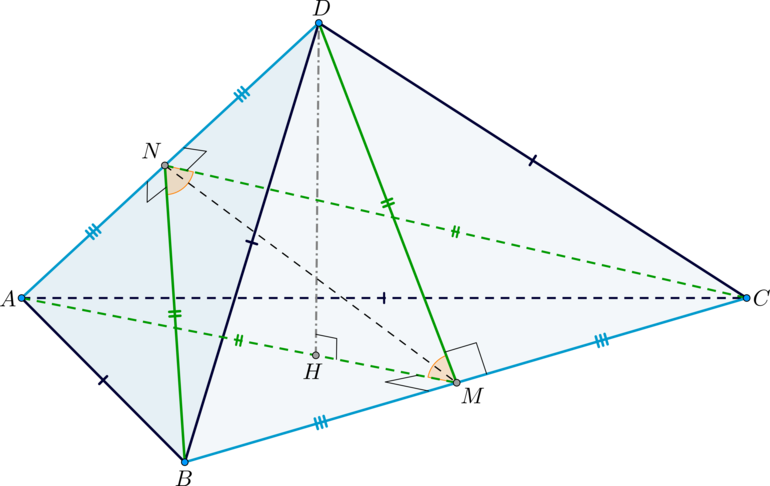
В треугольной пирамиде (DABC) двугранные углы при ребрах (AD) и (BC) равны. Известно также, что (AB=BD=DC=AC=sqrt{15}).

а) Докажите, что (AD=BC).

б) Найдите объем пирамиды, если двугранные углы при (AD) и (BC) равны по (60^circ).

а) Рассмотрим пирамиду (DABC), (AB=BD=DC=CA), (angle
(BAD,CAD)=angle (BAC,BDC)).

Т.к. (triangle ABD) и (triangle ACD) – равнобедренные, причем (AD) – общее основание, то высоты к основаниями попадут в одну точку – в середину стороны (AD), точку (N). То есть (BNperp AD), (CNperp AD). Таким образом, (angle BNC) – линейный угол двугранного угла (angle(BAD,CAD)).

Аналогичным образом строится угол (angle AMD) – линейный угол двугранного угла (angle (BAC,BDC)), где (M) – середина (BC). Таким образом, (angle BNC=angle AMD).

Т.к. (triangle ABD=triangle ACD) по трем сторонам, то (BN=CN). Аналогично (AM=DM). Значит, (triangle AMD) и (triangle BNC) – равнобедренные и подобные (по двум пропорциональным сторонам и углу между ними).

Заметим, что плоскости ((AMD)) и ((BNC)) имеют две общие точки – это точки (N) и (M). Следовательно, они пересекаются по прямой (MN). Отрезок (NM) – это высота в (triangle AMD) и (triangle BNC) к основаниям (AD) и (BC) соответственно. Следовательно, эти треугольники равны. Следовательно, (AD=BC), чтд.

б) Из пункта а) также следует, что (AM=DM=BN=CN). Т.к. двугранные углы равны (60^circ), то (triangle AMD) и (triangle BNC) – равносторонние.
Пусть (AM=DM=BN=CN=AD=BC=x).

Проведем высоту пирамиды (DH). Т.к. (DMperp BC), то по теореме о трех перпендикулярах (HMperp BC). Таким образом, точка (H) должна лежать на (AM), причем на середине, т.к. (triangle AMD) – равносторонний.

(DH=frac{sqrt3}2cdot AD=frac{sqrt3}2x). Найдем по теореме Пифагора (x) из (triangle ABM):

(AM=x), (BM=frac x2), (AB=sqrt{15}), следовательно, (x=2sqrt3).

Таким образом, [V_{DABC}=frac13cdot DHcdot S_{ABC}=dfrac13cdot
frac{sqrt3}2xcdot frac12x^2=6]

Ответ:

б) (6)

Задание
4

#1265

Уровень задания: Равен ЕГЭ

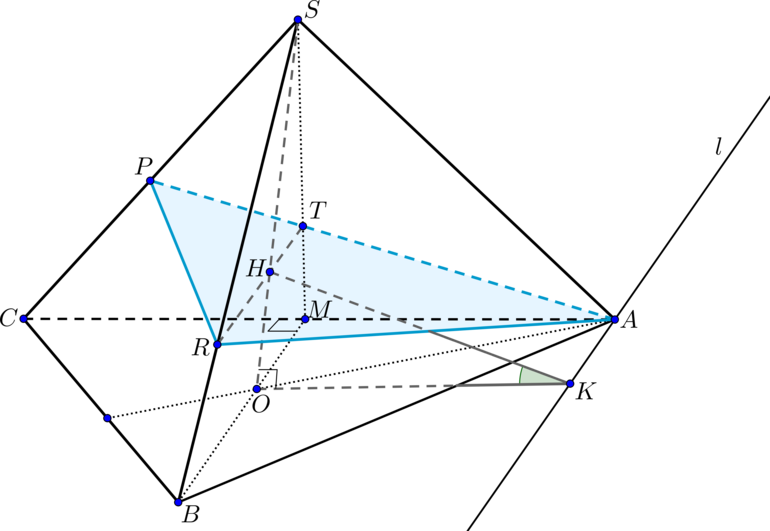
Дан правильный тетраэдр (SABC), (H) – такая точка на высоте (SO), что (OH:HS=1:3). Плоскость (alpha) проходит через точки (A) и (H) параллельно медиане (BM) треугольника (ABC) и пересекает ребро (CS) в точке (P).

а) Докажите, что (CP:PS=2:3).

б) Найдите угол между плоскостями (alpha) и (ABC).

а)

Правильный тетраэдр — это правильная треугольная пирамида, у которой все ребра равны. Пусть ребро пирамиды равно (a).
Т.к. пирамида правильная, то высота (SO) падает в точку пересечения медиан (bigtriangleup ABC). Рассмотрим плоскость (BSM), точка (H) лежит в этой плоскости. Т.к. плоскость (alpha) параллельна (BM), то она пересекает плоскость (BSM) по прямой, параллельной (BM).

Проведем (RTparallel BM, Hin RT). Тогда по теореме Фалеса (dfrac{SH}{HO}=dfrac{ST}{TM}=dfrac{3}{1}).

Прямая (AT) пересечет (CS) в точке (P). (bigtriangleup APR) – сечение пирамиды плоскостью (alpha).
Напишем теорему Менелая для (bigtriangleup CSM) и прямой (AP):
[dfrac{CP}{PS}cdot dfrac{ST}{TM}cdot dfrac{MA}{AC}=1] Из этого равенства находим, что (dfrac{CP}{PS}=dfrac{2}{3})

б) Докажем, что линия пересечения плоскостей (alpha) и (ABC) параллельна прямой (BM). Пусть это не так: пусть (l) – линия пересечения (alpha) и (ABC) и (lcap BM=Z). Тога прямая (BMcap
alpha=Z), следовательно, не может быть параллельна (alpha). Получили противоречие, следовательно, (lparallel BM). Заметим, что прямая (l) проходит через точку (A).

Построим линейный угол двугранного угла между (alpha) и (ABC). Т.к. (HOperp ABC), проведем (OKperp l), следовательно, по теореме о трех перпендикулярах (HKperp l). Таким образом, (angle HKO) – искомый угол.

1) Найдем (HO).
(BO=dfrac{2}{3}cdot BM=dfrac{2}{3}cdot
dfrac{sqrt3}{2}a=dfrac{a}{sqrt3})

Тогда (SO=sqrt{a^2 -dfrac{a^2}{3}}=sqrt{dfrac{2}{3}}a
Rightarrow HO=dfrac{1}{4}SO=dfrac{sqrt2a}{4sqrt3})

2) Найдем (OK).
(BMperp AC, BMparallel l Rightarrow ACperp l). Т.к. (OKperp l
Rightarrow OKparallel AC). Таким образом, (OMAK) – параллелограмм, следовательно, (OK=MA=dfrac{1}{2}a).
Треугольник (HOK) – прямоугольный, следовательно, (mathrm{ctg},angle
HKO=dfrac{OK}{HO}=sqrt6)
Тогда (angle HKO= mathrm{arcctg},sqrt6).

Ответ:

б) (mathrm{arcctg},sqrt6)

Задание
5

#3059

Уровень задания: Равен ЕГЭ

Дана правильная четырехугольная призма (ABCDA_1B_1C_1D_1), стороны основания которой равна (4), а боковые ребра равны (5).

а) Постройте сечение призмы плоскостью (DMN), где (M) и (N) – середины отрезков (A_1B_1) и (B_1C_1).

б) Найдите угол между данным сечением и плоскостью (ABC).

(Задача от подписчиков)

а) Из условия следует, что призма прямая и основаниями являются квадраты.
(MN) – средняя линия в (triangle A_1B_1C_1), следовательно, (MNparallel A_1C_1). Тогда плоскость (DMN) пересечет плоскость (A_1C_1CA) по прямой (l), параллельной (A_1C_1) (в противном случае (l) пересечет (A_1C_1) в некоторой точке (K), которая будет лежать и на (A_1C_1), и в плоскости (DMN), следовательно, должна будет лежать и на (MN), что невозможно, так как (MN) не пересекает (A_1C_1)).
Таким образом, найдем точку, в которой плоскость (DMN) пересекает плоскость (A_1C_1CA).

Пусть плоскость (B_1D_1DB) пересекает (MN) в точке (T). Тогда (DTin
(DMN)). Если (O) и (O_1) – точки пересечения диагоналей оснований, то прямые (DT) и (OO_1) лежат в плоскости (B_1D_1DB). Пусть точка их пересечения – точка (K). Тогда (K) – искомая точка пересечения плоскости (DMN) и плоскости (A_1C_1CA).
Проведем через точку (K) прямую (l) параллельно (A_1C_1). Пусть она пересекла (AA_1) в точке (P), (CC_1) в точке (L). Таким образом, получили сечение (DPMNL) призмы плоскостью (DMN).

б) Заметим, что (KOperp (ABC)), следовательно, так как (ODperp
AC), то и (KDperp AC) по теореме о трех перпендикулярах. Значит, (angle KDO) равен углу между плоскостями (DMN) и (ABC).
По теореме Фалеса [dfrac{A_1M}{MB_1}=dfrac11=dfrac{O_1T}{TB_1}
quadRightarrowquad O_1T=TB_1.] (triangle TO_1Ksim triangle DOK), следовательно, [dfrac{O_1T}{OD}=dfrac12=dfrac{O_1K}{OK}] Следовательно, (OK=frac23OO_1=frac23AA_1=frac23cdot
5=frac{10}3).

(OD=frac12 BD=frac12cdot sqrt2AB=2sqrt2.)

Тогда [mathrm{tg},angle KDO=dfrac{OK}{OD}=dfrac56sqrt2
quadRightarrowquad
angle KDO=mathrm{arctg},dfrac56sqrt2.]

Ответ:

б) (mathrm{arctg},dfrac56sqrt2)

Задание
6

#3064

Уровень задания: Равен ЕГЭ

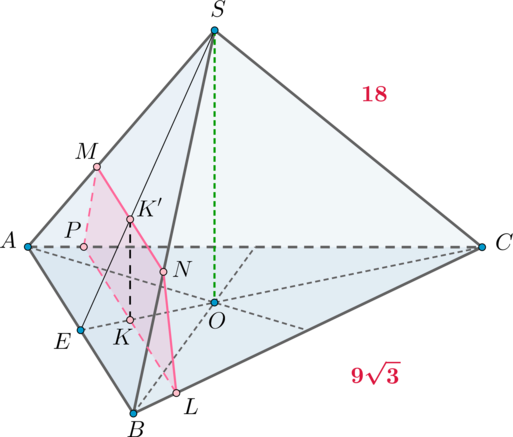
В правильной треугольной пирамиде (SABC) с основанием (ABC) на медиане основания (CE) взята точка (K) так, что (CK:KE=8:1). Через точку (K) проведена плоскость (alpha), которая перпендикулярна прямой (CE) и пересекает боковые ребра (SA) и (SB) в точках (M) и (N) соответственно.

а) Докажите, что (MN:AB=2:3).

б) Найдите объем пирамиды, вершиной которой является точка (C), а основанием – сечение пирамиды (SABC) плоскостью (alpha), если известно, что (AB=9sqrt3), (SA=18).

(Задача от подписчиков)

а) Пусть (SO) – высота пирамиды, (O) – точка пересечения медиан. Следовательно, [dfrac{CO}{OE}=dfrac21] Так как по условию (CK:KE=8:1), то можно обозначить (CK=8x), (KE=x). Тогда (CE=9x). Следовательно, (CO=frac23CE=6x), (OE=3x), (OK=2x).
Так как (CE) перпендикулярна плоскости (alpha), то нужно построить две пересекающиеся прямые в плоскости (alpha), которым (CE) будет перпендикулярна.
Первая прямая: так как (CEperp AB), то проведем через точку (K) прямую (PLparallel AB). Тогда (CEperp PL) ((Pin AC, Lin BC)).
Вторая прямая: так как (SOperp (ABC)), то (SOperp CE). Следовательно, проведем (KK’parallel SO), тогда (KK’perp CE) ((K’in SE)).
Следовательно, (alpha) проходит через точки (P, L, K’).

Заметим, что (alpha) пересечет плоскость (ASB) по прямой, параллельной (AB) (в противном случае (alpha) будет иметь общую точку с (AB), что невозможно, так как (ABparallel PL
quadRightarrowquad ABparallel alpha)).
Следовательно, (MNparallel AB) и проходит через (K’).
Из подобия (triangle K’EKsim triangle SEO): [dfrac{SE}{K’E}=dfrac{OE}{KE}=dfrac31 quadRightarrowquad K’E=
dfrac13SE
quadRightarrowquad SK’=dfrac23SE.] Из подобия (triangle
MSNsim triangle ASB): [dfrac{MN}{AB}=dfrac{SK’}{SE}=dfrac23.]

б) Рассмотрим пирамиду (CPMNL). (CK) – высота этой пирамиды, (PMNL) – трапеция ((MNparallel ABparallel PL)).
Следовательно, [V=dfrac13cdot CKcdot dfrac{MN+PL}2cdot KK’] Так как (BC=9sqrt3), то (CE=sqrt{BC^2-EB^2}=frac{27}2). Следовательно, [CK=dfrac89CE=12.] Из подобия (triangle PCLsim triangle ACB): [dfrac{PL}{AB}=dfrac{CK}{CE}=dfrac89quadRightarrowquad PL=
8sqrt3.] Из пункта а) [MN=dfrac23AB=6sqrt3.] Из подобия (triangle
EK’Ksim triangle ESO): [KK’=dfrac13SO=dfrac13sqrt{SC^2-CO^2}=dfrac13sqrt{18^2-9^2}=
3sqrt3.] Следовательно, [V=dfrac13cdot 12cdot dfrac{6sqrt3+8sqrt3}2cdot 3sqrt3=252.]

Ответ:

б) 252

Задание
7

#3063

Уровень задания: Равен ЕГЭ

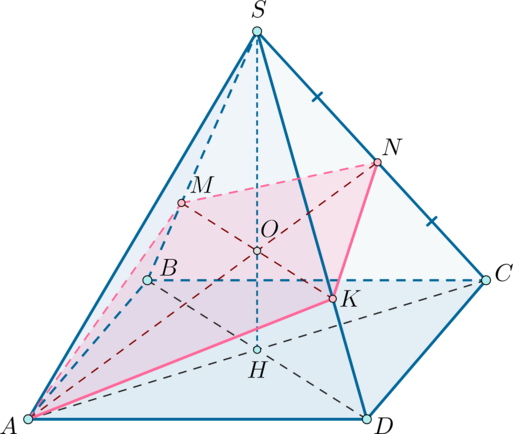
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S), стороны основания которой равны (6sqrt2), а боковые ребра равны (21).

а) Постройте сечение пирамиды плоскостью, проходящей через точку (A) и середину ребра (SC) параллельно прямой (BD).

б) Найдите площадь построенного сечения.

(Задача от подписчиков)

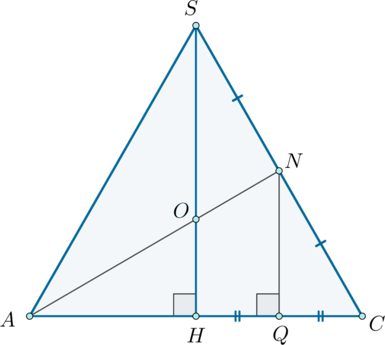
а) Пусть (N) – середина ребра (SC), (SH) – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную (BD). Рассмотрим плоскость (ASC). Прямая (AN) пересекает (SH) в точке (O). Теперь рассмотрим (BSD). Проведем в этой плоскости через точку (O) прямую, параллельную (BD). Пусть она пересечет ребра (SB) и (SD) в точках (M) и (K) соответственно. Таким образом, (AMNK) – искомое сечение.

б) Заметим, что по теореме о трех перпендикулярах (так как (OHperp
(ABC), AHperp BD)) (AOperp BD). Так как (BDparallel MK), то (AOperp MK), следовательно, (ANperp MK). Следовательно, у четырехугольника (AMNK) диагонали взаимно перпендикулярны. Значит, его площадь можно найти как [S=dfrac12 ANcdot MK.]

Заметим сразу, что (BD=AC=ABsqrt2=12).
Рассмотрим плоскость (ASC).

По теореме Менелая: [dfrac{SN}
{NC}cdot dfrac{CA}{AH}cdot dfrac{HO}{OS}=1 quadRightarrow
quad dfrac{HO}{OS}=dfrac12 quadRightarrowquad OS=2OH
quadRightarrowquad dfrac{SO}{SH}=dfrac23.] (это нам понадобится позже для поиска (MK))

Проведем (NQperp AC). Тогда из подобия (triangle SHC) и (triangle
NQC): [dfrac{SH}{NQ}=dfrac{SC}{NC}=2 quadRightarrowquad
NQ=dfrac12SH=dfrac12sqrt{SC^2-HC^2}=dfrac12sqrt{21^2-6^2}=
dfrac12sqrt{81cdot 5}] (Q) – середина (HC), следовательно, (AQ=frac34AC=frac34cdot 12=9). Тогда по теореме Пифагора [AN=sqrt{AQ^2+NQ^2}=sqrt{dfrac{81cdot 5}4+81}=dfrac{27}2.]
Рассмотрим (BSD). Так как (triangle MSKsim triangle BSD), то [dfrac{MK}{BD}=dfrac{SO}{SH}=dfrac23 quadRightarrowquad
MK=dfrac23BD=dfrac23cdot 12=8.] Следовательно, площадь сечения равна [S=dfrac12cdot 8cdot dfrac{27}2=54.]

Ответ:

б) 54

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

По теме: методические разработки, презентации и конспекты

Решение стереометрической задачи тремя различными способами

Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…

Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».

ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…

Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…

Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.

Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…

Источник

Задание 13 Профильного ЕГЭ (Стереометрия) многие старшеклассники считают самой сложной задачей в варианте. И напрасно! Ничего особенного в ней нет. Просто начинать надо вовремя, лучше всего в десятом классе. И конечно, не с самых сложных задач. Действуем по порядку!

1. Подготовительный этап — решение задач по стереометрии из первой части ЕГЭ. Повторите формулы объемов и площадей поверхности многогранников и тел вращения. Посмотрите, как решаются типовые задачи.

2. Повторите необходимую теорию. Вот краткая Программа по стереометрии. Проверьте себя. Все ли вы знаете? В освоении стереометрии вам поможет наш ЕГЭ-Справочник.

3. Посмотрите, как правильно строить чертежи.

4. Выучили теорию? Применяем на практике — строим сечения.

5. Решаем простые задачи по стереометрии. И после этого — переходим к реальным задачам ЕГЭ.

6. Задачи 13 по стереометрии из Профильного ЕГЭ по математике обычно относятся к одному из типов. Смотрите нашу Классификацию задач по стереометрии и методы их решения.

Вот примеры простых подготовительных задач по стереометрии:

1. Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.

Посмотреть решение

2. В правильной шестиугольной призме , все ребра которой равны 1, точка G — середина ребра A_1B_1. Найдите угол между прямой АG и плоскостью BDD_1.

Посмотреть решение

3. В правильной шестиугольной призме все рёбра равны 1. Найдите расстояние от точки В до плоскости

Посмотреть решение

4. В основании прямой призмы лежит ромб. Найти угол между прямыми и BD_1.

Посмотреть решение

5. Точка E — середина ребра CC_1 куба Найдите угол между прямыми и B_1D.

Посмотреть решение

6. В правильной треугольной призме , все рёбра которой равны sqrt{3} . Найдите расстояние между прямыми AA_1 и BC_1.

Посмотреть решение

7. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 5. Найдите площадь сечения конуса плоскостью ABP.

Посмотреть решение

А теперь — реальные задачи по стереометрии, встретившиеся выпускникам на Профильном ЕГЭ по математике.

8. Точки М и N — середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О — точка пересечения медиан грани АВС.

а) Докажите, что прямая DO проходит через середину отрезка MN.

б) Найдите угол между прямыми MN и ВС, если АВСD — правильный тетраэдр.

Посмотреть решение

9. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C_1 , причём CC_1 — образующая цилиндра, а AC — диаметр основания. Известно, что $angle ACB=30^circ , , AB=sqrt{2}, , CC_1=2.$

а) Докажите, что угол между прямыми AC_1 и равен

б)Найдите объём цилиндра.

Посмотреть решение

10. В основании призмы лежит правильный треугольник, вершина C_1 проецируется в центр Q основания АВС.

а) Докажите, что плоскости ABC_1 и QCC_1 перпендикулярны.

б) Найдите угол между прямой AA_1 и плоскостью ABC_1, если боковое ребро призмы равно стороне основания.

Посмотреть решение

11. Сечением прямоугольного параллелепипеда $ABCDA_{1}B_{1}C_{1} D_{1}$ плоскостью alpha , содержащей прямую $B D_{1}$ и параллельной прямой АС, является ромб.

а) Докажите, что грань ABCD — квадрат.

б) Найдите угол между плоскостями alpha и $BCC_{1}$ , если $AA_{1} = 6, , AB = 4.$

Посмотреть решение

12. На ребрах АВ и ВС треугольной пирамиды АВСD отмечены точки М и N соответственно, причем

Точки P и Q — середины ребер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите, в каком отношении эта плоскость делит объем пирамиды.

Посмотреть решение

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 14

7 лайфхаков для решения задач по стереометрии:

1. Задача по стереометрии не решается без хорошего чертежа! Чертеж строим по линейке, черной ручкой, на клетчатой бумаге, по правилам построения чертежей. На ЕГЭ можно и нужно пользоваться линейкой! А бланк будет в клеточку.

2. Все, что нужно, на чертеже должно быть хорошо видно! Если вам не понравился чертеж — не сидите над ним, бросьте и нарисуйте другой. Одного объемного чертежа будет недостаточно — понадобится один или несколько плоских.

3. Учимся записывать решение кратко. Вспомним основные обозначения

— точка M принадлежит плоскости АВС.

— прямые а и b пересекаются в точке О.

— прямые а и b параллельны.

abot b — прямые а и b перпендикулярны.

4. Почти в каждой задаче по стереометрии встречаются «особенные треугольники»

Давайте вспомним:

— В прямоугольном равнобедренном треугольнике гипотенуза в sqrt{2} раз больше катета.

— В треугольнике с углами 30, 60 и 90 градусов гипотенуза в 2 раза больше меньшего катета, а больший катет в sqrt{3} раз больше меньшего.

5. Формула для площади прямоугольной проекции фигуры помогает найти угол между плоскостями. Здесь varphi — угол между плоскостью фигуры и плоскостью проекции.

6. Метод объемов помогает найти расстояние от точки до плоскости. Надо выбрать треугольную пирамиду, записать ее объем двумя способами и найти из полученного уравнения нужное расстояние.

7. Сначала изучаем «классику». После этого, если время есть, можно браться и за координатный метод

Почему именно в таком порядке?

Конечно, координатный метод удобен. Однако большинство задач по стереометрии из вариантов ЕГЭ «заточены» под классику.

И если в решении задачи координатным методом вы сделаете арифметическую ошибку — можете потерять все баллы. Эксперт не будет разбираться, правильно ли вы посчитали определитель или смешанное произведение векторов. Потому что эти темы не входят в школьную программу, и составители «конструировали» задачи по стереометрии так, чтобы они решались обычными, «классическими» способами.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 13 Профильного ЕГЭ по математике. Стереометрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник


3618	Основание прямой призмы ABCDA1B1C1D — параллелограмм АВСD, диагонали которого пересекаются в точке О. Известно, что АА1 : АВ : АD = 1 : 2 : √5. На ребре АА1 отметили такую точку М, что прямые ОМ и BD1 перпендикулярны. а) Докажите, что точка М — середина ребра АА1. б) Найдите расстояние от точки М до прямой B1D1, если АВ=2 , BD=3 Решение	Основание прямой призмы ABCDA1B1C1D — параллелограмм АВСD, диагонали которого пересекаются в точке О ! Тренировочная работа №1 по математике 10 класс Статград 08-02-2023 Вариант МА2200109 Задание 13

3599	В правильной шестиугольной пирамиде SABCDEF сторона основания AB равна 2, а боковое ребро SA равно 8. Точка M — середина ребра AB. Плоскость альфа перпендикулярна плоскости ABC и содержит точки M и D. Прямая SC пересекает плоскость альфа в точке K. а) Докажите, что KM=KD. б) Найдите объём пирамиды CDKM Решение	В правильной шестиугольной пирамиде SABCDEF сторона основания AB равна 2, а боковое ребро SA равно 8. Точка M — середина ребра AB ! 36 вариантов ФИПИ Ященко 2023 Вариант 21 Задание 13

3577	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD Решение	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525

3545	Грань ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 является вписанной в основание конуса, а сечением конуса плоскостью A1B1C1 является круг, вписанный в четырёхугольник A1B1C1D1; AB=a, AA1=sqrt2a. а) Высота конуса равна h. Докажите, что 4,5a < h < 5a. б) Найдите угол между плоскостями ABC и SD1C, где S — вершина конуса Решение	Грань ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 является вписанной в основание конуса, а сечением конуса плоскостью A1B1C1 является круг, вписанный в четырёхугольник A1B1C1D1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 10 Задание 13

3535	Грань ABCD куба ABCDA1B1C1D1 является вписанной в основание конуса, а сечением конуса плоскостью A1B1C1 является круг, вписанный в четырёхугольник A1B1C1D1. а) Высота конуса равна h, ребро куба равно a. Докажите, что 3a < h < 3,5a. б) Найдите угол между плоскостями ABC и SA1D, где S — вершина конуса Решение	Грань ABCD куба ABCDA1B1C1D1 является вписанной в основание конуса, а сечением конуса плоскостью A1B1C1 является круг, вписанный в четырёхугольник A1B1C1D1 ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 13

3527	Сторона основания правильной четырёхугольной пирамиды SABCD относится к боковому ребру как 1 : sqrt2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M. а) Докажите, что сечение пирамиды SABCD плоскостью альфа — это четырёхугольник, диагонали которого перпендикулярны. б) Найдите площадь этого сечения, если боковое ребро пирамиды равно 6 Решение	Докажите, что сечение пирамиды SABCD плоскостью альфа — это четырёхугольник, диагонали которого перпендикулярны ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 13

3516	Сторона основания правильной четырёхугольной пирамиды SABCD относится к боковому ребру как 1 : sqrt2. Через вершину D проведена плоскость α, перпендикулярная боковому ребру SB и пересекающая его в точке M. а) Докажите, что M — середина SB. б) Найдите расстояние между прямыми AC и DM, если высота пирамиды равна 6sqrt3 Решение	Сторона основания правильной четырёхугольной пирамиды SABCD относится к боковому ребру как ! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 13

3504	В правильную треугольную пирамиду с боковым ребром sqrt13 и стороной основания 6 вписан шар. Плоскость α перпендикулярна высоте пирамиды и проходит через её середину. а) Докажите, что плоскость α и шар пересекаются более, чем в одной точке. б) Найдите площадь сечения шара плоскостью α Решение	В правильную треугольную пирамиду с боковым ребром sqrt13 и стороной основания 6 вписан шар ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 13

3479	В основании пирамиды SABCD лежит трапеция ABCD, с большим основанием AD. Диагонали трапеции пересекаются в точке O. Точки M и N — середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO. а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией. б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD=9, BC=7, SO=6, а прямая SO перпендикулярна прямой AD Решение	В основании пирамиды SABCD лежит трапеция ABCD, с большим основанием AD ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 13 # ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 13 Санкт-Петербург, Центр # Задачи-Аналоги 3357 3361

3470	В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней Решение	В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13

Показана страница 1 из 37

Источник