Задачи про кофейные автоматы в егэ по математике 2022 - Помощь в подготовке к экзаменам и поступлению

В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,25. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

В торговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,18. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после закрытия центра. Известно, что вероятность события «К вечеру в первом автомате закончится кофе» равна 0,25. Такая же вероятность события «К вечеру во втором автомате закончится кофе». Вероятность того, что кофе к вечеру закончится в обоих автоматах, равна 0,15. Найдите вероятность того, что к вечеру дня кофе останется в обоих автоматах.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,2. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,14. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,3. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

В тоговом центре два одинаковых автомата продают жвачку. Вероятность того, что к концу дня в автомате закончится жвачка, равна 0,25. Вероятность того, что жвачка закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня жвачка останется в обоих автоматах.

Источник

Тема 3.

Введение в теорию вероятностей

Сумма вероятностей совместных событий

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

введение в теорию вероятностей

3.01Вероятность как отношение «подходящих» исходов ко всем исходам

3.02Сумма вероятностей несовместных событий

3.03Сумма вероятностей совместных событий

3.04Произведение вероятностей независимых событий

Решаем задачу:

В торговом центре есть три одинаковых кофейных автомата. Вероятность того, что к концу дня в кофейном автомате закончится
кофе, равна 0,3. Вероятность того, что к концу дня кофе закончится во всех трех кофейных автоматах, равна 0,05. Какова
вероятность того, что к концу дня в торговом центре еще можно выпить кофе, но в первом автомате весь кофе
закончился?

Показать ответ и решение

У каждого автомата есть два исхода: кофе в нем закончился (будем обозначать «»), и кофе в нем остался (будем обозначать
«»). По условию вероятность того, что в первом автомате кофе закончился, равна 0,3. Заметим, что в событие «в первом
автомате закончился кофе» входят следующие элементарные исходы:

1) когда во втором и в третьем автоматах тоже нет кофе

2) когда во втором и третьем автоматах есть кофе

3) когда только во втором автомате остался кофе

4) когда толька в третьем автомате остался кофе

Также по условию вероятность того, что во всех автоматах нет кофе равна 0,05.

Тогда вероятность того, что в первом автомате кофе закончился, а во втором или в третьем еще есть кофе, то есть
вероятность события равна

Источник

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Источники: fipi, Ященко ЕГЭ 2022 (36 вар)

Решение:

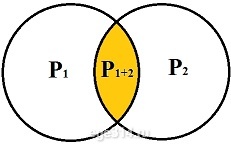
Р₁ = 0,25 кончится в 1-м автомате
Р₂ = 0,25 кончится во 2-м автомате
Р₁₊₂ = 0,1 кончатся и в 1-м и во 2-м автомате

Найдём вероятность того, что кофе закончится или в 1-м автомате, или во 2-м автомате, или в обоих сразу автоматах с учетом совместных событий (вся область внутри двух кругов):

Если сложим Р₁ + Р₂ вероятность Р₁₊₂ посчитается дважды от каждого из автоматов, поэтому один раз её вычитаем:

Р₁ + Р₂ – Р₁₊₂ = 0,25 + 0,25 – 0,1 = 0,4

Полная вероятность, всегда равна 1. Вероятность того, что кофе останется в обоих автоматах обратная тому, что кофе закончится хотя бы в одном автомате:

1 – 0,4 = 0,6

Ответ: 0,6.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.5 / 5. Количество оценок: 240

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Теория для решения задач здесь

Задача 1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна Вероятность того, что это вопрос на тему «Вписанная окружность», равна Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:+ показать

Задача 2.При изготовлении подшипников диаметром мм вероятность того, что диаметр будет отличаться от заданного не больше чем на мм, равна Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем мм или больше чем мм.

Решение:+ показать

Задача 3. В тоговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна Вероятность того, что кофе закончится в обоих автоматах, равна Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение: + показать

Задача 4. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Решение:+ показать

Задача 5. Биатлонист раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна Найдите вероятность того, что биатлонист первые раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение: + показать

Задача 6. Вероятность того, что новый пылесос прослужит больше года, равна Вероятность того, что он прослужит больше двух лет, равна Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение: + показать

Задача 7. Вероятность того, что на тесте по математике учащийся У. верно решит больше задач, равна Вероятность того, что У. верно решит больше задач, равна Найдите вероятность того, что У. верно решит ровно задач.

Решение: + показать

Задача 8. Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение: + показать

Задача 9. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает % этих стекол, вторая – %. Первая фабрика выпускает % бракованных стекол, а вторая – %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение:+ показать

Задача 10. Агрофирма закупает куриные яйца в двух домашних хозяйствах. % яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — % яиц высшей категории. Всего высшую категорию получает % яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение: + показать

Задача 11. Ковбой Джон попадает в муху на стене с вероятностью , если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью На столе лежит револьверов, из них только пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение: + показать

Задача 12. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы очков в двух играх. Если команда выигрывает, она получает очков, в случае ничьей — очко, если проигрывает — очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны

Решение: + показать

Задача 13. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент А. получит не менее баллов по математике, равна , по русскому языку — , по иностранному языку — и по обществознанию — .

Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Решение: + показать

Задача 14. На фабрике керамической посуды % произведённых тарелок имеют дефект. При контроле качества продукции выявляется % дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Решение: + показать

Задача 15. В кармане у Пети было монеты по рублю и монеты по два рубля. Петя, не глядя, переложил какие-то монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.

Решение: + показать

Задача 16. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью погода завтра будет такой же, как и сегодня. 3 августа погода в Волшебной стране хорошая. Найдите вероятность того, что 6 августа в Волшебной стране будет отличная погода.

Решение: + показать

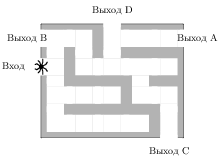
Задача 17. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.

Решение: + показать

Задача 18. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ дает положительный результат с вероятностью Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью Известно, что у % пациентов с подозрением на гепатит анализ дает положительный результат. Найдите вероятность того, что пациент, поступивший с подозрением на гепатит, действительно болен гепатитом. Ответ округлите до тысячных.

Решение: + показать

Задача 19. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна , а при каждом последующем — . Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее ?

Решение: + показать

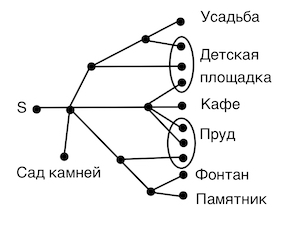
Задача 20. Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану.

Решение: + показать

Задача 21. Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа , и встречаются по два раза. В остальном кубики одинаковые.

Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали и очков. Какова вероятность того, что бросали первый кубик?

Решение: + показать

Задача 22. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс.

У Маши уже есть четыре разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?

Решение: + показать

Вы можете пройти Тест

Источник

2 марта 2022

В закладки

Обсудить

Жалоба

Для успешного решения новых задач под №10 необходимо уметь моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.

Задачи: 10.pdf

1. Плейлист айпода содержит 25 треков, из которых 9 исполняет группа Битлз. Функция «shuffle» воспроизводит все треки в случайном порядке, каждый по одному разу. Какова вероятность того, что трек Битлз будет играть вторым, причем первым будет воспроизведен трек другого исполнителя?

2. Игральный кубик бросают дважды. Известно, что в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.

3. Игральный кубик бросают три раза. Найдите вероятность того, что в сумме выпало 13 очков, при условии, что единица выпала ровно один раз.

4. В коробке 6 синих, 9 красных и 10 черных носков. Случайным образом выбирают два носка. Найдите вероятность того, что выбранные носки окажутся разноцветными.

5. Службе безопасности стало известно, что среди 1000 участников межгалактической конференции скрывается шпион, проникший в зал под чужой внешностью. Определить, кто из гуманоидов преступник, можно с помощью рамки шпионоискателя. Прибор всегда реагирует на чужака. Однако в 5% случаев сигнализация срабатывает без причины, и невинные гуманоиды могут оказаться в числе подозреваемых. Служба безопасности просит всех участников конференции пройти через рамку шпионоискателя. Проход первого же гуманоида вызывает сигнал тревоги. Какова вероятность того, что в ловушку угодил настоящий шпион? Ответ округлите до сотых.

6. Есть странный шестигранный игральный кубик, на гранях которого написаны какие-то натуральные числа, причем среди них ровно x четных. Реализуется следующий эксперимент: сначала совершают бросок странного кубика; затем, если на странном кубике выпало четное число, подбрасывают симметричную монетку, если же выпало нечетное число, подбрасывают стандартный игральный кубик с числами от 1 до 6 на гранях. Известно, что вероятность того, что во втором броске выпал орел, либо тройка, либо шестерка, равна 7 . Сколько
четных чисел было написано на странном игральном кубике?

7. Дана колода из 20 карт, по 5 карт каждой из четырех мастей. Из колоды случайным образом тянут 3 карты. Найдите вероятность того, что не все 3 карты окажутся одной масти. Ответ округлите до сотых.

8. Симметричную монету подбрасывают четыре раза. Известно, что в четвертом броске выпал орел. Какова при этом вероятность того, что за все броски орел выпал ровно два раза?

9. В торговом центре есть три одинаковых кофейных автомата. Вероятность того, что к концу дня в кофейном автомате закончится кофе, равна 0, 3. Вероятность того, что к концу дня кофе закончится во всех трех кофейных автоматах, равна 0, 05. Какова вероятность того, что к концу дня в торговом центре еще можно выпить кофе, но в первом автомате весь кофе закончился?

10. Пин-код на телефоне — случайная комбинация из четырех цифр. Какова вероятность того, что пин-код будет содержать ровно три различных цифры?

Ответы

1. 0,24
2. 0,2
3. 0,04
4. 0,68
5. 0,02
6. 2
7. 0,96
8. 0,375
9. 0,25
10. 0,432

Источник: vk.com/shkolkovo_ege

Источник

Пошаговое объяснение:

цифры дадут 9999 варианто + 1 вариант (0000), т. е. 10000 вариантов.

Теперь разберемся с 32 буквами. Представим их трехзначные сочетания, как число, записанное в 32 ричной системе, где А соответствует цифре 0, а Я соответствует цифре 31 (да, да в 32-ричной системе может есть цифра 31!)

Тогда максимальное число из трех цифр в этой системе будет записано как ЯЯЯ.

Переведем это число в привычную нам десятичную систему счисления:

ЯЯЯ(32) = 31×32² + 31×32¹+31 = 31×(32²+32+1)=32767. По аналогии с 4 цифрами прибавим еще один вариант (ААА), соответствующий нулю в этой системе и получим, сочетание из 3-х букв 32 буквенного алфавита дает нам 32767+1=32768 вариантов. Каждому этому варианту может соответствовать любой из 10000 вариантов из 4 цифр. Поэтому для нахождения общего количества возможных вариантов их надо перемножить:

32768×10000=327680000 возможных вариантов номеров

Введем два события:

А: выбор вопроса по теме «Вписанная окружность»;

B: выбор вопроса по теме «Параллелограмм».

Так как нет вопросов, относящихся одновременно к этим двум темам, то события A и B несовместные. Вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем – это сумма вероятности событий A и B, имеем:

ответ: 0,35.

Т.к. 0,3*0,3 ≠ 0,12, то события «кофе закончится в первом автомате» и «кофе закончится во втором автомате» совместны (т.е. зависимы).

Обозначим событие А = «кофе останется в первом автомате», событие В = «кофе останется во втором автомате». Р(А)=Р(В)= 1-0,3=0,7.

Событие «кофе остался хотя бы в одном автомате» — это объединение событий А U B -событие, противоположное событию «кофе закончится в обоих автоматах).

Р(АUB) = 1-0,12=0,88

С другой стороны » кофе остался хотя бы в одном автомате» означает, что кофе остался или в первом или во втором или в обоих вместе .

Т.е. AUB = AUB U A∩B , тогда Р(AUB) = Р(А) + Р(B) — Р(A∩B)

Р(A∩B) = Р(А) + Р(B) — Р(AUB) = 0,7+0,7 — 0,88 = 0,52

ответ: 0,52

Общаться в чате

1) сдаст оба 0,7*0,3=0,21

2) не сдаст ни одного =такая же вероятность 0,3*0,7=0,21

3)сдаст хотя бы один — это противоположное событию, не сдаст не одного: р(А)=1-0,21=0,79

Поскольку в условии задачи не менее 2 вопросов, то задача распадается на две:

1) студенту попадётся билет с 3-мя вопросами, которые он знает;

2) студенту попадётся билет с 2-мя вопросами, которые он знает.

Решаем 1-ую задачу:

События зависимые:

а — он знает 1 вопрос, благоприятных событий 20 из 25, т.е. Р(а) = 20/25.

в — он знает 2-й вопрос (а известных ему осталось 19 из оставшихся всех 24), т.е Р(в) = 19/24

с — он знает 3-й вопрос (а известных ему осталось 18 из оставшихся всех 23), т.е Р(с) = 18/23

Итак, вероятность того, что студенту достанутся три выученных вопроса) равна

Р(а×в×с) = Р(а)·Р(в)·Р(с) = 20/25 · 19/24 · 18/23 = 57/115.

inghethawh207

Вопрос по алгебре:

В торговом центре два одинаковых автомата продают кофе.Вероятность того, что к концу дня в каком-либо автомате закончится кофе, равна 0.2 независимо от другого автомата. Найдтевеочтноть того,что к концу дня кофе останется в обоих томатах.Помогите пожалуйста!

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

mincant235

1-0.2=0.8 — вероятность что кофе останется в 1 из автоматов.
0.8*0.8=0.64 — вероятность что кофе останется в двух автоматах.

Знаете ответ? Поделитесь им!

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

4:25ЕГЭ 2017 | Задание 4 | В торговом центре два одинаковых автомата продают кофе … ✘ Школа ПифагораШкола Пифагора ОГЭ и БАЗА

lượt xem 4,6 N6 năm trước

ЕГЭ 2015 (Профильный уровень) Задача #63 из списка пятых заданий Школы Пифагора …

7:15Задание 4 ЕГЭ по математике. Урок 19Valery Volkov

lượt xem 22 N7 năm trước

… ВКонтакте: volkovvalery В торговом центре два одинаковых автомата продают кофе. Вероятность того, что …

2:26В торговом центре два одинаковых автомата продают кофе.Екатерина Игоревна

lượt xem 202Năm trước

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе …

1:2728.В торговом центре два одинаковых автомата продают кофе.Вероятность того,что к концу дняТамара Остроушко

lượt xem 1,6 N2 năm trước

В торговом центре два одинаковых автомата продают кофе.Вероятность того,что к концу дня в каком либо автомате …

2:22В торговом центре два автомата продают кофе. Вероятность, что в автомате закончится кофе, равна 0,3.Патрик Физматик

lượt xem 346Năm trước

Поддержать автора www.donationalerts.com/r/patrickey В торговом центре два одинаковых автомата продают кофе.

11:00Вероятность на ЕГЭ! Задача на кофеавтоматы???100балльный репетитор

lượt xem 63 N3 năm trước

Узнать подробности и записаться на мои курсы можно тут — vk.cc/cbpGk9 Ищешь крутой контент по другим …

5:24ЕГЭ 4 номер (Теория вероятностей). Разбор задачи про кофейные автоматыИван Абрамов

lượt xem 61010 tháng trước

В торговом центре два одинаковых автомата продают кофе. Обслуживание автоматов происходит по вечерам после …

1:00:08✓ Новая задача на вероятность в ЕГЭ | Задание 10. ЕГЭ-2022. Профильный уровень | Борис ТрушинБорис Трушин

lượt xem 108 N4 tháng trước

0:30:00 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

3:40Теория Вероятностей| Задача на кофеавтоматы с помощью таблицыТатьяна Нарушева

lượt xem 1,4 N2 năm trước

Универсальный метод решения задачи про автоматы с кофе с ПОМОЩЬЮ ТАБЛИЦЫ. еще больше задач на моем …

3:25Теория вероятностей Два одинаковых автомата продают чай 4 вариант Ященко 36 вариантов ФИПИ ЕГЭ 2022Татьяна Нарушева

lượt xem 2184 tháng trước

Задача по теории вероятностей : В торговом центре два одинаковых автомата продают чай. Вероятность, что в автомате …

4:20ЕГЭ 2017 | Задание 4 | В торговом центре … ✘ Школа ПифагораШкола Пифагора ОГЭ и БАЗА

lượt xem 2,4 N7 năm trước

Подпишись! ¯¯/¯¯¯¯¯¯ ☻/ /· / Задача #321 из Списка Пифагора Условие: В торговом центре два одинаковых автомата …

3:44Сложная задача из ЕГЭ 2019 ( Теория вероятностей #11)Данил Лебедев

lượt xem 1,9 N3 năm trước

… обращайтесь Я Вконтакте — d_lebedev0 В торговом центре два одинаковых автомата продают кофе.

12:36Задача 4 ЕГЭ по математике. Урок 25Valery Volkov

lượt xem 13 N8 năm trước

… В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, …

17:36ЕГЭ задание 4 Задачи на вероятность Что надо знатьСавченко Елена

lượt xem 66310 tháng trước

9:27Совместные и несовместные, зависимые и независимые событияУчиться легко со Славой

lượt xem 7274 tháng trước

7:15Задача про кофейные аппаратыИван Абрамов

lượt xem 52Tháng trước

Решение проблемной задачи на теорию вероятностей В торговом центре два одинаковых автомата продают кофе.

17:34ЕГЭ задание 4 Разные типы задач на вероятностьСавченко Елена

lượt xem 50310 tháng trước

6:37«Вероятность». Задача на Зависимые События. ЕГЭ, Профиль. Математика для гуманитариевegeDoktor

lượt xem 42 tháng trước

В этом видео мы разберем задачу с таким УСЛОВИЕМ: В торговом центре два одинаковых автомата продают кофе.

4:06ЕГЭ 2017. Задание 4. Теория вероятностей. Автоматы в торговом центре. Совместные события.Математика для всех

lượt xem 4,8 N5 năm trước

В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, …

14:43Задание 4 профильного ЕГЭ по математике. Задача по теории вероятностей про автоматы с кофеРепетитор по математике Инна Леонидовна

lượt xem 2549 tháng trước

0:31Как продают кофе в супермаркетах на МанхеттенеSTUDIO413

lượt xem 2,2 N7 năm trước

8:24Кофейные автоматы (ЕГЭ. Профиль. Задача 4)Сергей Кузин

lượt xem 1602 năm trước

Классическая задача с ЕГЭ, по которой обычно много вопросов. Vk: zormex.

1:01:02ЕГЭ 2022 Ященко 3 вариант ФИПИ школе полный разбор!mrMathlesson Виктор Осипов

lượt xem 20 N3 tháng trước

00:14:03 — В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

2:12Теория вероятностей в задачах ОГЭ и ЕГЭ задача №24 #26Андрей Никитин

lượt xem 1,1 N2 năm trước

2:48ЕГЭ Математика профиль Задание 4 #510117Данил Лебедев / Нарезки математики

lượt xem 147Năm trước

2:52ЕГЭ математика Задание 4 #510117Лебедев Данил

lượt xem 80Năm trước

3:03:32Вариант ФИПИ на 100 баллов #20 (математика ЕГЭ профиль)Школа Пифагора ЕГЭ по математике

lượt xem 24 N2 năm trước

Задача 4 — 09:57 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате …

1:18ЕГЭ математика Задание 4 #320172Лебедев Данил

lượt xem 118Năm trước

25:40РАЗБОР ЕГЭ ПО МАТЕМАТИКЕ 359 ВАРИАНТ ЛАРИН. ЕГЭ ПО МАТЕМАТИКЕ 2022. ПЕРВАЯ ЧАСТЬ 1- 11 ЗАДАНИЯЮлия Гиперболическая

lượt xem 1,4 N5 tháng trước

Разбираю 1- 11 задания 359 варианта ЕГЭ Ларина. задания 12, 14, 15 vnclip.net/video/VUf2RZP7uXo/video.html задание 17 …

5:10Задача про кофейные автоматыГрани

lượt xem 1,1 N5 năm trước

Готовимся к ЕГЭ по математике. Разбор задачи из теории вероятностей про кофейные автоматы.

1:15ЕГЭ Математика профиль Задание 4 #320172Данил Лебедев / Нарезки математики

lượt xem 7Năm trước

36:44урок 3. вероятность,сложнее обычного. задание 10 ЕГЭ 2022Вера Волыхина математика просто

lượt xem 2303 tháng trước

Ященко 36 вариантов ЕГЭ вероятность задание 10 все получится.

1:27ОГЭ Ященко 2015. Вариант 34, задача №19. Ответselfedu

lượt xem 1796 năm trước

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в каком-либо автомате …

Kế tiếp

Источник