Задачи про конус егэ по математике - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите

Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?

Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?

Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на Пи .

Пройти тестирование по этим заданиям

Источник

09
Сен 2013

Категория: 02 Стереометрия

02. Конус

2013-09-09
2022-09-11

Задача 1. Высота конуса равна , образующая равна Найдите его объем, деленный на .

Решение: + показать

Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного Найдите его объем, деленный на .

Решение: + показать

Задача 3. Высота конуса равна а диаметр основания – Найдите образующую конуса.

Решение: + показать

Задача 4. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом В ответе укажите $frac{V}{pi}.$

Решение: + показать

Задача 5. Длина окружности основания конуса равна образующая равна Найдите площадь боковой поверхности конуса.

Решение: + показать

Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?

Решение: + показать

Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?

Решение: + показать

Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?

Решение: + показать

Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Решение: + показать

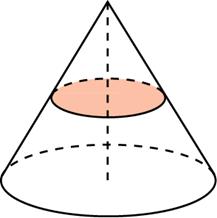
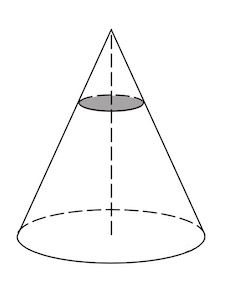
Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение: + показать

Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Решение: + показать

Задача 12. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом $30^{circ}.$ В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен °. Вычислите объем конуса, деленный на .

Решение: + показать

Задача 14. Площадь основания конуса равна , высота — Найдите площадь осевого сечения конуса.

Решение: + показать

Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной и считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Решение: + показать

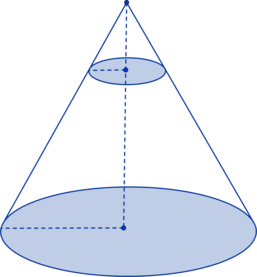
Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает $frac{1}{2}$ высоты. Объём жидкости равен мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение: + показать

Вы можете пройти тест

Автор: egeMax |

комментариев 10

Печать страницы

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по теме «Конус»

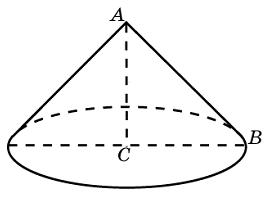
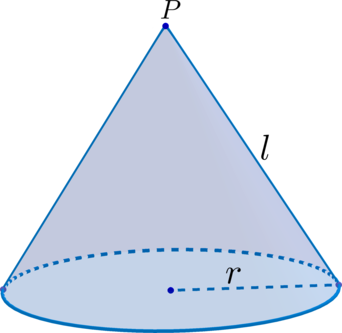
(blacktriangleright) Точка (P) – вершина конуса.

(blacktriangleright) Отрезок, соединяющий вершину конуса с границей основания, называется образующей (все образующие равны между собой).

(blacktriangleright) Отрезок, соединяющий вершину конуса с центром основания-круга, является высотой конуса.

(blacktriangleright) Площадь боковой поверхности конуса ({large{S_{text{бок.пов.}}=pi rl}}), где (r) – радиус основания, (l) – образующая.

(blacktriangleright) Площадь полной поверхности конуса – эта сумма площади боковой поверхности и площади основания. [{large{S_{text{полн.пов.}}=pi rl+pi r^2=pi r(r+l)}}]

(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}S_{text{осн.}}cdot h=dfrac{1}{3}pi
r^2h}}), где (h) – высота конуса.

Заметим, что конус имеет некоторое сходство с пирамидой, только в основании пирамиды лежит многоугольник (граница которого – ломаная), а в основании конуса – круг (граница которого – гладкая).
Поэтому можно сказать, что поверхность пирамиды “ребристая” , а конуса – “гладкая”.

Задание
1

#1886

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности конуса равна (48pi), а площадь основания равна (36pi). Найдите длину образующей конуса.

Если радиус окружности, лежащей в основании конуса обозначить за (r), а длину образующей за (l), то площадь основания и площадь боковой поверхности конуса выразятся по формулам: (S_{text{осн.}} =
pi r^2), (S_{text{бок.пов.}} = pi r l). Из первой формулы следует: (pi r^2 = 36pi) (Rightarrow) (r^2 = 36) (Rightarrow) (r
= 6) (Rightarrow) (6pi l = 48pi) (Rightarrow) (6l = 48) (Rightarrow) (l = .

Ответ: 8

Задание
2

#1887

Уровень задания: Равен ЕГЭ

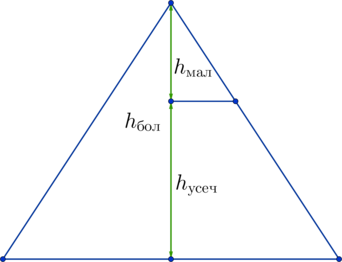
Площадь боковой поверхности конуса равна (48pi), а площадь боковой поверхности усеченного конуса с такими же основанием и углом наклона образующей к плоскости основания равна (36pi). Найдите высоту усеченного конуса, если высота исходного конуса равна (10).

Площадь боковой поверхности меньшего конуса, который дополняет усеченный конус до полного, равна разности их площадей поверхностей: (S_{text{мал}} = 48pi — 36pi = 12pi). Отношение площадей боковых поверхностей большого и малого конусов равно квадрату коэффициента подобия между ними: [frac{S_{text{бол}}}{S_{text{мал}}} = k^2 =
frac{48pi}{12pi} = 4Rightarrow k = 2]

Тогда высоты конусов относятся друг к другу: (dfrac{h_{text{бол}}}{h_{text{мал}}} = dfrac{10}{h_{text{мал}}}
= k = 2). Тогда

[h_{text{мал}} = 5Rightarrow h_{text{усеч}} = h_{text{бол}}
— h_{text{мал}} = 10 — 5 = 5]

Ответ: 5

Задание
3

#962

Уровень задания: Сложнее ЕГЭ

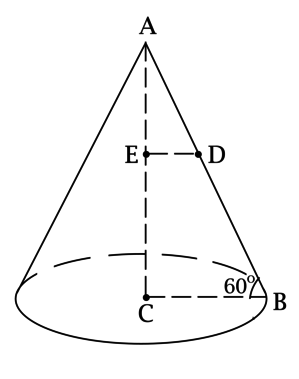
На высоте конуса с вершиной (A), центром основания (C) и радиусом основания (R = 4) отметили точку (E) такую, что расстояние от неё до основания равно (sqrt{3}(4-pi^{-0,5})). Известно, что угол между образующей конуса и плоскостью основания равен (60^circ). Найдите площадь сечения (T) конуса, проходящего через точку (E) и параллельного основанию конуса.

Рассмотрим треугольник (ABC), где (B) – некоторая точка на окружности основания. Так как (AC) – высота конуса, то (ACperp CB), тогда (angle CAB = 90^circ — angle ABC = 30^circ), следовательно, (AB = 2CB = . По теореме Пифагора [AC = sqrt{AB^2 — CB^2} = 4sqrt{3}.]

Обозначим через (D) точку пересечения плоскости сечения (T) и (AB). Рассмотрим треугольник (AED): [AE = AC — CE = 4sqrt{3} — sqrt{3}(4 — pi^{-0,5}) = sqrt{dfrac{3}{pi}}.]

Так как сечение (T) параллельно плоскости основания, а (AC) – высота конуса, то (ACperp ED), тогда (triangle AED) – прямоугольный и (angle EAD = 30^circ), откуда [ED = AEcdot mathrm{tg}, angle EAD = sqrt{dfrac{3}{pi}}cdot dfrac{1}{sqrt{3}} = dfrac{1}{sqrt{pi}} = r] – радиус сечения (T).

Таким образом, площадь сечения (T) равна (pi r^2 = picdotdfrac{1}{pi} = 1).

Ответ: 1

Задание
4

#963

Уровень задания: Сложнее ЕГЭ

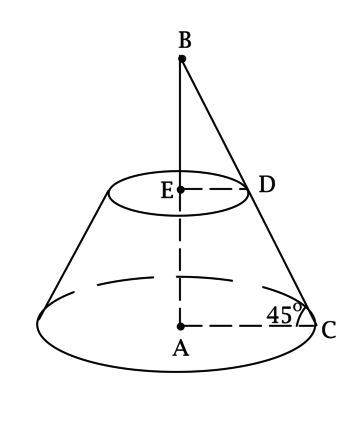
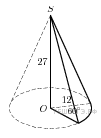
Радиусы оснований усечённого конуса равны [r = dfrac{2}{sqrt[4]{2}sqrt{pi}}qquad text{и}qquad R = dfrac{10}{sqrt[4]{2}sqrt{pi}},] а угол между его образующей и основанием равен (45^circ). Найдите площадь боковой поверхности этого усечённого конуса.

Обозначим центры оснований усечённого конуса через (A) и (E), так что (A) – центр большего основания. Отметим на большем основании точку (C), а точку меньшего основания, через которую проходит образующая, выходящая из (C), обозначим через (D).

Высота (AE) и образующая (CD) лежат в одной плоскости. Обозначим точку их пересечения через (B).

Так как (AE) – высота, то (AEperp CD) и (AEperp AC).

Рассмотрим прямоугольный треугольник (BAC):
в нём (angle BCA = 45^circ), тогда [AB = R = dfrac{10}{sqrt[4]{2}sqrt{pi}},qquadqquad BC = Rsqrt{2} = dfrac{10sqrt{2}}{sqrt[4]{2}sqrt{pi}}.]

Рассмотрим прямоугольный треугольник (BED):
так как (angle EBD = 45^circ), то [BE = r = dfrac{2}{sqrt[4]{2}sqrt{pi}},qquadqquad BD = rsqrt{2} = dfrac{2sqrt{2}}{sqrt[4]{2}sqrt{pi}},] тогда (EA = AB — BE = R — r), (DC = BC — BD = Rsqrt{2} — rsqrt{2} = sqrt{2}(R — r)). [S_{text{бок}} = pi(R + r)cdot I,] где (I) – образующая, тогда [S_{text{бок}} = pi(R + r)cdotsqrt{2}(R — r) = sqrt{2}pi(R^2 — r^2) = sqrt{2}pileft(dfrac{100}{sqrt{2}pi} — dfrac{4}{sqrt{2}pi}right) = 96.]

Ответ: 96

Старшеклассникам, которые готовятся к сдаче ЕГЭ по математике, непременно стоит научиться вычислять площадь и другие неизвестные параметры конуса. Как показывает практика предыдущих лет, подобные задания из раздела «Геометрия в пространстве» вызывают у выпускников определенные сложности.

При этом понимать, как найти площадь боковой поверхности или, к примеру, сечения конуса, параллельного основанию, должны все учащиеся, независимо от уровня их подготовки. Это позволит им успешно пройти аттестационное испытание по математике.

Базовая информация, которую стоит запомнить

Конус представляет собой геометрическое тело, которое образовано совокупностью круга, точки, находящейся вне его плоскости, и лучей, соединяющих заданную точку с точками круга. Его высотой называется перпендикуляр, который опущен из вершины на плоскость основания.
Все образующие конуса равны между собой.
Осевое сечение конуса представляет собой равнобедренный треугольник. Основание этой фигуры равняется двум радиусам. Боковые стороны треугольника равны образующим конуса.

Занимайтесь вместе с сайтом «Школково»!

Чтобы не допускать распространенных ошибок при решении задач по теме «Конус», выбирайте наш математический портал. Здесь есть весь необходимый материал для изучения разделов, требующих повторения.

Специалисты образовательного проекта «Школково» предлагают новый подход к подготовке к экзамену, предполагающий переход от простого к сложному. Вначале мы даем полную теорию, основные формулы и элементарные практические задачи с решением, в том числе и по теме «Конус», а затем постепенно переходим к заданиям экспертного уровня, которые также встречаются в ЕГЭ. Вся необходимая информация представлена в разделе «Теоретическая справка».

Вы также можете сразу приступить к решению онлайн-задач на вычисление высоты усеченного конуса, площади его боковой поверхности, объема, а также похожих задач на вычисление, например, нахождению объема или площади сечения куба. Большая база упражнений представлена в разделе «Каталог». Перечень заданий систематически обновляется.

Проверьте, насколько легко вы сможете определить площадь конуса в режиме онлайн. Если упражнение потребовало от вас минимальных усилий, рекомендуем вам не тратить время на простые задачи и переходить к более сложным. А если затруднения все же возникли, тогда вам непременно стоит находить время в своем ежедневном расписании на дистанционные занятия вместе со «Школково». С нами вы сможете быстро усвоить алгоритм решения задач на расчет объема конуса и других неизвестных параметров.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Тема 2.

Геометрия в пространстве (стереометрия)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия в пространстве (стереометрия)

2.01Теорема о трех перпендикулярах

2.02Угол между прямыми

2.03Угол между прямой и плоскостью

2.04Угол между плоскостями и двугранный угол

2.05Пирамида

2.06Правильная и прямоугольная пирамиды

2.07Призма

2.08Правильная и прямая призмы

2.09Параллелепипед как частный случай призмы

2.10Прямоугольный параллелепипед

2.11Куб как частный случай прямоугольного параллелепипеда

2.12Конус

2.13Цилиндр

2.14Сфера и шар

2.15Комбинированные тела: их объемы и площади поверхностей

2.16Отношение площадей поверхностей и отношение объемов тел

2.17Вписанные и описанные тела

Решаем задачи

Площадь боковой поверхности конуса равна 48π, а площадь боковой поверхности усеченного конуса с такими же большим
основанием и углом наклона образующей к плоскости основания равна 36π. Найдите высоту усеченного конуса, если высота
исходного конуса равна 10.

Показать ответ и решение

Площадь боковой поверхности меньшего конуса, который дополняет усеченный
конус до полного, равна разности их площадей поверхностей:

S = 48π − 36π = 12π
мал

Отношение площадей боковых поверхностей большого и малого конусов равно
квадрату коэффициента подобия треугольников, являющихся осевыми сечениями
этих конусов:

k2 = Sбол-= 48π = 4 ⇒ k = 2
Sмал 12π

Тогда отношение высот конусов равно коэффициенту подобия:

-10-= hбол =k = 2
hмал hмал

Отсюда найдем высоту малого и усеченного конусов:

Площадь боковой поверхности конуса равна 48π, а площадь основания равна 36π. Найдите длину образующей
конуса.

Показать ответ и решение

Если радиус окружности, лежащей в основании конуса, обозначить за , а длину образующей за , то площадь основания и
площадь боковой поверхности конуса выразятся по формулам:

2
Sосн. = πr, Sбок.пов. = πrl

Из первой формулы получаем:

2 2
πr = 36π ⇒ r = 36 ⇒ r = 6

Из второй формулы получаем:

Диаметр основания конуса равен 32, а длина образующей равна 20. Найдите
площадь осевого сечения этого конуса.

Радиусы оснований усечённого конуса равны

r = √-2√--- и R = √-10√--,
4 2 π 42 π

а
угол между его образующей и основанием равен ∘
45 . Найдите площадь боковой поверхности этого
усечённого конуса.

Показать ответ и решение

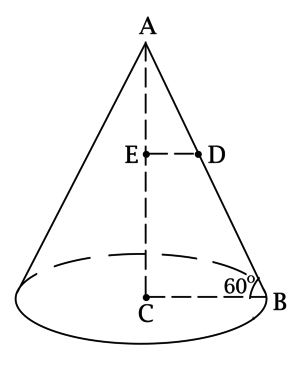
Рассмотрим треугольник ABC , где – некоторая точка на окружности основания. Так как
– высота конуса, то , тогда , следовательно, . По
теореме Пифагора

√----2------2 √ --
AC = AB − CB = 4 3.

Обозначим через точку пересечения плоскости сечения и . Рассмотрим треугольник
AED :

∘ --
√ -- √-- −0,5 3-
AE = AC − CE = 4 3 − 3 (4 − π ) = π.

Так как сечение параллельно плоскости основания, а – высота конуса, то , тогда
△AED – прямоугольный и , откуда

∘ -3 1 1
ED = AE ⋅ tg∠EAD = -- ⋅√---= √--- = r
π 3 π

–
радиус сечения .

Таким образом, площадь сечения равна 1
πr2 = π ⋅--= 1
π .

Источник

Скачать материал

Сейчас обучается 1079 человек из 83 регионов

Сейчас обучается 28 человек из 12 регионов

Сейчас обучается 140 человек из 45 регионов

Описание презентации по отдельным слайдам:

1 слайд

Подготовка к ЕГЭ, подборка задач
по теме «Конус» (базовый уровень)
2 слайд

Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
3 слайд

Задача №1
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Решение.
Т.к. площадь боковой поверхности конуса: S=πrl.
Значит S1= π·3·9= 27π, S2= π·6·9= 54π.
Тогда S2: S1= 54π : 27π = 2
4 слайд

Задача №2
Объём конуса равен 135. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Отношение объемов конусов равно кубу их коэффициента подобия. Высоты конусов относятся как 1:3, поэтому их объемы относятся как 1:27. Следовательно, объем отсекаемого конуса равен 135 : 33 = 5.
5 слайд

К задаче №2
Объём конуса равен 32. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Решение.
Отношение объемов конусов равно кубу их коэффициента подобия k. Так как высоты конусов относятся как 1:2, то k равно одной второй, а значит объем отсекаемого конуса будет равен 32 : 2³ = 4.
6 слайд

Задача №3
Объём конуса равен 50π а его высота равна 6 . Найдите радиус основания конуса.
Найдём радиус основания конуса по формуле: V=1/3·πR²h
Откуда R²=3V:πh => R²= 150π : 6π = 25. Тогда R=5
7 слайд

Задача №4
Во сколько раз уменьшится объем конуса, если
его высоту уменьшить в 3 раза?
Объем конуса вычисляется по формуле V=1/3·Soc.·h .
Значит, если высоту увеличить в 3 раза, то и объём увеличится в 3 раза
8 слайд

Задача №5
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Объем конуса вычисляется по формуле
V=1/3·Soc.·h = 1/3·πR²·h.
Значит, если радиус основания увеличить в 1,5 раза, то и объём конуса увеличится в 2,25 раза
9 слайд

Задача №6
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?
Площадь боковой поверхности конуса вычисляется по формуле
S= πR·L, где L-образующая.
Значит если увеличить L в 3 раза, то площадь боковой поверхности конуса тоже увеличится в 3 раза.
10 слайд

Задача №7
Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?

Площадь боковой поверхности конуса вычисляется по формуле S= πR·L. Значит, если радиус основания уменьшится в 1,5 раза, то площадь боковой поверхности конуса тоже уменьшится в 1,5 раза.
11 слайд

Задача №8
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
По теореме Пифагора
12 слайд

Задача №9
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
По теореме Пифагора….
Ответ: 6.
13 слайд

Задача №10
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
По теореме Пифагора….
Ответ: 4.
14 слайд

Задача №11
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
15 слайд

Задача №12
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
16 слайд

Решение
Пусть х — высота налитой жидкости, у — радиус окружности в основании конуса. Тогда 2х — высота сосуда, 2у — радиус окружности в основании сосуда (так как поверхность жидкости отсекает от конического сосуда конус подобный данному). Найдем отношения объёмов конусов,
Таким образом, объём сосуда в 8 раз больше объёма налитой жидкости: 1600 : 8 = 200
17 слайд

Задача №13
Объём конуса равен 96π, а его высота равна 8. Найдите радиус основания конуса.
Найдём радиус основания конуса из формулы: V=1/3·πR²h
Откуда R²=3V:πh =>
18 слайд

Задача №14
Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
19 слайд

Решение
Найдём площадь боковой поверхности первого конуса: S1=π·R1·L1 = π·2·4=8π
2) Найдём площадь боковой поверхности второго конуса: S2=π·R2·L2 = π·6·8=48π
3) Найдём отношение площадей этих конусов:
S2 : S1 = 48π : 8π = 6
20 слайд

Задача №15
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.
21 слайд

Решение
Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна Sб.п.= 2πR·h, но R=h следовательно Sб.п.= 2πR² и =3√2 => πR² =1,5√2
2) Площадь боковой поверхности конуса равна S=πR·L, Но L² = R²+h², но R=h => L² = 2R² => L = R√2.
Значит Sб.п.= πR·L= πR· R√2 = πR²·√2 =
= 1,5√2·√2 = 3
22 слайд

Задача №16
Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Осевым сечением конуса является равнобедренный треугольник, основание которого —это диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² => h = √100-36=√64=8
Следовательно, площадь осевого сечения
равна 0,5 · 12 · 8 = 48.
23 слайд

Задача №17
Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Осевым сечением конуса является равнобедренный треугольник, основание которого — диаметр основания конуса, а высота совпадает с высотой конуса.
Но L² = R²+h² => R=√100-64=√36=6
Следовательно, диаметр осевого сечения конуса равен 12, а площадь осевого сечения равна 0,5 · 12 · 8 = 48.
24 слайд

Задача №18
Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью
25 слайд

Решние
Сечение плоскостью, параллельной основанию, представляет собой круг, радиус которого относится к радиусу основания конуса как 3 : 9. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому площадь сечения в 9 раз меньше площади основания. Тем самым, она равна 2.
26 слайд

Задача №19
Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.

Осевым сечением конуса является равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание является диаметром основания конуса. Поэтому площадь осевого сечения равна половине произведения высоты конуса на диаметр его основания или произведению высоты конуса на радиус основания R. Поскольку по условию πR²=16π, то радиус основания конуса равен 4, а тогда искомая площадь осевого сечения равна 24.
27 слайд

Задача №20
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:
28 слайд

Задача №21
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Формулу для объёма шара:
V=4/3 ·πR³, а формула объёма конуса: V=1/3 ·πR³.
Значит объём конуса в 4 раза меньше объёма шара.
Тогда объём конуса равен 28 : 4 = 7

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 784 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Тема

§ 2. Конус

Больше материалов по этой теме

Другие материалы

Все о конусе (теория)

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема: § 2. Конус

14.03.2019
2015
28

Урок по теме «Конус»

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема: § 2. Конус

12.12.2018
336
1

Презентация по теме «Конус. Площадь поверхности конуса»

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема: § 2. Конус

Рейтинг:
4 из 5

22.11.2018
3947
679

Открытый урок по теме «Конус».

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема: § 2. Конус

23.10.2018
1045
6

Презентация по геометрии на тему «Конус»

Учебник: «Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
Тема: § 2. Конус

10.07.2018
3172
13

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Финансы: управление структурой капитала»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

Источник

Конус

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30. В ответе укажите V/π

Ответ: 1

Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π.

Ответ: 128

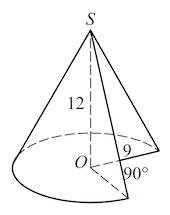
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.

Ответ: 9

4. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на π.

Ответ: 72

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.

Ответ: 16

Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

Ответ: 3

Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на π.

Ответ: 144

Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Ответ: 60

Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π.

Ответ: 24

10.

Найдите объем части конуса, изображенной на рисунке. В ответе укажите .

Ответ: 87,75

11.

Н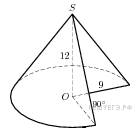айдите объем части конуса, изображенной на рисунке. В ответе укажите .

Ответ: 243

12.

Найдите объем части конуса, изображенной на рисунке. В ответе укажите .

Ответ: 216

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Ответ: 7

15. Задание 16 № 324453

Площадь основания конуса равна 16π, высота — 6. Найдите площадь осевого сечения конуса.

Ответ: 24

16. Задание 16 № 324454

Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Ответ: 2

17.

Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.

Ответ: 48

18. Задание 16 № 324456

Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.

Ответ: 48

19. Задание 16 № 324458

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Ответ: 3

20. Задание 16 № 500893

Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 5 раз?

Ответ: 5

21. Задание 16 № 501191

Во сколько раз уменьшится объём конуса, если его высоту уменьшить в 8 раз, а радиус основания оставить прежним?

Ответ: 8

22. Задание 16 № 505149

Высота конуса равна 12, а диаметр основания равен 10. Найдите образующую конуса.

Ответ: 13

23. Задание 16 № 505170

Высота конуса равна 4, а диаметр основания равен 6. Найдите образующую конуса.

Ответ: 5

24. Задание 16 № 506339

бъём конуса равен 50π, а его высота равна 6. Найдите радиус основания конуса.

Ответ: 5

25. Задание 16 № 509601

Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?

Ответ: 6

26. Задание 16 № 509661

Объём конуса равен 96π, а его высота равна 8. Найдите радиус основания конуса.

Ответ: 6

27. Задание 16 № 510129

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

Ответ: 200

Источник

Слайд 1

Решение задач по теме «Конус» МБОУ «СОШ №1 г.Суздаля» Учитель : Плотникова Татьяна Владимировна

Слайд 2

Тела вращения

Слайд 3

Цилиндр

Слайд 4

Конус

Слайд 5

Усечённый конус

Слайд 6

Цилиндр Конус Усечённый конус Площадь боковой поверхности S бок =2πRh S бок = πRl S бок = πl ( R+R 1 ) Площадь полной поверхности S пол =2 πRh +2π R 2 S пол = πRl +π R 2 S пол = πl ( R+R 1 ) +π R 2 + πR l 2 Объём V= π R 2 h V= π R 2 h V= π h(R 2 + R 1 2 + RR 1 )

Слайд 7

Устные упражнения: Высота конуса равна 4 см, радиус основания – 3 см. Найти образующую конуса. 1 5

Слайд 8

Радиус конуса равен 5 см, образующая равна 8 см. Найдите площадь боковой поверхности конуса. 2 40 π

Слайд 9

Образующая конуса равна 13 см, радиус основания – 5 см. Найдите высоту конуса. 3 12

Слайд 10

Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? 4 3

Слайд 11

Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза? 5 2,25

Слайд 12

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? 6 3

Слайд 13

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней? 7 1,5

Слайд 14

Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π . 8 128

Слайд 15

Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на π . 9 72

Слайд 16

Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π . . 10 24

Слайд 17

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27. 11 81

Слайд 18

12 Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. 2

Слайд 19

1. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса. 2. Высота конуса 12 см, образующая – 13 см. Найти площадь полной поверхности конуса. Работа в парах: 50 π 90 π 3. Высота конуса равна 2√3 см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником. 8π, 2√3

Слайд 20

Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π . 9

Слайд 21

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π . . 16

Слайд 22

Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. 6

Слайд 23

Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. 60

Слайд 24

Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. 3

Слайд 25

Найдите объем части конуса, изображенной на рисунке. В ответе укажите . 87,75

Слайд 26

. Найдите объем части конуса, изображенной на рисунке. В ответе укажите 243

Слайд 27

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? 490

Слайд 28

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса. 3

Слайд 29

Конусообразная палатка высотой 3,5 м и диаметром основания 4 м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку? Образующая конуса , что примерно составляет 8,06 м. Тогда площадь боковой поверхности конуса равна что примерно составляет 5,3 м 2 . На палатку пошло примерно 25,3 м 2 парусины. Ответ: 25,3 м 2 Решение. 25,3

Слайд 30

Домашнее задание: Подобрать по теме «Конус» 5 задач из банка данных по математике и решить их . Дополнительные задачи: Радиусы оснований усеченного конуса 10√3 и 6√3 , а образующая наклонена к плоскости основания под углом 60 о . Найти высоту усеченного конуса. Отношение площадей боковой и полной поверхности конуса равно Найти угол между образующей и плоскостью основания конуса .

Слайд 31

Источники: http://reshuege.ru/?theme=144&print=true — КАТАЛОГ ЗАДАНИЙ Геометрия, 10–11класс: Учебник для общеобразовательных учреждений: базовый и профильный уровни / Л.С. Атанасян , В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2011.

Источник