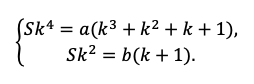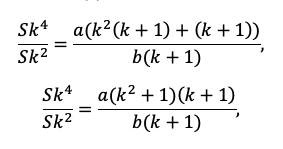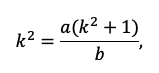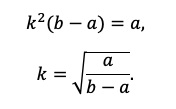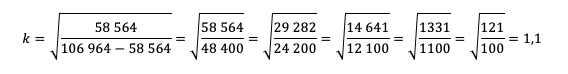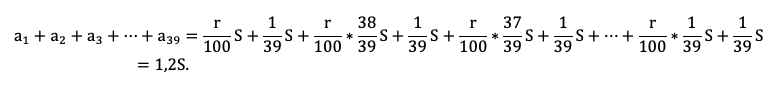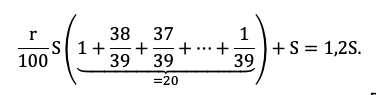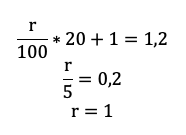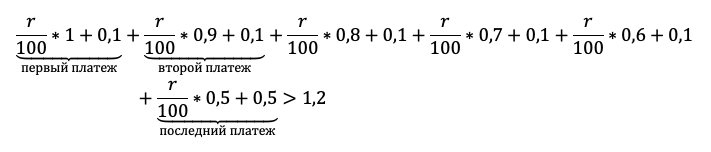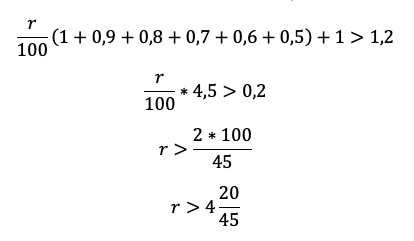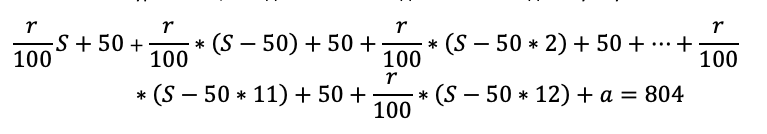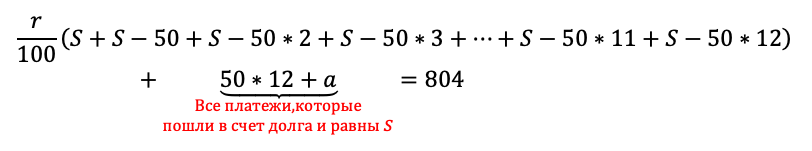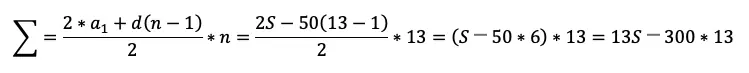Всего: 258 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 8 млн.
Савелий хочет взять в кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Савелий взять кредит, чтобы ежегодные выплаты были не более 330 тысяч рублей?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
Источник: А. Ларин. Тренировочный вариант № 322 (часть C).
1 января 2015 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С)., Задания 17 (С4) ЕГЭ 2015
В июле планируется взять кредит на сумму 2 320 500 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
Наш добрый герой В. взял в банке кредит в размере 20 192 020 рублей по очень знакомой схеме:
— в конце очередного месяца пользования кредитом банк начисляет проценты за пользование заемными средствами по специальной ставке данного варианта 2,96%;
— в этот же день клиент выплачивает часть долга и сумму начисленных процентов;
— после выплаты долг должен быть на одну и ту же величину меньше долга на конец предыдущего месяца.
Но дальше все пошло не по сценарию. Наш герой решил каждый месяц, начиная с первого, платить банку сверх прочего дополнительную сумму на погашение долга, при этом долг по‐прежнему ежемесячно уменьшался на одну и ту же величину (бóльшую, чем планировалось изначально) до полного погашения. В итоге срок кредита сократился на 52%. На какое наименьшее число процентов могла уменьшиться при этом переплата банку?
Источник: А. Ларин. Тренировочный вариант № 296.
Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Источник: А. Ларин: Тренировочный вариант № 85.
31 декабря 2014 года Никита взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Никита переводит очередной транш. Если он будет платить каждый год по 2 073 600 рублей, то выплатит долг за 4 года. Если по 3 513 600 рублей, то за 2 года. Под какой процент Никита взял деньги в банке?
15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015 по математике. Основная волна 04.06.2015. Вариант 1 (Часть С)., Задания 17 (С4) ЕГЭ 2015
В начале года фирма «Жилстройсервис» выбирает банк для получения кредита среди нескольких банков, кредитующих под разные проценты. Полученным кредитом фирма фирма планирует распорядится следующим образом: 75% кредита направить на строительство коттеджей, а остальные 25% на оказание риэлтерских услуг населению. Первый проект может принести прибыль в размере от 36% до 44% годовых, а второй — от 20% до 24% годовых. В конце года фирма должна вернуть кредит банку с процентами и при этом рассчитывает на чистую прибыль от указанных видов деятельности от не менее 13%, но и не более 21% годовых от всего полученного кредита. Какими должны быть наименьшая и наибольшая процентные ставки кредитования выбираемых банков, чтобы фирма гарантированно обеспечила себе указанный выше уровень прибыли.
Источник: А. Ларин: Тренировочный вариант № 157.
В январе 2020 года Борис взял кредит в банке на сумму 4 200 000 рублей. По договору с банком Борис должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 10%. В феврале 2021 года Борис сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 7%. Какую сумму сэкономит Борис на рефинансировании своего кредита?
Источник: Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №1
В январе 2020 года Василий взял кредит в банке на сумму 3 300 000 рублей. По договору с банком Василий должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 20%. В феврале 2021 года Василий сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 16%. Какую сумму сэкономит Василий на рефинансировании своего кредита?
Источник: А. Ларин. Тренировочный вариант № 348., Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2
Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?
В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в млн рублей) |
S | 0,7S | 0,4S | 0 |
Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
Источник: Задания 17 (С5) ЕГЭ 2016
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 825 тыс рублей?
Источник: РЕШУ ЕГЭ
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 2% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 327 тысяч рублей.
Всего: 258 1–20 | 21–40 | 41–60 | 61–80 …
17. Сложные задачи прикладного характера
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
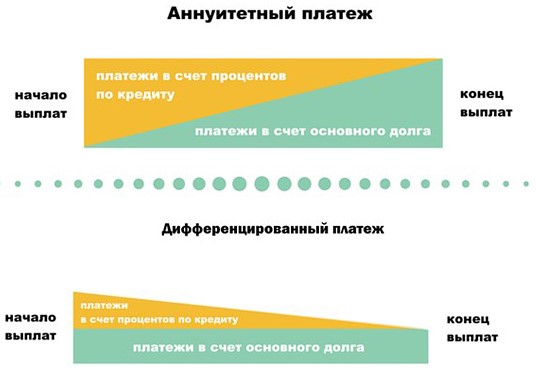
Задачи про банковский кредит: дифференцированный платеж
Дифференцированный платеж – это такая система выплат, при которой сама сумма долга уменьшается равномерно, то есть на одну и ту же величину каждый год (месяц).
При этом платежи каждый год разные.
Таким образом, если кредит взят на (n) лет, то это значит, что сумму кредита (A) разделили на (n) равных частей и что каждый год после платежа сумма долга уменьшается на (dfrac1n A) по сравнению с долгом на начало года.
Пример: Александр взял в банке кредит на (50,000) рублей на (3) месяца, причем выплачивать кредит он должен ежемесячными выплатами так, чтобы сумма долга каждый месяц уменьшалась на одну и ту же величину. Сколько рублей составит переплата Александра по кредиту, если процентная ставка в банке (10%)?
Т.к. кредит взят на (3) месяца, то после первой выплаты долг должен составить (A-frac13A=frac23 A), после второй (frac23A-frac13A=frac13A), а после третьей — (frac13A-frac13A=0) рублей. Составим таблицу, производя все вычисления в тыс. рублей: [begin{array}{|l|c|c|c|c|}
hline text{Месяц}&text{Сумма долга}&text{Сумма долга}&text{Сумма долга}&text{Выплата}\
&text{до начисления} %&text{после начисления }%&text{после выплаты}&\
hline 1&50&50+0,1cdot 50&frac23cdot 50&0,1cdot 50+frac13cdot 50\
hline 2&frac23cdot 50&frac23cdot 50+0,1cdotfrac23cdot 50&frac13cdot 50&0,1cdot frac23cdot 50+frac13cdot50\
hline 3&frac13cdot 50&frac13cdot 50+0,1cdot frac13cdot
50&0&0,1cdot frac13cdot 50+frac13cdot 50\
hline
end{array}]
Таким образом, всего Александр заплатил банку (big(0,1cdot
50+dfrac13cdot 50big)+big(0,1cdot dfrac23cdot
50+dfrac13cdot50big)+big(0,1cdot dfrac13cdot 50+dfrac13cdot
50big)) тыс.рублей.
Перегруппируем слагаемые и вынесем за скобки общие множители:
(0,1cdot 50 left(1+dfrac23+dfrac13right)+3cdot dfrac13cdot
50=0,1cdot 50cdot 2+50)
Для того, чтобы найти переплату по кредиту, необходимо из того, что он в итоге заплатил банку, отнять сумму кредита:
(big(0,1cdot 50cdot 2+50big)-50=10) тыс. рублей.
Таким образом, его переплата составила (10,000) рублей.
Заметим,
I. что каждая выплата состоит из двух частей:
первая часть — это сумма “набежавших” процентов на текущий долг (в первый год это (0,1cdot 50), во второй — (0,1cdot big(frac23cdot
50big)) и т.д.)
вторая часть всегда фиксирована — это та часть, на которую должен уменьшаться долг каждый год (в нашем примере это (frac13cdot 50)).
Действительно, когда клиент выплачивает “набежавшие” проценты, сумма его долга становится равна той, которая была до начисления процентов (например, в первый год становится равна (A)). А далее он еще вносит (frac 1n) часть от этого долга. И таким образом сумма долга уменьшается на (frac 1n) часть, что и подразумевает дифференцированная система платежей.
II. переплата по кредиту всегда равна сумме “набежавших” процентов на долг в первый год, во второй год, в третий год и т.д.
В нашем примере переплата как раз равна (0,1cdot 50+0,1cdot
frac23cdot 50+0,1cdot frac13cdot 50).
Формула для выплаты в (i)-ый год: [{Large{x_i=dfrac{r}{100}cdot dfrac{n-i+1}{n}A+dfrac1n A}}] где (n) – количество лет, на которое взят кредит, (A) – сумма кредита, (r%) – процентная ставка.
Задание
1
#1194
Уровень задания: Легче ЕГЭ
(16) августа на покупку телефона стоимостью (60,000) рублей в банке был взят кредит на (3) месяца. Условия пользования кредитом таковы:
– (10) числа каждого месяца, начиная с сентября, банк начисляет на остаток долга (10%);
– с (11) по (15) числа каждого месяца, начиная с сентября, клиент обязан внести в банк платеж;
– суммы платежей подбираются так, чтобы долг каждый месяц уменьшался на одну и ту же величину (так называемый дифференцированный платеж). Сколько рублей в итоге составит переплата по данному кредиту?
Т.к. кредит был взят на (3) месяца, то долг каждый месяц должен уменьшаться на (dfrac{1}{3}) часть.
Составим таблицу, все суммы будем вычислять в тыс.руб.: [begin{array}{|l|c|c|c|c|}
hline text{Месяц}&text{Долг до} & text{Долг после} & text{Сумма}& text{Долг после}\
& text{начисления }%& text{начисления }% &text{платежа}& text{платежа} \
hline &&&&\
1& dfrac{3}{3}cdot 60=60&60+0,1cdot 60 &0,1cdot 60+dfrac{1}{3}cdot 60& dfrac{2}{3}cdot 60\
&&&&\
hline &&&&\
2&dfrac{2}{3}cdot 60 & dfrac{2}{3}cdot 60+0,1cdot dfrac{2}{3}cdot 60&0,1cdot dfrac{2}{3}cdot 60+dfrac{1}{3}cdot 60&dfrac{1}{3}cdot 60 \
&&&&\
hline &&&&\
3&dfrac{1}{3}cdot 60 &dfrac{1}{3}cdot 60+0,1cdot dfrac{1}{3}cdot 60 &0,1cdot dfrac{1}{3}cdot 60+dfrac{1}{3}cdot 60&0 \
&&&&\
hline
end{array}]
Заметим, что каждый платеж состоит из (dfrac{1}{3}cdot 60) и из процентов, начисленных на остаток долга (т.е. все платежи – разные). Именно поэтому удобнее долг после начисления процентов записывать в виде (A+0,1cdot A), а не в виде (1,1cdot A).
Общая выплата по кредиту равна сумме всех платежей по кредиту, т.е.
(0,1cdot 60+dfrac{1}{3}cdot 60+0,1cdot dfrac{2}{3}cdot
60+dfrac{1}{3}cdot 60+0,1cdot dfrac{1}{3}cdot
60+dfrac{1}{3}cdot 60=60+0,1cdot 60cdot
(1+dfrac{2}{3}+dfrac{1}{3}))
Следовательно, переплата составит: (60+0,1cdot 60cdot
(1+frac{2}{3}+frac{1}{3})-60=0,1cdot 60cdot 2=12) тыс.руб.
Ответ:
(12,000) рублей.
Задание
2
#1196
Уровень задания: Равен ЕГЭ
(10) лет назад Григорий брал в банке кредит на (4) года, причем Григорий помнит, что выплачивал он кредит дифференцированными платежами и переплата по кредиту составила (32,5%) от кредита. Под какой годовой процент был взят тогда кредит?
Обозначим за (y) — годовой процент по кредиту, а за (A) руб. – сумму кредита. Составим таблицу: [begin{array}{|l|c|c|c|c|}
hline text{Год}&text{Долг до} & text{Долг после} & text{Сумма}& text{Долг после}\
& text{начисления }%& text{начисления }% &text{платежа}& text{платежа} \
hline &&&&\
1& A&A+dfrac{y}{100}cdot A &dfrac{y}{100}cdot A+dfrac{1}{4}cdot A& dfrac{3}{4}cdot A\
&&&&\
hline &&&&\
2&dfrac{3}{4}cdot A & dfrac{3}{4}cdot A+dfrac{y}{100}cdot dfrac{3}{4}cdot A&dfrac{y}{100}cdot dfrac{3}{4}cdot A+dfrac{1}{4}cdot A&dfrac{2}{4}cdot A \
&&&&\
hline &&&&\
3&dfrac{2}{4}cdot A &dfrac{2}{4}cdot A+dfrac{y}{100}cdot dfrac{2}{4}cdot A &dfrac{y}{100}cdot dfrac{2}{4}cdot A+dfrac{1}{4}cdot A&dfrac{1}{4}A \
&&&&\
hline &&&&\
4&dfrac{1}{4}cdot A &dfrac{1}{4}cdot A+dfrac{y}{100}cdot dfrac{1}{4}cdot A &dfrac{y}{100}cdot dfrac{1}{4}cdot A+dfrac{1}{4}cdot A&0 \
&&&&\
hline
end{array}]
Переплата по кредиту составит:
(dfrac{y}{100}cdot A +dfrac{y}{100}cdot dfrac{3}{4}cdot
A+dfrac{y}{100}cdot dfrac{2}{4}cdot A+dfrac{y}{100}cdot
dfrac{1}{4}cdot A=dfrac{y}{100}cdot Acdot
dfrac{5}{2}=dfrac{yA}{40})
Т.к. переплата в итоге составила (32,5%) от суммы кредита, то (dfrac{yA}{40}=0,325A Rightarrow y=13%)
Ответ:
(13 %).
Задание
3
#2890
Уровень задания: Равен ЕГЭ
Родион хочет взять кредит на некоторую сумму и выбирает между двумя банками. Первый банк предлагает кредит на 15 лет под (6%) годовых, второй – на 6 лет под (14%) годовых, причем в обоих банках дифференцированная система платежей. Определите, в какой банк выгоднее обратиться Родиону и сколько процентов от кредита составляет эта выгода.
Выгоднее будет предложение от того банка, по которому будет меньше переплата. Пусть (A) – сумма, которую Родион хочет взять в кредит. Заметим, что так как система выплат дифференцированная, то переплата по кредиту равна сумме “набежавших” на долг процентов на начало каждого года.
1) Первый банк предлагает кредит на 15 лет, следовательно, каждый год после платежа основной долг уменьшается на (frac1{15}) часть. То есть если в начале 1-ого года долг равен (A), то в начале 2-ого — (A-frac1{15}A=frac{14}{15}A), в начале 3-его — (frac{13}{15}A), в начале 4-ого — (frac{12}{15}A) и т.д. Значит, “набежавшие” в 1-ый год проценты — это (0,06cdot A), во 2-ой год — это (0,06cdot frac{14}{15}A), в 3-ий — это (0,06cdot
frac{13}{15}A) и т.д. Следовательно, переплата: [begin{aligned}&Per_1=0,06cdot A+0,06cdot frac{14}{15}A+dots+
0,06cdot frac2{15}A+0,06cdot frac1{15}A=\[2ex] &=0,06Acdot
left(1+frac{14}{15}+dots+frac2{15}+frac1{15}right)=0,06Acdot
8=0,48Aend{aligned}]
2) Второй банк предлагает кредит на 6 лет, следовательно, применяя те же рассуждения, получим: [Per_2=0,14Acdot left(1+frac56+frac46+frac36+frac26+frac16right)=
0,14Acdot 3,5=0,49A]
Следовательно, в первом банке переплата меньше, значит, обратиться в этот банк будет более выгодно.
Выгода равна (0,49A-0,48A=0,01A), значит, она составляет (1%) от суммы кредита.
Ответ: 1
Задание
4
#3147
Уровень задания: Равен ЕГЭ
Банк выдает кредит на следующих условиях:
— раз в год банк начисляет на текущий долг некоторый процент годовых;
— раз в год после начисления процентов клиент обязан внести платеж в счет погашения кредита, причем платежи вносятся таким образом, чтобы сумма долга уменьшалась каждый год на одну и ту же величину;
— отношение наибольшего платежа к наименьшему платежу равно (17:9).
Сколько процентов составит переплата от кредита, если взять такой кредит на 9 лет?
Из условия следует, что кредит должен выплачиваться дифференцированными платежами.
Пусть в банке взято (A) рублей в кредит. Если (r%) – процентная ставка в банке, то обозначим величину (0,01r=p). Тогда можно составить таблицу: [begin{array}{|l|c|c|c|}
hline text{Год} & text{Долг до начисления проц.} & text{Долг
после
начисления проц.} & text{Платеж}\
hline 1 & A & A+pA & pA+frac19A\
hline 2 & frac89A & frac89A+pcdot frac89A & pcdot
frac89A+frac19A\
hline … &… & … & …\
hline 9 & frac19A & frac19A+pcdot frac19A & pcdot
frac19A+frac19A\ hline end{array}]
Так как система выплат дифференцированная, то наибольший платеж – первый, а наименьший – последний. Следовательно, [dfrac{pA+frac19A}{pcdot frac19A+frac19A}=dfrac{17}9 quadLeftrightarrow
quad p=dfrac18] Тогда переплата по кредиту равна [pA+pcdot dfrac89A+pcdot dfrac79A+dots+pcdot dfrac19A=
pcdot Acdot left(1+dfrac89+dfrac79+dots+dfrac19right)=5pA] Следовательно, переплата составила от кредита [dfrac{5pA}{A}cdot 100%=500p%=62,5%.]
Ответ: 62,5
Задание
5
#2016
Уровень задания: Равен ЕГЭ
Павлу банком был предложен кредит на следующих условиях:
– сумма кредита не должна превышать (150,000) рублей;
– раз в месяц банк начисляет на остаток долга (22%);
– после начисления процентов Павел вносит в банк некоторый платеж, причем весь кредит должен быть выплачен тремя платежами так, чтобы сумма долга уменьшалась равномерно.
Помогите посчитать Павлу, сколько процентов от первоначального долга составит переплата по данному кредиту?
Т.к. долг должен уменьшаться равномерно, то схема выплаты кредита – дифференцированные платежи. Т.к. платежей должно быть (3), значит, кредит дается на (3) месяца, следовательно, долг каждый месяц должен уменьшаться на (dfrac{1}{3}) часть. Составим таблицу, обозначив за (A) – сумму кредита:
[begin{array}{|l|c|c|c|c|}
hline text{Месяц}&text{Долг до} & text{Долг после} & text{Сумма}& text{Долг после}\
& text{начисления }%& text{начисления }% &text{платежа}& text{платежа} \
hline &&&&\
1& A&A+0,22cdot A &0,22cdot A+dfrac{1}{3}cdot A& dfrac{2}{3}cdot A\
&&&&\
hline &&&&\
2&dfrac{2}{3}cdot A & dfrac{2}{3}cdot A+0,22cdot dfrac{2}{3}cdot A&0,22cdot dfrac{2}{3}cdot A+dfrac{1}{3}cdot A&dfrac{1}{3}cdot A \
&&&&\
hline &&&&\
3&dfrac{1}{3}cdot A &dfrac{1}{3}cdot A+0,22cdot dfrac{1}{3}cdot A &0,22cdot dfrac{1}{3}cdot A+dfrac{1}{3}cdot A&0 \
&&&&\
hline
end{array}]
Таким образом, переплата по кредиту составит:
(left(0,22cdot A+dfrac{1}{3}cdot A+0,22cdot dfrac{2}{3}cdot
A+dfrac{1}{3}cdot A+0,22cdot dfrac{1}{3}cdot
A+dfrac{1}{3}cdot Aright) — A=)
(=0,22cdot Acdot
left(1+dfrac{2}{3}+dfrac{1}{3}right)=0,44A)
Следовательно, процент, который составит переплата относительно первоначального долга, равен:
(dfrac{0,44A}{A}cdot 100% = 44 %).
Заметим, что информация о том, что сумма кредита не должна превышать (150,000) рублей, на самом деле не нужна для того, чтобы ответить на вопрос задачи.
Ответ:
(44 %).
Задание
6
#2929
Уровень задания: Равен ЕГЭ
15-го января планируется взять кредит в банке на 31 месяц. Условие его возврата таковы:
— 1-го числа каждого месяца долг возрастает на (3%) по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на 16-й месяц кредитования нужно сделать платеж в размере 29,6 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
(Задача от подписчиков)
Пусть (A) тыс. рублей – сумма, взятая в кредит. Фраза “долг должен быть на одну и ту же величину меньше” означает, что кредит выплачивается дифференцированными платежами. Каждый такой платеж состоит из двух частей: первая часть всегда одинаковая – это (dfrac1{31}) часть от (A); вторая часть состоит из процентов, “набежавших” на долг в этом месяце.
Составим таблицу:
[begin{array}{|l|c|c|c|c|}
hline text{Месяц} &text{Долг до} & text{Долг после} & text{Сумма} & text{Долг после}\
& text{начисления }%& text{начисления }% &text{платежа} & text{платежа} \
hline &&&&\
1& A&A+0,03cdot A &0,03cdot A+dfrac{1}{31}cdot A& dfrac{30}{31}cdot A\
&&&&\
hline &&&&\
2&dfrac{30}{31}cdot A & dfrac{30}{31}cdot A+0,03cdot dfrac{30}{31}cdot A
&0,03cdot dfrac{30}{31}cdot A+dfrac{1}{31}cdot A&dfrac{29}{31}cdot A \
&&&&\
hline &&&&\
3&dfrac{29}{31}cdot A &dfrac{29}{31}cdot A+0,03cdot
dfrac{29}{31}cdot A
&0,03cdot dfrac{29}{31}cdot A+dfrac{1}{31}cdot A&dfrac{28}{31}cdot A \
&&&&\
hline &&&&\
…&… &… &…&… \
&&&&\
hline &&&&\
16&dfrac{16}{31}cdot A &dfrac{16}{31}cdot A+0,03cdot dfrac{16}{31}cdot A
&0,03cdot dfrac{16}{31}cdot A+dfrac{1}{31}cdot A=29,6&dfrac{15}{31}cdot A \
&&&&\
hline &&&&\
…&… &… &…&… \
&&&&\
hline &&&&\
31&dfrac{1}{31}cdot A &dfrac{1}{31}cdot A+0,03cdot dfrac{1}{31}cdot A
&0,03cdot dfrac{1}{31}cdot A+dfrac{1}{31}cdot A&0 \
&&&&\
hline
end{array}]
Из полученного уравнения (0,03cdot dfrac{16}{31}cdot
A+dfrac{1}{31}cdot A=29,6) можно найти [A=620.]
Тогда за все месяцы кредитования будет выплачено банку:
(0,03cdot A+dfrac1{31}A+0,03cdot
dfrac{30}{31}A+dfrac1{31}A+dots+0,03cdot
dfrac1{31}A+dfrac1{31}A= 31cdot dfrac1{31}A+0,03cdot Acdot
left(1+dfrac{30}{31}+dfrac{29}{31}+dots+dfrac1{31}right)=)
(=A+0,03cdot Acdot dfrac{1+frac1{31}}2cdot
31=dfrac{37}{25}A=dfrac{37}{25}cdot 620=917,6) тыс. рублей.
Ответ: 917,6
Задание
7
#3871
Уровень задания: Равен ЕГЭ
В июле планируется взять кредит в банке на сумму (14) млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на (25%) по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплачивать часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась (24,5) млн. рублей?
Пусть (n) – число лет, на которое взят кредит. Так как годовой процент в банке равен (25%), то это значит, что каждый год долг увеличивается на четверть. Из условия следует, что система выплат дифференцированная, следовательно, каждый год долг должен уменьшаться на (frac 1n) часть, то есть на (frac{14}n) млн. рублей. Составим таблицу: [begin{array}{|l|c|c|c|}
hline text{Год} & text{Долг до начисления }% & text{Долг после
начисления
} % & text{Выплата}\
hline 1 & 14 & 14+frac14cdot 14 & frac{14}n+frac14cdot 14\
hline 2 & frac{n-1}ncdot 14 & frac{n-1}ncdot 14+frac14cdot
frac{n-1}ncdot 14 & frac{14}n + frac14cdot frac{n-1}ncdot
14\
hline … & … & … & …\
hline n & frac{14}n & frac{14}n+frac14cdot frac{14}n &
frac{14}n +frac14cdot frac{14}n \
hline end{array}] Таким образом, общая сумма выплат составляет [begin{aligned}
&dfrac{14}n+dfrac14cdot 14+dfrac{14}n + dfrac14cdot
dfrac{n-1}ncdot 14+dots+dfrac{14}n +dfrac14cdot
frac{14}n=\[1ex]
&=dfrac14cdot 14cdot left(1+dfrac{n-1}n+dots+dfrac1nright)+
ncdot dfrac{14}n=\[1ex]
&=dfrac14cdot 14cdot dfrac{1+frac1n}2cdot
n+14=dfrac74(n+1)+14 end{aligned}] (в скобках мы получили сумму арифметической прогрессии, где первый член равен (frac1n), (n)-ый равен (1), соответственно, количество членов равно (n))
Таким образом, так как общая сумма выплат равна по условию (24,5) млн. рублей, то получаем: [dfrac74(n+1)+14=24,5quadLeftrightarrowquad n=5]
Ответ: 5
Курс современной математики, которая преподается будущим выпускникам в старших классах, регулярно меняется. В настоящее время учащийся, который готовится к сдаче ЕГЭ по этому предмету, должен уметь правильно решать задачи на дифференцированные платежи. В аттестационном испытании профильного уровня задания, затрагивающие сферу финансовой математики, встречаются регулярно. Решение задач ЕГЭ по дифференцированным платежам за кредит предполагает наличие у школьника базовых навыков анализа числовых данных и осуществление практических расчетов по формулам.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимое умение. Базовый теоретический и практический материал по данной теме представлен в соответствующих разделах сайта таким образом, чтобы все учащиеся могли без особых затруднений справляться с задачами ЕГЭ на дифференцированные платежи.
Основные моменты
При выполнении заданий из области финансовой математики необходимо запомнить несколько важных нюансов:
- Общая выплата по кредиту состоит из тела кредита и процентов, которые начисляются банком. Эта важная формула лежит в основе практически всех задач по данной тематике.
- В процессе расчета дифференцированного платежа общая сумма первоначального кредита должна быть поделена на равные части. Как правило, их количество соответствует числу проводимых платежей.
- Если в условии задачи фигурируют словосочетания «равными частями», «долг уменьшается на одну и ту же величину» и т. п., вероятнее всего, речь идет именно о дифференцированном платеже.
Для того чтобы выпускник мог не только усвоить теоретический материал, но и отточить навык выполнения практических заданий, рекомендуем сделать соответствующие упражнения. Для каждого из них специалисты «Школково» прописали алгоритм решения и привели правильный ответ. Тренироваться в решении задач на дифференцированные платежи при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь в Москве или любом другом городе России.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
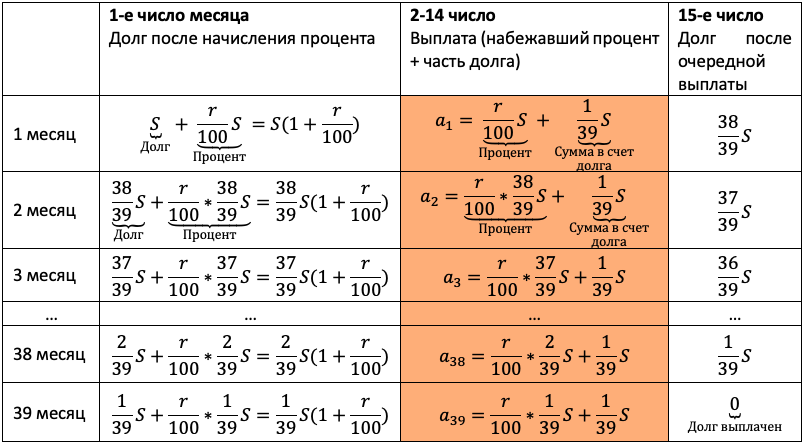
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
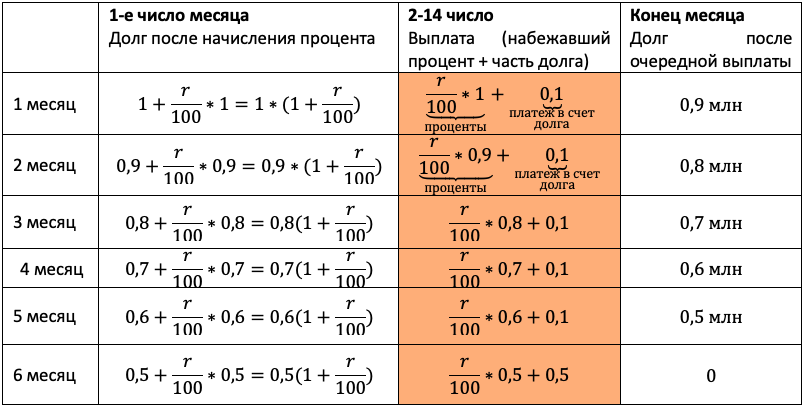
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
ЕГЭ Профиль №15. Задачи о вкладах и кредитовании
Скачать файл в формате pdf.
ЕГЭ Профиль №15. Задачи о вкладах и кредитовании
1В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 400 000 рублей.
Какое минимальное число рублей может составлять долг через год после взятия кредита?
1 000 000 рублей – сумма кредита. Через год долг возрастёт на 20%, то есть станет (1 000 000 cdot 1,2 = 1 200 000) рублей. Чтобы долг через год был наименьшим, платёж должен быть наибольшим, то есть 400 000 рублей. Следовательно, долг будет составлять минимальное число рублей, равное (1 200 000 — 400 000 = 800 000) рублей.
Ответ: 800 000 рублей.
2В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 300 000 рублей.
Какое минимальное число рублей может составлять долг через год после взятия кредита?
1 000 000 рублей – сумма кредита. Через год долг возрастёт на 10%, то есть станет ( 1000 000 cdot 1,1 = 1 100 000)рублей. Чтобы долг через год был наименьшим, платёж должен быть наибольшим, то есть 300000 рублей. Следовательно, долг будет составлять минимальное число рублей, равное (1 100 000 — 300 000 = 800 000) рублей.
Ответ: 800 000 рублей.
3В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 400 000 рублей.
Какое минимальное число рублей может составить последний платёж, если кредит нужно выплатить за минимальное количество лет?
Для того чтобы последний платёж был наименьшим, при условии, что кредит необходимо выплатить за минимальное количество лет, платежи должны быть наибольшими, то есть по 400 000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1,000,000 cdot 1,2 = 1,200,000) | 400 000 | 800 000 |
| 2 | (800,000 cdot 1,2 = 960,000) | 400 000 | 560 000 |
| 3 | (560,000 cdot 1,2 = 672,000) | 400 000 | 272 000 |
| 4 | (272,000 cdot 1,2 = 326,400) | 326 400 | 0 |
Таким образом, последний платёж составит 326 400 рублей.
Ответ: 326 400 рублей.
4В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 300 000 рублей.
Какое минимальное число рублей может составить последний платёж, если кредит нужно выплатить за минимальное количество лет?
Для того чтобы последний платёж был наименьшим, при условии, что кредит необходимо выплатить за минимальное количество лет, платежи должны быть наибольшими, то есть по 300 000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1,000,000 cdot 1,1 = 1,,100,000) | 300 000 | 800 000 |
| 2 | (800,000 cdot 1,1 = 880,000) | 300 000 | 580 000 |
| 3 | (580,000 cdot 1,1 = 638,000) | 300 000 | 338 000 |
| 4 | (338,,000 cdot 1,1 = 371,,800) | 300 000 | 71 800 |
| 5 | (71,,800 cdot 1,1 = 78,,980) | 78 980 | 0 |
Таким образом, последний платёж составит 78 980 рублей.
Ответ: 78 980 рублей.
5В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 300 000 рублей.
На какое минимальное число рублей сумма выплат может превышать размер кредита?
Чтобы сумма выплат превышала размер кредита на минимальное число рублей, ежегодные выплаты должны быть наибольшими, то есть по 300000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1000000 cdot 1,1 = 1100000) | 300 000 | 800 000 |
| 2 | (800000 cdot 1,1 = 880000) | 300 000 | 580 000 |
| 3 | (580000 cdot 1,1 = 638000) | 300 000 | 338 000 |
| 4 | (338000 cdot 1,1 = 371800) | 300 000 | 71 800 |
| 5 | (71800 cdot 1,1 = 78980) | 78 980 | 0 |
Таким образом, общая сумма выплат: (4 cdot 300000 + 78980 = 1278980) рублей, что на 278 980 рублей больше суммы кредита, равного 1 000 000 рублей.
Ответ: 278 980 рублей.
6В. В июле планируется взять кредит на сумму 1 000 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
- ежегодные выплаты не превышают 400 000 рублей.
На какое минимальное число рублей сумма выплат может превышать размер кредита?
Чтобы сумма выплат превышала размер кредита на минимальное число рублей, ежегодные выплаты должны быть наибольшими, то есть по 400 000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1000000 cdot 1,2 = 1200000) | 400 000 | 800 000 |
| 2 | (800000 cdot 1,2 = 960000) | 400 000 | 560 000 |
| 3 | (560000 cdot 1,2 = 672000) | 400 000 | 272 000 |
| 4 | (272000 cdot 1,2 = 326400) | 326 400 | 0 |
Таким образом, общая сумма выплат: (3 cdot 400000 + 326400 = 1526400) рублей, что на 526 400 рублей больше суммы кредита, равного 1 000 000 рублей.
Ответ: 526 400 рублей.
7В. Дмитрий мечтает о собственной квартире, которая стоит 3 млн руб. Дмитрий может купить её в кредит, при этом банк готов выдать эту сумму сразу, а погашать кредит Дмитрию придётся 20 лет равными ежемесячными платежами, при этом ему придётся выплатить сумму, на 180% превышающую исходную. Вместо этого Дмитрий может какое-то время снимать квартиру (стоимость аренды—15 тыс. руб. в месяц), откладывая каждый месяц на покупку квартиры сумму, которая останется от его возможного платежа банку (по первой схеме) после уплаты арендной платы за съёмную квартиру. За сколько лет в этом случае Дмитрий сможет накопить на квартиру, если считать, что её стоимость не изменится?
Так как Дмитрию придётся выплатить банку на 180% больше суммы кредита, то общая выплата составит 280% от суммы кредита: (3000000 cdot 2,8 = 8400000) рублей.
Так как срок кредита 20 лет (240 месяцев), то ежемесячные платежи составят: (frac{{8400000}}{{240}} = 35000) рублей.
Из 35 000 рублей откладывать удастся 20 000 рублей, так как стоимость аренды 15 000 рублей.
Учитывая, что стоимость квартиры не изменится то, откладывая по 20 000 рублей, Дмитрий накопит на квартиру за: (frac{{3000000}}{{20000}} = 150) месяцев, что составляет 12,5 лет.
Ответ: 12,5 лет.
8В. Сергей мечтает о собственной квартире, которая стоит 2 млн руб. Сергей может купить её в кредит, при этом банк готов выдать эту сумму сразу, а погашать кредит Сергею придётся 20 лет равными ежемесячными платежами, при этом ему придётся выплатить сумму, на 260% превышающую исходную. Вместо этого Сергей может какое-то время снимать квартиру (стоимость аренды—14 тыс. руб. в месяц), откладывая каждый месяц на покупку квартиры сумму, которая останется от его возможного платежа банку (по первой схеме) после уплаты арендной платы за съёмную квартиру. За сколько месяцев в этом случае Сергей сможет накопить на квартиру, если считать, что её стоимость не изменится?
Так как Сергею придётся выплатить банку на 260% больше суммы кредита, то общая выплата составит 360% от суммы кредита: (2000000 cdot 3,6 = 7200000) рублей.
Так как срок кредита 20 лет (240 месяцев), то ежемесячные платежи составят: (frac{{7200000}}{{240}} = 30000) рублей.
Из 30000 рублей откладывать удастся 16000 рублей, так как стоимость аренды 14000 рублей.
Учитывая, что стоимость квартиры не изменится то, откладывая по 16000 рублей, Сергей накопит на квартиру за: (frac{{2000000}}{{16000}} = 125) месяцев.
Ответ: 125.
9В. Ольга хочет взять в кредит 100 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет Ольга может взять кредит, чтобы ежегодные выплаты были не более 24 000 рублей?
Чтобы срок кредита был наименьшим необходимо, чтобы платежи были наибольшими, то есть по 24 000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (100000 cdot 1,1 = 110000) | 24 000 | 86 000 |
| 2 | (86000 cdot 1,1 = 94600) | 24 000 | 70 600 |
| 3 | (70600 cdot 1,1 = 77660) | 24 000 | 53 660 |
| 4 | (53660 cdot 1,1 = 59026) | 24 000 | 35 026 |
| 5 | (35026 cdot 1,1 = 38528,6) | 24 000 | 14 528,6 |
| 6 | (14528,6 cdot 1,1 = 15981,46) | 15 981,46 | 0 |
Таким образом, кредит будет выплачен за 6 лет.
Ответ: 6.
10В. Семен хочет взять в кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет Семен может взять кредит, чтобы ежегодные выплаты были не более 330 тысяч рублей?
Чтобы срок кредита был наименьшим необходимо, чтобы платежи были наибольшими, то есть по 330 000 рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1400000 cdot 1,1 = 1540000) | 330 000 | 1 210 000 |
| 2 | (1210000 cdot 1,1 = 1331000) | 330 000 | 1 001 000 |
| 3 | (1001000 cdot 1,1 = 1101100) | 330 000 | 771 100 |
| 4 | (771100 cdot 1,1 = 848210) | 330 000 | 518 210 |
| 5 | (518210 cdot 1,1 = 570031) | 330 000 | 240 031 |
| 6 | (240031 cdot 1,1 = 264034,1) | 264 034,1 | 0 |
Таким образом, кредит будет выплачен за 6 лет.
Ответ: 6 лет.
11В. 1 июня 2013 года Всеволод Ярославович взял в банке 900 000 рублей в кредит. Схема выплаты кредита следующая—1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т. е. увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платёж. На какое минимальное количество месяцев Всеволод Ярославович мог взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?
Чтобы срок кредита был наименьшим необходимо, чтобы платежи были наибольшими, то есть по 300 000 рублей.
| Месяц | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (900000 cdot 1,01 = 909000) | 300000 | 609000 |
| 2 | (609000 cdot 1,01 = 615090) | 300000 | 315090 |
| 3 | (315090 cdot 1,01 = 318240,9) | 300000 | 18240,9 |
| 4 | (18240,9 cdot 1,01 = 18423,309) | 18423,309 | 0 |
Таким образом, кредит будет выплачен за 4 месяца.
Ответ: 4.
12В. 1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т. е. увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич мог взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. руб.?
Чтобы срок кредита был наименьшим необходимо, чтобы платежи были наибольшими, то есть по 125 000 рублей.
| Месяц | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (1000000 cdot 1,01 = 1010000) | 125 000 | 885 000 |
| 2 | (885000 cdot 1,01 = 893850) | 125 000 | 768 850 |
| 3 | (768850 cdot 1,01 = 776538,5) | 125 000 | 651 538,5 |
| 4 | (651538,5 cdot 1,01 = 658053,89) | 125 000 | 533 053,9 |
| 5 | (533053,9 cdot 1,01 = 538384,4) | 125 000 | 413 384,4 |
| 6 | (413384,4 cdot 1,01 = 417518,3) | 125 000 | 292 518,3 |
| 7 | (292518,3 cdot 1,01 = 295443,5) | 125 000 | 170 443,5 |
| 8 | (170443,5 cdot 1,01 = 172147,9) | 125 000 | 47 147,9 |
| 9 | (47147,9 cdot 1,01 = 47619,4) | 47 619,4 | 0 |
Таким образом, кредит будет выплачен за 9 месяцев.
Ответ: 9.
13В. В начале года Алексей приобрёл ценные бумаги на сумму 9 тыс. рублей. В середине каждого года стоимость ценных бумаг возрастает на 2 тыс. рублей. В любой момент Алексей может продать ценные бумаги и положить вырученные деньги на банковский счёт. В середине каждого года сумма на счёте будет увеличиваться на 9%. В начале какого года после покупки Алексей должен продать ценные бумаги, чтобы через двадцать лет после покупки ценных бумаг сумма на банковском счёте была наибольшей?
Алексей должен продать ценные бумаги и положить деньги в банк, когда 9% от стоимости ценных бумаг будет больше 2000 рублей.
(A cdot frac{9}{{100}} > 2000;,,,,,,A > 22222frac{2}{9}) рублей.
Через 7 лет цена ценных бумаг будет: (9000 + 7 cdot 2000 = 23000 > 22222frac{2}{9}).
Поэтому, в начале 8-го года Алексей должен продать ценные бумаги и тогда через 20 лет сумма на банковском счёте будет наибольшей.
Ответ: 8.
14В. В начале года Виктор приобрёл ценные бумаги на сумму 7 тыс. рублей. В середине каждого года стоимость ценных бумаг возрастает на 1,5 тыс. рублей. В любой момент Виктор может продать ценные бумаги и положить вырученные деньги на банковский счёт. В середине каждого года сумма на счёте будет увеличиваться на 12%. В начале какого года после покупки Виктор должен продать ценные бумаги, чтобы через пятнадцать лет после покупки ценных бумаг сумма на банковском счёте была наибольшей?
Виктор должен продать ценные бумаги и положить деньги в банк, когда 12% от стоимости ценных бумаг будут больше 1500 рублей.
(A cdot frac{{12}}{{100}} > 1500;,,,,,,A > 12500) рублей.
Через 4 года цена ценных бумаг будет: (7000 + 4 cdot 1500 = 13000 > 12500).
Поэтому, в начале 5-го года Виктор должен продать ценные бумаги и тогда через 15 лет сумма на банковском счёте будет наибольшей.
Ответ: 5.
15В. Какой вклад выгоднее: первый—на 1 год под 16% годовых или второй—на 4 месяца (с автоматической пролонгацией каждые четыре месяца в течение года с момента открытия вклада) под 15% годовых? При расчётах считайте, что один месяц равен (frac{1}{{12}}) части года.
Пусть А – сумма вклада.
1 вклад: через год будет равен 1,16 А.
2 вклад: 15% годовых.
4 месяца это (frac{1}{3}) часть от года. Следовательно, за 4 месяца банк начислит 5%, а за год три раза по 5%:
(1,05 cdot 1,05 cdot 1,05A = 1,157625A.)
Так как (1,16A > 1,157625A), то первый вклад выгоднее.
Ответ: первый.
16В. Какой вклад выгоднее: первый—на 1 год под 15% годовых или второй—на 6 месяцев (с автоматической пролонгацией каждые шесть месяцев в течение года с момента открытия вклада) под 14% годовых? При расчётах считайте, что один месяц равен (frac{1}{{12}}) части года.
Пусть А – сумма вклада.
1 вклад: через год будет равен 1,15 А.
2 вклад: 14% годовых.
6 месяцев это полгода. Следовательно, за 6 месяцев банк начислит 7%, а за год два раза по 7%:
(1,07 cdot 1,07A = 1,1449A.)
Так как (1,15A > 1,1449A), то первый вклад выгоднее.
Ответ: первый.
17В. 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая—31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 14,5%), затем Дмитрий переводит в банк x рублей. Какой должна быть сумма x, чтобы Дмитрий выплатил долг двумя равными платежами (т.е. за два года)?
А = 4 290 000 рублей – сумма кредита.
Через год долг увеличивается на 14,5%, то есть в (frac{{100 + 14,5}}{{100}} = 1,145 = t) раз.
х – ежегодная выплата (в рублях).
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | х | ()(At — x) |
| 2 | (left( {At — x} right)t) | х | (left( {At — x} right)t — x) |
Так как долг выплачен за 2 года, то остаток в конце второго года равен нулю.
(left( {At — x} right)t — x = 0,,,,,,, Leftrightarrow ,,,,,,A,{t^2} — x,t — x = 0,,,,,, Leftrightarrow ,,,,,,x = frac{{A,{t^2}}}{{t + 1}})
(x = frac{{4290000 cdot {{1,145}^2}}}{{1,145 + 1}} = frac{{4290000 cdot {{1,145}^2}}}{{2,145}} = 2000 cdot 1145 cdot 1,145 = 2,622,050) рублей.
Ответ: 2 622 050 рублей.
18В. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая—31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (т. е. за четыре года)?
А = 6 902 000 рублей – сумма кредита.
Через год долг увеличивается на 12,5%, т.е. в (frac{{100 + 12,5}}{{100}} = 1,125 = frac{9}{8} = t) раз.
х – ежегодная выплата (в рублях).
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Так как долг выплачен за 4 года, то остаток в конце четвертого года равен нулю.
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(x = frac{{A{t^4}}}{{{t^3} + {t^2} + t + 1}} = frac{{6902000 cdot {{left( {frac{9}{8}} right)}^4}}}{{{{left( {frac{9}{8}} right)}^3} + {{left( {frac{9}{8}} right)}^2} + frac{9}{8} + 1}} = frac{{6902000 cdot {9^4}}}{{8 cdot left( {{9^3} + {9^2} cdot 8 + 9 cdot {8^2} + {8^3}} right)}} = )
( = frac{{862750 cdot 6561}}{{2465}} = 350 cdot 6561 = 2296350) рублей.
Ответ: 2296350 рублей.
19В. 31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (т. е. за четыре года)?
А – сумма кредита (в рублях)
Через год долг увеличивается на 12,5%, т.е. в (frac{{100 + 12,5}}{{100}} = 1,125 = frac{9}{8} = t) раз.
х = 2 132 325 рублей – ежегодная выплата.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left| {} right|} right)} right))(left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Так как долг выплачен за 4 года, то остаток в конце четвёртого года равен нулю.
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(A = frac{{xleft( {{t^3} + {t^2} + t + 1} right)}}{{{t^4}}} = frac{{2132325 cdot left( {frac{{{9^3}}}{{{8^3}}} + frac{{{9^2}}}{{{8^2}}} + frac{9}{8} + 1} right)}}{{frac{{{9^4}}}{{{8^4}}}}} = frac{{2132325 cdot 8 cdot left( {{9^3} + {9^2} cdot 8 + 9 cdot {8^2} + {8^3}} right)}}{{9 cdot 9 cdot 9 cdot 9}} = )( = 325 cdot 8 cdot 2465 = 6409000) рублей.
Ответ: 6 409 000 рублей.
20В. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
A = 9930000 рублей – сумма кредита. Через год долг увеличивается на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – ежегодная выплата (в рублях).
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Так как долг выплачен за 3 года, то остаток в конце третьего года равен нулю.
(left( {left( {At — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,,A{t^3} — x{t^2} — xt — x = 0,,,,A,{t^3} = xleft( {{t^2} + t + 1} right))
(x = frac{{A{t^3}}}{{{t^2} + t + 1}} = frac{{9930000 cdot {{1,1}^3}}}{{{{1,1}^2} + 1,1 + 1}} = frac{{9930 cdot 11 cdot 11 cdot 11}}{{3,31}} = = 3000 cdot 1331 = 3993000) рублей.
Ответ: 3 993 000 рублей.
21В. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (т. е. за четыре года)?
A = 8 052 000 рублей – сумма кредита. Через год долг увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2 = t).
x – ежегодная выплата (в рублях).
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Так как долг выплачен за 4 года, то остаток в конце четвёртого года равен нулю
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(x = frac{{A{t^4}}}{{{t^3} + {t^2} + t + 1}} = frac{{8052000 cdot {{1,2}^4}}}{{{{1,2}^3} + {{1,2}^2} + 1,2 + 1}} = frac{{805,2 cdot {{12}^4}}}{{5,368}} = = 150 cdot 144 cdot 144 = 3110400) рублей.
Ответ: 3 110 400 рублей.
22В. В июле планируется взять кредит на сумму 9 282 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (т. е. за четыре года)?
A = 9282000 рублей – сумма кредита. Через год долг увеличивается на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – ежегодная выплата (в рублях).
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Так как долг выплачен за 4 года, то остаток в конце четвёртого года равен нулю.
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(x = frac{{A{t^4}}}{{{t^3} + {t^2} + t + 1}} = frac{{9,282,000 cdot {{1,1}^4}}}{{{{1,1}^3} + {{1,1}^2} + 1,1 + 1}} = frac{{928,2 cdot {{11}^4}}}{{4,641}} = 200 cdot 121 cdot 121 = 2,928,200) рублей.
Ответ: 2 928 200 рублей.
23В. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 399 300 рублей.
Сколько рублей было взято в банке, если известно, что кредит был полностью погашен тремя равными платежами (т. е. за три года)?
A = сумма кредита (в рублях). Через год долг увеличивается на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x = 399 300 рублей – ежегодная выплата.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Так как долг выплачен за 3 года, то остаток в конце третьего года равен нулю
(left( {left( {At — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,,A{t^3} — x{t^2} — xt — x = 0,,,,A,{t^3} = xleft( {{t^2} + t + 1} right))
(A = frac{{xleft( {{t^2} + t + 1} right)}}{{{t_3}}} = frac{{399300 cdot left( {{{1,1}^2} + 1,1 + 1} right)}}{{{{1,1}^3}}} = frac{{399300 cdot 3,31}}{{1,331}} = 3000 cdot 331 = 993000) рублей.
Ответ: 993 000 рублей.
24В. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 207 360 рублей.
Сколько рублей было взято в банке, если известно, что кредит был полностью погашен четырьмя равными платежами (т.е. за четыре года)?
A = сумма кредита (в рублях). Через год долг увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2 = t) раз.
x = 207 360 рублей – ежегодная выплата.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Так как долг выплачен за 4 года, то остаток в конце четвёртого года равен нулю
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(A = frac{{xleft( {{t^3} + {t^2} + t + 1} right)}}{{{t^4}}} = frac{{207360 cdot left( {{{1,2}^3} + {{1,2}^2} + 1,2 + 1} right)}}{{{{1,2}^4}}} = frac{{207360 cdot 5,368}}{{2,0736}} = 100000 cdot 5,368 = 536800) рублей.
Ответ: 536 800 рублей.
25В. 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
A = 7007000 рублей – сумма кредита. Через год долг увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2 = t) раз.
x – ежегодная выплата на 3 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Остаток в конце третьего года равен нулю.
(left( {left( {At — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,,A{t^3} — x{t^2} — xt — x = 0,,,,A,{t^3} = xleft( {{t^2} + t + 1} right))
(x = frac{{A{t^3}}}{{{t^2} + t + 1}} = frac{{7007000 cdot {{1,2}^3}}}{{{{1,2}^2} + 1,2 + 1}} = 3326400) рублей.
Следовательно, выплаты за 3 года составили: (3x = 3 cdot 3326400 = 9,,979,,200) рублей.
y – ежегодная выплата на 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | y | (At — y) |
| 2 | (left( {At — y} right)t) | y | (left( {At — y} right)t — y) |
Остаток в конце второго года равен нулю.
(left( {At — y} right)t — y = 0,,,,,, Leftrightarrow ,,,,,A{t^2} — yt — y = 0,,,,, Leftrightarrow ,,,,,A{t^2} = yleft( {t + 1} right))
(y = frac{{A{t^2}}}{{t + 1}} = frac{{7007000 cdot {{1,2}^2}}}{{1,2 + 1}} = 4586400) рублей.
Следовательно, выплаты за 2 года составили: (2y = 2 cdot 4586400 = 9,,172,,800) рублей.
Таким образом, разница составит: (3x — 2y = 9,,979,,200 — 9,,172,,800 = 806,,400) рублей.
Ответ: 806 400 рублей.
26В. 31 декабря 2014 года Савелий взял в банке 7 378 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 12,5%), затем Савелий переводит в банк платёж. Весь долг Савелий выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
A = 7378000 рублей – сумма кредита. Через год долг увеличивается на 12,5%, то есть в (frac{{100 + 12,5}}{{100}} = 1,125 = frac{9}{8} = t) раз.
x – ежегодная выплата на 3 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Остаток в конце третьего года равен нулю.
(left( {left( {At — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,,A{t^3} — x{t^2} — xt — x = 0,,,,A,{t^3} = xleft( {{t^2} + t + 1} right))
(x = frac{{A{t^3}}}{{{t^2} + t + 1}} = frac{{7378000 cdot {{left( {frac{9}{8}} right)}^3}}}{{{{left( {frac{9}{8}} right)}^2} + frac{9}{8} + 1}} = 3098250) рублей.
Следовательно, выплаты за 3 года составили: (3x = 3 cdot 3098250 = 9,,294,,750) рублей.
y – ежегодная выплата на 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | y | (At — y) |
| 2 | (left( {At — y} right)t) | y | (left( {At — y} right)t — y) |
Остаток в конце второго года равен нулю.
(left( {At — y} right)t — y = 0,,,,,, Leftrightarrow ,,,,,A{t^2} — yt — y = 0,,,,, Leftrightarrow ,,,,,A{t^2} = yleft( {t + 1} right))
(y = frac{{A{t^2}}}{{t + 1}} = frac{{7378000 cdot {{left( {frac{9}{8}} right)}^2}}}{{frac{9}{8} + 1}} = 4394250) рублей.
Следовательно, выплаты за 2 года составили: (2y = 2 cdot 4394250 = 8,,788,,500) рублей.
Таким образом, разница составит: (3x — 2y = 9,,294,,750 — 8,,788,,500 = 506,,250) рублей.
Ответ: 506 250 рублей.
27В. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей меньше придётся отдать в случае, если кредит будет полностью погашен двумя равными платежами (т. е. за два года), по сравнению со случаем, если кредит будет полностью погашен четырьмя равными платежами (т. е. за четыре года)?
A = 8052000 рублей – сумма кредита. Через год долг увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2 = t)раз.
x – ежегодный платёж на 4 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Остаток в конце четвёртого года равен нулю.
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(x = frac{{A{t^4}}}{{{t^3} + {t^2} + t + 1}} = frac{{8052000 cdot {{1,2}^4}}}{{{{1,2}^3} + {{1,2}^2} + 1,2 + 1}} = 3110400) рублей.
Следовательно, выплаты за 4 года составили: (4x = 4 cdot 3110400 = 12,,441,,600) рублей.
y – ежегодный платёж на 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | y | (At — y) |
| 2 | (left( {At — y} right)t) | y | (left( {At — y} right)t — y) |
Остаток в конце второго года равен нулю.
(left( {At — y} right)t — y = 0,,,,,, Leftrightarrow ,,,,,A{t^2} — yt — y = 0,,,,, Leftrightarrow ,,,,,A{t^2} = yleft( {t + 1} right))
(y = frac{{A{t^2}}}{{t + 1}} = frac{{8052000 cdot {{1,2}^2}}}{{1,2 + 1}} = 5270400) рублей.
Следовательно, выплаты за 2 года составили: (2y = 2 cdot 5270400 = 10,,540,,800) рублей.
Таким образом, разница составит: (4x — 2y = 12,,441,,600 — 10,,540,,800 = 1,,900,,800) рублей.
Ответ: 1 900 800 рублей.
28В. В июле планируется взять кредит на сумму 9 282 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей меньше придётся отдать в случае, если кредит будет полностью погашен двумя равными платежами (т. е. за два года), по сравнению со случаем, если кредит будет полностью погашен четырьмя равными платежами (т. е. за четыре года)?
A = 9282000 рублей – сумма кредита. Через год долг увеличивается на 10%, то есть (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – ежегодный платёж на 4 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right) cdot t — x} right)t) | x | (left( {left( {At — x} right) cdot t — x} right)t — x) |
| 4 | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t) | x | (left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x) |
Остаток в конце четвёртого года равен нулю.
(left( {left( {left( {At — x} right)t — x} right)t — x} right)t — x = 0,,,,, Leftrightarrow ,,,,A,{t^4} — x,{t^3} — x,{t^2} — x,t — x = 0,,,, Leftrightarrow ,,,A{t^4} = xleft( {{t^3} + {t^2} + t + 1} right))
(x = frac{{A{t^4}}}{{{t^3} + {t^2} + t + 1}} = frac{{9282000 cdot {{1,1}^4}}}{{{{1,1}^3} + {{1,1}^2} + 1,1 + 1}} = 2928200) рублей.
Следовательно, выплаты за 4 года составили: (4x = 4 cdot 2928200 = 11,,712,,800) рублей.
y – ежегодный платёж на 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | y | (At — y) |
| 2 | (left( {At — y} right)t) | y | (left( {At — y} right)t — y) |
Остаток в конце второго года равен нулю.
(left( {At — y} right)t — y = 0,,,,,, Leftrightarrow ,,,,,A{t^2} — yt — y = 0,,,,, Leftrightarrow ,,,,,A{t^2} = yleft( {t + 1} right))
(y = frac{{A{t^2}}}{{t + 1}} = frac{{9282000 cdot {{1,1}^2}}}{{1,1 + 1}} = 5348200) рублей.
Следовательно, выплаты за 2 года составили: (2y = 2 cdot 5348200 = 10,,696,,400) рублей.
Таким образом, разница составит: (4x — 2y = 11,,712,,800 — 10,,696,,400 = 1,,016,,400) рублей.
Ответ: 1 016 400 рублей.
29В. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга.
Известно, что кредит был полностью погашен за два года, причём в первый год было переведено 75 000 рублей, а во второй год—46 000 рублей. Найдите число r.
A = 100 000 рублей – сумма кредита. Через год долг увеличивается на r %, то есть в (frac{{100 + r}}{{100}} = t) раз.
Платежи: a = 75 000 рублей в 1–й год; b = 46 000 рублей во 2–й год.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | a | (At — a) |
| 2 | (left( {At — a} right)t) | b | (left( {At — a} right)t — b) |
Так как долг выплачен за 2 года, то остаток в конце второго года равен нулю.
(left( {At — a} right)t — b = 0,,,,, Leftrightarrow ,,,,,100000{t^2} — 75000t — 46000 = 0,,,, Leftrightarrow ,,,,100{t^2} — 75t — 46 = 0;)
(D = 5625 + 18400 = 24025 = {155^2};,,,,,{t_1} = frac{{23}}{{20}};,,,,,,,,,{t_2} = — frac{2}{5}) не подходит.
(frac{{100 + r}}{{100}} = frac{{23}}{{20}};,,,,,,100 + r = 115;,,,,,,r = 15)%.
Ответ: 15.
30В. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга.
Известно, что кредит был полностью погашен за два года, причём в первый год было переведено 68 000 рублей, а во второй год—59 000 рублей. Найдите число r.
А = 100 000 рублей – сумма кредита. Через год долг увеличивается на r%, то есть в (frac{{100 + r}}{{100}} = t) раз.
Платежи: a = 68 000 рублей в 1–й год; b = 59 000 рублей во 2–й год.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | a | (At — a) |
| 2 | (left( {At — a} right)t) | b | (left( {At — a} right)t — b) |
Так как долг выплачен за 2 года, то остаток в конце 2–го года равен нулю.
(left( {At — a} right)t — b = 0,,,,,, Leftrightarrow ,,,,,,100000{t^2} — 68000t — 59000 = 0,,,,,, Leftrightarrow ,,,,,100{t^2} — 68t — 59 = 0;)
(D = {68^2} + 400 cdot 59 = 28224;,,,,,,sqrt D = 168;,,,,,,{t_1} = frac{{68 + 168}}{{200}} = frac{{118}}{{100}};,,,,,,,{t_2} = frac{{68 — 168}}{{200}} = — frac{1}{2}.)
({t_2} = — frac{1}{2}) не подходит. Следовательно: (frac{{100 + r}}{{100}} = frac{{118}}{{100}};,,,,,,,,,,r = 18)%.
Ответ: 18.
31В. Дмитрий взял кредит в банке на сумму 270 200 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 процентов оставшуюся сумму долга, а затем Дмитрий переводит в банк свой очередной платеж. Известно, что Дмитрий погасил кредит за три года, причем каждый его следующий платеж был ровно втрое больше предыдущего. Какую сумму Дмитрий заплатил в первый раз? Ответ дайте в рублях.
А = 270 200 рублей – сумма кредита.
Через год долг увеличился на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – первый платёж (в рублях); 3x – второй; 9x – третий.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | 3x | (left( {At — x} right)t — 3x) |
| 3 | (left( {left( {At — x} right)t — 3x} right)t) | 9x | (left( {left( {At — x} right)t — 3x} right)t — 9x) |
Так как долг выплачен за 3 года, то остаток в конце третьего года равен нулю.
(left( {left( {At — x} right)t — 3x} right)t — 9x = 0,,,,, Leftrightarrow ,,,,,A{t^3} — x{t^2} — 3xt — 9x = 0,,,,, Leftrightarrow ,,,,,A{t^3} = xleft( {{t^2} + 3t + 9} right))
(x = frac{{A{t^3}}}{{{t^2} + 3t + 9}} = frac{{270200 cdot {{1,1}^3}}}{{{{1,1}^2} + 3 cdot 1,1 + 9}} = frac{{270200 cdot 1,331}}{{13,51}} = 20000 cdot 1,331 = 26620) рублей.
Следовательно, первый платёж составил 26 620 рублей.
Ответ: 26 620 рублей.
32В. Георгий взял кредит в банке на сумму 804 000 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 процентов оставшуюся сумму долга, а затем Георгий переводит в банк свой очередной платеж. Известно, что Георгий погасил кредит за три года, причем каждый его следующий платеж был ровно вдвое меньше предыдущего. Какую сумму Георгий заплатил в третий раз? Ответ дайте в рублях.
А = 804 000 рублей – сумма кредита
Через год долг увеличился на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
4x – первый платёж (в рублях); 2x – второй; x – третий.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | 4x | (At — 4x) |
| 2 | (left( {At — 4x} right)t) | 2x | (left( {At — 4x} right)t — 2x) |
| 3 | (left( {left( {At — 4x} right)t — 2x} right)t) | x | (left( {left( {At — 4x} right)t — 2x} right)t — x) |
Так как долг выплачен за 3 года, то остаток в конце третьего года равен нулю.
(left( {left( {At — 4x} right)t — 2x} right)t — x = 0;,,,,,,,,,,A{t^3} — 4x{t^2} — 2xt — x = 0)
(x = frac{{A{t^3}}}{{4{t^2} + 2t + 1}} = frac{{804000 cdot {{1,1}^3}}}{{4 cdot {{1,1}^2} + 2 cdot 1,1 + 1}} = frac{{804000 cdot 1,331}}{{8,04}} = 100 cdot 1331 = 133100) рублей.
Следовательно, третий платёж составил 133 100 рублей.
Ответ: 133 100 рублей.
33В. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредит банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 156 060 рублей больше суммы взятого кредита.
А = сумма кредита (в рублях). Через год долг увеличился на 30%, то есть в (frac{{100 + 30}}{{100}} = 1,3 = t) раз.
x – ежегодный платёж (в рублях)
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Общая сумма выплат равна 3x, а остаток в конце третьего года равен нулю.
(left{ {begin{array}{*{20}{c}} {3x — A = 156060;} \ {left( {left( {At — x} right)t — x} right)t — x = 0.} end{array}} right.)
Из второго уравнения: (A{t^3} — x{t^2} — xt — x = 0,,,,, Leftrightarrow ,,,,A cdot {1,3^3} = x cdot {1,3^2} + 1,3x + x,,,,, Leftrightarrow ,,,,,A = frac{{3,99x}}{{2,197}})
Подставим в первое уравнение:
(3x — frac{{3,99x}}{{2,197}} = 156060,,,,, Leftrightarrow ,,,,x = frac{{156060 cdot 2197}}{{2601}})
Тогда: (A = frac{{3990 cdot 156060 cdot 2197}}{{2197 cdot 2601}} = 3990 cdot 60 = 239400) рублей.
Ответ: 239 400 рублей.
34В. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредита банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78 030 рублей больше суммы взятого кредита.
А = сумма кредита (в рублях). Через год долг увеличился на 30%, то есть в (frac{{100 + 30}}{{100}} = 1,3 = t) раз.
x – ежегодный платёж (в рублях)
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | x | (At — x) |
| 2 | (left( {At — x} right)t) | x | (left( {At — x} right)t — x) |
| 3 | (left( {left( {At — x} right)t — x} right)t) | x | (left( {left( {At — x} right)t — x} right)t — x) |
Общая сума выплат равна 3x, а остаток в конце третьего года равен нулю.
(left{ {begin{array}{*{20}{c}} {3x — A = 78030;} \ {left( {left( {At — x} right)t — x} right)t — x = 0.} end{array}} right.)
Из второго уравнения: (A{t^3} — x{t^2} — xt — x = 0,,,,, Leftrightarrow ,,,,A cdot {1,3^3} = x cdot {1,3^2} + 1,3x + x,,,,, Leftrightarrow ,,,,,A = frac{{3,99x}}{{2,197}})
Подставим в первое уравнение:
(3x — frac{{3,99x}}{{2,197}} = 78030,,,,, Leftrightarrow ,,,,x = frac{{78030 cdot 2197}}{{2601}})
Тогда: (A = frac{{3990 cdot 78030 cdot 2197}}{{2197 cdot 2601}} = 3990 cdot 30 = 119700) рублей.
Ответ: 119 700 рублей.
35В. Светлана Михайловна взяла кредит в банке на 4 года на сумму 4 420 000 рублей. Условия возврата кредита таковы: в конце каждого года банк увеличивает текущую сумму долга на 10 %. Светлана Михайловна хочет выплатить весь долг двумя равными платежами — в конце второго и четвертого годов. При этом платежи в каждом случае выплачиваются после начисления процентов. Сколько рублей составит каждый из этих платежей?
А = 4420000 рублей – сумма кредита, которая через год увеличивается на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – платежи в конце второго и четвёртого годов.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | 0 | (At) |
| 2 | (A{t^2}) | x | (A{t^2} — x) |
| 3 | (left( {A{t^2} — x} right)t) | 0 | (left( {A{t^2} — x} right)t) |
| 4 | (left( {A{t^2} — x} right){t^2}) | x | (left( {A{t^2} — x} right){t^2} — x) |
Остаток в конце четвёртого года равен нулю.
(left( {A{t^2} — x} right){t^2} — x = 0,,,,, Leftrightarrow ,,,,A{t^4} — x,{t^2} — x = 0,,,,, Leftrightarrow ,,,,,A,{t^4} = xleft( {{t^2} + 1} right))
(x = frac{{A{t^4}}}{{{t^2} + 1}} = frac{{4420000 cdot {{1,1}^4}}}{{{{1,1}^2} + 1}} = frac{{442 cdot {{11}^4}}}{{2,21}} = 200 cdot 121 cdot 121 = 2928200) рублей.
Следовательно, каждый из платежей составляет по 2 928 200 рублей.
Ответ: 2 928 200 рублей.
36В. Агата Артуровна взяла кредит в банке на 4 года на сумму 7 320 000 рублей. Условия возврата кредита таковы: в конце каждого года банк увеличивает текущую сумму долга на 20%. Агата Артуровна хочет выплатить весь долг двумя равными платежами — в конце второго и четвертого годов. При этом платежи в каждом случае выплачиваются после начисления процентов. Сколько рублей составит каждый из этих платежей?
А = 7 320 000 рулей – сумма кредита, которая через год увеличивается на 20% , то есть в (frac{{100 + 20}}{{100}} = 1,2 = )t раз
x – платежи в конце второго и четвёртого годов.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (At) | 0 | (At) |
| 2 | (A{t^2}) | x | (A{t^2} — x) |
| 3 | (left( {A{t^2} — x} right)t) | 0 | (left( {A{t^2} — x} right)t) |
| 4 | (left( {A{t^2} — x} right){t^2}) | x | (left( {A{t^2} — x} right){t^2} — x) |
Остаток в конце четвёртого года равен нулю.
(left( {A{t^2} — x} right){t^2} — x = 0,,,,, Leftrightarrow ,,,,A{t^4} — x,{t^2} — x = 0,,,,, Leftrightarrow ,,,,,A,{t^4} = xleft( {{t^2} + 1} right))
(x = frac{{A{t^4}}}{{{t^2} + 1}} = frac{{7320000 cdot {{1,2}^4}}}{{{{1,2}^2} + 1}} = frac{{732 cdot {{12}^4}}}{{2,44}} = 300 cdot 144 cdot 144 = 6,220,800) рублей.
Следовательно, каждый из платежей составляют по 6 220 800 рублей.
Ответ: 6 220 800 рублей.
37В. Банк предоставляет кредит сроком на 10 лет под 19% годовых на следующих условиях: ежегодно заёмщик возвращает банку 19% от непогашенной части кредита и (frac{1}{{10}}) суммы кредита. Так, в первый год заёмщик выплачивает (frac{1}{{10}}) суммы кредита и 19% от всей суммы кредита, во второй год заёмщик выплачивает (frac{1}{{10}}) суммы кредита и 19% от (frac{9}{{10}}) суммы кредита и т. д. Во сколько раз сумма, которую выплатит банку заёмщик, будет больше суммы кредита, если заёмщик не воспользуется досрочным погашением кредита?
А – сумма кредита; срок 10 лет.
Каждый год банк начисляет 19% на остаток, а заёмщик выплачивает эти проценты и десятую часть от суммы кредита, то есть (frac{A}{{10}}). Таким образом, через 1 год остаток долга будет (frac{{9A}}{{10}}), через 2 года (frac{{8A}}{{10}}), через 3 года (frac{{7A}}{{10}}) и так далее.
| Год | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{{19}}{{100}}) | (A — frac{A}{{10}} = frac{{9A}}{{10}})() |
| 2 | (frac{{9A}}{{10}} cdot frac{{19}}{{100}}) | (frac{{9A}}{{10}} — frac{A}{{10}} = frac{{8A}}{{10}})()() |
| 3 | (frac{{8A}}{{10}} cdot frac{{19}}{{100}}) | (frac{{8A}}{{10}} — frac{A}{{10}} = frac{{7A}}{{10}}) |
| … | … | … |
| 10 | (frac{A}{{10}} cdot frac{{19}}{{100}}) | (frac{A}{{10}} — frac{A}{{10}} = 0) |
Общая сумма выплат за 10 лет равна сумме кредита А и начисленным процентам:
(A + frac{{10A}}{{10}} cdot frac{{19}}{{100}} + frac{{9A}}{{10}} cdot frac{{19}}{{100}} + frac{{8A}}{{10}} cdot frac{{19}}{{100}} + … + frac{A}{{10}} cdot frac{{19}}{{100}} = A + frac{{19}}{{100}} cdot frac{A}{{10}} cdot left( {10 + 9 + 8 + … + 1} right) = )
( = A + frac{{19}}{{100}} cdot frac{A}{{10}} cdot frac{{1 + 10}}{2} cdot 10 = A + frac{{209A}}{{200}} = frac{{409A}}{{200}} = 2,045A)
Таким образом, сумма выплаченная банку заёмщиком в 2,045 раз больше суммы кредита.
Ответ: 2,045.
38В. Банк предоставляет ипотечный кредит сроком на 20 лет под 12% годовых на следующих условиях: ежегодно заёмщик возвращает банку 12% от непогашенной части кредита и (frac{1}{{20}}) суммы кредита. Так, в первый год заёмщик выплачивает (frac{1}{{20}}) суммы кредита и 12% от всей суммы кредита, во второй год заёмщик выплачивает (frac{1}{{20}}) суммы кредита и 12% от (frac{{19}}{{20}}) суммы кредита и т. д. Во сколько раз сумма, которую выплатит банку заёмщик, будет больше суммы кредита, если заёмщик не воспользуется досрочным погашением кредита?
А – сумма кредита; срок 20 лет.
Каждый год банк начисляет 12% на остаток, а заёмщик выплачивает эти проценты и двадцатую часть от суммы кредита, то есть (frac{A}{{20}}).Таким образом, через 1 год остаток долга будет (frac{{19A}}{{20}}), через 2 года (frac{{18A}}{{20}}), через 3 года (frac{{17A}}{{20}}) и так далее.
| Год | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{{12}}{{100}}) | (A — frac{A}{{20}} = frac{{19A}}{{20}})() |
| 2 | (frac{{19A}}{{20}} cdot frac{{12}}{{100}}) | (frac{{19A}}{{20}} — frac{A}{{20}} = frac{{18A}}{{20}})()() |
| 3 | (frac{{18A}}{{20}} cdot frac{{12}}{{100}}) | (frac{{18A}}{{20}} — frac{A}{{20}} = frac{{17A}}{{20}}) |
| … | … | … |
| 20 | (frac{A}{{20}} cdot frac{{12}}{{100}}) | (frac{A}{{20}} — frac{A}{{20}} = 0) |
Общая сумма выплат за 20 лет равна сумме кредите А и сумме начисленных процентов.
(A + frac{{20A}}{{20}} cdot frac{{12}}{{100}} + frac{{19A}}{{20}} cdot frac{{12}}{{100}} + frac{{18A}}{{20}} cdot frac{{12}}{{100}} + … + frac{A}{{20}} cdot frac{{12}}{{100}} = A + frac{A}{{20}} cdot frac{{12}}{{100}} cdot left( {20 + 19 + 18 + … + 1} right) = )
( = A + frac{A}{{20}} cdot frac{{12}}{{100}} cdot frac{{1 + 20}}{2} cdot 20 = A + frac{{252A}}{{200}} = frac{{452A}}{{200}} = 2,26A)
Таким образом, сумма выплаченная банку заёмщиком в 2,26 раз больше суммы кредита.
Ответ: 2,26.
39В. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 30 млн рублей. Ответ дайте в млн рублей.
А = 10 млн. рублей – первоначальный вклад.
x – сумма на которую пополняется вклад в начале третьего и четвёртого годов (целое число млн. руб.).
В конце каждого года вклад увеличивается на 10%, то есть увеличивается в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (At) |
| 2 | (At) | (A{t^2}) |
| 3 | (A{t^2} + x) | (left( {A{t^2} + x} right)t) |
| 4 | (left( {A{t^2} + x} right)t + x) | (left( {left( {A{t^2} + x} right)t + x} right)t) |
По условию задачи вклад в конце четвёртого года должен быть не меньше 30 млн. руб.
(left( {left( {A{t^2} + x} right)t + x} right)t ge 30,,,,, Leftrightarrow ,,,,10 cdot {1,1^4} + x cdot {1,1^2} + x cdot 1,1 ge 30,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,2,31x ge 15,359,,,,, Leftrightarrow ,,,,x ge frac{{15359}}{{2310}},,,,,, Leftrightarrow ,,,,,x ge 6frac{{1499}}{{2310}}.)
Так как, х наименьшее целое, то х = 7 млн. руб
Ответ: 7.
40В. Вклад в размере 6 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 15 млн рублей. Ответ дайте в млн рублей.
А = 6 млн. рублей – первоначальный вклад.
В коне каждого года вклад увеличивается на 10%, то есть увеличивается в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
x – сумма на которую наполняется вклад в начале третьего и четвёртого годов (целое число млн. рублей).
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (At) |
| 2 | (At) | (A{t^2}) |
| 3 | (A{t^2} + x) | (left( {A{t^2} + x} right)t) |
| 4 | (left( {A{t^2} + x} right)t + x) | (left( {left( {A{t^2} + x} right)t + x} right)t) |
По условию задачи вклад в коне четвёртого года должен быть не меньше 15 млн. рублей.
(left( {left( {A{t^2} + x} right)t + x} right)t ge 15,,,, Leftrightarrow ,,,,,6 cdot {1,1^4} + {1,1^2} cdot x + 1,1x ge 15,,,,, Leftrightarrow ,,,,,2,31x ge 6,2154,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,x ge frac{{62154}}{{23100}},,,,,, Leftrightarrow ,,,,,,x ge 2frac{{2659}}{{3850}}.)
Так как х наименьшее целое, то х = 3 млн. руб.
Ответ: 3.
41В. По бизнес-плану предполагается вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
А = 10 млн. рублей – первоначальные вложения.
В конце каждого года вклад увеличивается на 15%, то есть увеличивается в (frac{{100 + 15}}{{100}} = 1,15 = t) раз.
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (At + n) |
| 2 | (At + n) | (left( {At + n} right)t + n) |
| 3 | (left( {At + n} right)t + n) | (left( {left( {At + n} right)t + n} right)t + m) |
| 4 | (left( {left( {At + n} right)t + n} right)t + m) | (left( {left( {left( {At + n} right)t + n} right)t + m} right)t + m) |
В конце второго года вложенные средства как минимум удвоятся:
(left( {At + n} right)t + n ge 20,,,,,, Leftrightarrow ,,,,,10 cdot {1,15^2} + 1,15 cdot n + n ge 20,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,2,15n ge 6,775,,,,,,, Leftrightarrow ,,,,,n ge frac{{6775}}{{2150}},,,,,, Leftrightarrow ,,,,,,n ge 3frac{{13}}{{86}}.)
Так как n наименьшее целое число, то n = 4 млн. рублей.
В конце четвёртого года вложенные средства как минимум утроятся:
(left( {left( {left( {At + n} right)t + n} right)t + m} right)t + m ge 30,,,,,, Leftrightarrow ,,,,,,10 cdot {1,15^4} + 4 cdot {1,15^3} + 4 cdot {1,15^2} + 1,15m + m ge 30,,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,2,15m ge 1,1364375,,,,,,, Leftrightarrow ,,,,,,,m ge frac{{11364375}}{{21500000}}.)
Так как m наименьшее целое, то m = 1 млн. рублей.
Ответ: n = 4; m = 1.
42В. По бизнес-плану предполагается вложить в четырёхлетний проект 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 13% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.
A = 20 млн. рублей – первоначальные вложения
В конце каждого года вклад увеличивается на 13%, то есть увеличивается в (frac{{100 + 13}}{{100}} = 1,13 = t) раз.
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (A cdot t + n) |
| 2 | (A cdot t + n) | (left( {A cdot t + n} right) cdot t + n) |
| 3 | (left( {A cdot t + n} right) cdot t + n) | (left( {left( {A cdot t + n} right) cdot t + n} right) cdot t + m) |
| 4 | (left( {left( {A cdot t + n} right) cdot t + n} right) cdot t + m) | (left( {left( {left( {A cdot t + n} right) cdot t + n} right) cdot t + m} right) cdot t + m) |
В конце второго года вложенные средства как минимум удвоятся:
((A cdot t + n) cdot t + n ge 40,,,,, Leftrightarrow ,,,,,,20 cdot {1,13^2} + 1,13 cdot n + n ge 40,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,2,13 cdot n ge 14,462,,,,,, Leftrightarrow ,,,,,n ge frac{{14462}}{{2130}},,,,,,, Leftrightarrow ,,,,,,n ge 6,,frac{{1682}}{{2130}}.)
Так как n наименьшее целое, то n = 7 млн. руб.
В конце четвёртого года вложенные средства как минимум утроятся:
(left( {left( {left( {A cdot t + n} right) cdot t + n} right) cdot t + m} right) cdot t + m ge 60,,,,, Leftrightarrow ,,,,,20 cdot {1,13^4} + 7 cdot {1,13^3} + 7 cdot {1,13^2} + 1,13 cdot m + m ge 60,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,2,13 cdot m ge 8,3519488,,,,,, Leftrightarrow ,,,,,m ge frac{{83519488}}{{21300000}},,,,,,, Leftrightarrow ,,,,,,m ge 3,,frac{{19619488}}{{21300000}}.)
Так как m наименьшее целое, то m = 4 млн. руб.
Ответ: n = 7, m = 4.
43В. По бизнес-плану предполагается вложить в четырёхлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 млн рублей в первый и второй годы, а также по 10 млн рублей в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 150 млн, а за четыре года—станут больше 250 млн рублей.
A – первоначальные вложения (целое число млн. руб).
В конце каждого года вклад увеличивается на 20%, то есть увеличивается в (frac{{100 + 20}}{{100}} = 1,2 = t) раз.
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (A cdot t + 20) |
| 2 | (A cdot t + 20) | (left( {A cdot t + 20} right) cdot t + 20) |
| 3 | (left( {A cdot t + 20} right) cdot t + 20) | (left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10) |
| 4 | (left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10) | (left( {left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10} right) cdot t + 10) |
В конце второго года сумма должна быть больше 150 млн. руб, а в конце четвёртого больше 250 млн. руб.
(left{ {begin{array}{*{20}{c}}{left( {A cdot t + 20} right) cdot t + 20 > 150}\{left( {left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10} right) cdot t + 10 > 250}end{array}} right.)
Из первого неравенства: (A cdot {1,2^2} + 20 cdot 1,2 > 130,,,,, Leftrightarrow ,,,,,1,44A > 106,,,,,, Leftrightarrow ,,,,,A > 73frac{{11}}{{18}}.)
Из второго неравенства:
(A cdot {1,2^4} + 20 cdot {1,2^3} + 20 cdot {1,2^2} + 10 cdot 1,2 > 240,,,, Leftrightarrow ,,,,2,0736A > 164,64,,,,, Leftrightarrow ,,,,A > 79frac{{43}}{{108}}.)
(left{ {begin{array}{*{20}{c}}{A > 73frac{{11}}{{18}}}\{A > 79frac{{43}}{{108}}}end{array}} right.) ( = > ,,,,,,A > 79frac{{43}}{{108}}.)
Так как A наименьшее целое, то A = 80 млн. руб.
Ответ: 80.
44В. По бизнес-плану предполагается вложить в четырёхлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 10% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 млн рублей в первый и второй годы, а также по 10 млн рублей в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 200 млн, а за четыре года станут больше 270 млн рублей.
A – первоначальные вложения (целое число млн. руб).
В конце каждого года вклад увеличивается на 10%, то есть увеличивается в (frac{{100 + 10}}{{100}} = 1,1 = t) раз.
| Год | Вклад в начале года (в млн. руб) | Вклад в конце года (в млн. руб) |
| 1 | (A) | (A cdot t + 20) |
| 2 | (A cdot t + 20) | (left( {A cdot t + 20} right) cdot t + 20) |
| 3 | (left( {A cdot t + 20} right) cdot t + 20) | (left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10) |
| 4 | (left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10) | ()(left( {left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10} right) cdot t + 10) |
В конце второго года сумма должна быть больше 200 млн. руб, а в конце четвёртого больше 270 млн. руб.
(left{ {begin{array}{*{20}{c}}{left( {A cdot t + 20} right) cdot t + 20 > 200}\{left( {left( {left( {A cdot t + 20} right) cdot t + 20} right) cdot t + 10} right) cdot t + 10 > 270}end{array}} right.)
Из первого неравенства: (A cdot {1,1^2} + 20 cdot 1,1 > 180,,,,, Leftrightarrow ,,,,,1,21A > 158,,,,,, Leftrightarrow ,,,,,A > 130frac{{70}}{{121}}.)
Из второго неравенства:
(A cdot {1,1^4} + 20 cdot {1,1^3} + 20 cdot {1,1^2} + 10 cdot 1,1 > 260,,,, Leftrightarrow ,,,,1,4641A > 198,18,,,,, Leftrightarrow ,,,,A > 135frac{{5265}}{{14641}}.)
(left{ {begin{array}{*{20}{c}}{A > 130frac{{70}}{{121}}}\{A > 135frac{{5265}}{{14641}}}end{array}} right.) ( = > ,,,,,,A > 135frac{{5265}}{{14641}}.)
Так как A наименьшее целое, то A = 136 млн. руб.
Ответ: 136.
45В. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Известно, что если каждый год выплачивать по 292 820 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 534 820 рублей, то кредит будет полностью погашен за 2 года. Найдите число r.
A – сумма кредита (в рублях).
Каждый год сумма кредита увеличивается на r%, то есть увеличивается в (frac{{100 + r}}{{100}} = t) раз.
(a = 292820) рублей ежегодная выплата, если срок кредита 4 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | a | (A cdot t — a) |
| 2 | (left( {A cdot t — a} right) cdot t) | a | (left( {A cdot t — a} right) cdot t — a) |
| 3 | (left( {left( {A cdot t — a} right) cdot t — a} right) cdot t) | a | (left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a) |
| 4 | (left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t) | a | ()(left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t — a) |
(b = 534820) рублей ежегодная выплата, если срок кредита 2 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | b | (A cdot t — b) |
| 2 | (left( {A cdot t — b} right) cdot t) | b | (left( {A cdot t — b} right) cdot t — b) |
(left{ {begin{array}{*{20}{c}}{left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t — a = 0}\{left( {A cdot t — b} right) cdot t — b = 0}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{A cdot {t^4} = aleft( {{t^3} + {t^2} + t + 1} right)}\{A cdot {t^2} = b cdot left( {t + 1} right)}end{array}} right.} right.)
Разделим первое уравнение на второе:
(frac{{A cdot {t^4}}}{{A cdot {t^2}}} = frac{{a cdot ({t^2} cdot (t + 1) + (t + 1))}}{{b cdot (t + 1)}},,,,,, Leftrightarrow ,,,,,,{t^2} = frac{{a cdot (t + 1) cdot ({t^2} + 1)}}{{b cdot (t + 1)}},,,,,,,, Leftrightarrow ,,,,,b cdot {t^2} = a cdot {t^2} + a,,,,, Leftrightarrow ,,,,,(b — a) cdot {t^2} = a)(t = sqrt {frac{a}{{b — a}}} = sqrt {frac{{292820}}{{534820 — 292820}}} = sqrt {frac{{292820}}{{242000}}} = sqrt {frac{{121}}{{100}}} = frac{{11}}{{10}})
(frac{{100 + r}}{{100}} = frac{{11}}{{10}},,,,,, Leftrightarrow ,,,,,r = 10% .)
Ответ: 10.
46В. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Известно, что если каждый год выплачивать по 216 000 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 366 000 рублей, то кредит будет полностью погашен за 2 года. Найдите число r.
A – сумма кредита (в рублях).
Каждый год сумма кредита увеличивается на r%, то есть увеличивается в (frac{{100 + r}}{{100}} = t)раз.
(a = 216000) рублей ежегодная выплата, если срок 4 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | a | (A cdot t — a) |
| 2 | (left( {A cdot t — a} right) cdot t) | a | (left( {A cdot t — a} right) cdot t — a) |
| 3 | (left( {left( {A cdot t — a} right) cdot t — a} right) cdot t) | a | (left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a) |
| 4 | (left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t) | a | ()(left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t — a) |
(b = 366000) рублей ежегодная выплата, если срок 2 года
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | b | (A cdot t — b) |
| 2 | (left( {A cdot t — b} right) cdot t) | b | (left( {A cdot t — b} right) cdot t — b) |
(left{ {begin{array}{*{20}{c}}{left( {left( {left( {A cdot t — a} right) cdot t — a} right) cdot t — a} right) cdot t — a = 0}\{left( {A cdot t — b} right) cdot t — b = 0}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{A cdot {t^4} = aleft( {{t^3} + {t^2} + t + 1} right)}\{A cdot {t^2} = b cdot left( {t + 1} right)}end{array}} right.} right.)
Разделим первое уравнение на второе:
(frac{{A cdot {t^4}}}{{A cdot {t^2}}} = frac{{a cdot ({t^2} cdot (t + 1) + (t + 1))}}{{b cdot (t + 1)}},,,,,, Leftrightarrow ,,,,,,{t^2} = frac{{a cdot (t + 1) cdot ({t^2} + 1)}}{{b cdot (t + 1)}},,,,,,,, Leftrightarrow ,,,,,b cdot {t^2} = a cdot {t^2} + a,,,,, Leftrightarrow ,,,,,(b — a) cdot {t^2} = a)(t = sqrt {frac{a}{{b — a}}} = sqrt {frac{{216000}}{{366000 — 216000}}} = sqrt {frac{{36}}{{25}}} = frac{6}{5})
(frac{{100 + r}}{{100}} = frac{6}{5},,,,,, Leftrightarrow ,,,,,r = 20% .)
Ответ: 20.
47В. Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита (в млн рублей), при котором общая сумма выплат заёмщика будет меньше 8 млн.
A – сумма кредита (в млн. рублей).
Каждый год сумма кредита увеличивается на 10%, то есть в (frac{{100 + 10}}{{100}} = 1,1) раз.
Первые 3 года заёмщик выплачивает только проценты, то есть по (0,1A), а в конце четвёртого и пятого годов платежи составляют по x рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | 1,1A | 0,1A | A |
| 2 | 1,1A | 0,1A | A |
| 3 | 1,1A | 0,1A | A |
| 4 | 1,1A | x | (1,1A — x) |
| 5 | ((1,1A — x)1,1) | x | (left( {1,1A — x} right)1,1 — x) |
Остаток в конце пятого года долг полностью погашен, поэтому остаток равен нулю, а общая сумма выплат (0,3A + 2x) должна быть меньше 8 млн. руб.
(left{ begin{array}{l}(1,1A — x)1,1 — x = 0;\0,3A + 2x < 8.end{array} right.)
Выразим из уравнения x и подставим в неравенство: (1,21A = 2,1x,,,,,,,, Leftrightarrow ,,,,,,x = frac{{1,21A}}{{2,1}}.)
(0,3A + frac{{2,42A}}{{2,1}} < 8,,,,,,, Leftrightarrow ,,,,,,0,63A + 2,42A < 16,8,,,,, Leftrightarrow ,,,,3,05A < 16,8,,,,,, Leftrightarrow ,,,,,A < frac{{1680}}{{305}},,,,,,, Leftrightarrow ,,,A < 5frac{{31}}{{61}}.)
Так как A должно быть наибольшим и целым, то A = 5 млн. рублей.
Ответ: 5.
48В. Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита (в млн рублей), при котором общая сумма выплат заёмщика превысит 10 млн.
A – сумма кредита (в млн. рублей).
Каждый год сумма кредита увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2) раз.
Первые 3 года заёмщик выплачивает только проценты, то есть по (0,2A), а в конце четвёртого и пятого годов платежи составляют по x рублей.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | 1,2A | 0,2A | A |
| 2 | 1,2A | 0,2A | A |
| 3 | 1,2A | 0,2A | A |
| 4 | 1,2A | x | (1,2A — x) |
| 5 | ((1,2A — x)1,2) | x | (left( {1,2A — x} right)1,2 — x) |
Остаток в конце пятого года долг полностью погашен, поэтому остаток равен нулю, а общая сумма выплат (0,6A + 2x) должна быть больше 10 млн. руб.
(left{ begin{array}{l}(1,2A — x)1,2 — x = 0;\0,6A + 2x > 10.end{array} right.)
Выразим из уравнения x и подставим в неравенство: (1,44A = 2,2x,,,,, Leftrightarrow ,,,,x = frac{{1,44A}}{{2,2}}.)
(0,6A + frac{{1,44A}}{{1,1}} > 10;,,,,,,0,66A + 1,44A > 11,,,,,, Leftrightarrow ,,,,2,1A > 11,,,, Leftrightarrow ,,,,,A > 5frac{5}{{21}}).
Так как A должно быть наименьшим и целым, то A = 6 млн. рублей.
Ответ: 6.
49В. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее 0,6 млн рублей.
A = 4,5 млн. рублей сумма кредита.
Каждый год долг возрастает на r% и уменьшается заёмщиком на одну и ту же сумму, то есть на (frac{{4,5}}{9} = 0,5) млн. руб.
Следовательно, ежегодные платежи равны 0,5 млн. руб плюс начисленные проценты за год.
| Год | Начисленные % (руб) | Платёж (руб) | Остаток (руб) |
| 1 | (4,5 cdot frac{r}{{100}}) | (4,5 cdot frac{r}{{100}} + 0,5) | 4 |
| 2 | (4 cdot frac{r}{{100}}) | (4 cdot frac{r}{{100}} + 0,5) | 3,5 |
| … | … | … | … |
| 9 | (0,5 cdot frac{r}{{100}}) | (0,5 cdot frac{r}{{100}} + 0,5) | 0 |
Наибольший годовой платёж первый (4,5 cdot frac{r}{{100}} + 0,5), а наименьший последний (0,5 cdot frac{r}{{100}} + 0,5). Следовательно:
(left{ begin{array}{l}4,5 cdot frac{r}{{100}} + 0,5 le 1,4\0,5 cdot frac{r}{{100}} + 0,5 ge 0,6end{array} right.,,,,,,, Leftrightarrow ,,,,,,left{ begin{array}{l}4,5r le 90\0,5r ge 10end{array} right.,,,,,, Leftrightarrow ,,,,,left{ begin{array}{l}r le 20\r ge 20end{array} right.,,,,, Rightarrow ,,,r = 20% .)
Ответ: 20.
50В. В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн рублей, а наименьший—не менее 0,5 млн рублей.
A = 6 млн. рублей сумма кредита.
Каждый год долг возрастает на r% и уменьшается заёмщиком на одну и ту же сумму, то есть на (frac{6}{{15}} = 0,4)млн. руб.
Следовательно, ежегодные платежи равны 0,4 млн. руб. плюс начисленные проценты на остаток за год.
| Год | Начисленные % (руб) | Платёж (руб) | Остаток (руб) |
| 1 | (6 cdot frac{r}{{100}}) | (6 cdot frac{r}{{100}} + 0,4) | 5,6 |
| 2 | (5,6 cdot frac{r}{{100}}) | (5,6 cdot frac{r}{{100}} + 0,4) | 5,2 |
| … | … | … | … |
| 15 | (0,4 cdot frac{r}{{100}}) | (0,4 cdot frac{r}{{100}} + 0,4) | 0 |
Наибольший годовой платёж первый (6 cdot frac{r}{{100}} + 0,4), а наименьший последний (0,4 cdot frac{r}{{100}} + 0,4). Следовательно:
(left{ begin{array}{l}6 cdot frac{r}{{100}} + 0,4 le 1,9\0,4 cdot frac{r}{{100}} + 0,4 ge 0,5end{array} right.,,,,,,,, Leftrightarrow ,,,,,,left{ begin{array}{l}6r le 150\0,4r ge 10end{array} right.,,,,,,, Leftrightarrow ,,,,,,,left{ begin{array}{l}r le 25\r ge 25end{array} right.,,,,,,, Rightarrow ,,,r = 25% .)
Ответ: 25.
51В. В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат (в млн рублей) после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
A = 28 млн. рублей сумма кредита сроком на n лет, где n – целое.
Каждый год долг возрастает на 25%, то есть увеличивается в 1,25 раза и уменьшается заёмщиком на одну и ту же величину, то есть на (frac{{28}}{n}).
Следовательно, ежегодные платежи равны (frac{{28}}{n}) плюс начисленные проценты на остаток за год.
| Год | Начисленные % (руб) | Платёж (руб) | Остаток (руб) |
| 1 | (28 cdot frac{{25}}{{100}}) | (28 cdot frac{{25}}{{100}} + frac{{28}}{n}) | (frac{{28(n — 1)}}{n}) |
| 2 | (frac{{28(n — 1)}}{n} cdot frac{{25}}{{100}}) | (frac{{28(n — 1)}}{n} cdot frac{{25}}{{100}} + frac{{28}}{n}) | (frac{{28(n — 2)}}{n}) |
| … | … | … | … |
| n | (frac{{28}}{n} cdot frac{{25}}{{100}}) | (frac{{28}}{n} cdot frac{{25}}{{100}} + frac{{28}}{n}) | 0 |
Наибольший годовой платёж первый, то есть: (28 cdot frac{{25}}{{100}} + frac{{28}}{n} = 9,,,,,, Leftrightarrow ,,,,,frac{{28}}{n} = 2,,,,, Leftrightarrow ,,,,n = 14.)
Общая сумма выплат равна начисленным процентам за 14 лет плюс сумма самого кредита 28 млн. рублей.
(28 + 28 cdot frac{{25}}{{100}} + 26 cdot frac{{25}}{{100}} + … + 2 cdot frac{{25}}{{100}} = 28 + frac{{25}}{{100}} cdot (28 + 26 + … + 2) = 28 + frac{1}{4} cdot frac{{2 + 28}}{2} cdot 14 = )( = 28 + frac{{105}}{2} = 28 + 52,5 = 80,5)млн. рублей.
Ответ: 80,5.
52В. В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат (в млн рублей) после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн рублей?
A = 9 млн. рублей сумма кредита сроком на n лет, где n – целое.
Каждый год долг возрастает на 25%, то есть в 1,25 раза и уменьшается заёмщиком на одну и ту же величину, то есть на (frac{9}{n}).
Следовательно, ежегодные платежи равны (frac{9}{n})плюс начисленные проценты на остаток за год.
| Год | Начисленные % (руб) | Платёж (руб) | Остаток (руб) |
| 1 | (9 cdot frac{{25}}{{100}}) | (9 cdot frac{{25}}{{100}} + frac{9}{n}) | (frac{{9(n — 1)}}{n}) |
| 2 | (frac{{9(n — 1)}}{n} cdot frac{{25}}{{100}}) | (frac{{9(n — 1)}}{n} cdot frac{{25}}{{100}} + frac{9}{n}) | (frac{{9(n — 2)}}{n}) |
| … | … | … | … |
| n | (frac{9}{n} cdot frac{{25}}{{100}}) | (frac{9}{n} cdot frac{{25}}{{100}} + frac{9}{n}) | 0 |
Наименьший годовой платёж последний, то есть: (frac{9}{n} cdot frac{{25}}{{100}} + frac{9}{n} = 1,25,,,,, Leftrightarrow ,,,,,frac{9}{n}left( {frac{1}{4} + 1} right) = frac{5}{4},,,,, Leftrightarrow ,,,,,n = 9.)
Общая сумма выплат равна начисленным процентам за 9 лет плюс сумма самого кредита 9 млн. руб.
(9 + 9 cdot frac{{25}}{{100}} + 8 cdot frac{{25}}{{100}} + … + 1 cdot frac{{25}}{{100}} = 9 + frac{{25}}{{100}} cdot (9 + 8 + … + 1) = 9 + frac{1}{4} cdot frac{{1 + 9}}{2} cdot 9 = 20,25) млн. руб.
Ответ: 20,25.
53В. В августе 2017 года взяли кредит. Условия возврата таковы:
— каждый январь долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за три года равными платежами по 38 016 рублей, или за два года равными платежами по 52 416 рублей. Найдите r.
A – сумма кредита ( в рублях).
Каждый год сумма кредита увеличивается на r %, то есть в (frac{{100 + r}}{{100}} = t) раз.
a = 38016 руб. ежегодная выплата, если срок кредита 3 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | a | (A cdot t — a) |
| 2 | ((A cdot t — a) cdot t) | a | ((A cdot t — a) cdot t — a) |
| 3 | (((A cdot t — a) cdot t — a)t) | a | (((A cdot t — a) cdot t — a) cdot t — a) |
b = 52416 руб. ежегодная выплата, если срок кредита 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | b | (A cdot t — b) |
| 2 | ((A cdot t — b) cdot t) | b | ((A cdot t — b) cdot t — b) |
(left{ begin{array}{l}((A cdot t — a) cdot t — a) cdot t — a = 0\(A cdot t — b) cdot t — b = 0end{array} right.,,,,,,, Leftrightarrow ,,,,,left{ begin{array}{l}A cdot {t^3} = a cdot ({t^2} + t + 1)\A cdot {t^2} = b cdot (t + 1)end{array} right.)
Разделим первое уравнение на второе:
(frac{{A cdot {t^3}}}{{A cdot {t^2}}} = frac{{a cdot ({t^2} + t + 1)}}{{b cdot (t + 1)}},,,,,, Leftrightarrow ,,,,,b cdot {t^2} + b cdot t = a cdot {t^2} + a cdot t + a,,,,, Leftrightarrow ,,,,,(b — a) cdot {t^2} + (b — a) cdot t — a = 0,,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,14400,{t^2} + 14400,t — 38016 = 0,,,,,, Leftrightarrow ,,,,,25,{t^2} + 25,t — 66 = 0,,,,, Leftrightarrow ,,,,,{t_1} = frac{6}{5};,,,,,{t_2} = — frac{{11}}{5}.)
({t_2} = — frac{{11}}{5}) не подходит. Следовательно: (frac{{100 + r}}{{100}} = frac{6}{5},,,,, Leftrightarrow ) (r = 20% ).
Ответ: 20.
54В. В августе 2017 года взяли кредит. Условия возврата таковы:
— каждый январь долг увеличивается на r%;
— с февраля по июль необходимо выплатить часть долга.
Кредит можно выплатить за три года равными платежами по 56 595 рублей, или за два года равными платежами по 81 095 рублей. Найдите r.
A – сумма кредита ( в рублях)
Каждый год сумма кредита увеличивается на r %, то есть в (frac{{100 + r}}{{100}} = t) раз.
a = 56595 рублей ежегодная выплата, если срок кредита 3 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | a | (A cdot t — a) |
| 2 | ((A cdot t — a) cdot t) | a | ((A cdot t — a) cdot t — a) |
| 3 | (((A cdot t — a) cdot t — a)t) | a | (((A cdot t — a) cdot t — a) cdot t — a) |
b = 81095 рублей ежегодная выплата, если срок кредита 2 года.
| Год | Долг после начисления процентов (руб) | Платёж (руб) | Остаток после платежа (руб) |
| 1 | (A cdot t) | b | (A cdot t — b) |
| 2 | ((A cdot t — b) cdot t) | b | ((A cdot t — b) cdot t — b) |
(left{ begin{array}{l}((A cdot t — a) cdot t — a) cdot t — a = 0\(A cdot t — b) cdot t — b = 0end{array} right.,,,,,,, Leftrightarrow ,,,,,left{ begin{array}{l}A cdot {t^3} = a cdot ({t^2} + t + 1)\A cdot {t^2} = b cdot (t + 1)end{array} right.)
Разделим первое уравнение на второе:
(frac{{A cdot {t^3}}}{{A cdot {t^2}}} = frac{{a cdot ({t^2} + t + 1)}}{{b cdot (t + 1)}},,,,,, Leftrightarrow ,,,,,b cdot {t^2} + b cdot t = a cdot {t^2} + a cdot t + a,,,,, Leftrightarrow ,,,,,(b — a) cdot {t^2} + (b — a) cdot t — a = 0,,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,24500 cdot {t^2} + 24500 cdot t — 56595 = 0,,,,,, Leftrightarrow ,,,,,100 cdot {t^2} + 100 cdot {t^2} — 231 = 0,,,,,, Leftrightarrow ,,,,,,{t_1} = frac{{11}}{{10}};,,,,,{t_2} = — frac{{21}}{{10}}.)
({t_2} = — frac{{21}}{{10}}) не подходит. Следовательно: (frac{{100 + r}}{{100}} = frac{{11}}{{10}},,,,, Leftrightarrow ) (r = 10% ).
Ответ: 10.
55В. По вкладу ≪А≫ банк в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫ увеличивает эту сумму на 11% в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу ≪Б≫, при котором за все три года этот вклад будет менее выгоден, чем вклад ≪А≫.
Пусть на каждый вклад внесена сумма равная S.
Вклад «A» каждый год увеличивается на 10%, то есть в 1,1 раза. Поэтому через 3 года он будет равен: ({1,1^3} cdot S).
Вклад «Б» первые 2 года увеличивается на 11%, то есть в 1,11 раз, а третий год на n%, то есть в (frac{{100 + n}}{{100}}) раз. Поэтому через 3 года он будет равен: ({1,11^2} cdot S cdot frac{{100 + n}}{{100}}).
Вклад «Б» должен быть менее выгоден, то есть:
({1,11^2} cdot frac{{100 + n}}{{100}} cdot S < {1,1^3} cdot S,left| {,:,S,} right.,,,, Leftrightarrow ,,,,,1,2321 cdot frac{{100 + n}}{{100}} < 1,331,,,,, Leftrightarrow ,,,,,100 + n < frac{{133,1}}{{1,2321}},,,, Leftrightarrow )
( Leftrightarrow ,,,,,,n < frac{{9,89}}{{1,2321}},,,,,, Leftrightarrow ,,,,,n < frac{{98900}}{{12321}},,,,,, Leftrightarrow ,,,,n < 8frac{{332}}{{12321}}.)
Так как n наибольшее натуральное, то n = 8%.
Ответ: 8.
56В. По вкладу ≪А≫ банк в конце каждого года увеличивает на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫ увеличивает эту сумму на 25% в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу ≪Б≫, при котором за все три года этот вклад будет менее выгоден, чем вклад ≪А≫.
Пусть на каждый вклад внесена сумма равная S.
Вклад «A» каждый год увеличивается на 20%, то есть в 1,2 раза. Поэтому через 3 года он будет равен: ({1,2^3} cdot S).
Вклад «Б» первые 2 года увеличивается на 25%, то есть в 1,25 раза, а третий год на n%, то есть в (frac{{100 + n}}{{100}}) раз. Поэтому через 3 года он будет равен: ({1,25^2} cdot S cdot frac{{100 + n}}{{100}}).
Вклад «Б» должен быть менее выгоден, то есть:
({1,25^2} cdot S cdot frac{{100 + n}}{{100}} < {1,2^3} cdot Sleft| {,:,S} right.,,,,,, Leftrightarrow ,,,,,1,5625 cdot frac{{100 + n}}{{100}} < 1,728,,,,,, Leftrightarrow ,,,,,100 + n < frac{{172,8}}{{1,5625}},,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,n < frac{{16,55}}{{1,5625}},,,,,, Leftrightarrow ,,,,,n < frac{{1324}}{{125}},,,,,, Leftrightarrow ,,,,,,n < 10frac{{74}}{{125}}.)
Так как n наибольшее натуральное, то n = 10%.
Ответ: 10.
57В. По вкладу ≪А≫ банк в течение трёх лет в конце каждого года увеличивает на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫ увеличивает эту сумму на 21% в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу ≪Б≫, при котором за все три года этот вклад всё ещё останется выгоднее вклада ≪А≫.
Пусть на каждый вклад внесена сумма равная S.
Вклад «A» каждый год увеличивается на 20%, то есть в 1,2 раза. Поэтому через 3 года он будет равен: ({1,2^3} cdot S)
Вклад «Б» первые 2 года увеличивается на 21%, то есть в 1,21 раз, а третий год на n%, то есть в (frac{{100 + n}}{{100}})раз. Поэтому через 3 года он будет равен:({1,21^2} cdot S cdot frac{{100 + n}}{{100}}).
Вклад «Б» должен быть более выгоден, то есть:
({1,21^2} cdot S cdot frac{{100 + n}}{{100}} > {1,2^3} cdot Sleft| {,:,S} right.,,,,,,, Leftrightarrow ,,,,,,1,4641 cdot frac{{100 + n}}{{100}} > 1,728,,,,,, Leftrightarrow ,,,,,,100 + n > frac{{172,8}}{{1,4641}},,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,n > frac{{26,39}}{{1,4641}},,,,, Leftrightarrow ,,,,n > frac{{263900}}{{14641}},,,,,, Leftrightarrow ,,,,,,n > 18frac{{362}}{{14641}}.)
Так как n наименьшее целое, то n = 19%.
Ответ: 19.
58В. По вкладу ≪А≫ банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫ увеличивает эту сумму на 11% в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу ≪Б≫, при котором за все три года этот вклад всё ещё останется выгоднее вклада ≪А≫.
Пусть на каждый вклад внесена сумма равная S.
Вклад «А» каждый год увеличивается на 10% , то есть в 1,1 раза. Поэтому через 3 года он будет равен ({1,1^3} cdot S).
Вклад «Б» первые 2 года увеличивается на 1% , то есть в 1,11 раза, а третий год на n% то есть в (frac{{100 + n}}{{100}}) раз. Поэтому через 3 года он будет равен: ({1,11^2} cdot Sfrac{{100 + n}}{{100}})
Вклад «Б» должен быть более выгоден, то есть:
({1,11^2} cdot S cdot frac{{100 + n}}{{100}} > {1,1^3} cdot S,left| {,:,S} right.,,,,,,, Leftrightarrow ,,,,,,1,2321 cdot frac{{100 + n}}{{100}} > 1,331,,,,,, Leftrightarrow ,,,,,100 + n > frac{{133,1}}{{1,2321}},,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,n > frac{{98900}}{{12321}},,,,,, Leftrightarrow ,,,,,,,n > 8frac{{332}}{{12321}}.)
Так как n наименьшее целое, то n = 9%.
Ответ: 9.
59В. По вкладу ≪А≫ банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫—увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад ≪Б≫ окажется выгоднее вклада ≪А≫ при одинаковых суммах первоначальных взносов.
Пусть на каждый вклад внесена сумма равная S.
Вклад «А» каждый год увеличивается на 20%, то есть в 1,2 раза. Поэтому через 3 года он будет равен ({1,2^3} cdot S).
Вклад «Б» первый год увеличивается на 10%, то есть в 1,1 раза, а второй и третий на n%, то есть в (frac{{100 + n}}{{100}}) раз. Поэтому через 3 года он будет равен: (1,1 cdot S cdot {left( {frac{{100 + n}}{{100}}} right)^2})
Вклад «Б» должен быть выгоднее, то есть:
(1,1 cdot S cdot {left( {frac{{100 + n}}{{100}}} right)^2} > {1,2^3} cdot S,,left| {,:S} right.,,,,,,, Leftrightarrow ,,,,,,1,1 cdot {left( {frac{{100 + n}}{{100}}} right)^2} > {1,2^3})
Решить последнее неравенство без калькулятора достаточно сложно, поэтому решим его подбором. Так как n целое, то проверим n = 25: левая принимает значение 1,71875, а правая – 1,728, то есть при n = 25 неравенство не выполняется. Проверим n = 26: левая часть 1,74636, а правая – 1,728, то есть неравенство выполняется. Следовательно, наименьшее целое значение n при котором вклад «Б» более выгоден 26%.
Ответ: 26.
60В. По вкладу ≪А≫ банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу ≪Б≫—увеличивать эту сумму на 5% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад ≪Б≫ окажется выгоднее вклада ≪А≫ при одинаковых суммах первоначальных взносов.
Пусть на каждый вклад внесена сумма равная S.
Вклад «А» каждый год увеличивается на 10%, то есть в 1,1 раза. Поэтому через 3 года он будет равен ({1,1^3} cdot S).
Вклад «Б» первый год увеличивается на 5%, то есть в 1,05 раза, а второй и третий год на n%, то есть в (frac{{100 + n}}{{100}}) раз. Поэтому через 3 года он будет равен: (1,05 cdot S cdot {left( {frac{{100 + n}}{{100}}} right)^2})
Вклад «Б» должен быть выгоднее, то есть:
(1,05 cdot S cdot {left( {frac{{100 + n}}{{100}}} right)^2} > {1,1^3} cdot S,left| {,:} right.,S,,,,,, Leftrightarrow ,,,,,,1,05 cdot {left( {frac{{100 + n}}{{100}}} right)^2} > {1,1^3})
Решить последнее неравенство без калькулятора достаточно сложно, поэтому решим его подбором. Так как n целое, то проверим n=12%: левая часть принимает значение 1,31712, а правая – 1,331, то есть при n =12 неравенство не выполняется. Проверим n = 13: левая часть 1,340745, а правая – 1,331, то есть неравенство выполняется. Следовательно, наименьшее целое значение n при котором вклад «Б» более выгоден 13%
Ответ: 13.
61В. В июле 2017 года планируется взять кредит в банке в размере S тыс. рублей (где S—натуральное число) сроком на 3 года. Условия его возврата таковы:
- каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в тыс. рублей) | S | 0,7 S | 0,4 S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
S – кредит тыс. рублей (S – натуральное). Каждый год остаток долга увеличивается на 15%. Первый год долг уменьшается на (S — 0,7S = 0,3S), второй год на (0,7S — 0,4S = 0,3S) и третий год на 0,4S.
| Год | Начисленные% (тыс. руб) | Выплата (тыс. руб) | Остаток (тыс. руб) |
| 2018 | (0,15 cdot S) | (0,15 cdot S + 0,3S) | (0,7S) |
| 2019 | (0,15 cdot 0,7S) | (0,15 cdot 0,7S + 0,3S) | 0,4S |
| 2020 | (0,15 cdot 0,4S) | (0,15 cdot 0,4S + 0,4S) | 0 |
Таким образом, первая выплата: (0,45S = frac{{45}}{{100}}S = frac{9}{{20}} cdot S)
вторая выплата: (0,405S = frac{{405}}{{1000}} cdot S = frac{{81}}{{200}} cdot S)
третья выплата: (0,46S = frac{{46}}{{100}}S = frac{{23}}{{50}}S)
Все выплаты будут целыми, если S делится на 20, 200 и 50, то есть необходимо найти наименьшее общее кратное (НОК) чисел 20, 200 и 50. Очевидно, что это 200. Следовательно, наименьшее значение S при котором каждая выплата целая: S = 200.
Ответ: 200.
62В. В июле 2017 года планируется взять кредит в банке в размере S тыс. рублей (где S—натуральное число) сроком на 3 года. Условия его возврата таковы:
- каждый январь долг увеличивается на 17,5% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в тыс. рублей) | S | 0,9 S | 0,4 S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
S – кредит тыс. рублей (S— натуральное)
Каждый год остаток долга увеличивается на 17,5%. Первый год долг уменьшается на (S — 0,9S = 0,1S), второй год на (0,9S — 0,4S = 0,5S) и третий год на 0,4S.
| Год | Начисленные% (тыс. руб) | Выплата (тыс. руб) | Остаток (тыс.руб) |
| 2018 | (0,175S) | (0,175S + 0,1S) | 0,9S |
| 2019 | (0,175 cdot 0,9S) | (0,175 cdot 0,9S + 0,5S) | 0,4S |
| 2020 | (0,175 cdot 0,4S) | (0,175 cdot 0,4S + 0,4S) | 0 |
Таким образом, первая выплата: (0,275S = frac{{275}}{{1000}}S = frac{{11}}{{40}}S)
вторая выплата: (0,6575S = frac{{6575}}{{10000}}S = frac{{263}}{{400}}S)
третья выплата: (0,47S = frac{{47}}{{100}}S)
Все выплаты будут целыми, если S делится на 40, 400 и 100, то есть необходимо найти наименьшее общее кратное (НОК) чисел 40, 400 и 100. Очевидно, что это 400. Следовательно, наименьшее значение S при котором каждая выплата целая: S = 400.
Ответ: 400.
63В. 15 января планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его возврата таковы:
- 1-го числа каждого месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r—целое число;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| Долг (в млн. рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором сумма выплат будет меньше 1,25 млн руб.
Сумма кредита 1 млн. рублей сроком на 6 месяцев под r%, где r – целое.
| Месяц | Начисленные % (млн. руб) | Остаток (млн. руб) |
| Февраль | (1 cdot frac{r}{{100}}) | 0,6 |
| Март | (0,6 cdot frac{r}{{100}}) | 0,4 |
| Апрель | (0,4 cdot frac{r}{{100}}) | 0,3 |
| Май | (0,3 cdot frac{r}{{100}}) | 0,2 |
| Июнь | (0,2 cdot frac{r}{{100}}) | 0,1 |
| Июль | (0,1 cdot frac{r}{{100}}) | 0 |
Общая сумма выплат равна начисленным процентам за 6 месяцев плюс сумма самого кредита 1 млн. рублей. По условию задачи общая сумма выплат должна быть меньше 1,25 млн. рублей.
(1 + 1 cdot frac{r}{{100}} + 0,6 cdot frac{r}{{100}} + 0,4 cdot frac{r}{{100}} + 0,3 cdot frac{r}{{100}} + 0,2 cdot frac{r}{{100}} + 0,1 cdot frac{r}{{100}} < 1,25)
(frac{r}{{100}} cdot (1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) < 0,25,,,,,, Leftrightarrow ,,,,,,frac{{2,6r}}{{100}} < 0,25,,,,,,, Leftrightarrow ,,,,,r < frac{{250}}{{26}},,,,,, Leftrightarrow ,,,,,,r < 9frac{8}{{13}}.)
Так как r наибольшее целое, то r = 9%.
Ответ: 9.
64В. 15 января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн. рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,2 млн рублей.
Сумма кредита 1 млн. рублей сроком на 6 месяцев под r%, где r – целое.
| Месяц | Начисленные % (млн. руб) | Остаток (млн. руб) |
| Февраль | (1 cdot frac{r}{{100}}) | 0,6 |
| Март | (0,6 cdot frac{r}{{100}}) | 0,4 |
| Апрель | (0,4 cdot frac{r}{{100}}) | 0,3 |
| Май | (0,3 cdot frac{r}{{100}}) | 0,2 |
| Июнь | (0,2 cdot frac{r}{{100}}) | 0,1 |
| Июль | (0,1 cdot frac{r}{{100}}) | 0 |
Общая сумма выплат равна начисленным процентам за 6 месяцев плюс сумма самого кредита 1 млн. рублей. По условию задачи общая сумма выплат должна быть меньше 1,2 млн. рублей.
(1 + 1 cdot frac{r}{{100}} + 0,6 cdot frac{r}{{100}} + 0,4 cdot frac{r}{{100}} + 0,3 cdot frac{r}{{100}} + 0,2 cdot frac{r}{{100}} + 0,1 cdot frac{r}{{100}} < 1,2)
(frac{r}{{100}} cdot (1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) < 0,2,,,,,, Leftrightarrow ,,,,,frac{{2,6r}}{{100}} < 0,2,,,,, Leftrightarrow ,,,,,r < frac{{20}}{{2,6}},,,,, Leftrightarrow ,,,,,r < 7frac{8}{{13}}.)
Так как r наибольшее целое, то r = 7%.
Ответ: 7.
65В. В июле 2017 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S—целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 | Июль 2021 |
| Долг (в млн. рублей) | S | 0,8 S | 0,6 S | 0,4 S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет больше 50 млн рублей.
S – кредит млн. рублей (S – целое).
Каждый год остаток долга увеличивается на 25%. Первый год долг уменьшается на (S — 0,8S = 0,2S), второй год на (0,8S — 0,6S = 0,2S), третий год на (0,6S — 0,4S = 0,2S) и четвертый год на 0,4S.
| Год | Начисленные % (млн. руб) | Выплата (млн. руб) | Остаток (млн. руб) |
| 2018 | (0,25S) | (0,25S + 0,2S = 0,45S) | (0,8S) |
| 2019 | (0,25 cdot 0,8S) | (0,25 cdot 0,8S + 0,2S = 0,4S) | (0,6S) |
| 2020 | (0,25 cdot 0,6S) | (0,25 cdot 0,6S + 0,2S = 0,35S) | (0,4S) |
| 2021 | (0,25 cdot 0,4S) | (0,25 cdot 0,4S + 0,4S = 0,5S) | 0 |
Чтобы все выплаты были больше 50 млн. рублей достаточно, чтобы наименьшая выплата была больше 50 млн. рублей. Наименьшей является третья выплата – 0,35S. Следовательно:
(0,35S > 50,,,,, Leftrightarrow ,,,,,S > frac{{5000}}{{35}},,,,,, Leftrightarrow ,,,,,,S > frac{{1000}}{7},,,,,, Leftrightarrow ,,,,,S > 142frac{6}{7}.)
Так как S наименьшее целое, то S = 143.
Ответ: 143.
66В. В июле 2017 года планируется взять кредит в банке на четыре года в размере S млн руб., где S— целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 | Июль 2021 |
| Долг (в млн. рублей) | S | 0,8 S | 0,5 S | 0,1 S | 0 |
Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.
S – кредит млн. рублей (S – целое).
Каждый год остаток долга увеличивается на 15%. Первый год долг уменьшается на (S — 0,8S = 0,2S), второй год на (0,8S — 0,5S = 0,3S), третий год на (0,5S — 0,1S = 0,4S) и четвертый на 0,1S.
| Год | Начисленные % (млн. руб) | Выплата (млн. руб) | Остаток (млн. руб) |
| 2018 | ($)0,15S$ | (0,15S + 0,2S = 0,35S) | (0,8S) |
| 2019 | (0,15 cdot 0,8S) | (0,15 cdot 0,8S + 0,3S = 0,42S) | (0,5S) |
| 2020 | (0,15 cdot 0,5S) | (0,15 cdot 0,5S + 0,4S = 0,475S) | (0,1S) |
| 2021 | (0,15 cdot 0,1S) | (0,15 cdot 0,1S + 0,1S = 0,115S) | 0 |
Тогда общая сумма выплат: (0,35S + 0,42S + 0,475S + 0,115S = 1,36S.)
По условию: (1,36S < 50,,,,,, Leftrightarrow ,,,,,S < frac{{5000}}{{136}},,,,,, Leftrightarrow ,,,,,,S < frac{{625}}{{17}},,,,, Leftrightarrow ,,,,S < 36frac{{13}}{{17}}.)
Так как S наибольшее целое, то S = 36 млн. руб.
Ответ: 36.
67В. В июле 2017 года планируется взять кредит в банке на три года в размере S млн руб., где S—целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в млн. рублей) | S | 0,7 S | 0,4 S | 0 |
Найдите наименьшее S, при котором каждая из выплат будет больше 5 млн рублей.
S – кредит млн. рублей (S – целое).
Каждый год остаток долга увеличивается на 25%. Первый год долг уменьшается на (S — 0,7S = 0,3S), второй год на (0,7S — 0,4S = 0,3S) и третий год на 0,4S.
| Год | Начисленные % (млн. руб) | Выплата (млн. руб) | Остаток (млн. руб) |
| 2018 | (0,25S) | (0,25S + 0,3S = 0,55S) | (0,7S) |
| 2019 | (0,25 cdot 0,7S) | (0,25 cdot 0,7S + 0,3S = 0,475S) | (0,4S) |
| 2020 | (0,25 cdot 0,4S) | (0,25 cdot 0,4S + 0,4 = 0,5S) | 0 |
Чтобы все выплаты были больше 5млн. рублей достаточно, чтобы наименьшая выплата была больше 5млн. рублей. Наименьшей является вторая выплата – 0,475S.
(0,475S > 5,,,,, Leftrightarrow ,,,,,,S > frac{{5000}}{{475}},,,,,, Leftrightarrow ,,,,,,S > frac{{200}}{{19}},,,,,, Leftrightarrow ,,,,,S > 10frac{{10}}{{19}}.)
Так как S наименьшее целое, то S = 11 млн. руб.
Ответ: 11.
68В. В июле 2017 года планируется взять кредит в банке на три года в размере S млн руб., где S— целое число. Условия его возврата таковы:
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг (в млн. рублей) | S | 0,7 S | 0,4 S | 0 |
Найдите наибольшее значение S, при котором разница между наибольшей и наименьшей выплатами будет меньше 1 млн рублей.
S – кредит млн. рублей (S – целое).
Каждый год остаток долга увеличивается на 25%. Первый год долг уменьшается на (S — 0,7S = 0,3S), второй год на (0,7S — 0,4S = 0,3S) и третий год на 0,4S.
| Год | Начисленные % (млн. руб) | Выплата (млн. руб) | Остаток (млн. руб) |
| 2018 | (0,25S) | (0,25S + 0,3S = 0,55S) | (0,7S) |
| 2019 | (0,25 cdot 0,7S) | (0,25 cdot 0,7S + 0,3S = 0,475S) | (0,4S) |
| 2020 | (0,25 cdot 0,4S) | (0,25 cdot 0,4S + 0,4S = 0,5S) | 0 |
Наибольшая выплата первая 0,55S, а наименьшая вторая 0,475S и разница между ними должна быть меньше 1млн. рублей:
(0,55S — 0,475S < 1,,,,,,,, Leftrightarrow ,,,,,,0,075S < 1,,,,,, Leftrightarrow ,,,,,,S < frac{{1000}}{{75}},,,,,,, Leftrightarrow ,,,,,,,S < frac{{40}}{3},,,,,,, Leftrightarrow ,,,,,,S < 13frac{1}{3}.)
Так как S наибольшее целое, то S = 13млн. руб.
Ответ: 13.
69В. В июле 2017 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2018, 2019 и 2020 гг. долг остаётся равным S тыс. рублей;
- выплаты в 2021 и 2022 годах равны по 625 тыс. рублей;
- к июлю 2022 года долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет. Ответ дайте в тыс. рублей.
S – кредит в тыс. рублей.
Каждый год остаток долга увеличивается на 25%, то есть в (frac{{100 + 25}}{{100}} = 1,25) раза.
Первые 3 года заёмщик выплачивает только проценты, то есть по (0,25S), а в конце четвёртого и пятого годов по 625 тыс. рублей.
| Год | Долг после начисления процентов (тыс. руб) | Платёж (тыс. руб) | Остаток после платежа (тыс. руб) |
| 2018 | (1,25S) | (0,25S) | S |
| 2019 | (1,25S) | (0,25S) | S |
| 2020 | (1,25S) | (0,25S) | S |
| 2021 | (1,25S) | 625 | (1,25S — 625) |
| 2022 | (left( {1,25S — 625} right)1,25) | 625 | (left( {1,25S — 625} right)1,25 — 625) |
Остаток в конце пятого года равен нулю:
(,left( {frac{5}{4}S — 625} right) cdot frac{5}{4} — 625 = 0,,,,, Leftrightarrow ,,,,,frac{{25}}{{16}}S = 625 cdot frac{5}{4} + 625,,,,,,,, Leftrightarrow ,,,,,,S = frac{{625 cdot 9 cdot 16}}{{4 cdot 25}} = 900.)
Общая сумма выплат за 5 лет равна: (3 cdot 0,25S + 2 cdot 625 = 0,75 cdot 900 + 1250 = 1925) тыс. рублей.
Ответ: 1925.
70В. В июле 2017 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2018, 2019 и 2020 гг. долг остаётся равным S тыс. рублей;
- выплаты в 2021 и 2022 годах равны по 360 тыс. рублей;
- к июлю 2022 года долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет. Ответ дайте в тыс. рублей.
S – кредит в тыс. рублей.
Каждый год остаток долга увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2) раза.
Первые 3 года заёмщик выплачивает только проценты, то есть по (0,2S), а в конце четвёртого и пятого годов по 360 тыс. рублей.
| Год | Долг после начисления процентов (тыс. руб) | Платёж (тыс. руб) | Остаток после платежа (тыс. руб) |
| 2018 | (1,2S) | (0,2S) | S |
| 2019 | (1,2S) | (0,2S) | S |
| 2020 | (1,2S) | (0,2S) | S |
| 2021 | (1,2S) | 360 | (1,2S — 360) |
| 2022 | (left( {1,2S — 360} right)1,2) | 360 | (left( {1,2S — 360} right)1,2 — 360) |
Остаток в конце пятого года равен нулю:
(left( {1,2S — 360} right)1,2 — 360 = 0,,,,,,, Leftrightarrow ,,,,,,{1,2^2} cdot S — 360 cdot 1,2 — 360 = 0,,,,,,, Leftrightarrow ,,,,,,S = frac{{360 cdot 2,2}}{{{{1,2}^2}}} = 550) тыс. рублей.
Общая сумма выплат за 5 лет равна: (3 cdot 0,2S + 2 cdot 360 = 0,6 cdot 550 + 720 = 1050) тыс. рублей.
Ответ: 1050.
71В. Пётр взял кредит в банке на срок 12 месяцев. По договору Пётр должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r% этой суммы, и своим ежемесячным платежом Пётр погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц. Известно, что общая сумма, выплаченная Петром банку за весь срок кредитования, оказалась на 13% больше, чем сумма, взятая им в кредит. Найдите r.
A – кредит сроком на 12 месяцев. Каждый месяц банк начисляет r % на остаток, а заемщик выплачивает эти проценты и двенадцатую часть от суммы кредита, то есть (frac{A}{{12}}). Таким образом, через 1 месяц остаток долга будет (frac{{11A}}{{12}}), через 2 месяца (frac{{10A}}{{12}}) и так далее.
| Месяц | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{r}{{100}}) | (A — frac{A}{{12}} = frac{{11A}}{{12}}) |
| 2 | (frac{{11A}}{{12}} cdot frac{r}{{100}}) | (frac{{11A}}{{12}} — frac{A}{{12}} = frac{{10A}}{{12}}) |
| … | … | … |
| 12 | (frac{A}{{12}} cdot frac{r}{{100}}) | 0 |
Так как общая сумма, выплаченная банку за весь срок кредитования, оказалась на 13% больше, чем сумма, взятая в кредит, то начисленные проценты равны 13% от суммы кредита, то есть (A cdot frac{{13}}{{100}})
(frac{{12A}}{{12}} cdot frac{r}{{100}} + frac{{11A}}{{12}} cdot frac{r}{{100}} + ….. + frac{A}{{12}} cdot frac{r}{{100}} = A cdot frac{{13}}{{100}},,,,,,, Leftrightarrow ,,,,,,,frac{A}{{12}} cdot frac{r}{{100}}(12 + 11 + ….. + 1) = frac{{13A}}{{100}},left| {,:,A} right.,,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,,frac{r}{{12}} cdot frac{{1 + 12}}{2} cdot 12 = 13,,,,,,, Leftrightarrow ,,,,,,frac{r}{{12}} cdot frac{{13}}{2} cdot 12 = 13,,,,,, Leftrightarrow ,,,,,,r = 2% .)
Ответ: 2.
72В. Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r% этой суммы, и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц. Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в кредит. Найдите r.
A – кредит сроком на 17 месяцев. Каждый месяц банк начисляет r % на остаток долга, а заемщик выплачивает эти проценты и семнадцатую часть от суммы кредита, то есть (frac{A}{{17}}). Таким образом, через 1 месяц остаток долга будет (frac{{16A}}{{17}}), через 2 месяца (frac{{15A}}{{17}}) и так далее.
| Месяц | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{r}{{100}}) | (A — frac{A}{{17}} = frac{{16A}}{{17}}) |
| 2 | (frac{{16A}}{{17}} cdot frac{r}{{100}}) | (frac{{16A}}{{17}} — frac{A}{{17}} = frac{{15A}}{{17}}) |
| … | … | … |
| 17 | (frac{A}{{17}} cdot frac{r}{{100}}) | 0 |
Так как общая сумма, выплаченная банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая в кредит, то начисленные проценты равны 27% от суммы кредита, то есть (A cdot frac{{27}}{{100}}).
(frac{{17A}}{{17}} cdot frac{r}{{100}} + frac{{16A}}{{17}} cdot frac{r}{{100}} + ….. + frac{A}{{17}} cdot frac{r}{{100}} = A cdot frac{{27}}{{100}},,,,,, Leftrightarrow ,,,,,frac{A}{{17}} cdot frac{r}{{100}}(17 + 16 + ….. + 1) = frac{{27A}}{{100}},left| {,:,A,,,,,,, Leftrightarrow } right.)
( Leftrightarrow ,,,,,,,,frac{r}{{17}} cdot frac{{1 + 17}}{2} cdot 17 = 27,,,,,,, Leftrightarrow ,,,,,,,frac{r}{{17}} cdot frac{{18}}{2} cdot 17 = 27,,,,,,, Leftrightarrow ,,,,,,,r = 3% .)
Ответ: 3.
73В. 15 января планируется взять кредит в банке на 48 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 49% больше, чем сумма, взятая в кредит. Найдите r.
A – кредит сроком на 48 месяцев. Каждый месяц банк начисляет r % на остаток, а заемщик выплачивает эти проценты и сорок восьмую часть от суммы кредита, то есть (frac{A}{{48}}). Таким образам, через 1 месяц остаток долга будет (frac{{47A}}{{48}}), через 2 месяца (frac{{46A}}{{48}}) и так далее.
| Месяц | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{r}{{100}}) | (A — frac{A}{{48}} = frac{{47A}}{{48}}) |
| 2 | (frac{{47A}}{{48}} cdot frac{r}{{100}}) | (frac{{47A}}{{48}} — frac{A}{{48}} = frac{{46A}}{{48}}) |
| … | … | … |
| 48 | (frac{A}{{48}} cdot frac{r}{{100}}) | 0 |
Так как общая сумма, выплаченная банку за весь срок кредитования, оказалась на 49% больше, чем сумма, взятая в кредит, то начисленные проценты равны 49% от суммы кредита, то есть (A cdot frac{{49}}{{100}})
(frac{{48A}}{{48}} cdot frac{r}{{100}} + frac{{47A}}{{48}} cdot frac{r}{{100}} + ….. + frac{A}{{48}} cdot frac{r}{{100}} = A cdot frac{{49}}{{100}},,,,,,, Leftrightarrow ,,,,,,,frac{A}{{48}} cdot frac{r}{{100}}(48 + 47 + ….. + 1) = A cdot frac{{49}}{{100}},left| {,:A,,,,, Leftrightarrow } right.)
( Leftrightarrow ,,,,,,,,,frac{r}{{48}} cdot frac{{1 + 48}}{2} cdot 48 = 49,,,,,,, Leftrightarrow ,,,,,,,frac{r}{{48}} cdot frac{{49}}{2} cdot 48 = 49,,,,,,, Leftrightarrow ,,,,,r = 2% .)
Ответ: 2.
74В. 15 января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 20% больше, чем сумма, взятая в кредит. Найдите r.
A – кредит сроком на 39 месяцев. Каждый месяц банк начисляет r % на остаток, а заемщик выплачивает эти проценты и тридцать девятую часть от суммы кредита, то есть (frac{A}{{39}}). Таким образам, через 1 месяц остаток долга будет (frac{{38A}}{{39}}), через 2 месяца (frac{{37A}}{{39}}) и так далее.
| Месяц | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{r}{{100}}) | (A — frac{A}{{39}} = frac{{38A}}{{39}}) |
| 2 | (frac{{38A}}{{39}} cdot frac{r}{{100}}) | (frac{{38A}}{{39}} — frac{A}{{39}} = frac{{37A}}{{39}}) |
| … | … | … |
| 39 | (frac{A}{{39}} cdot frac{r}{{100}}) | 0 |
Так как общая сумма, выплаченная банку за весь срок кредитования, оказалась на 20% больше, чем сумма, взятая в кредит, то начисленные проценты равны 20% от суммы кредита, то есть (A cdot frac{{20}}{{100}})
(frac{{39A}}{{39}} cdot frac{r}{{100}} + frac{{38A}}{{39}} cdot frac{r}{{100}} + ….. + frac{A}{{39}} cdot frac{r}{{100}} = A cdot frac{{20}}{{100}},,,,,,,, Leftrightarrow ,,,,,,,frac{A}{{39}} cdot frac{r}{{100}}(39 + 38 + ….. + 1) = frac{{20A}}{{100}},left| {,:A,,,,,, Leftrightarrow } right.)
( Leftrightarrow ,,,,,,,,frac{r}{{39}} cdot frac{{1 + 39}}{2} cdot 39 = 20,,,,,,,, Leftrightarrow ,,,,,,,frac{r}{{39}} cdot frac{{40}}{2} cdot 39 = 20,,,,,,, Leftrightarrow ,,,,,,r = 1% .)
Ответ: 1.
75В. В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
A = 16 млн. рублей кредит сроком на n лет так как каждый год долг должен уменьшатся на одну и ту же сумму, то заемщик каждый год выплачивает проценты начисленные за год на остаток и (frac{A}{n}). Тогда остаток через год будет(A — frac{A}{n} = frac{{A cdot (n — 1)}}{n},) через 2 года (frac{{A cdot (n — 2)}}{n}) и так далее.
| Год | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{{25}}{{100}}) | (frac{{A(n — 1)}}{n}) |
| 2 | (frac{{A(n — 1)}}{n} cdot frac{{25}}{{100}}) | (frac{{A(n — 2)}}{n}) |
| … | … | … |
| n | (frac{A}{n} cdot frac{{25}}{{100}}) | 0 |
Общая сумма выплат равна начисленным процентам за n лет плюс сам кредит A:
(frac{{A cdot n}}{n} cdot frac{{25}}{{100}} + frac{{A cdot (n — 1)}}{n} cdot frac{{25}}{{100}} + ….. + frac{A}{n} cdot frac{{25}}{{100}} + A = 38,,,,,, Leftrightarrow ,,,,,,frac{A}{n} cdot frac{{25}}{{100}} cdot (n + (n — 1) + ….. + 1) + A = 38,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,frac{A}{n} cdot frac{1}{4} cdot frac{{1 + n}}{2} cdot n + A = 38,,,,,, Leftrightarrow ,,,,,frac{{16 cdot (1 + n)}}{8} + 16 = 38,,,,,, Leftrightarrow ,,,,,2left( {1 + n} right) = 22,,,,,, Leftrightarrow ,,,,,n = 10.)
Ответ: 10.
76В. В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 47 млн рублей?
A = 20 млн. рублей кредит сроком на n лет так как каждый год долг должен уменьшатся на одну и ту же сумму, то заемщик каждый год выплачивает проценты начисленные за год на остаток и (frac{A}{n}). Тогда остаток через год будет,(A — frac{A}{n} = frac{{A cdot (n — 1)}}{n},) через 2 года (frac{{A cdot (n — 2)}}{n}) и так далее.
| Год | Начисленные % | Остаток после платежа |
| 1 | (A cdot frac{{30}}{{100}}) | (frac{{A(n — 1)}}{n}) |
| 2 | (frac{{A(n — 1)}}{n} cdot frac{{30}}{{100}}) | (frac{{A(n — 2)}}{n}) |
| … | … | … |
| n | (frac{A}{n} cdot frac{{30}}{{100}}) | 0 |
Общая сумма выплат равна начисленным процентам за n лет плюс сам кредит A:
(frac{{A cdot n}}{n} cdot frac{{30}}{{100}} + frac{{A cdot (n — 1)}}{n} cdot frac{{30}}{{100}} + ….. + frac{A}{n} cdot frac{{30}}{{100}} + A = 47,,,,, Leftrightarrow ,,,,frac{A}{n} cdot frac{{30}}{{100}} cdot (n + (n — 1) + ….. + 1) + A = 47,,,,, Leftrightarrow )
(frac{{20}}{n} cdot frac{3}{{10}} cdot frac{{1 + n}}{2} cdot n + 20 = 47,,,,, Leftrightarrow ,,,,,,3left( {1 + n} right) = 27,,,,,,, Leftrightarrow ,,,,,,n = 8.)
Ответ: 8.
77В. Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернет банку в течение первого года кредитования?
A = 1.2 млн. рублей кредит сроком на 24 месяца. Каждый месяц банк начисляет 2% на остаток долга, а заемщик выплачивает эти проценты и уменьшает сумму долга равномерно на одну и ту же величину, то есть на (frac{{1,2}}{{24}} = 0,05) млн. руб.
| месяц | Начисленные % (млн. руб) | Остаток (млн. руб) |
| 1 | (1,2 cdot frac{2}{{100}}) | 1,15 |
| 2 | (1,15 cdot frac{2}{{100}}) | 1,1 |
| … | … | … |
| 12 | (0,65 cdot frac{2}{{100}}) | 0,6 |
| 13 | (0,6 cdot frac{2}{{100}}) | 0,55 |
| … | … | … |
| 24 | (0,05 cdot frac{2}{{100}}) | 0 |
За первый год заемщик выплатит половину суммы кредита 0,6 млн. рублей плюс проценты начисленные за первые 12 месяцев.
(0,6 + 1,2 cdot frac{2}{{100}} + 1,15 cdot frac{2}{{100}} + … + 0,65 cdot frac{2}{{100}} = 0,6 + frac{2}{{100}}left( {1,2 + 1,15 + … + 0,65} right) = )
( = 0,6 + frac{2}{{100}} cdot frac{{1,2 + 0,65}}{2} cdot 12 = 0,6 + frac{{1,85 cdot 12}}{{100}} = 0,822) млн. рублей.
Ответ: 822 000 рублей.
78В. 15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
A = 2,4 млн. рублей кредит сроком на 24 месяца. Каждый месяц банк начисляет 3% на остаток долга, а заемщик выплачивает эти проценты и уменьшает сумму долга равномерно на одну и ту же величину, то есть на (frac{{2,4}}{{24}} = 0,1) млн. руб.
| месяц | Начисленные % (млн. руб) | Остаток (млн. руб) |
| 1 | (2,4 cdot frac{3}{{100}}) | 2,3 |
| 2 | (2,3 cdot frac{3}{{100}}) | 2,2 |
| … | … | … |
| 12 | (1,3 cdot frac{3}{{100}}) | 1,2 |
| 13 | (1,2 cdot frac{3}{{100}}) | 1,1 |
| … | … | … |
| 24 | (0,1 cdot frac{3}{{100}}) | 0 |
За первые 12 месяцев заемщик выплатит половину суммы кредита в 1,2 млн рублей плюс проценты начисленные за первые 12 месяцев.
(1,2 + 2,4 cdot frac{3}{{100}} + 2,3 cdot frac{3}{{100}} + … + 1,3 cdot frac{3}{{100}} = 1,2 + frac{3}{{100}} cdot (2,4 + 2,3 + … + 1,3) = )
( = 1,2 + frac{3}{{100}} cdot frac{{2,4 + 1,3}}{2} cdot 12 = 1,2 + frac{{3 cdot 3,7 cdot 6}}{{100}} = 1,866) млн. рублей.
Ответ: 1 866 000 рублей.
79В. В регионе A среднемесячный доход на душу населения в 2014 году составлял 43 740 рублей и ежегодно увеличивался на 25%. В регионе B среднемесячный доход на душу населения в 2014 году составлял 60 000 рублей. В течение трёх лет суммарный доход жителей региона B увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах A и B стал одинаковым. Найдите m.
В регионе A среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%, то есть в 1,25 раза. Поэтому в 2017 среднемесячный доход на душу населения составит (43740 cdot {1,25^3}).
В регионе B среднемесячный доход на душу населения в 2014 году составлял 60000 рублей. Пусть в 2014 году в регионе B было x жителей. Тогда их суммарный доход был (60000 cdot x), который в течение трех лет увеличивался на 17%, то есть в 1,17 раза и в 2017 году составил (60000 cdot x cdot {1,17^3}). Но при этом количество жителей увеличивалось на m% , то есть в (frac{{100 + m}}{{100}}) раз.
Поэтому количество жителей в 2017 году было (x cdot {left( {frac{{100 + m}}{{100}}} right)^3}). Тогда среднемесячный доход на душу населения в регионе B в 2017 году был ({frac{{60000 cdot x cdot 1,17}}{{x cdot {{left( {frac{{100 + m}}{{100}}} right)}^3}}}^3} = {frac{{60000 cdot 1,17}}{{{{left( {frac{{100 + m}}{{100}}} right)}^3}}}^3}.)
По условию среднемесячный доход на душу населения в регионах A и B в 2017 стал одинаковым.
(43740 cdot {1,25^3} = {frac{{60000 cdot 1.17}}{{{{left( {frac{{100 + m}}{{100}}} right)}^3}}}^3},,,, Leftrightarrow ,,,,,,,,{left( {frac{{100 + m}}{{100}}} right)^3} = frac{{60000 cdot {{1,17}^3}}}{{43740 cdot {{1,25}^3}}},,,,,,, Leftrightarrow )
({left( {frac{{100 + m}}{{100}}} right)^3} = frac{{1000 cdot {{1,17}^3}}}{{729 cdot {{1,25}^3}}},,,,,, Leftrightarrow ,,,,,,frac{{100 + m}}{{100}} = frac{{10 cdot 1,17}}{{9 cdot 1,25}},,,,,, Leftrightarrow ,,,,,,frac{{100 + m}}{{100}} = frac{{26}}{{25}},,,,,, Leftrightarrow ,,,,,,m = 4.)
Ответ: 4.
80В. В Чистополе среднемесячный доход на душу населения в 2015 году составлял 27 500 рублей и ежегодно увеличивался на 28%. В Казани среднемесячный доход на душу населения в 2015 году составлял 39 600 рублей. В течение двух лет суммарный доход жителей Казани увеличивался на 12% ежегодно, а население увеличивалось на x% ежегодно. В 2017 году среднемесячный доход на душу населения в Чистополе и Казани стал одинаковым. Найдите x.
В Чистополе среднемесячный доход на душу населения в 2015 году составлял 27500 рублей и ежегодно увеличивался на 28%, то есть в 1,28 раза. Поэтому в 2017 среднемесячный доход на душу населения составит (27500 cdot {1,28^2}).
В Казани среднемесячный доход на душу населения в 2015 году составлял 39600 рублей. Пусть в 2015 году в Казани было n жителей. Тогда их суммарный доход был (39600 cdot n), который в течении двух лет увеличивался на 12%, то есть в 1,12 раза и в 2017 году составил (39600 cdot n cdot {1,12^2}). Но при этом количество жителей увеличивалось на x%, то есть в (frac{{100 + x}}{{100}}) раз.
Поэтому количество жителей в 2017 году было (n cdot {left( {frac{{100 + x}}{{100}}} right)^2}). Тогда среднемесячный доход на душу населения в Казани 2017 году был:
({frac{{39600 cdot n cdot 1,12}}{{n cdot {{left( {frac{{100 + x}}{{100}}} right)}^2}}}^2} = {frac{{39600 cdot 1,12}}{{{{left( {frac{{100 + x}}{{100}}} right)}^2}}}^2}.)
По условию среднемесячный доход на душу населения в Чистополе и Казани в 2017 стал одинаковым.
(27500 cdot {1,28^2} = {frac{{39600 cdot 1,12}}{{{{left( {frac{{100 + x}}{{100}}} right)}^2}}}^2},,,,, Leftrightarrow ,,,,,,,,{left( {frac{{100 + x}}{{100}}} right)^2} = frac{{39600 cdot {{1,12}^2}}}{{27500 cdot {{1,28}^2}}},,,,,, Leftrightarrow );
( Leftrightarrow ,,,,,,,{left( {frac{{100 + x}}{{100}}} right)^2} = frac{{36 cdot {{1,12}^2}}}{{25 cdot {{1,28}^2}}},,,,, Leftrightarrow ,,,,,frac{{100 + x}}{{100}} = frac{{6 cdot 1,12}}{{5 cdot 1,28}},,,,, Leftrightarrow ,,,,,frac{{100 + x}}{{100}} = frac{{6 cdot 7}}{{5 cdot 8}},,,,, Leftrightarrow ,,,,x = 5.)
Ответ: 5.
81В. 15 января планируется взять кредит в банке на 16 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 2,34 млн рублей?
A — кредит в млн. рублей сроком на 16 месяцев. Каждый месяц банк начисляет 2% на остаток, а заемщик выплачивает эти начисленные проценты и шестнадцатую часть от суммы кредита, то есть (frac{A}{{16}}). Таким образом, через 1 месяц остаток долга будет (frac{{15A}}{{16}}), через 2 месяца (frac{{14A}}{{16}}) и так далее.
| Год | Начисленные % (млн. руб) | Остаток (млн. руб) |
| 1 | (A cdot frac{2}{{100}}) | (A — frac{A}{{16}} = frac{{15A}}{{16}}) |
| 2 | (frac{{15A}}{{16}} cdot frac{2}{{100}}) | (frac{{15A}}{{16}} — frac{A}{{16}} = frac{{14A}}{{16}}) |
| … | … | … |
| 16 | (frac{A}{{16}} cdot frac{2}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита А и начисленным процентам.
(A + frac{{16A}}{{16}} cdot frac{2}{{100}} + frac{{15A}}{{16}} cdot frac{2}{{100}} + … + frac{A}{{16}} cdot frac{2}{{100}} = 2,34,,,,, Leftrightarrow ,,,,,A + frac{A}{{16}} cdot frac{2}{{100}} cdot left( {16 + 15 + … + 1} right) = 2,34,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,A + frac{A}{{800}} cdot frac{{1 + 16}}{2} cdot 16 = 2,34,,,,,, Leftrightarrow ,,,,,A + frac{{17A}}{{100}} = 2,34,,,,, Leftrightarrow ,,,,1,17A = 2,34,,,,,,, Leftrightarrow ,,,,,A = 2.)
Ответ: 2 000 000 рублей.
82В. 15 января планируется взять кредит в банке на 10 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 4 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного погашения равнялась 1,83 млн рублей?
A — кредит в млн. рублей сроком на 10 месяцев. Каждый месяц банк начисляет 4% на остаток, а заемщик выплачивает эти проценты начисленные и десятую часть от суммы кредита, то есть (frac{A}{{10}}). Таким образом, через 1 месяц остаток долга будет (frac{{9A}}{{10}}), через 2 месяца (frac{{8A}}{{10}}) и так далее.
| Год | Начисленные % (млн. руб) | Остаток (млн. руб) |
| 1 | (A cdot frac{4}{{100}}) | (A — frac{A}{{10}} = frac{{9A}}{{10}}) |
| 2 | (frac{{9A}}{{10}} cdot frac{4}{{100}}) | (frac{{9A}}{{10}} — frac{A}{{10}} = frac{{8A}}{{10}}) |
| … | … | … |
| 10 | (frac{A}{{10}} cdot frac{4}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита А и начисленным процентам.
(A + frac{{10A}}{{10}} cdot frac{4}{{100}} + frac{{9A}}{{10}} cdot frac{4}{{100}} + … + frac{A}{{10}} cdot frac{4}{{100}} = 1,83,,,,,, Leftrightarrow ,,,,,,A + frac{A}{{10}} cdot frac{4}{{100}} cdot left( {10 + 9 + … + 1} right) = 1,83,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,A + frac{A}{{250}} cdot frac{{1 + 10}}{2} cdot 10 = 1,83,,,,,, Leftrightarrow ,,,,,A + frac{{11A}}{{50}} = 1,83,,,,,, Leftrightarrow ,,,,,1,22A = 1,83,,,,, Leftrightarrow ,,,,,,A = 1,5) млн. руб.
Ответ: 1 500 000.
83В. 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n + 1) месяц. Условия его возврата таковы:
—1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
—cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
—15-го числа n-го месяца долг составит 200 тысяч рублей;
—к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.
Так как в конце n– го месяца долг составил 200 тысяч рублей, то за n месяцев долг был уменьшен на (1000 — 200 = 800) тысяч рублей. Учитывая, что первые n месяцев долг уменьшался на 40 тысяч рублей каждый месяц, то (n = frac{{800}}{{40}} = 20).
| Год | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (1000 cdot frac{r}{{100}}) | (1000 — 40 = 960) |
| 2 | (960 cdot frac{r}{{100}}) | (960 — 40 = 920) |
| … | … | … |
| 20 | (240 cdot frac{r}{{100}}) | (240 — 40 = 200) |
| 21 | (200 cdot frac{r}{{100}}) | (200 — 200 = 0) |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно, начисленные проценты равны: (1378 — 1000 = 378) тысяч рублей.
(1000 cdot frac{r}{{100}} + 960 cdot frac{r}{{100}} + … + 240 cdot frac{r}{{100}} + 200 cdot frac{r}{{100}} = 378,,,,,, Leftrightarrow ,,,,,,)
( Leftrightarrow ,,,,,frac{r}{{100}} cdot left( {1000 + 960 + .. + 200} right) = 378,,,,, Leftrightarrow ,,,,,frac{r}{{100}} cdot frac{{1000 + 200}}{2} cdot 21 = 378,,,, Leftrightarrow ,,,,126 cdot r = 378,,,, Leftrightarrow ,,,,r = 3.)
Ответ: 3.
84В. 15-го декабря планируется взять кредит в банке на 1200 тысяч рублей на (n + 1) месяц. Условия его возврата таковы:
—1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
—cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—15-го числа каждого месяца с 1-го по n-й долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;
—15-го числа n-го месяца долг составит 400 тысяч рублей;
—к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1288 тысяч рублей.
Так как в конце n– го месяца долг составил 400 тысяч рублей, то за n месяцев долг был уменьшен на (1200 — 400 = 800) тысяч рублей. Учитывая, что первые n месяцев долг уменьшался на 80 тысяч рублей каждый месяц, то (n = frac{{800}}{{80}} = 10).
| Год | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (1200 cdot frac{r}{{100}}) | (1200 — 80 = 1120) |
| 2 | (1120 cdot frac{r}{{100}}) | (1120 — 80 = 1040) |
| … | … | … |
| 10 | (480 cdot frac{r}{{100}}) | (480 — 80 = 400) |
| 11 | (400 cdot frac{r}{{100}}) | (400 — 400 = 0) |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно, начисленные проценты равны: (1288 — 1200 = 88) тысяч рублей.
(1200 cdot frac{r}{{100}} + 1120 cdot frac{r}{{100}} + … + 480 cdot frac{r}{{100}} + 400 cdot frac{r}{{100}} = 88,,,,, Leftrightarrow )
(frac{r}{{100}} cdot left( {1200 + 1120 + … + 400} right) = 88,,,,, Leftrightarrow ,,,,,frac{r}{{100}} cdot frac{{1200 + 400}}{2} cdot 11 = 88,,,,, Leftrightarrow ,,,,,88 cdot r = 88,,,,,, Leftrightarrow ,,,,,r = 1.)
Ответ: 1.
85В. 15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?
A – кредит в тыс. рублей сроком на 26 месяцев.
В течение первых 25 месяцев банк начисляет 3% на остаток, а заемщик выплачивает эти проценты и еще 20 тыс. рублей. Таким образом, через 1 месяц остаток долга будет A–20, через 2 месяца A–40 и так далее, а через 25 месяцев A–500.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{3}{{100}}) | A–20 |
| 2 | ((A — 20) cdot frac{3}{{100}}) | A–40 |
| … | … | … |
| 25 | ((A — 480) cdot frac{3}{{100}}) | A–500 |
| 26 | ((A — 500) cdot frac{3}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно:
(A + A cdot frac{3}{{100}} + (A — 20) cdot frac{3}{{100}} + … + (A — 480) cdot frac{3}{{100}} + (A — 500) cdot frac{3}{{100}} = 1407,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,A + frac{3}{{100}}(A + (A — 20) + … + (A — 480) + (A — 500)) = 1407,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,A + frac{3}{{100}} cdot frac{{A + A — 500}}{2} cdot 26 = 1407,,,,, Leftrightarrow ,,,,,A + frac{{3 cdot (A — 250) cdot 26}}{{100}} = 1407,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,100 cdot A + 78 cdot A — 1950 = 140700,,,,, Leftrightarrow ,,,,178 cdot A = 160200,,,,, Leftrightarrow ,,,,,A = 900.)
Следовательно, долг в конце 25-го месяца равен: (A — 500 = 900 — 500 = 400) тысяч рублей.
Ответ: 400 000.
86В. 15-го декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца кредит должен быть полностью погашен. Какой долг будет 15-го числа 30-го месяца, если общая сумма выплат после полного погашения кредита составит 1503 тысячи рублей?
A = 1100 тыс. рублей кредит сроком на 31 месяц.
В течение первых 30 месяцев банк начисляет 2% на остаток, а заемщик выплачивает эти проценты и еще х тыс. рублей. Таким образом, через 1 месяц остаток долга будет A–х, через 2 месяца A–2х и так далее, а через 30 месяцев A–30х.
| месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{2}{{100}}) | A–х |
| 2 | ((A — x) cdot frac{2}{{100}}) | A–2x |
| … | … | … |
| 30 | ((A — 29x) cdot frac{2}{{100}}) | A–30x |
| 31 | ((A — 30x) cdot frac{2}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно, начисленные проценты равны: (1503 — 1100 = 403) тысяч рублей.
(A cdot frac{2}{{100}} + (A — x) cdot frac{2}{{100}} + … + (A — 29x) cdot frac{2}{{100}} + (A — 30x) cdot frac{2}{{100}} = 403,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,frac{2}{{100}}(A + (A — x) + … + (A — 29x) + (A — 30x)) = 403,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,frac{2}{{100}} cdot frac{{A + A — 30x}}{2} cdot 31 = 403,,,,, Leftrightarrow ,,,,,frac{{2A — 30x}}{{100}} = 13,,,,, Leftrightarrow ,,,,,2200 — 30x = 1300,,,, Leftrightarrow ,,,,x = 30.)
Таким образам, долг 15–го числа 30–го месяца будет равен: (A — 30x = 1100 — 30 cdot 30 = 200) тысяч рублей.
Ответ: 200 000.
87В. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
A – кредит в тыс. рублей сроком на 21 месяц.
В течение первых 20 месяцев банк начисляет 3% на остаток, а заёмщик выплачивает эти проценты и ещё 30 тысяч рублей. Таким образом, через 1 месяц остаток долга будет A–30, через 2 месяца A–60 и так далее, а через 20 месяцев A–600.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{3}{{100}}) | A–30 |
| 2 | ((A — 30) cdot frac{3}{{100}}) | A–60 |
| … | … | … |
| 20 | ((A — 570) cdot frac{3}{{100}}) | A–600 |
| 21 | ((A — 600) cdot frac{3}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно:
(A + A cdot frac{3}{{100}} + (A — 30) cdot frac{3}{{100}} + … + (A — 570) cdot frac{3}{{100}} + (A — 600) cdot frac{3}{{100}} = 1604,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,A + frac{3}{{100}} cdot (A + (A — 30) + … + (A — 570) + (A — 600)) = 1604,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,A + frac{3}{{100}} cdot frac{{A + A — 600}}{2} cdot 21 = 1604,,,,, Leftrightarrow ,,,,,A + frac{{63}}{{100}} cdot (A — 300) = 1604,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,100A + 63A — 18900 = 160400,,,,, Leftrightarrow ,,,,163A = 179300,,,,,,, Leftrightarrow ,,,,,A = 1100) тыс. рублей.
Ответ: 1 100 000 рублей.
88В. 15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
A – кредит в тыс. рублей сроком на 13 месяцев.
В течение первых 12 месяцев банк начисляет 2% на остаток, а заемщик выплачивает эти проценты и еще 50 тыс. рублей. Таким образом, через 1 месяц остаток долга будет A–50, через 2 месяца A–100 и так далее, а через 12 месяцев A–600.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{2}{{100}}) | A–50 |
| 2 | ((A — 50) cdot frac{2}{{100}}) | A–100 |
| … | … | … |
| 25 | ((A — 550) cdot frac{2}{{100}}) | A–600 |
| 26 | ((A — 600) cdot frac{2}{{100}}) | 0 |
Общая сумма выплат после полного погашения кредита равна сумме самого кредита и начисленным процентам. Следовательно:
(A + A cdot frac{2}{{100}} + (A — 50) cdot frac{2}{{100}} + … + (A — 550) cdot frac{2}{{100}} + (A — 600) cdot frac{2}{{100}} = 804,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,A + frac{2}{{100}}(A + (A — 50) + … + (A — 550) + (A — 600)) = 804,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,A + frac{{26}}{{100}} cdot (A — 300) = 804,,,,, Leftrightarrow ,,,,A + frac{2}{{100}} cdot frac{{A + A — 600}}{2} cdot 13 = 804,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,100 cdot A + 26 cdot A — 7800 = 80400,,,,, Leftrightarrow ,,,,126 cdot A = 88200,,,,, Leftrightarrow ,,,,,A = 700.)
Ответ: 700 000 рублей.
89В. 15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 20-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
(A = 300) тысяч рублей кредит сроком на 21 месяц.
Так как первые 20 месяцев долг уменьшался на одну и ту же сумму и 15–го числа 20–го месяца составил 100 тысяч рублей, то он уменьшался на (frac{{300 — 100}}{{20}} = 10) тысяч рублей.
Следовательно, 15–го числа 1–го месяца долг равен (300 — 10 = 290), 2–го месяца (290 — 10 = 280) и так далее, а в конце 20–го месяца 100 тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (300 cdot frac{2}{{100}}) | 290 |
| 2 | (290 cdot frac{2}{{100}}) | 280 |
| … | … | … |
| 20 | (110 cdot frac{2}{{100}}) | 100 |
| 21 | (100 cdot frac{2}{{100}}) | 0 |
Общая сумма выплат после полного погашение кредита равна сумме самого кредита (300 тысяч рублей) и начисленным процентам.
(begin{array}{l}300 + 300 cdot frac{2}{{100}} + 290 cdot frac{2}{{100}} + … + 110 cdot frac{2}{{100}} + 100 cdot frac{2}{{100}} = 300 + frac{2}{{100}} cdot left( {300 + 290 + … + 110 + 100} right) = \end{array})
( = 300 + frac{2}{{100}} cdot frac{{300 + 100}}{2} cdot 21 = 300 + 84 = 384) тыс. рублей.
Ответ: 384 000.
90В. 15-го декабря планируется взять кредит в банке на сумму 500 тысяч рублей на 31 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 30-го месяца долг составит 200 тысяч рублей;
— к 15-му числу 31-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
(A = 500) тысяч рублей кредит сроком на 31 месяц.
Так как первые 30 месяцев долг уменьшался на одну и ту же сумму и 15–го числа 30–го месяца составил 200 тысяч рублей то он уменьшался на (frac{{500 — 200}}{{30}} = 10) тысяч руб.
Следовательно, 15–го числа 1–го месяца долг равен (500 — 10 = 490), 2–го месяца (490 — 10 = 480) и так далее, а в конце 30–го месяца 200 тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (500 cdot frac{1}{{100}}) | 490 |
| 2 | ()(490 cdot frac{1}{{100}}) | 480 |
| … | … | … |
| 20 | (210 cdot frac{1}{{100}}) | 200 |
| 21 | (200 cdot frac{1}{{100}}) | 0 |
Общая сумма выплат после полного погашение кредита равна сумме самого кредита (500 тысяч рублей) и начисленным процентам.
(500 + 500 cdot frac{1}{{100}} + 490 cdot frac{1}{{100}} + .. + 210 cdot frac{1}{{100}} + 200 cdot frac{1}{{100}} = 500 + frac{1}{{100}} cdot left( {500 + 490 + … + 210 + 200} right) = )
( = 500 + frac{1}{{100}} cdot left( {500 + 490 + … + 210 + 200} right) = 500 + frac{1}{{100}} cdot frac{{500 + 200}}{2} cdot 31 = 500 + frac{{217}}{2} = 608,5) тысяч рублей.
Ответ: 608 500.
91В. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на 3 млн рублей. Найдите наименьший размер первоначального вклада, при котором банк за четыре года начислит на вклад больше 5 млн рублей.
А – первоначальный вклад (в млн. руб); А – целое. Срок кредита 4 года, под 10% годовых.
| Год | Сумма в начале года (млн. руб) | Сумма в конце года (млн. руб) |
| 1 | (A) | (A cdot 1,1) |
| 2 | ()(A cdot 1,1) | (A cdot 1,1 cdot 1.1) |
| 3 | (A cdot {1,1^2} + 3) | ((A cdot {1,1^2} + 3) cdot 1,1) |
| 4 | ((A cdot {1,1^2} + 3) cdot 1,1 + 3) | (((A cdot {1,1^2} + 3)1,1 + 3) cdot 1,1) |
Так как банк за 4 года, должен начислить больше 5 млн. рублей, то в конце четвёртого года сумма должна быть больше чем сумма положенная на вклад (это А+3+3 млн. руб.) и плюс к ней начисленные проценты (это 5 млн. рублей).
(left( {left( {A cdot {{1,1}^2} + 3} right) cdot 1,1 + 3} right)1,1,,, > ,,A + 3 + 3 + 5,,,,, Leftrightarrow ,,,,,A cdot {1,1^4} + 3 cdot {1,1^2} + 3 cdot 1,1,,, > A + 11,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,1,4641A — A,,, > ,,11 — 3,3 — 3,63,,,,, Leftrightarrow ,,,,,,0,4641A,,, > 4,07,,,,,, Leftrightarrow ,,,,,A,, > ,frac{{40700}}{{4641}},,,,,,, Leftrightarrow ,,,,,A,, > ,8frac{{3572}}{{4641}}.)
Так как А должно быть наименьшим и целым, то А = 9 млн. рублей.
Ответ: 9.
92В. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года банк увеличивает вклад на 20% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на 5 млн рублей. Найдите наименьший размер первоначального вклада, при котором банк за четыре года начислит на вклад больше 12 млн рублей.
А – первоначальный вклад (в млн. руб); А – целое. Срок кредита 4 года, под 20% годовых.
| Год | Сумма в начале года (млн. руб) | Сумма в конце года (млн. руб) |
| 1 | (A) | (A cdot 1,2) |
| 2 | ()(A cdot 1,2) | (A cdot 1,2 cdot 1.2) |
| 3 | (A cdot {1,2^2} + 5) | ((A cdot {1,2^2} + 5) cdot 1,2) |
| 4 | ((A cdot {1,2^2} + 5) cdot 1,2 + 5) | (((A cdot {1,2^2} + 5)1,2 + 5) cdot 1,2) |
Так как банк за 4 года, должен начислить больше 12 млн. рублей ,то в конце четвёртого года сумма должна быть больше чем сумма положенная на вклад (это А+5+5 млн. руб.) и плюс к ней начисленные проценты (это 12 млн. рублей).
(left( {left( {A cdot {{1,2}^2} + 5} right)1,2 + 5} right)1,2,, > ,,A + 5 + 5 + 12,,,,, Leftrightarrow ,,,,,,A cdot {1,2^4} + 5 cdot {1,2^2} + 5 cdot 1,2,, > ,,A + 10 + 12,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,2,0736A — A,,, > ,,22 — 6 — 7,2,,,,,, Leftrightarrow ,,,,,,1,0736A,,, > ,,8,8,,,,,, Leftrightarrow ,,,,,A,,, > ,,frac{{88000}}{{10736}},,,,,,, Leftrightarrow ,,,,A,, > ,,8frac{{12}}{{61}}.)
Так как А должно быть наименьшим и целым, то А = 9 млн. рублей.
Ответ: 9.
93В. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на x млн рублей, где x — целое число. Найдите наименьшее значение x, при котором банк за четыре года начислит на вклад больше 7 млн рублей.
А = 10 млн. рублей вклад сроком на 4 года, под 10% годовых.
| Год | Сумма в начале года (млн. руб) | Сумма в конце года (млн. руб) |
| 1 | (10) | (10 cdot 1,1) |
| 2 | (10 cdot 1,1) | (10 cdot 1,1 cdot 1,1) |
| 3 | (10 cdot {1,1^2} + x) | ((10 cdot {1,1^2} + x) cdot 1,1) |
| 4 | ((10 cdot {1,1^2} + x) cdot 1,1 + x) | (((10 cdot {1,1^2} + x) cdot 1,1 + x) cdot 1,1) |
Так как банк за 4 года должен начислить больше 7млн. рублей, то в конце четвёртого года сумма должна быть больше чем сумма положенная на вклад (это 10+х+х млн. рублей) и плюс к ней начисленные проценты (это 7млн. рублей).
(left( {left( {10 cdot {{1,1}^2} + x} right)1,1 + x} right)1,1,,, > ,,10 + x + x + 7,,,,,, Leftrightarrow ,,,,,,10 cdot {1,1^4} + {1,1^2}x + 1,1x,,, > ,,2x + 17,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,2,31x — 2x,,, > ,,17 — 14,641,,,,, Leftrightarrow ,,,,,,0,31x,,, > ,,2,359,,,,, Leftrightarrow ,,,,x,, > ,frac{{2359}}{{310}},,,,, Leftrightarrow ,,,,,x,, > ,7frac{{189}}{{310}}.)
Так как х должен быть наименьшим и целым, то х = 8 млн. рублей.
Ответ: 8.
94В. Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 20% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на x млн рублей, где x — целое число. Найдите наименьшее значение x, при котором банк за четыре года начислит на вклад больше 24 млн рублей.
А = 20 млн. рублей вклад сроком на 4 года, под 20% годовых.
| Год | Сумма в начале года (млн. руб) | Сумма в конце года (млн. руб) |
| 1 | (20) | (20 cdot 1,2) |
| 2 | (20 cdot 1,2) | (20 cdot 1,2 cdot 1,2) |
| 3 | (20 cdot {1,2^2} + x) | ((20 cdot {1,2^2} + x) cdot 1,2) |
| 4 | ((20 cdot {1,2^2} + x) cdot 1,2 + x) | (((20 cdot {1,2^2} + x) cdot 1,2 + x) cdot 1,2) |
Так как банк за 4 года должен начислить больше 24млн. рублей, то в конце четвёртого года сумма должна быть больше чем сумма положенная на вклад (это 20+х+х млн. рублей) и плюс к ней начисленные проценты (это 24млн.рублей).
(left( {left( {20 cdot {{1,2}^2} + x} right)1,2 + x} right)1,12,, > ,,20 + x + x + 24,,,,, Leftrightarrow ,,,,20 cdot {1,2^4} + {1,2^2}x + 1,2x,,, > ,,2x + 44,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,frac{{{6^2}}}{{{5^2}}}x + frac{6}{5}x — 2x,,, > ,,44 — 20 cdot frac{{{6^4}}}{{{5^4}}},,,,, Leftrightarrow ,,,,,frac{{36 + 30 — 50}}{{{5^2}}}x,,, > ,,44 — frac{{4 cdot {6^4}}}{{{5^3}}},,,, Leftrightarrow ,,,,)
( Leftrightarrow ,,,,,,frac{{16}}{{{5^2}}}x,, > ,frac{{4 cdot left( {11 cdot {5^3} — {6^4}} right)}}{{{5^3}}},,,,,, Leftrightarrow ,,,,,,,x,, > ,frac{{79}}{{20}},,,,,,, Leftrightarrow ,,,,,x,, > ,,3frac{{19}}{{20}}.)
Так как х должен быть наименьшим и целым, то х = 4 млн. рублей.
Ответ: 4.
95В. В банке A начисляют на вклад 40% годовых, а в банке Б 60% годовых. Иван Петрович положил часть денег в банк А, а оставшуюся сумму в банк Б. Через два года сумма положенная в банки увеличилась на 150%. Какую часть денег он положил в банк А?
Пусть Иван Петрович владеет суммой S из которой х он положил в банк А, а (S — x) в банк Б. В банке А за год вклад увеличивается на 40%, то есть в (frac{{100 + 40}}{{100}} = 1,4) раза, а в банке Б на 60%, то есть (frac{{100 + 60}}{{100}} = 1,6) раза.
Таким образом, через 2 года в банке А сумма на вкладе будет равна ({1,4^2} cdot x), а в банке Б ({1,6^2} cdot left( {S — x} right)).
Так как через 2 года сумма положенная в банки (S) увеличилась на 150%, то она увеличилась в (frac{{100 + 150}}{{100}} = 2,5) раза, то есть стала равна (2,5S).
({1,4^2} cdot x + {1,6^2}left( {S — x} right) = 2,5S,,,,, Leftrightarrow ,,,,,1,96x + 2,56S — 2,56x = 2,5S,,,,,, Leftrightarrow ,,,,,0,6x = 0,06S,,,,, Leftrightarrow ,,,,x = frac{1}{{10}}S.)
Следовательно, Иван Петрович положил в банк А (frac{1}{{10}}) часть от суммы которой владел.
Ответ: (frac{1}{{10}}).
96В. Инна Николаевна получила кредит в банке под определенный процент годовых. В конце первого и второго года в счет погашения кредита она возвращала в банк 1/9 от всей суммы, которую она должна была банку к этому времени. В конце третьего года в счет полного погашения кредита Инна Николаевна внесла в банк сумму, которая на 12,5% превышала величину полученного кредита. Какой процент годовых по кредиту в данном банке?
Пусть Инна Николаевна получила кредит сумма которого равна А под х% годовых. Следовательно, в конце каждого года остаток долга увеличивался в (frac{{100 + x}}{{100}} = t) раз. Так как в конце первого и второго годов она возвращала в банк (frac{1}{9}) от всей суммы, которую она должна была банку к этому времени, то ее долг оставался (frac{8}{9}) от этой суммы.
| Год | Долг в конце года до выплаты | Выплата | Остаток долга после выплаты |
| 1 | (At) | (frac{1}{9}At) | (frac{8}{9}At) |
| 2 | (frac{8}{9}A{t^2}) | (frac{1}{9} cdot frac{8}{9}A{t^2}) | ({left( {frac{8}{9}} right)^2}A{t^2}) |
| 3 | ({left( {frac{8}{9}} right)^2}A{t^3}) | ({left( {frac{8}{9}} right)^2}A{t^3}) | 0 |
По условию задачи третья выплата на 12,5% больше суммы кредита, то есть она равна 112,5% от А, то есть (frac{{112,5}}{{100}}A = 1,125A = 1frac{1}{8}A = frac{9}{8}A.) Следовательно:
({left( {frac{8}{9}} right)^2} cdot A{t^3} = frac{{112,5}}{{100}}A,,,,,, Leftrightarrow ,,,,,,{left( {frac{8}{9}} right)^2} cdot A{t^3} = frac{9}{8}A,,,,,, Leftrightarrow ,,,,,,{left( {frac{8}{9}} right)^2}{t^3} = frac{9}{8},,,,, Leftrightarrow ,,,,,{t^3} = {left( {frac{9}{8}} right)^3},,,,,, Leftrightarrow ,,,,,,t = frac{9}{8}.)
(frac{{100 + x}}{{100}} = frac{9}{8},,,,,, Leftrightarrow ,,,,,,800 + 8x = 900,,,,, Leftrightarrow ,,,,,,x = frac{{100}}{8} = 12,5% ,.,,,,)
Ответ: 12,5.
97В. Ангелина Денисовна Курбанова открыла вклад в банке на 1 млн рублей сроком на 3 года. В конце каждого года на сумму лежащую в банке начисляется 20%. В конце каждого из первых 2-х лет (после начисления процентов) Ангелина Денисовна снимает одинаковую сумму. Эта сумма должна быть такой, чтобы через 3 года после начисления процентов на 3-й год у нее на счету было не менее 1,1 млн рублей. Какую максимальную сумму она может снимать? Ответ округлите до целой тысячи рублей в меньшую сторону.
А = 1 млн. рублей вклад сроком на 3 года. В конце каждого года вклад увеличивается на 20%, то есть в (frac{{100 + 20}}{{100}} = 1,2) раза. Пусть в конце первого и второго годов Ангелина Денисовна снимает сумму х тысяч рублей. Тогда в конце первого года на вкладе останется сумма: (1,2A — x); в конце второго года: (left( {1,2A — x} right)1,2 — x); в конце третьего года: (left( {left( {1,2A — x} right)1,2 — x} right)1,2).
По условию задачи: (left( {left( {1,2A — x} right)1,2 — x} right)1,2,, ge ,,1100.)
Так как х в тыс. рублей, то А = 1000 тыс. рублей. Следовательно:
({1,2^3} cdot 1000 — {1,2^2}x — 1,2x,, ge ,,1100,,,,, Leftrightarrow ,,,,, — 2,64x,, ge ,,1100 — 1728,,,,, Leftrightarrow )
( Leftrightarrow ,,,,, — 2,64x,, ge ,, — 628,,,,,, Leftrightarrow ,,,,,x,, le ,,frac{{62800}}{{264}},,,,,,, Leftrightarrow ,,,,,,x,, le ,,frac{{7850}}{{33}},,,,,,, Leftrightarrow ,,,,,,x,, le ,,237frac{{29}}{{33}}.)
Так как х наибольшее и целое, то х = 237 тысяч рублей.
Ответ: 237.
98В. Предприниматель Олег Михайлович вложил 2/5 своего капитала в покупку товара A, 50% оставшегося капитала в покупку товара Б, а оставшиеся средства в покупку товара В. При реализации товара А Олег Михайлович получил прибыль в размере 20%, а при реализации товара Б убыток 10%. Какой процент прибыли получил Олег Михайлович от реализации товара В, если общая прибыль от реализации всех трех товаров составила 11%?
Пусть капитал равен S. Тогда (frac{2}{5}S) вложили в покупку товара А; оставшийся капитал (frac{3}{5}S), 50% (то есть половину) вложили в покупку товара Б, то есть (frac{3}{{10}}S) и оставшиеся средства (left( {S — frac{2}{5}S — frac{3}{{10}}S = frac{3}{{10}}S} right)) в покупку товара В.
После реализации товара А Олег Михайлович получил сумму: (frac{2}{5}S cdot 1,2). После реализации товара Б сумму: (frac{3}{{10}}S cdot 0,9).
Пусть при реализация товара В была получена прибыль х%, то есть сумма (frac{3}{{10}}S cdot frac{{100 + x}}{{100}}.) Тогда:
(frac{2}{5}S cdot 1,2 + frac{3}{{10}}S cdot 0,9 + frac{3}{{10}}S cdot frac{{100 + x}}{{100}} = S cdot frac{{111}}{{100}},,left| {,:,} right.,S,,,,, Leftrightarrow ,,,,,frac{2}{5} cdot frac{6}{5} + frac{3}{{10}} cdot frac{9}{{10}} + frac{3}{{10}} cdot frac{{100 + x}}{{100}} = frac{{111}}{{100}},,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,frac{3}{{10}} cdot frac{{100 + x}}{{100}} = frac{{36}}{{100}},,,,,, Leftrightarrow ,,,,,,100 + x = 120,,,,,,, Leftrightarrow ,,,,,,x = 20.)
Ответ: 20.
99В. Алина Алексеевна взяла в кредит 1,8 млн. рублей на 36 месяцев. По договору Алина Алексеевна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 3%, а затем уменьшается на сумму, уплаченную Алиной Алексеевной банку в конце месяца. Суммы, выплачиваемые Алиной Алексеевной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и те же величину каждый месяц. На сколько рублей больше Алина Алексеевна вернет банку в течение первого года кредитования по сравнению с третьим годом?
Сумма долга уменьшается равномерно на (frac{{1,8}}{{36}} = 0,05) млн. рублей в месяц.
| Месяц | Начисленные % (млн. руб) | Остаток (млн. руб) |
| 1 | (1,8 cdot frac{3}{{100}}) | 1,75 |
| 2 | ()(1,75 cdot frac{3}{{100}}) | 1,7 |
| … | … | … |
| 12 | (1,25 cdot frac{3}{{100}}) | 1,2 |
| …… | ……. | …… |
| 25 | (0,6 cdot frac{3}{{100}}) | 0,55 |
| 26 | (0,55 cdot frac{3}{{100}}) | 0,5 |
| … | … | … |
| 36 | (0,05 cdot frac{3}{{100}}) | 0 |
Сумма, выплаченная за первый год равна (12 cdot 0,05) плюс проценты, начисленные за первые 12 месяцев:
(12 cdot 0,05 + 1,8 cdot frac{3}{{100}} + 1,75 cdot frac{3}{{100}} + … + 1,25 cdot frac{3}{{100}} = 0,6 + frac{3}{{100}} cdot frac{{1,8 + 1,25}}{2} cdot 12 = 0,6 + 0,549 = 1,149)
Сумма, выплаченная за третий год равна (12 cdot 0,05) плюс проценты, начисленные с 25–го по 36–й месяц:
(12 cdot 0,05 + 0,6 cdot frac{3}{{100}} + 0,55 cdot frac{3}{{100}} + … + 0,05 cdot frac{3}{{100}} = 0,6 + frac{3}{{100}} cdot frac{{0,6 + 0,05}}{2} cdot 12 = 0,6 + 0,117 = 0,717.)
Следовательно, разница между первым и третьим годом: (1,149 — 0,717 = 0,432) млн. рублей.
Ответ: 432 000.
100В. Данил Витальевич 1 апреля планирует взять кредит в банке на 24 месяца. Условия возврата таковы:
— 15 числа каждого месяца долг возрастает на r% (r – целое число) по сравнению с началом текущего месяца;
— с 16 по 28 число необходимо выплатить часть долга так, чтобы на начало каждого следующего месяца долг уменьшался на одну и ту же сумму по сравнению с предыдущим месяцем.
Найдите наименьшую возможную ставку r, если известно, что за второй год было выплачено более чем на 20% меньше, нежели за первый год.
А – кредит сроком на 24 месяца под r% в месяц.
Долг в течение 24 месяцев уменьшается равномерно, то есть на (frac{A}{{24}}).
| Месяц | Начисленные % | Остаток |
| 1 | (A cdot frac{r}{{100}}) | (A — frac{A}{{24}} = frac{{23A}}{{24}}) |
| 2 | ()(frac{{23A}}{{24}} cdot frac{r}{{100}}) | (frac{{23A}}{{24}} — frac{A}{{24}} = frac{{22A}}{{24}}) |
| ….. | …… | …… |
| 12 | (frac{{13A}}{{24}} cdot frac{r}{{100}}) | (frac{{13A}}{{24}} — frac{A}{{24}} = frac{{12A}}{{24}}) |
| 13 | (frac{{12A}}{{24}} cdot frac{r}{{100}}) | (frac{{12A}}{{24}} — frac{A}{{24}} = frac{{11A}}{{24}}) |
| …… | ……. | …… |
| 24 | (frac{A}{{24}} cdot frac{r}{{100}}) | 0 |
Выплаты за первый год: (12 cdot frac{A}{{24}} + frac{r}{{100}} cdot frac{{A + frac{{13A}}{{24}}}}{2} cdot 12 = frac{A}{2} + frac{{37A cdot r}}{{400}}.)
Выплаты за второй год: (12 cdot frac{A}{{24}} + frac{r}{{100}} cdot frac{{frac{{12A}}{{24}} + frac{A}{{24}}}}{2} cdot 12 = frac{A}{2} + frac{{13A cdot r}}{{400}}.)
(begin{array}{*{20}{c}}{frac{A}{2} + frac{{37Ar}}{{400}} — 100% }\{frac{A}{2} + frac{{13Ar}}{{400}} — 80% }end{array},,,,,,,, Rightarrow ,,,,,0,8left( {frac{A}{2} + frac{{37Ar}}{{400}}} right),,, > ,,frac{A}{2} + frac{{13Ar}}{{400}},,,,, Leftrightarrow ,)
( Leftrightarrow ,,,,,frac{{0,8 cdot 37 cdot A cdot r}}{{400}} — frac{{13Ar}}{{400}},,, > ,,frac{A}{2} — 0,8frac{A}{2},,left| {,:} right.,A,,,,, Leftrightarrow ,,,,frac{{16,6r}}{{400}},, > ,,0,1,,,, Leftrightarrow ,,,,r,, > ,,frac{{400}}{{166}},,,,,, Leftrightarrow ,,,,,r,, > ,,frac{{200}}{{83}},,,,,, Leftrightarrow ,,,,,r,, > ,,2frac{{34}}{{83}},.)
Так как r целое и наименьшее, то r = 3%.
Ответ: 3.
101В. Кирилл Николаевич положил в банк некоторую сумму на 5 лет под определенный процент. За второй год вклад увеличился на 8100 рублей, а за четвертый на 14400 рублей. На сколько рублей увеличился вклад у Кирилла Николаевича за пятый год?
А – вклад сроком на 5 лет под х% годовых. Каждый год вклад увеличивается в (frac{{100 + x}}{{100}} = t) раз.
| Год | Сумма в начале года | Сумма в конце года |
| 1 | (A) | (A cdot t) |
| 2 | (A cdot t) | (A cdot {t^2}) |
| 3 | (A cdot {t^2}) | (A cdot {t^3}) |
| 4 | (A cdot {t^3}) | (A cdot {t^4}) |
| 5 | (A cdot {t^4}) | (A cdot {t^5}) |
За второй год вклад увеличился на: (A{t^2} — At), а за четвёртый год на: (A{t^4} — A{t^3}).
(left{ {begin{array}{*{20}{c}}{A{t^4} — A{t^3} = 14400;}\{A{t^2} — At = 8100.}end{array}} right.)
Разделим первое уравнение на второе:
(frac{{A{t^4} — A{t^3}}}{{A{t^2} — At}} = frac{{14400}}{{8100}},,,,,,, Leftrightarrow ,,,,,,frac{{A{t^2}left( {{t^2} — t} right)}}{{Aleft( {{t^2} — t} right)}}, = frac{{144}}{{81}},,,,,, Leftrightarrow ,,,,,{t^2} = frac{{144}}{{81}},,,,,,,, Leftrightarrow ,,,,,,{t_1} = frac{4}{3};,,,,,,{t_2} = — frac{4}{3}.)
({t_2} = — frac{4}{3}) не подходит.
За пятый год вклад увеличился на: (A{t^5} — A{t^4} = t cdot left( {A{t^4} — A{t^3}} right) = frac{4}{3} cdot 14400 = 19200) рублей.
Ответ: 19 200.
102В. Гражданин Гусев взял кредит в банке, рассчитывая погасить долг равными ежегодными платежами, каждый из которых (кроме, возможно, последнего) составляет половину суммы S, взятой в кредит. Схема выплата кредита следующая: в конце каждого года банк увеличивает на 25% оставшуюся сумму долга, а затем гражданин Гусев переводит в банк очередной платеж. После двух лет выплат банк снизил процентную ставку до 20% годовых, и гражданин Гусев внес третий платеж. Четвертым платежом долг был погашен полностью. Сколько процентов от первоначальной суммы S составлял четвертый платеж по кредиту гражданина Гусева?
S – кредит сроком на 4 года. Первые 2 года остаток кредита увеличивается в 1,25 раза, а 3-й и 4-й в 1,2 раза. Первые 3 выплаты (frac{S}{2}), а последняя х.
| Год | Долг после начисления процентов | Выплата | Остаток после выплаты |
| 1 | (frac{5}{4}S) | (frac{1}{2}S) | (frac{5}{4}S — frac{1}{2}S = frac{3}{4}S) |
| 2 | (frac{5}{4} cdot frac{3}{4}S) | (frac{1}{2}S) | (frac{{15}}{{16}}S — frac{1}{2}S = frac{7}{{16}}S) |
| 3 | (frac{6}{5} cdot frac{7}{{16}}S) | (frac{1}{2}S) | (frac{{21}}{{40}}S — frac{1}{2}S = frac{1}{{40}}S) |
| 4 | (frac{6}{5} cdot frac{1}{{40}}S) | x | (frac{3}{{100}}S — x = 0) |
Так как (x = frac{3}{{100}}S), то четвертый платеж составляет 3% от первоначальной суммы S.
Ответ: 3.
103В. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа месяца и все следующие месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на 50 тысяч рублей, в течении 1-го года, на 30 тысяч рублей в течении 2-го года.
Найдите сумму выплаченную банку?
Так как в течении первого года долг уменьшался на 50 тысяч рублей каждый месяц, а в течении второго года на 30 тысяч рублей и за 2 года был полностью выплачен, то сумма кредита равна: (50 cdot 12 + 30 cdot 12 = 960) тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (960 cdot frac{1}{{100}}) | 910 |
| 2 | (910 cdot frac{1}{{100}}) | 860 |
| … | … | … |
| 12 | (410 cdot frac{1}{{100}}) | 360 |
| 13 | (360 cdot frac{1}{{100}}) | 330 |
| 14 | (330 cdot frac{1}{{100}}) | 300 |
| … | … | … |
| 24 | (30 cdot frac{1}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (960 тысяч рублей) и начисленным процентам.
(960 + 960 cdot frac{1}{{100}} + 910 cdot frac{1}{{100}} + … + 410 cdot frac{1}{{100}} + 360 cdot frac{1}{{100}} + 330 cdot frac{1}{{100}} + … + 30 cdot frac{1}{{100}} = )
( = 960 + frac{1}{{100}} cdot left( {960 + 910 + … + 410} right) + frac{1}{{100}} cdot left( {360 + 330 + … + 30} right) = )
( = 960 + frac{1}{{100}} cdot frac{{960 + 410}}{2} cdot 12 + frac{1}{{100}} cdot frac{{360 + 30}}{2} cdot 12 = 960 + 82,2 + 23,4 = 1065,6) тысяч рублей.
Ответ: 1 065 600.
104В. 15-го декабря планируется взять кредит в банке на сумму 600 тысяч рублей на (n + 1) месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
На сколько месяцев был взят кредит, если известно, что общая сумма выплат после полного погашения кредита составит 852 тысячи рублей.
А = 600 тысяч рублей кредит сроком на n+1 месяц. Пусть первые n месяцев долг уменьшался на х тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{3}{{100}}) | (A — x) |
| 2 | ()(left( {A — x} right) cdot frac{3}{{100}}) | (A — 2x) |
| … | … | … |
| n | (left( {A — left( {n — 1} right)x} right) cdot frac{3}{{100}}) | (A — nx = 200) |
| n+1 | (left( {A — nx} right) cdot frac{3}{{100}}) | 0 |
Так как общая сумма выплаченная банку равна 852 тысячи рублей, то переплата, то есть начисленные проценты, равна: (852 — 600 = 252) тыс. рублей.
(left{ {begin{array}{*{20}{c}}{A cdot frac{3}{{100}} + left( {A — x} right) cdot frac{3}{{100}} + … + left( {A — nx} right) cdot frac{3}{{100}} = 252;}\{A — nx = 200.}end{array}} right.)
Из первого уравнения: (frac{3}{{100}} cdot frac{{A + A — nx}}{2} cdot left( {n + 1} right) = 252). Так как (A — nx = 200,) то:
(left( {A + 200} right)left( {n + 1} right) = 16800,,,, Leftrightarrow ,,,,,,left( {600 + 200} right)left( {n + 1} right) = 16800,,,,, Leftrightarrow ,,,,n = 20.)
Следовательно, кредит был взят на (n + 1 = 21) месяц.
Ответ: 21.
105В. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
А – кредит в тыс. рублей сроком на 21 месяца под 1% в месяц.
| Месяц | Начисленные % (тыс. руб) | Платёж (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{1}{{100}}) | (A cdot frac{1}{{100}} + frac{A}{{21}}) | (A — frac{A}{{21}} = frac{{20A}}{{21}}) |
| 2 | (frac{{20A}}{{21}} cdot frac{1}{{100}}) | (frac{{20A}}{{21}} cdot frac{1}{{100}} + frac{A}{{21}}) | (frac{{20A}}{{21}} — frac{A}{{21}} = frac{{19A}}{{21}}) |
| … | … | … | … |
| 11 | (frac{{11A}}{{21}} cdot frac{1}{{100}}) | (frac{{11A}}{{21}} cdot frac{1}{{100}} + frac{A}{{21}}) | (frac{{11A}}{{21}} — frac{A}{{21}} = frac{{10A}}{{21}}) |
| … | … | … | … |
| 21 | (frac{A}{{21}} cdot frac{1}{{100}}) | (frac{A}{{21}} cdot frac{1}{{100}} + frac{A}{{21}}) | (frac{A}{{21}} — frac{A}{{21}} = 0) |
Воспользуемся тем, что 11–я выплата равна 44,4тыс.рублей:
(frac{{11A}}{{21}} cdot frac{1}{{100}} + frac{A}{{21}} = 44,4,,,,,,, Leftrightarrow ,,,,,,,frac{{111A}}{{21 cdot 100}} = 44,4,,,,, Leftrightarrow ,,,,111A = 4440 cdot 21,,,,,,, Leftrightarrow ,,,,,,A = 40 cdot 21 = 840) тыс. рублей.
Общая сумма выплат равна сумме кредита А = 840 тысяч рублей плюс начисленные проценты:
(A + frac{{21A}}{{21}} cdot frac{1}{{100}} + frac{{20A}}{{21}} cdot frac{1}{{100}} + … + frac{A}{{21}} cdot frac{1}{{100}} = A + frac{1}{{100}} cdot frac{A}{{21}} cdot left( {21 + 20 + … + 1} right) = )
( = A + frac{A}{{2100}} cdot frac{{21 + 1}}{2} cdot 21 = A + frac{{11A}}{{100}} = frac{{111A}}{{100}} = frac{{840 cdot 111}}{{100}} = 932,4) тыс. рублей.
Ответ: 932 400.
106В. 15 декабря планируется взять кредит в банке на 1240 тысяч рублей на (n + 2) месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1,5% по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа первые два месяца долг должен уменьшиться на 220 тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на а тысяч рублей.
Найдите n, если всего было выплачено банку 1519,9 тысяч рублей?
А = 1240 тысяч рублей кредит сроком на (n+2) месяца под 1,5% в месяц.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (1240 cdot frac{{1,5}}{{100}}) | 1020 |
| 2 | ()(1020 cdot frac{{1,5}}{{100}}) | 800 |
| 3 | (800 cdot frac{{1,5}}{{100}}) | (800 — a) |
| 4 | (left( {800 — a} right) cdot frac{{1,5}}{{100}}) | (800 — 2a) |
| … | … | … |
| n+2 | (left( {800 — left( {n — 1} right)a} right) cdot frac{{1,5}}{{100}}) | (800 — an = 0) |
Так как сумма кредита 1240 тысяч рублей, а общая сумма выплат 1519,9 тыс. рублей, то переплата, то есть начисленные проценты составляют: (1519,9 — 1240 = 279,9) тыс. рублей.
(left{ {begin{array}{*{20}{c}}{1240 cdot frac{{1,5}}{{100}} + 1020 cdot frac{{1,5}}{{100}} + 800 cdot frac{{1,5}}{{100}} + left( {800 — a} right) cdot frac{{1,5}}{{100}} + … + left( {800 — left( {n — 1} right)a} right) cdot frac{{1,5}}{{100}} = 279,9,}\{800 — an = 0.,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)
Из второго уравнения: (a,n = 800.) Из первого уравнения:
(frac{{1,5}}{{100}}left( {1240 + 1020 + frac{{800 + 800 — left( {n — 1} right)a}}{2} cdot n} right) = 279,9,,,,, Leftrightarrow ,,,,,)
( Leftrightarrow ,,,,,frac{{800 + 800 — an + a}}{2} cdot n = 18660 — 2260,,,,, Leftrightarrow ,,,,,frac{{800 + 800 — 800 + a}}{2} cdot n = 16400,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,frac{{800n + an}}{2} = 16400,,,,,,, Leftrightarrow ,,,,,,,,frac{{800n + 800}}{2} = 16400,,,,, Leftrightarrow ,,,,400n + 400 = 16400,,,,, Leftrightarrow ,,,,,,n = 40.)
Ответ: 40.
107В. 15 декабря планируется взять кредит в банке на 950 тысяч рублей на (n + 2) месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа последние два месяца долг должен уменьшиться на 300 тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на а тысяч рублей.
Найдите n, если всего было выплачено банку 1188,5 тысяч рублей?
А = 950 тысяч рублей кредит сроком на (n+2) месяца под 2% в месяц.
| Месяц | Начисленные % | Остаток |
| 1 | (950 cdot frac{2}{{100}}) | (950 — a) |
| 2 | ()(left( {950 — a} right)frac{2}{{100}}) | (950 — 2a) |
| … | … | … |
| n | (left( {950 — aleft( {n — 1} right)} right)frac{2}{{100}}) | (950 — an) |
| n+1 | (left( {950 — an} right) cdot frac{2}{{100}}) | (950 — an — 300) |
| n+2 | (left( {950 — an — 300} right) cdot frac{2}{{100}}) | (950 — an — 600 = 0) |
Так как сумма кредита 950 тысяч рублей, а общая сумма выплат 1188,5 тыс. рублей, то переплата, то есть начисленные проценты составляют: (1188,5 — 950 = 238,5) тыс. рублей.
(left{ {begin{array}{*{20}{c}}{950 cdot frac{2}{{100}} + left( {950 — a} right)frac{2}{{100}} + … + left( {950 — aleft( {n — 1} right)} right) cdot frac{2}{{100}} + left( {950 — an} right) cdot frac{2}{{100}} + left( {950 — an — 300} right) cdot frac{2}{{100}} = 238,5}\{950 — a,n — 600 = 0.,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)
Из второго уравнения: (a,n = 350.) Из второго уравнения:
(frac{2}{{100}} cdot left( {frac{{950 + 950 — an}}{2} cdot left( {n + 1} right) + 300} right) = 238,5,,,,, Leftrightarrow ,,,,,frac{{1900 — 350}}{2} cdot left( {n + 1} right) = 11925 — 300,,,,, Leftrightarrow ,,,,n = 14.)
Ответ: 14.
108В. 15 декабря планируется взять кредит в банке на 1750 тысяч рублей на 28 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа первые три месяца долг должен уменьшиться на а тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на в тысяч рублей.
Найдите а, если всего было выплачено банку 1925 тысяч рублей?
А = 1750 тысяч рублей кредит сроком на 28 месяцев под 1% в месяц.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{1}{{100}}) | (A — a) |
| 2 | ()(left( {A — a} right) cdot frac{1}{{100}}) | (A — 2a) |
| 3 | ()(left( {A — 2a} right) cdot frac{1}{{100}}) | (A — 3a) |
| 4 | ()(left( {A — 3a} right) cdot frac{1}{{100}}) | (A — 3a — b) |
| 5 | ()(left( {A — 3a — b} right) cdot frac{1}{{100}}) | (A — 3a — 2b) |
| … | … | … |
| 28 | ()(left( {A — 3a — 24b} right) cdot frac{1}{{100}}) | (A — 3a — 25b = 0) |
Так как сумма кредита 1750 тысяч рублей, а общая сумма выплат 1925 тыс. рублей, то переплата, то есть начисленные проценты составляют: (1925 — 1750 = 175) тыс. рублей.
(left{ {begin{array}{*{20}{c}}{frac{1}{{100}} cdot left( {frac{{A + A — 2a}}{2} cdot 3 + frac{{A — 3a + A — 3a — 24b}}{2} cdot 25} right) = 175;}\{A — 3a — 25b = 0.,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)
Из второго уравнения: (25b = A — 3a.) Из первого уравнения:
(3A — 3a + 25A — 75a — 300b = 17500,,,,,, Leftrightarrow ,,,,,28A — 78a — 12 cdot left( {A — 3a} right) = 17500,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,16 cdot 1750 — 42a = 17500,,,,,, Leftrightarrow ,,,,,a = 250) тысяч рублей.
Ответ: 250.
109В. 15 декабря планируется взять кредит в банке на 480 тысяч рублей на 27 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа первые два месяца и последний долг должен уменьшиться на а тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на в тысяч рублей.
Найдите а, если всего было выплачено банку 656,4 тысяч рублей?
А = 480 тысяч рублей кредит сроком на 27 месяцев под 3% в месяц.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{3}{{100}}) | (A — a) |
| 2 | ()(left( {A — a} right) cdot frac{3}{{100}}) | (A — 2a) |
| 3 | ()(left( {A — 2a} right) cdot frac{3}{{100}}) | (A — 2a — b) |
| 4 | ()(left( {A — 2a — b} right) cdot frac{3}{{100}}) | (A — 2a — 2b) |
| … | … | … |
| 26 | ()(left( {A — 2a — 23b} right) cdot frac{3}{{100}}) | (A — 2a — 24b) |
| 27 | ()(left( {A — 2a — 24b} right) cdot frac{3}{{100}}) | (A — 3a — 24b = 0) |
Так как сумма кредита 480 тысяч рублей, а общая сумма выплат 656,4 тыс. рублей, то переплата, то есть начисленные проценты составляют: (656,4 — 480 = 176,4) тыс. рублей.
(left{ {begin{array}{*{20}{c}}{frac{3}{{100}} cdot left( {A + A — a + frac{{A — 2a + A — 2a — 24b}}{2} cdot 25} right) = 176,4}\{A — 3a — 24b = 0,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.,,,, Leftrightarrow ,,,,,left{ {begin{array}{*{20}{c}}{2A — a + 25A — 50a — 300b = 5880}\{480 — 3a — 24b = 0;,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.,,,, Leftrightarrow )
Из второго уравнения: (b = frac{{160 — a}}{8}.) Подставим в первое:
(27 cdot 480 — 51a — 300 cdot frac{{160 — a}}{8} = 5880,,,,, Leftrightarrow ,,,,,4320 — 17a — 2000 + frac{{25}}{2}a = 1960,,,, Leftrightarrow ,,,,,a = 80) тысяч рублей.
Ответ: 80.
110В. 15 декабря планируется взять кредит в банке на S тысяч рублей на 68 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1,5 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа последние три месяца долг должен уменьшиться на 300 тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на а тысяч рублей.
Найдите S, если всего было выплачено банку 3748 тысяч рублей?
S – кредит (в тыс. рублей) сроком на 68 месяцев под 1,5% в месяц.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (S cdot frac{{1,5}}{{100}}) | (S — a) |
| 2 | ()(left( {S — a} right) cdot frac{{1,5}}{{100}}) | (S — 2a) |
| … | … | … |
| 65 | ()(left( {S — 64a} right) cdot frac{{1,5}}{{100}}) | (S — 65a = 900) |
| 66 | (900 cdot frac{{1,5}}{{100}}) | 600 |
| 67 | (600 cdot frac{{1,5}}{{100}}) | 300 |
| 68 | ()(300 cdot frac{{1,5}}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (S) плюс начисленные проценты.
(left{ {begin{array}{*{20}{c}}{S + frac{{1,5}}{{100}} cdot left( {frac{{S + S — 64a}}{2} cdot 65 + 900 + 600 + 300} right) = 3748}\{S — 65a = 900;,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.,,, Leftrightarrow ,,,,left{ {begin{array}{*{20}{c}}{S + frac{{1,5}}{{100}} cdot left( {65S — 32 cdot 65a + 1800} right) = 3748}\{65a = S — 900,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)
(S + frac{{1,5}}{{100}} cdot left( {65S — 32 cdot S + 32 cdot 900 + 1800} right) = 3748,,,,,,, Leftrightarrow ,,,,,,S + frac{{49,5 cdot S}}{{100}} + 459 = 3748,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,149,5S = 328900,,,,,, Leftrightarrow ,,,,,,S = 2200) тысяч рублей.
Ответ: 2 200.
111В. 15 декабря планируется взять кредит в банке на S тысяч рублей на 32 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа первый и последний месяцы долг должен уменьшиться на 250 тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на а тысяч рублей.
Найдите S, если всего было выплачено банку 2061,5 тысяч рублей?
S – кредит (в тыс. рублей) сроком на 32 месяца под 2% в месяц.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (S cdot frac{2}{{100}}) | (S — 250) |
| 2 | ()(left( {S — 250} right) cdot frac{2}{{100}}) | (S — 250 — a) |
| 3 | ()(left( {S — 250 — a} right) cdot frac{2}{{100}}) | (S — 250 — 2a) |
| … | … | … |
| 31 | ()(left( {S — 250 — 29a} right) cdot frac{2}{{100}}) | (S — 250 — 30a = 250) |
| 32 | ()(left( {S — 250 — 30a} right) cdot frac{2}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (S) плюс начисленные проценты.
(left{ {begin{array}{*{20}{c}}{S + frac{2}{{100}} cdot left( {S + frac{{S — 250 + S — 250 — 30a}}{2} cdot 31} right) = 2061,5}\{S — 250 — 30a = 250;,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.,, Leftrightarrow ,,,left{ {begin{array}{*{20}{c}}{50S + S + left( {S — 250 — frac{{30}}{2}a} right)31 = 103075}\{30a = S — 500,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.)
(51S + 31S — 250 cdot 31 — frac{{31}}{2} cdot 30a = 103075,,,, Leftrightarrow ,,,,,82S — 250 cdot 31 — frac{{31}}{2}left( {S — 500} right) = 103075,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,82S — 250 cdot 31 — 15,5S + 250 cdot 31 = 103075,,,,, Leftrightarrow ,,,,,66,5S = 103075,,,,, Leftrightarrow ,,,,S = 1550) тысяч рублей.
Ответ: 1 550.
112В. В июле планируется взять кредит в банке на 12 лет. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту в 2 раза больше наименьшего платежа.
А – кредит сроком на 12 лет под r % годовых. Так как долг уменьшается каждый год на одну и ту же сумму, то эта сумма равна (frac{A}{{12}}). Следовательно, ежегодные выплаты равны (frac{A}{{12}}) плюс начисленные проценты на остаток.
| Год | Начисленные % | Выплата | Остаток |
| 1 | (A cdot frac{r}{{100}}) | (frac{A}{{12}} + A cdot frac{r}{{100}}) | (A — frac{A}{{12}} = frac{{11A}}{{12}}) |
| 2 | (frac{{11A}}{{12}} cdot frac{r}{{100}}) | (frac{A}{{12}} + frac{{11A}}{{12}} cdot frac{r}{{100}}) | (frac{{11A}}{{12}} — frac{A}{{12}} = frac{{10A}}{{12}}) |
| … | … | … | … |
| 12 | (frac{A}{{12}} cdot frac{r}{{100}}) | (frac{A}{{12}} + frac{A}{{12}} cdot frac{r}{{100}}) | (frac{A}{{12}} — frac{A}{{12}} = 0) |
Наибольшая выплата первая: (frac{A}{{12}} + A cdot frac{r}{{100}}).
Наименьшая выплата последняя: (frac{A}{{12}} + frac{A}{{12}} cdot frac{r}{{100}}).
Следовательно:
(frac{A}{{12}} + A cdot frac{r}{{100}} = 2 cdot left( {frac{A}{{12}} + frac{A}{{12}} cdot frac{r}{{100}}} right),,,,, Leftrightarrow ,,,,frac{A}{{12}} cdot left( {1 + frac{{12r}}{{100}}} right) = 2 cdot frac{A}{{12}} cdot left( {1 + frac{r}{{100}}} right),,left| {:,A} right.,,,, Leftrightarrow ,,,,,)
( Leftrightarrow ,,,,,,1 + frac{{12r}}{{100}} = 2 + frac{{2r}}{{100}},,,,,, Leftrightarrow ,,,,,,,frac{{10r}}{{100}} = 1,,,,,, Leftrightarrow ,,,,,r = 10% .)
Ответ: 10.
113В. В июле планируется взять кредит в банке на 13 лет. Условия его возврата таковы:
- каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту в 3 раза больше наименьшего платежа.
А – кредит сроком на 13 лет под r % годовых. Так как долг уменьшается каждый год на одну и ту же сумму, то эта сумма равна (frac{A}{{13}}). Следовательно, ежегодные выплаты равны (frac{A}{{13}}) плюс начисленные проценты на остаток.
| Год | Начисленные % | Выплата | Остаток |
| 1 | (A cdot frac{r}{{100}}) | (frac{A}{{13}} + A cdot frac{r}{{100}}) | (A — frac{A}{{13}} = frac{{12A}}{{13}}) |
| 2 | (frac{{12A}}{{13}} cdot frac{r}{{100}}) | (frac{A}{{13}} + frac{{12A}}{{13}} cdot frac{r}{{100}}) | (frac{{12A}}{{13}} — frac{A}{{13}} = frac{{11A}}{{13}}) |
| … | … | … | … |
| 13 | (frac{A}{{13}} cdot frac{r}{{100}}) | (frac{A}{{13}} + frac{A}{{13}} cdot frac{r}{{100}}) | (frac{A}{{13}} — frac{A}{{13}} = 0) |
Наибольшая выплата первая: (frac{A}{{13}} + A cdot frac{r}{{100}}).
Наименьшая выплата последняя: (frac{A}{{13}} + frac{A}{{13}} cdot frac{r}{{100}}).
Следовательно:
(frac{A}{{13}} + A cdot frac{r}{{100}} = 3 cdot left( {frac{A}{{13}} + frac{A}{{13}} cdot frac{r}{{100}}} right),,,,,, Leftrightarrow ,,,,,frac{A}{{13}} cdot left( {1 + frac{{13r}}{{100}}} right) = frac{A}{{13}} cdot 3 cdot left( {1 + frac{r}{{100}}} right),,left| {:,A} right.,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,1 + frac{{13r}}{{100}} = 3 + frac{{3r}}{{100}},,,,,, Leftrightarrow ,,,,,,frac{{10r}}{{100}} = 2,,,,, Leftrightarrow ,,,,,r = 20% .)
Ответ: 20.
114В (ЕГЭ 2021). В июле 2025 года планируется взять кредит в банке на сумму 700 тыс. рублей на 10 лет. Условия его возврата таковы:
- в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
- в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- к июлю 2035 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
ОТВЕТ: 1 400 тыс. рублей.
А = 700 тысяч рублей кредит сроком на 10 лет. Так как кредит уменьшается каждый год на одну и ту же сумму, то эта сумма равна (700:10 = 70) тысяч рублей.
| Год | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (700 cdot frac{{19}}{{100}}) | 630 |
| 2 | (630 cdot frac{{19}}{{100}}) | 560 |
| … | … | … |
| 5 | (420 cdot frac{{19}}{{100}}) | 350 |
| 6 | (350 cdot frac{{16}}{{100}}) | 280 |
| 7 | (280 cdot frac{{16}}{{100}}) | 210 |
| … | … | … |
| 10 | (70 cdot frac{{16}}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (700 тысяч рублей) плюс начисленные проценты.
(700 + 700 cdot frac{{19}}{{100}} + 630 cdot frac{{19}}{{100}} + … + 420 cdot frac{{19}}{{100}} + 350 cdot frac{{16}}{{100}} + 280 cdot frac{{16}}{{100}} + … + 70 cdot frac{{16}}{{100}} = )
( = 700 + frac{{19}}{{100}} cdot frac{{700 + 420}}{2} cdot 5 + frac{{16}}{{100}} cdot frac{{350 + 70}}{2} cdot 5 = 700 + 532 + 168 = 1400) тысяч рублей.
Ответ: 1 400 тыс. рублей.
115В (ЕГЭ 2021). В июле 2025 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года долг должен быть полностью погашен.
Чему равно r, если общая сумма выплат составит 930 тысяч рублей?
А = 600 тысяч рублей кредит сроком на 6 лет. Так как кредит уменьшается каждый год на одну и ту же сумму, то эта сумма равна (600:6 = 100) тысяч рублей.
| Год | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (600 cdot frac{r}{{100}}) | 500 |
| 2 | (500 cdot frac{r}{{100}}) | 400 |
| 3 | (400 cdot frac{r}{{100}}) | 300 |
| 4 | (300 cdot frac{{15}}{{100}}) | 200 |
| 5 | (200 cdot frac{{15}}{{100}}) | 100 |
| 6 | (100 cdot frac{{15}}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (600 тысяч рублей) плюс начисленные проценты.
(600 + 600 cdot frac{r}{{100}} + 500 cdot frac{r}{{100}} + 400 cdot frac{r}{{100}} + 300 cdot frac{{15}}{{100}} + 200 cdot frac{{15}}{{100}} + 100 cdot frac{{15}}{{100}} = 930,,,,, Leftrightarrow )
( Leftrightarrow ,,,,left( {600 + 500 + 400} right) cdot frac{r}{{100}} = 930 — 600 — 45 — 30 — 15,,,, Leftrightarrow ,,,15r = 240,,,,, Leftrightarrow ,,,,r = 16% .)
Ответ: 16.
116В (ЕГЭ 2021). 15 декабря 2024 года планируется взять кредит в банке на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й (с января 2025 года по июнь 2027 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15 июня 2027 года долг составит 100 тысяч рублей;
— 15 июля 2027 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 555 тысяч рублей?
А – кредит (в тыс. рублей) сроком на 31 месяц под 2% в месяц. Так как кредит первые 30 месяцев каждый месяц уменьшался на одну и ту же величину и в конце 30–го месяца составил 100 тысяч рублей, то он уменьшался на (frac{{A — 100}}{{30}} = t) тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{2}{{100}}) | (A — t) |
| 2 | (left( {A — t} right) cdot frac{2}{{100}}) | (A — 2t) |
| … | … | … |
| 30 | (left( {A — 29t} right) cdot frac{2}{{100}}) | (A — 30t) |
| 31 | (left( {A — 30t} right) cdot frac{2}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (А) плюс начисленные проценты.
(A + A cdot frac{2}{{100}} + left( {A — t} right) cdot frac{2}{{100}} + … + left( {A — 30t} right) cdot frac{2}{{100}} = 555,,,,, Leftrightarrow ,,,,A + frac{2}{{100}} cdot frac{{A + A — 30t}}{2} cdot 31 = 555,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,A + frac{1}{{50}} cdot left( {A — 15t} right) cdot 31 = 555,,,,, Leftrightarrow ,,,,,50A + 31A — 15 cdot 31 cdot frac{{A — 100}}{{30}} = 555 cdot 50,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,81A — frac{{31}}{2}A + 1550 = 27750,,,,, Leftrightarrow ,,,,,frac{{131A}}{2} = 26200,,,,,,,, Leftrightarrow ,,,,,,A = 400) тысяч рублей.
Ответ: 400 тыс. рублей.
117В (ЕГЭ 2021). 15 декабря 2024 года планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й (с января 2025 года по август 2026 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15 августа 2026 года долг составит 200 тысяч рублей;
— 15 сентября 2026 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 905 тысяч рублей?
А – кредит (в тыс. рублей) сроком на 21 месяц под 1% в месяц. Так как кредит первые 20 месяцев каждый месяц уменьшался на одну и ту же величину и в конце 20–го месяца составил 200 тысяч рублей, то он уменьшался на (frac{{A — 200}}{{20}} = t) тысяч рублей.
| Месяц | Начисленные % (тыс. руб) | Остаток (тыс. руб) |
| 1 | (A cdot frac{1}{{100}}) | (A — t) |
| 2 | (left( {A — t} right) cdot frac{1}{{100}}) | (A — 2t) |
| … | … | … |
| 20 | (left( {A — 19t} right) cdot frac{1}{{100}}) | (A — 20t) |
| 21 | (left( {A — 20t} right) cdot frac{1}{{100}}) | 0 |
Общая сумма выплат равна сумме кредита (А) плюс начисленные проценты.
(A + A cdot frac{1}{{100}} + left( {A — t} right) cdot frac{1}{{100}} + … + left( {A — 20t} right) cdot frac{1}{{100}} = 905,,,, Leftrightarrow ,,,,A + frac{1}{{100}} cdot frac{{A + A — 20t}}{2} cdot 21 = 905,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,A + frac{1}{{100}} cdot left( {A — 10t} right) cdot 21 = 905,,,,,, Leftrightarrow ,,,,,,,100A + 21A — 10 cdot 21 cdot frac{{A — 200}}{{20}} = 90500,,,,,, Leftrightarrow )
( Leftrightarrow ,,,,,,121A — frac{{21}}{2}A + 2100 = 90500,,,,,, Leftrightarrow ,,,,,,,110,5A = 88400,,,,,,, Leftrightarrow ,,,,,,,A = 800) тысяч рублей.
Ответ: 800 тыс. рублей.
118В (ЕГЭ 2020). В июле 2026 года планируется взять кредит на 5 лет в размере 630 тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле 2027, 2028 и 2029 годов долг остаётся равным 630 тыс. рублей;
— выплаты в 2030 и 2031 годах равны;
— к июлю 2031 года долг будет выплачен полностью.
Найдите r, если известно, что долг будет выплачен полностью и общий размер выплат составит 915 тыс. рублей.
А = 630 тысяч рублей кредит сроком на 5 лет под r % годовых, то есть каждый год остаток долга увеличивается в (frac{{100 + r}}{{100}} = 1 + frac{r}{{100}} = 1 + t) раз, где (t = frac{r}{{100}}). Пусть х выплата в конце 4–го и 5–го годов.
| Год | Долг после начисления процентов (тыс. руб) | Платёж (тыс. руб) | Остаток после платежа (тыс. руб) |
| 1 | (Aleft( {1 + t} right)) | (At) | А |
| 2 | (Aleft( {1 + t} right)) | (At) | А |
| 3 | (Aleft( {1 + t} right)) | (At) | А |
| 4 | (Aleft( {1 + t} right)) | х | (Aleft( {1 + t} right) — x) |
| 5 | (left( {Aleft( {1 + t} right) — x} right)left( {1 + t} right)) | х | (left( {Aleft( {1 + t} right) — x} right)left( {1 + t} right) — x) |
(left{ {begin{array}{*{20}{c}}{3At + 2x = 915;,,,,,,,,,,,,,,,,,,,,,}\{A{{left( {1 + t} right)}^2} — xleft( {1 + t} right) — x = 0;}end{array}} right.,,,,, Leftrightarrow ,,,,,left{ {begin{array}{*{20}{c}}{2x = 915 — 3At;,,,,,,,,,,,,,,,,,,,,,}\{Aleft( {1 + 2t + {t^2}} right) = xleft( {2 + t} right).}end{array}} right.)
Из первого уравнения: (x = frac{{915 — 3At}}{2}). Подставим во второе уравнение
(Aleft( {1 + 2t + {t^2}} right) = frac{{915 — 3At}}{2} cdot left( {2 + t} right),,,,, Leftrightarrow ,,,,,1260 + 2520t + 1260{t^2} = 1830 + 915t — 3780t — 1890{t^2},,,, Leftrightarrow )
( Leftrightarrow ,,,,,,3150{t^2} + 5385t — 570 = 0,,,,, Leftrightarrow ,,,,,210{t^2} + 359t — 38 = 0,,,,, Leftrightarrow ,,,,,{t_1} = frac{1}{{10}};,,,,,,,,,,,,{t_2} = — frac{{38}}{{21}}.)
Корень ({t_2} = — frac{{38}}{{21}}) не подходит. Следовательно: (frac{r}{{100}} = frac{1}{{10}},,,,,, Leftrightarrow ,,,,,,r = 10% .)
Ответ: 10.
119В (ЕГЭ 2020). В кредит взяли 21 млн. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трёх лет задолженность остаётся неизменной и равной 21 млн. рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r, если известно, что сумма всех выплат составит 30,5 млн. рублей.
А = 21 млн. рублей кредит сроком на 5 лет под r % годовых, то есть каждый год остаток долга увеличивается в (frac{{100 + r}}{{100}} = 1 + frac{r}{{100}} = 1 + t) раз, где (t = frac{r}{{100}}). Пусть х выплата в конце 4–го и 5–го годов.
| Год | Долг после начисления процентов (млн. руб) | Платёж (млн. руб) | Остаток после платежа (млн. руб) |
| 1 | (Aleft( {1 + t} right)) | (At) | А |
| 2 | (Aleft( {1 + t} right)) | (At) | А |
| 3 | (Aleft( {1 + t} right)) | (At) | А |
| 4 | (Aleft( {1 + t} right)) | х | (Aleft( {1 + t} right) — x) |
| 5 | (left( {Aleft( {1 + t} right) — x} right)left( {1 + t} right)) | х | (left( {Aleft( {1 + t} right) — x} right)left( {1 + t} right) — x) |
(left{ {begin{array}{*{20}{c}}{3At + 2x = 30,5;,,,,,,,,,,,,,,,,,,,,,}\{A{{left( {1 + t} right)}^2} — xleft( {1 + t} right) — x = 0;}end{array},,,,, Leftrightarrow ,,,,,left{ {begin{array}{*{20}{c}}{2x = 30,5 — 3At;,,,,,,,,,,,,,,,,,,,}\{Aleft( {1 + 2t + {t^2}} right) = xleft( {2 + t} right).}end{array}} right.} right.)
Из первого уравнения: (x = frac{{30,5 — 3At}}{2}). Подставим во второе уравнение.
(Aleft( {1 + 2t + {t^2}} right) = frac{{30,5 — 3At}}{2} cdot left( {2 + t} right),,,,,, Leftrightarrow ,,,,,,42 + 84t + 42{t^2} = 61 + 30,5t — 126t — 63{t^2},,,,, Leftrightarrow )
(105{t^2} + 179,5t — 19 = 0,,,,,, Leftrightarrow ,,,,,{t_1} = frac{1}{{10}};,,,,,,,,,,,,{t_2} = — frac{{38}}{{21}}.)
Корень ({t_2} = — frac{{38}}{{21}}) не подходит. Следовательно: (frac{r}{{100}} = frac{1}{{10}},,,,,,, Leftrightarrow ,,,,,,r = 10% .)
Ответ: 10.
2 декабря 2021
В закладки
Обсудить
Жалоба
В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию.
Разобраны 8 типов заданий
→ 1 тип: Нахождение количества лет (месяцев) выплаты кредита. (Аннуитетные платежи) — 3 задачи.
→ 2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи) – 3 задачи.
→ 3 тип: Нахождение суммы кредита. (Аннуитетные платежи)- 3 задачи.
→ 4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные платежи)- 3 задачи.
→ 5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи.
→ 6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)- 3 задачи.
→ 7 тип: Задачи, связанные с дифференцированными платежами.- 3 задачи.
→ 8 тип: Нестандартные задачи, связанные с кредитом.- 4 задачи.
50ek.docx
Решение задачи можно разбить на 4 этапа:
- Подготовка
- Заполнение таблицы
- Составление математической модели
- Решение и получение искомого результата
Немного вводной теории.
1) От момента получения кредита до полного его погашения циклически повторяются 3 шага:
А) начисление процентов;
Б) внесение выплат;
В) формирование оставшегося долга
ВАЖНО!!! Каждый новый период проценты начисляются НА ОСТАТОК ДОЛГА!!!
2) Для удобства и сокращения записи в таблице перед началом ее заполнения введем переменные: S — сумма кредита, х — процентный коэффициент. Если в задаче известна процентная ставка и сумма кредита, то при решении эти данные будут использованы
Рассмотрим задачу. Это одна из самых простых задач.
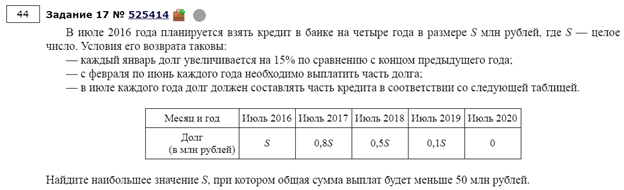
1) Подготовка
S-сумма кредита. Х=1+0,15 = 1,15
2) Заполнение таблицы. В условии сразу даны все значения третьего столбца (долга). С него и начнем заполнение
|
Проценты |
Выплаты |
Долг |
|
|
1 |
0,8S |
||
|
2 |
0,5S |
||
|
3 |
0,1S |
||
|
4 |
0 |
Далее начисляем проценты на остаток долга. Первый долг — это взятый кредит
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
0,8S |
|
|
2 |
0,8SX |
0,5S |
|
|
3 |
0,5SX |
0,1S |
|
|
4 |
0,1SX |
0 |
Выражаем ВЫПЛАТЫ из двух заполненных, как разность начальной и конечной суммы
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
SX — 0,8S |
0,8S |
|
2 |
0,8SX |
0,8SX — 0,5S |
0,5S |
|
3 |
0,5SX |
0,5SX — 0,1S |
0,1S |
|
4 |
0,1SX |
0,1SX |
0 |
3) Составление математической модели.
Известно, что общая сумма выплат будет меньше 50 млн рублей
SX — 0,8S + 0,8SX — 0,5S + 0,5SX — 0,1S + 0,1SX < 50
4) Решение и получение искомого результата
Для удобства сгруппируем множители: в одни скобки с процентным коэффициентом, в другие — без него.
(SX + 0,8SX + 0,5SX + 0,1SX) — (0,8S + 0,5S + 0,1S ) < 50
Вынесем общие множители за скобки
SX(1 + 0,8 + 0,5 + 0,1) — S(0,8 + 0,5 + 0,1 ) < 50
SX*2,4 — S*1,4 <50
S(2,4X — 1,4) <50
Теперь можно подставить значение Х
S(2,4*1.15 — 1,4) <50
S< 50/1.36. Так как S-целое число и нам требуется наибольшее, S=36
Рассмотрим задачу с неизвестной процентной ставкой.
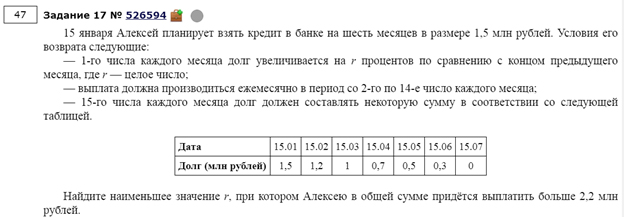
1) Подготовка
S=1,5 млн. — сумма кредита. Х=1+0,01r
2) Заполнение таблицы. В условии сразу даны все значения третьего столбца (долга). С него и начнем заполнение
|
Проценты |
Выплаты |
Долг |
|
|
1 |
1,2 |
||
|
2 |
1 |
||
|
3 |
0,7 |
||
|
4 |
0,5 |
||
|
5 |
0,3 |
||
|
6 |
0 |
Далее начисляем проценты на остаток долга. Первый долг — это взятый кредит.
|
Проценты |
Выплаты |
Долг |
|
|
1 |
1,5X |
1,2 |
|
|
2 |
1,2X |
1 |
|
|
3 |
1X |
0,7 |
|
|
4 |
0,7X |
0,5 |
|
|
5 |
0,5X |
0,3 |
|
|
6 |
0,3X |
0 |
Выражаем ВЫПЛАТЫ из двух заполненных, как разность начальной и конечной суммы
|
Проценты |
Выплаты |
Долг |
|
|
1 |
1,5X |
1,5X — 1,2 |
1,2 |
|
2 |
1,2X |
1,2X — 1 |
1 |
|
3 |
1X |
1X — 0,7 |
0,7 |
|
4 |
0,7X |
0,7X — 0,5 |
0,5 |
|
5 |
0,5X |
0,5X — 0,3 |
0,3 |
|
6 |
0,3X |
0,3X |
0 |
3) Составление математической модели.
Известно, что общая сумма выплат будет больше 2,2 млн рублей
1,5X — 1,2 + 1,2X — 1 + 1X — 0,7 + 0,7X — 0,5 + 0,5X — 0,3 + 0,3X >2,2
4) Решение и получение искомого результата
Для удобства сгруппируем множители: в одни скобки с процентным коэффициентом, в другие — без него. Вынесем общие множители за скобки.
Х(1,5 + 1,2 + 1 + 0,7 + 0,5 + 0,3) — (1,2 + 1 + 0,7 + 0,5 + 0,3) > 2,2
5,2Х — 3,7 >2,2
X > 59/52 Так как Х=1+0,01r и r — наименьшее, получаем r=14
Рассмотрим задачу с большим сроком выплаты кредита.

1) Подготовка
S — сумма кредита. Х=1+0,01*2=1,02
2) Заполнение таблицы. В условии сразу даны все значения третьего столбца (долга). С него и начнем заполнение
Так как срок большой, ограничимся первыми тремя и последними тремя месяцами.
Если в условии сказано, что «долг должен быть на одну и ту же сумму меньше предыдущего», то сумма кредита делится на количество месяцев и каждый месяц долг уменьшается на 1/18
|
Проценты |
Выплаты |
Долг |
|
|
1 |
17/18*S |
||
|
2 |
16/18*S |
||
|
3 |
15/18*S |
||
|
…………………………………………………. |
|||
|
16 |
2/18*S |
||
|
17 |
1/18*S |
||
|
18 |
0 |
Далее начисляем проценты на остаток долга. Первый долг — это взятый кредит
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
17/18*S |
|
|
2 |
17/18*S*X |
16/18*S |
|
|
3 |
16/18*S*X |
15/18*S |
|
|
…………………………………………………. |
|||
|
16 |
3/18*S*X |
2/18*S |
|
|
17 |
2/18*S*X |
1/18*S |
|
|
18 |
1/18*S*X |
0 |
Выражаем ВЫПЛАТЫ из двух заполненных, как разность начальной и конечной суммы
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
SX — 17/18*S |
17/18*S |
|
2 |
17/18*S*X |
17/18*S*X — 16/18*S |
16/18*S |
|
3 |
16/18*S*X |
16/18*S*X — 15/18*S |
15/18*S |
|
…………………………………………………. |
|||
|
16 |
3/18*S*X |
3/18*S*X — 2/18*S |
2/18*S |
|
17 |
2/18*S*X |
2/18*S*X — 1/18*S |
1/18*S |
|
18 |
1/18*S*X |
1/18*S*X |
0 |
3) Составление математической модели.
В задаче стоит вопрос об общей сумме выплат. Следовательно
SX — 17/18*S + 17/18*S*X — 16/18*S + 16/18*S*X — 15/18*S + … + 3/18*S*X — 2/18*S + 2/18*S*X — 1/18*S + 1/18*S*X =
4) Решение и получение искомого результата
Для удобства сгруппируем множители: в одни скобки с процентным коэффициентом, в другие — без него. Вынесем общие множители за скобки.
= SX/18 (18 + 17+ 16 + … + 3+ 2 + 1) — S/18* (17 + 16 + 15 +…+ 2 + 1) =
В скобках сумма арифметической прогрессии от 1 до 18 и от 1 до 17
= —
= 19SX/2 — 17S/2 = S(9,5*1,02 — 8,5) = S*1,19.
То есть сумма выплат составляет 119% от суммы взятого кредита.
Рассмотрим задачу с неизвестным сроком выплаты кредита.

1) Подготовка
S=5 — сумма кредита. Х=1+0,01*20=1,2
2) Заполнение таблицы. В условии сразу даны все значения третьего столбца (долга). С него и начнем заполнение
Так как срок большой, ограничимся первыми тремя и последними тремя месяцами.
Если в условии сказано, что «долг должен быть на одну и ту же сумму меньше предыдущего», то сумма кредита делится на количество месяцев и каждый месяц долг уменьшается на 1/n
|
Проценты |
Выплаты |
Долг |
|
|
1 |
(n-1)/n*S |
||
|
2 |
(n-2)/n *S |
||
|
3 |
(n-3)/n *S |
||
|
…………………………………………………. |
|||
|
n-2 |
2/n*S |
||
|
n-1 |
1/n*S |
||
|
n |
0 |
Далее начисляем проценты на остаток долга. Первый долг — это взятый кредит
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
(n-1)/n*S |
|
|
2 |
(n-1)/n*S*X |
(n-2)/n *S |
|
|
3 |
(n-2)/n *S*X |
(n-3)/n *S |
|
|
…………………………………………………. |
|||
|
n-2 |
3/n*s*x |
2/n*S |
|
|
n-1 |
2/n*S*X |
1/n*S |
|
|
n |
1/n*S*X |
0 |
Выражаем ВЫПЛАТЫ из двух заполненных, как разность начальной и конечной суммы
|
Проценты |
Выплаты |
Долг |
|
|
1 |
SX |
SX — (n-1)/n*S |
(n-1)/n*S |
|
2 |
(n-1)/n*S*X |
(n-1)/n*S*X-(n-2)/n *S |
(n-2)/n *S |
|
3 |
(n-2)/n *S*X |
(n-2)/n *SX-(n-3)/n *S |
(n-3)/n *S |
|
…………………………………………………. |
|||
|
n-2 |
3/n*s*x |
3/n*s*x-2/n*S |
2/n*S |
|
n-1 |
2/n*S*X |
2/n*S*X-1/n*S |
1/n*S |
|
n |
1/n*S*X |
1/n*S*X |
0 |
3) Составление математической модели.
В задаче стоит вопрос об общей сумме выплат. Следовательно
SX — (n-1)/n*S + (n-1)/n*S*X-(n-2)/n *S + (n-2)/n *SX-(n-3)/n *S + …+3/n*S*X-2/n*S + 2/n*S*X-1/n*S + 1/n*S*X = 7,5
4) Решение и получение искомого результата
Для удобства сгруппируем множители: в одни скобки с процентным коэффициентом, в другие — без него. Вынесем общие множители за скобки.
SX/n*(n + (n-1) + (n-2) + …+3 + 2+ 1) -S/ n* ((n-1)/ +(n-2) + (n-3) +…+2 +1) = 7,5
В скобках сумма арифметической прогрессии от 1 до n и от 1 до (n-1)
—
=7,5
Сокращая дроби и подставляя значения S и Х, получаем =7,5
n=4
Рассмотрим другой тип задач, в которых известен не долг, а сумма выплат.

1) Подготовка
S — сумма кредита. Х=1+0,01*10=1,1
2) Заполнение таблицы. В условии говорится о трех платежах, то есть
|
Проценты |
Выплаты |
Долг |
|
|
1 |
Х |
||
|
2 |
2Х |
||
|
3 |
3Х |
Начисляя проценты, получаем
|
Проценты |
Выплаты |
Долг |
|
|
1 |
1,1S |
Х |
1,1S — X |
|
2 |
(1,1S — X)*1,1 |
2Х |
(1,1S — X)*1,1-2X |
|
3 |
((1,1S — X)*1,1-2X)*1,1 |
3Х |
((1,1S — X)*1,1-2X)*1,1-3X |
3) Составление математической модели.
Учитывая, что последний долг должен быть равен нулю, получаем
((1,1S — X)*1,1-2X)*1,1-3X = 0
4) Решение и получение искомого результата
А также известна сумма, выплаченная за три года, то есть
Х+2Х+3Х=2395800, откуда получаем Х=399300
Подставляя найденное значение и решая первое уравнение, получаем S=1923000 рублей
Секрет: существуют только два вида уравнений:
- Сумма выплат;
- Последний остаток равен нулю.
Других видов уравнений нет!
Желаю всем легких решений!
|
VI районная научно-исследовательская конференция обучающихся обучающихся общеобразовательных организаций Октябрьского муниципального района |
|
Финансовая математика в задачах ЕГЭ. Решение задач на кредиты |
|
Исследовательская работа по математике |
Автор работы: Кутепова Анна, ученица 10 класса
Руководитель: Моторина Ольга Робертовна, преподаватель математики «МОУ ОСОШ №1»
с. Октябрьское, 2022 г.
СОДЕРЖАНИЕ
Введение 2
Банковские кредиты и математика 4
Схемы решения экономических задач на кредиты 8
- Задача на определение величины выплаты/дифференцированные платежи 8
- Задача на определение ежегодной (ежемесячной) выплаты /аннуитетные платежи 10
- Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи 12
- Задача на определение суммы кредита/аннуитетные платежи 14
- Нахождение количества лет (месяцев) выплаты кредита /дифференцированные платежи 16
Заключение 20
Список информационных источников 22
Введение
В современном, информационно-развитом мире, встречаются люди, которые не умеют правильно распоряжаться своими финансами и контролировать свои доходы и расходы. В этих случаях необходима финансовая грамотность, ведь благодаря данным знаниям мы сможем не только управлять деньгами, правильно инвестировать свои средства, но также будем в безопасности во время сложных жизненных обстоятельств и не потеряем свои доходы. Наша жизнь сегодня настоятельно требует, чтобы каждый человек имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений. Финансовая грамотность необходима при решении экономических задач в ЕГЭ профильного уровня по математике. Данные задания проверяют практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Учащиеся при подходе к итоговой аттестации в 9-х и 11-х классах сталкиваются с проблемой решения задач на проценты, а они есть и в ОГЭ и в ЕГЭ. На данный момент я являюсь ученицей 10 класса. В следующем году мне предстоит сдать ЕГЭ. Я уже ознакомлена с заданиями данного экзамена и знаю, что среди них есть задачи экономической направленности повышенного уровня сложности, которые в курсе старшей общеобразовательной школы не рассматриваются. Для меня стал актуален вопрос о том, каким образом подойти к решению таких задач. Кроме того я выбрала эту тему еще и потому, что в 7 классе мной был выполнен проект «Сам себе финансист: проценты и скидки».В этой исследовательской работе я хочу углубить и расширить свои знания в области финансовой математики. На выбор темы повлияло и то, что в будущем я планирую поступить на экономический факультет ВУЗа.
Тема моей работы: Финансовая математика в экономических задачах ЕГЭ. Решение задач на кредиты.
Гипотеза: Не смотря многообразие типов экономических задач профильного экзамена по математике, их можно классифицировать и вывести единую схему решения.
Цель работы: Изучить основные типы экономических задач на кредиты ЕГЭ по профильной математике и научиться их решать.
Задачи:
- Изучить теоретические аспекты решения экономических задач;
- Познакомиться с прототипами экономических задач, представленных в открытом банке заданий ЕГЭ;
- Создать обучающую презентацию по различным типам задач на кредиты.
Объект исследования: Экономические задачи на кредиты №15 в ЕГЭ.
Предмет исследования: Схемы и алгоритмы решения задач на кредиты.
Методы исследования:
- Изучение и анализ литературы и интернет-источников по данной теме.
- Математическое моделирование
- Классификация
- Анализ
Банковские кредиты и математика
Финансовая математика – раздел прикладной математики, имеющий дело с математическими задачами, связанными с экономическими расчётами.
В единый государственный экзамен по математике (ЕГЭ) профильного уровня экономические задачи были включены в 2015 г. Это задания высокого уровня сложности с практическим содержанием, проверяющее навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
Экономические задачи предполагают:
- Умение работать с процентами, частями и долями.
- Владение понятием «Математическая модель».
- Умение строить математическую модель задачи.
- Владение вычислительными навыками.
- Умение применять математические методы для решения содержательных задач из различных областей науки и практики.
- Умение интерпретировать полученный результат, учитывать реальные ограничения.
Экономические задачи под номером 15 в ЕГЭ по профильной математике делятся на три основные группы:
- Задачи на кредиты.
- Задачи на вклады и ценные бумаги.
- Задачи на оптимальный выбор.
Данную работу я посвятила разбору примеров задач первого типа.
Банковский кредит – денежная сумма, предоставляемая банком на определённый срок и на определённых условиях; определённая технология удовлетворения заявленной заёмщикомфинансовой потребности.
Потребность в кредите возникает при оплате значительныхпо стоимости объектов потребления без предварительного накопления достаточных ресурсов, необходимости обеспечения своевременных платежей по товарам, приобретенным в рассрочку, оплате эксклюзивных покупок случайного характера, кассовых разрывах при замене старых объектов потребления на новые, покрытии потерь при наступлении рисков, оплате значительных расходов и т. д.
Понимание и структурирование данных условия задачи – важный шаг на пути правильного ее решения. Для упорядочивания данных условия задачи я использовала таблицы, хотя это и не единственный способ решения 15-го задания, можно использовать и другие методы: последовательности, прикладные методы. Метод решения текстовых задач с помощью таблиц универсальный, знаком каждому школьнику. С помощью таблицможно выработать единый алгоритм решения большинства банковских задач.
В решениях, представленных в работе задач,мною будут использоваться следующие обозначения:
выплатить кредит
Кредитные операции играют основную роль в деятельности банков. Экономические задачи, конечно, несколько упрощают реальную ситуацию, в жизни банковские операции по кредитам значительно сложнее, тем не менее, именно они дают начальные представления о действиях в мире финансов. При решении экономических задач не обойтись без вычисления процентов, при этом используются «простые» и «сложные проценты». Задачи простые проценты изучаются в школьном курсе математике и включены в тестовую часть заданий профильного экзамена. Вычислять же «сложные проценты» приходится в тех случаях, когда в задаче идет речь о величине, подверженной поэтапному изменению. При этом каждый раз ее изменениесоставляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе.Существуют разные формулы, по которым происходит вычисление сложных процентов. При выдаче кредитов на срок n проценты могут, например, начисляться по формуле:

Проанализировав условия задач на кредиты профильного ЕГЭ, я обнаружила, что классифицировать задачи можно разными способами:
- По типу ежемесячных (ежегодных) платежей.
- Разделить на простые (используется одна формула) или сложные (применяются несколько формул, используются системы, неравенства).
- По неизвестной величине, которую требуется найти в условии (процентной ставке, величине выплаты, суммы кредита и др.)
По типу платежей задачи ЕГЭ задачами самыми распространенными являются задачи на фиксированный, аннуитетный и дифференцированный платежи.
Фиксированный платеж – это платеж, величина которого четко определена в задаче.
Аннуитетный платеж– это платеж, которыйустанавливается в равной сумме через равные промежутки времени, то есть остаётся постоянным на всём периоде кредитования. Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом, авторая часть идёт на погашение суммы долга. Главная особенность таких платежей в том, что вначале ежемесячный платеж практически полностью состоит из суммы процентов, тогда как основной долг заемщика не уменьшается. Постепенно это соотношение выравнивается: если первое времязаемщик гасит в основном проценты, то потом основные средства идут в счет погашения задолженности.
Дифференцированный платеж – это способ ежемесячного платежа по кредиту, при котором размер ежемесячной выплаты по погашению кредита постепенно уменьшается к концу периода кредитования. Ежемесячный платёж, как и при аннуитетной схеме погашения кредита, складывается тоже из двух составляющих. Но в дифференцированной схеме первая часть называется основным платежом, размер которого не изменяется на всём сроке кредитования. Этот платёж идет на погашение основного долга по кредиту. Вторая часть платежа непостоянная, она уменьшается к концу срока кредитования. Данная часть платежа при дифференцированной схеме идет на погашение процентов по кредиту. При дифференцированной схеме погашения кредита, ежемесячный платеж рассчитывается как сумма основного платежа и проценты, начисляемые на оставшийся размер долга. Естественно, что оставшийся размер долга уменьшается к концу срока кредитования, отсюда и получается уменьшение размера ежемесячной выплаты.
Схемы решения экономических задач на кредиты
В практической части своей работы я представляюпримеры решений нескольких задач на кредиты. Это задачи на нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.) выплат, определения срока кредитования.
-
Задача на определение величины выплаты
/дифференцированные платежи
15-го января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Решение:
Фраза «15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца» — это означает, что каждый месяц мы должны выплачивать часть начального долга 

|
№ мес. |
Начальная сумма, млн. руб. |
Сумма начисленных процентов, млн. руб. |
Выплата, млн. руб. |
Конечная сумма, млн. руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
24 |
… |
… |
… |
0 |
Первая сумма 



Ответ: 1 866 000 рублей
Примеры задач банка ЕГЭ на определение величины выплаты:
1. В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторыйсрок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн. рублей?
2. В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн. рублей?
-
Задача на определение ежегодной (ежемесячной) выплаты/аннуитетные платежи
В июле планируется взять кредит на сумму 6409000 рублей. Условия его возврата таковы:
— Каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года.
— С февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами.
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 год |
|
|
x |
|
|
2 год |
|
|
x |
|
Ответ: 3817125 руб.
Примеры задач банка ЕГЭна определение ежегодной (ежемесячной) выплаты:
- В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?
-
Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи
15-го января планируется взять кредит в банке на шесть месяцев в размере 
– 1-го числа каждого месяца долг увеличивается на

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
|
Дата |
|
|
|
|
|
|
|
|
Долг (млн. руб.) |
|
|
|
|
|
|
|
Найдите наибольшее значение
Решение:
|
|
Начальная сумма, млн. руб. |
Сумма долга после начисления процентов,млн. руб. |
Выплата, млн. руб. |
Конечная сумма,млн. руб. |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что общая сумма выплат меньше 1,2 млн. руб., составим и решим неравенство:
Ответ: 7%
Примеры задач банка ЕГЭна определение величины процента ставки кредита:
- 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн. руб.) |
1 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн. рублей.
- В июле планируется взять кредит в банке на сумму 4,5 млн. рублей на срок 9 лет. Условия его возврата таковы:
– каждый январь долг возрастает на r % по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн рублей.
-
Задача на определение суммы кредита
/аннуитетные платежи
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 156 060 рублей больше суммы, взятой в кредит?
Решение:
|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим величину ежегодной выплаты, решив уравнение относительно x:
Известно, что сумма трех выплат на 156060 руб. больше суммы кредита:
Ответ: 239 400руб.
Примеры задач банка ЕГЭна определение суммы кредита:
- В июле 2020 года планируется взять кредит в банке на сумму 419 375 рублей. Условия его возврата таковы:
– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?
- В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 40 980 рублей больше суммы, взятой в кредит?
-
Нахождение количества лет (месяцев) выплаты кредита/дифференцированные платежи
В июле планируется взять кредит в банке на сумму 5 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?
Решение:
«В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» — это означает, что каждый год мы должны выплачивать часть начального долга 

|
№ года |
Начальная сумма, руб. |
Сумма долга после начисления процентов, руб. |
Выплата, руб. |
Конечная сумма, руб. |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Сложим все платежи, чтобы определить общую сумму выплат по кредиту:
Сложив все слагаемые 


Выражение в скобках – арифметическая прогрессия.Найдём её сумму по формуле:
Подставим полученную сумму в выражение для нахождения общей выплаты:
Вместо буквенных символов подставим известные нам значения величин и найдем n:
Ответ: 4 года
Примеры задач банка ЕГЭна нахождение срокавыплаты кредита:
- В июле планируется взять кредит в банке на сумму 14 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 24,5 млн. рублей?
- В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн. рублей?
Заключение
Подводя итоги своей работы, целью которой было познакомиться с типами задач с экономическим содержанием и научиться решать задачи на кредиты, я считаю, что мне удалось достичь этой цели, хотя есть еще к чему стремиться, так как предстоит изучить и задачи других видов.
Проанализировав условия и решения банковских задач, я пришла к заключению, что в большинстве случаев схему решения можно использовать таблицу такого вида:
В ходе своего исследования, разбирая примеры задач и решая задачи самостоятельно, я заметила, что:
- Практически все экономические задачи из банка ЕГЭ можно разделить на несколько основных видов
- Решение экономических задач можно выполнять по одному алгоритму, а именно:
- Занести данные условия задачи в таблицу.
- Составить уравнение или неравенство (систему уравнений/неравенств).
- В ходе решения появится формула, с помощью которой будет найден ответ на вопрос задачи.
Моя гипотеза о том, что, несмотря на сложность и многообразие типов экономических задач их можно классифицировать и вывести единую схему решения, подтвердилась. Я убедилась в ее истинности на примере изучения задач на кредиты.Работу по изучению экономических задач буду продолжать и дальше, так как впереди экзамен по профильной математике и, кроме того, считаю, что решение таких задач позволило мне лучше разобраться в базовых понятиях банковских процессов, что будет полезно мне в моей будущей профессии.
Думаю, что эта работа будет полезна ученикам 10 и 11 класса, учителям для подготовки к ЕГЭ профильного уровня по математике. В ходе работы мною была создана презентация с примерами задач на кредиты и их подробными решениями. Эту презентацию можно предложить ребятам для самостоятельной подготовки, кроме решенных примеров она содержит задачи из банка ЕГЭ по математике.
Список информационных источников
- Лукашин Ю.П. Финансовая математика / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003. https://kpsu.ru/upload/medialibrary/606/606fd86fd3cd2272b6f1f3f1b0e4f96c.pdf
- https://ru.wikipedia.org
- https://ege.sdamgia.ru/
- http://fipi.ru/
- Курс лекций по финансовой математике https://lfirmal.com/predmet-finansovaya-matematika/
- Материалы для подготовки к ЕГЭ по математике https://www.time4math.ru/ege