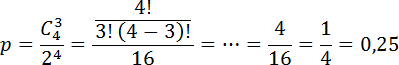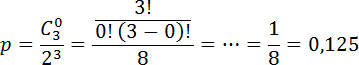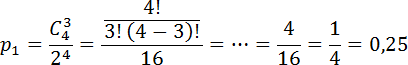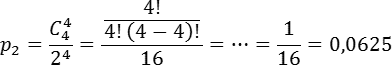Задачи про монету егэ

Всего: 10    1–10

Добавить в вариант

В обменном пункте можно совершить одну из двух операций:

1)  за 3 золотых монеты получить 4 серебряных и одну медную;

2)  за 6 серебряных монет получить 4 золотых и одну медную.

У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?

Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166082., Пробный экзамен Саратов 2016. Вариант 4.

В обменном пункте можно совершить одну из двух операций:

1)  за 3 золотых монеты получить 4 серебряных и одну медную;

2)  за 7 серебряных монет получить 4 золотых и одну медную.

У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медных. На сколько уменьшилось количество серебряных монет у Николы?

Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 152742.

В обменном пункте можно совершить одну из двух операций:

1)  за 2 золотых монеты получить 3 серебряных и одну медную;

2)  за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

Источник: ЕГЭ по базовой математике 26.03.2015. Досрочная волна

В обменном пункте можно совершить одну из двух операций:

 · за 2 золотые монеты получить 3 серебряные и одну медную;

 · за 5 серебряных монет получить 3 золотые и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 100 медных. На сколько уменьшилось количество серебряных монет у Николая?

В обменном пункте можно совершить одну из двух операций:

1)  за 4 золотых монеты получить 5 серебряных и одну медную;

2)  за 7 серебряных монет получить 5 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?

Источник: Пробный экзамен Саратов 2016. Вариант 1.

В обменном пункте можно совершить одну из двух операций:

1)  за 5 золотых монеты получить 6 серебряных и одну медную;

2)  за 8 серебряных монет получить 6 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 55 медных. На сколько уменьшилось количество серебряных монет у Николая?

Источник: Пробный экзамен Саратов 2016. Вариант 2.

В обменном пункте можно совершить одну из двух операций:

— за 5 золотых монет получить 7 серебряных и одну медную;

— за 10 серебряных монет получить 7 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 60 медных. На сколько уменьшилось количество серебряных монет у Николая?

В обменном пункте можно совершить одну из двух операций:

— за 3 золотые монеты получить 4 серебряных и одну медную;

— за 7 серебряных монет получить 4 золотые и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медные. На сколько уменьшилось количество серебряных монет у Николая?

В обменном пункте можно совершить одну из двух операций:

1)  за 4 золотые монеты получить 5 серебряных и одну медную;

2)  за 8 серебряных монет получить 5 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?

В обменном пункте можно совершить одну из двух операций:

1)  за 2 золотые монеты получить 3 серебряные и одну медную;

2)  за 5 серебряных монет получить 3 золотые и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

Всего: 10    1–10

Источник

В США тоже есть ЕГЭ — причём он был задолго до нас. Вот одна задачка оттуда. Мы перевели её на русский и заменили центы на привычные рубли. Сама задача звучит так:

Эту задачку можно решить на листочке за несколько минут. Попробуйте сами, а если не получится — кат в помощь ↓

Это звучит удивительно, но для решения нам не нужно считать точное количество монет обоих видов у каждого (хотя никто не мешает вам попробовать это сделать). Вместо этого мы применим хитрость и смекалку.

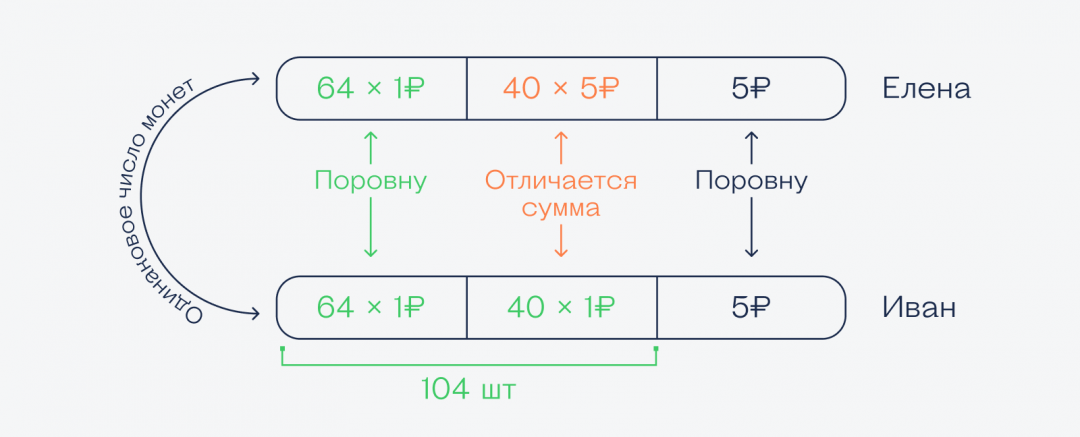
Нам неважно, сколько у кого монет, главное, что их одинаковое количество и у Елены, и у Ивана, а вот количество рублёвых монет разное. Зная это, достаточно нарисовать простую картинку, по которой легко найти ответ на этот вопрос:

Убойная задача из американского ЕГЭ про монеты

Глядя на неё становится понятно, что общую часть из 64 рублёвых монет можно выкинуть у обоих, потому что и там и там одинаковая сумма. А то, что осталось, и даст нужную разницу.

👉 Так как количество монет у каждого одинаковое, то у Ивана вместо 40 пятирублёвок лежит 40 рублёвых монет, а остальные пятирублёвки снова у обоих в одинаковом количестве, и их тоже можно отбросить. Получается, разница в деньгах такая:

  • у Елены — 40 × 5 ₽ = 200 ₽
  • у Ивана — 40 × 1 ₽ = 40 ₽

Значит, у Елены на 200 − 40 = 160 ₽ больше.

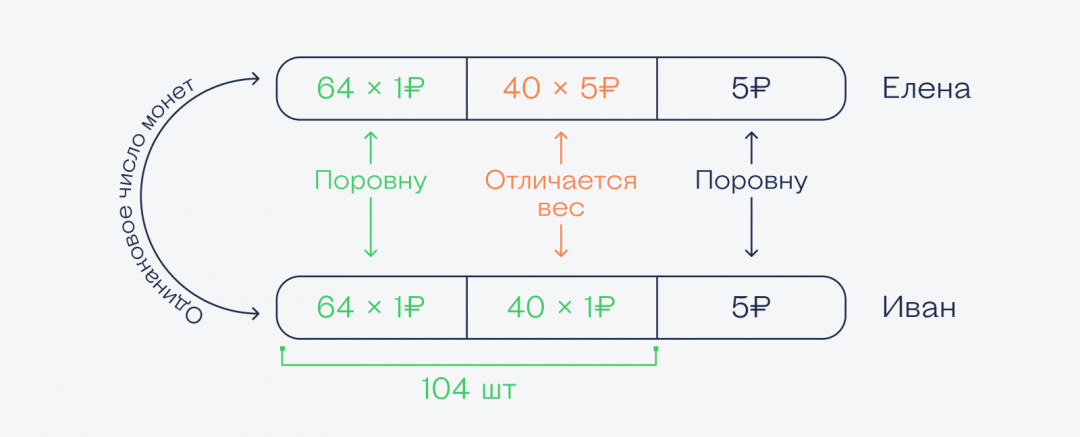
На этом этапе спотыкается большинство решающих, потому что они пытаются найти точное количество монет Ивана. Но мы-то с вами уже знаем, что это необязательно — достаточно найти разницу в весе и по ней посчитать вес монет.

Используем тот же рисунок, но уже в разрезе веса монет:

Убойная задача из американского ЕГЭ про монеты

Получается, что разница в весе зависит от тех же монет, что мы считали в первой части. 

Так как одна рублёвая монета легче одной пятирублёвой на 2,7 грамма, то у 40 монет разница в весе будет 40 × 2,7 = 108 грамм. А раз у Ивана пятирублёвок меньше, чем у Елены, то и монеты будут весить как раз на эти 108 грамм легче: 1,134 − 0,108 = 1,026 килограмма.

Источник

29
Янв 2016

База ЕГЭ Задание 20

Задача с монетами (Задание 20 базовый ЕГЭ )

В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций:

 · за 2 зо­ло­тые мо­не­ты по­лу­чить 3 се­реб­ря­ные и одну мед­ную;

 · за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тые и одну мед­ную.

У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 100 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая?

Решение.

Во время операции первого типа Николай отдает 2  золотых монеты, и взамен получает 3 серебряных и одну медную. Запишем это так:

12

Во время операции второго типа Николай отдает 5  серебряных монет, и взамен получает 3 золотых и одну медную. Запишем это так:

12

Пусть было проведено х операций первого типа, и у операций второго типа.

12

12

Тогда в результате проведения этих операций число медных монет увеличится на 100:

Подготовка к ГИА и ЕГЭ

Число золотых монет не изментся:

Подготовка к ГИА и ЕГЭ

Получили систему уравнений:

    Решение задач на сайте www.ege-ok.ru

Выразим из первого уравнения Подготовка к ГИА и ЕГЭ  и подставим во второе уравнение:

 Подготовка к ГИА и ЕГЭ,

Подготовка к ГИА и ЕГЭ

Подготовка к ГИА и ЕГЭ

То есть было проведено 60 операций первого типа, и 40 второго.

Тогда количество серебряных монет изменится на

Подготовка к ГИА и ЕГЭ

Итак, количество серебряных уменьшится на 20.

Ответ: 20.

И.В. Фельдман, репетитор по математике.

Задача с монетами (Задание 20 базовый ЕГЭ )

Источник

abacus-addition

Так называемые задачи на смекалку – это олимпиадные задачи, которые включены в программу средней школы. Чтобы преуспеть в их решении можно применять математическое моделирование или решать методом подбора.

Данные задачи попадаются последними в базовом уровне математики ЕГЭ в школе. Разберем те из них, которые непосредственно можно решить, составляя математически модели – уравнения.

Задача 1.

Источник: ЕГЭ — 2015. До­сроч­ная волна.

В об­мен­ном пункте можно со­вер­шить одну из двух операций:
• за 2 зо­ло­тых монеты по­лу­чить 3 се­реб­ря­ных и одну медную;
• за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тых и одну медную.
У Ни­ко­лая были толь­ко серебряные монеты. После нескольких посещений об­мен­но­го пункта се­реб­ря­ных монет у него стало меньше, зо­ло­тых не появилось, зато по­яви­лось 50 медных. На сколь­ко уменьшилось ко­ли­че­ство серебряных монет у Николая?

Решение задачи 1.

Составим математическую модель:

[ begin{equation*}  begin{cases}    2з=3с+1м    \   5c=3з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}    2з=3с+1м    \   3з=5с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    2з=3с+1м    \   1з={{5}over{3}}с-{1over3}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    2({{5}over{3}}с-{1over3}м)=3с+1м    \   1з={{5}over{3}}с-{1over3}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   {{10}over{3}}с-{2over3}м=3с+1м    \   1з={{5}over{3}}с-{1over3}мend{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{1}over{3}}с={{5}over{3}}м    \   1з={{5}over{3}}с-{1over3}мс end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=5м    \   1з={{5}over{3}}с-{1over3}м end{cases} end{equation*} ]

Т.к. у Николая появилось 50 медных монет, следовательно, количество серебряных монет уменьшилось на 10.

Ответ: 10.

Задача 2.

Источник: Апро­ба­ция ба­зо­во­го ЕГЭ по ма­те­ма­ти­ке, 13—17 октября: ва­ри­ант 166082.

В об­мен­ном пунк­те можно со­вер­шить одну из двух операций:
1) за 3 зо­ло­тых мо­не­ты по­лу­чить 4 се­реб­ря­ных и одну медную;
2) за 6 се­реб­ря­ных монет по­лу­чить 4 зо­ло­тых и одну медную.
У Ни­ко­лы были толь­ко се­реб­ря­ные монеты. После по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало меньше, зо­ло­тых не появилось, зато по­яви­лось 35 медных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Николы?

Решение задачи 2.

Составим математическую модель:

[ begin{equation*}  begin{cases}    3з=4с+1м    \   6c=4з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}    3з=4с+1м    \   4з=6с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   3з=4с+1м    \   1з={6over4}с-{1over4}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    3({6over4}с-{1over4}м)=4с+1м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{18}over{4}}с-{3over4}м=4с+1м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{2}over{4}}с={{7}over{4}}м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=7м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

Тогда

[ 35м=10с ]

Т.к. у Николая появилось 35 медных монет, следовательно, количество серебряных монет уменьшилось на 10.

Ответ: 10.

Задача 3.

Источник: Пробный экзамен Саратов 2016. Вариант 1.

В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?

Решение задачи 3.

Составим математическую модель:

[ begin{equation*}  begin{cases}    4з=5с+1м    \   7c=5з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}   4з=5с+1м    \   5з=7с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   4з=5с+1м   \   1з={7over5}с-{1over5}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    4({7over5}с-{1over5}м)=5с+1м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{28}over{5}}с-{4over5}м=5с+1м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{3}over{5}}с={{9}over{5}}м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=3м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

Тогда

[ 90м=30с ]

Т.к. у Николая появилось 90 медных монет, следовательно, количество серебряных монет уменьшилось на 30.

Ответ: 30.

Источник

В обменном пункте можно совершить одну из двух операций:

1) за 2 золотые монеты получить 3 серебряные и одну медную;

2) за 7 серебряных монет получить 3 золотые и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 20 медных. На сколько уменьшилось количество серебряных монет у Николая?

Решение.

Условно обозначим через a – число золотых монет, через b – число серебряных монет, а через c – число медных монет. Тогда операции 1 и 2 могут быть записаны в виде

Изначально у Николая a=0, с=0 и b>0. Поэтому первой операцией он может обменять только серебряные монеты на золотые и медные. Для этого ему понадобится взять первые 7 серебряных монет, в результате получит:

1. .

Второй операцией он может использовать две золотые (из трех) монеты для получения двух серебряных и одной медной монеты и еще останется одна золотая и медная монета с предыдущей операции:

2.  

Затем, Николай может достать еще 4 серебряные монеты, чтобы получить 7b серебряных монет для выполнения первой операции:

3. 

Наконец, следующей операцией он может обменять 4a золотых монет на 6b+2c монет других достоинств:

4. .

В результате этих четырех операций избавились от золотых монет (a=0), но приобрели медные. При этом, число серебряных монет, взятых во время операций обмена, составило 7b+4b=11b, а в результате получилось только 6b этих монет, то есть, серебряных монет стало на 11b-6b = 5b меньше.

По условию задания необходимо получить 20 медных монет. Этого можно достичь на 4 итерации, так как 5c∙4=20c. Тогда серебряных монет станет меньше на 5b∙4=20b, то есть на 20 монет.

Ответ: 20.

Источник

30 мая 2012

Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

Основная формула теории вероятностей

где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.

Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n. В этом и состоит вся сложность.

Тем не менее, существует как минимум два принципиально различных метода решения:

  1. Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
  2. Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!

Метод перебора комбинаций

Этот метод еще называется «решение напролом». Состоит из трех шагов:

  1. Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n;
  2. Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k;
  3. Осталось найти вероятность: p = k : n.

К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:

Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.

Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):

OO OP PO PP

Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

OP PO

Таких вариантов оказалось k = 2. Находим вероятность:

Вероятность для n = 4 и k = 2

Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем все возможные комбинации орлов и решек:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:

Вероятность для n = 16 и k = 1

Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности

Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:

Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:

Специальная формула вероятности для задачи B6

Где Cnk — число сочетаний из n элементов по k, которое считается по формуле:

Формула числа сочетани из n элементов по k элементов

Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.

Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:

Специальная формула вероятности для n = 4 и k = 3

С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же.

Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:

Специальная формула вероятности для n = 3 и k = 0

Напомню, что 0! = 1 по определению. Поэтому C30 = 1.

Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.

Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.

Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:

Специальная формула вероятности для n = 4 и k = 3

Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:

Специальная формула вероятности для n = 4 и k = 4

Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:

p = p1 + p2 = 0,25 + 0,0625 = 0,3125

Смотрите также:

  1. Правила комбинаторики в задаче B6
  2. Комбинаторика в задаче B6: легкий тест
  3. Что такое числовая дробь
  4. Задачи B12, сводящиеся к линейным уравнениям
  5. Сложные задачи на проценты
  6. Задача B4 с таблицами: тарифы на интернет
Источник

22 февраля 2022

В закладки

Обсудить

Жалоба

Задачи с монетой по теории вероятностей на профильном ЕГЭ по математике

Задание №2.

1) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет хотя бы 1 раз.

2) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.

Теория: zadachi_s_monetoy.pdf

Задачи с монетой по теории вероятностей на профильном ЕГЭ по математике

Источник: vk.com/clubinnaleonidovna

Источник

Понравилась статья? Поделить с друзьями:
  • Задачи про кофейные автоматы в егэ по математике 2022
  • Задачи про конус егэ по математике
  • Задачи про заводы егэ математика
  • Задачи про бактерии егэ математика
  • Задачи при сдаче экзамена на судью