Задачи про трапецию егэ


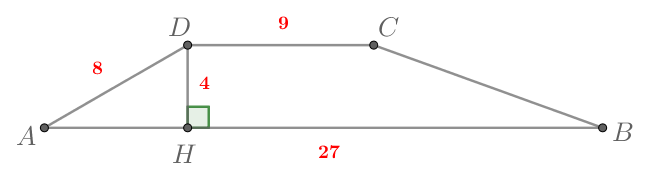
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

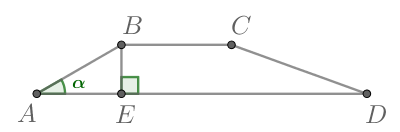
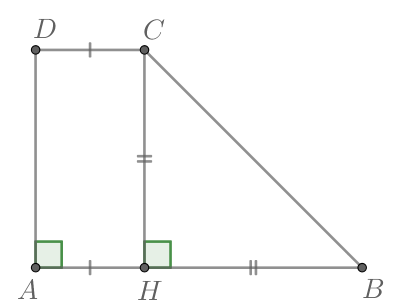
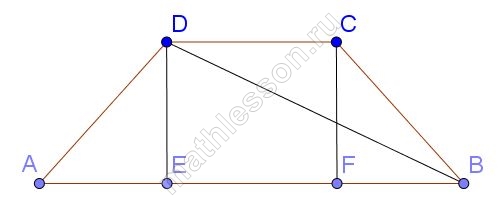
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

2

Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен дробь: числитель: 5, знаменатель: 7 конец дроби . Найдите боковую сторону.

3

Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен дробь: числитель: 2 корень из 10, знаменатель: 7 конец дроби . Найдите меньшее основание.

4

Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен дробь: числитель: 5, знаменатель: 11 конец дроби . Найдите высоту трапеции.

5

Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен дробь: числитель: 13, знаменатель: 8 конец дроби . Найдите большее основание.

Пройти тестирование по этим заданиям

Источник

25
Июл 2013

Категория: 01 Геометрия

01. Трапеция

2013-07-25
2022-09-11

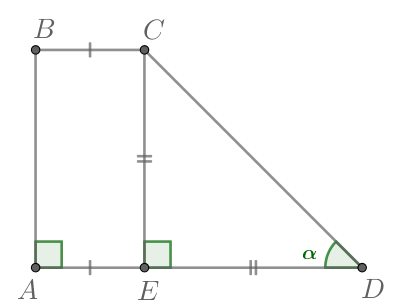
Задача 1. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

Решение: + показать


Задача 2. Большее основание равнобедренной трапеции равно 18. Боковая сторона равна 3. Синус острого угла равен frac{sqrt5}{3}.  Найдите меньшее основание.

Решение: + показать


Задача 3. Основания равнобедренной трапеции равны 28 и 15. Тангенс острого угла равен frac{11}{13}. Найдите высоту трапеции.

Решение: + показать


Задача 4. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 70^{circ}? Ответ дайте в градусах.

Решение: + показать


Задача 5.  Найдите среднюю линию трапеции, если ее основания равны 24 и 9.

Решение: + показать


Задача 6. Средняя линия трапеции равна 45, а меньшее основание равно 37. Найдите большее основание трапеции.

Решение: + показать


Задача 7. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Решение: + показать


Задача 8. Основания трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение: + показать


Задача 9. В равнобедренной трапеции основания равны 29 и 50, острый угол равен 60^{circ}. Найдите ее периметр.

Решение: + показать


Задача 10. Основания трапеции равны 14 и 24, боковая сторона равна 12. Площадь трапеции равна 114. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

 

Решение: + показать


Задача 11. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.

Решение: + показать


Задача 12. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 74 и 41. Найдите среднюю линию этой трапеции.

Решение: + показать


Задача 13.  Основания трапеции относятся как 4:5, а средняя линия равна 54. Найдите меньшее основание.

Решение: + показать


Задача 14.  В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите ее среднюю линию.

Решение: + показать


Задача 15. Найдите площадь прямоугольной трапеции, основания которой равны 16 и 24, большая боковая сторона составляет с основанием угол 45^{circ}.

Решение: + показать


Задача 16. Основания равнобедренной трапеции равны 17 и 23, а ее периметр равен 50. Найдите площадь трапеции.

Решение: + показать


Задача 17. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны sqrt2.

g

Решение: + показать


тестВы можете пройти тест по теме «Трапеция»

Автор: egeMax |

комментариев 14

Печать страницы

Источник

3. Геометрия на плоскости (планиметрия). Часть I


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

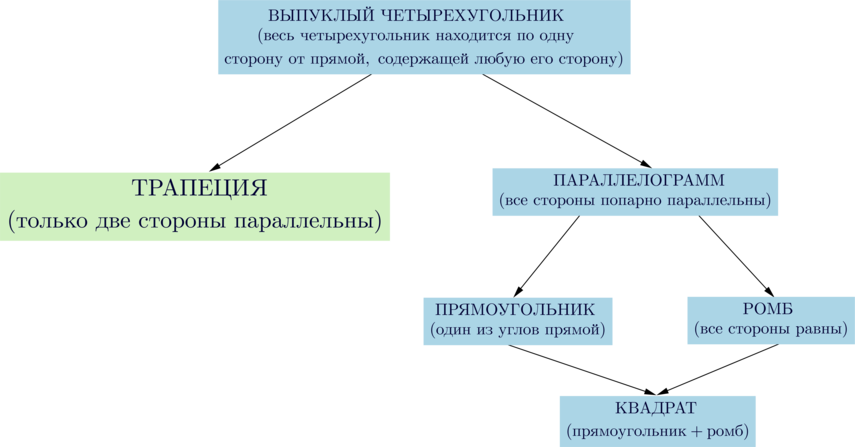
Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства трапеции:

(blacktriangleright) Сумма углов при боковой стороне равна (180^circ).

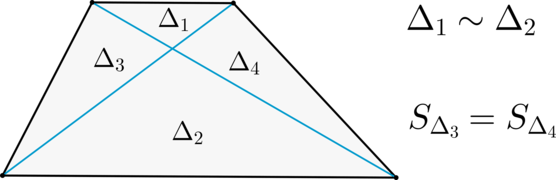
(blacktriangleright) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

(blacktriangleright) Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.


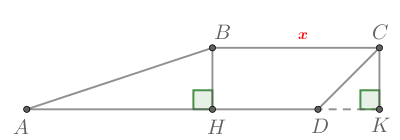
Задание
8

#1695

Уровень задания: Сложнее ЕГЭ

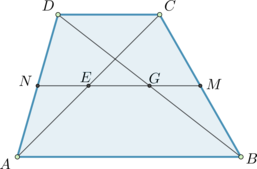
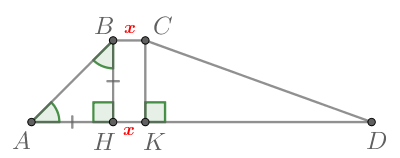
В трапеции (ABCD) с основаниями (AD) и (BC): отрезки (QR) и (PS) параллельны основаниям, причем (AP = QB) и (CR = SD). Найдите основание (BC), если (QR = 6,75), (PS = 8,25), а (AD = 12).

Т.к. (QR) и (PS) параллельны основаниям, то четырехугольник (PQRS) также будет трапецией, причем среднии линии (ABCD) и (PQRS) совпадают. Средняя линия равна (frac{1}{2}cdot(QR + PS) = frac{1}{2}cdot(6,75 + 8,25) = 7,5). Тогда можно выразить верхнее основание через среднюю линию и нижнее основание следующим образом: (BC = 2cdot7,5 — 12 = 3).

Ответ: 3


Задание
9

#291

Уровень задания: Сложнее ЕГЭ

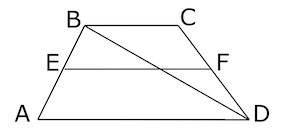
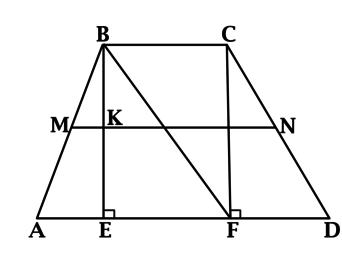
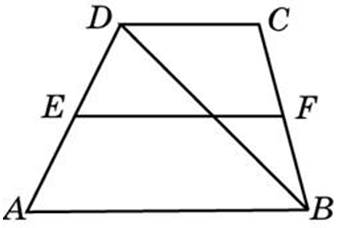
В трапеции (ABCD) с основаниями (BC = 3) и (AD > BC) проведены высоты (BE) и (CF). (BE) пересекает среднюю линию (MN) в точке (K). Известно, что (MK = 1), (DF = 2,4), (BF = 5). Найдите площадь трапеции (ABCD).

Площадь трапеции равна произведению полусуммы оснований на высоту. Так как (BC || AD), то в (BCFE) все углы прямые, следовательно, (BCFE) – прямоугольник и (EF = BC = 3). Средняя линия в трапеции параллельна её основаниям, тогда (MK || AE). При этом, (M) – середина (AB), значит, (MK) – средняя линия в треугольнике (ABE). Средняя линия треугольника равна половине его основания, тогда (AE = 2cdot MK = 2).

(AD = AE + EF + FD = 2 + 3 + 2,4 = 7,4). Треугольник (BCF) – прямоугольный. (BC = 3), (BF = 5), откуда по теореме Пифагора: (CF^2 = BF^2 — BC^2 = 25 — 9 = 16), то есть, (CF = 4).

Площадь (ABCD) равна (0,5(3 + 7,4)cdot 4 = 20,8).

Ответ: 20,8


Задание
10

#3690

Уровень задания: Равен ЕГЭ

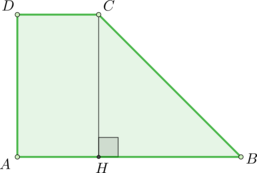
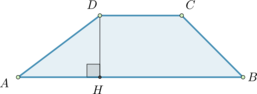
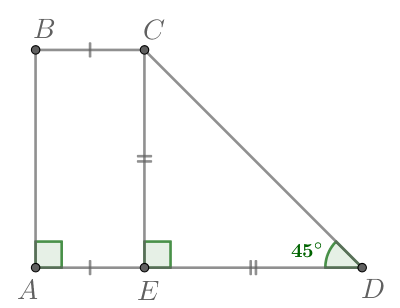
Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.

Проведем высоту (CH).

(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).

Ответ: 45


Задание
11

#3691

Уровень задания: Равен ЕГЭ

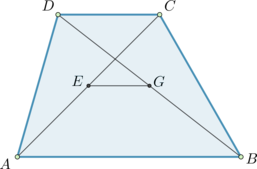
Основания трапеции равны (3) и (2). Найдите отрезок, соединяющий середины диагоналей трапеции.

Пусть (M) и (N) – середины боковых сторон трапеции. Отрезок (MN) пересекает диагонали в серединах: (E) и (G).

Действительно, так как (MN) – средняя линия, то (MNparallel ABparallel CD). Следовательно, если рассмотреть (triangle ADC), то (NEparallel CD). Так как к тому же (N) – середина (AD), то по теореме Фалеса (E) – середина (AC). Аналогично доказывается, что (G) – середина (DB).
Так как средняя линия равна полусумме оснований, то (MN=0,5(3+2)=2,5). Так как (NE) и (GM) – средние линии в треугольниках (ADC) и (BDC) соответственно, параллельные (CD), то (NE=GM=0,5CD=0,5cdot 2=1). Следовательно, (EG=MN-NE-GM=2,5-1-1=0,5).

Ответ: 0,5


Задание
12

#3692

Уровень задания: Равен ЕГЭ

Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.

Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).

Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]

Ответ: 42


Задание
13

#3693

Уровень задания: Равен ЕГЭ

Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

Пусть (AD=8). Проведем (DHperp AB).

Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).

Ответ: 30


Задание
14

#3694

Уровень задания: Равен ЕГЭ

Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).

Проведем высоту (CH).

Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]

Ответ: 16

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

1

.

11

Трапеция и ее свойства

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

1.01Треугольник: внутренние и внешние углы

1.02Треугольник: высота, биссектриса, медиана

1.03Треугольник: задачи на подобие

1.04Прямоугольный треугольник и теорема Пифагора

1.05Треугольник: площадь и периметр

1.06Параллелограмм и его свойства

1.07Параллелограмм и свойство его биссектрисы

1.08Прямоугольник и его свойства

1.09Ромб и его свойства

1.10Квадрат и его свойства

1.11Трапеция и ее свойства

1.12Равнобедренная трапеция

1.13Окружность: центральный и вписанный углы

1.14Окружность: углы, образованные хордами, секущими, касательными

1.15Окружность: отрезки хорд, секущих, касательных

1.16Окружность: описанная около многоугольника

1.17Окружность: вписанная в многоугольник или угол

1.18Длина окружности или дуги и площадь круга или сектора

1.19Правильный шестиугольник и его свойства

1.20Площадь многоугольника: различные формулы

1.21Внешние углы многоугольника и тригонометрия

1.22Решение треугольника и других фигур с помощью тригонометрии

1.23Теорема синусов и теорема косинусов

1.24Координатная плоскость

1.25Векторы: сложение, вычитание, координаты

1.26Задачи на клетчатой бумаге

Решаем задачи

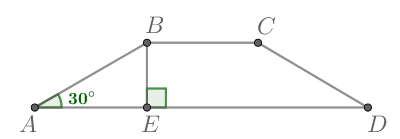
Один из углов прямоугольной трапеции равен ∘ 113 . Найдите меньший угол этой трапеции. Ответ дайте в градусах.

PIC

Показать ответ и решение

В трапеции сумма углов, прилежащих боковой стороне, равна ∘ 180 , то есть если один из таких углов равен ∘ 113 , то другой
равен

180∘− 113∘ = 67∘

Оставшиеся два угла равны ∘ 90 , так как трапеция — прямоугольная. Тогда меньший угол равен ∘ 67 .

В трапеции ABCD известно, что AB = CD, ∘ ∠BDA = 14 и ∘ ∠BDC = 106. Найдите угол ABD. Ответ дайте в
градусах.

PIC

Показать ответ и решение

PIC

Трапеция равнобедренная, то есть

∘ ∘ ∘ ∠BAD = ∠CDA = ∠BDA + ∠BDC = 106 + 14 = 120

По сумме углов треугольника ABD имеем:

∘ ∘ ∘ ∘ ∘ ∠ABD = 180 − ∠BAD − ∠ADB = 180 − 120 − 14 = 46

Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.

PIC

Показать ответ и решение

Средняя линия трапеции равна полусумме оснований, то есть равна

1 12 2(3 +9)= 2-= 6

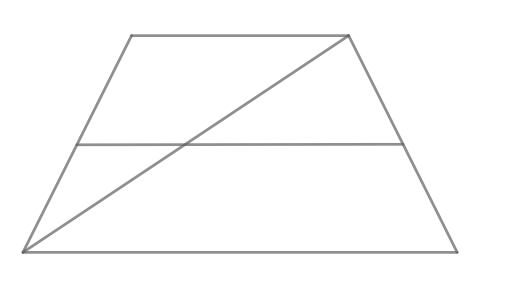
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

PIC

Показать ответ и решение

PIC

Пусть AB = 11, DC = 10.

Так как EF — средняя линия трапеции, EO и OF — средние линии треугольников ADC и ACB соответственно.
Значит,

EO = 1DC = 1⋅10= 5 2 2

1 1 OF = 2 AB = 2 ⋅11 =5,5

Больший из этих отрезков равен 5,5.

Средняя линия трапеции равна 20. Одна из диагоналей трапеции делит среднюю линию в отношении 1 к 4. Найдите большее
основание трапеции.

Основания трапеции равны 6 и 8. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

PIC

Показать ответ и решение

Для начала найдем длину средней линии трапеции: она равна полусумме оснований, то есть

6+ 8 -2-- =7

Так как EF — средняя линия трапеции ABCD , то EF || AB, и при этом E — середина AD.

Тогда в треугольнике ADB отрезок EO параллелен основанию AB и при этом проходит через середину стороны AD.
Значит, EO — средняя линия треугольника ADB и

EO = 1AB = 4 2

Тогда

OF =EF − EO = 7− 4= 3

Следовательно, наибольший из отрезков равен 4.

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ выразите в градусах.

PIC

Показать ответ и решение

Опустим высоту BE на AD. В прямоугольном треугольнике ABE катет BE напротив угла α равен BE = AB sinα = 8sinα.

PIC

Запишем площадь трапеции, чтобы найти sinα

1 2SABCD SABCD = 2(AD + BC )⋅BE ⇒ BE = AD-+-BC-= 4

Тогда

sin α= BE- = 0,5 ⇒ α= 30∘ 8

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ∘ 150. Найдите
площадь трапеции.

PIC

Показать ответ и решение

Пусть ∘ ∠ABC =150 , тогда из параллельности ∘ ∠DAB = 30 . Опустим высоту BE на AD. В прямоугольном треугольнике
ABE катет BE напротив угла в 30∘ равен половине гипотенузы

1 BE = 2AB = 3,5

PIC

Тогда площадь трапеции

SABCD = 1(AD +BC )⋅BE = 1 (6 +18)⋅3,5= 42 2 2

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

PIC

Показать ответ и решение

Опустим высоту CE на основание AD трапеции. ABCE — прямоугольник и AE =BC = 4. Тогда ED = AD − AE =8.

Запишем площадь трапеции, чтобы найти длину высоты CE :

1 2S 2⋅64 SABCD = 2(BC + AD )⋅CE ⇒ CE = BC-A+BCADD- = 12+-4 = 8

Получили, что EC =ED = 8. Тогда треугольник CDE — прямоугольный с равными катетами, значит, его острый угол
равен 45∘.

PIC

Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием
угол 45∘.

PIC

Показать ответ и решение

Опустим высоту CE на основание AD трапеции. ABCE — прямоугольник и AE =BC = 2. Тогда ED = AD − AE =4.

PIC

Треугольник CDE — прямоугольный с углом в ∘ 45 , следовательно, он равнобедренный и CE =ED = 4. Тогда площадь
трапеции

SABCD = 1(BC + AD)⋅CE = 1(2+ 6) ⋅4 = 16 2 2

Показать ответ и решение

Рассмотрим треугольники ABC и ACD :

  1. ∠BCA =∠CAD;
  2. BC- 1 AC- AC = 2 = AD .

Тогда треугольники ABC и ACD подобны по пропорциональности двух сторон и равенству углов между ними, следовательно,
их площади относятся как квадрат коэффициента подобия:

( )2 SABC-= BC- = 1 ⇒ SACD = 4 ⋅SABC = 8 SACD AC 4

Таким образом,

SABCD = SABC + SACD = 2+ 8= 10

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ дайте в градусах.

PIC

Показать ответ и решение

Пусть AD = 8. Проведем DH ⊥ AB.

PIC

Тогда площадь трапеции равна

AB-+DC-- 27-+9- 72= 2 ⋅DH = 2 ⋅DH ⇒ DH = 4

Рассмотрим прямоугольный △ADH. Так как катет DH равен половине гипотенузы AD, то угол DAH равен
30∘.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

PIC

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

PIC

Показать ответ и решение

Проведем высоту CH.

PIC

Тогда ADCH — прямоугольник, следовательно,

AH = DC = 4 ⇒ HB = 12 − 4 = 8

Площадь трапеции равна

AB-+-DC- 4+-12 64 = 2 ⋅CH = 2 ⋅CH ⇒ CH =8

Заметим, что мы получили, что CH = HB = 8. Тогда △CHB равнобедренный, значит, углы при основании равны, то есть
∠HCB = ∠HBC. Так как сумма острых углов в прямоугольном треугольнике равна 90∘, то

∘ ∘ ∠B =∠HBC =90 :2 = 45

Одно из оснований трапеции в 5 раз меньше ее средней линии. Во сколько раз это основание меньше другого основания
трапеции?

Показать ответ и решение

PIC

Обозначим меньшее основание трапеции за x, большее — за y. Тогда 5x — длина средней линии трапеции. Так как средняя
линия равна полусумме оснований, то

x+ y = 2 ⋅5x ⇔ y = 9x

Следовательно, меньшее основание в 9 раз меньше большего основания.

В трапеции боковые стороны равны 12 и 12√5, угол при меньшей боковой стороне равен 135∘. Найдите отношение меньшего
основания к большему, если площадь трапеции равна 156.

Если задача допускает несколько вариантов ответа, внесите в бланк меньший из них.

PIC

Показать ответ и решение

Рассмотрим трапецию ABCD, где AB = 12, CD = 12√5, ∠A =45∘, ∠B =135∘, и проведем в ней высоты BH и CK. При этом
трапеция может выглядеть двумя разными способами.

1 способ.

PIC

Заметим, что △ABH — прямоугольный и равнобедренный, тогда

BH = AH = AB√- = 1√2-= 6√2 2 2

Значит, из прямоугольного △DCK можно найти KD :

√- √ - √-------- √- KD2 = CD2 − CK2 = (12 5)2− (6 2)2 = 648 ⇒ KD = 9⋅9 ⋅4 ⋅2= 18 2

Т.к. площадь трапеции равна 156 , то имеем следующее уравнение:

√ - √ - 6--2+-18-2+-x+-x ⋅6√2 = 156 ⇒ x =√2 2

Тогда

√- √- BC :AD = ( 2):(25 2)= 1:25

2 способ.

PIC

В этом случае, поступая аналогично первому способу, находим

CK = DK = BH = 6√2- √ - AH =18 2 √ - √- √ - AD = 18 2+ x− 6 2= 12 2+ x

Из уравнения 12√2+ x+ x √- 156 = -----2-----⋅6 2 находим √ - x =7 2.

Значит,

BC :AD = (7√2-):(19√2) =7 :19

Т.к. 125 < 719, то в ответ пойдет 125 = 0,04.

В трапеции ABCD CD = BC, ∠BCD = 140∘, ∠ABD = 100∘. Найдите модуль разности острых углов трапеции.

PIC

Показать ответ и решение

△BCD — равнобедренный, следовательно,

∘ ∠CBD = ∠CDB =20 ∠BAD = 180∘ − ∠ABD − ∠CBD = 180∘− 100∘− 20∘ = 60∘ ∘ ∘ ∘ ∠ADC = 180 − 140 = 40

Тогда

∘ ∘ ∘ ∘ |∠ADC − ∠BAD |=|40 − 60|= |− 20|= 20

Источник

Самостоятельная работа

I вариант

№1(2532)  Найдите среднюю линию трапеции, если
ее основания равны 14 и 28

№2(2535)  Средняя линия трапеции равна 19,5, а
меньшее основание равно 17. Найдите большее основание трапеции

№3(2544) Прямая, проведенная параллельно
боковой стороне трапеции через конец меньшего основания, равного 16, отсекает
треугольник, периметр которого равен 33. Найдите периметр трапеции.

№4(2550) Основания трапеции относятся как 4:5,
а средняя линия равна 27. Найдите меньшее основание.

№5(2556) Средняя линия трапеции равна 38. Одна
из диагоналей делит её на два отрезка, разность которых равна 12. Найдите
большее основание трапеции.

II вариант

№1(2533)  Найдите среднюю линию трапеции, если
ее основания равны 37 и 35

№2(2536)  Средняя линия трапеции равна 25,5, а
меньшее основание равно 21. Найдите большее основание трапеции

№3(2545) Прямая, проведенная параллельно
боковой стороне трапеции через конец меньшего основания, равного 14, отсекает
треугольник, периметр которого равен 29. Найдите периметр трапеции.

№4(2551) Основания трапеции относятся как 5:7,
а средняя линия равна 30. Найдите меньшее основание.

№5(2557) Средняя линия трапеции равна 20. Одна
из диагоналей делит её на два отрезка, разность которых равна 6. Найдите большее
основание трапеции.

Источник
Skip to content

ЕГЭ Профиль №1. Трапеция

ЕГЭ Профиль №1. Трапецияadmin2022-10-19T14:49:14+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №1. Трапеция

Задача 1. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Ответ

ОТВЕТ: 0,96.
Задача 2. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен (frac{5}{7}). Найдите боковую сторону.

Ответ

ОТВЕТ: 21.
Задача 3. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (frac{{2sqrt {10} }}{7}). Найдите меньшее основание.

Ответ

ОТВЕТ: 22.
Задача 4. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен (frac{5}{{11}}). Найдите высоту трапеции.

Ответ

ОТВЕТ: 10.
Задача 5. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен (frac{{13}}{8}). Найдите большее основание.

Ответ

ОТВЕТ: 71.
Задача 6. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Ответ

ОТВЕТ: 0,4.
Задача 7. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Ответ

ОТВЕТ: 8.
Задача 8. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Ответ

ОТВЕТ: 7.
Задача 9. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Ответ

ОТВЕТ: 15.
Задача 10. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Ответ

ОТВЕТ: 8.
Задача 11. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Ответ

ОТВЕТ: 160.
Задача 12. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Ответ

ОТВЕТ: 30.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.

Ответ

ОТВЕТ: 16.
Задача 14. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.
Задача 15. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Ответ

ОТВЕТ: 160.
Задача 16. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Ответ

ОТВЕТ: 5.
Задача 17. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Ответ

ОТВЕТ: 42.
Задача 18. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Ответ

ОТВЕТ: 30.
Задача 19. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50°? Ответ дайте в градусах.

Ответ

ОТВЕТ: 115.
Задача 20. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Ответ

ОТВЕТ: 38.
Задача 21. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Ответ

ОТВЕТ: 5.
Задача 22. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60°. Найдите меньшее основание.

Ответ

ОТВЕТ: 15.
Задача 23. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр.

Ответ

ОТВЕТ: 69.
Задача 24. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Ответ

ОТВЕТ: 23.
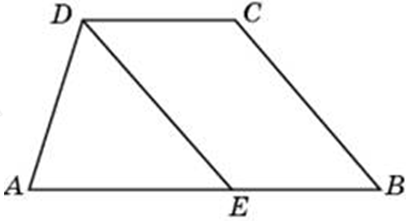Задача 25. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Ответ

ОТВЕТ: 10.
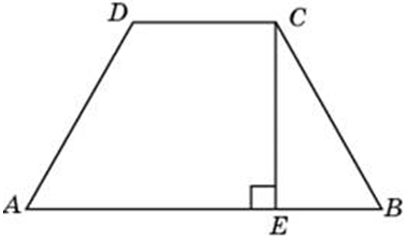Задача 26. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45°. Найдите высоту трапеции.

Ответ

ОТВЕТ: 3.
Задача 27. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Ответ

ОТВЕТ: 0,5.
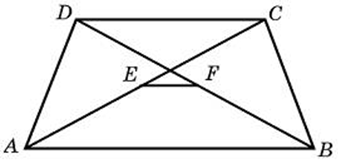Задача 28. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Ответ

ОТВЕТ: 12.
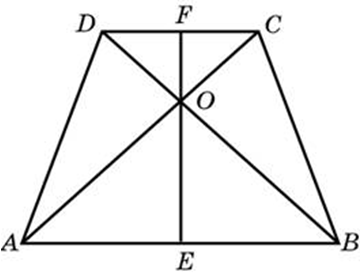Задача 29. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Ответ

ОТВЕТ: 5.

Источник

Задание 972

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Ответ: 30

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

Площадь трапеции вычисляется по формуле $$S=frac{a+b}{2}*h$$. Получаем $$40=frac{7+13}{2}*CH$$. Отсюда CH = 4.

Из треугольника CHD по теореме Пифагора находим CD = 5. Отсюда периметр равен 7 + 13 + 5 + 5 = 30

Задание 1858

Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° со­от­вет­ствен­но.

Ответ: 105

Скрыть

$$angle A=angle BAC+angle CAD=30+45=75^{circ}$$, тогда по свойству углов трапеции: $$angle B=180-angle A=105^{circ}$$

Задание 1859

Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 50° со­от­вет­ствен­но.

Ответ: 80

Скрыть

$$angle A=angle BAC+angle CAD=30+50=80^{circ}$$

Задание 1860

Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол тра­пе­ции. Ответ дайте в гра­ду­сах.

Ответ: 110

Скрыть

Так как дана равнобедренная трапеция, то сумма острых углов при большем основании будет составлять 140 градусов, $$angle A=angle B=frac{140}{2}=70^{circ}$$, по свойству углов трапеции: $$angle D=180-angle A=110^{circ}$$

Задание 1861

Най­ди­те мень­ший угол рав­но­бед­рен­ной тра­пе­ции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в гра­ду­сах.

Ответ: 60

Скрыть

Пусть меньший угол равен х, тогда больший угол равен 2х. По свойству углов трапеции получаем, что $$x+2x=180Leftrightarrow$$$$x=60$$, то есть меньший угол составляет $$60^{circ}$$

Задание 1863

Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен $$frac{5}{6}$$. Най­ди­те её боль­шее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

Ответ: 33

Скрыть

Опустим высоту CF, тогда из прямоугольного треугольника CFB: $$FB=frac{CF}{tgB}=frac{15}{frac{5}{6}}=18$$. DC=AF=15, тогда AB=15+18=33.

Задание 1864

В рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та 4, мень­шее ос­но­ва­ние 8 и угол при ос­но­ва­нии $$45^{circ}$$. Най­ди­те боль­шее ос­но­ва­ние.

Ответ: 16

Скрыть

Опустим высоты DE=CF=4, тогда из прямоугольного треугольника ADE: так как $$angle A=45^{circ}$$, то $$angle ADE=90-45=45^{circ}$$, следовательно, реугольник AED — равнобедренный, и AE=DE=4, аналогично FB=4. Но EF=DC=8, тогда AB=4+4+8=16.

Задание 1865

Ос­но­ва­ния тра­пе­ции равны 4 и 10. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

Ответ: 5

Скрыть

EG — средняя линия треугольника ADB, тогда $$EG=frac{1}{2}=AB=5$$, аналогично GF — средняя линия треугольника DCB, тогда $$GF=frac{1}{2}DC=2$$, наибольший в таком случае равен 5

Примечение: больший из отрезков всегда будет равен половине большего основания

Задание 1866

Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

Ответ: 85

Скрыть

Опустим две высоты DE=CF, тогда AE=FB (из равенства прямоугольных треугольников ADE и CFB по катету и гипотенузе), и DC=EF=50, тогда $$AE=FB=frac{104-50}{2}=27$$. Тогда из прямоугольного треугольника ADE : $$DE=sqrt{AD^{2}-AE^{2}}=sqrt{45^{2}-27^{2}}=36$$, следовательно, EB=AB-AE=104-27=77. Тогда из прямоугольного треугольника DEB: $$DB=sqrt{DE^{2}+EB^{2}}=sqrt{77^{2}+36^{2}}=85$$

Задание 1867

Около тра­пе­ции, один из углов ко­то­рой равен 49°, опи­са­на окруж­ность. Най­ди­те осталь­ные углы тра­пе­ции.

За­пи­ши­те ве­ли­чи­ны углов в ответ через точку с за­пя­той в по­ряд­ке не­убы­ва­ния.

Ответ: 49; 131; 131

Скрыть

По свойству вписанного четырехугольник $$angle A+angle C=180^{circ}$$, пусть $$angle A=49^{circ}Rightarrow$$$$angle C=180-49=131^{circ}$$. По свойству углов трапеции $$angle B=180-angle C=180-131=49^{circ}$$, аналогично $$angle D=180-angle A=131^{circ}$$

Задание 1868

В тра­пе­цию, сумма длин бо­ко­вых сто­рон ко­то­рой равна 24, впи­са­на окруж­ность. Най­ди­те длину сред­ней линии тра­пе­ции.

Ответ: 12

Скрыть

По свойству описанного четырехугольника AD+BC=AB+CD, тогда сумма оснований тоже 24, средняя линия же равна полусумме оснований, то есть 24/2=12.

Задание 1965

Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен $$frac{1}{3}$$. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 30

Скрыть

  1. Опустим высоту CE. Пусть $$sin D=frac{1}{3}$$, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2$$
  2. Из формулы площади трапеции: $$S_{ABCD}=frac{18+12}{2}*2=30$$

Задание 1966

Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен $$frac{2sqrt{2}}{3}$$. Най­ди­те пло­щадь тра­пе­ции.

Ответ: 30

Скрыть

  1. Пусть $$cos D =frac{2sqrt{2}}{3}$$, опустим высоту CE. Тогда из треугольника  CED: $$ED=CD*cos D=6*frac{2sqrt{2}}{3}=4sqrt{2}$$
  2. По теореме Пифагора из треугольника CED: $$CE=sqrt{6^{2}-(4sqrt{2})^{2}}=2$$
  3. Из формулы площади трапеции $$S_{ABCD}=frac{18+12}{2}*2=30$$

Задание 1967

Сред­няя линия тра­пе­ции равна 11, а мень­ше ос­но­ва­ние равно 5. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ответ: 17

Скрыть

Пусть a — большее основание, тогда из формулы длины средней линии трапеции : $$a=2*11-5=17$$

Задание 1968

Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

Ответ: 15

Скрыть

  1. Пусть $$angle D=30^{circ}$$. Опустим высоту CE, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2,5$$
  2. По формуле площади трапеции $$S_{ABCD}=frac{3+9}{2}*2,5=15$$

Источник

Понравилась статья? Поделить с друзьями:
  • Задачи про сплавы егэ по математике
  • Задачи про сплав егэ
  • Задачи про семью егэ
  • Задачи про растворы егэ по математике
  • Задачи про рабочих егэ математика