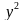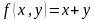Задачи на оптимальный выбор
Версия для печати и копирования в MS Word
1
В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
2
В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у. е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у. е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Источник: А. Ларин: Тренировочный вариант № 123.
3
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Считайте, что перекресток не T-образный, обе дороги продолжаются за перекрестком.
Источник: А. Ларин: Тренировочный вариант № 124.
4
Алексей вышел из дома на прогулку со скоростью υ км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение υ, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
Источник: А. Ларин: Тренировочный вариант № 116.
5
В бассейн проведены три трубы. Первая труба наливает 30 м3 воды в час. Вторая труба наливает в час на 3V м3 меньше, чем первая (0 < V < 10), а третья труба наливает в час на 10V м3 больше первой. Сначала первая и вторая трубы, работая вместе, наливают 30% бассейна, а затем все три трубы, работая вместе, наливают оставшиеся 0,7 бассейна. При каком значении V бассейн быстрее всего наполнится указанным способом?
Источник: А. Ларин: Тренировочный вариант № 117.
6
Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость одного контейнера типа А составляет 2 тонны и 5 млн. руб., контейнера типа В – 5 тонн и 7 млн. руб.соответственно. Определите наибольшую возможную суммарную стоимость (в млн. руб.) всех контейнеров, перевозимых баржей при данных условиях.
Источник: А. Ларин: Тренировочный вариант № 134.
7
Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t3 часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t3 часов в неделю, они производят t приборов.
За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?
Источник: А. Ларин: Тренировочный вариант № 140.
8
На каждом из двух заводов работает по 100 человек. На первом заводе один рабочий изготавливает за смену 3 детали А или 1 деталь В. На втором заводе для изготовления t деталей (и А, и В) требуется t2 человеко-смен. Оба завода поставляют детали на комбинат, где собирают изделие, причем для его изготовления нужна 1 деталь А и 3 детали В. При этом заводы договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
9
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
| Вид начинки | Себестоимость (за 1 тонну) |
Отпускная цена (за 1 тонну) |
Производственные возможности |
| ягоды | 70 тыс. руб. | 100 тыс. руб. | 90 (тонн в мес.) |
| творог | 100 тыс. руб. | 135 тыс. руб. | 75 (тонн в мес.) |
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
10
В январе 2000 года ставка по депозитам в банке «Возрождение» составляла х% годовых, тогда как в январе 2001 года она составила у% годовых, причем известно, что x + y = 30. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной.
Источник: А. Ларин: Тренировочный вариант № 88.
11
Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации, 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Источник: Материалы для экспертов ЕГЭ
12
Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)
13
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара.
За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.
14
Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
15
Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
16
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
17
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
18
В двух шахтах добывают алюминий и никель. В первой шахте имеется 20 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
19
В двух областях есть по 20 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,2 кг никеля. Во второй области для добычи х кг алюминия в день требуется человеко-часов труда, а для добычи y кг никеля в день требуется
человеко-часов труда.
Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
20
В двух областях работают по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,3 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется y2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую суммарную массу металлов можно добыть в двух областях за сутки?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
21
Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
22
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?
Источник: Пробный экзамен МЦНМО, Москва, 2017
23
Источник: ЕГЭ по математике 31.03.2017. Досрочная волна.
24
Пенсионный фонд владеет ценными бумагами, которые стоят 10t тыс. рублей в конце года t (t = 1; 2;…). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 24%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на его счёте была наибольшей?
Источник: ЕГЭ — 2017.Вариант 610 (C часть).
25
Источник: ЕГЭ по математике 25.06.2018. Резервная волна. Вариант 502 (C часть), Задания 17 (С5) ЕГЭ 2018
26
Зависимость объёма Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют
рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Источник: ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Вариант 992 (C часть), Задания 17 (С5) ЕГЭ 2018
27
Строительство нового завода стоит 159 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При этом в первый год p = 10, а далее каждый год возрастает на 1. За сколько лет окупится строительство?
Источник: ЕГЭ по математике 10.04.2019. Досрочная волна, резервная волна, Задания 17 (С5) ЕГЭ 2019
28
Для перевозки 500 маленьких и 26 больших блоков был выделен автомобиль грузоподъемностью 9,75 т. По техническим условиям он может перевозить не более 38 маленьких блоков. Габариты блоков таковы, что перевозка одного большого блока приравнивается к перевозке 18 маленьких. Большой блок весит 3,5 т, а маленький 0,25 т. Какое минимальное количество перевозок потребуется для перемещения всех блоков?
Источник: А. Ларин. Тренировочный вариант № 295.
29
Эпицентр циклона, движущийся прямолинейно, во время первого измерения находился в 24 км к северу и 5 км к западу от метеостанции, а во время второго измерения находился в 20 км к северу и км к западу от метеостанции. Определите наименьшее расстояние, на которое эпицентр циклона приблизится к метеостанции.
Источник: А. Ларин. Тренировочный вариант № 297.
30
Завод закупает станки двух типов, на приобретение которых выделено 34 миллиона рублей. Станок первого типа занимает площадь 7 м2 (с учетом проходов), производит за смену 5000 единиц продукции и стоит 4 миллиона рублей. Станок второго типа занимает площадь 4 м2 (с учетом проходов), производит за смену 3000 единиц продукции и стоит 3 миллиона рублей. Станки должны быть размещены на площади, не превышающей 50 м2. Сколько станков каждого типа нужно приобрести, чтобы производить за смену наибольшее количество продукции?
Источник: А. Ларин. Тренировочный вариант № 299.
31
В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес изделия составляют 400 тыс. руб. и 12 кг для первого типа, 500 тыс. руб. и 16 кг для второго типа, 600 тыс. руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определите минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
Источник: А. Ларин. Тренировочный вариант № 300.
32
Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым тратится 52 миллиона рублей. Строительство одного нового завода с персоналом 170 человек стоит 43 млн руб., а одной фабрики с персоналом 110 человек — 20 млн руб. Чему равно максимально возможное увеличение суммарного числа новых рабочих мест, если известно, что сумма всех затрат правительства составила ровно 714 млн руб.?
Источник: А. Ларин. Тренировочный вариант № 310. (Часть C)
33
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими начинками: ягодная, творожная и мясная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
| Вид начинки | Себестоимость за тонну | Отпускная цена за тонну | Производственные возможности |
|---|---|---|---|
| Ягоды | 70 тыс. руб. | 100 тыс. руб. | 90 тонн в мес. |
| Творог | 100 тыс. руб. | 135 тыс. руб. | 75 тонн в мес. |
| Мясо | 145 тыс. руб. | 145 тыс. руб. | 60 тонн в мес. |
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.
Источник: А. Ларин. Тренировочный вариант № 312. (Часть C)
34
Необходимо произвести отделку здания, имеющего форму прямоугольного параллелепипеда объемом 432 м3. Отделка стены здания, примыкающей к внутреннему строению, обходится в 1000 руб. за квадратный метр. Отделка трех фасадных стен обходится в 2000 руб. за квадратный метр. А заливка крыши, форма которой является квадратом, обходится в 7000 руб. за квадратный метр. Найдите размеры здания, отделочные работы которого при данных условиях являются наименьшими по стоимости.
Источник: А. Ларин. Тренировочный вариант № 335.
35
Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 25%. Какую наименьшую сумму (в рублях) нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Источник: А. Ларин. Тренировочный вариант № 346.
Источник/автор: Сборник заданий ФИПИ под редакцией И. В. Ященко, 2021
36
В начале года Алексей приобрёл ценные бумаги на сумму 9 тыс. рублей. В середине каждого года стоимость ценных бумаг возрастает на 2 тыс. рублей. В любой момент Алексей может продать ценные бумаги и положить вырученные деньги на банковский счёт. В середине каждого года сумма на счёте будет увеличиваться на 9%. В начале какого года после покупки Алексей должен продать ценные бумаги, чтобы через двадцать лет после покупки ценных бумаг сумма на банковском счёте была наибольшей?
37
Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1 806 000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено в таблице.
| Вариант 1 |
− Каждый январь долг возрастает на 15% по сравнению с концом предыдущего года; − с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; − кредит должен быть полностью погашен за два года двумя равными платежами. |
|---|---|
| Вариант 2 |
−1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; − со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; − 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; − к 15-му числу 24 месяца кредит должен быть полностью погашен. |
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?
Источник: Избранные задания по математике из последних сборников ФИПИ
38
Цена ценной бумаги на конец года вычисляется по формуле S = 1,1S0 + 2000, где S0 — цена ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12%. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тысяч рублей, которые он может положит на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.
Источник: Избранные задания по математике из последних сборников ФИПИ
39
Бригаду из 30 рабочих нужно распределить по двум объектам. Если на первом объекте работает p человек, то каждый из них получает в сутки 200p рублей. Если на втором объекте работает p человек, то каждый из них получает в сутки (50p + 300) руб. Как нужно распределить рабочих по объектам, чтобы их суммарная суточная зарплата оказалась наименьшей? Сколько рублей в этом случае придётся заплатить за сутки всем рабочим?
Источник: Избранные задания по математике из последних сборников ФИПИ
40
В январе 2005 года ставка по депозитам в банке «Фантазия» составила x% годовых, а в январе 2006 года — y% годовых, причем известно, что x + y = 30. В январе 2005 года вкладчик открыл депозитный счёт в банке «Фантазия», положив на него некоторую сумму. В январе 2006 года, по прошествии года со дня открытия счёта, вкладчик снял со счёта пятую часть этой суммы. Укажите значение x, при котором сумма на счёте вкладчика в январе 2007 года является максимально возможной.
Источник: А. Ларин. Тренировочный вариант № 351.
41
Строительство нового завода стоит 140 млн руб. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,2x2 + 3x + 1 млн руб. в год. Если продукцию завода продать по цене p тыс. руб. за единицу, то прибыль фирмы (в млн руб.) за один год составит px − (0,2x2 + 3x + 1). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки завода цена на продукцию p = 7 тыс. руб. за единицу. Каждый последующий год цена увеличивается на 2 тыс. руб. за единицу. За сколько лет окупится строительство завода?
Источник: А. Ларин. Тренировочный вариант № 364.
42
В начале 1977 года Алишер положил в пустой сейф 1 млн руб. В начале каждого последующего года он вынимает из сейфа m% имеющихся там рублей. При каком значении m он вынет из сейфа в начале 1982 года максимальную сумму?
Источник: А. Ларин. Тренировочный вариант № 365.
43
Фабрика получила заказ на изготовление 1005 деталей типа А и 2010 деталей типа В. Каждый из 192 рабочих фабрики затрачивает на изготовление двух деталей типа А время, за которое он мог бы изготовить одну деталь типа В. Каким образом следует разделить рабочих фабрики на две бригады, чтобы выполнить заказ за наименьшее время, при условии, что обе бригады приступят к работе одновременно и каждая из бригад будет занята изготовлением деталей только одного типа?
Источник: А. Ларин. Тренировочный вариант № 370.
Источник/автор: Вступительный экзамен по математике, экономический факультет МГУ, 1992 год
44
В растворе Х содержится 30% вещества А и 50% вещества В, в растворе Y содержится 50% вещества А и 40% вещества В, в растворе Z содержится 80% вещества А и 10% вещества В. В результате смешивания получился раствор, содержащий 60% вещества А. Найдите наименьшее возможное содержание вещества В в получившемся растворе.
Источник: А. Ларин. Тренировочный вариант № 372.
45
Шарона Абрамовна планирует взять кредит на некоторую сумму и выбирает между двумя банками. Первый банк предлагает кредит на 10 лет под 3% годовых, второй — на 6 лет под 9% годовых, причем в обоих банках применяется дифференцированная съема погашения кредита (ежегодно долг уменьшается каждый год на одну и ту же величину по сравнению с предыдущим годом). В какой банк выгоднее обратиться Шароне Абрамовне и сколько процентов от кредита составит эта выгода?
Источник: А. Ларин. Тренировочный вариант № 379.
46
Источник: А. Ларин. Тренировочный вариант № 392.
47
Инвестору предлагаются два проекта для вложения денежных средств. В каждом проекте зависимость прибыли y (в тысячах рублей) от вложений x (тыс. руб.) определяется квадратичной функцией с коэффициентами a и b, зависящими от проекта. Известно, что при инвестировании средств только в первый проект максимальная прибыль в 200 тыс. руб. достигается при вложении 100 тыс. руб., а при инвестировании только во второй проект максимальная прибыль в 150 тыс. руб. достигается при вложении 150 тыс. руб. Инвестор решил вложить 290 тыс. рублей в оба проекта. Какую сумму ему следует вложить в каждый из проектов, чтобы общая прибыль была максимальной? Найдите эту максимальную общую прибыль.
Источник: А. Ларин. Тренировочный вариант № 393.
48
Паром грузоподъёмностью 109 тонн перевозит джипы и грузовики. Количество перевозимых на пароме грузовиков не менее чем на 20% превосходит количество перевозимых джипов. Вес и стоимость перевозки одного джипа составляют 3 тонны и 600 рублей, грузовика — 5 тонн и 700 рублей соответственно. Определите наибольшую возможную суммарную стоимость перевозки всех джипов и грузовиков при данных условиях.
Источник: А. Ларин. Тренировочный вариант № 395.
49
Цена за единицу товара зависит от объема заказа и определяется следующим образом:
1. Если объём заказа не превышает 4000 единиц товара, то цена единицы товара равна 300 рублей.
2. Если объём заказа превышает 4000 единиц товара, то на каждую единицу товара от цены 300 рублей предоставляется скидка в размере рублей, где x — количество единиц товара в заказе.
При каком объёме заказа фирма, продающая товар, получит наибольшую выручку при условии, что объём заказа не может превышать 16 000 единиц товара?
Источник: А. Ларин. Тренировочный вариант № 399.
50
Строительство нового цеха по производству роботов-пылесосов стоит 300 миллионов рублей. Затраты на производство x тысяч единиц продукции на такой линии равны млн руб. в год. Если продукцию продавать по цене p тыс. руб. за единицу, то прибыль фирмы (в млн руб.) за один год составит
млн руб. Когда цех будет построен, каждый год фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки цеха цена продукции p = 12 тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство цеха?
Источник: А. Ларин. Тренировочный вариант № 404.
51
У инвестора есть 50 миллионов рублей. Часть денег он планирует вложить в проект. Если он вложит в проект млн руб., то по завершении проекта он получит x млн руб. Невложенные в проект деньги инвестор планирует разместить на банковском счете. По завершении проекта инвестор получит из банка сумму, увеличенную на 20%.
Инвестор собирается распределить деньги так, чтобы общая сумма полученных им денег от вложения в проект и размещения в банке оказалась наибольшей. Прибыль от проекта — это разность между полученной от проекта и вложенной в проект суммами денег. Найдите, сколько процентов составит прибыль от проекта от вложенной в него суммы денег.
Источник: А. Ларин. Тренировочный вариант № 407.
52
Предприниматель взял в кредит под 20% годовых сумму S на целое число лет. Кредит должен быть погашен равными ежегодными платежами. Через некоторое целое число лет после исполнения очередного платежа предприниматель обнаружил, что выплатил банку сумму, большую S, при этом сумма оставшихся платежей также была больше S. Найдите минимальный срок, на который предприниматель мог взять кредит.
Источник: А. Ларин. Тренировочный вариант № 408.
53
Предприятие производит детские санки и является убыточным. Известно, что при изготовлении x санок в месяц расходы предприятия на выпуск одних санок составляют
а цена реализации каждой единицы продукции равна тыс. руб. Определите ежемесячный объем производства (в тысячах санок), при котором ежемесячные убытки могут быть снижены до наименьшего возможного уровня.
Источник: А. Ларин. Тренировочный вариант № 412.
54
На каждом из двух комбинатов изготавливают детали А и В. На первом комбинате работает 500 человек, и один рабочий изготавливает за смену 8 деталей А или 2 детали В. На втором комбинате работает 200 человек, и один рабочий изготавливает за смену 2 детали А или 8 деталей В. Оба эти комбината поставляют детали на комбинат, на котором собирают изделие, для изготовления которого нужна 1 деталь A и 3 детали В. При этом комбинаты договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
Источник: А. Ларин. Тренировочный вариант № 417.
55
Наталья Дмитриевна владеет облигациями, которые стоят n2 тысяч рублей в конце года n В конце любого года Наталья Дмитриевна может их продать и положить деньги на счет в банке, при этом в конце каждого следующего года сумма на счете будет увеличиваться в 1 + m раз.
Наталья Дмитриевна хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать восьмого года сумма на ее счете была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать третьего года. При каких положительных значениях m это возможно?
Источник: А. Ларин. Тренировочный вариант № 418.
Разные задачи
Версия для печати и копирования в MS Word
1
В одной стране в обращении находилось 1 000 000 долларов, 20% из которых были фальшивыми. Некая криминальная структура стала ввозить в страну по 100 000 долларов в месяц, 10% из которых были фальшивыми. В это же время другая структура стала вывозить из страны 50 000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержание фальшивых долларов в стране составит 5% от общего количества долларов?
Источник: А. Ларин: Тренировочный вариант № 92.
2
Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% — в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект — от 22 до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.
Источник: А. Ларин: Тренировочный вариант № 93.
3
При рытье колодца глубиной свыше 10 м за первый метр заплатили 1000 руб., а за каждый следующий на 500 руб. больше, чем за предыдущий. Сверх того за весь колодец дополнительно было уплачено 10 000 руб. Средняя стоимость 1 м оказалась равной 6250 руб. Определите глубину колодца.
Источник: А. Ларин: Тренировочный вариант № 102.
4
Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?
Источник: А. Ларин: Тренировочный вариант № 106.
5
Садовод привез на рынок 91 кг яблок, которые после транспортировки разделил на три сорта. Яблоки первого сорта он продавал по 40 руб., второго сорта – по 30 руб., третьего сорта – по 20 руб. за килограмм. Выручка от продажи всех яблок составила 2170 руб. Известно, что масса яблок 2-го сорта меньше массы яблок 3-го сорта на столько же процентов, на сколько процентов масса яблок 1-го сорта меньше массы яблок 2-го сорта. Сколько килограммов яблок второго сорта продал садовод?
Источник: А. Ларин: Тренировочный вариант № 119.
6
В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объема закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив ее на закупку нефти?
Источник: А. Ларин: Тренировочный вариант № 89.
7
Транcнациональная компания Amako Inc. решила провести недружественное поглощение компании First Aluminum Company (FAC) путем скупки акций миноритарных акционеров. Известно, что Amako было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3. В результате второго предложения Amako сумела увеличить число выкупленных акций на 20% (после второй скупки общее число выкупленных акций увеличилось на 20%), а в результате скупки по третьей цене — еще на 20%. Найдите цену за одну акцию при третьем предложении и общее количество скупленных акций, если начальное предложение составляло $27 за одну акцию, а по второй цене Amako скупила 15 тысяч акций.
Источник: А. Ларин: Тренировочный вариант № 90., А. Ларин: Тренировочный вариант № 90.
8
Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?
Источник: А. Ларин: Тренировочный вариант № 91., А. Ларин: Тренировочный вариант № 91.
9
Вася мечтает о собственной квартире, которая стоит 3 млн.руб. Вася может купить ее в кредит, при этом банк готов выдать эту сумму сразу, а погашать кредит Васе придется 20 лет равными ежемесячными платежами, при этом ему придется выплатить сумму, на 180% превышающую исходную. Вместо этого, Вася может какое-то время снимать квартиру (стоимость аренды ― 15 тыс. руб. в месяц), откладывая каждый месяц на покупку квартиры сумму, которая останется от его возможного платежа банку (по первой схеме) после уплаты арендной платы за съемную квартиру. За какое время в этом случае Вася сможет накопить на квартиру, если считать, что стоимость ее не изменится?
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1., А. Ларин: Тренировочный вариант № 227.
10
Цена производителя на некоторое изделие составляет 25 рублей. Прежде чем попасть на прилавок магазина, изделие проходит через несколько фирм-посредников, каждая из которых увеличивает цену в 1,5 или 2 раза, осуществляя услуги по хранению и транспортировке изделий. Магазин делает наценку 20%, после чего изделие поступает в продажу по цене 405 рублей. Сколько посредников было между магазином и производителем?
11
В регионе A среднемесячный доход на душу населения в 2014 году составлял 43 740 рублей и ежегодно увеличивался на 25%. В регионе B среднемесячный доход на душу населения в 2014 году составлял 60 000 рублей. В течение трёх лет суммарный доход жителей региона B увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах A и B стал одинаковым. Найдите m.
Источник: ЕГЭ по математике 11.04.2018. Досрочная волна, резервная волна. Запад (часть С)
12
В аграрной стране А производство пшеницы на душу населения в 2015 году составляло 192 кг и ежегодно увеличивалось на 20%. В аграрной стране В производство пшеницы на душу населения в 2015 году составляло 375 кг. В течение трех лет производство зерна в стране В увеличивалось на 14% ежегодно, а ее население увеличивалось на m% ежегодно. В 2018 году производство зерна на душу населения в странах А и В стало одинаковым. Найдите m.
Источник: А. Ларин. Тренировочный вариант № 298.
13
Борис и Иван вложили деньги в общий бизнес. После этого один из них добавил ещё 1 миллион рублей, в результате чего его доля в бизнесе увеличилась на 0,05, а когда он добавил ещё 1 миллион рублей, его доля увеличилась ещё на 0,04. Сколько миллионов рублей ему ещё нужно добавить, чтобы увеличить свою долю ещё на 0,06?
Источник: А. Ларин. Тренировочный вариант № 323. (часть C).
14
Евгений хочет купить пакет акций компании. 15 февраля он отложил определённую сумму денег и планирует откладывать такую же сумму денег 15 числа каждого месяца. Первого февраля пакет акций стоил 195 000 рублей. Первого числа каждого месяца пакет акций дорожает на 40%. Какую наименьшую сумму нужно Евгению откладывать каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
15
Имеются три пакета акций. Суммарное количество акций первых двух пакетов совпадает с количеством акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммарная стоимость первого и второго пакетов совпадает со стоимостью третьего пакета. Одна акция из второго пакета дороже одной акции из первого пакета на величину, заключенную в пределах от 16 тысяч рублей до 20 тысяч рублей, а цена одной акции из третьего пакета не меньше 42 тысяч рублей и не больше 60 тысяч рублей. Определить, какой наименьший и наибольший процент от общего количества акций может содержаться в первом пакете.
Источник: А. Ларин. Тренировочный вариант № 342.
16
Страховая компания положила в банк некоторую сумму денег под 10% годовых для обеспечения страховых выплат. Какова была эта сумма (в рублях), если она оказалась полностью истрачена за три года на следующие выплаты: 880 000 рублей в конце первого года, 605 000 рублей в конце второго года и 1 331 000 рублей в конце третьего года (все выплаты производились после начисления банком процентов).
Источник: А. Ларин. Тренировочный вариант № 354.
17
Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% в проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Источник: А. Ларин. Тренировочный вариант № 366.
Производительность труда в задаче 17
2 октября 2015
Задачи этого типа появились в ЕГЭ относительно недавно, но застали врасплох как учеников, так и многих учителей. А всё потому что решаются они с помощью производной — инструмента, совершенно непривычного для второй части экзамена.
Задача 17. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $3t$единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $4t$единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
В приведённом условии есть важный момент, после осознания которого у вас вообще не будет проблем с решением подобных задач. Дело в том, что величина $t$, указанная для первого завода и для второго — это не одно и то же число! Другими словами, суммарное время рабочих на первом и другом заводе будет разным.
Для решения введём новые переменные: ${{a}^{2}}$ — суммарное время рабочих на первом заводе, ${{b}^{2}}$ — суммарное время на втором. С учётом производительности получим:
$begin{align}& {{a}^{2}}to 3a \& {{b}^{2}}to 4b \end{align}$
Таким образом, затратив суммарно ${{a}^{2}}+{{b}^{2}}$ часов времени, мы получим $3a+4b$ единиц продукции в неделю. Всё остальное — элементарная математика, подробно описанная в видеоуроке:
В прошлый раз мы рассматривали довольно «противные» задачи, связанные с вычислением времени в задачах про кредиты. Но это было очень просто по сравнению с тем, что мы будем рассматривать сегодня, а именно экономическую задачу 17 про производительность труда, в которой требуется применять производную. Эти задачи появились в ЕГЭ по математике относительно недавно, и те, кто уже с ними столкнулся, оценили, что, во-первых, условие таких задач довольно длинное, а, во-вторых, в каждой из таких задач есть неприятная зацепка, на которой «прогорели» очень многие ученики.
Думаю, вы уже догадались, что речь идет о той самой задачи 17, когда у Григория есть два завода, и еще указана производительность труда, и требуется оценить, какое наибольшее количество продукции можно произвести на этих двух заводах, если распределить нагрузку оптимально. Но на самом деле, в этих задачах 17 нет ничего сложного, даже чуть проще, чем многие задачи на кредиты. Поэтому сейчас мы рассмотрим одно из таких заданий, внимательно пробежимся по каждому пункту и посмотрим, как именно должно выглядеть идеальное ее решение.
Задача № 1
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $3t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $4t$. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Шаг первый: вводим переменные
Прежде всего, перед тем как переходить к непосредственному решению задачи 17 из ЕГЭ по математике, попытаться что-то посчитать, составить какие-то формулы, поймите одну простую вещь: величина ${{t}^{2}}$, данная и в первом, и во втором предложении, никак не связаны друг с другом. Коэффициент $t$ нам дан исключительно для того, чтобы сравнить производительность на разных заводах при одинаковом расходе времени. Думаю, это сравнение абсолютно очевидно: на первом производительность составляет $3t$, а на втором — $4t$, т.е. чуть побольше. На практике это означает следующее: давайте распишем, что происходит на каждом из них.
На первом заводе у нас расходуется ${{a}^{2}}$ времени (после замены) и производится $3a$ единиц продукции. На втором — ${{b}^{2}}$ времени и $4b$ продукции.
А теперь давайте сложим расходы времени и суммарный выпуск продукта.
Получим, что суммарный расход времени составляет ${{a}^{2}}+{{b}^{2}}$, а суммарный расход продукции — $3a+4b$. При этом еще раз обращаю ваше внимание: никто не говорил, что ${{a}^{2}}$ и ${{b}^{2}}$ должны быть равны. Ключевое слово здесь «если» и в первом, и во втором случае. Именно поэтому мы так смело меняем коэффициенты $t$ на $a$ в первом случае и на $b$ во втором случае.
Шаг второй: составляем и решаем уравнение
Давайте посмотрим, что у нас получилось. ${{a}^{2}}+{{b}^{2}}$ — это суммарный расход времени. Поскольку Григорий платит рабочему 500 рублей за каждый час работы, то всего он сможет заплатить такую сумму:
[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000]
Вот и первое уравнение.
На самом деле, основная сложность этой задачи 17 про производительность труда — вовсе не составление уравнения. Она состоит в том, что нужно понять, что на первом и на втором заводе время разное. Именно поэтому для первого мы везде заменили $t$ на $a$, а для второго — $t$ на $b$. В итоге как вы сейчас увидите, мы получим одно уравнение с двумя неизвестными, которое легко упрощается — одна неизвестная легко выражается через другую. И поэтому вся функция, выражающая количество произведенного товара, на самом деле зависит от одной-единственной переменной, в нашем случае это будет переменная $a$.
Далее, я думаю, все понятно: у нас есть функция, отрезок, на котором эта функция рассматривается, а все, что нам требуется найти — это наибольшее значение этой функции на данном отрезке. Вообщем, классическая задача для применения производных, в нашем случае новая задача 17 из ЕГЭ по математике.
Суммарный выпуск продукции ($S$) равен:
[S=3a+4bto max ]
Вот теперь задача и проявилась: имея ограничение на $a$ и $b$, нам нужно добиться того, чтобы $S$ принимала свое максимальное значение. Для начала давайте немножко поработаем с уравнением: $$
[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000left| :500 right.]
[{{a}^{2}}+{{b}^{2}}=10000]
Отсюда выразим $b$:
[{{b}^{2}}=10000-{{a}^{2}}]
[b=sqrt{10000-{{a}^{2}}}]
Конечно, тут следовало бы перед выражением поставить $pm $, однако у нас речь идет о времени, а оно не может быть отрицательным, поэтому мы берем положительное значение. Итого суммарный объем выпускаемого товара может быть выписан как функция от одной-единственной переменной $a$:
[S=3a+4sqrt{10000-{{a}^{2}}}]
Шаг третий: находим максимальное значение функции
Теперь нам нужно найти максимальное значение этой функции на всей области определения, а совершенно очевидно, что величину $a$, т.е. количество товара, выпущенного на первом заводе, увеличивать до бесконечности нельзя, просто потому что корень имеет конкретную область определения — величина, стоящая под корнем, не должна быть отрицательной. Давайте запишем это:
[10000-{{a}^{2}}ge 0]
[{{a}^{2}}le 10000]
[left| a right|le 100]
[ain left[ 0;100 right]]
Итого мы получили классическую задачу из первой части ЕГЭ по математике: у нас есть функция, есть интервал, соответственно, нужно найти максимальное значение этой функции на заданном интервале. Давайте считать производную:
[{S}’=3+4cdot frac{1cdot left( 10000-{{a}^{2}} right)}{2sqrt{10000-{{a}^{2}}}}=3+frac{4cdot left( -2a right)}{2sqrt{10000-{{a}^{2}}}}=]
[=3-frac{4a}{sqrt{10000-{{a}^{2}}}}]
[3-frac{4a}{sqrt{10000-{{a}^{2}}}}=0]
Решаем полученное уравнение:
[3=frac{4a}{sqrt{sqrt{10000-{{a}^{2}}}}}]
[3sqrt{10000-{{a}^{2}}}=4a]
[9left( 10000-{{a}^{2}} right)=16{{a}^{2}}]
[90000-9{{a}^{2}}=16{{a}^{2}}]
[25{{a}^{2}}=90000]
[5a=3cdot 100]
[a=frac{3cdot 100}{5}=60]
Теперь, зная, чему равно $a$, легко найти $b$:
[b=sqrt{10000-3600}=sqrt{6400}=80]
Однако для полного и обоснованного решения необходимо понять знак производной. Давайте начертим числовую прямую и отметим на ней $a=60$ и посмотрим, что происходит при $a gt 60$:
Например, если взять $a=99$ мы получим следующее:
[10000-{{99}^{2}}={{100}^{2}}-{{99}^{2}}=left( 100-99 right)left( 100+99 right)=199]
Если посмотрим на исходное выражение, то очевидно, что $sqrt{199} lt 99$, но посчитав его, получаем в ответе отрицательное число.
Отсюда следует, что$a=60$является точкой максимума, т.е. именно той, которую мы и хотели найти. Именно в ней наша исходная функция принимает исходное значение. Осталось подставить в $S$ полученное значение $a$ и $b$:
[S=3cdot 60+4cdot 80=180+320=500]
Окончательный ответ: 500 единиц товара.
Нюансы решения
Как видите, все оказалось не так уж и сложно. Единственно, что нам нужно запомнить — это то, что величина ${{t}^{2}}$, когда речь идет о первом заводе дает нам информацию о производительности труда именно на нем, т.е. связывает время, затраченное на производство и количество продукции в рамках только него.
Величина ${{t}^{2}}$, относящаяся ко второму заводу, говорит нам именно о нем и никак не связана с первым.
Более того, считать, что количество времени, затраченного рабочими на первом и на втором заводах, абсолютно одинаково — это вообще глупость, потому что в этом случае полученное уравнение оказалось бы намного проще и решалось бы как элементарное линейное: нам бы не потребовалось никаких производных, никаких доказательств, что мы получили точку максимума — мы просто бы разделили зарплату между рабочими первого и второго производств пополам.
Поэтому запомните: время, потраченное на первом и на втором заводах, разное, поэтому пусть на первом потрачено ${{a}^{2}}$ времени, а на втором — ${{b}^{2}}$. В этом случае задача действительно становится сложнее, при этом интересней и вполне достойной называться задачей 17 из ЕГЭ по математике.
Задача № 2
А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.
Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.
Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?
Шаг первый: вводим переменные
Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.
Шаг второй: составляем и решаем уравнение
Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:
[500cdot left( {{x}^{2}}+{{y}^{2}} right)=30250000]
[{{x}^{2}}+{{y}^{2}}=60500]
Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.
Теперь необходимо записать сумму:
[S=x+2yto max ]
Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:
[{{y}^{2}}=60500-{{x}^{2}}]
[y=sqrt{60500-{{x}^{2}}}]
Подставляем найденное значение $y$ в нашу формулу и получаем:
[S=x+2cdot sqrt{60500-{{x}^{2}}}]
Находим производную этой конструкции:
[{S}’=1+2frac{1left( -2x right)}{2sqrt{60500-{{x}^{2}}}}=1-frac{2x}{sqrt{60500-{{x}^{2}}}}]
Вновь приравниваем полученное выражение к нулю:
[1-frac{2x}{sqrt{60500-{{x}^{2}}}}=0]
[frac{1}{1}=frac{2x}{sqrt{60500-{{x}^{2}}}}]
[sqrt{60500-{{x}^{2}}}=2x]
[60500-{{x}^{2}}=4{{x}^{2}}]
[60500=5{{x}^{2}}]
[{{x}^{2}}=frac{60500}{5}=121cdot 100]
[x=11cdot 10=110]
Шаг третий: находим максимальное значение функции
Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:
[y=2x=220]
Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:
Давайте подставим:
${S}’left( 220 right)=1-frac{2cdot 220}{sqrt{60500-{{220}^{2}}}}=1-frac{440}{sqrt{60500-48400}}=$
$=1-frac{440}{sqrt{12100}}=1-frac{440}{110}=1-4=-3$
Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.
Итого 110 — точка максимума. Это является строгим обоснованием.
Теперь подставляем в выражение $x$ и $y$, которые мы нашли:
[S=110+2cdot 220=110+440=550]
Ответ: 550 единиц товара.
Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике
Все, что нам нужно знать — это:
- Правило вычисления производных сложных функций.
- Правила решения несложных уравнений.
Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:
- ${{a}^{2}}to a$ и ${{b}^{2}}to 2b$ — как связано затраченное время с объемом выпущенного товара;
- $S=a+2bto max $ — суммарный объем товара находится по несложной формуле.
Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.
А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.
Надеюсь, это видео поможет вам построить собственный завод, где вы будете платить рабочим по 30 млн. рублей в неделю, если такой суммы вам окажется недостаточно, заходите на наш сайт, подписывайтесь на паблик ВКонтакте и на канал в YouTube. До новых встреч!
Смотрите также:
- Задачи на кредит с плавающим платежом
- Задачи с экономическим содержанием — основные формулы
- Тест к уроку «Что такое логарифм» (средний)
- Решение задач B12: №440—447
- Как решать задачу 18: графический подход
- Нестандартные задачи B2: кредит в банке
Задание 17 ЕГЭ по математике (профиль). Задачи на оптимальный выбор. Владельцы заводов. Объем производства
Задача 1. (№ 517742)
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:
Составим таблицу:
|
Завод |
Количество часов в неделю |
Количество единиц товара |
Оплата труда, руб. |
|
I |
|
х |
200 |
|
II |
|
y |
300 |
|
Сумма |
|
1200000 |
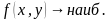
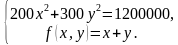
Из первого уравнения выразим y через x:
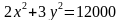
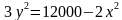
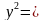
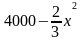
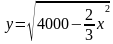
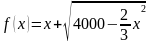
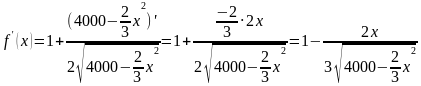
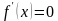
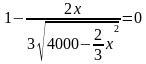
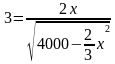
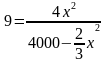
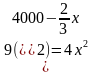
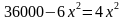
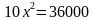
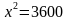
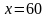
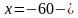
f
’(x) +
f
60
(x)
Значит, точка максимума функции и в ней функция принимает наибольшее значение:
Следовательно, наибольшее количество единиц товара равно 100.
Ответ: 100 единиц товара.
Задания для самостоятельного решения:
1. (№ 517753)
Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 300 рублей.
Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 80 единиц товара.
2. (№ 509824)
Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 90 единиц товара.
Строительство нового завода стоит 220 млн рублей. Затраты на производство х тыс. единиц продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки завода цена продукции p = 9 тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство завода?
Скачать решение
Решение
ЕГЭ 2022
Автор Ольга Андрющенко На чтение 12 мин Просмотров 19.1к. Опубликовано 7 февраля, 2019
За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.
Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.
Можно выделить несколько блоков заданий:
1. Вклады и кредиты
2. Акции и другие ценные бумаги
3. Методы оптимальных решений
Рассмотрим каждый из вышеперечисленных блоков.
Вклады и кредиты
Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.
Формула выглядит следующим образом:
где FV – будущая сумма.
PV – текущая сумма.
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента.
Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:
,
где
FV – будущая сумма
PV – текущая сумма
p – процент, в соответствии с которым происходит начисление
n – количество лет начисления процента
m – количество начислений в год (например, m=4, если начисления ежеквартальные).
Давайте отработаем эту формулу на подготовительной задаче.
Задача 1
Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?
Решение:
Рассчитаем по формуле сложного процента сумму через год:
Теперь сумму через 2 года:
Теперь сумму через 3 года:
Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения/неравенства.
Задача 2
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.
Решение:
Пусть искомая сумма составит a млн рублей.
Составим таблицу, чтобы упорядочить данные и построить математическую модель.
По условию, нужно найти наименьшее целое x, для которого выполнено неравенство
14,641 + 2,31a ≥ 28
a ≥
Наименьшее целое число, при котором знак неравенства выполняется, это число 6.
Значит, искомая сумма — 6 млн рублей.
Ответ: 6 млн рублей.
Акции и другие ценные бумаги
Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.
Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.
Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.
Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.
Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.
Задача 3.
Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.
К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:
9000 + 2000n
Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.
Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.
Либо можем составить уравнение, которое объединит все строчки нашей таблицы:
По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.
Ответ: 2020
Методы оптимальных решений
Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.
Основные типы заданий в этом блоке:
1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;
2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);
3. Транспортная задача.
Разберём несколько задач с основными методами решения.
Задача.
У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.
Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?
Решение:
Имеем 2 поля с различными характеристиками.
В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.
Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:
10·500· 9000= 45000000 рублей
Ситуация с первым полем не так очевидна.
Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).
Поэтому необходимо сравнить соотношения этих величин:
Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.
Доход с первого поля:
10 · 500 ·7000 = 35000000 рублей
Суммарный доход составит:
35000000 рублей + 45000000 рублей = 80000000 рублей
Ответ: 80000000 рублей
Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.
Задача.
На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.
Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?
Решение:
Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.
Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.
Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.
На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.
Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:
Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:
1. Найти производную функции;
2. Приравнять производную к 0, получить точки, подозрительные на экстремум;
3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.
Проведём такую последовательность действий с нашей производственной функцией.
Приведём к общему знаменателю.
Приравняем числитель к 0.
Возведём в квадрат.
Получили единственную точку экстремума.
- Проверим, является ли она точкой максимума.
Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.
Ответ: 600 кг
Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.
Самое главное – внимательно прочитать и понять условие.
Примеры решения задач
Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.
Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму
Воспользуемся этой формулой, считаяS0= 100 000, r = 11 , m = 30 (так как в ноябре 30 дней).
Получим:
Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.
Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?
Решение:
Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.
Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».
Решение:
Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на
умножается на коэффициент 1,1.
Тогда по вкладу «А» после первого года сумма станет равна ;
после второго года: 1,21S;
после третьего года: 1,331S.
По вкладу «Б» после первого года сумма станет равна1,11S;
после второго года 1,2321S.
Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна
, где r— натуральное число,
коэффициент повышения в третий год.
По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:
Так как r— натуральное число, то наименьший процент равен 9%.
Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?
Решение.
Во второй год цена ценной бумаги составит: (7+2) тысячи рублей
В третий год (7+2)+2= 7+2∙2 тысячи рублей
В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей
.
Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.
10% от цены бумаги на
Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.
Получаем неравенство:
Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.
Задача 5.
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?
Решение:
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Решение №1
Нам дано: 5 000 000 рублей — вся сумма, 500 р/ч — ставка рабочего. Отсюда мы можем найти, сколько суммарно времени будут трудиться все рабочие:
(5, 000,000: 500 = 10,000,ч.)
Пусть рабочие на первом заводе трудились (x^2) часов, тогда они произвели (3x) единиц товара. Пусть рабочие на втором заводе трудились (y^2) часов, тогда они произвели (4y) единиц товара. Получаем условие:
(x^2+y^2=10,000.)
Обозначим (S = 3x+4y) — суммарное количество единиц товара с двух заводов. В задаче требуется найти наибольшее значение этой функции. Будем его находить с помощью производной.
Из условия (x^2 + y^2 = 10,000) выразим переменную (y = sqrt{10,000-x^2}) и подставим в нашу функцию:
(S = 3x + 4sqrt{10,000 — x^2};)
(S’ = 3 + 4cdotdisplaystylefrac{1}{2sqrt{10,000-x^2}}cdot(-2x)=3-frac{4x}{sqrt{10,000-x^2}};)
Ищем точку экстремума, приравнивая производную к нулю:
(3-displaystylefrac{4x}{sqrt{10,000-x^2}}=0;)
(3sqrt{10,000-x^2}=4x;)
(9cdotleft(10,000-x^2right)=16x^2;)
(25x^2=90,000 Rightarrow x^2 = 3600 Rightarrow x = pm 60.)
Отрицательное значение можно не рассматривать, т.к. речь идет о часах. Для нахождения нужного нам значения осталось полученное число подставить в функцию (S:)
(S_{max} = S(60) = 3cdot 60 + 4sqrt{10,000 — 60^2} = 180 + 4cdot 80 = 500.)
Ответ: 500.
Решение задачи предоставлено компанией: Юниум
Юниум — федеральная сеть образовательных центров для школьников по всей России. Мы проводим занятия по подготовке к ЕГЭ и ГИА. Каждый год наши выпускники поступают в лучшие ВУЗы страны, а их результаты выше, чем в среднем по России.