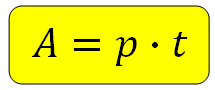Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
2
Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?
3
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
4
На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
5
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Пройти тестирование по этим заданиям
25
Окт 2013
Категория: 09 Текстовые задачиТекстовые задачи
09. Задачи на работу
2013-10-25
2022-09-11
Возможно, при решении задач вы столкнетесь с громоздким дискриминантом… Что делать в таком случае смотрите здесь и здесь
Задача 1. Заказ на деталей первый рабочий выполняет на
часа быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на
детали больше?
Решение: + показать
Задача 2. Первая труба пропускает на литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом
литров она заполняет на
минуты дольше, чем вторая труба?
Решение: + показать
Задача 3. Первая труба пропускает на литр воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом
литров она заполняет на
минуты дольше, чем вторая труба заполняет резервуар объемом
литра?
Решение: + показать
Задача 4. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за
дней выполняет такую же часть работы, какую второй — за
дня?
Решение: + показать
Задача 5. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за часов. Через
часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение: + показать
Задача 6. Один мастер может выполнить заказ за часов, а другой — за
часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Решение: + показать
Задача 7. Игорь и Паша красят забор за часов. Паша и Володя красят этот же забор за
час, а Володя и Игорь — за
часов. За сколько часов мальчики покрасят забор, работая втроем?
Решение: + показать
Задача 8. Две трубы наполняют бассейн за часов
минут, а одна первая труба наполняет бассейн за
часов. За сколько часов наполняет бассейн одна вторая труба?
Решение: + показать
Задача 9. Петя и Митя выполняют одинаковый тест. Петя отвечает за час на вопросов текста, а Митя — на
Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Мити на
минут. Сколько вопросов содержит тест?
Решение: + показать
Задача 10. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было рабочих, а во второй —
рабочих. Через
дней после начала работы в первую бригаду перешли
рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Решение: + показать
Вы можете пройти тест по задачам на работу
Автор: egeMax |
комментария 3
Печать страницы
ЕГЭ Профиль №9. Задачи на работу
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на работу
| Задача 1. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Пусть x дет/ч делает второй рабочий, тогда (x + 1) дет/ч делает первый рабочий.
Первый рабочий на изготовление 110 деталей тратит на 1 час меньше. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,;,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то второй рабочий делает 10 деталей в час. Ответ: 10. |
||||||||||||
| Задача 2. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Пусть x дет/ч делает первый рабочий, тогда (x — 3) дет/ч делает второй рабочий.
Первый рабочий тратит на 6 часов меньше. Следовательно: (frac{{550}}{{x — 3}} — frac{{475}}{x} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475x + 475 cdot 3}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,) (6xleft( {x — 3} right) = 75x + 475 cdot 3,,left| {,:,} right.3,,,, Leftrightarrow ,,,,2{x^2} — 6x = 25x + 475,,,, Leftrightarrow ,,,,2{x^2} — 31x — 475 = 0;) (D = 961 + 8 cdot 475 = 4761;,,,,,,,,sqrt D = 69;) ({x_1} = frac{{31 + 69}}{4} = 25;,,,,{x_2} = frac{{31 — 69}}{4} = — frac{{19}}{2}.) Так как (x > 3), то первый рабочий делает 25 деталей за час. Ответ: 25. |
||||||||||||
| Задача 3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Пусть первый рабочий, работая отдельно, выполнил работу за х дней. Так как второй рабочий за 3 дня выполняет такую часть работы, которую первый за 2 дня, то он выполнит всю работу за (frac{3}{2}x) дней. Пусть объём равен А:
Работая вместе, то есть с общей производительностью (frac{A}{x} + frac{{2A}}{{3x}}), рабочие выполняют всю работу (А) за 12 дней. Следовательно: (left( {frac{A}{x} + frac{{2A}}{{3x}}} right) cdot 12 = A,,,, Leftrightarrow ,,,,frac{{3A + 2A}}{{3x}} cdot 12 = A,,,, Leftrightarrow ,,,,frac{{5A cdot 4}}{x} = A,,,left| {:A} right.,,,,,, Leftrightarrow ,,,,,,,frac{{20}}{x} = 1,,,, Leftrightarrow ,,,,x = 20.) Таким образом, первый рабочий, работая отдельно, выполнит работу за 20 дней. Ответ: 20. |
||||||||||||
| Задача 4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 1 мин больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 5. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 2 минуты больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{99}}{{x + 1}} = 2,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,frac{{110x + 110 — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,2xleft( {x + 1} right) = 11x + 110,,,, Leftrightarrow ,,,,2{x^2} + 2x = 11x + 110,,,,, Leftrightarrow ,,,,2{x^2} — 9x — 110 = 0) (D = 81 + 8 cdot 110 = 961;,,,,,,,{x_1} = frac{{9 + 31}}{4}, = 10;,,,,,{x_2} = frac{{9 — 31}}{4} = — frac{{11}}{2}.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 6. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Пусть вторая труба пропускает x литров в минуту, тогда первая пропускает (x — 5) литров в минуту.
Первая труба тратит на 10 минут больше чем вторая. Следовательно: (frac{{500}}{{x — 5}} — frac{{375}}{x} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375left( {x — 5} right)}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375x + 375 cdot 5}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,10xleft( {x — 5} right) = 125x + 375 cdot 5,,left| {,:} right.,5,,,, Leftrightarrow ,,,,2{x^2} — 10x = 25x + 375,,,, Leftrightarrow ,,,,2{x^2} — 35x — 375 = 0;) (D = {35^2} + 8 cdot 375 = {5^2} cdot {7^2} + 8 cdot {5^2} cdot 15 = {5^2}left( {49 + 120} right) = {5^2} cdot 169;,,,,,,,,,,sqrt D = 5 cdot 13 = 65;) ({x_1} = frac{{35 + 65}}{4}, = 25;,,,,,{x_2} = frac{{35 — 65}}{4} = — frac{{15}}{2}.) Так как (x > 0), то вторая труба пропускает 25 литров в минуту. Ответ: 25. |
||||||||||||
| Задача 7. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
После 3 часов работы первому на выполнение заказа осталось работать ещё 12 часов, но так как к нему присоединился второй рабочий, и они стали работать вместе, то им на завершение заказа потребуется 6 часов. Следовательно, заказ будет выполнен за 3 + 6 = 9 часов. Ответ: 9. |
||||||||||||
| Задача 8. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Первый мастер за 1 час выполняет (frac{1}{{12}}) часть работы, а второй (frac{1}{6}). Следовательно, работая вместе, два мастера выполняют (frac{1}{{12}} + frac{1}{6} = frac{1}{4}) часть работы. Поэтому всю работу мастера выполнят за 4 часа. Ответ: 4. Замечание: Выведем формулу для совместной работы двух рабочих. Пусть первый рабочий может выполнить работу А за время ({t_1}), а второй за время ({t_2}). Тогда производительность первого рабочего ({W_1} = frac{A}{{{t_1}}}), второго ({W_2} = frac{A}{{{t_2}}}). Следовательно, при совместной работе их общая производительность будет равна: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}). Пусть ({t_{совм}}) — время за которое будет выполнена работа А при совместной работе. Тогда (frac{A}{{{t_{совм}}}}) будет общая производительность двух рабочих, которая равна (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}), то есть: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}} = frac{A}{{{t_{совм}}}}). Сократив на А, получим: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}). Если работа выполняется тремя субъектами за время ({t_1}), ({t_2}) и ({t_3}) соответственно, то время совместного выполнения того же объёма работы равно: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Так как первый рабочий выполняет заказ за 12 часов, а второй за 6 часов, то ({t_1} = 12), ({t_2} = 6). Тогда: (frac{1}{{12}} + frac{1}{6} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{1}{4} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,,{t_{совм}} = 4). |
||||||||||||
| Задача 9. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). В данном случае ({t_1} = 20) минут, ({t_2} = 30) минут, ({t_3} = 1) час = 60 минут: (frac{1}{{20}} + frac{1}{{30}} + frac{1}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,frac{{3 + 2 + 1}}{{60}} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{6}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 10). Ответ: 10. |
| Задача 10. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Пусть Игорь, Паша и Володя каждый покрасят забор за время ({t_1}), ({t_2}) и ({t_3})соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{12}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{12}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{4},left| {,:2,,,,, Leftrightarrow } right.,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{8}.) Так как спрашивают, за сколько часов мальчики покрасят забор, работая втроем, то: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Следовательно: (frac{1}{{{t_{совм}}}} = frac{1}{8},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8.) Ответ: 8. |
||||||||||||
| Задача 11. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 20) минут время, за которое Маша пропалывает грядку, а ({t_2}) – время за которое Даша. При этом ({t_{совм}} = 12) минут. (frac{1}{{20}} + frac{1}{{{t_2}}} = frac{1}{{12}},,,,, Leftrightarrow ,,,,,frac{1}{{{t_2}}} = frac{1}{{12}} — frac{1}{{20}},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{{30}},,,,,, Leftrightarrow ,,,,,{t_2} = 30) минут. Ответ: 30. |
||||||||||||
| Задача 12. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 6) часов время, за которое первая труба наполняет бассейн, а ({t_2}) – время второй трубы. При этом ({t_{совм}} = 3) часа 36 минут = (3frac{{36}}{{60}}) часа = (frac{{18}}{5}) часа. (frac{1}{6} + frac{1}{{{t_2}}} = frac{5}{{18}},,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{5}{{18}} — frac{1}{6},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{9},,,,, Leftrightarrow ,,,,{t_2} = 9) часов. Ответ: 9. |
||||||||||||
| Задача 13. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть x – минут время, за которое вторая труба наполняет резервуар, а x + 6 минут время первой трубы. При этом ({t_{совм}} = 4) минуты: (frac{1}{{x + 6}} + frac{1}{x} = frac{1}{4},,,,, Leftrightarrow ,,,,,,frac{{x + x + 6}}{{xleft( {x + 6} right)}} = frac{1}{4},,,,, Leftrightarrow ,,,,{x^2} + 6x = 4left( {2x + 6} right),,,, Leftrightarrow ,,,,,{x^2} — 2x — 24 = 0;) (D = 4 + 4 cdot 24 = 100;,,,,,,{x_1} = frac{{2 + 10}}{2} = 6;,,,,,{x_2} = frac{{2 — 10}}{2} = — 4.) Так как (x > 0), то вторая труба наполнит резервуар за 6 минут. Ответ: 6. |
||||||||||||
| Задача 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
Первый нанос перекачивает (frac{5}{2}) л/мин, а второй (frac{5}{3}) л/мин. Тогда вместе они перекачивают (frac{5}{2} + frac{5}{3} = frac{{25}}{6}) л/мин. Следовательно, 25 литров они перекачают за (25:frac{{25}}{6} = 6) минут. Ответ: 6. |
||||||||||||
| Задача 15. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Пусть тест содержит х вопросов.
Так как Петя закончил свой тест на 20 минут ((frac{1}{3}) часа) позже Вани, то: (frac{x}{8} — frac{x}{9} = frac{1}{3},,,, Leftrightarrow ,,,,frac{x}{{72}} = frac{1}{3},,,,, Leftrightarrow ,,,,x = 24.) Следовательно, тест содержит 24 вопроса. Ответ: 24. |
||||||||||||
| Задача 16. Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Пусть плиточник планирует укладывать х м2 плитки в день.
Следовательно: (frac{{175}}{x} — frac{{175}}{{x + 10}} = 2,,,, Leftrightarrow ,,,,frac{{175left( {x + 10} right) — 175x}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ,,,,frac{{175 cdot 10}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 10} right) = 175 cdot 10,,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 10x — 875 = 0) (D = 100 + 4 cdot 875 = 3600;,,,,,{x_1} = frac{{ — 10 + 60}}{2} = 25;,,,,,{x_2} = frac{{ — 10 — 60}}{2} = — 35.) Так как (x > 0), то плиточник планировал укладывать 25 м2 плитки в день. Ответ: 25. |
||||||||||||
| Задача 17. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Пусть первый, второй и третий насосы заполняют бассейн за время ({t_1}), ({t_2}) и ({t_3}) соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: ()(left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{14}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{14}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{5}{{21}},left| {,:2,,,,, Leftrightarrow } right.,,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{5}{{42}}.) Так как спрашивается, за сколько минут три насоса заполнят бассейн, работая вместе, то: (frac{1}{{{t_{совм}}}} = frac{5}{{42}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8,4) минуты. Ответ: 8,4. |
||||||||||||
| Задача 18. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых дома. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады, в результате чего оба дома были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе?
Количество рабочих будем считать производительностью. Пусть в новом составе рабочие доделывали дома t дней. В сумме до и после перехода рабочих каждая из бригад выполнила всю работу. Тогда: (16 cdot 7 + 24 cdot t = 25 cdot 7 + 17t,,,, Leftrightarrow ,,,,7t = 25 cdot 7 — 16 cdot 7,,,, Leftrightarrow ,,,,t = 9.) Следовательно, рабочим понадобилось 9 дней, чтобы закончить работу в новом составе. Ответ: 9. |
Примем объем работы за единицу. Пусть x — количество дней, за которое необходимо выполнить всю работу Виктору; за y дней работу выполнит Алексей, Андрей выполнит всю работу за z дней; тогда frac{1}{x} — производительность Виктора, frac{1}{y} — производительность Алексея, frac{1}{z} — производительность Андрея.
По первому условию Виктор и Алексей сделают всю работу за 8 дней, значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{y}=frac18.
По второму условию Виктор и Андрей сделают всю работу за 8 дней. Значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{z}=frac18.
По третьему условию Андрей и Алексей выполнят всю работу за 12 дней. Значит, их общая производительность frac{1}{12}. Составим уравнение frac{1}{y}+frac{1}{z}=frac{1}{12}.
Получим систему уравнений:
begin{cases} frac{1}{x}+frac{1}{y}=frac18,\ frac{1}{x}+frac{1}{z}=frac18,\ frac{1}{y}+frac{1}{z}=frac{1}{12}; end{cases}
2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac18+frac18+frac{1}{12},
2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac13,
frac{1}{x}+frac{1}{y}+frac{1}{z}=frac16,
1:frac16=6 (дней).
Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.
Задачи на работу решаются просто. В этой статье мы с вами рассмотрим типовые задания условия которых связаны с рабочими изготавливающими детали. Алгоритм решения задач идентичен алгоритму решения задач на движение. Перед дальнейшим изучением материала обязательно посмотрите статью, где мы решали задания на движение. Итак, формула:
Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, Вася красит забор. Количество метров, которые он красит за час — это и есть его производительность. То есть это скорость работы.
Правила решения задач на работу:
1. А = р∙t, из этой формулы легко найти t или p.
2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды — работа как раз и равна этому количеству.
3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша…) или трое (не важно) — их производительности суммируются. Очень логичное правило.
4. В качестве переменной «х» удобно взять (в абсолютном большинстве задач) именно производительность. Так же, как в задах на движение мы за «х» принимаем скорость.
Вы убедитесь, что задачи на работу и движение очень схожи.
Рассмотрим задачи:
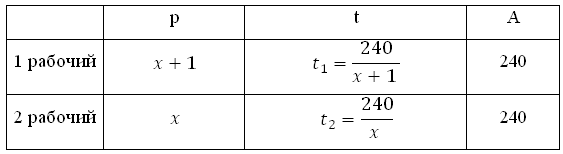
Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Как и в задачах на движение, заполним таблицу.
В колонке «работа» и для первого, и для второго рабочего запишем: 240. В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем её за х. Тогда производительность первого рабочего равна х + 1 (он делает на одну деталь в час больше).
Поскольку t = A/p, время работы первого рабочего равно t2 = 240/(х + 1), время работы второго равно t2 = 240/х.
Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть t1 на 1 меньше, чем t2, значит
Мы уже решали такие уравнения. Оно легко сводится к квадратному:
Очевидно, производительность рабочего не может быть отрицательной величиной. Значит, отрицательный корень не подходит.
Ответ: 15
Решить самостоятельно:
Посмотреть решение
26593. Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?
В колонке «работа» и для первого, и для второго рабочего запишем 156.
В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её за х (деталей в час). Тогда производительность второго рабочего будет равна х–1 (он делает на одну деталь в час меньше).
Поскольку t=A/p, то время работы первого рабочего будет равно:

Первый рабочий выполнил заказ на час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй. Значит

Очевидно, что производительность рабочего не может быть отрицательной величиной. Таким образом производительность первого рабочего равна 13 деталей в час.
Ответ: 13
На изготовление 40 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 70 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий?
Данная задача практически не отличается от предыдущей, разница лишь в объёме работы. Примем производительность второго рабочего за х.
Тогда производительность первого рабочего равна х + 3 (он делает в час на три детали больше). Заполним графу «время» в таблице:
Сравнение будем проводить по времени. Сказано, что первый затрачивает на 6 часов меньше, чем второй. Значит
Таким образом, второй рабочий в час делает 7 деталей.
Ответ: 7
26594. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Для удобства занесём данные в таблицу.
В колонке «работа» для первого запишем 475, для второго рабочего запишем 550. В задаче спрашивается, сколько деталей в час делает первый рабочий, то есть какова его производительность. Примем её за х (деталей в час).
Тогда производительность второго рабочего будет равна х–3 (он делает на три детали в час меньше).
Поскольку t=A/p, то время работы первого рабочего будет равно


Сказано, что первый рабочий тратит на свой заказ на 6 часов меньше. Можем записать:

Очевидно, что производительность рабочего не может быть величиной. Первый рабочий делает 25 деталей в час.
Ответ: 25
Решить самостоятельно:
Посмотреть решение
На этом всё. В будущем мы рассмотрим задачи на работу, которые несколько отличаются от представленных выше. Но вы увидите, что и в них нет ничего особо сложного, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Основные особенности решения задач на производительность:
- Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
- Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
- Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:
$ t=frac{1}{upsilon}. $
- В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v1 и v2, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v1 + v2, а время совместной работы будет равно:
$ t=frac{1}{upsilon_{1}+upsilon_{2}} $
Пример:
Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение:
В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.
| v, дет/ч | t, ч | V, дет | |
|---|---|---|---|
|
Первый рабочий |
x + 5 |
$ frac{200}{x+5} $ |
200 |
|
Второй рабочий |
x |
$ frac{200}{x} $ |
200 |
В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:
$ {frac{200}{x+5}+2=frac{200}{x} frac{200+2x+10}{x+5}=frac{200}{x}.} $
2x2 + 210x = 200x + 1000;
x2 + 5x – 500 = 0.
Получаем два корня, x1= 20 и x2= –25. Второй корень не подходит, так как производительность не может быть отрицательной.
Ответ: 20 дет/ч.
Виды задач на производительность:
1. Задачи на совместную работу:
Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.
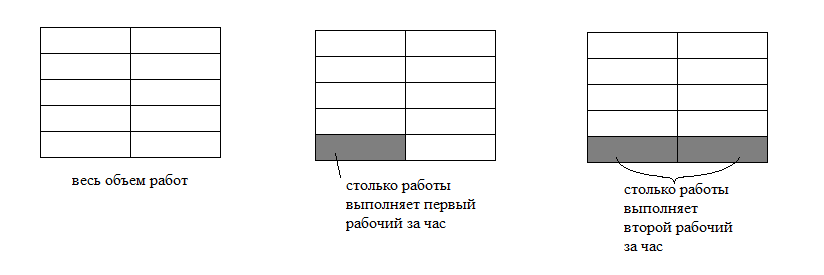
Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.
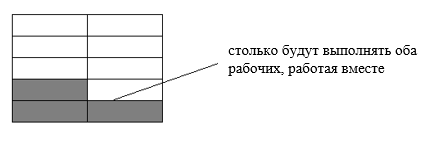
Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ frac{1}{10} $ всей работы за час, а второй $ frac{1}{10} $ то есть $ frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ frac{1}{10}+ frac{1}{5}= frac{3}{10} $ всей работы за час, или 3 «кирпичика»:
Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:
$ 1/frac{3}{10}=frac{10}{3}=3frac{1}{3} $
То есть вместе рабочие справятся с работой за 3 $ frac{1}{3} $ часа, или за 3 часа 20 минут.
2. Задачи на бассейны и трубы:
Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.
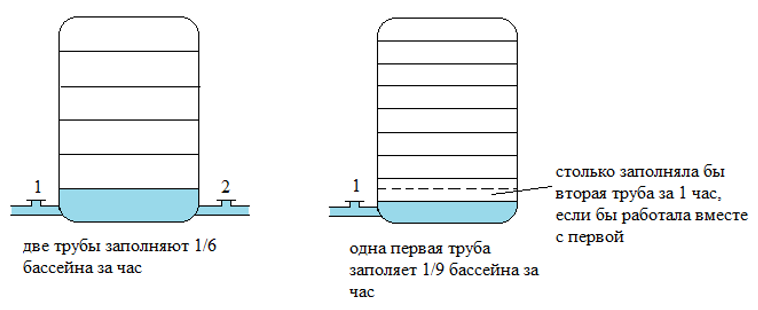
Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
Получается, что за 1 час две трубы наполняют $ frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ frac{1}{6}- frac{1}{9}= frac{1}{18} $.
Таким образом, вторая труба заполнит бассейн за $ 1/frac{1}{18}=18 $ часов.