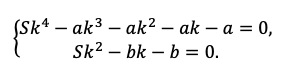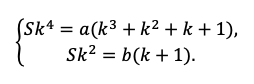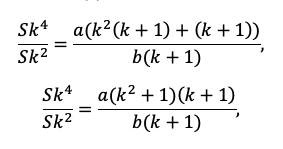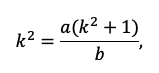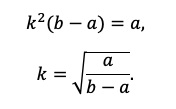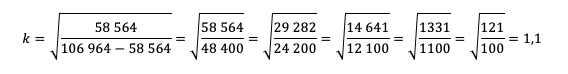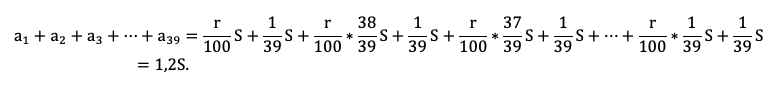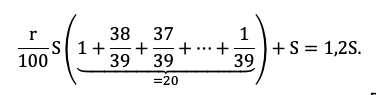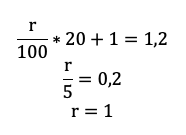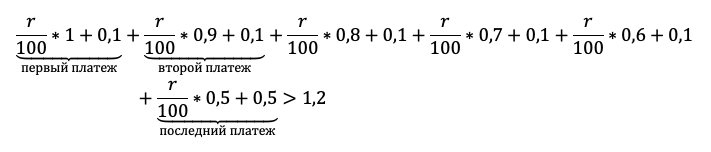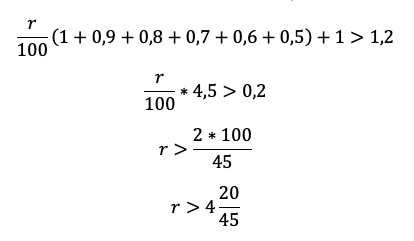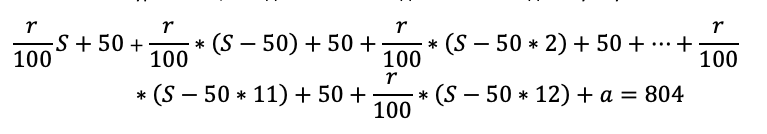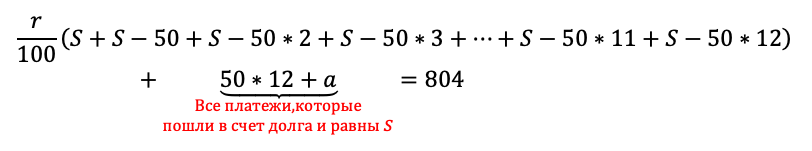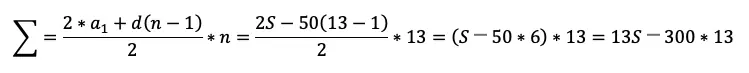Задачи с фунтами егэ

1

---

2

---

3

---

4

---

5

---

6

---

7

---

8

---

9

---

10

---

11

---

12

---

13

---

14

---

15

---

16

---

17

---

18

---

19

---

20

---

21

---

22

---

23

---

24

---

25

---

26

---

27

---

28

---

29

---

30

---

31

---

32

---

33

---

34

---

35

---

36

---

37

---

38

---

39

---

40

---

41

---

42

---

43

---

44

---

45

---

46

---

47

---

48

---

49

---

50

---

51

• Альфашкола
• Статьи
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 10)

Задача № 1

Рост человека 6 футов 1 дюйм. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.

Решение

Выразим рост человека в дюймах, получим:

6 футов 1 дюйм = 6 · 12 + 1 = 73 дюйма

Тогда рост человека составит:

73 · 2,54 = 185,42 см.

Округляя, получаем 185 см.

Ответ: 185.

Задача № 2

Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

Решение

Средняя скорость бегуна равна:

50 : 5 = 10 м/с.

Переведем метры в секунду в километры в час:

1 м/с = 60 м/мин = 3600 м/ч = 3,6 км/ч.

Поэтому 10 м/с равно:

3,6 · 10 = 36 км/ч.

Ответ: 36.

Задача № 3

В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 10 человек следует взять 1/10 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 3 человек? Считайте, что 1 фунт равен 0,4 кг.

Решение

Представим:

1/10 = 0,1

По условию задачи на 10 человек следует взять 0,1 фунта чернослива, следовательно, на одного человека следует взять:

0,1 : 10 = 0,01 фунта чернослива

Тогда на трех человек потребуется:

0,01 · 3 = 0,03 фунта чернослива, что составляет:

0,03 · 0,4 = 0,012 кг

Выразим полученный результат в граммах:

1 кг = 1000 г

0,012 кг · 1000 = 12 граммов.

Ответ: 12.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Репетитор по математике

Тираспольский государственный университет

Репетитор по математике

Новосибирский государственный педагогический университет

Репетитор по математике

Мозырский государственный педагогический университет им. И.П. Шамякина

13 января 2014

Задача B4. В первом банке один фунт стерлингов стоит 45,2 рубля. Во втором банке 30 фунтов стоят 1383 рубля. В третьем банке 12 фунтов стоят 534 рубля. Какую наименьшую сумму в рублях придется заплатить за 20 фунтов стерлингов?

Это стандартная задача на перебор трех вариантов без использования таблиц. Считается легкой задачей B4 и может встречаться в реальном ЕГЭ по математике.

Смотрите также:

1. Задача B4: Цены на продукты в трех городах
2. Задача B4 про три дороги — стандартная задача на движение
3. Как сдать ЕГЭ по математике
4. Не пишите единицы измерения в задаче B12
5. Деление многочленов уголком
6. Углы и отрезки в пирамиде

1

При температуре  рельс имеет длину  м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где  — коэффициент теплового расширения,  — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

25

2

Некоторая компания продает свою продукцию по цене  руб. за единицу, переменные затраты на производство одной единицы продукции составляют  руб., постоянные расходы предприятия  руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле . Определите месячный объём производства (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 300000 руб.

5000

3

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.

1

4

Зависимость объёма спроса  (единиц в месяц) на продукцию предприятия-монополиста от цены  (тыс. руб. за ед.) задаётся формулой . Выручка предприятия  (в тыс. руб. за месяц) вычисляется по формуле . Определите наибольшую цену , при которой месячная выручка  составит не менее 240 тыс. руб. Ответ приведите в тыс. руб. за ед.

6

5

Высота над землeй подброшенного вверх мяча меняется по закону , где h- высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?    

1,2

6

Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна , где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с      

2

7

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону  , где t — время в секундах, прошедшее с момента открытия крана, H0 = 20 м — начальная высота столба воды,  — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

50

8

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , где м — начальный уровень воды,  м/мин2, и м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах        

20

9

Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой , где  м-1, — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?  

90

10

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:, где  — время в минутах,  К,  К/мин,  К/мин. Известно, что при температуре нагревательного элемента свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

2

11

Для сматывания кабеля на заводе используют лебeдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону , где t — время в минутах, — начальная угловая скорость вращения катушки, а — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки  достигнет 12000. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.  

20

12

Мотоциклист, движущийся по городу со скоростью  км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением а = 12 км/ч. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах        

30

13

Автомобиль, движущийся в начальный момент времени со скоростью  м/с, начал торможение с постоянным ускорением а = 5 м/с. За t секунд после начала торможения он прошёл путь  (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.  

2

14

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 10 см, и двух боковых с массами M= 1 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг . см2, даeтся формулой . При каком максимальном значении h момент инерции катушки не превышает предельного значения 625 кг . см2? Ответ выразите в сантиметрах.  

5

15

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая сила, выражаемая в ньютонах, будет определяться по формуле: , где l — длина ребра куба в метрах, — плотность воды, а g — ускорение свободного падения (считайте g=9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400Н? Ответ выразите в метрах  

2

16

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где  — постоянная, r — радиус аппарата в метрах,  — плотность воды, а g — ускорение свободного падения (считайте g=10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ  в метрах    

2

17

Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: , где  — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь  м2, а излучаемая ею мощность P не менее  Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина    

4000

18

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием  см.Расстояние  от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние  от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах  

36

19

Перед отправкой тепловоз издал гудок с частотой Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону  (Гц), где c — скорость звука в воздухе (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а с=315 м/с. Ответ выразите в м/с        

7

20

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна , где — ЭДС источника (в вольтах),  Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания ? (Ответ выразите в Омах)  

4

21

Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах    

55

22

Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле , где  — частота вынуждающей силы (в ),  — постоянный параметр,  — резонансная частота. Найдите максимальную частоту , меньшую резонансной, для которой амплитуда колебаний превосходит величину не более чем на 12,5%. Ответ выразите в    

120

23

В розетку электросети подключены приборы, общее сопротивление которых составляет  Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями  Ом и  Ом их общее сопротивление даeтся формулой  (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах  

10

24

Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой , где  — температура нагревателя (в градусах Кельвина),  — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя КПД этого двигателя будет не меньше 15%, если температура холодильника  К? Ответ выразите в градусах Кельвина  

400

25

Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой (в килограммах) от температуры до температуры (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы  кг. Он определяется формулой , где Дж/(кгК) — теплоёмкость воды, Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть кг воды от 100С до кипения, если известно, что КПД кормозапарника не больше 21%. Ответ в килограммах

18

26

Опорные башмаки шагающего экскаватора, имеющего массу  тонн представляют собой две пустотелые балки длиной  метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой , где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте м/с). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах  

2,5

27

К источнику с ЭДС  В и внутренним сопротивлением  Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даeтся формулой . При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в Омах

5

28

При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приeмником, не совпадает с частотой исходного сигнала  Гц и определяется следующим выражением: (Гц), где c — скорость распространения сигнала в среде (в м/с), а  м/с и  м/с — скорости приeмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приeмнике f будет не менее 160 Гц

390

29

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле , где  м/с — скорость звука в воде,  — частота испускаемых импульсов (в МГц), f — частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала f, если скорость погружения батискафа не должна превышать 2 м/с

751

30

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением  км/ч. Скорость  вычисляется по формуле , где  — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость 100 км/ч. Ответ выразите в км/ч.

5000

31

При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где  м — длина покоящейся ракеты,  км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с

180000

32

Наблюдатель находится на высоте , выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле , где  км — радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 4 километров? Ответ выразите в метрах.

1250

33

Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле , где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?

1,4

34

Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле , где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?

7

35

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением  км/ч. Скорость  вычисляется по формуле , где  — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.

1

36

Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле , где m=1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g=10 м/с, а , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах

0,2

37

Автомобиль, масса которого равна m=2160 кг, начинает двигаться с ускорением, которое в течение t секунд остаeтся неизменным, и проходит за это время путь S=500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно . Определите наибольшее время после начала движения автомобиля, за которое он пройдeт указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ в секундах  

30

38

При адиабатическом процессе для идеального газа выполняется закон  Па, где  — давление в газе в паскалях,  — объём газа в кубических метрах, . Найдите, какой объём  (в куб. м) будет занимать газ при давлении , равном  Па.

0,125

39

В ходе распада радиоактивного изотопа его масса уменьшается по закону , где  — начальная масса изотопа,  — время, прошедшее от начального момента,  — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.

30

40

Уравнение процесса, в котором участвовал газ, записывается в виде , где p (Па) — давление в газе, V — объeм газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?

2

41

Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением , где  и  — давление газа (в атмосферах) в начальном и конечном состояниях,  и  — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 1,6 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах

0,05

42

В телевизоре ёмкость высоковольтного конденсатора  Ф. Параллельно с конденсатором подключён резистор с сопротивлением  Ом. Во время работы телевизора напряжение на конденсаторе  кВ. После выключения телевизора напряжение на конденсаторе убывает до значения  (кВ) за время, определяемое выражением  (с), где  — постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 21 с. Ответ дайте в киловольтах.

2

43

Для обогрева помещения, температура в котором поддерживается на уровне , через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды  кг/с. Проходя по трубе расстояние , вода охлаждается от начальной температуры  до температуры , причём , где  — теплоёмкость воды,  — коэффициент теплообмена, а  — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.

30

44

Водолазный колокол, содержащий в начальный момент времени  моля воздуха объёмом  л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма . Работа, совершаемая водой при сжатии воздуха, определяется выражением , где   — постоянная, а  К — температура воздуха. Найдите, какой объём  (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 10350 Дж.

2

45

        Водолазный колокол, содержащий  моля воздуха при давлении атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления . Работа, совершаемая водой при сжатии воздуха, определяется выражением , где   — постоянная,  К — температура воздуха. Найдите, какое давление  (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 6900 Дж.

6

46

Мяч бросили под острым углом  к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле . При каком значении угла  (в градусах) время полёта составит 3 секунды, если мяч бросают с начальной скоростью  м/с? Считайте, что ускорение свободного падения  м/с.

30

47

Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нм) определяется формулой , где  — сила тока в рамке,  Тл — значение индукции магнитного поля,  м — размер рамки,  — число витков провода в рамке,  — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла  (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,75 Нм?

30

48

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону , где  — время в секундах, амплитуда В, частота /с, фаза . Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

50

49

Очень лeгкий заряженный металлический шарик зарядом  Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет  м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол  с направлением движения шарика. Значение индукции поля  Тл. При этом на шарик действует сила Лоренца, равная  (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла  шарик оторвeтся от поверхности, если для этого нужно, чтобы сила  была не менее чем  Н? Ответ дайте в градусах.

30

50

Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой , где  м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте  м/с). При каком наименьшем значении угла  (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?

30

51

Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле  (м), где  м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте  м/с). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?

15

52

Плоский замкнутый контур площадью  м находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой , где  — острый угол между направлением магнитного поля и перпендикуляром к контуру,  Тл/с — постоянная, S — площадь замкнутого контура, находящегося в магнитном поле (в м). При каком минимальном угле (в градусах) ЭДС индукции не будет превышать  В?

60

53

Трактор тащит сани с силой  кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной  м вычисляется по формуле . При каком максимальном угле (в градусах) совершeнная работа будет не менее 2000 кДж?

60

54

Двигаясь со скоростью  м/с, трактор тащит сани с силой  кН, направленной под острым углом  к горизонту. Мощность, развиваемая трактором, вычисляется по формуле . Найдите, при каком угле (в градусах) эта мощность будет равна 75 кВт (кВт — это ).

60

55

При нормальном падении света с длиной волны  нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол  (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением . Под каким минимальным углом  (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1600 нм?

30

56

Два тела, массой  кг каждое, движутся с одинаковой скоростью  м/с под углом  друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле , где  — масса в килограммах,  — скорость в м/с. Найдите, под каким наименьшим углом (в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 50 джоулей.

60

57

Катер должен пересечь реку шириной  м и со скоростью течения  м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением , где  — острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом  (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?

45

58

Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью  м/с под острым углом  к рельсам. От толчка платформа начинает ехать со скоростью  (м/с), где  кг — масса скейтбордиста со скейтом, а  кг — масса платформы. Под каким максимальным углом (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?

60

59

Груз массой 0,08 кг колеблется на пружине. Его скорость  меняется по закону , где  — время с момента начала колебаний,  с — период колебаний,  м/с. Кинетическая энергия  (в джоулях) груза вычисляется по формуле , где  — масса груза в килограммах,  — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.

0,0025

60

Груз массой 0,08 кг колеблется на пружине. Его скорость  меняется по закону , где  — время с момента начала колебаний,  с — период колебаний,  м/с. Кинетическая энергия  (в джоулях) груза вычисляется по формуле , где  — масса груза в килограммах,  — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.

0,0025

61

Скорость колеблющегося на пружине груза меняется по закону  (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

0,17

62

Независимое агентство намерено ввести рейтинг новостных изданий на основе показателей информативности , оперативности  и объективности публикаций. Каждый отдельный показатель — целое число от -2 до 2.

Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вдвое дороже, чем оперативность. Таким образом, формула приняла вид

Найдите, каким должно быть число , чтобы издание, у которого все показатели максимальны, получило бы рейтинг 30.

0,4

63

Рейтинг  интернет-магазина вычисляется по формуле , где ,  — средняя оценка магазина покупателями,  — оценка магазина, данная экспертами,  — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.

0,71

64

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе показателей информативности , оперативности , объективности публикаций, а также качества  сайта. Каждый отдельный показатель — целое число от 1 до 5.

Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

Найдите, каким должно быть число , чтобы издание, у которого все показатели максимальны, получило бы рейтинг 1.

35

65

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности , оперативности , объективности публикаций, а также качества  сайта. Каждый отдельный показатель — целое число от -2 до 2.

Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

Если по всем четырём показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число , при котором это условие будет выполняться.

10

66

На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось  направим вертикально вдоль одного из пилонов, а ось  направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой  где  и  измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.

7,3

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• на ценные бумаги,
• задачи на оптимальный выбор. 

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

• Как работает процент по кредиту?
• На какую сумму начисляется?
• Из каких частей состоит платеж?
• Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

• Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
• Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
• Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг. 

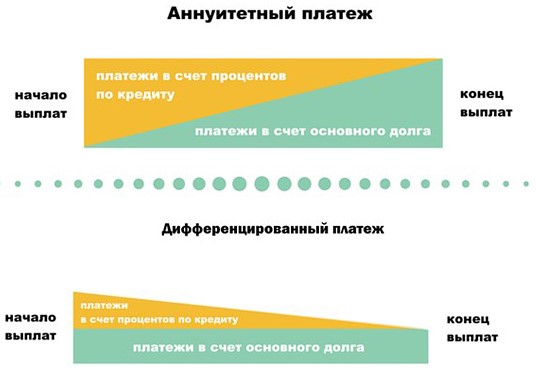
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается. 

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!   

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.  

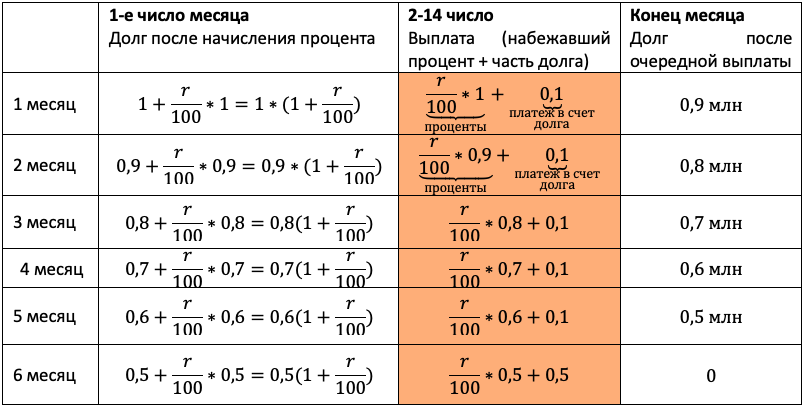
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

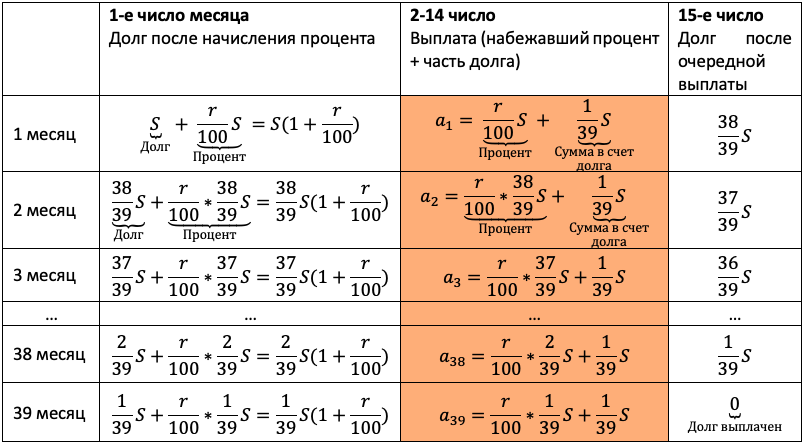
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

• Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
• Повторите типы задач и механизм распределения платежа на проценты и долг;
• Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
• Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа. 

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги. 

Так называемые задачи на смекалку – это олимпиадные задачи, которые включены в программу средней школы. Чтобы преуспеть в их решении можно применять математическое моделирование или решать методом подбора.

Данные задачи попадаются последними в базовом уровне математики ЕГЭ в школе. Разберем те из них, которые непосредственно можно решить, составляя математически модели – уравнения.

Задача 1.

Источник: ЕГЭ — 2015. До­сроч­ная волна.

В об­мен­ном пункте можно со­вер­шить одну из двух операций:
• за 2 зо­ло­тых монеты по­лу­чить 3 се­реб­ря­ных и одну медную;
• за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тых и одну медную.
У Ни­ко­лая были толь­ко серебряные монеты. После нескольких посещений об­мен­но­го пункта се­реб­ря­ных монет у него стало меньше, зо­ло­тых не появилось, зато по­яви­лось 50 медных. На сколь­ко уменьшилось ко­ли­че­ство серебряных монет у Николая?

Решение задачи 1.

Составим математическую модель:

[ begin{equation*}  begin{cases}    2з=3с+1м    \   5c=3з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}    2з=3с+1м    \   3з=5с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    2з=3с+1м    \   1з={{5}over{3}}с-{1over3}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    2({{5}over{3}}с-{1over3}м)=3с+1м    \   1з={{5}over{3}}с-{1over3}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   {{10}over{3}}с-{2over3}м=3с+1м    \   1з={{5}over{3}}с-{1over3}мend{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{1}over{3}}с={{5}over{3}}м    \   1з={{5}over{3}}с-{1over3}мс end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=5м    \   1з={{5}over{3}}с-{1over3}м end{cases} end{equation*} ]

Т.к. у Николая появилось 50 медных монет, следовательно, количество серебряных монет уменьшилось на 10.

Ответ: 10.

Задача 2.

Источник: Апро­ба­ция ба­зо­во­го ЕГЭ по ма­те­ма­ти­ке, 13—17 октября: ва­ри­ант 166082.

В об­мен­ном пунк­те можно со­вер­шить одну из двух операций:
1) за 3 зо­ло­тых мо­не­ты по­лу­чить 4 се­реб­ря­ных и одну медную;
2) за 6 се­реб­ря­ных монет по­лу­чить 4 зо­ло­тых и одну медную.
У Ни­ко­лы были толь­ко се­реб­ря­ные монеты. После по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало меньше, зо­ло­тых не появилось, зато по­яви­лось 35 медных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Николы?

Решение задачи 2.

Составим математическую модель:

[ begin{equation*}  begin{cases}    3з=4с+1м    \   6c=4з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}    3з=4с+1м    \   4з=6с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   3з=4с+1м    \   1з={6over4}с-{1over4}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    3({6over4}с-{1over4}м)=4с+1м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{18}over{4}}с-{3over4}м=4с+1м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{2}over{4}}с={{7}over{4}}м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=7м    \   1з={6over4}с-{1over4}м end{cases} end{equation*} ]

Тогда

[ 35м=10с ]

Т.к. у Николая появилось 35 медных монет, следовательно, количество серебряных монет уменьшилось на 10.

Ответ: 10.

Задача 3.

Источник: Пробный экзамен Саратов 2016. Вариант 1.

В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?

Решение задачи 3.

Составим математическую модель:

[ begin{equation*}  begin{cases}    4з=5с+1м    \   7c=5з+1м  end{cases} end{equation*} ]

Выразим золотые монеты через серебряные и медные:

[ begin{equation*}  begin{cases}   4з=5с+1м    \   5з=7с-1м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}   4з=5с+1м   \   1з={7over5}с-{1over5}м  end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    4({7over5}с-{1over5}м)=5с+1м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{28}over{5}}с-{4over5}м=5с+1м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    {{3}over{5}}с={{9}over{5}}м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

[ begin{equation*}  begin{cases}    1с=3м    \   1з={7over5}с-{1over5}м end{cases} end{equation*} ]

Тогда

[ 90м=30с ]

Т.к. у Николая появилось 90 медных монет, следовательно, количество серебряных монет уменьшилось на 30.

Ответ: 30.

01
Июн 2013

Категория: A1 Простейшие текст/задачи (нет в ЕГЭ-22)

Задания №1. Простейшие текстовые задачи на проценты

2013-06-01
2021-09-11

Автор: egeMax |

комментария 4