1
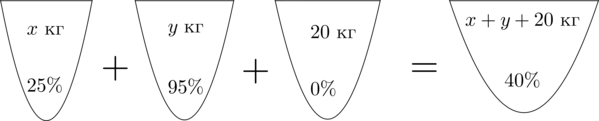
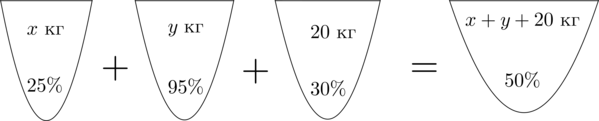
Смешав 11-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?
2
Смешав 55-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 65-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 55-процентного раствора использовали для получения смеси?
3
Смешав 41-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 41-процентного раствора использовали для получения смеси?
4
Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
5
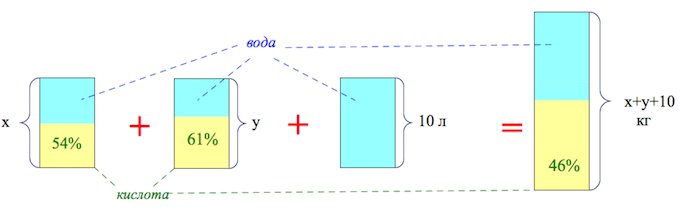
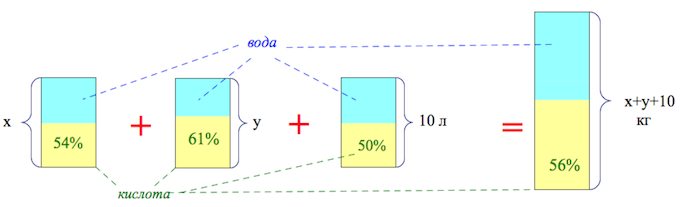
Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
6
Смешав 62-процентный и 93-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 67-процентный раствор кислоты. Сколько килограммов 62-процентного раствора использовали для получения смеси?
7
Смешав 14-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 70-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 74-процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?
8
Смешав 40-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
9
Смешав 48-процентный и 94-процентный растворы кислоты и добавив 10 кг чистой воды, получили 80-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 85-процентный раствор кислоты. Сколько килограммов 48-процентного раствора использовали для получения смеси?
10
Смешав 5-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 39-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
11
Смешав 8-процентный и 96-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
12
Смешав 68-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 39-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 68-процентного раствора использовали для получения смеси?
13
Смешав 76-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 76-процентного раствора использовали для получения смеси?
14
Смешав 63-процентный и 77-процентный растворы кислоты и добавив 10 кг чистой воды, получили 56-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 66-процентный раствор кислоты. Сколько килограммов 63-процентного раствора использовали для получения смеси?
15
Смешав 12-процентный и 64-процентный растворы кислоты и добавив 10 кг чистой воды, получили 28-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 48-процентный раствор кислоты. Сколько килограммов 12-процентного раствора использовали для получения смеси?
16
Смешав 4-процентный и 32-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 4-процентного раствора использовали для получения смеси?
17
Смешав 13-процентный и 34-процентный растворы кислоты и добавив 10 кг чистой воды, получили 12-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 32-процентный раствор кислоты. Сколько килограммов 13-процентного раствора использовали для получения смеси?
18
Смешав 45-процентный и 66-процентный растворы кислоты и добавив 10 кг чистой воды, получили 51-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
19
Смешав 27-процентный и 69-процентный растворы кислоты и добавив 10 кг чистой воды, получили 51-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 61-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
20
Смешав 13-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 24-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 29-процентный раствор кислоты. Сколько килограммов 13-процентного раствора использовали для получения смеси?
21
Смешав 3-процентный и 17-процентный растворы кислоты и добавив 10 кг чистой воды, получили 5-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
22
Смешав 7-процентный и 41-процентный растворы кислоты и добавив 10 кг чистой воды, получили 11-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 31-процентный раствор кислоты. Сколько килограммов 7-процентного раствора использовали для получения смеси?
23
Смешав 32-процентный и 91-процентный растворы кислоты и добавив 10 кг чистой воды, получили 61-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 71-процентный раствор кислоты. Сколько килограммов 32-процентного раствора использовали для получения смеси?
24
Смешав 85-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 70-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 80-процентный раствор кислоты. Сколько килограммов 85-процентного раствора использовали для получения смеси?
25
Смешав 65-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 65-процентного раствора использовали для получения смеси?
26
Смешав 8-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
27
Смешав 24-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 68-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 73-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
28
Смешав 37-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 37-процентного раствора использовали для получения смеси?
29
Смешав 25-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси?
30
Смешав 71-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 86-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 91-процентный раствор кислоты. Сколько килограммов 71-процентного раствора использовали для получения смеси?
31
Смешав 12-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 21-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 12-процентного раствора использовали для получения смеси?
32
Смешав 49-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 49-процентного раствора использовали для получения смеси?
33
Смешав 19-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 19-процентного раствора использовали для получения смеси?
34
Смешав 33-процентный и 34-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 33-процентного раствора использовали для получения смеси?
35
Смешав 45-процентный и 59-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
36
Смешав 40-процентный и 48-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
37
Смешав 50-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 48-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 58-процентный раствор кислоты. Сколько килограммов 50-процентного раствора использовали для получения смеси?
38
Смешав 58-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 65-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 70-процентный раствор кислоты. Сколько килограммов 58-процентного раствора использовали для получения смеси?
39
Смешав 83-процентный и 84-процентный растворы кислоты и добавив 10 кг чистой воды, получили 67-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 77-процентный раствор кислоты. Сколько килограммов 83-процентного раствора использовали для получения смеси?
40
Смешав 22-процентный и 64-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
41
Смешав 72-процентный и 93-процентный растворы кислоты и добавив 10 кг чистой воды, получили 78-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 82-процентный раствор кислоты. Сколько килограммов 72-процентного раствора использовали для получения смеси?
42
Смешав 40-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 39-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 43-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
43
Смешав 3-процентный и 24-процентный растворы кислоты и добавив 10 кг чистой воды, получили 12-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 16-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
44
Смешав 86-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 78-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 83-процентный раствор кислоты. Сколько килограммов 86-процентного раствора использовали для получения смеси?
45
Смешав 16-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 20-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 25-процентный раствор кислоты. Сколько килограммов 16-процентного раствора использовали для получения смеси?
46
Смешав 52-процентный и 96-процентный растворы кислоты и добавив 10 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 60-процентный раствор кислоты. Сколько килограммов 52-процентного раствора использовали для получения смеси?
47
Смешав 14-процентный и 30-процентный растворы кислоты и добавив 10 кг чистой воды, получили 11-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?
48
Смешав 40-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 38-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 42-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
49
Смешав 69-процентный и 71-процентный растворы кислоты и добавив 10 кг чистой воды, получили 56-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 66-процентный раствор кислоты. Сколько килограммов 69-процентного раствора использовали для получения смеси?
50
Смешав 46-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 49-процентный раствор кислоты. Сколько килограммов 46-процентного раствора использовали для получения смеси?
51
Смешав 42-процентный и 56-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 42-процентного раствора использовали для получения смеси?
52
Смешав 52-процентный и 94-процентный растворы кислоты и добавив 10 кг чистой воды, получили 72-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 77-процентный раствор кислоты. Сколько килограммов 52-процентного раствора использовали для получения смеси?
53
Смешав 34-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 29-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 34-процентного раствора использовали для получения смеси?
54
Смешав 20-процентный и 25-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
55
Смешав 15-процентный и 25-процентный растворы кислоты и добавив 10 кг чистой воды, получили 15-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
56
Смешав 46-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 38-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 48-процентный раствор кислоты. Сколько килограммов 46-процентного раствора использовали для получения смеси?
57
Смешав 53-процентный и 91-процентный растворы кислоты и добавив 10 кг чистой воды, получили 67-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 71-процентный раствор кислоты. Сколько килограммов 53-процентного раствора использовали для получения смеси?
58
Смешав 6-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 12-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 16-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
59
Смешав 35-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 54-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 35-процентного раствора использовали для получения смеси?
60
Смешав 42-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 42-процентного раствора использовали для получения смеси?
61
Смешав 29-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 29-процентного раствора использовали для получения смеси?
62
Смешав 25-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 28-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 33-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси?
63
Смешав 33-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 33-процентного раствора использовали для получения смеси?
64
Смешав 20-процентный и 25-процентный растворы кислоты и добавив 10 кг чистой воды, получили 13-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 33-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
65
Смешав 19-процентный и 52-процентный растворы кислоты и добавив 10 кг чистой воды, получили 27-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 32-процентный раствор кислоты. Сколько килограммов 19-процентного раствора использовали для получения смеси?
66
Смешав 50-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 64-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 68-процентный раствор кислоты. Сколько килограммов 50-процентного раствора использовали для получения смеси?
67
Смешав 14-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 22-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 42-процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?
68
Смешав 50-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 52-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 50-процентного раствора использовали для получения смеси?
69
Смешав 10-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 35-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 40-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
70
Смешав 41-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 35-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 41-процентного раствора использовали для получения смеси?
71
Смешав 65-процентный и 83-процентный растворы кислоты и добавив 10 кг чистой воды, получили 37-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 62-процентный раствор кислоты. Сколько килограммов 65-процентного раствора использовали для получения смеси?
72
Смешав 61-процентный и 79-процентный растворы кислоты и добавив 10 кг чистой воды, получили 35-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 60-процентный раствор кислоты. Сколько килограммов 61-процентного раствора использовали для получения смеси?
73
Смешав 20-процентный и 68-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
74
Смешав 50-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 54-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 50-процентного раствора использовали для получения смеси?
75
Смешав 32-процентный и 59-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 32-процентного раствора использовали для получения смеси?
76
Смешав 70-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 70-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 74-процентный раствор кислоты. Сколько килограммов 70-процентного раствора использовали для получения смеси?
77
Смешав 2-процентный и 18-процентный растворы кислоты и добавив 10 кг чистой воды, получили 13-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 18-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
78
Смешав 1-процентный и 27-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 15-процентный раствор кислоты. Сколько килограммов 1-процентного раствора использовали для получения смеси?
79
Смешав 17-процентный и 21-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 17-процентного раствора использовали для получения смеси?
80
Смешав 45-процентный и 65-процентный растворы кислоты и добавив 10 кг чистой воды, получили 51-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 55-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
81
Смешав 42-процентный и 69-процентный растворы кислоты и добавив 10 кг чистой воды, получили 57-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 61-процентный раствор кислоты. Сколько килограммов 42-процентного раствора использовали для получения смеси?
82
Смешав 29-процентный и 36-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 29-процентного раствора использовали для получения смеси?
83
Смешав 22-процентный и 23-процентный растворы кислоты и добавив 10 кг чистой воды, получили 18-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 28-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
84
Смешав 22-процентный и 66-процентный растворы кислоты и добавив 10 кг чистой воды, получили 22-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
85
Смешав 40-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 63-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 68-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
86
Смешав 37-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 27-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 37-процентного раствора использовали для получения смеси?
87
Смешав 46-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 59-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 46-процентного раствора использовали для получения смеси?
88
Смешав 33-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 33-процентного раствора использовали для получения смеси?
89
Смешав 32-процентный и 84-процентный растворы кислоты и добавив 10 кг чистой воды, получили 34-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 39-процентный раствор кислоты. Сколько килограммов 32-процентного раствора использовали для получения смеси?
90
Смешав 91-процентный и 93-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 91-процентного раствора использовали для получения смеси?
91
Смешав 5-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 12-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 22-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
92
Смешав 75-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 76-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 81-процентный раствор кислоты. Сколько килограммов 75-процентного раствора использовали для получения смеси?
93
Смешав 31-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 65-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 69-процентный раствор кислоты. Сколько килограммов 31-процентного раствора использовали для получения смеси?
94
Смешав 67-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 65-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 69-процентный раствор кислоты. Сколько килограммов 67-процентного раствора использовали для получения смеси?
95
Смешав 16-процентный и 18-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 16-процентного раствора использовали для получения смеси?
96
Смешав 8-процентный и 14-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
97
Смешав 7-процентный и 49-процентный растворы кислоты и добавив 10 кг чистой воды, получили 35-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 39-процентный раствор кислоты. Сколько килограммов 7-процентного раствора использовали для получения смеси?
98
Смешав 44-процентный и 92-процентный растворы кислоты и добавив 10 кг чистой воды, получили 78-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 83-процентный раствор кислоты. Сколько килограммов 44-процентного раствора использовали для получения смеси?
99
Смешав 35-процентный и 75-процентный растворы кислоты и добавив 10 кг чистой воды, получили 53-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 35-процентного раствора использовали для получения смеси?
100
Смешав 3-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 34-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 44-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
101
Смешав 8-процентный и 20-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
102
Смешав 35-процентный и 73-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 35-процентного раствора использовали для получения смеси?
103
Смешав 35-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 43-процентный раствор кислоты. Сколько килограммов 35-процентного раствора использовали для получения смеси?
104
Смешав 11-процентный и 84-процентный растворы кислоты и добавив 10 кг чистой воды, получили 61-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 66-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?
105
Смешав 60-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 60-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 65-процентный раствор кислоты. Сколько килограммов 60-процентного раствора использовали для получения смеси?
106
Смешав 5-процентный и 15-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
107
Смешав 5-процентный и 32-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 14-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
108
Смешав 71-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 58-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 68-процентный раствор кислоты. Сколько килограммов 71-процентного раствора использовали для получения смеси?
109
Смешав 19-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 19-процентного раствора использовали для получения смеси?
110
Смешав 36-процентный и 73-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 36-процентного раствора использовали для получения смеси?
111
Смешав 78-процентный и 96-процентный растворы кислоты и добавив 10 кг чистой воды, получили 72-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 77-процентный раствор кислоты. Сколько килограммов 78-процентного раствора использовали для получения смеси?
112
Смешав 2-процентный и 44-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
113
Смешав 38-процентный и 47-процентный растворы кислоты и добавив 10 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 44-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?
114
Смешав 14-процентный и 91-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 52-процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?
115
Смешав 26-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 29-процентный раствор кислоты. Сколько килограммов 26-процентного раствора использовали для получения смеси?
116
Смешав 15-процентный и 86-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
117
Смешав 10-процентный и 48-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
118
Смешав 25-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 27-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 31-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси?
119
Смешав 26-процентный и 38-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 38-процентный раствор кислоты. Сколько килограммов 26-процентного раствора использовали для получения смеси?
120
Смешав 15-процентный и 29-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 29-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
121
Смешав 89-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 84-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 89-процентный раствор кислоты. Сколько килограммов 89-процентного раствора использовали для получения смеси?
122
Смешав 18-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 18-процентного раствора использовали для получения смеси?
123
Смешав 27-процентный и 33-процентный растворы кислоты и добавив 10 кг чистой воды, получили 15-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 40-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
124
Смешав 4-процентный и 92-процентный растворы кислоты и добавив 10 кг чистой воды, получили 60-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 4-процентного раствора использовали для получения смеси?
125
Смешав 49-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 69-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 73-процентный раствор кислоты. Сколько килограммов 49-процентного раствора использовали для получения смеси?
126
Смешав 54-процентный и 83-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
127
Смешав 38-процентный и 81-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?
128
Смешав 27-процентный и 91-процентный растворы кислоты и добавив 10 кг чистой воды, получили 28-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 38-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
129
Смешав 22-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 66-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 71-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
130
Смешав 48-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 51-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 48-процентного раствора использовали для получения смеси?
131
Смешав 40-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 45-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
132
Смешав 59-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 39-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 59-процентного раствора использовали для получения смеси?
133
Смешав 8-процентный и 30-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 21-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
134
Смешав 48-процентный и 92-процентный растворы кислоты и добавив 10 кг чистой воды, получили 52-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 48-процентного раствора использовали для получения смеси?
135
Смешав 44-процентный и 77-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 53-процентный раствор кислоты. Сколько килограммов 44-процентного раствора использовали для получения смеси?
136
Смешав 23-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 66-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 70-процентный раствор кислоты. Сколько килограммов 23-процентного раствора использовали для получения смеси?
137
Смешав 22-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 21-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
138
Смешав 3-процентный и 9-процентный растворы кислоты и добавив 10 кг чистой воды, получили 3-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 13-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
139
Смешав 27-процентный и 59-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
140
Смешав 7-процентный и 33-процентный растворы кислоты и добавив 10 кг чистой воды, получили 10-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 7-процентного раствора использовали для получения смеси?
141
Смешав 40-процентный и 53-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
142
Смешав 36-процентный и 39-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 38-процентный раствор кислоты. Сколько килограммов 36-процентного раствора использовали для получения смеси?
143
Смешав 15-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 60-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
144
Смешав 60-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 59-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 60-процентного раствора использовали для получения смеси?
145
Смешав 42-процентный и 58-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 42-процентного раствора использовали для получения смеси?
146
Смешав 6-процентный и 18-процентный растворы кислоты и добавив 10 кг чистой воды, получили 6-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 31-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
147
Смешав 64-процентный и 71-процентный растворы кислоты и добавив 10 кг чистой воды, получили 54-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 64-процентный раствор кислоты. Сколько килограммов 64-процентного раствора использовали для получения смеси?
148
Смешав 57-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 38-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 63-процентный раствор кислоты. Сколько килограммов 57-процентного раствора использовали для получения смеси?
149
Смешав 15-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 18-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 23-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
150
Смешав 91-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 77-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 87-процентный раствор кислоты. Сколько килограммов 91-процентного раствора использовали для получения смеси?
151
Смешав 23-процентный и 81-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 53-процентный раствор кислоты. Сколько килограммов 23-процентного раствора использовали для получения смеси?
152
Смешав 5-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 13-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 23-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
153
Смешав 8-процентный и 51-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 38-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
154
Смешав 36-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 45-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 36-процентного раствора использовали для получения смеси?
155
Смешав 25-процентный и 75-процентный растворы кислоты и добавив 10 кг чистой воды, получили 39-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 43-процентный раствор кислоты. Сколько килограммов 25-процентного раствора использовали для получения смеси?
156
Смешав 9-процентный и 88-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 66-процентный раствор кислоты. Сколько килограммов 9-процентного раствора использовали для получения смеси?
157
Смешав 20-процентный и 40-процентный растворы кислоты и добавив 10 кг чистой воды, получили 34-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 39-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
158
Смешав 15-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 29-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
159
Смешав 17-процентный и 23-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 17-процентного раствора использовали для получения смеси?
160
Смешав 22-процентный и 38-процентный растворы кислоты и добавив 10 кг чистой воды, получили 26-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
161
Смешав 20-процентный и 81-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
162
Смешав 5-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 29-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 49-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
163
Смешав 6-процентный и 18-процентный растворы кислоты и добавив 10 кг чистой воды, получили 12-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 17-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
164
Смешав 60-процентный и 90-процентный растворы кислоты и добавив 10 кг чистой воды, получили 57-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 67-процентный раствор кислоты. Сколько килограммов 60-процентного раствора использовали для получения смеси?
165
Смешав 45-процентный и 95-процентный растворы кислоты и добавив 10 кг чистой воды, получили 37-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
166
Смешав 14-процентный и 38-процентный растворы кислоты и добавив 10 кг чистой воды, получили 21-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?
167
Смешав 56-процентный и 58-процентный растворы кислоты и добавив 10 кг чистой воды, получили 45-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 55-процентный раствор кислоты. Сколько килограммов 56-процентного раствора использовали для получения смеси?
168
Смешав 1-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 4-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 9-процентный раствор кислоты. Сколько килограммов 1-процентного раствора использовали для получения смеси?
169
Смешав 47-процентный и 57-процентный растворы кислоты и добавив 10 кг чистой воды, получили 26-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 47-процентного раствора использовали для получения смеси?
170
Смешав 38-процентный и 47-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?
171
Смешав 8-процентный и 40-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 8-процентного раствора использовали для получения смеси?
172
Смешав 26-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 45-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 26-процентного раствора использовали для получения смеси?
173
Смешав 44-процентный и 68-процентный растворы кислоты и добавив 10 кг чистой воды, получили 54-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 44-процентного раствора использовали для получения смеси?
174
Смешав 10-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
175
Смешав 3-процентный и 36-процентный растворы кислоты и добавив 10 кг чистой воды, получили 15-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
176
Смешав 77-процентный и 79-процентный растворы кислоты и добавив 10 кг чистой воды, получили 70-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 77-процентного раствора использовали для получения смеси?
177
Смешав 27-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 29-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
178
Смешав 18-процентный и 86-процентный растворы кислоты и добавив 10 кг чистой воды, получили 57-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 62-процентный раствор кислоты. Сколько килограммов 18-процентного раствора использовали для получения смеси?
179
Смешав 30-процентный и 66-процентный растворы кислоты и добавив 10 кг чистой воды, получили 24-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 49-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
180
Смешав 24-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
181
Смешав 61-процентный и 99-процентный растворы кислоты и добавив 10 кг чистой воды, получили 40-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 65-процентный раствор кислоты. Сколько килограммов 61-процентного раствора использовали для получения смеси?
182
Смешав 21-процентный и 87-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 40-процентный раствор кислоты. Сколько килограммов 21-процентного раствора использовали для получения смеси?
183
Смешав 22-процентный и 46-процентный растворы кислоты и добавив 10 кг чистой воды, получили 33-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 38-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
184
Смешав 21-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 21-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 21-процентного раствора использовали для получения смеси?
185
Смешав 12-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 48-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 52-процентный раствор кислоты. Сколько килограммов 12-процентного раствора использовали для получения смеси?
186
Смешав 3-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 40-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
187
Смешав 15-процентный и 25-процентный растворы кислоты и добавив 10 кг чистой воды, получили 13-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 23-процентный раствор кислоты. Сколько килограммов 15-процентного раствора использовали для получения смеси?
188
Смешав 68-процентный и 96-процентный растворы кислоты и добавив 10 кг чистой воды, получили 74-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 84-процентный раствор кислоты. Сколько килограммов 68-процентного раствора использовали для получения смеси?
189
Смешав 83-процентный и 94-процентный растворы кислоты и добавив 10 кг чистой воды, получили 52-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 83-процентного раствора использовали для получения смеси?
190
Смешав 3-процентный и 79-процентный растворы кислоты и добавив 10 кг чистой воды, получили 48-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 58-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
191
Смешав 10-процентный и 58-процентный растворы кислоты и добавив 10 кг чистой воды, получили 38-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 42-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
192
Смешав 74-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 71-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 76-процентный раствор кислоты. Сколько килограммов 74-процентного раствора использовали для получения смеси?
193
Смешав 27-процентный и 34-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
194
Смешав 11-процентный и 65-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 53-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?
195
Смешав 4-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 7-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 12-процентный раствор кислоты. Сколько килограммов 4-процентного раствора использовали для получения смеси?
196
Смешав 26-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 26-процентного раствора использовали для получения смеси?
197
Смешав 40-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 35-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
198
Смешав 45-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 37-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
199
Смешав 5-процентный и 55-процентный растворы кислоты и добавив 10 кг чистой воды, получили 7-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 12-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
200
Смешав 37-процентный и 76-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 50-процентный раствор кислоты. Сколько килограммов 37-процентного раствора использовали для получения смеси?
201
Смешав 66-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 64-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 74-процентный раствор кислоты. Сколько килограммов 66-процентного раствора использовали для получения смеси?
202
Смешав 18-процентный и 66-процентный растворы кислоты и добавив 10 кг чистой воды, получили 24-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 34-процентный раствор кислоты. Сколько килограммов 18-процентного раствора использовали для получения смеси?
203
Смешав 47-процентный и 76-процентный растворы кислоты и добавив 10 кг чистой воды, получили 56-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 60-процентный раствор кислоты. Сколько килограммов 47-процентного раствора использовали для получения смеси?
204
Смешав 22-процентный и 39-процентный растворы кислоты и добавив 10 кг чистой воды, получили 30-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 35-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
205
Смешав 60-процентный и 80-процентный растворы кислоты и добавив 10 кг чистой воды, получили 58-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 68-процентный раствор кислоты. Сколько килограммов 60-процентного раствора использовали для получения смеси?
206
Смешав 18-процентный и 26-процентный растворы кислоты и добавив 10 кг чистой воды, получили 16-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 26-процентный раствор кислоты. Сколько килограммов 18-процентного раствора использовали для получения смеси?
207
Смешав 2-процентный и 71-процентный растворы кислоты и добавив 10 кг чистой воды, получили 57-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 62-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
208
Смешав 30-процентный и 98-процентный растворы кислоты и добавив 10 кг чистой воды, получили 58-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 68-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
209
Смешав 47-процентный и 81-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 47-процентного раствора использовали для получения смеси?
210
Смешав 30-процентный и 46-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 44-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
211
Смешав 23-процентный и 44-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 23-процентного раствора использовали для получения смеси?
212
Смешав 18-процентный и 87-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 52-процентный раствор кислоты. Сколько килограммов 18-процентного раствора использовали для получения смеси?
213
Смешав 3-процентный и 56-процентный растворы кислоты и добавив 10 кг чистой воды, получили 8-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 13-процентный раствор кислоты. Сколько килограммов 3-процентного раствора использовали для получения смеси?
214
Смешав 44-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 29-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 44-процентного раствора использовали для получения смеси?
215
Смешав 23-процентный и 64-процентный растворы кислоты и добавив 10 кг чистой воды, получили 43-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 53-процентный раствор кислоты. Сколько килограммов 23-процентного раствора использовали для получения смеси?
216
Смешав 37-процентный и 68-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 52-процентный раствор кислоты. Сколько килограммов 37-процентного раствора использовали для получения смеси?
217
Смешав 2-процентный и 79-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 52-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
218
Смешав 92-процентный и 94-процентный растворы кислоты и добавив 10 кг чистой воды, получили 83-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 88-процентный раствор кислоты. Сколько килограммов 92-процентного раствора использовали для получения смеси?
219
Смешав 43-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 59-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 63-процентный раствор кислоты. Сколько килограммов 43-процентного раствора использовали для получения смеси?
220
Смешав 16-процентный и 58-процентный растворы кислоты и добавив 10 кг чистой воды, получили 27-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 32-процентный раствор кислоты. Сколько килограммов 16-процентного раствора использовали для получения смеси?
221
Смешав 46-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 42-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 46-процентного раствора использовали для получения смеси?
222
Смешав 59-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 55-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 59-процентный раствор кислоты. Сколько килограммов 59-процентного раствора использовали для получения смеси?
223
Смешав 50-процентный и 70-процентный растворы кислоты и добавив 10 кг чистой воды, получили 34-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 50-процентного раствора использовали для получения смеси?
224
Смешав 10-процентный и 34-процентный растворы кислоты и добавив 10 кг чистой воды, получили 15-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 20-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
225
Смешав 26-процентный и 93-процентный растворы кислоты и добавив 10 кг чистой воды, получили 61-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 71-процентный раствор кислоты. Сколько килограммов 26-процентного раствора использовали для получения смеси?
226
Смешав 67-процентный и 89-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 69-процентный раствор кислоты. Сколько килограммов 67-процентного раствора использовали для получения смеси?
227
Смешав 2-процентный и 8-процентный растворы кислоты и добавив 10 кг чистой воды, получили 3-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 8-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
228
Смешав 5-процентный и 10-процентный растворы кислоты и добавив 10 кг чистой воды, получили 4-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
229
Смешав 17-процентный и 54-процентный растворы кислоты и добавив 10 кг чистой воды, получили 21-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 31-процентный раствор кислоты. Сколько килограммов 17-процентного раствора использовали для получения смеси?
230
Смешав 16-процентный и 35-процентный растворы кислоты и добавив 10 кг чистой воды, получили 22-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 27-процентный раствор кислоты. Сколько килограммов 16-процентного раствора использовали для получения смеси?
231
Смешав 91-процентный и 94-процентный растворы кислоты и добавив 10 кг чистой воды, получили 86-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 90-процентный раствор кислоты. Сколько килограммов 91-процентного раствора использовали для получения смеси?
232
Смешав 10-процентный и 14-процентный растворы кислоты и добавив 10 кг чистой воды, получили 11-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 16-процентный раствор кислоты. Сколько килограммов 10-процентного раствора использовали для получения смеси?
233
Смешав 5-процентный и 84-процентный растворы кислоты и добавив 10 кг чистой воды, получили 52-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
234
Смешав 4-процентный и 48-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 4-процентного раствора использовали для получения смеси?
235
Смешав 33-процентный и 82-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 33-процентного раствора использовали для получения смеси?
236
Смешав 57-процентный и 59-процентный растворы кислоты и добавив 10 кг чистой воды, получили 47-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 57-процентный раствор кислоты. Сколько килограммов 57-процентного раствора использовали для получения смеси?
237
Смешав 22-процентный и 43-процентный растворы кислоты и добавив 10 кг чистой воды, получили 32-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 36-процентный раствор кислоты. Сколько килограммов 22-процентного раствора использовали для получения смеси?
238
Смешав 32-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 44-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 48-процентный раствор кислоты. Сколько килограммов 32-процентного раствора использовали для получения смеси?
239
Смешав 2-процентный и 59-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
240
Смешав 20-процентный и 75-процентный растворы кислоты и добавив 10 кг чистой воды, получили 29-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 34-процентный раствор кислоты. Сколько килограммов 20-процентного раствора использовали для получения смеси?
241
Смешав 59-процентный и 73-процентный растворы кислоты и добавив 10 кг чистой воды, получили 58-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 63-процентный раствор кислоты. Сколько килограммов 59-процентного раствора использовали для получения смеси?
242
Смешав 27-процентный и 85-процентный растворы кислоты и добавив 10 кг чистой воды, получили 39-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 49-процентный раствор кислоты. Сколько килограммов 27-процентного раствора использовали для получения смеси?
243
Смешав 24-процентный и 87-процентный растворы кислоты и добавив 10 кг чистой воды, получили 27-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 47-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
244
Смешав 59-процентный и 78-процентный растворы кислоты и добавив 10 кг чистой воды, получили 43-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 63-процентный раствор кислоты. Сколько килограммов 59-процентного раствора использовали для получения смеси?
245
Смешав 2-процентный и 34-процентный растворы кислоты и добавив 10 кг чистой воды, получили 5-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 10-процентный раствор кислоты. Сколько килограммов 2-процентного раствора использовали для получения смеси?
246
Смешав 5-процентный и 57-процентный растворы кислоты и добавив 10 кг чистой воды, получили 15-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 19-процентный раствор кислоты. Сколько килограммов 5-процентного раствора использовали для получения смеси?
247
Смешав 36-процентный и 50-процентный растворы кислоты и добавив 10 кг чистой воды, получили 38-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 43-процентный раствор кислоты. Сколько килограммов 36-процентного раствора использовали для получения смеси?
248
Смешав 40-процентный и 45-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 45-процентный раствор кислоты. Сколько килограммов 40-процентного раствора использовали для получения смеси?
249
Смешав 68-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 64-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 69-процентный раствор кислоты. Сколько килограммов 68-процентного раствора использовали для получения смеси?
250
Смешав 16-процентный и 30-процентный растворы кислоты и добавив 10 кг чистой воды, получили 17-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 27-процентный раствор кислоты. Сколько килограммов 16-процентного раствора использовали для получения смеси?
251
Смешав 24-процентный и 28-процентный растворы кислоты и добавив 10 кг чистой воды, получили 25-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 30-процентный раствор кислоты. Сколько килограммов 24-процентного раствора использовали для получения смеси?
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Возможно, вам нужно заглянут сюда – “Простейшие задачи на проценты”
Задача 1. В сосуд, содержащий литров
-процентного водного раствора некоторого вещества, добавили
литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение: + показать
Задача 2. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством
-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: + показать
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй —
% никеля. Из этих двух сплавов получили третий сплав массой
кг, содержащий
% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение: + показать
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Решение: + показать
Задача 5. Имеются два сосуда. Первый содержит кг, а второй —
кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий
% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий
% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение: + показать
Задача 6. Виноград содержит % влаги, а изюм —
%. Сколько килограммов винограда требуется для получения
килограммов изюма?
Решение: + показать
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на
%, а в 2010 году — на
% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Решение: + показать
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за
рублей.
Решение: + показать
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение: + показать
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео*
Решение: + показать
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на
%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение: + показать
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес
% уставного капитала, Андрей —
рублей, Гриша —
уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли
рублей причитается Коле? Ответ дайте в рублях.
Решение: + показать
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на
рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Решение: + показать
Вы можете пройти Тест по задачам на проценты, сплавы, смеси
Задача на кислоты егэ математика
Задачи на смеси, сплавы и растворы
Рассмотрим смесь (сплав, раствор) из нескольких веществ.
Определение 1. Концентрацией (процентной концентрацией, процентным содержанием) вещества A в смеси (сплаве, растворе) называют число процентов pA, выраженное формулой
Где MA – масса вещества A в смеси (сплаве, растворе), а M – масса всей смеси (сплава, раствора).
Часто в задачах на растворы указаны не массы входящих в них веществ, а их объёмы. В этом случае вместо формулы (1) для концентрации (процентной концентрации, процентного содержания) вещества A в растворе используется формула
Где VA, – объём вещества А в растворе, а V – объем всего раствора.
Определение 2 . Формулу (1) называют формулой для массовой концентрации вещества A в смеси (сплаве, растворе), а формулу (2) – формулой для объёмной концентрации вещества A в растворе.
При решении задач считается, что При слиянии нескольких растворов (сплавов) Масса и объем полученной смеси равны сумме масс и объемов смешиваемых компонентов соответственно.
Приёмы, используемые при решении задач на массовые концентрации смесей (сплавов, растворов), а также при решении задач на объёмные концентрации растворов, являются общими, что мы и увидим при решении следующих типовых задач
Примеры решения задач на смеси, сплавы и растворы
Задача 1 . Смешали 16 литров 30% раствора кислоты в воде с 9 литрами 80% раствора кислоты в воде. Найти концентрацию полученного раствора кислоты в воде.
Решение. В 16 литрах 30% раствора кислоты в воде содержится
Литров кислоты. В 9 литрах 80% раствора кислоты в воде содержится
Литров кислоты. Поэтому в смеси этих растворов содержится
Литров кислоты. Поскольку полученный в результате смешивания раствор имеет объем
Литров, то концентрация кислоты в этом растворе равна
Задача 2 . Имеется 27 килограммов смеси цемента с песком с 40% содержанием цемента. Сколько килограммов песка нужно добавить в эту смесь, чтобы процентное содержание цемента в ней стало 30% ?
Решение. Обозначим буквой x количество килограммов песка, которые нужно добавить в смесь. Поскольку в 27 килограммах смеси с 40% содержанием цемента содержится
Килограммов цемента, а после добавления x килограммов песка масса смеси станет равной
Килограммов, то после добавления песка процентное содержание цемента в получившейся смеси будет составлять
По условию задачи
Ответ. 9 килограммов.
Задача 3 . Смешав 8% и 13% растворы соли и добавив 200 миллилитров 5% раствора соли, получили 7% раствор соли. Если бы вместо 200 миллилитров 5% раствора соли добавили 300 миллилитров 17% раствора соли, то получили бы 15% раствор соли. Сколько миллилитров 8% и 13% растворов соли использовали для получения раствора?
Решение. Обозначив буквой x массу 8% раствора соли, а буквой y – массу 13% раствора соли, рассмотрим рисунки 1 и 2.
На рисунке 1 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 200 миллилитров 9% раствора соли. Объем этого раствора равен (x + y + 200) миллилитров.
На рисунке 2 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 300 миллилитров 17% раствора соли. Объем этого раствора равен (x + y + 300) миллилитров.
Записывая баланс соли в растворе, структура которого изображена на рисунке 1, а также баланс соли в растворе, структура которого изображена на рисунке 2, получим систему из двух уравнений с двумя неизвестными x и y :
Раскрывая скобки и приводя подобные члены, получаем
Ответ. Смешали 70 мл 8% раствора и 55 мл 13% раствора.
Задача 4 . Имеются два сплава меди с цинком. Если сплавить 1 килограмм первого сплава с 2 килограммами второго сплава, то получится сплав с 50% содержанием меди. Если же сплавить 4 килограмма первого сплава с 1 килограммом второго сплава, то получится сплав с 36% содержанием меди. Найти процентное содержание меди в первом и во втором сплавах.
Решение. Обозначим x % и y % — процентные содержания меди в первом и во втором сплавах соответственно и рассмотрим рисунки 3 и 4.
На рисунке 3 изображена структура сплава, состоящего из 1 килограмма первого сплава и 2 килограммов второго сплава. Масса этого сплава – 3 килограмма.
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Записывая баланс меди в сплаве, структура которого изображена на рисунке 3, а также баланс меди в сплаве, структура которого изображена на рисунке 4, получим систему из двух уравнений с двумя неизвестными x и y :
Ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .
Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть раздел нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».
Приемы, используемые для решения задач на выполнение работ, представлены в разделе нашего справочника «Задачи на выполнение работ».
С примерами решения задач на движение можно ознакомиться в разделе нашего справочника «Задачи на движение».
С методами решения систем уравнений можно ознакомиться в разделах нашего справочника «Системы линейных уравнений» , «Системы с нелинейными уравнениями» и в нашем учебном пособии «Системы уравнений».
С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Условие задачи: Имеется два сосуда. Первый содержит 75 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 42% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Поскольку в 27 килограммах смеси с 40 содержанием цемента содержится.
Resolventa. ru
09.03.2018 5:55:16
2018-03-09 05:55:16
Текстовые задачи на растворы, сплавы, смеси. Подготовка к ЕГЭ и ГИА по математике.
Условие задачи: Имеется два сосуда. Первый содержит 75 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 42% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
Ответ. В первом сплаве содержание меди 30% , во втором сплаве содержание меди 60% .
На рисунке 4 изображена структура сплава, состоящего из 4 килограммов первого сплава и 1 килограмма второго сплава. Масса этого сплава – 5 килограммов.
Решаем задание 13 B14 профильного уровня ЕГЭ по математике.
Www. uchportal. ru
08.08.2019 15:26:44
2019-08-08 15:26:44
Задача на кислоты егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 8 № 99578
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть концентрация первого раствора кислоты – а концентрация второго – Если смешать эти растворы кислоты, то получится раствор, содержащий 68% кислоты: Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты: Решим полученную систему уравнений:
На рисунке 2 изображена структура раствора, полученного при смешении x миллилитров 8% раствора соли, y миллилитров 13% раствора соли и 300 миллилитров 17% раствора соли. Объем этого раствора равен (x + y + 300) миллилитров.
Определение 1. Концентрацией (процентной концентрацией, процентным содержанием) вещества A в смеси (сплаве, растворе) называют число процентов pA, выраженное формулой
Если же сплавить 4 килограмма первого сплава с 1 килограммом второго сплава, то получится сплав с 36 содержанием меди.
Ege. sdamgia. ru
15.12.2018 16:52:29
2018-12-15 16:52:29
Источники:
Http://resolventa. ru/spr/algebra/mix. htm
Http://www. uchportal. ru/video/vip/165/egeh_po_matematike_profilnyj_uroven/zadanie_13/reshaem_zadanie_13_b14_profilnogo_urovnja_egeh_po_matematike_urok_5_zadacha_pro_rastvor_kisloty
Http://ege. sdamgia. ru/problem? id=99578
В14 егэ по математике. Текстовые задачи на сплавы, растворы | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; } Задача на кислоты егэ математика
08. Задачи на смеси и сплавы и т. п
Задачи на проценты из вариантов ЕГЭ по математике
Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.
Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за мы принимаем ту величину, с которой сравниваем.
Мы также вывели полезные формулы:
Если величину увеличить на процентов, получим.
Если величину уменьшить на процентов, получим.
Если величину увеличить на процентов, а затем уменьшить на, получим.
Если величину дважды увеличить на процентов, получим
Если величину дважды уменьшить на процентов, получим
Воспользуемся ими для решения задач.
. В году в городском квартале проживало человек. В году, в результате строительства новых домов, число жителей выросло на, а в году — на по сравнению с годом. Сколько человек стало проживать в квартале в году?
По условию, в году число жителей выросло на, то есть стало равно человек.
А в году число жителей выросло на, теперь уже по сравнению с годом. Получаем, что в году в квартале стало проживать жителей.
Следующая задача предлагалась на пробном ЕГЭ по математике в декабре года. Она проста, но справились с ней немногие.
. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили рублей. К вечеру понедельника они подорожали на и стали стоить. Теперь уже эта величина принимается за, и к вечеру вторника акции подешевели на по сравнению этой величиной. Соберем данные в таблицу:
| В понедельник утром | В понедельник вечером | Во вторник вечером |
| Стоимость акций |
По условию, акции в итоге подешевели на.
Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения.
По смыслу задачи, величина положительна.
Получаем, что.
. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил рублей. Его цена два раза уменьшилась на, и теперь она равна
. Четыре рубашки дешевле куртки на. На сколько процентов пять рубашек дороже куртки?
Пусть стоимость рубашки равна, стоимость куртки. Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет от цены куртки, то есть.
Стоимость одной рубашки — в раза меньше:
А стоимость пяти рубашек:
Получили, что пять рубашек на дороже куртки.
. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на. Сколько процентов от общего дохода семьи составляет зарплата жены?
Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась. ») назовем «ситуация » и «ситуация ».
| Муж | Жена | Дочь | Общий доход |
| В реальности | |||
| Ситуация | |||
| Ситуация |
Осталось записать систему уравнений.
Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти, и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму. Получим:
Это значит, что зарплата мужа составляет от общего дохода семьи.
Во втором уравнении мы тоже вычтем из обеих частей выражение, упростим и получим, что
Значит, стипендия дочки составляет от общего дохода семьи. Тогда зарплата жены составляет общего дохода.
А так как проценты уставного капитала Димы и Гриши % и % соответственно, то уставной процент Коли – %.
Стало быть, рубашек составляют % по отношению к цене куртки.
Описание презентации по отдельным слайдам:
Изучить полученное решение, провести критический анализ результата.
Ege-study. ru
18.10.2020 19:21:17
2020-10-18 19:21:17
08. Задачи на смеси и сплавы и т. п.
Задача 1. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
После того, как в сосуд долили литров воды, жидкости стало л, а некоторого вещества – по-прежнему л.
Пусть – процентная доля некоторого вещества в получившемся растворе.
Задача 2. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть – вес первого раствора. В нем некоторого вещества.
Второго раствора по весу взяли столько же, – . В нем того же некоторого вещества.
Тогда в смешанном растворе будет то есть по весу некоторого вещества.
Пусть концентрация получившегося раствора – %, тогда
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй — % никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть кг – масса первого сплава. Тогда согласно условию кг – масса второго сплава.
В первом сплаве кг никеля, во втором – кг никеля.
В новом сплаве кг никеля.
Значит, масса второго сплава – кг, что на кг больше массы первого сплава.
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Пусть вес первого расвора литров. В нем согласно условию л кислоты.
Пусть вес второго раствора литров. В нем согласно условию л кислоты.
При смешивании двух растворов и добавлении 10 л воды, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Рассмотрим второй случай.
При смешивании двух растворов и добавлении л %-го раствора кислоты, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Итак, нам предстоит решить систему уравнений:
Вычитая строки, получаем:
Задача 5. Имеются два сосуда. Первый содержит кг, а второй — кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть % – концентрация кислоты в первом растворе, % – концентрация кислоты во втором растворе.
Пусть вес каждого смешиваемого раствора – кг.
Итак, нам предстоит работать с системой уравнений:
Складывая уравнения системы, получаем:
Тогда в первом растворе содержится кг кислоты.
Задача 6. Виноград содержит % влаги, а изюм — %. Сколько килограммов винограда требуется для получения килограммов изюма?
Обратите внимание! Что очень важно понимать для решения данной задачи?
«Твердая часть винограда» = «твердая часть изюма»!
Начнем с изюма.
Твердая часть винограда (изюма) составляет % веса изюма, то есть
Итак, в изюме массой кг, также как и в винограде, из которого он получен, твердая часть – кг.
Переходим к винограду.
Пусть кг – вес винограда. Твердая часть в винограде занимает % веса, поэтому
Итак, необходимо взять кг винограда (чтобы получить 40 кг изюма) .
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на %, а в 2010 году — на % по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
В 2009 году число жителей составляет % от числа жителей в 2008 году, то есть их столько:
В 2010 году число жителей составляет % от числа жителей в 2009 году, то есть их столько:
Итак, количество жителей в 2010 году есть
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Пусть цена холодильника ежегодно уменьшаетя на процентов.
Тогда через год после выставления на продажу он будет стоить
Еще через год цена на холодильник будет такой:
А поскольку холодильник через два года был продан за рублей, то составим уравнение:
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
1) Пусть в понедельник акции компании подорожали на %, а до повышения цены стоимость акций обозначим за.
Итак, в понедельник цена акций будет составлять % по отношению к стоимости акций до повышения.
Поэтому новая цена акций на понедельник:
2) Вторник. Цена акций будет составлять % по отношению к стоимости акций в понедельник.
Поэтому новая цена акций на вторник:
3) Что мы имеем? На открытие торгов в понедельнки стоимость акций – , во вторник стоимость акций – при этом последняя стоимость акций составляет % от стоимости на открытие торгов. Составим уравнение:
Откуда получаем, что %.
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео *
Согласно условию цена рубашек составляет % по отношению к цене куртки.
А значит, рубашка составляет % по отношению к цене куртки.
Стало быть, рубашек составляют % по отношению к цене куртки.
То есть рубашек дороже куртки на %.
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на %. Сколько процентов от общего дохода семьи составляет зарплата жены?
Пусть зарплата мужа – рублей, жены – , стипендия дочери – .
Тогда общий доход семьи –
Если бы зарплата мужа увеличилась вдвое, то есть стала бы, то общий доход семьи увеличился бы на рублей.
То есть, согласно условию, рублей составляет % от общего дохода семьи (до повышения зарплаты мужа).
Если бы стипендия дочери уменьшилась вдвое, то есть стала бы, то общий доход семьи уменьшился бы на рублей, что соответствует, согласно условию, % от первоначального общего дохода семьи. Значит, стипендия дочери () составляет % от дохода семьи.
Выясним, наконец, сколько процентов от общего дохода семьи составляет зарплата жены:
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес % уставного капитала, Андрей — рублей, Гриша — уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли рублей причитается Коле? Ответ дайте в рублях.
Найдем процент уставного капитала Андрея:
А так как проценты уставного капитала Димы и Гриши % и % соответственно, то уставной процент Коли – %.
А значит, от прибыли в рублей он получит рублей.
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Пусть банковский процент –
Тогда через год клиент А. будет иметь на счету рублей.
Еще через год клиент А. будет иметь на счету рублей.
Клиент В. через год после открытия вклада будет иметь на счету рублей.
Поскольку клиент А. получил на рубля больше клиента Б., составим уравнение:
2-й способ (алгебраический) m1• ω 1 + m2• ω 2 = ω3(m1 + m2 ). Отсюда ω3 = (m1• ω 1 + m2• ω2)/(m1 + m2). В результате находим: ω3 = (150•30 + 250•10)/(150 + 250) = 17,5%. (ω3 – 10)/(30 – ω3) = 150/250. Тогда (30 – ω3)•150 = (ω3 – 10)•250, 4500 – 150ω3 = 250ω3 – 2500, 4500 – 2500 = 250 ω3 – 150 ω3, 7000 = 400 ω3, ω3 = 7000/400 = 17,5%. Ответ. При слиянии взятых растворов получится новый раствор с концентрацией ω3 = 17,5%. 3-й способ (правило креста).
Задачи на смеси и сплавы и т. п.
Задача 1. В сосуд, содержащий литров — процентного водного раствора некоторого вещества, добавили литров воды. Сколько процентов составляет концентрация получившегося раствора?
После того, как в сосуд долили литров воды, жидкости стало л, а некоторого вещества – по-прежнему л.
Пусть – процентная доля некоторого вещества в получившемся растворе.
Задача 2. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пусть – вес первого раствора. В нем некоторого вещества.
Второго раствора по весу взяли столько же, – . В нем того же некоторого вещества.
Тогда в смешанном растворе будет то есть по весу некоторого вещества.
Пусть концентрация получившегося раствора – %, тогда
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй — % никеля. Из этих двух сплавов получили третий сплав массой кг, содержащий % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть кг – масса первого сплава. Тогда согласно условию кг – масса второго сплава.
В первом сплаве кг никеля, во втором – кг никеля.
В новом сплаве кг никеля.
Значит, масса второго сплава – кг, что на кг больше массы первого сплава.
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Пусть вес первого расвора литров. В нем согласно условию л кислоты.
Пусть вес второго раствора литров. В нем согласно условию л кислоты.
При смешивании двух растворов и добавлении 10 л воды, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Рассмотрим второй случай.
При смешивании двух растворов и добавлении л %-го раствора кислоты, мы получим раствор весом л и кислоты в нем будет л.
Посколько в новом растворе % кислоты, то составим уравнение:
Итак, нам предстоит решить систему уравнений:
Вычитая строки, получаем:
Задача 5. Имеются два сосуда. Первый содержит кг, а второй — кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть % – концентрация кислоты в первом растворе, % – концентрация кислоты во втором растворе.
Пусть вес каждого смешиваемого раствора – кг.
Итак, нам предстоит работать с системой уравнений:
Складывая уравнения системы, получаем:
Тогда в первом растворе содержится кг кислоты.
Задача 6. Виноград содержит % влаги, а изюм — %. Сколько килограммов винограда требуется для получения килограммов изюма?
Обратите внимание! Что очень важно понимать для решения данной задачи?
«Твердая часть винограда» = «твердая часть изюма»!
Начнем с изюма.
Твердая часть винограда (изюма) составляет % веса изюма, то есть
Итак, в изюме массой кг, также как и в винограде, из которого он получен, твердая часть – кг.
Переходим к винограду.
Пусть кг – вес винограда. Твердая часть в винограде занимает % веса, поэтому
Итак, необходимо взять кг винограда (чтобы получить 40 кг изюма) .
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на %, а в 2010 году — на % по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
В 2009 году число жителей составляет % от числа жителей в 2008 году, то есть их столько:
В 2010 году число жителей составляет % от числа жителей в 2009 году, то есть их столько:
Итак, количество жителей в 2010 году есть
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за рублей.
Пусть цена холодильника ежегодно уменьшаетя на процентов.
Тогда через год после выставления на продажу он будет стоить
Еще через год цена на холодильник будет такой:
А поскольку холодильник через два года был продан за рублей, то составим уравнение:
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
1) Пусть в понедельник акции компании подорожали на %, а до повышения цены стоимость акций обозначим за.
Итак, в понедельник цена акций будет составлять % по отношению к стоимости акций до повышения.
Поэтому новая цена акций на понедельник:
2) Вторник. Цена акций будет составлять % по отношению к стоимости акций в понедельник.
Поэтому новая цена акций на вторник:
3) Что мы имеем? На открытие торгов в понедельнки стоимость акций – , во вторник стоимость акций – при этом последняя стоимость акций составляет % от стоимости на открытие торгов. Составим уравнение:
Откуда получаем, что %.
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео *
Согласно условию цена рубашек составляет % по отношению к цене куртки.
А значит, рубашка составляет % по отношению к цене куртки.
Стало быть, рубашек составляют % по отношению к цене куртки.
То есть рубашек дороже куртки на %.
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на %. Сколько процентов от общего дохода семьи составляет зарплата жены?
Пусть зарплата мужа – рублей, жены – , стипендия дочери – .
Тогда общий доход семьи –
Если бы зарплата мужа увеличилась вдвое, то есть стала бы, то общий доход семьи увеличился бы на рублей.
То есть, согласно условию, рублей составляет % от общего дохода семьи (до повышения зарплаты мужа).
Если бы стипендия дочери уменьшилась вдвое, то есть стала бы, то общий доход семьи уменьшился бы на рублей, что соответствует, согласно условию, % от первоначального общего дохода семьи. Значит, стипендия дочери () составляет % от дохода семьи.
Выясним, наконец, сколько процентов от общего дохода семьи составляет зарплата жены:
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес % уставного капитала, Андрей — рублей, Гриша — уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли рублей причитается Коле? Ответ дайте в рублях.
Найдем процент уставного капитала Андрея:
А так как проценты уставного капитала Димы и Гриши % и % соответственно, то уставной процент Коли – %.
А значит, от прибыли в рублей он получит рублей.
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Пусть банковский процент –
Тогда через год клиент А. будет иметь на счету рублей.
Еще через год клиент А. будет иметь на счету рублей.
Клиент В. через год после открытия вклада будет иметь на счету рублей.
Поскольку клиент А. получил на рубля больше клиента Б., составим уравнение:
2. Объясните значение высказываний: а) Концентрация раствора 23 %; (В 100 г раствора содержится 23 г вещества). б) Молоко имеет 1,8 % жирности; (В100 г молока содержится 1,8 г жира). в) Сколько сахара содержится в 200 г 10%–сахарного сиропа? Теперь давайте попробуем решить устно несколько задач. 3. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора? (1: 5 ·100 = 20 %) 4. Килограмм соли растворили в 9 л воды. Какова концентрация раствора?
В нем согласно условию л кислоты.
Egemaximum. ru
23.05.2018 17:15:42
2018-05-23 17:15:42
Решение задач по математике на тему «Задачи на кислоты»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Международный конкурс по экологии «Экология России»
Доступно для всех учеников 1-11 классов и дошкольников
Описание презентации по отдельным слайдам:
Подробнее рассмотрим задачи на концентрации растворов и на процентное содержание, то есть на смеси. Понятие концентрации и процентного содержания одного вещества в другом. Пусть смесь состоит из m1 и m2 массы первого и второго веществ. Тогда в этой смеси: С1= m1 m1+m2 — массовая концентрация первого в-ва С2= m2 m1+m2 — массовая концентрация второго в-ва т. о., массовая концентрация данного в-ва в смеси выражает количество частей массы, приходящихся на данное в-во в смеси. При этом количество частей массы всей смеси принято за единицу, так как сумма концентраций всех компонентов смеси равна единице: С1+ С2= m1 + m2 =1 m1+m2 m1+m2
Аналогично понятию массовой концентрации вводится понятие объёмной концентрации, если массы входящих в смесь в-в заменить на объёмы. При слиянии двух растворов, имеющих объёмы V1 и V2, получается смесь, объём которой равен V1+V2, т. е. V= V1+V2, Отношение объема чистой компоненты (VA) в растворе ко всему объему смеси (V): cA= = ; называется объёмной концентрацией этой компоненты.
Наконец, отметим, что в элементарных математических задачах на смеси предполагается, что смешиваемые вещества не вступают в химическую реакцию, так что, если m1 и m2 – массы смешиваемых в-в, то масса смеси m= m1 +m2 .
Концентрацию вещества в смеси можно выразить в процентах. Считая, что вся смесь составляет 100%,заключаем, что процентное содержание первого и второго веществ равны соответственно: Р1=С1*100%, Р2=С2*100%, при этом Р1+Р2=(С1+ С2)*100%=100%.
2. Объясните значение высказываний: а) Концентрация раствора 23 %; (В 100 г раствора содержится 23 г вещества). б) Молоко имеет 1,8 % жирности; (В100 г молока содержится 1,8 г жира). в) Сколько сахара содержится в 200 г 10%–сахарного сиропа? Теперь давайте попробуем решить устно несколько задач. 3. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора? (1: 5 ·100 = 20 %) 4. Килограмм соли растворили в 9 л воды. Какова концентрация раствора?
Алгоритм решения задачи на сплавы, растворы и смеси: Изучить условия задачи. Выбрать неизвестные величины (их обозначают буквами х, у и т. д.), относительно которых составить пропорции, этим, мы создаем математическую модель ситуации, описанной в условии задачи. Используя условия задачи, определить все взаимосвязи между данными величинами. Составить математическую модель задачи и решить ее. Изучить полученное решение, провести критический анализ результата
Можно воспользоваться диагональной схемой В этой схеме а и b — концентрации исходных растворов, с — требуемая концентрация кислоты в процентах, а — записаны их разности (b — с) и (с — а), соответствующие отношению масс растворов а и b.
Правило креста ЗАДАЧА 1 Определите концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10%-го растворов какой-либо соли. Дано: m1 = 150 г, m2 = 250 г, ω 1 = 30%, ω 2 = 10%. Найти: ω 3.
Решение 1-й способ (метод пропорций). Общая масса раствора: m3 = m1 + m2 = 150 + 250 = 400 г. Массу вещества в первом растворе находим методом пропорций, исходя из определения: процентная концентрация раствора показывает, сколько граммов растворенного вещества находится в 100 г раствора: 100 г 30%-го р-ра – 30 г в-ва, 150 г 30%-го р-ра – х г в-ва, х = 1,5•30 = 45 г. Для второго раствора составляем аналогичную пропорцию: 100 г 10%-го р-ра – 10 г в-ва, 250 г 10%-го р-ра – y г в-ва, y = 2,5•10 = 25 г. Следовательно, 400 г нового раствора содержит 45 + 25 = 70 г растворенного вещества. Теперь можно определить концентрацию нового раствора: 400 г р-ра – 70 г в-ва, 100 г р-ра – х г в-ва, х = 70/400 • 100 = 17,5 г, или 17,5%.
2-й способ (алгебраический) m1• ω 1 + m2• ω 2 = ω3(m1 + m2 ). Отсюда ω3 = (m1• ω 1 + m2• ω2)/(m1 + m2). В результате находим: ω3 = (150•30 + 250•10)/(150 + 250) = 17,5%. (ω3 – 10)/(30 – ω3) = 150/250. Тогда (30 – ω3)•150 = (ω3 – 10)•250, 4500 – 150ω3 = 250ω3 – 2500, 4500 – 2500 = 250 ω3 – 150 ω3, 7000 = 400 ω3, ω3 = 7000/400 = 17,5%. Ответ. При слиянии взятых растворов получится новый раствор с концентрацией ω3 = 17,5%. 3-й способ (правило креста).
Теперь решим задачи посложнее ЗАДАЧА 2 Определите, сколько нужно взять 10%-го раствора соли и 30%-го раствора этой же соли для приготовления 500 г 20%-го раствора. Дано: ω1 = 10%,ω 2 = 30%, ω 3 = 20%,m3 = 500 г. Найти: m1, m2. Решение Используем правило креста. Для приготовления 500 г 20%-го раствора соли нужно взять по 10 частей растворов исходных концентраций Ответ. Для приготовления 500 г 20%-го раствора нужно взять исходные растворы по 250 г (m1 = 250 г, m2 = 250 г).
ЗАДАЧА 3 Определите, сколько нужно взять растворов соли 60%-й и 10%-й концентраций для приготовления 300 г раствора 25%-й концентрации. Дано: ω 1 = 60%, ω 2 = 10%, ω 3 = 25%, m3 = 300 г. Найти: m1, m2. Решение Масса одной части: 300/50 = 6 г. Тогда m1 = 6•15 = 90 г, m2 = 6•35 = 210 г. Проверим правильность решения. 100 г 60%-го р-ра – 60 г соли,90 г 60%-го р-ра – х г соли, х = 54 г. 100 г 10%-го р-ра – 10 г соли, 210 г 30%-го р-ра – y г соли, y = 21 г. m(соли) = 54 + 21 = 75 г. Находим концентрацию нового раствора: 300 г р-ра – 75 г соли, 100 г р-ра – z г соли, z = 100•75/300 = 25 г, или 25%. Ответ. m1 = 90 г, m2 = 210 г.
Правило креста можно применять и в тех случаях, когда нужно получить раствор меньшей концентрации путем разбавления водой более концентрированного раствора или получить более концентрированный раствор путем добавления к исходному раствору сухой смеси. Рассмотрим это на примерах ЗАДАЧА 5 Сколько воды нужно добавить к 250 г раствора соли для понижения его концентрации с 45% до 10%? Дано: ω1 = 45%, ω3 = 10%, m1 = 250 г. Найти: m2. Решение Принимаем, что концентрация для добавляемой воды – ω2 = 0%. Используем правило креста. Определяем массу одной части через первый раствор: 250/10 = 25 г. Тогда масса необходимой воды равна: m2 = 25•35 = 875 г.
ЗАДАЧА 6 Сколько сухой соли нужно добавить к 250 г раствора 10%-й концентрации для ее увеличения до 45%? Дано: ω 1 = 10%, m1 = 250 г, ω 3 = 45%. Найти: m(с. с.). Решение Принимаем, что сухая соль – это раствор с ω2 = 100%. Используем правило креста. Определяем массу одной части через первый раствор: 250/55 = 4,5 г. Определяем массу сухой соли: m(с. с.) = 4,5•35 = 158 г. Ответ. m(с. с.) = 158 г.
Рассмотрим несколько задач: Задача №1 Сколько воды надо добавить в 1 л раствора, содержащего 96% спирта, чтобы получить раствор с содержанием спирта 40 %? Решение: 1 л раствора, в котором содержится 96% спирта содержит этого спирта 1* 0,96=0,96 л. Это же количество спирта должны содержать и х л раствора с содержанием спирта 40%. Следовательно, 0,96= х *0,4, х=2,4 л, и надо добавить 2,4 – 1 = 1,4 л. Ответ: 1,4 л.
Задача №2 Процент содержания меди в первом сплаве на 40% меньше, чем во втором сплаве. После того, как эти слитки сплавили вместе, получили новый сплав с содержанием меди 30%.Определить процентное содержание меди в первоначальных сплавах, если в первом сплаве меди было 6 кг, а во втором 12 кг. Решение: Пусть х процентов меди содержалось в первом сплаве, тогда х + 40 процентов её содержалось во втором. В первом сплаве меди было 6 кг, а во втором 12кг, следовательно,1% первого и второго сплавов имели массы 6:х и 12 :(х + 40)кг соответственно. Поскольку каждый сплав составляет 100%, то их массы будут М1=600:х кг и М2=1200:(х+40) соответственно.
Новый сплав содержит меди то же количество, которое было до сплавления в двух слитках, т. е. 6+12=18 кг. Это по условию задачи составляет 36% нового сплава, поэтому масса нового сплава есть: 18:36*100=50 кг. Масса нового сплава состоит из масс двух старых сплавов, так что: 50=М1+М2=(600:х)+ 1200:(х+40) 1= (12:х)+ 24:(х+40). Решая полученное уравнение, находим х1=20, х2=-24. Так как х>0,то х=20. Следовательно, в первоначальных сплавах было 20 и 20+40=60 процентов меди. Ответ:20%, 60%
Задача 2. Смешали некоторое количество — процентного раствора некоторого вещества с таким же количеством — процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
А значит, от прибыли в рублей он получит рублей.
M1 90 г, m2 210 г.
Infourok. ru
30.07.2020 13:44:22
2020-07-30 13:44:22
Источники:
Http://ege-study. ru/ru/ege/materialy/matematika/zadachi-ege-na-procenti/
Http://egemaximum. ru/13-zadachi-na-smesi-i-splavy/
Http://infourok. ru/reshenie-zadach-po-matematike-na-temu-zadachi-na-kisloti-769183.html
Задачи на растворы, смеси и сплавы с решениями | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; } Задача на кислоты егэ математика
Задачи на растворы, смеси и сплавы
Задачи ОГЭ на проценты, сплавы и смеси
Решение текстовых задач на проценты, смеси и сплавы при подготовке к ОГЭ и ЕГЭ по математике. Методические рекомендации и практические задания.
Для демоверсии ОГЭ 2021 года это задание №21, для демоверсии ЕГЭ — №11. В материале рассмотрены решение нескольких задач и предложены задания для самостоятельного решения.
Автор: Колесник Марина Анатольевна
Из демоверсии ЕГЭ:
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты.
Сколько килограммов 45-процентного раствора использовали для получения смеси?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
Так как в итоге жира оказалось (dfrac cdot 5 = 0,23) литра, то:
Blacktriangleright Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Vpr-ege. ru
27.06.2017 14:22:45
2017-06-27 14:22:45
Задачи на растворы, смеси и сплавы
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfracx) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac cdot 4 = 1,3) литра, то:
[dfracx + dfrac(4 — x) = 1,3,] откуда находим (x = 1,5) .
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac(x + 300)) грамм – масса кислорода в первом газе,
(dfracx) грамм – масса кислорода во втором газе,
Тогда масса кислорода в третьем газе составляет (dfrac(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac(x + 300) + dfracx = dfrac(2x + 300),] откуда находим (x = 600) . Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%) . В итоге у него получилось 5 литров молока жирностью (4,6%) . Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfracx) – объём жира в молоке жирностью (2,5%) , (dfrac(5 — x)) – объём жира в молоке жирностью (6%) .
Так как в итоге жира оказалось (dfrac cdot 5 = 0,23) литра, то:
(dfracx + dfrac(5 — x) = 0,23) , откуда находим (x = 2) .
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100 (%) . До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac cdot 100% = 18,4%.]
Во сколько раз больше должен быть объём (5) — процентного раствора кислоты, чем объём (10) — процентного раствора той же кислоты, чтобы при смешивании получить (7) — процентный раствор?
Пусть объём (5) — процентного раствора кислоты равен (x) литров, а объём (10) — процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac) при условии [0,05x + 0,1y = 0,07(x + y) qquadLeftrightarrowqquad dfrac = dfrac = 1,5,,] таким образом, ответ: (1,5) .
Во сколько раз больше должен быть объём (20) — процентного раствора кислоты, чем объём (14) — процентного раствора той же кислоты, чтобы при смешивании получить (18) — процентный раствор?
Пусть объём (20) — процентного раствора кислоты равен (x) литров, а объём (14) — процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac) при условии [0,2x + 0,14y = 0,18(x + y) qquadLeftrightarrowqquad dfrac = 2,,] таким образом, ответ: (2) .
Смешав (25) — процентный и (95) — процентный растворы кислоты и добавив (20) кг чистой воды, получили (40) — процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30) — процентного раствора той же кислоты, то получили бы (50) — процентный раствор кислоты. Сколько килограммов (25) — процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25) — процентным содержанием кислоты, (y) кг – масса раствора с (95) — процентным содержанием кислоты. Составим схему, описывающую получение (40) — процентного раствора:

Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfraccdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
Аналогично составим схему, описывающую получение (50) — процентного раствора:

Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
Таким образом, решив систему из полученных двух уравнений, найдем (x) . Для этого можно умножить оба уравнения на (100) , чтобы сделать их проще на вид:
[begin 25x+95y+0=40(x+y+20)\ 25x+95y+30cdot 20=50(x+y+20) end]
Вычтем из второго уравнения первое и получим новую систему:
[begin &begin 25x+95y=40(x+y+20)\ 30cdot 20=10(x+y+20) end quad Rightarrow quad begin 5x+19y=8(x+y+20)\ y=40-x end quad Rightarrow \[2ex] Rightarrow quad &begin 3x-11(40-x)+160=0\ y=40-x end quad Rightarrow quad begin x=20\y=20end end]
Теперь у нас достаточно данных, чтобы составить первое уравнение системы. (Поскольку у нас две неизвестных величины, мы должны составить два уравнения.)
Задание B13 (№ 99577)
Dfrac x 300 dfracx dfrac 2x 300 , откуда находим x 600.
Shkolkovo. net
05.04.2018 1:19:58
2018-04-05 01:19:58
Задача на растворы. Задание В13
Я уже объясняла принцип решения задач на растворы здесь. В этой статье я приведу пример решения чуть более сложной задачи.
Решим задачу: из Открытого банка заданий для подготовки к ЕГЭ по математике:
Задание B13 (№ 99577)
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Вспомним, что процентное содержание выражается формулой: >*100% » />. В этой формуле
Р — процентное содержание;
M — масса чистого вещества;
M — масса раствора или сплава.

Чтобы решить эту задачу, составим таблицу:
Поскольку в задаче не дана масса каждого раствора, примем массу первого раствора за, а второго за, и, исходя из этого, найдем массу чистого вещества в каждом растворе:
Теперь будем заносить в таблицу все действия, которые описаны в условии задачи. По условию в раствор добавили 10 кг чистой воды. При этом масса раствора увеличилась на 10 кг, а масса чистого вещества не изменилась. В результате получили 36-процентный раствор кислоты:
Теперь у нас достаточно данных, чтобы составить первое уравнение системы. (Поскольку у нас две неизвестных величины, мы должны составить два уравнения.)
/>*100=36″ />
Читаем условие дальше:
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты. Добавляем в таблицу эти данные:
То получили бы 41-процентный раствор кислоты:
Можем записать второе уравнение системы:
/>*100=41″ />
Получили систему уравнений:
/>*100=36> />*100=41> >>< >» />
>>< >» />
>>< >» />
>>< >» />
>>< >» />
>>< >» />
>>< >» />
В ответе нужно записать, сколько килограммов 30-процентного раствора использовали для получения смеси, то есть х.
Для демоверсии ОГЭ 2021 года это задание №21, для демоверсии ЕГЭ — №11. В материале рассмотрены решение нескольких задач и предложены задания для самостоятельного решения.
Вспомним, что процентное содержание выражается формулой: >*100% » />. В этой формуле
Методические рекомендации и практические задания.
Ege-ok. ru
04.09.2019 10:51:26
2017-02-21 20:22:53
Источники:
Http://vpr-ege. ru/oge/matematika/1102-zadachi-oge-na-protsenty-splavy-i-smesi
Http://shkolkovo. net/catalog/syuzhetnye_tekstovye_zadachi/na_rastvory_smesi_i_splavy
Http://ege-ok. ru/2012/03/16/zadacha-na-rastvoryi-zadanie-v13
Тренажер задания 8 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 8 — текстовые задачи на концентрации (смеси и сплавы). Это задание на применение математических знаний при решении текстовых задач. Номер заданий соответствует номеру заданий в базе mathege.ru.
Задачи на концентрации (смеси и сплавы)
99571 В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
99572 Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
99573 Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
99574 Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
99575 Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
99576 Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
99577 Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
109213 Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
99578 Имеется два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?