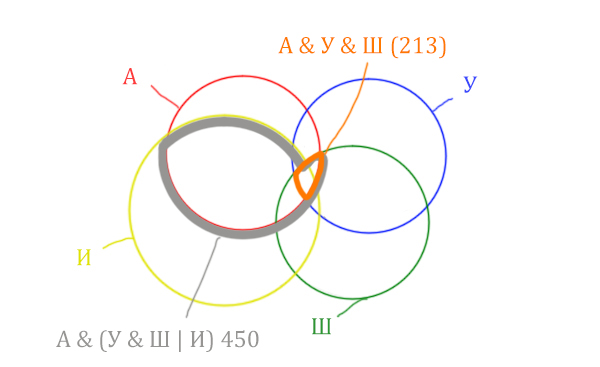Задачи с кругами эйлера егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Ключевое слово	Найдено страниц
сканер	200
принтер	250
монитор	450

Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор»  — 40, а по запросу «сканер & монитор»  — 50.

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Запрос	Количество страниц (тыс.)
торты \| пироги	12000
торты & пироги	6500
пироги	7700

Сколько страниц (в тысячах) будет найдено по запросу торты

Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Ключевое слово	Количество сайтов,для которых данное слово является ключевым
принтеры	400
сканеры	300
мониторы	500

Сколько сайтов будет найдено по запросу (принтеры | мониторы) & сканеры

если по запросу принтеры | сканеры было найдено 600 сайтов,

по запросу принтеры | мониторы – 900,

а по запросу сканеры | мониторы – 750.

Запрос	Найдено страниц (в тысячах)
Лебедь & (Рак \| Щука)	320
Лебедь & Рак	200
Лебедь & Рак & Щука	50

Какое количество страниц (в тысячах) будет найдено по запросу

Лебедь & Щука

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пекин & (Москва \| Токио)	338
Пекин & Москва	204
Пекин & Москва & Токио	50

Какое количество страниц (в тысячах) будет найдено по запросу Пекин & Токио?

Пройти тестирование по этим заданиям

Источник

Сегодня разберём задачи на круги Эйлера в информатике.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

Задача (Простая)

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин \| Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.

Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.

Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?

Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.

Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».

В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».

Отсюда получается:

Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.

Это и будет ответ!

Теперь решим эту задачу с помощью Кругов Эйлера!

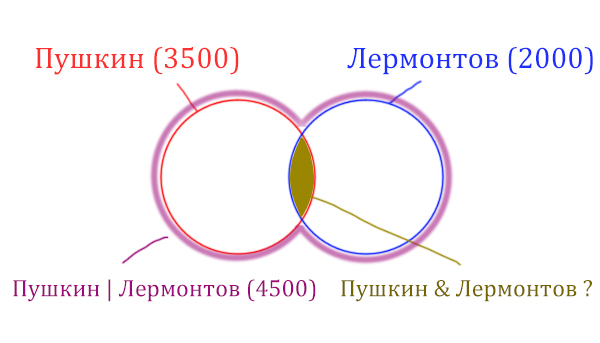
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.

Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

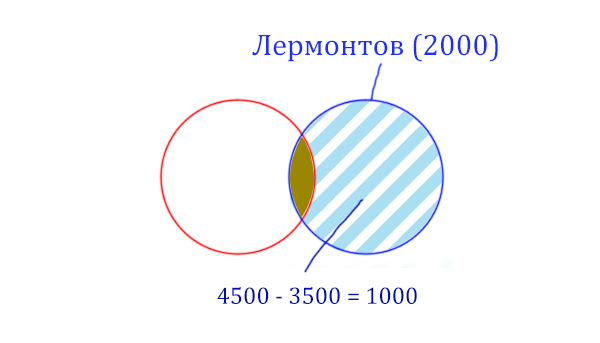
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

Рассмотрим ещё одну не сложную разминочную задачу.

Задача (Разминочная)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Кокос \| Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Решение:

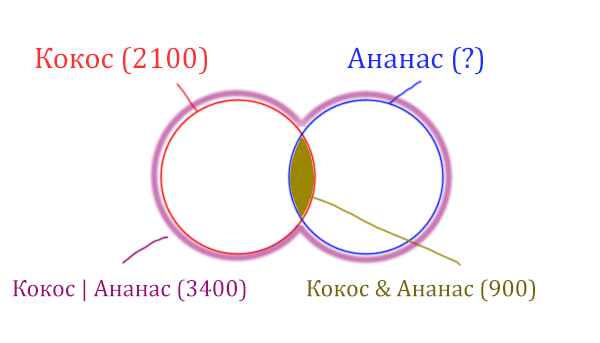
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть красного круга.

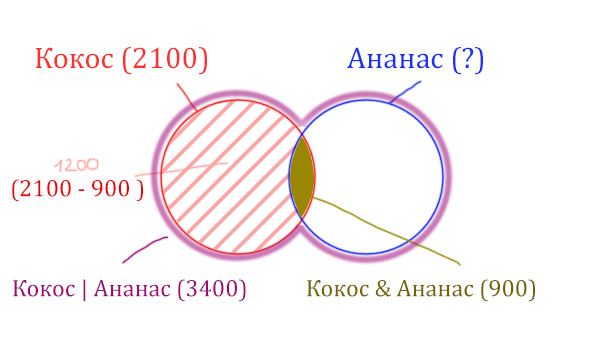
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 — 1200 = 2200

Ответ: 2200

Разберём классическую задачу из информатики по кругам Эйлера.

Задача (Классическая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
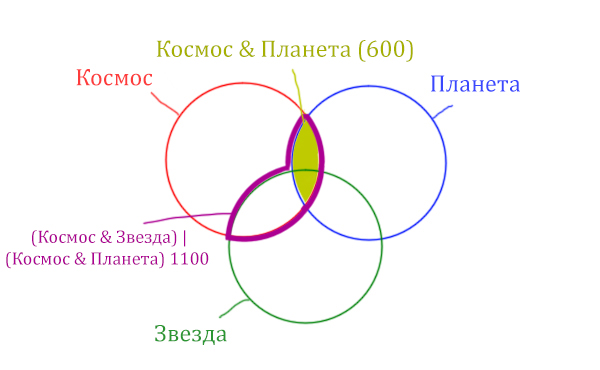
(Космос & Звезда) \| (Космос & Планета)	1100
Космос & Планета	600
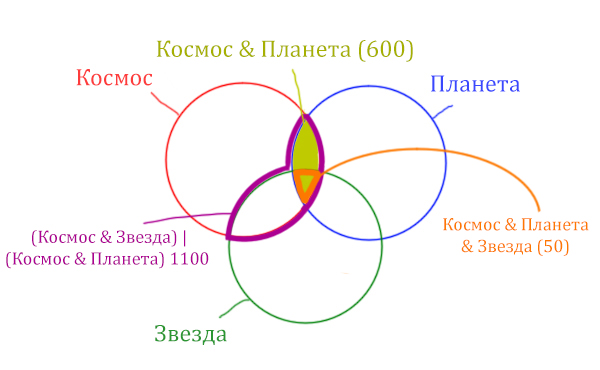
Космос & Планета & Звезда	50

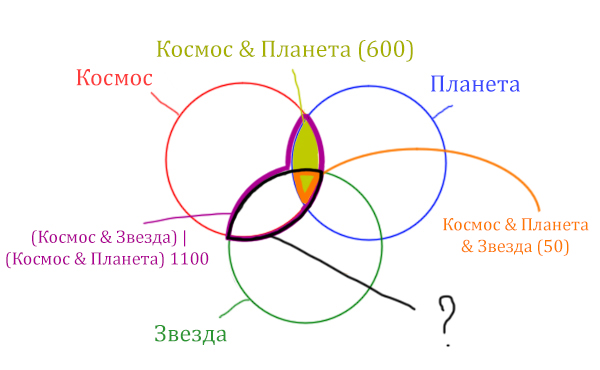
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?

Решение:

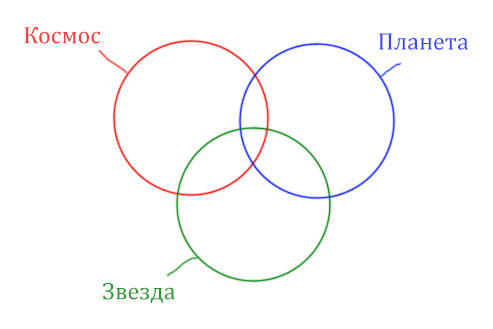
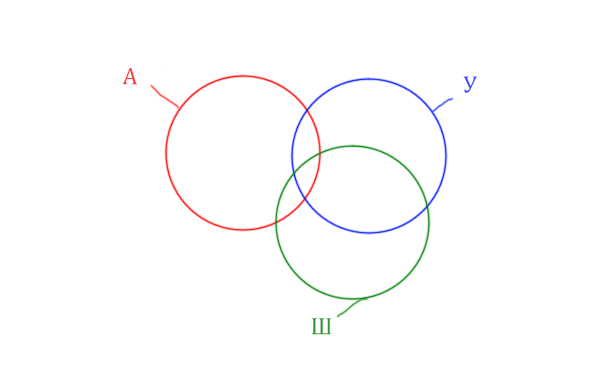
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».

Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

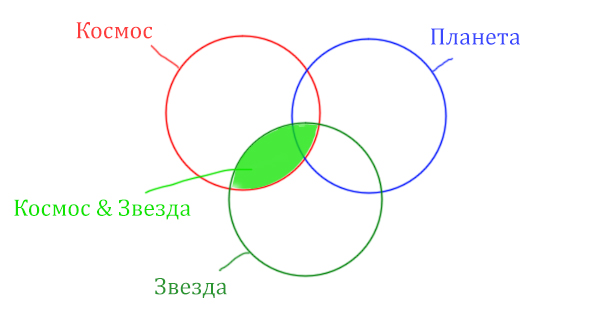
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

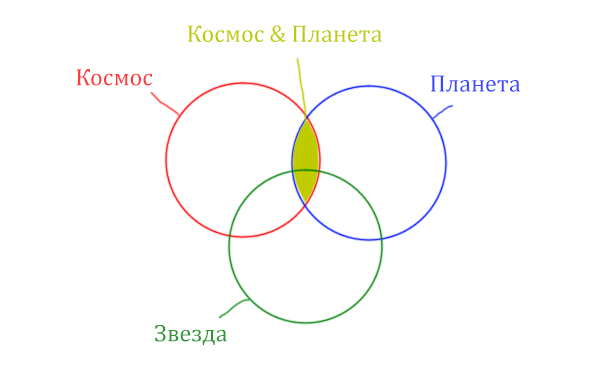
Теперь отметим вторую скобку Космос & Планета.

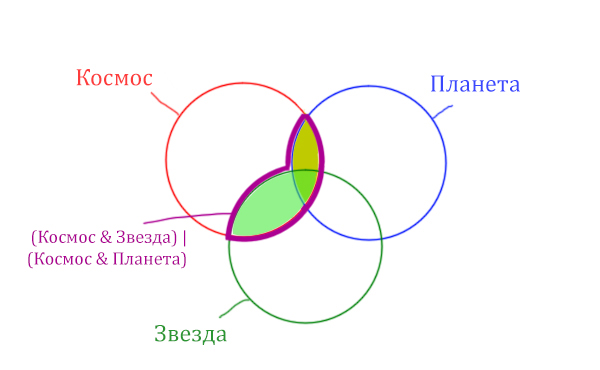
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.

Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

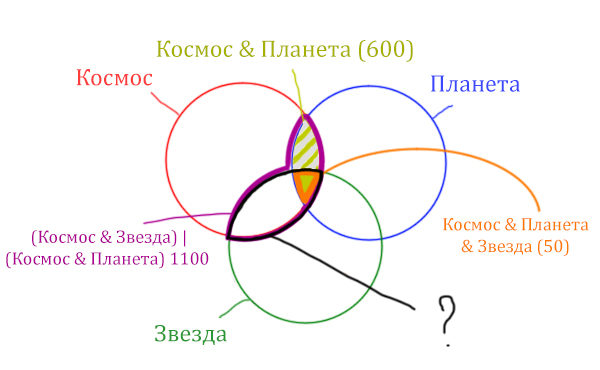
Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

Количество страниц в заштрихованной части = 600 — 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550

Ответ: 550

Закрепляем материал по задачам на Круги Эйлера.

Задача (На закрепление)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
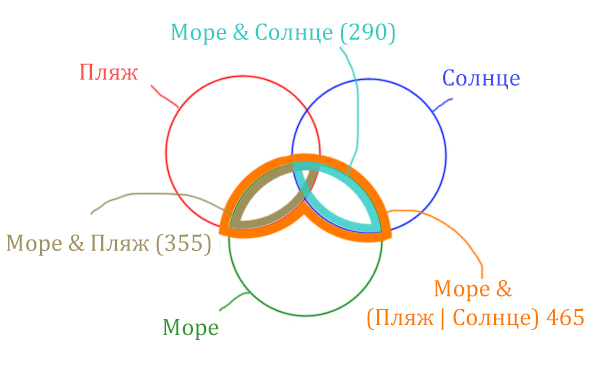
Море & (Пляж \| Солнце)	465

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

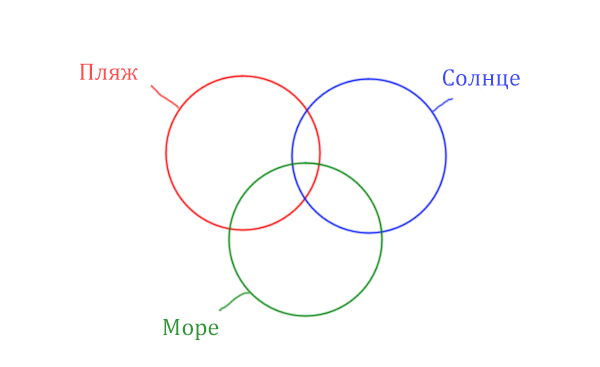
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

Отметим все области для которых нам даны количество страниц.

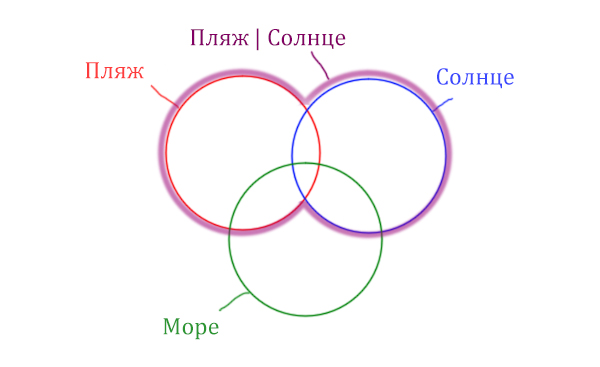
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

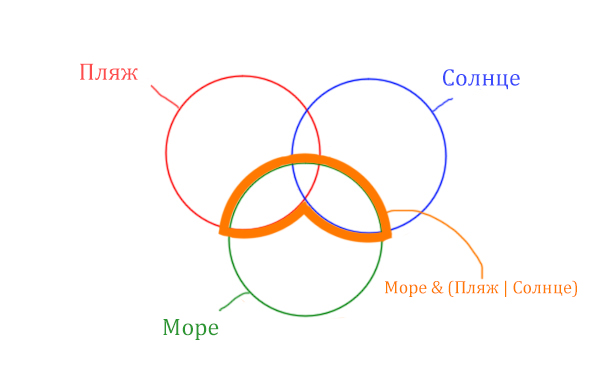
Теперь отметим Море & Пляж.

Теперь отметим Море & Солнце.

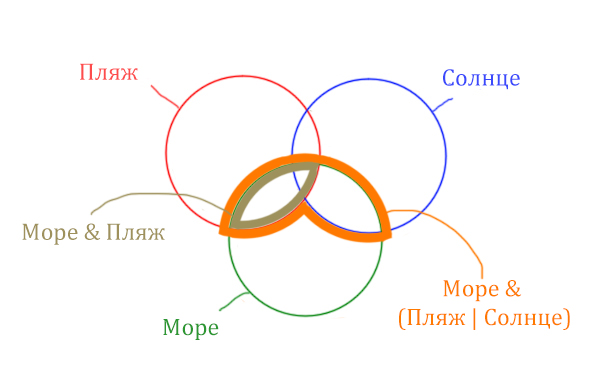
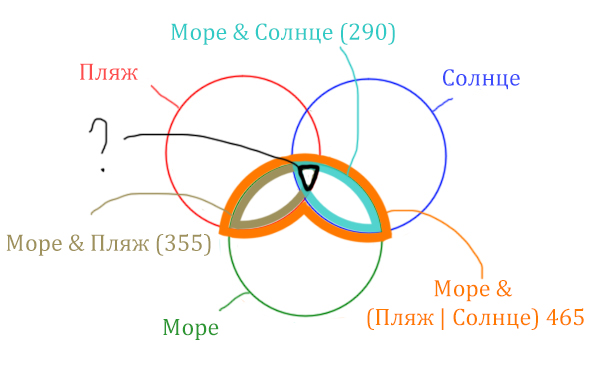
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

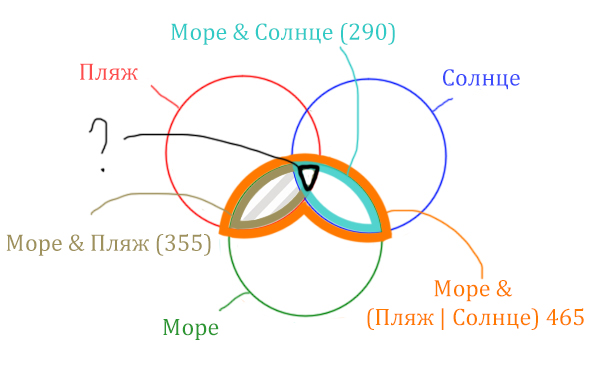
Найдём заштрихованную область!

Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).

Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180

Ответ: 180

Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.

Задача (с 4 сущностями)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия \| Ирландия)	450
Англия & Уэльс & Шотландия	213
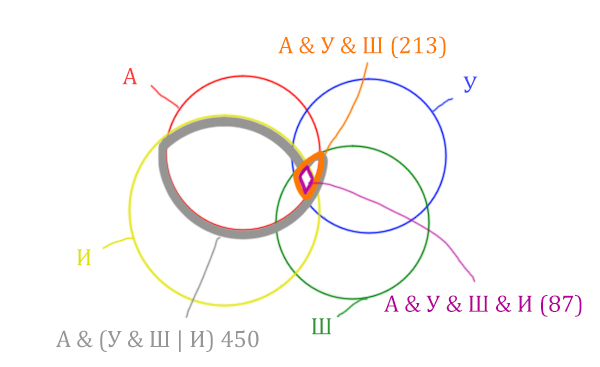
Англия & Уэльс & Шотландия & Ирландия	87

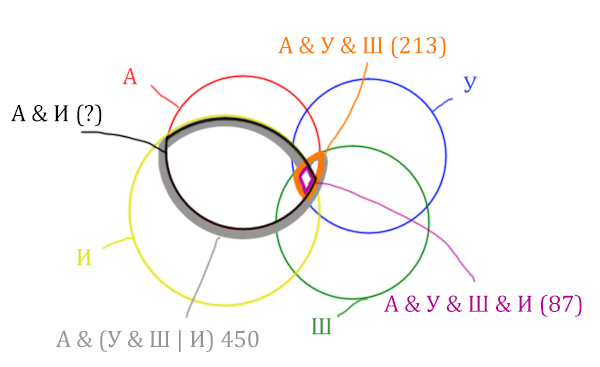
Какое количество страниц (в тысячах) будет найдено по запросу

Англия & Ирландия?

Решение:

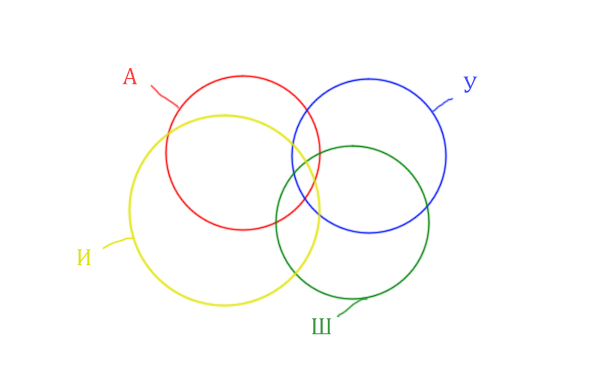
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

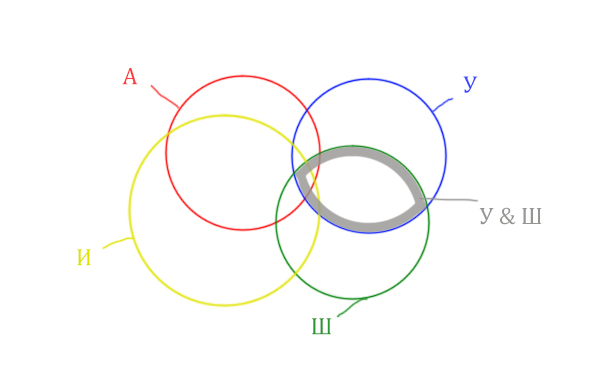
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

Область Уэльс & Шотландия выглядит так:

Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

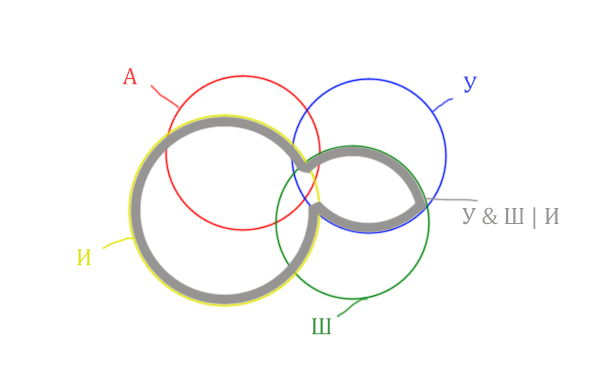
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

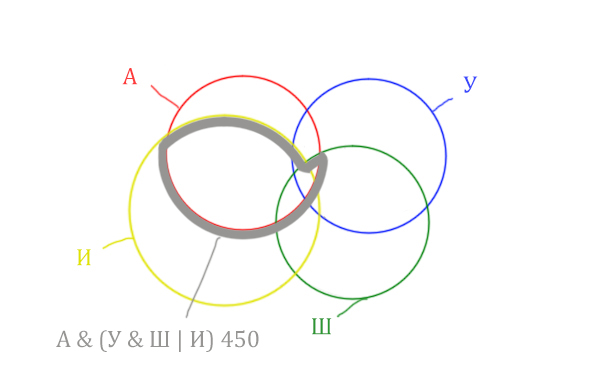
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

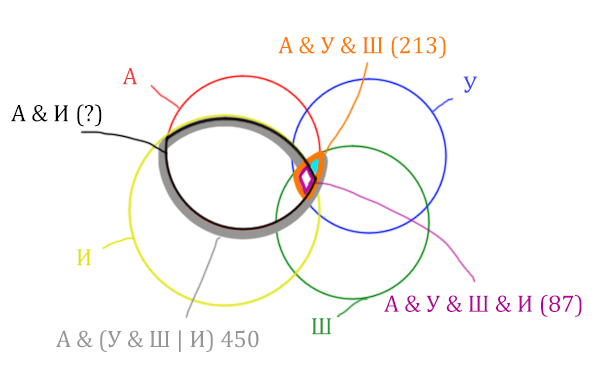
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =

450 — 126 = 324

Это и будет ответ!

Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

Сколько страниц (в тысячах) будет найдено по запросу

Суфле | Корзина | Эклер

Решение:

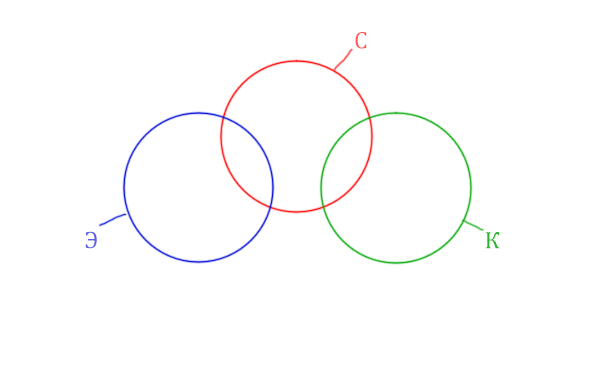
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.

Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

Отметим всё, что нам дано в условии.

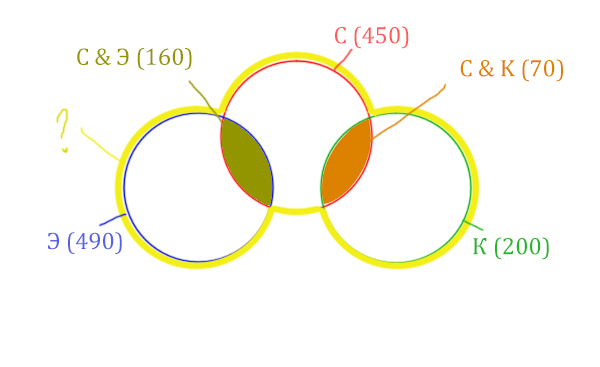
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

Левая заштрихованная область находится просто:

Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330

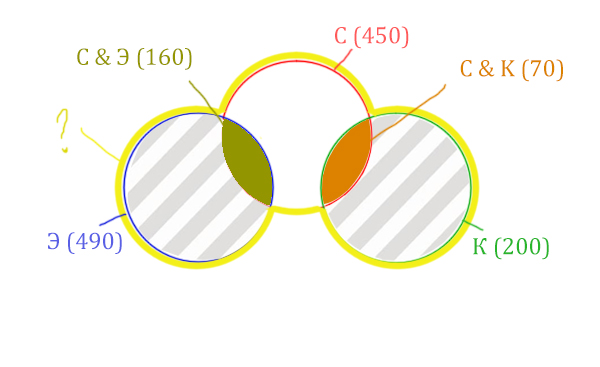
Так же найдём площадь правой заштрихованной области:

Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130

Теперь можно найти искомую жёлтую область

Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910

Задача решена, можно писать ответ.

Ответ: 910

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
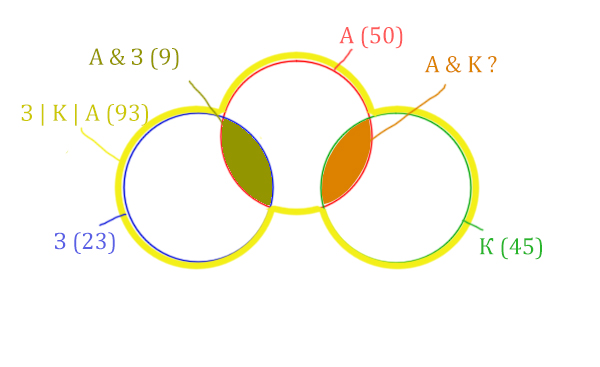
Заря \| Крейсер \| Аврора	93

Сколько страниц (в тысячах) будет найдено по запросу

Аврора & Крейсер

Решение:

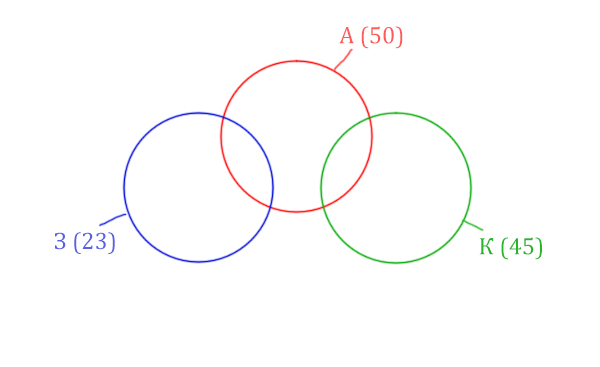
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

Нарисуем все данные на рисунке.

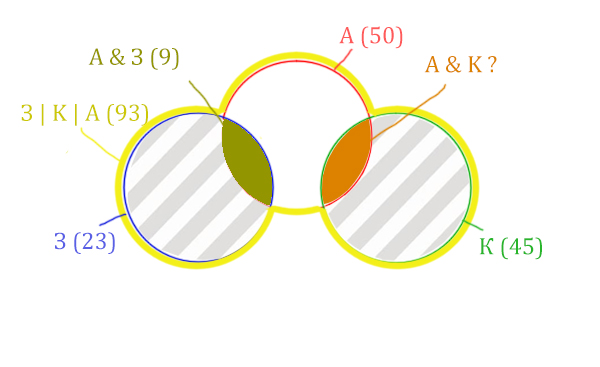
Нужно найти для начала заштрихованную правую часть.

Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43

Левую заштрихованную область легко найти.

Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14

Тогда для правой заштрихованной области получается:

Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29

Тогда искомую область легко найти:

Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16

Ответ: 16

На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.

Интересно…

как быть , когда идет произведение3 предметов + произведниее 3 педметов..

ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++

Источник

Круги Эйлера —
геометрическая схема, с помощью которой можно изобразить отношения между
подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других
прикладных направлениях.

Задача №1

В
языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а
для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц
некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Торты \| Пироги	12000
Торты & Пироги	6500
Пироги	7700

Какое количество страниц (в тысячах) будет найдено по запросу Торты?Считается,
что все запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение задачи №1

Для решения задачи отобразим множества Тортов и Пирогов в виде
кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Торты │Пироги = А+Б+В =
12000

Торты & Пироги = Б = 6500

Пироги = Б+В =
7700

Чтобы найти количество Тортов (Торты = А+Б),
надо найти сектор А, для этого из общего множества
(Торты│Пироги) отнимем множество Пироги.

Торты│Пироги – Пироги = А+Б+В-(Б+В)
= А = 1200 – 7700 = 4300

Сектор А равен 4300,
следовательно

Торты = А+Б =
4300+6500 = 10800

Задача №2

В
языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а
для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц
некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое \| Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по
запросу Выпечка?

Считается,
что все запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.Решение
задачи №2

Для решения задачи отобразим множества Пироженых и
Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Пироженое & Выпечка = Б =
5100

Пироженое = А+Б =
9700

Пироженое │ Выпечка = А+Б+В =
14200

Чтобы
найти количество Выпечки (Выпечка = Б+В),
надо найти сектор В, для этого из общего множества
(Пироженое │ Выпечка ) отнимем множество Пироженое.

Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500

Сектор В равен 4500,
следовательно Выпечка = Б + В =
4300+5100 = 9400

Задача №3
В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ
«|», а для логической операции «И» — символ
«&».

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры \| овчарки

Решение задачи №3

Представим множества овчарок, терьеров и спаниелей в виде кругов
Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

спаниели │(терьеры & овчарки) = Г + Б

спаниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Из сумм секторов мы видим какой запрос выдал больше количества
страниц.

Расположим номера запросов в порядке убывания количества
страниц: 3 2 1 4

Задача №4

В таблице приведены запросы к поисковому серверу. Расположите
номера запросов в порядке возврастанияколичества страниц, которые
найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ
«|», а для логической операции «И» — символ
«&».

1	барокко \| классицизм \| ампир
2	барокко \| классицизм & ампир
3	классицизм & ампир
4	барокко \| классицизм

Решение задачи №4

Представим
множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим
сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества
страниц.

Расположим номера запросов в порядке возрастания количества
страниц: 3 2 4 1

Источник

(Старый формат ЕГЭ) 17. Запросы в поисковых системах

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Диаграммы Эйлера

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{ноутбук}&100\
hline
text{монитор}&200\
hline
text{стол}&350\
hline
text{ноутбук | стол}&450\
hline
text{ноутбук} & text{монитор}&50\
hline
text{стол} & text{монитор}&40\
hline
end{array}]

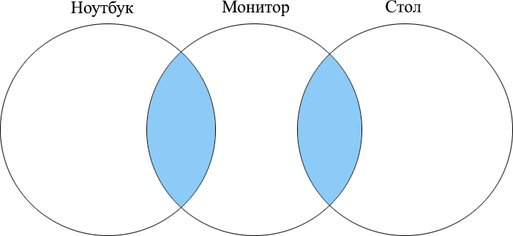
Сколько страниц будет найдено по запросу (ноутбук | стол) & монитор?

Если сложить количество страниц, найденных отдельно по запросам ”ноутбук” и ”монитор”, получим 450. Можно заметить, что (ноутбук | стол) так же равно 450. Это значит, что эти два множества не пересекаются, то есть (text{(ноутбук} & text{монитор)}=0).

Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:

Исходя из рисунка, нам нужно найти сумму (text{(ноутбук} & text{монитор)}+text{(стол} & text{монитор)}). Все данные приведены в таблице, значит, наш ответ (50+40=90).

Ответ: 90

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{чайка}&200\
hline
text{утка}&150\
hline
text{курица}&120\
hline
text{чайка} & text{утка}&80\
hline
text{утка} & text{курица}&70\
hline
text{чайка} & text{курица}&60\
hline
text{чайка} & text{курица} & text{утка}&10\
hline
end{array}]

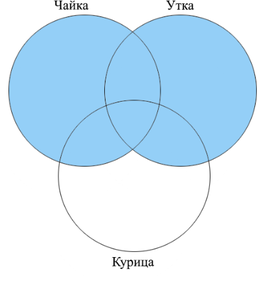
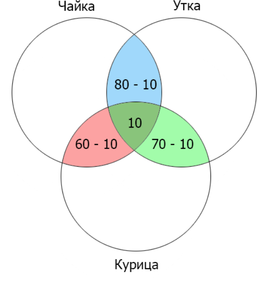
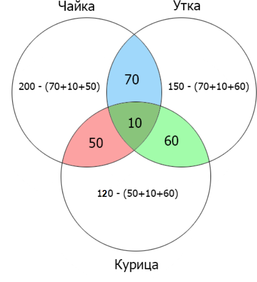
Сколько страниц будет найдено по запросу (чайка | утка)?

Первый способ решения

Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:

Посчитаем количество найденных страниц для каждого пересечения:

Посчитаем оставшиеся данные:

Затем складываем все данные, входящие в круги ”чайка” и ”утка”: (70+70+50+10+60+10=270)

Второй способ решения

Чтобы найти объединение (операция «ИЛИ») множеств, необходимо сложить отдельно количество страниц, найденных по каждому запросу, а затем вычесть их пересечение (операция «И»): (200+150-80=270)

Ответ: 270

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{карандаш}&300\
hline
text{линейка}&200\
hline
text{ручка}&280\
hline
text{ручка} & text{линейка}&80\
hline
text{ручка} & text{карандаш}&70\
hline
text{линейка} & text{карандаш}&0\
hline
end{array}]

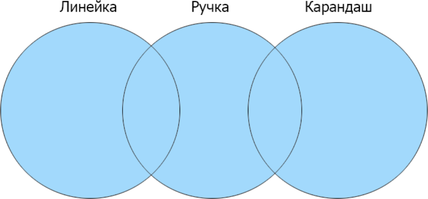
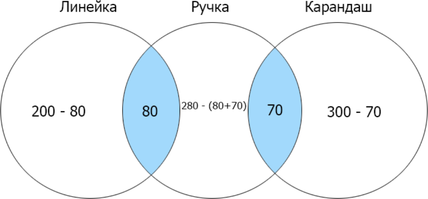
Сколько страниц будет найдено по запросу (линейка | ручка | карандаш)?

Первый способ решения

Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:

Отметим известные данные и посчитаем недостающее:

Затем складываем все данные, входящие в искомую область: (120+130+230+80+70=630).

Второй способ решения

Заметим, что по условию нам необходимо найти сумму всех найденных страниц по введенным запросам. Если мы сложим все отдельные значения найденных страниц, мы учтем по 2 раза каждое из двух пересечений. Таким образом, можем посчитать искомое по формуле: (линейка) + (ручка) + (карандаш) — (ручка & линейка) — (ручка & карандаш) (=300+200+280-80-70=630).

Ответ: 630

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{конверт}&100\
hline
text{книга}&200\
hline
text{журнал}&400\
hline
text{конверт | книга}&300\
hline
text{конверт} & text{журнал}&50\
hline
text{журнал} & text{книга}&60\
hline
end{array}]

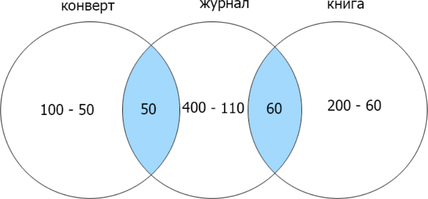
Сколько страниц будет найдено по запросу (конверт | книга | журнал)?

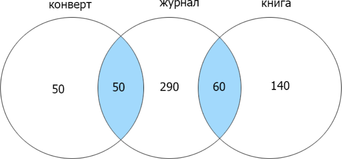
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к. сумма количества страниц, найденных по запросам конверт и книга = 300, а (конверт | книга) = 300, (конверт & книга) = 0. Теперь отобразим известные данные:

Отметим найденные данные и сложим каждую отдельную область для нахождения объедиения трех множеств:

(50+50+290+60+140=590).

Ответ: 590

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{шкаф} & text{стул}&50\
hline
text{стул} & text{стол}&60\
hline
text{стол} & text{шкаф}&70\
hline
text{(шкаф} & text{стул) | (стул} & text{стол) | (стол} & text{шкаф)}&120\
hline
end{array}]

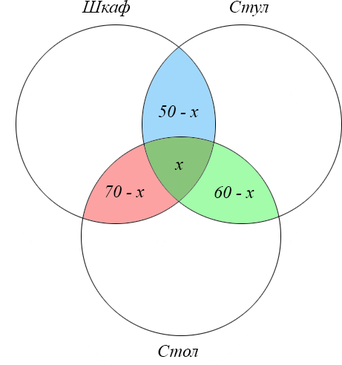
Сколько страниц будет найдено по запросу (шкаф & стул & стол)?

Обозначим искомую область за (x) и выразим данные через (x):

Из последней строки таблицы нам известно, что сумма всех отмеченных элементов равна 120. Значит, можем найти (x) через следующее уравнение:

((50-x)+(70-x)+(60-x)+x=120)

(180-2x=120)

(2x=60)

(x=30)

Ответ: 30

[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{злодеи}&150\
hline
text{мягкие пушистики}&210\
hline
text{злодеи | мягкие пушистики}&300\
hline
end{array}]

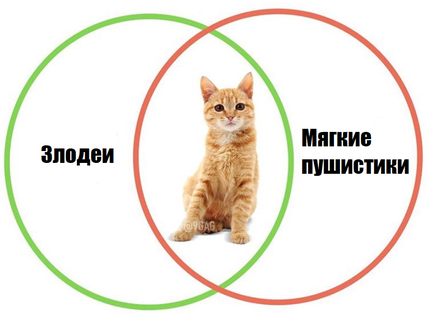
Сколько страниц будет найдено по запросу кот, если известно, что коты находятся на пересечении множеств злодеев и мягких пушистиков?

Отметим искомую область:

Заметим, что кот = (злодеи & мягкие пушистики) = злодеи + пушистики — (злодеи | мягкие пушистики) = (150+210-300=60).

Ответ: 60

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
textbf{Запрос} & textbf{Найдено страниц (в тысячах)}\
hline
text{сок}&100\
hline
text{фрукты}&100\
hline
text{сахар | фрукты | сок}&300\
hline
text{сок | фрукты}&200\
hline
text{сок} ; & ; text{сахар}&20\
hline
text{сахар} ; & ; text{фрукты}&30\
hline
end{array}]
Сколько страниц будет найдено по запросу сахар?

Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к.сумма количества страниц, найденных по запросам сок и фрукты = 200, а (сок | фрукты) = 200, (сок & фрукты) = 0. Теперь отобразим известные данные: 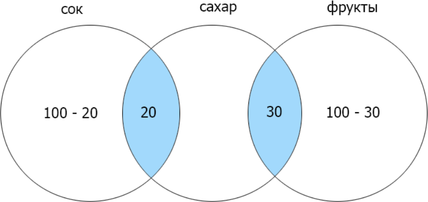Заметим, что сахар = (сок | сахар | фрукты) — сок — фрукты + (сок & сахар) + (сахар & фрукты) = (300-100-100+20+30=150).

Ответ: 150

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Круги Эйлера.

Круги Эйлера для решения задач ЕГЭ

11 класса.

Максимова Дарья, Иванова Дарья ученицы 7 В класса

МБОУ «Гимназия № 24»

Руководитель: Данилина Ольга Сергеевна

учитель математики

Шел урок математики: «Действия с десятичными дробями». Вторая смена, урок был далеко не первый, все устали и думали о том, как бы поскорей оказаться дома. Но тут, учитель, пройдя по классу, поглядывая в тетради моих одноклассников, вдруг заявил: «Так. Так. 11 человек научились и умножать и делить и складывать дроби, 16 — умножать и делить, 14 – делить и складывать, 11 — умножать и складывать.

Тут все неожиданно встрепенулись, сон сняло как рукой. «Не понял» — проговорил Зюзин. «И как такое может быть?» — озадаченно заявил Илья. Но, дело было сделано. Все забыли про теплые мысли о доме.

«Да-да, продолжал учитель. Всего же научились делить 19 человек, умножать — 19, складывать — 15. А в классе сегодня 25 человек. Скажите, сколько человек сегодня ничему не научились?» Тут наперебой все стали предлагать свои версии, складывали, умножали, делили, когда наконец наша отличница Василина, которая в таких случаях всегда отмалчивается и при этом всегда сосредоточенно размышляет, и в конечном итоге всегда, с довольным видом выдает правильный ответ, выпалила: «Их двое». Все замолчали. — «Почему?». -«Ну, мне сложно объяснить, но я знаю, что двое» . — «Правильно» — подтвердила учительница. Предлагая позже доучить эту «сладкую парочку». Но прежде я покажу как разобраться с такой задачей, тем более, что это проще простого. И на доске появились круги.

умножать

Все, кто чему – нибудь научился: 3+5+1+3+11+1 = 23. Осталось – 2.

Вся это жутко запутанная история была разложена по полочках и все стало на свои места. –«А теперь — продолжала учительница_ мы будем доучивать эту «сладкую парочку»

Так я познакомилась с кругами Эйлера. Великий̆ ученый ̆Леонард Эйлер занимает одно из первых мест в истории мировой науки. Полное собрание его трудов составляет 72 тома, более 850 научных работ. . Уже в 13 лет Леонард Эйлер стал студентом факультета искусств Базельского университета. В 17 лет был удостоен ученой̆ степени магистра. В 19 лет Эйлер был включен в число кандидатов на должность профессора физики.

В 1726 был приглашён в Петербургскую Академию наук. В 20 лет стал членом Петербургской̆ академии наук. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни.

Однажды, находясь около учительского стола, я заметила текст задачи, которая привлекла мое внимание , и неспроста, вчитавшись внимательно в текст, я подумала., что при решении можно воспользоваться кругами Эйлера. Текст задачи был из материалов ЕГЭ 11 класса. В последствии, мы рассмотрели еще несколько задач.

Вот, например, задачи из материалов ЕГЭ для выпускников 11 класс.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос Найдено страниц (в тысячах)

Крейсер или Линкор — 7000

Крейсер — 4800

Линкор — 4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

4800 + 4500 = 9300 9300-7000 = 2300

Использование этого метода делает и условие и решение задачи понятным для всех. Вот еще несколько задач.

Всего 40 печений

40 – (10+20) = 10

Всего 20

Всего 50 рогаликов

Как, видно, из представленных рисунков. Отвечать на предложенные вопросы к задачам, имея перед собой рисунки Эйлера, очень просто. И не стоит думать, что эти задачи просты и не представляют никакой сложности для взрослых одиннадцатиклассников. Так, во время проведения сессии процент выполнения хоть и был высоким, (85%), но как видно все же не все ответили правильно. Мы провели эксперимент: объяснили старшеклассникам. Как можно использовать круги Эйлера, и как ожидалось выполнение задания набрало заветные 100%.

Порешав большое количество задач на предложенную тему, нам пришла в голову идея изучить жизнь детей нашего класса, их интересы и предпочтения, составили опросники, собрали данные, обработали и представляем вам результаты нашей работы. При этом хочется особо подчеркнуть, что нам очень нравятся круги Эйлера тем, что при ответе на вопрос можно предпочесть не только один из ответов, а выбрать одновременно все предложенные варианты

Данную задачу мы решали двумя способами, кроме привычного нам, мы учились решать с помощью более для нас трудного — с помощью уравнения. Так как уравнения мы не изучали в такой степени, чтобы мы могли использовать без труда.

Способ 2: 13+17+12 – (5+7+8) = 22. 25-22 = 3. Ответ6 3 человека любят все три вида спорта.

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в городской

Всего — 35

Вопросы, которые можно задать к задаче:

Сколько шестиклассников являются: 1. Являются читателями обеих библиотек? 2.Не являются читателями городской библиотеки? 3. Не являются читателями школьной библиотеки? 4. Являются читателями только городской библиотеки? 5. Являются читателями только школьной библиотеки?

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в понимании,

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение в популярных сериалах. Таких, как «Теория большого взрыва» и «4 числа». Но этому иы посвятим нашу следующую работу.

Источник

На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 17 задания. Объясняется тема о программной обработке числовой информации.

Содержание:

ЕГЭ по информатике 17 задания объяснение
Выполнение 17 задания ЕГЭ
- Работа с цифрами числа в n-й системе счисления

17-е задание: «Программная обработка целочисленной информации»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— да,

Максимальный балл

— 1,

Примерное время выполнения

— 15 минут.

Проверяемые элементы содержания: Умение создавать собственные программы (20–40 строк) для обработки целочисленной информации

Выполнение 17 задания ЕГЭ

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

17_1: Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [1016; 7937], которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них.
В ответе запишите два целых числа: сначала количество, затем максимальное число.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Типовые задания для тренировки

Ответ: 1568 | 7935

Видео

✍ Решение:

✎ Решение с использованием программирования:

Паскаль:

var
  i, k, max: integer;
 
begin
  k := 0;
  max := 0;
  for i := 1016 to 7937 do 
  begin
    if (i mod 3 = 0) and (i mod 7 > 0) and (i mod 17 > 0) and (i mod 19 > 0) and (i mod 27 > 0) then
    begin
      max:= i;
      inc(k);
    end;
  end;
  writeln(k, ' ', max)
end.

PascalABC.NET:

begin
 var s := Range( 1017, 7937, 3).Where( i -> not i.DivsAny(7, 17, 19, 27) );
 print( s.Count, s.Max );            
end.

Python:

1
2
3

a = [n for n in range(1016,7937+1) 
     if (n%3==0 and n%7!=0 and n%17!=0 and n%19!=0 and n%27!=0)]
print(len(a),max(a))

Список a формируем, используя генератор списка: то есть в список попадут только не числа из диапазона [1016,7937], которые удовлетворяют всем перечисленным условиям: n%3==0 (число делится на 3), n%7!=0 (число не делится на 7) и т.п.

C++:

#include <iostream>
int main()
{
  int count = 0;
  int maxGood = 0;
  for(int n=1016; n<=7937; n++)
    if( (n % 3 == 0) and (n % 7 != 0) and 
        (n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0) ) {
      maxGood = n;    
      count += 1;
      }  
  std::cout << count << " " << maxGood;
}

✎ Решение с помощью Excel:

Первое значение диапазона введем в ячейку A1:

Используем прогрессию для заполнения всего диапазона числами. Для это выберите вкладку Главная и щелкните по кнопке Прогрессия:

Столбец B будем использовать для поиска чисел, которые делятся на 3. Для этого в ячейку B1 введите формулу с рисунка:

Двойным щелчком по маркеру заполнения скопируйте формулу на весь столбец:

Столбец С будем использовать для поиска чисел, которые НЕ делятся на 7. Для этого в ячейку С1 введите формулу с рисунка:

Заполните весь столбец двойным щелчком по маркеру заполнения.
Cтолбцы D, E, F таким же образом будем использовать для поиска чисел столбца А, которые не делятся на 17, 19 и 27

Для поиска всех истинных значений используем столбец G. В ячейку G1 введите функцию ЕСЛИ: если все значения ячеек в столбцах B-F в этой строке истинны, выводим число из А1, иначе – пустую строку:

Заполните весь столбце, используя маркер автозаполнения.

Ячейку H1 будем использовать для подсчета таких чисел, которые удовлетворяют всем условиям, т.е. для подсчета непустых ячеек столбца G:

Ячейку H2 будем использовать для подсчета такого наибольшего числа:

Видеоразбор 17 задания ЕГЭ:
📹 YouTube здесь

Видеорешение на RuTube здесь

Работа с цифрами числа в n-й системе счисления

17_2:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [3712; 8432], которые удовлетворяют следующим условиям:
− запись в двоичной и четверичной системах счисления заканчивается одинаковой цифрой;
− кратны 13, 14 или 15.

Найдите количество таких чисел и минимальное из них.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Типовые задания для тренировки

Ответ: 471 3720
✍ Решение:

✎ Решение с использованием программирования:

Паскаль:

var
 var k, n, min:integer;
 
begin
  k:=0; min:=8433;
  for n:= 3712 to 8432 do
    if (n mod 2 = n mod 4) and ((n mod 13=0) or (n mod 14=0) or (n mod 15=0)) then
      begin
        if min>n then
        min:=n;
        k:=k+1;
      end;
      Writeln (k,' ',min);
End.

PascalABC.NET:

begin
 var s := Range( 3712, 8432)
   .Where(i -> ((i mod 13=0) or (i mod 14=0) or (i mod 15=0)) and (i mod 2 = i mod 4));
    // или: .Where( i -> (i.DivsAny(13,14,15)) and (i mod 2 = i mod 4));
 s.Count.Print;
 s.Min.Print;  
end.

Python:

1 2	L = [x for x in range(3712, 8432+1) if (x % 13 == 0 or x % 14 == 0 or x % 15 == 0) and ( x % 2 == x % 4)] print(len(L),' ',L[0])

Формируем список (массив) L только из подходящих элементов, то есть удовлетворяющих всем, перечисленным в задании, условиям. Затем выводим длину списка (len(L)), т.е. найденное количество таких чисел, и нулевой элемент, он же минимальный, поскольку числа упорядочены по возрастанию (L[0])

C++:

#include <iostream>
int main()
{
	int count = 0;
	int min = 8433;
	for (int n = 3712; n <= 8432; n++)
		if (((n % 2 == n % 4) && ((n % 13 == 0) || (n % 14 == 0) || (n % 15 == 0))) )
		{
			if (n < min) min = n;
			count += 1;
		}
	std::cout << count << " " << min;
}

✎ Решение с помощью Excel:

Первое значение диапазона введем в ячейку A1:

Используем прогрессию для заполнения всего диапазона числами. Для это выберите вкладку Главная и щелкните по кнопке Прогрессия:

Столбец B будем использовать для поиска чисел, которые кратны 13, 14 или 15. Для этого в ячейку B1 введите формулу с рисунка:

Двойным щелчком по маркеру заполнения скопируйте формулу на весь столбец:

Столбец С будем использовать для поиска чисел, запись которых в двоичной и четверичной системах счисления заканчивается одинаковой цифрой. Для этого в ячейку С1 введите формулу с рисунка:

Заполните весь столбец двойным щелчком по маркеру заполнения.

Для поиска всех истинных значений используем столбец D. В ячейку D1 введите функцию ЕСЛИ: если все значения ячеек в столбцах B, C в этой строке истинны, выводим число из А1, иначе – пустую строку:

Заполните весь столбце, используя маркер автозаполнения.

Ячейку E1 будем использовать для подсчета таких чисел, которые удовлетворяют всем условиям, т.е. для подсчета непустых ячеек столбца D:

Ячейку E2 будем использовать для подсчета такого наименьшего числа (или просмотрите столбец D визуально и найдите первое значение):

17_3:

Рассматривается множество целых чисел, принадлежащих числовому отрезку [1000; 9999], запись которых в пятеричной системе имеет не менее 6 цифр и заканчивается на 21 или 23.

Найдите количество таких чисел и минимальное из них.

! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц

Ответ: 550 3136

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.NET:

### uses school;
var s := Range(1000, 9999)
   .Where(i -> (i.ToString.ToBase(5).Length=6) and (i div 5 mod 5 = 2)
       and((i mod 5 = 1) or (i mod 5 = 3)));
s.Count.Print;
s.Min.Print;

Python:

numb=''
result=list()
for i in range(1000, 9999+1):
    if ((i // 5) % 5 ==2) and (( i % 5 == 1) or ( i % 5 == 3)):
        while i>=5: #Цикл перевода числа из 10-й в 5-ю сс
            s=i%5
            numb=str(s)+numb
            i=i//5
            if i<5:
                numb=str(i)+numb
        n=len(numb)
        if n>5:
            result.append(numb) # список из чисел в 5-й с.с
        numb=""
kolvo=len(result)
minNumb=int(min(result),5) # перевод в десятичную с.с и поиск min
print(kolvo,minNumb)

Источник

Пояснительная записка

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

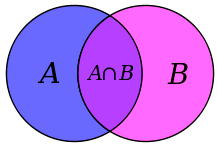
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

2. Решение задач с помощью кругов Эйлера

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

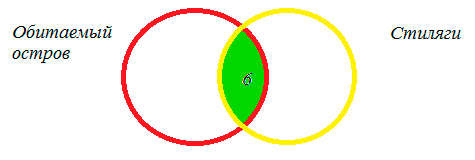
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Получаем:

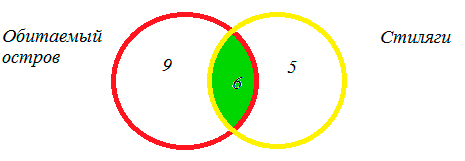
Ответ: 5 человек.

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.

Сколько шестиклассников:

Являются читателями обеих библиотек;
Не являются читателями районной библиотеки;
Не являются читателями школьной библиотеки;
Являются читателями только районной библиотеки;
Являются читателями только школьной библиотеки?

Решение:

Чертим два множества таким образом:

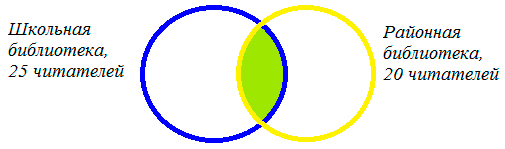
1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

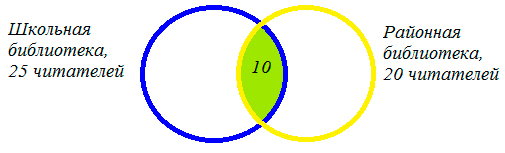
2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

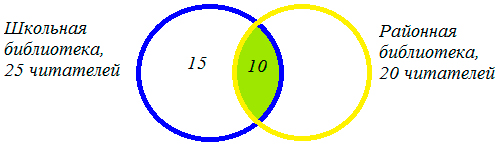
3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

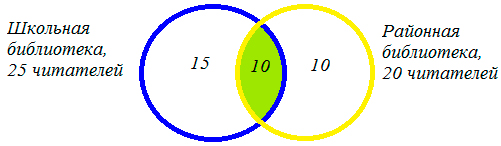
4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Решение:

Учитывая условия задачи, сделаем чертеж:

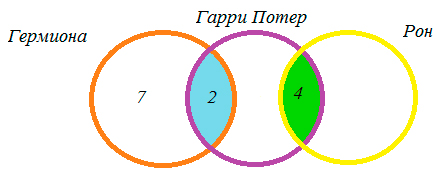
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

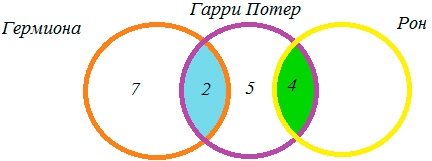
Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Чертим три круга, таким образом:

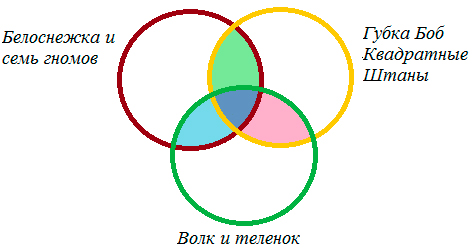
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

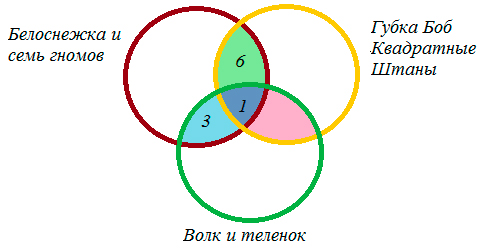
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

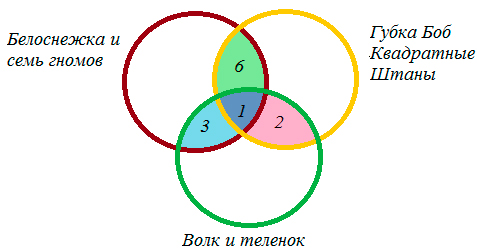
1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

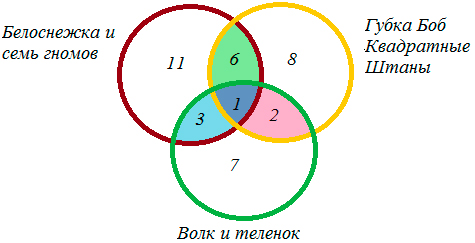
4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц, тыс.
Крейсер и Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)

Решение:

При помощи кругов Эйлера изобразим условия задачи.

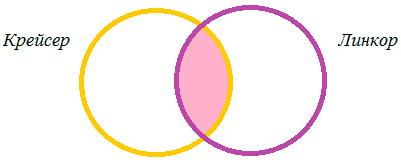
1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

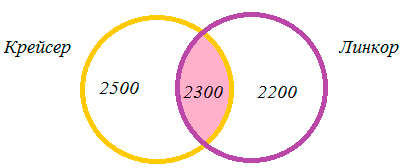
Ответ: 2300 тыс. страниц.

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

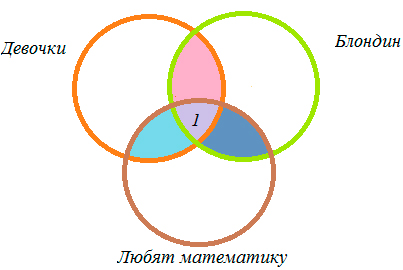
1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

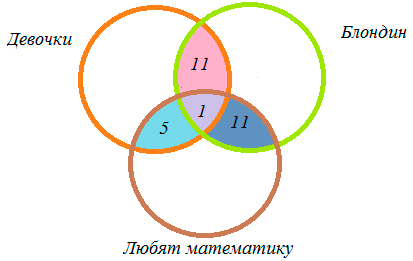
4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

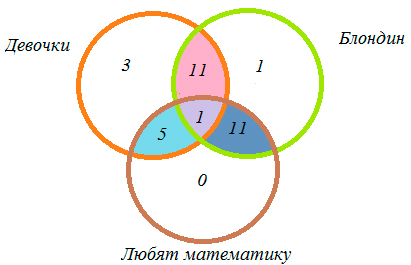
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.

Ответ: 32 ученика.

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение:

Учитывая условия задачи, сделаем чертеж:

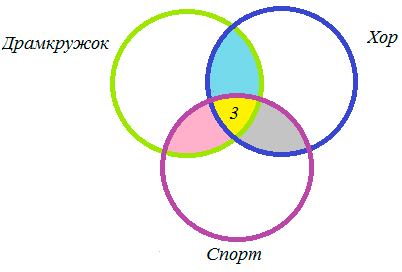
1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

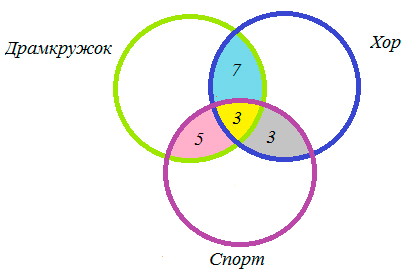
4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

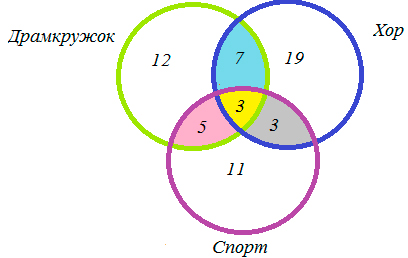
7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Ответ: 10 человек и 11 человек.

Задачи для самостоятельного решения

1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Список использованных источников

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

3. https://ru.wikipedia.org/wiki/

4. http://logika.vobrazovanie.ru

5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22

6. http://urok.1sept.ru/articles/550092/

7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera

Источник

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры \| овчарки

1	барокко \| классицизм \| ампир
2	барокко \| классицизм & ампир
3	классицизм & ампир
4	барокко \| классицизм