Задачи с линзами егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Рациональные уравнения и неравенства

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 8 № 27970

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d_1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d_2 от линзы до экрана  — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

Аналоги к заданию № 27970: 28205 41891 41895 519511 519537 541052 541257 28207 28209 28211 … Все

Классификатор алгебры: Рациональные уравнения и неравенства

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения, Разные задачи с прикладным содержанием

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 8 № 27971

Перед отправкой тепловоз издал гудок с частотой Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону (Гц), где c − скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.

Аналоги к заданию № 27971: 28215 41955 530821 530896 28217 28219 28221 28223 41897 41899 … Все

Классификатор алгебры: Рациональные уравнения и неравенства

Кодификатор ФИПИ/Решу ЕГЭ: 2.2.2 Рациональные неравенства, Разные задачи с прикладным содержанием

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 8 № 27972

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна где − ЭДС источника (в вольтах), r = 1 Ом  — его внутреннее сопротивление, R − сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания  ? (Ответ выразите в омах.)

Аналоги к заданию № 27972: 28225 41987 28227 28229 28231 28233 41957 41959 41961 41963 … Все

Классификатор алгебры: Рациональные уравнения и неравенства

Кодификатор ФИПИ/Решу ЕГЭ: 2.2.2 Рациональные неравенства, Разные задачи с прикладным содержанием

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 8 № 27973

Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: где U − напряжение в вольтах, R − сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.

Аналоги к заданию № 27973: 28235 41999 28237 28239 28241 28243 41989 41991 41993 41995 … Все

Классификатор алгебры: Рациональные уравнения и неравенства

Кодификатор ФИПИ/Решу ЕГЭ: 2.2.2 Рациональные неравенства, Разные задачи с прикладным содержанием

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 8 № 27974

Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле где omega − частота вынуждающей силы (в ), A_0 − постоянный параметр, − резонансная частота. Найдите максимальную частоту omega , меньшую резонансной, для которой амплитуда колебаний превосходит величину A_0 не более чем на 12,5%. Ответ выразите в

Аналоги к заданию № 27974: 28245 42045 28247 28249 28251 28253 28255 42001 42003 42005 … Все

Классификатор алгебры: Рациональные уравнения и неравенства

Кодификатор ФИПИ/Решу ЕГЭ: 2.2.2 Рациональные неравенства, Разные задачи с прикладным содержанием

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 60 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 92 до 115 см, а расстояние d₂ от линзы до экрана – в пределах от 140 до 160 см. Изображение на экране будет четким, если выполнено соотношение frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{f}. На каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.

Источники: fipi, os.fipi, Пробный ЕГЭ 2018, Основная волна 2017

Решение:

f = 60 см

frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{f}\frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{60}\frac{1}{d_{1}}=frac{1}{60}-frac{1}{d_{2}}

По условию расстояние до лампочки d₁ должно быть наименьшим, тогда выражение frac{1}{d_{1}} будет наибольшим, что бы оно было наибольшим в правой части должны вычитать как можно меньше frac{1}{d_{1}}, тогда d₂ должно быть максимальным, т.е. d₂ = 160.

frac{1}{d_{1}}=frac{1}{60}-frac{1}{160}\frac{1}{d_{1}}=frac{8-3}{480}\frac{1}{d_{1}}=frac{5}{480}\frac{1}{d_{1}}=frac{1}{96}\d_{1}=96

Ответ: 96.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4 / 5. Количество оценок: 32

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

15
Мар 2012

07 Задание (2022)

Расстояние от линзы до лампочки. Задание 10.

Решение задачи на оптику из Задания 10 из Открытого банка заданий для подготовки к ЕГЭ по математике традиционно вызывают затруднения. Давайте рассмотрим решение такой задачи, и вы поймете, что они решаются совсем просто.

Задание 10 (№ 27970)

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение $1/{d_1}+1/{d_2}=1/{f}$ . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

Решение.

Расстояние от линзы до лампочки — это по условию d_1 . Выразим d_1 через остальные переменные:

$1/{d_1}=1/{f}-1/{d_2}$

По условию величина d_1 должна принимать наименьшее значение, следовательно, обратная ей величина $1/{d_1}$ должна принимать наибольшее значение.

Посмотрим, при каких условиях правая часть равенства $1/{f}-1/{d_2}$ принимает наибольшее значение.

1/f — фиксированная величина, .

$1/{30}-1/{d_2}$ принимает наибольшее значение, когда $1/{d_2}$ принимает наименьшее значение, и, значит, обратная величина d_2 должна принимать наибольшее значение, то есть d_2=180 .

Получаем: $1/{d_1}=1/{30}-1/{180}=5/{180}$

$d_1=180/{5}=36$

Ответ: 36.

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Выразим d₁ из соотношения, при выполнении которого увеличенное изображение будет чётким:

frac{1}{d_{1}} + frac{1}{d_{2}} = frac{1}{f}

frac{1}{d_{1}} = frac{1}{f} — frac{1}{d_{2}}

Приводим правую часть к общему знаменателю и выражаем d₁:

frac{1}{d_{1}} = frac{d_{2}-f}{fcdot d_{2}}

d_{1} = frac{fcdot d_{2}}{d_{2}-f}

Определим, какое расстояние d₁ будет при граничных значениях d₂ (d₂ = 90 см и d₂ = 120 см) и найдем среди них наименьшее. Фокусное расстояние линзы f = 30 см.

Для d₂ = 120 см получим:

d_{1} = frac{30 cdot 120}{120-30} = frac{30 cdot 120}{90} = 40 см

Для d₂ = 90 см:

d_{1} = frac{30 cdot 90}{90-30} = frac{30 cdot 90}{60} = 45 см

Наименьшее из них – 40 см.

Источник

Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.

Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.

Тонкая линза: задачи

Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению.

Задача №1. Формула тонкой линзы

Условие

Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?

Решение

Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:

1F=1d+1f

Учтем, что F=1D, подставим значения из условия, и запишем:

2,5=10,5+1+ff=2 м

Ответ: 2м

Задача №2. Формула тонкой линзы

Условие

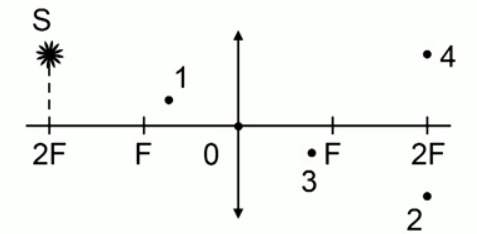
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению светящейся точки.

Решение

Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.

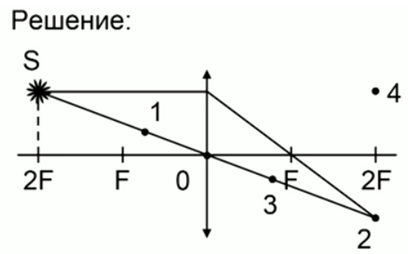
Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.

Ответ: изображению точки S соответствует точка 2.

Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.

Задача №3. Формула тонкой линзы

Условие

Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.

Решение

Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:

1F=1d+1f ; Г=Hh=fd

Перепишем эти соотношения, с учетом того, что F=1D

H=h·fd1f=D-1d

Отсюда найдем f:

f=dD·d-1

Осталось подставить значения в формулу для H и вычислить:

H=hdD·d-1=0,03·0,44·0,4-1=0,05 м

Ответ: 0,05 м.

Задача №4. Формула тонкой линзы

Условие

Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?

Решение

Фокусное расстояние найдем из формулы линзы:

1F=1d+1fF=fdd+f

Запишем формулу увеличения линзы и выразим d:

Г=Hh=fd ; d=fhH

Запишем окончательный ответ:

F=hfH+h≈0,08 м

Ответ: 0,08 м.

Задача №5. Формула тонкой линзы

Условие

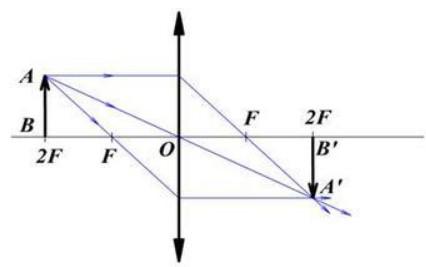
Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?

Решение

Посторим изображение в соответствии с правилами геометрической оптики:

Данное изображение:

действительное;
перевернутое;
равное предмету.

Ответ: см. выше.

Вопросы на тему «Тонкая линза»

Вопрос 1. Какое равенство называют формулой тонкой линзы?

Ответ. Формула тонкой линзы имеет следующий вид:

1F=1d+1±f

Здесь:

F – фокусное расстояние;
d – расстояние от линзы до предмета;
f – расстояние от линзы до изображения.

Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?

Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.

Вопрос 3. Что такое фокусное расстоняние линзы?

Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.

Вопрос 4. Что такое оптическая сила линзы?

Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.

Вопрос 5. Может ли оптическая сила линзы быть отрицательной?

Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.

Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!

Источник

Предлагаю вашему вниманию несколько задач, в которых обязательно присутствуют две линзы. Линзы могут быть – обе — собирающими, и собирающей в комбинации с рассеивающей.

Задача 1.

Две собирающие линзы с фокусными расстояниями см и см расположены вдоль общей главной оптической оси на расстоянии см друг от друга. Где следует поместить точечный источник света, чтобы идущие от него лучи по прохождении обеих линз образовали пучок лучей, параллельных главной оптической оси?

Решение.

К задаче 1

Чтобы лучи после системы линз шли параллельным потоком, необходимо, чтобы после первой линзы лучи прошли бы через фокус второй. То есть изображение, даваемое первой линзой, должно попасть в фокус второй (на расстоянии 20 см от первой). Тогда запишем формулу линзы для первой:

Понятно, что первой может стоять линза с фокусным расстоянием 15 см. Тогда расчет немного изменится:

Ответ: 30 см или 60 см

Задача 2.

На собирающую линзу с фокусным расстоянием см падает параллельный пучок лучей. Где следует поместить рассеивающую линзу с фокусным расстоянием см, чтобы пучок лучей после прохождения двух линз остался параллельным?

К задаче 2

Решение. Ход световых лучей обратим. Если бы лучи падали на рассеивающую линзу слева параллельным потоком, то они далее рассеивались и шли бы за линзой расходящимся потоком. То есть, чтобы обеспечить параллельный ход лучей за линзой, нужно, чтобы фокус рассеивающей линзы совпадал с фокусным расстоянием собирающей. Тогда падающий на рассеивающую линзу сходящийся поток лучей преобразуется ею в параллельный.

Ответ 25 см.

Задача 3.

Система состоит из двух линз с одинаковыми по модулю фокусными расстояниями. Одна из линз собирающая, другая рассеивающая. Линзы расположены на одной оси на некотором расстоянии друг от друга. Известно, что если поменять линзы местами, то действительное изображение Луны, даваемое этой системой, сместится на см. Найдите фокусное расстояние каждой из линз.

Решение. Пусть первой стоит рассеивающая линза, а затем собирающая. Сначала ход лучей был таким:

Рисунок 1 к задаче 3

Для собирающей линзы тогда

Откуда

Теперь поменяем линзы местами (действительное изображение может получиться только, если на рассеивающую линзу падает сходящийся пучок, то есть при мнимом предмете):

Запишем уравнение для рассеивающей линзы.

Как видно из обеих картинок, изображение переместилось на расстояние :

Откуда

Ответ 10 см

Задача 4.

Собирающая линза дает на экране изображение светящейся точки , лежащей на главной оптической оси. Между линзой и экраном на расстоянии см от экрана поместили рассеивающую линзу. Отодвигая экран от рассеивающей линзы, получили новое изображение светящейся точки . При этом расстояние нового положения экрана от рассеивающей линзы равно см.

Определите фокусное расстояние F рассеивающей линзы и ее оптическую силу в диоптриях.

Решение.

К задаче 4

Запишем уравнение линзы (рассеивающей)

Здесь снова использована обратимость световых лучей (показана с помощью зеленого луча).

Ответ: фокусное расстояние 30 см, оптическая сила -3,3 дптр.

Задача 5.

Параллельный пучок света падает перпендикулярно на собирающую линзу, оптическая сила которой дптр. На расстоянии 20 см от нее находится рассеивающая линза с оптической силой дптр. Диаметр линз равен 5 см. На расстоянии 30 см от рассеивающей линзы расположен экран Э. Каков диаметр светлого пятна, создаваемого линзами, на экране?

Решение. Определим фокусные расстояния линз.

Значит, задние фокусы обеих линз совпадают! А это означает, что, как и во второй задаче, падающий на рассеивающую линзу сходящийся поток лучей преобразуется ею в параллельный.

К задаче 5

Если бы рассеивающей линзы не было, то ширина светового пучка в месте ее установки была бы вдвое уже диаметра линзы – из подобия треугольников. Поэтому диаметр светлого пятна будет равен 2,5 см.

Ответ: 2,5 см.

Задача 6.

Две собирающие линзы с оптическими силами дптр и дптр расположены на расстоянии см друг от друга. Найдите, используя построение в линзах, где находится изображение предмета, расположенного на расстоянии см от первой линзы, и поперечное увеличение системы.

Решение. Фокусное расстояние первой линзы равно 20 см.

Поэтому предмет расположен в двойном фокусе и его изображение получится тоже в двойном фокусе, то есть в 20 см от второй линзы. Составим уравнение линзы для второй:

Изображение получится в метре от второй линзы. Так как первая линза не увеличивает, то увеличение системы равно увеличению второй линзы. А это

Ответ: изображение получится в 1 м от второй линзы; увеличение системы равно 5.

3 комментария

Николай
✉️
11.02.2022 19:12:39

Здравствуйте, Анна!
Мне кажется, что задача 3 решена неверно.
По условию задачи в обоих случаях система дает действительное изображение. У вас во втором случае, когда свет сначала падает на собирающую линзу, а после нее падает расходящимся пучком на рассеивающую линзу, в принципе не может получиться действительное изображение.
Задача имеет решение только в случае, когда расстояние между линзами меньше фокусного расстояния.

Николай
✉️
11.02.2022 19:15:19

Не нашел возможности прикрепить файл с верным решением. Если интересно, могу прислать. Ответ тот же, что и у вас. Так как вы допустили две ошибки (чертеж и знаки в формуле линзы), в результате получили верный ответ.

Анна Валерьевна
✨
14.02.2022 08:26:50

Спасибо! Конечно, вы абсолютно правы. Исправила.

Источник

Предлагаем разобрать три задачи, приведенные ниже. Это варианты задания №27 из ЕГЭ прошлых лет, рекомендованные как тренировочные.

Задача № 1

Коллекционер разглядывает при помощи лупы элемент марки, имеющий размер 0,2 мм, и видит его мнимое изображение, увеличенное до 1,2 мм. Рассматриваемый элемент расположен на расстоянии 7 мм от лупы. На каком расстоянии от лупы находится изображение? Ответ приведите в миллиметрах.

Решение

Составим чертеж, согласно условию задачи (Рис. 1):

Рис. 1

Лупа представляет собой собирающую линзу. Чтобы получать в ней неперевернутые увеличенные изображения, необходимо размещать предмет ближе фокусного расстояния. При этом изображение будет мнимым.

Из рисунка (Рис. 1) видно, что в силу подобия треугольников расстояние от предмета до лупы «d», расстояние от лупы до изображения «f», размер предмета «h» и размер изображения «H» связаны соотношением:

Выразим из этой формулы «f»:

f =

Подставим числовые значения:

f = = 42

Таким образом, изображение находится от лупы на расстоянии 42 мм.

Ответ: 42 мм.

Задача № 2

Линза с фокусным расстоянием F = 0,1 м даёт на экране изображение предмета, увеличенное в 6 раз. Каково расстояние от линзы до изображения? Ответ приведите в метрах.

Решение

Фокусное расстояние связано с расстоянием от предмета до линзы и расстоянием от линзы до изображения формулой линзы:

= +

Увеличение линзы равно отношению высоты изображения к высоте объекта:

Г =

Из геометрического построения найдем, что:

Г =

Тогда получим:

= 6 => = + = => f = 7F = 7 · 0,1 = 0,7 м

Ответ: 0,7 м.

Задача № 3

Линза с фокусным расстоянием F = 0,3 м даёт на экране изображение предмета, увеличенное в 3 раза. Каково расстояние от линзы до изображения? Ответ приведите в метрах.

Решение

= +