Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на
Определите срок хранения вклада.
Источник: А. Ларин: Тренировочный вариант № 81.
2
Семен Кузнецов планировал вложить все свои сбережения на сберегательный счет в банк «Навроде» под 500%, рассчитывая через год забрать А рублей. Однако крах банка «Навроде» изменил его планы, предотвратив необдуманный поступок. В результате часть денег г-н Кузнецов положил в банк «Первый Муниципальный», а остальные – в банку из-под макарон. Через год «Первый Муниципальный» повысил процент выплат в два с половиной раза, и г-н Кузнецов решил оставить вклад еще на год. В итоге размер суммы, полученной в «Первом Муниципальном», составил рублей. Определите, какой процент за первый год начислил банк «Первый Муниципальный», если в банку из-под макарон Семен «вложил»
рублей.
Источник: А. Ларин: Тренировочный вариант № 94.
3
8 марта Леня Голубков взял в банке 53 680 рублей в кредит на 4 года под 20% годовых, чтобы купить своей жене Рите новую шубу. Схема выплаты кредита следующая: утром 8 марта следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), а вечером того же дня Леня переводит в банк определенную сумму ежегодного платежа (все четыре года эта сумма одинакова). Какую сумму сверх взятых 53 680 рублей должен будет выплатить банку Леня Голубков за эти четыре года?
Источник: А. Ларин: Тренировочный вариант № 95.
4
В 8-литровой колбе находится смесь азота и кислорода, содержащая 32% кислорода. Из колбы выпустили некоторое количество смеси и добавили столько же азота, затем снова выпустили такое же, как и в первый раз, количество новой смеси и добавили столько же азота. В итоге процентное содержание кислорода в смеси составило 12,5%. Сколько литров смеси выпускали каждый раз?
Источник: А. Ларин: Тренировочный вариант № 98.
5
Молодой семье на покупку квартиры банк выдает кредит под 20% годовых. Схема выплаты кредита следующая: ровно через год после выдачи кредита банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем эта семья в течение следующего года переводит в банк определенную (фиксированную) сумму ежегодного платежа. Семья Ивановых планирует погашать кредит равными платежами в течение 4 лет. Какую сумму может предоставить им банк, если ежегодно Ивановы имеют возможность выплачивать по кредиту 810 000 рублей?
Источник: А. Ларин: Тренировочный вариант № 99.
Пройти тестирование по этим заданиям
Задачи с практическим содержанием
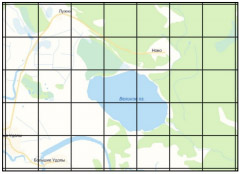
На рисунке изображен план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображенного на плане. Ответ округлите до целого числа.
#901
Марина Павловна внимательно изучает цены в каталогах, прежде чем пойти за покупками. На сей раз она составила таблицу с ценами на продукты для выпечки из разных магазинов. Мука продаётся килограммами, а дрожжи и ванилин — пакетиками по 10 г.
| Магазин | Мука, 1 кг | Дрожжи, 10 г | Ванилин, 10 г |
| «Пекарь» | 62 руб. | 18 руб. | 18 руб. |
| «Повар» | 49 руб. | 12 руб. | 14 руб. |
| «Булка» | 52 руб. | 13 руб. | 12 руб. |
Для булочек к чаю ей нужно купить 1 кг муки, 1 пакетик дрожжей, 2 пакетика ванилина. При этом она знает, что в «Пекаре» скидка 15% на все три продукта, а в «Булке» — 5% на муку. Вычисли, в каком магазине Марина Павловна сможет сделать наименее выгодные покупки. В ответ внеси суммарную стоимость покупки.
#872
На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы (сторона каждой клетки на плане равна 20 м). Въезд и выезд осуществляются через единственные ворота.
При входе на территорию хозяйства слева от ворот находится кукурузное поле. Рядом с ним расположен яблоневый сад. Также имеется цех по переработке овощей и фруктов, расположенный рядом с полем, засеянным капустой. При входе справа от ворот находится стоянка для грузовиков и сельхозтехники. На территории стоянки расположен склад готовой продукции. Участок с теплицами, в которых выращивают клубнику, граничит с яблоневым садом и капустным полем. К хозяйству подведено электричество.
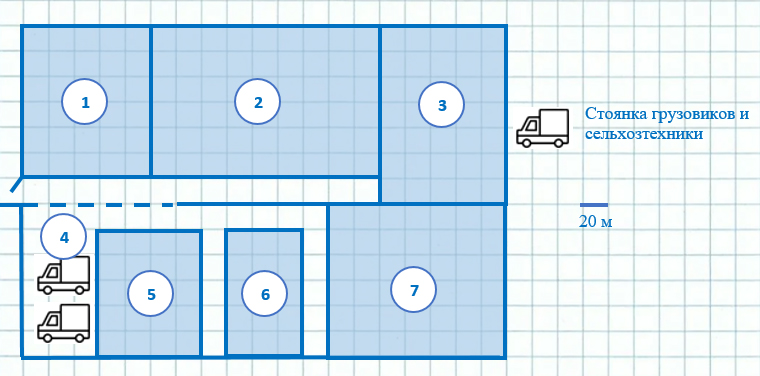
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Яблоневый сад | Капустное поле | Цех по переработке овощей и фруктов | Теплицы с клубникой |
| Цифры |
2. Урожайность кукурузы в этом хозяйстве в среднем составила 4 тонны с одного гектара земли. Цех по переработке выпускает банки консервированной кукурузы массой нетто основного продукта 280 грамм каждая. Какое максимальное количество банок кукурузы выпустил цех?
3. Найдите суммарную площадь участков земли, занятых под сельскохозяйственные культуры. Ответ дайте в гектарах.
4. По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).
5. Собственник хозяйства рассматривает два варианта водоснабжения: централизованное и автономное из артезианской скважины. Цены на оборудование и стоимость его установки, данные о расходе воды и ее стоимости даны в таблице.
| Водоснабжение | Стоимость оборудования, руб. | Стоимость монтажа, руб. | Средний расход воды, м3/ч | Тариф, руб./м3 |
| Централизованное | 180 960 | 210 700 | 20 | 20,2 |
| Автономное | 205 710 | 480 350 | 20 | 11 |
Обдумав оба варианта, собственник решил оборудовать автономное водоснабжение. Через сколько часов непрерывной работы водоснабжения экономия от использования автономного водоснабжения вместо централизованного компенсирует разность в стоимости установки оборудования и монтажа?
#853
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счет гибкости спиц и эластичности ткани, из которой изготовлен зонт.
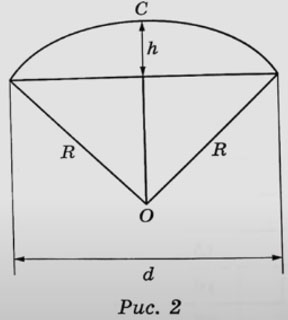
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами, образующих дугу окружности, проходящей через вершину зонта, — равно 100 см.
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
#847
Брюки дороже рубашки на 20%, а пиджак дороже рубашки на 44%. На сколько процентов пиджак дороже брюк?
#841
В соревновании по стрельбе за каждый промах в серии из 20 выстрелов стрелок получал штрафные очки: за первый промах — два штрафных очка, за каждый последующий промах — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 11 штрафных очков?
#836
Прототипы задания 1 из ЕГЭ по математике (профильный уровень).
#789
На плане изображен многофункциональный культурно-образовательный комплекс, который состоит из нескольких корпусов и обнесен забором прямоугольной формы (сторона каждой клетки на плане 3 м). Вход на территорию комплекса и выход осуществляется через единственные ворота. От входа через весь комплекс проходит главная аллея, вдоль которой стоят восемь фонарей. При входе на территорию комплекса разбит яблоневый сад (цифра 3 на плане). В начале сада находится подсобное помещение, а в глубине — детская площадка площадью 144 кв. м. За яблоневым садом расположено административное здание. Справа от входа — здание магазина (цифра 6 на плане) и образовательная оранжерея. Главная аллея площадью 153 кв. м. вымощена тротуарной плиткой 1,5 м х 1,5 м. Дорожка от главной аллеи к административному зданию имеет ширину 1,5 м и вымощена такой же плиткой. В ночное время территория комплекса освещается фонарями.
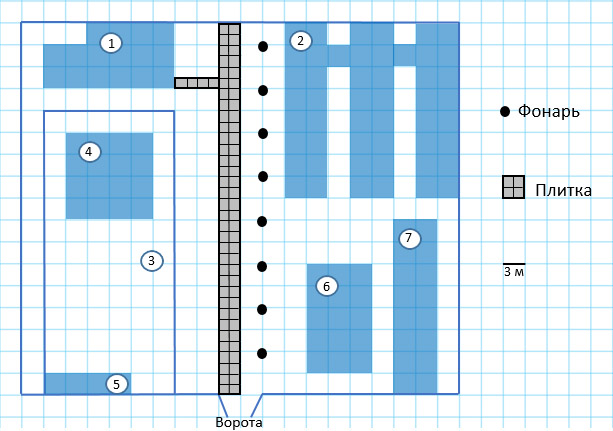
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность цифр.
| Объекты | Подсобное помещение | Образовательная оранжерея | Административный комплекс | Детская площадка | Прогулочная оранжерея |
| Цифры |
2. Во время строительства комплекса была использована тротуарная плитка, которую доставляли на стройку в виде упаковок по 5 штук в каждой. Сколько упаковок плитки понадобилось, чтобы уложить аллею и дорожку?
3. Какую часть яблоневого сада занимает подсобное помещение? Ответ дать в процентах, при необходимости округлить с точностью до 0,01.
4. Какое максимальное количество детей может одновременно находится на детской площадке, если по нормам на каждого ребенка положено не менее 7 квадратных метров?
5. В образовательной оранжерее решили посадить редкие виды цветов. Какое максимальное количество растений можно посадить, если количество посадок не должно превосходить числа, которое вычисляется по формуле n = sa, где s — площадь оранжереи, а = 75%.
6. Руководство комплекса планирует заменить уличные фонари. Они есть двух видов: с классическими светильниками или светодиодными. В таблице указаны стоимость опоры, стоимость лампы, монтаж для одного фонаря, средняя потребляемая мощность и стоимость электроэнергии.
| Стоимость опоры | Стоимость лампы | Монтаж | Средняя потребляемая мощность | Стоимость электроэнергии | |
| Фонарь с классическим светильником | 5 400 руб | 200 руб | 16 300 руб | 440 кВт | 3,7 руб/кВт · ч |
| Фонарь со светодиодным светильником | 6 830 руб | 440 руб | 18 330 руб | 40 кВт | 3,7 руб/кВт · ч |
Изучив предлагаемые варианты, руководство решило устанавливать фонари со светодиодными светильниками. Через сколько часов непрерывной работы таких фонарей экономия от их использования компенсирует разность в стоимости установки по сравнению с фонарями с классическими светильниками.
7. Найдите площадь, которую занимает административный комплекс. Ответ дайте в квадратных метрах.
8. Найдите расстояние от административного здания до магазина (расстояние между двумя ближайшими точками по прямой) в метрах.
9. В прогулочной оранжерее решили повесить праздничные флажки. Для этого натянули два троса, каждый через две максимально удаленные точки (по диагонали). Под каким углом пересекаются эти тросы?
10. В яблоневом саду решили вырыть пруд круглой формы, радиус которого 6 м. Какая площадь останется для яблонь после появления пруда? Ответ дайте в квадратных метрах. Площадь круга вычисляется по формуле S = πR2, где π = 3, R — радиус.
#769
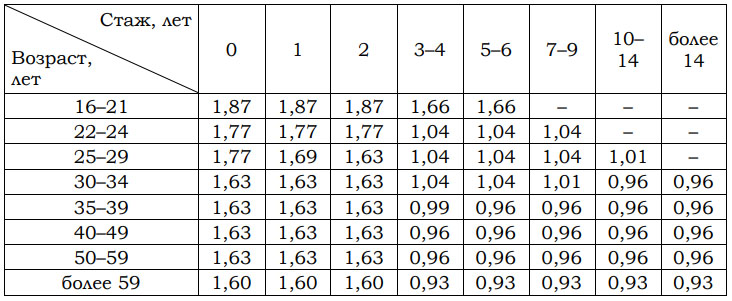
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
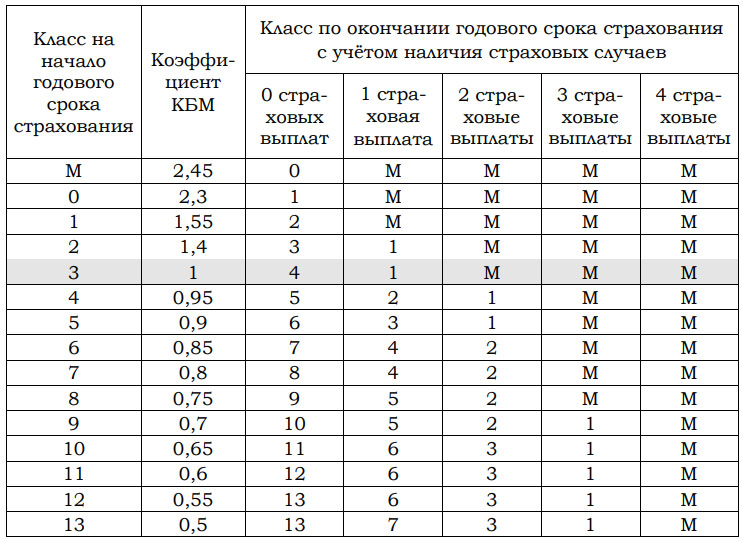
1. Борис страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Борису на начало третьего года страхования?
2. Чему равен КБМ на начало третьего года страхования?
3. Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу).
Когда Борис получил водительские права и впервые оформил полис, ему было 20 лет. Чему равен КВС на начало 3-го года страхования?
4. В начале второго года страхования Борис заплатил за полис 28 985 руб. Во сколько рублей обойдётся Борису полис на третий год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
5. Борис въехал на участок дороги протяжённостью 3,8 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге – 80 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Борис въехал на участок в 14:28:23, а покинул его в 14:30:47. Нарушил ли Борис скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
#760
Для маркировки автомобильных шин применяется единая система обозначений. Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рисунок). Второе число — отношение высоты боковины Н к ширине шины В в процентах. Последующая буква указывает конструкцию шины. Например, буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Последний символ в маркировке — индекс скорости. Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие. Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 185/70 R14. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
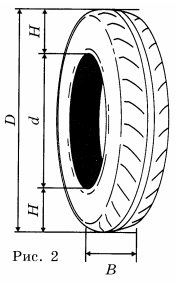
1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам?
2. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
3. На сколько миллиметров увеличится диаметр колеса, если заменить шины, установленные на заводе, на шины 195/70 R14?
4. На сколько метров увеличится путь, пройденный автомобилем, когда колесо сделает 1000 оборотов, если заменить шины установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до целых.
5. Спидометр автомобиля, собранного на заводе, показывает скорость точно. На сколько процентов показания спидометра будут отличаться от реальной скорости, если заменить шины, установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до десятых.
#759
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.
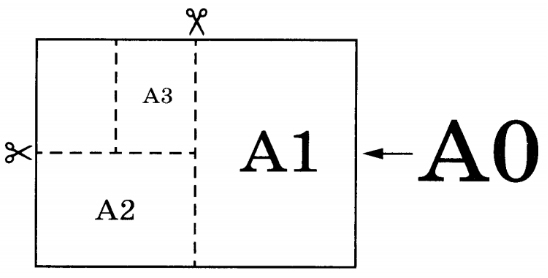
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 210 | 297 |
| 2 | 297 | 420 |
| 3 | 105 | 148 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А6 | А5 | А4 | А3 |
2. Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину меньшей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата А5. Ответ дайте в квадратных сантиметрах.
5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, т.е. 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
#720
Для маркировки автомобильных шин применяется единая система обозначений (см. таблицу). Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рисунок). Второе число — отношение высоты боковины Н к ширине шины В в процентах. Последующая буква указывает конструкцию шины. Например, буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие. Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 175/60 R15. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.

1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с маркировкой 195/60 R14 больше, чем радиус колеса с маркировкой 165/70 R14?
3. Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4. На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/45 R16?
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/55 R15? Округлите результат до десятых.
#718
Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе — через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки — 36 км, а от Берёзовки до Игнатьево 15 км.
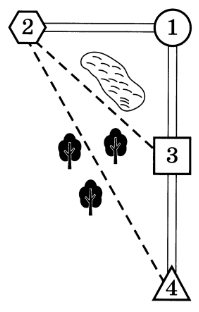
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры |
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.
#717
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
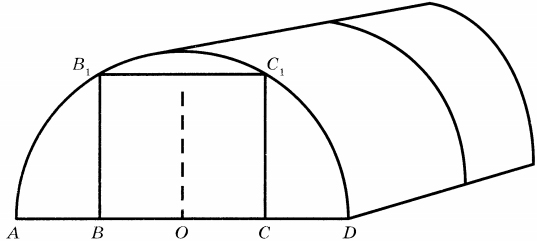
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
#716
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.

| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
2. Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
5. Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.
#715
Скачать материал

Скачать материал


- Сейчас обучается 54 человека из 29 регионов


- Сейчас обучается 36 человек из 28 регионов


- Сейчас обучается 132 человека из 48 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Тема урока:
«Решение задач с практическим содержанием при подготовке к ЕГЭ по математике на профильном уровне» -
2 слайд
Анализ банка задач ЕГЭ по математике, а также демоверсии ЕГЭ 2021 года позволил выделить основные подходы к решению задач с практическим содержанием:
1. решение с помощью формул;
2. решение задач в общем виде;
3. решение задач с использованием свойства степеней;
4. решение задач с помощью математического анализа;
5. решение задач методом сравнения -
3 слайд
4 вида экономических задач:
1. Простые проценты, налоги;
2. Сложные проценты, вклады;
3. Кредиты;
4. Задачи на оптимизацию. -
4 слайд
Задача
Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? -
5 слайд
Решение
Через год клиент должен будет выплатить
12 000 + 0,16 * 12 000 = 13 920 рублей.
Разделим 13 920 руб. на 12 мес.:
13 920/12 = 1 1160 руб./мес.
Значит, клиент должен вносить ежемесячно в банк
1 160 рублей.Ответ: 1 160.
-
6 слайд
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12 500 рублей. Сколько рублей он получит после вычета налога на доходы?
Задача -
7 слайд
Решение
Налог на зарплату Ивана Кузьмича составит 12 500 * 0,13 = 1 625 рублей. Значит, после вычета налога на доходы он получит 12 500 – 1 625 = 10 875 рублей.Ответ: 10 875
-
8 слайд
Задача
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 112%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены? -
9 слайд
Решение
Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 112%, то есть зарплата мужа составляет 56% дохода семьи. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 3%, то есть вся стипендия дочери составляет 6% дохода семьи. Таким образом, доход жены составит 100%-56%-6% = 38% дохода семьи.Ответ: 38.
-
10 слайд
Задача
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены? -
11 слайд
Решение
𝑥+𝑦+𝑧=100 100+2𝑥+2𝑦=288 𝑥=67 𝑥+𝑦+𝑧=100 𝑥+𝑦=94 𝑥=67
𝑥+𝑦+𝑧=100 𝑦=94−67 𝑥=67
𝑧=100−27−67 𝑦=27 𝑥=67
Ответ: 27 -
12 слайд
Задача
Четыре рубашки дешевле куртки на 8%. На сколько процентов пять таких рубашек дороже куртки? -
13 слайд
Цена четырех рубашек составляет 92% цены куртки. Значит цена одной рубашки составляет 23% цены куртки. Поэтому цена пяти рубашек составляет 115% цены куртки. Это превышает цену на 15%.
Решение -
14 слайд
Кредиты
На сумму выплачиваемых процентов влияет не только ставка, но и метод погашения кредита.
Таких методов существует два: дифференцированные платежи и аннуитетные платежи. -
15 слайд
Схемы погашения кредита
Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но увеличивает общую сумму начисляемых процентов.Дифференцированные — платежи характерны тем, что задолженность по кредиту погашается равномерно, начиная с самых первых выплат, а проценты начисляются на фактический остаток. Таким образом, каждый последующий платеж меньше предыдущего.
-
-
17 слайд
Задача: Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10 %. Существуют 2 схемы выплаты кредита.
-
18 слайд
Формулы для аннуитетных расчетов
n- платежные периоды
Sо- сумма кредита
m= 1+0,01q
q%- процентная ставка
Х- постоянные выплаты
Sn-величина текущего долга -
19 слайд
Формулы для дифференцированных платежей
n- платежные периоды Sо- сумма кредита
q% — процентная ставка, причем, каждый платежный период, долг сначала возрастает, по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода
Х- постоянные выплаты П-величина переплаты
В- полная величина выплат -
20 слайд
31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Задача -
21 слайд
Аннуитетный вид платежа.
Решение
-
22 слайд
Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?Задача
-
23 слайд
Предложение:
«Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму, без учета процентов, возвращал равными долями. Это значит дифференцированный платеж.Решение
-
24 слайд
Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
Задача -
25 слайд
Дифференцированный платеж.
-
26 слайд
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?Задача
-
27 слайд
Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма Х, которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет откуда
Ответ: 124 809 100 рублей
Решение -
28 слайд
Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма будет на счете у Василия через 4 года?
Задача -
29 слайд
1. После первого года хранения вклада:
Сумма вклада возрастает до 1 000 000 · 1,1 = 1 100 000 (р);
Дополнительное пополнение счета 1 100 000 + 133 000 = 1 233 000 (р);
2. После второго года хранения вклада:
Сумма вклада возрастает до 1 233 000 · 1,1 = 1 356 300 (р);
Дополнительное пополнение счета 1 356 300 + 133000 = 1 489 300 (р);
3. После третьего года хранения вклада:
Сумма вклада возрастает до 1 489 300 · 1,1 = 1 638 230 (р);
Дополнительное пополнение счета 1 638 230 + 133 000 = 1 771 230 (р);
4. После четвертого года хранения вклада:
Сумма вклада возрастает до 1 771 230 · 1,1 = 1 948 353 (р).Ответ: 1 948 353 рубля.
Решение
-
Краткое описание документа:
«Решение задач с практическим содержанием при подготовке к ЕГЭ по математике на профильном уровне» Анализ банка задач ЕГЭ по математике, а также демоверсии ЕГЭ 2021 года позволил выделить основные подходы к решению задач с практическим содержанием:1. решение с помощью формул; 2. решение задач в общем виде; 3. решение задач с использованием свойства степеней; 4. решение задач с помощью математического анализа; 5. решение задач методом сравнения
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 785 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы






- 09.05.2021
- 138
- 1

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
По теме: методические разработки, презентации и конспекты
Реализация принципа практической направленности подготовки обучающихся на уроках математики в 5 – 9 классах
Тема исследования: «Реализация принципа практической направленности подготовки обучающихся на уроках математики в 5 – 9 классах».Объектом исследования является процесс обучения математике обучаю…
Решение задач практической направленности на уроках математики в старших классах коррекционной школы.
Решение задач практической направленности на уроках математики в старших классах коррекционной школы….
Обобщение педагогического опыта учителя математики I квалификационной категории Куликовой Татьяны Николаевны по теме:«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ».
Существенную роль в повышении эффективности обучения школьников играет сформированность у них практических умений и навыков, которые необходимы как для изучения математики, так и для повседневно…
Тетрадь по математике для учащихся 4 классов коррекционных школ VIII вида «Задачи практической направленности».
В данном материале представлена тетрадь по математике для учащихся 4 классов коррекционных школ VIII вида «Задачи практической направленности».Вышеназванная тетрадь создана по сборнику «Дополнит…
Презентация к уроку математики «Решение задач практической направленности на нахождение площади»
Презентация к уроку математики в 8 классе по учебнику В.В. Эк…
Задачи для марафона по решению математических задач практической направленности
Подобраны задания для решения прикладных задач…
Использование задач практической направленности при обучении математике детей с интеллектуальной недостаточностью.
Требования современного общества к выпускникам школ определили необходимость пересмотра стандартов как общего, так и специального образования. Система специального образования имеет определённую …
Решение задач с физическим и практическим содержанием ЕГЭ по математике.
Учитель: Васильева Вадия Фаритовна
Тип урока: формирование новых знаний и их применение.
Межпредметные связи: математика, физика.
Методы работы: кейс-технология.
Тип кейса: обучающий
Цели урока:
1. Подготовка к ЕГЭ. Разработка и составление рекомендаций по решению задач физического и практического содержания №10 профильного уровня ЕГЭ по математике.
2.Развитие исследовательских навыков, умения анализировать, систематизировать, интерпретировать полученные результаты.
3.Повышение интереса учащихся к математике. Расширение кругозора через решение задач связанными с жизненными ситуациями.
Задачи урока:
Образовательные: Систематизировать знания и умения учащихся по решению задач физического и практического содержания.
Развивающие: Развивать умение работать с информацией в нестандартной ситуации; развивать логическое мышление, память, наблюдательность, умение представлять решение; развивать самостоятельную, творческую, исследовательскую деятельность; развивать способность к самооценке.
Воспитательные: Воспитывать уважительное отношение к товарищам, умение работать в команде; умение критически относиться к мнению одноклассников.
Метапредметные УУД:
1.Регулятивные:
1)определять цели, включая постановку новых целей, преобразование практической задачи в познавательную;
2)принимать решения в проблемной ситуации на основе переговоров;
2. Познавательные:
1) учиться основам реализации проектно-исследовательской деятельности;
2) осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
3.Коммуникативные:
1) учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
2)формулировать собственное мнение и позицию, аргументировать и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности;
3)работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
Содержание кейса.
1. Текст «Трудности ЕГЭ»
2. План работы группы.
3. Правила работы с кейсом.
4. Характеристика задания.
5. Задания группам.
6. Лист достижений группы.
7. Домашнее задание.
ХОД УРОКА.
1этап. Постановка проблемы, определение темы и цели урока. (10 мин)
Слово учителя:
-Здравствуйте ребята! Сегодня я хочу начать урок словами Д.Пойа «Если хочешь научиться плавать — смело входи в воду, а если хочешь научиться решать задачи — бери и решай».
-В последнее время вся деятельность на уроке направлена на то, чтобы качественно подготовиться к ЕГЭ. Сегодня мы будем это делать с помощью кейсов, работая в группах. Что это такое вы уже знаете, но я ещё раз напомню. Кейс — это набор документов, направленных на решение задач определённого типа. Работая вместе, вы чётко соблюдаете правила работы в группе (эти правила вы найдёте в кейсе). Чтобы определить тему урока и цель, предлагаю ознакомиться с первым документом кейса.
Один из учеников зачитывает текст из кейса вслух.
Первый документ. Текст «Трудности ЕГЭ»
Усилия практически всех выпускников 11 класса направлены на поступление в любой достаточно престижный ВУЗ. С этой целью они и выбирают сдавать профильный уровень ЕГЭ по математике. В настоящий момент выявилась одна из жестких проблем: как показал обзор источников информации по подготовке к ЕГЭ, зачастую, вместо стандартно сформулированных математических задач, на экзаменах появляются задания, отражающие «какие-то связи» с реальной жизнью. Ситуация усугубляется тем, что встреча с любыми величинами, напоминающими таковые в учебниках физики, приводит некоторых учеников в состояние стойкого оцепенения (ну не получается у них подружиться с физикой). Решая задания с кратким ответом, некоторые ребята сразу узнают своего «противника» — задание №10 с физическим и практическим содержанием. Им сложно оценить величие и различие слов «доход», «прибыль», «выручка», «рейтинг», мелькающих в этих задачах. Более того, там встречаются и худшие монстры: брошенные камни, то вертикально вниз, то вертикально вверх, перегревающиеся приборы, законы излучения звезд и другие не менее «интересные» задачи. Просмотрев учебник математики, мы понимаем, что там нет таких задач. К счастью, у нас много друзей. И почему бы не сосредоточить их интеллектуальные ресурсы во времени и пространстве на выработку каких -то подходов и тактик решения этой проблемы: как одолеть задание №10? Может, кто-то уже его победил? Может у кого-то есть верный способ, как обойти проблему? И как понять, нужно ли вообще волноваться по данному поводу?
Слово учителя:
-Итак, определяем тему урока: (Решение задачи №10 с физическим и прикладным содержанием)
-Какую цель вы сегодня поставите перед собой на уроке? (овладение приёмами решения задачи №10 профильного ЕГЭ по математике, разработка рекомендаций к решению задач этого типа)
-Как вы кратко охарактеризуете эту задачу? (Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства средствами математики).
-Каждой группе нужно разработать и представить на уроке сколько получится, но, желательно, не менее пяти рекомендаций по решению задания № 10 профильного ЕГЭ по математике. Доказать преимущества своих рекомендаций. У каждой группы будет ровно одна задача. На эту работу отводится 10 мин. Если группа справится раньше, представитель сразу выходит на презентацию и защиту решения.
2 этап. Работа над проблемой. (10 мин)
Далее учащиеся сначала самостоятельно изучают содержимое кейса, затем задают уточняющие вопросы, учитель даёт необходимые комментарии.
Второй документ. «План работы группы»
1. Определить руководителя группы, перед которым будет стоять задача координировать работу группы и оценивать работу её участников.
2. Определить секретаря, который будет фиксировать предложенные решения и представителя, который будет защищать эти решения.
3. Внимательно изучить материалы кейса
4. Проанализировать материал и обсудить изученную информацию
5. Обменяться мнениями и составить план работы над задачей
6. Зафиксировать основные и второстепенные проблемы.
7. Работать сообща над проблемой (дискуссия)
8. Выработать решение задачи с оформлением.
9. Представить решение и общие рекомендации по решению задач этого типа.
10. Доказать его оптимальность (чем выгодно это решение).
Третий документ. Правила работы с кейсом в группе.
|
Этапы |
Цель этапа |
|
Знакомство с конкретным случаем |
Понимание проблемной ситуации и ситуации принятия решения |
|
Поиск: оценка информации, полученной из материалов задания, и самостоятельно привлеченной информации |
Научиться добывать информацию, необходимую для поиска решения и оценивать ее |
|
Обсуждение: обсуждение возможностей альтернативных решений |
Развитие альтернативного мышления |
|
Резолюция: нахождение решения в группах |
Сопоставление и оценка вариантов решения. |
|
Диспут: отдельные группы защищают свое решение |
Аргументированная защита решений |
|
Сопоставление итогов: сравнение решений, принятых в группах |
Оценить взаимосвязь интересов, в которых находятся отдельные решения |
Четвёртый документ. Характеристика задания.
Задачи с физическим содержанием
Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства.
Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ (имеются задачи, в которых нужно выбрать одно из двух решений, имеются и другие нюансы).
Есть задачи которые сводятся к решению показательных, логарифмических, тригонометрических уравнений и неравенств. Ответ в любом случае, должен получиться в виде целого числа или конечной десятичной дроби.
На экзамене с этим заданием успешно справляются около 40%.выпускников. Наибольшая трудность в заданиях такого типа – чтение, понимание условия, применение математических знаний. Около 15% участников экзамена просто не взялись за эту технически простую задачу.
На что необходимо обратить внимание:
1.Если в вопросе прозвучало «определить наибольшее значение», «определить наименьшее значение», то задача в большинстве случаев решается через составление неравенства.
2. Правильно определяйте знак при составлении неравенства. Например: b не менее 21 записывается как b≥21.
3. Если в вопросе задачи прозвучало «сколько», то составляется уравнение.
4. Не забывайте про единицы измерения, если это необходимо (переводим метры в сантиметры, наоборот и пр.) Все величины подставлять в одних единицах измерения.
5. Не упускайте из виду, в каких единицах измерения требуется записать ответ (например, решив задачу, вы получили 0,5 часа, в условии сказано записать ответ в минутах, получается 30 минут; если запишите 0,5 – это ошибка и потерянный бал, хотя задача решена, верно).
Пятый документ Задачи для групп.
1 группа
№10 . Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: T(t)=T0 +b t+a t2, где t — время (в мин.), T0 =1380 К, a=− 15 К / мин2, b=165 К / мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
2 группа
№10. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+13 t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?
3 группа
№10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a=9000 км /ч. Скорость v (в км/ч) вычисляется по формуле v=√2la, где l — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 120 км/ч.
4 группа
№10. Груз массой 0,38 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону v=v0sin
в секундах, T=8 с — период колебаний, v0=2 м /с. Кинетическая
энергия E (в Дж) груза вычисляется по формуле E=(mv2)/2, где m — масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.
5 группа
№10. Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель — целое число от 0 до 3. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вчетверо дороже, чем оперативность, то есть R=(3In+Op+4Tr)/A. Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило рейтинг 30.
3 этап. Защита своих идей. (10 мин)
На этом этапе дети в произвольной форме проводят презентацию решений и формулирование рекомендаций. Скорее всего все группы не успеют выступить, поэтому, защита может быть перенесена на следующий урок с последующим фронтальным закреплением.
ПРОЕКТ ПРЕДЛОЖЕНИЙ, как общий вывод, записывается в тетрадь.
4 этап. Подведение итогов (рефлексия) (5 мин)
Подведение итогов проходит в форме пресс-конференции, в ходе которой учащиеся отвечают на вопросы:
• Что общего в представленных заданиях?
• Что отличает группу заданий №10 от других заданий?
• Есть ли такие задачи в наших учебниках?
• Что хотят проверить составители подобных заданий?
• Хватит ли времени решить все задачи открытого банка задач?
• Стоит ли это делать?
• Являются ли задачи с практическим содержанием №10 отражением реальных жизненных ситуаций?
• Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?
• Можете ли вы сами найти информацию для подготовки к ЕГЭ в сети Интернет, полезные ссылки на on-line тестирование? Все ли они помогут при подготовке к экзаменам?
• Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие?
5 этап. Домашнее задание. (в кейсе)
Задания практического содержания №10из открытого банка задач ФИПИ на карточках с полным оформленным решением в тетради.
Приложение
Лист достижений группы № ______
Руководитель группы _______________________________
Секретарь_________________________________________
Участники группы
_________________________________________
_________________________________________
_________________________________________
Количество набранных баллов группы
I этап работы в группе ( поиск, обсуждение, нахождение решений) (от 0 до 5 баллов)
II этап работы в группе (составление рекомендаций по решению) (от 0 до 5 баллов)
III этап (защита решений и представление рекомендаций)
Оценивание работы отметкой каждого участника группы.
Тема урока: Решение задач с практическим содержанием при подготовке к ЕГЭ по математике на профильном уровне. Сколько стоит кредит?
Цель урока: создать условия для формирования практических навыков решения проблемной ситуации, приближенной к жизни, посредством кейс-технологии.
Задачи урока:
дидактическая (обучающая):
—формирование у учащихся представления о сути операции «потребительский кредит» и порядка расчеты суммы платежей, используя кредитный калькулятор банков для применения знаний обучающимися комплекса знаний и способов действий при покупке товара в кредит;
развивающая:
-совершенствовать развитие логического мышления, умения анализировать, сравнивать, обобщать и делать выводы; развивать навыки аргументировано доказывать свое мнение, участвовать в дискуссии;
воспитательная:
-воспитывать уважение к кредитной политике и правовому самосознанию; формировать у учащихся финансовую грамотность, гражданскую ответственность и активную жизненную позицию.
Тип урока: урок-практикум.
Метод обучения: проблемный метод, кейс-метод, интерактивный метод. (критического?)
Формы организации учебной деятельности: фронтальная, групповая, использование ИКТ.
Элементы образовательных педагогических технологий: кейс-технология, технология проблемного обучения, технология сотрудничества, информационно-коммуникационная технология.
Форма оценивания: самооценка по накопительной системе. Максимальный балл за урок — 30 баллов, в том числе: решение кроссворда — до 10 баллов, работа с кейсом — до 15 баллов, активность на уроке — до 5 баллов.
Оборудование: персональный компьютер преподавателя, мультимедийный проектор, презентация с видеофрагментом проблемной ситуации, ноутбуки или телефоны для учащихся с выходом в Интернет, раздаточный материал для групповой работы.
Ход урока
Девиз урока:
«Дорогу осилит идущий, а математику — мыслящий»
Цитата урока: «Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, как располагать своими средствами для достижения по возможности большей выгоды» П. Л. Чебышев.
I. Мотивирование на учебную деятельность (Урок сопровождается компьютерной презентацией.)
— Здравствуйте ребята.
Прочитайте высказывание русского математика и механика П. Л. Чебышева на экране. (один из учащихся читает высказывание вслух)
— Как вы думаете, чем мы сегодня на уроке будем заниматься?
— Правильно, мы сегодня будем решать задачи с практическим содержанием.
Математика – царица всех наук, она нужна практически всем. Ее нужно знать для экономики, для повседневной жизни и т.д. На сегодняшнем уроке мы и попытаемся установить связь между экономикой и математикой. (Учащиеся определили тему и задачи урока)
У вас на столах оценочные листы, которые вы заполняете в ходе выполнения работ.
II.Актуализация опорных знаний.
— какие задания ЕГЭ имеют практическую направленность? (задание 15)
1.Устная работа по заданиям ЕГЭ (фронтальная работа)
1.Какие виды экономических задач вы знаете?
1).Задачи на кредиты.
2).Задачи на вклады.
3).Задачи на оптимизацию.
2.Назовите этапы решения экономических задач.
1).Составление математической модели.
2).Работа с математической моделью.
3).Анализ решения. Ответ на вопрос задачи.
2.Текстовая работа
Тест создан с помощью Google – формы. Учащиеся выполняют задания теста в тетради (возможно устное решение) и заносят ответ в Google – форму. Все ответы фиксируются в общей таблице и учащиеся сразу получают оценку.
1. Платежи по кредиту не должны превышать 40% доходов. Каков максимальный платеж по кредиту при доходах 10 000 руб. в месяц?
2. Под какой максимальный процент в месяц выгодно брать кредит при инфляции 24% в год?
3. Покупатель приобрел фотоаппарат за 10 тыс. руб. в кредит на 1 год под 20% годовых. Стоимость фотоаппарата через год составила 13 тыс. руб. Был ли выгоден кредит?
4. Кредит на сумму 10 000 руб. выдан на год под 36% годовых с единовременным погашением с процентами в конце срока. Какова будет переплата?
5. Кредит на сумму 10 000 руб. выдан на год под 1% в день с единовременным погашением с процентами в конце срока. Сколько рублей нужно будет уплатить в конце года?
6. Кредит на сумму 10 000 руб. взят на три месяца с единовременным погашением с процентами в конце срока. В конце срока за банку было уплачено 10 330 руб. Какому проценту годовых с единовременным погашением с процентами в конце срока это соответствует?
Самопроверка по готовым ответам (слайд презентации)(Оценочный лист)
3. Решение задач №15 из открытого банка задач «Решу ЕГЭ»(слайд10)
О каких видах кредита вы слышали или знаете? (Ответы учащихся)
Сегодня на занятии речь пойдет о потребительском кредите. Вопрос нашего урока: «Сколько стоит кредит?»
III. Создание проблемной ситуации.
Учитель.
Давайте представим простую житейскую ситуацию. Внимание на слайд.
1.К какому виду кредита относится покупка ноутбука? (Ответы учащихся)
2.С какой проблемой столкнулись герои сюжета? (Ответы учащихся)
3.Как эту проблему хочет решить семья? (Ответы учащихся)
Семья Ивановых намерена рассмотреть предложения трех известных банков: Сбербанк, Россельхозбанк и ВТБ банк. Вам необходимо помочь семье Ивановых определить, в каком банке выгоднее взять кредит.
-Что семье Ивановых необходимо знать при оформлении кредита? (Ответы учащихся)
Заемщику необходимо знать:
-
годовую процентную ставку;
-
ежемесячный платеж;
-
полную стоимость кредита.
Что такое полная стоимость кредита? (Ответы учащихся)
Полная стоимость кредита – это сумма, которая максимально близко отражает стоимость кредита для заемщика. Она рассчитывается банком по специальной формуле и указывается в виде процентов годовых и суммы кредита.
IV. Этап построения выхода из проблемной ситуации.
Ваша задача на уроке помочь семье Ивановых, ответив на вопрос: на каких условиях семья Ивановых сможет оформить кредит в банке.
Для этого вы будете работать в паре. На столах у вас есть кейс с ситуацией, вопросом к ситуации и алгоритм решения. Также есть таблица, куда вы будете вносить данные.
Кейс
Ситуация
Семья Ивановых Максим и София решили купить своему сыну Роману в подарок на день рождения ноутбук за 59990 рублей. У них есть 10000 рублей на первоначальный взнос. Заработанная плата Максима оставляет 37000 рублей, а Софии — 25000 рублей. Совокупный доход семьи позволяет им взять кредит сроком на 15 месяцев.
Вопрос
Определите ежемесячный платеж, процентную ставку кредитования, полную стоимость кредита и переплату по кредиту.
Учитель
Как можем узнать ежемесячный платёж? (Ответы учащихся)
Есть несколько способов, например, в офисе банка, по формуле и с помощью кредитного калькулятора на сайте банка.
Мы с вами сегодня научимся пользоваться кредитным калькулятором на сайте банков.
Алгоритм действий у вас прописан в кейс-задании. Время на выполнения задания 7 минут. По истечении времени один представитель от группы (докладчик) представит результаты работы, а секретарь внесет данные в сравнительную таблицу.
Сравнительная таблица (на слайде)
|
Вопросы для сравнения |
Сбербанк |
Россельхоз банк |
ВТБ банк |
|
Срок кредита |
15 месяцев |
15 месяцев |
15 месяцев |
|
Сумма кредита |
50000 |
50000 |
50000 |
|
Процент по кредиту |
|||
|
Ежемесячная выплата по кредиту |
|||
|
Полная стоимость кредита |
|||
|
Переплата по кредиту |
|||
|
Выгодное предложение |
V. Рассмотрение предложенных вариантов, поиск оптимального решения.
Учитель
Итак, время закончилось. Проанализируем, что у вас получилось. Докладчик от группы представит результаты работы.
Учитель
В какой банк выгоднее обратиться семье Ивановых? (Ответы учащихся)
Судя по переплате — да, выгоднее обратиться в ….. банк. Кроме того, размер ежемесячного платежа там тоже меньше и не превышает 30% совокупного дохода семьи.
Оцените свою работу с кейс-заданием и проставьте баллы в оценочный лист.
VI. Закрепление приобретенных знаний.
Учитель
Какова была тема занятия? (Ответы учащихся)
О каком виде кредита мы с вами сегодня говорили? (Ответы учащихся)
Выберите, какая покупка отвечает условиям потребительского кредита?
-
Покупка мобильного телефона
-
Покупка нового автомобиля
-
Покупка мебели
-
Покупка бытовой техники
-
Покупка жилья
Ответы учащихся
Учитель
1.Что нового вы узнали сегодня на уроке? (Ответы учащихся)
2.Вы узнали, что при оформлении потребительского кредита необходимо учитывать процент по кредиту, сумму ежемесячного, полную стоимость кредита и научились работать с кредитным калькулятором на сайте банка.
А для того, чтобы вы всегда помнили о нюансах потребительского кредита, я дарю вам на память буклеты с полезной информацией.
Учитель
Оцените свою работу и сдайте мне оценочные листы.
VII. Домашнее задание.
Используя ситуацию кейса, в качестве домашнего задания учащимся предлагается найти график платежей по потребительскому кредиту (возможно в семье приобретались товары в кредит и сохранились документы или поинтересоваться условиями предоставления кредита в любом магазине).
Задание: сделайте анализ платежного документа и ответьте на вопросы:
-
Какую годовую ставку предлагает банк по потребительскому кредиту?
-
На какой срок оформляется кредит?
-
Какую сумму составит переплата по кредиту? Равна ли она заявленной процентной ставке?
-
Почему сумма основного долга увеличивается от первого платежа к последнему, а сумма процентов уменьшается?
-
Предусмотрены ли комиссии и штрафные санкции за просрочку платежа? Какие именно
VIII. Рефлексия учебной деятельности.
Итак, вы хорошо поработали на занятии, но мне хотелось бы услышать, какие выводы вы сделали на нашем уроке.
Жизнь современного человека полна соблазнов. Если раньше люди по несколько лет стояли в очереди на квартиры, машины, как говорится
«наживали добро годами», то сегодня ситуация изменилась коренным образом. Можно взять кредит и удовлетворить все свои потребности разом.
Что это- дань моде, которая пришла к нам с Запада, или на самом деле действительно возможность решить все свои проблемы?
А может это просто желание быстро разбогатеть?
-
Тема нашего урока была какая?
-
В случае необходимости, что же вы сможете рассказать вашим друзьям о потребительском кредите?
-
Будут ли вам полезны эти знания? Ребята, где вам пригодятся знания, полученные на этом уроке? (Ответы учащихся)
Спасибо за ответы и работу на уроке.
Урок окончен. До свидания.
Интернет-ресурсы:
-
Россельхозбанк : официальный сайт. – URL: https://www. .ru (дата обращения 12.04.2022).
-
Сбербанк России : официальный сайт. – URL: https://www.sberbank.ru (дата обращения 12.04.2022).
-
ВТБ банк : официальный сайт. – URL: https://www.vtb.ru (дата обращения 12.04.2022).
Самоанализ.
В ходе урока обучающиеся осваивают основные понятия финансовой грамотности, изучают устройство банковской системы кредитования, системы страхования; осваивают способы разумного взаимодействия семьи с различными финансовыми институтами, знакомятся с правами потребителя финансовых услуг, учатся их защищать. Важно сформировать у обучающихся представления о ценности ответственного, грамотного поведения в сфере личных и семейных финансов, в том числе через ведение семейного бюджета
Учебное время на уроке использовалось эффективно, запланированный объём урока выполнен. Интенсивность урока была оптимальной с учётом физических и психологических особенностей детей.
Учащиеся сразу включились в процесс урока, они были заинтересованы, проявляли активность и ответственность при выполнении заданий. Задания, данные преподавателем, они выполняли с интересом. Эмоциональный фон урока положительный.
Предложенная нагрузка была оптимальной для занимающихся. В ходе урока учитель способствовал формированию интереса, убеждений и потребностей в занятиях экономикой.
План урока выполнен. Поставленные перед уроком цели были реализованы в полной степени.
Оценочный лист: _________________________________
|
Устный опрос (max 3б) |
Текстовая работа (max 6б) |
Решение задач типа задание 15 (max 2б) |
Решение кейса (max -15б) |
Активность на уроке (max -4б) |
Итого |
Оценка |
|
Максимальное количество баллов – 30 баллов 26 — 30 баллов – оценка «5»; 21 — 25 баллов – оценка «4»; 15 — 20 баллов – оценка «3»; 0 -14 баллов – оценка «2». |
Оценочный лист: _______________________________
|
Устный опрос (max 3б) |
Текстовая работа (max 3б) |
Решение задач типа задание 15 (max 2б) |
Решение кейса (max -15б) |
Активность на уроке (max -5б) |
Итого |
Оценка |
|
Максимальное количество баллов – 30 баллов 26 — 30 баллов – оценка «5»; 21 — 25 баллов – оценка «4»; 15 — 20 баллов – оценка «3»; 0 -14 баллов – оценка «2». |
Приложение 2
РАБОЧИЙ ЛИСТ
Тема урока_____________________________________________________
Кроссворд
|
1 |
|||||||||||
|
2 |
3 |
||||||||||
|
4 |
|||||||||||
|
5 |
|||||||||||
|
7 |
|||||||||||
|
8 |
|||||||||||
|
9 |
|||||||||||
|
10 |
|||||||||||
По горизонтали:
4. Документ, который регламентирует отношения банка и заемщика.
5. Объект потребительского кредита.
7. Единица измерения кредитной ставки.
8. Способ погашения кредита равными платежами.
10. Документ, необходимый для получения потребительского кредита.
По вертикали:
-
Банк, предоставляющий кредит, по отношению к заемщику.
-
Лучшая участь любого кредита.
-
На какой период обычно рассчитывается процентная ставка в банке.
-
Первым условием кредита является возвратность. Что является вторым?
9. «Наказание» для нерадивого плательщика.
КЕЙС-ЗАДАНИЕ
Ситуация
Семья Ивановых Максим и София решили купить своему сыну Роману в подарок на день рождения ноутбук за 59990 рублей. У них есть 10000 рублей на первоначальный взнос. Заработанная плата Максима оставляет 37000 рублей, а Софии — 25000 рублей. Совокупный доход семьи позволяет им взять кредит сроком на 15 месяцев.
Вопрос
Определите ежемесячный платеж, процентную ставку кредитования, полную стоимость кредита и переплату по кредиту.
Алгоритм действия
-
Зайдите на сайт банка по ссылке:
https://www. .ru/; https://www.sberbank.ru/, https://www.vtb.ru
2.Найдите вкладку кредит, из списка выберите кредит наличными,
рассчитать кредит.
3.Введите данные по кредиту:
-
сумма кредита (стоимость ноутбука минус первоначальный взнос)
-
срок кредита
4.Внесите данные в таблицу рабочего листа.
5.Рассчитайте полную стоимость кредита.
6.Рассчитайте переплату по кредиту.
|
Вопросы для сравнения |
Сбербанк |
Россельхоз банк |
ВТБ банк |
|
Срок кредита |
|||
|
Сумма кредита |
|||
|
Процент по кредиту |
|||
|
Ежемесячная выплата по кредиту |
|||
|
Полная стоимость кредита |
|||
|
Переплата по кредиту |
Алгоритм расчета размера единовременного платежа при оформлении потребительского кредита:
-
Находим сумму выплаты при покупке;
-
Находим сумму кредита
-
Находим наращенную сумму, подлежащую выплате;
-
Находим сумму единовременного платежа.
Многие старшеклассники считают, что задача 8 Профильного ЕГЭ по математике — это «физика». А поскольку с физикой дружат не все, то и задачу считают «сложной» и обходят стороной.
С другой стороны, на Ютьюбе и вообще в интернете появляются «полезные» советы по решению этой задачи. Условие, мол, читать не надо, главное — найти формулу, подставить в нее все «буковки» и посчитать, что получилось.
На самом деле это, конечно, не физика. Это обычная математика, школьный курс. Правда, знать нужно немало. И обязательно читать условие. И очень внимательно.
Первая задача — простая.
1. При сближении источника и приемника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала Гц и определяется следующим выражением:
(Гц), где
— скорость распространения сигнала в среде (в м/с), а
м/с и
м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмникеf будет не менее 120 Гц?
По условию, частота сигнала Гц.
Подставим данные в выражение для . Получим:
Значит, наибольшее возможное значение
равно 279.
Ответ: 279.
Линейные уравнения и неравенства (и сводящиеся к ним)
Следующая — настоящая ловушка для старшеклассников. Сколько раз эта задача встречалась и на диагностических работах, и на реальных ЕГЭ! И все равно многие в ней ошибаются.
2. При температуре рельс имеет длину
м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону
, где
— коэффициент теплового расширения,
— температура (в градусах Цельсия). При какой температуре рельс удлинится на 3мм? Ответ выразите в градусах Цельсия.
Решите самостоятельно — и проверьте, что получилось. Дело в том, что учащиеся часто получают в этой задаче абсурдные ответы. Например, говорят, что рельс удлинится на 3 миллиметра при температуре 7000 градусов. Но это больше, чем температура на поверхности Солнца! Рельс расплавится.
Зависимость — это функция длины рельса от температуры. Длина рельса зависит от температуры по определенному правилу. Мы помним из физики, что при нагревании тела расширяются, а при охлаждении — сжимаются, и особенно это заметно для металлов. При изменении температуры длина металлического рельса может измениться на несколько миллиметров.
Подставим в эту формулу начальные значения: м и
. Рельс удлинился на 3 мм, то есть в какой-то момент его длина стала на 3 мм больше. Значит, при определенной температуре длина рельса
стала равной 10 м + 3 мм.
Теперь переведем миллиметры в метры. Один миллиметр — это одна тысячная часть метра
().
. (м)
Получим:
Это линейное уравнение с одной переменной . Раскроем скобки в правой части
Находим :
При температуре 25 градусов Цельсия рельс удлинится на 3 мм.
Ответ: 25.
Парабола и квадратные неравенства
Темы для повторения:
Квадратичная функция
Квадратичные неравенства
3. Зависимость объёма спроса (единиц в месяц) на продукцию предприятия-монополиста от цены
(тыс.руб.) задаётся формулой
. Выручка предприятия за месяц
(в тыс.руб.) вычисляется по формуле
. Определите наибольшую цену
, при которой месячная выручка
составит не менее 210 тыс.руб. Ответ приведите в тыс.руб.
Здесь точно придется читать условие. И решать именно неравенство, а не уравнение.
Поскольку месячная выручка не менее 210 тысяч рублей,
График функции в левой части неравенства — квадратичная парабола с ветвями вниз.
Заметим, что это неравенство не превращается в уравнение . Уравнение здесь нужно для того, чтобы найти, при каких значениях
выручка равна 210. Решив его, получим:
или
. Решения неравенства:
Наибольшее значение равно 14.
Ответ: 14.
— «Отлично, — скажете вы. Берем больший из корней квадратного уравнения, и готово». Так ли это? — Конечно, нет. Надо внимательно прочитать условие и понять, что же будет ответом задачи.
4. Выcота над землёй подброшенного вверх мяча меняетcя по закону , где
— выcота в метрах,
— время в cекундах, прошедшее c момента броcка. Cколько cекунд мяч будет находитьcя на выcоте не менее трёх метров?
Запишем, что
Построим график функции в левой части — то есть зависимость высоты мяча от времени.
Мы видим, что через секунд после начала полёта мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота увеличивалась. Затем началось снижение, высота уменьшалась, и в момент времени
снова стала равна трём метрам над землей. Получается, что мяч находился на высоте не менее трёх метров в течение
секунд.
Осталось найти разность
Для этого решим квадратичное неравенство
Работать с дробными коэффициентами неудобно. Умножим обе части неравенства на 5:
Найдем корни соответствующего уравнения
Разность
Ответ: 1,2.
Вот еще одна задача из первой части варианта профильного ЕГЭ, в которой больше решающих получают неправильный ответ. Только потому, что не пользуются графиком.
5. Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экcпериментально и на иccледуемом интервале температур определяетcя выражением , где
— время в минутах,
K,
K/мин,
K/мин. Извеcтно, что при температуре нагревателя cвыше 1760 K прибор может иcпортитьcя, поэтому его нужно отключать. Определите, через какое наибольшее время поcле начала работы нужно отключать прибор. Ответ выразите в минутах.
Решите самостоятельно. Какой ответ у вас получился?
По условию, зависимость температуры нагревательного элемента от времени определяется формулой:
В нормальном режиме работы прибора должно выполняться неравенство , или
Нарисуем график зависимости температуры нагревателя от времени:
. Это квадратичная парабола с ветвями вниз.
Мы включаем прибор в момент времени Температура нагревателя повышается и в момент времени
достигает 1760 К. Если в этот момент прибор не выключить, температура продолжает повышаться. Но это значит, что прибор испортится, то есть сгорит! Ясно, что отключать его надо в момент времени
Осталось найти Решим квадратичное неравенство:
Корни соответствующего квадратного уравнения:
Мы нашли, что
Ответ: 2.
Ну как? Вы все еще считаете, что условие можно не читать? : -)
Квадратичные функции в задании №8 Профильного ЕГЭ — это еще не всё. Впереди степенные, показательные, логарифмические и тригонометрические уравнения и даже неравенства.
Степенные уравнения и неравенства
Тема для повторения: Степенная функция
6. При адиабатическом процессе для идеального газа выполняется закон где
— давление в газе в паскалях, V — объeм газа в кубических метрах,
Найдите, какой объём
(в куб. м) будет занимать газ при давлении
, равном
.
Подставим данные в уравнение
Ответ: 8.
Показательные уравнения и неравенства
Темы для повторения:
Показательная функция.
Показательные неравенства.
7. Уравнение процесса, в котором участвовал газ, записывается в виде , где
(Па) — давление в газе,
— объём газа в кубических метрах,
— положительная константа. При каком наименьшем значении константы
уменьшение вдвое раз объёма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Согласно понятиям термодинамики, в каждом состоянии газ характеризуется определенными параметрами — давлением, объемом, температурой. По условию задачи, газ переходит из одного состояния в другое так, что Это значит, что
Объем уменьшился вдвое, то есть
Поскольку , получим, что
Тогда
Наименьшее значение записываем в ответ.
Ответ: 2.
Логарифмические уравнения и неравенства
Темы для повторения:
Логарифмы.
Логарифмические неравенства.
8. Водолазный колокол, содержащий моля воздуха при давлении
атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления
Работа, совершаемая водой при сжатии воздуха, определяется выражением
, где
— постоянная,
— температура воздуха. Найдите, какое давление
(в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 29100 Дж.
Подставим все данные в уравнение для совершенной водой работы:
Ответ: 7.
Тригонометрические уравнения и неравенства
Темы для повторения: Тригонометрия
9. При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом
нм наблюдают серию дифракционных максимумов. При этом острый угол
(отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума
связаны соотношением
. Под каким минимальным углом
(вградусах) можно наблюдать третий максимум на решeтке с периодом, не превосходящим 2400 нм?
Запишем условие задачи в виде неравенства. Заметим, что нам нужен третий максимум, то есть номер максимума .
Поскольку угол — острый,
Ответ: 30.
Это была простая задача по тригонометрии. А закончим мы самыми сложными, какие только могут встретиться в этой теме, — тригонометрическими неравенствами.
10. Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону , где
— время в секундах. Кинетическая энергия груза, измеряемая в джоулях, вычисляется по формуле
, где
— масса груза (в кг), — скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5
Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
. Применим формулу понижения степени:
Нарисуем график функции при
Значения этой функции не больше нуля ровно половину времени из первой секунды.
Ответ: 0,5.
11. Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по закону , где
— время в секундах. Кинетическая энергия груза вычисляется по формуле
, где
— масса груза (вкг),
— скорость груза (вм/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее
Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
По формуле понижения степени
Отсюда
Построим график функции при
(при
);
(при
);
(при
);
(при
);
(при
);
(при
).
Найдем, каждую часть из первой секунды выполняется неравенство
Получим, что при
на
и
Вместе эти отрезки составляют от первой секунды;
Ответ: 0,33.
Кому-то удобнее рисовать в этой задаче не график, а тригонометрический круг. Это дело вкуса. Главное — не решать тригонометрические неравенства в уме. И конечно, внимательно читать и анализировать условие : -)
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание №8. Задачи с прикладным содержанием u0026#8212; профильный ЕГЭ по математике.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023