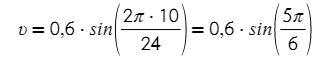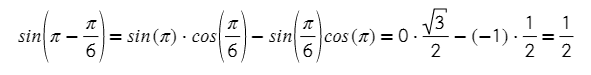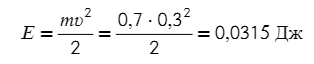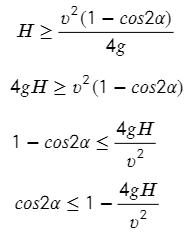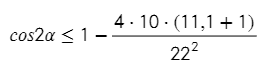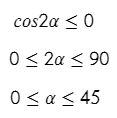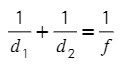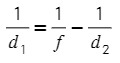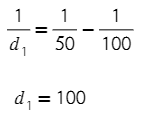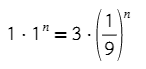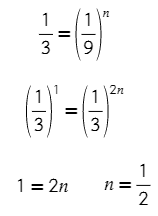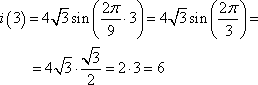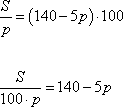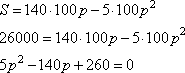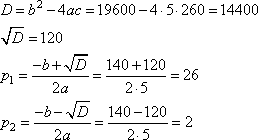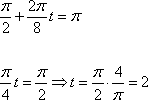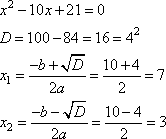Задачи с прикладным содержанием математика егэ как решать - Помощь в подготовке к экзаменам и поступлению

В этой статье мы рассмотрим общие подходы, позволяющие решать задачи из Задания В11.

Не смотря на ужасающие формулы и неведомые физические величины и константы, в конечном итоге, все эти задачи сводятся к решению несложных неравенств или уравнений. В большинстве случев они решаются на уровне здравого смысла.

Я рекомендую решать их в таком порядке.

1. Внимательно читаем задачу, и, не обращая внимание на подробности в виде формул и констант, стараемся представить, о чем в задаче идет речь.

2. Читаем вопрос, смотрим, о какой величине спрашивается в задаче, и что именно нам нужно о ней узнать.

3. Записываем вопрос задачи в виде уравнения или неравенства, в левой части которого стоит указанная величина.

4. Ищем в условии задачи, какой формулой эта величина выражается.

5. Подставляем в эту формулу указанные в условии константы.

6. Решаем получившееся уравнение или неравенство.

7. Прежде чем записать ответ, еще раз читаем вопрос, и проверяем, то ли мы нашли.

Решим этим способом несколько задач.

1. Задание B11 (№ 27954)

Некоторая компания продает свою продукцию по цене руб. за единицу, переменные затраты на производство одной единицы продукции составляют руб., постоянные расходы предприятия руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле . Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.

Лично я не представляю, о чем в задаче идет речь. Переходим к п. 2 — читаем вопрос задачи: «Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000руб».

Месячная операционная прибыль — что бы это ни значило — это, по условию задачи {pi}(q) . Эта величина должна быть не меньше 300000руб. Значит, наша задача решить неравенство .

Эта величина выражается формулой

Следовательно, нам нужно решить неравенство .

Подставим в это выражение константы из условия задачи:

Получим неравенство:

Отсюда: q>=5000 .

Теперь еще раз читаем вопрос задачи: определите наименьший месячный объeм производства q (единиц продукции). То есть в ответе надо указать наименьшее q, удовлетворяющее неравенству.

Ответ: 5000.

Задание B11 (№ 27956)

Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле . Определите наибольшую цену p, при которой месячная выручка составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

Как и в предыдущем примере, не будем вдаваться в физический смысл процесса. Читаем вопрос задачи: «Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тыс. руб.»

Месячная выручка в условии задачи — это величина r(p) . То есть нам надо решить неравенство .

Месячная выручка вычисляется по формуле r(p)=qp , где , в свою очередь, задаeтся формулой . Получаем неравенство:

Решим это неравенство:

4<=p<=6

Еще раз читаем вопрос задачи: определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

То есть в ответе надо указать наибольшее значение р, удовлетворяющее неравенству.

Ответ: 6.

Задание B11 (№ 27957)

Высота над землeй подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?

В этой задаче понятно что происходит. Мяч сначала двигается вверх, затем достигает верхней точки и начинает двигаться вниз. В какой-то момент времени мяч достигает 3-х метров, затем некоторое время находится выше трех метров, и потом снова оказывается ниже.

Нам нужно решить неравенство h>=3 . Высота меняется по закону , следовательно решаем неравенство:

Корни этого квадратного трехчлена: x_1=0,2 , x_2=1,4

Нанесем корни на координатную прямую и расставим знаки:

В задаче требуется найти, сколько секунд мяч будет находиться на высоте не менее трeх метров, то есть нас интересует длина промежутка, на котором выполняется неравенство:

Ответ: 1,2 сек.

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Новотроицкий ММЦ

Задачи с прикладным содержанием в ЕГЭ по математике.

Учитель математики МБОУ

«средняя общеобразовательная

школа №7 г. Медногорска»

Загоруйко Ольга Анатольевна

Март 2022

Задание №7. Задачи с прикладным содержанием —

профильный ЕГЭ по математике.

Многие старшеклассники считают, что задача 7 Профильного ЕГЭ по
математике — это «физика». А поскольку с физикой дружат не все, то и задачу
считают «сложной» и обходят стороной.

С другой стороны, на Ютьюбе и вообще в интернете появляются
«полезные» советы по решению этой задачи. Условие, мол, читать не надо, главное
— найти формулу, подставить в нее все «буковки» и посчитать, что получилось.

На самом деле это, конечно, не физика. Это обычная математика,
школьный курс. Правда, знать нужно немало и обязательно внимательно читать
условие.

Начнем
с простой задачи.

1.
При сближении источника и приемника звуковых сигналов, движущихся в некоторой
среде по прямой навстречу друг другу, частота звукового сигнала,
регистрируемого приёмником, не совпадает с частотой исходного сигнала  Гц
и определяется следующим выражением: $f=f_0frac{c+u}{c-v}$ (Гц), где  —
скорость распространения сигнала в среде (в м/с), а  м/с
и  м/с
— скорости приёмника и источника относительно среды соответственно. При какой
максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала
в приёмникеf будет не менее 120 Гц?

По
условию, частота сигнала Гц.

Подставим
данные в выражение для . Получим: $110cdot frac{c+9}{c-15}ge 120$

$frac{c+9}{c-15}ge frac{12}{11}$

$frac{11c+99-12c+180}{11(c-15)}ge 0,$

$frac{279-c}{c-15}ge 0$

Значит, наибольшее
возможное значение равно 279.

Ответ:
279.

Линейные уравнения и неравенства (и сводящиеся к ним)

Следующая
— настоящая ловушка для старшеклассников. Сколько раз эта задача встречалась и
на диагностических работах, и на реальных ЕГЭ! И все равно многие в ней
ошибаются.

2.
При температуре $0^{circ}C$ рельс
имеет длину $l {}_{0} =10$ м.
При возрастании температуры происходит тепловое расширение рельса, и его длина,
выраженная в метрах, меняется по закону ,
где $alpha =1,2cdot {10}^{-5}$ —
коэффициент теплового расширения, —
температура (в градусах Цельсия). При какой температуре рельс удлинится на 3мм?
Ответ выразите в градусах Цельсия.

Решите
самостоятельно — и проверьте, что получилось. Дело в том, что учащиеся часто
получают в этой задаче абсурдные ответы. Например, говорят, что рельс удлинится
на 3 миллиметра при температуре 7000 градусов. Но это больше, чем температура
на поверхности Солнца! Рельс расплавится.

Зависимость — это функция длины рельса от
температуры. Длина рельса зависит от температуры по определенному правилу. Мы
помним из физики, что при нагревании тела расширяются, а при охлаждении —
сжимаются, и особенно это заметно для металлов. При изменении температуры длина
металлического рельса может измениться на несколько миллиметров.

Подставим
в эту формулу начальные значения: $l {}_{0 } =10$ м и $alpha=1,2cdot {10}^{-5}$ . Рельс удлинился на 3 мм, то есть в какой-то
момент его длина стала на 3 мм больше. Значит, при определенной температуре
длина рельса стала равной 10 м + 3
мм.

Теперь
переведем миллиметры в метры. Один миллиметр — это одна тысячная часть метра ().

$lleft(tright)=10+3cdot {10}^{-3}$ (м)

Получим:

$10+3cdot {10}^{-3}=10(1+1,2cdot {10}^{-5}cdot t)$

Это
линейное уравнение с одной переменной . Раскроем скобки в правой
части

$10+3cdot {10}^{-3}=10+12cdot {10}^{-5}cdot t$

Находим :

$t=frac{3cdot {10}^{-3}}{12cdot {10}^{-5}}=frac{1}{4}cdot {10}^2=frac{100}{4}=25.$

При
температуре 25 градусов Цельсия рельс удлинится на 3 мм.

Ответ:
25.

Парабола и квадратные неравенства

Темы
для повторения:

Квадратичная
функция

Квадратичные
неравенства

3.
Зависимость объёма спроса  (единиц
в месяц) на продукцию предприятия-монополиста от цены  (тыс.руб.) задаётся формулой . Выручка предприятия за месяц  (в
тыс.руб.) вычисляется по формуле . Определите наибольшую
цену ,
при которой месячная выручка  составит
не менее 210 тыс.руб. Ответ приведите в тыс.руб.

Здесь
точно придется читать условие. И решать именно неравенство, а не уравнение.

Поскольку
месячная выручка не менее 210 тысяч рублей,

График
функции в левой части неравенства — квадратичная парабола с ветвями вниз.

Заметим,
что это неравенство не превращается в уравнение .
Уравнение здесь нужно для того, чтобы найти, при каких значениях выручка равна 210. Решив его, получим: или . Решения неравенства:

Наибольшее
значение равно 14.

Ответ:
14.

—
«Отлично, — скажете вы. Берем больший из корней квадратного уравнения, и
готово». Так ли это? — Конечно, нет. Надо внимательно прочитать условие и
понять, что же будет ответом задачи.

4.
Выcота над землёй подброшенного вверх мяча меняетcя по   t²
закону $h(t) = 1,6 + 8t - 5t {}^{2}$ ,
где  —
выcота в метрах,  —
время в cекундах, прошедшее c момента броcка. Cколько cекунд мяч будет
находитьcя на выcоте не менее трёх метров?

Запишем,
что

Построим
график функции в левой части — то есть зависимость высоты мяча от времени.

Мы
видим, что через $t_1 {}_{ }$ секунд после начала полёта
мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота
увеличивалась. Затем началось снижение, высота уменьшалась, и в момент
времени снова стала равна трём метрам над
землей. Получается, что мяч находился на высоте не менее трёх метров в
течение секунд.

Осталось
найти разность

Для
этого решим квадратичное неравенство $5t {}^{2 } - 8t + 1,4 leq 0.$

Работать
с дробными коэффициентами неудобно. Умножим обе части неравенства на 5:

$25t {}^{2 } - 40t + 7 leq 0.$

Найдем
корни соответствующего уравнения $25t {}^{2} - 40t+7 = 0.$

$t {}_{1 } = 0,2; , , t {}_{2 } = 1,4.$

Разность $t {}_{2 } - t {}_{1} {}_{ } = 1,4 - 0,2 = 1,2.$

Ответ:
1,2.

Вот
еще одна задача из первой части варианта профильного ЕГЭ, в которой
больше решающих получают неправильный
ответ. Только потому, что не пользуются графиком.

5.
Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента
некоторого прибора была получена экcпериментально и на иccледуемом интервале
температур определяетcя выражением $T(t) = T {}_{0 } + bt + at {}^{2}$ ,
где —
время в минутах, $T {}_{0 } = 1400$ K, K/мин, K/мин. Извеcтно, что при
температуре нагревателя cвыше 1760 K прибор может иcпортитьcя, поэтому его
нужно отключать. Определите, через какое наибольшее время поcле начала работы
нужно отключать прибор. Ответ выразите в минутах.

Решите
самостоятельно. Какой ответ у вас получился?

По
условию, зависимость температуры нагревательного элемента от времени
определяется формулой:

$T(t) = 1400 + 200t - 10t {}^{2}.$

В
нормальном режиме работы прибора должно выполняться неравенство , или

Нарисуем
график зависимости температуры нагревателя от времени:

. Это квадратичная
парабола с ветвями вниз.

Мы
включаем прибор в момент времени Температура
нагревателя повышается и в момент времени $t {}_{1}$ достигает
1760 К. Если в этот момент прибор не выключить, температура продолжает
повышаться. Но это значит, что прибор испортится, то есть сгорит! Ясно, что
отключать его надо в момент времени $t {}_{1} {}_{} .$

Осталось
найти $t {}_{1} {}_{ }.$ Решим квадратичное
неравенство:

Корни
соответствующего квадратного уравнения: $t {}_{1 } = 2, , , t {}_{2 } = 18$

Мы
нашли, что $t {}_{1} {}_{ } = 2.$

Ответ:
2.

Ну
как? Вы все еще считаете, что условие можно не читать? : -)

Квадратичные
функции в задании №7 Профильного ЕГЭ — это еще не всё. Впереди степенные,
показательные, логарифмические и тригонометрические уравнения и даже
неравенства.

Степенные уравнения и неравенства

Тема
для повторения: Степенная
функция

6.
При адиабатическом процессе для идеального газа выполняется закон где — давление в газе в паскалях, V — объeм газа в кубических
метрах, $k=frac{4}{3}$ Найдите,
какой объём (в
куб. м) будет занимать газ при давлении , равном .

Подставим
данные в уравнение $pV^k=3,2cdot {10}^6:$

$2cdot {10}^5cdot V^{frac{4}{3}}=3,2cdot {10}^6$

$V^{frac{4}{3}}=16$

$V^{frac{1}{3}}=2$

Показательные уравнения и неравенства

Темы
для повторения:

Показательная
функция.

Показательные
неравенства.

7.
Уравнение процесса, в котором участвовал газ, записывается в виде , где (Па) — давление в газе, — объём газа в кубических метрах, — положительная константа. При
каком наименьшем значении константы уменьшение вдвое раз объёма газа,
участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4
раза?

Согласно
понятиям термодинамики, в каждом состоянии газ характеризуется определенными
параметрами — давлением, объемом, температурой. По условию задачи, газ
переходит из одного состояния в другое так, что Это
значит, что

$p_1{V_1}^{alpha }=p_2{V_2}^{alpha }.$

$frac{rho _2}{rho _1}= ({frac{V_1}{V_2})}^{alpha }$

Объем
уменьшился вдвое, то есть $frac{V_1}{V_2}=2.$

Поскольку $frac{rho _2}{rho _1}ge 4$ , получим, что $2^{alpha }ge 4.$ Тогда

Наименьшее
значение записываем в ответ.

Логарифмические
уравнения и неравенства

Темы
для повторения:

Логарифмы.

Логарифмические
неравенства.

8.
Водолазный колокол, содержащий  моля воздуха при давлении  атмосферы, медленно
опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до
конечного давления  Работа,
совершаемая водой при сжатии воздуха, определяется выражением $A=alpha v T{log}_2frac{rho_2}{rho_1}$ ,
где  —
постоянная,  —
температура воздуха. Найдите, какое давление  (в атм) будет иметь воздух в
колоколе, если при сжатии воздуха была совершена работа в 29100 Дж.

Подставим
все данные в уравнение для совершенной водой работы:

$9,7cdot 5cdot 300cdot {log}_2frac{rho_2}{1,75}=29100$

$9,7cdot 5cdot {log}_2frac{rho_2}{1,75}=97$

${log}_2frac{rho_2}{1,75}=2$

$frac{rho_2}{1,75}=4rho_2=7.$

Тригонометрические уравнения и неравенства

Темы
для повторения: Тригонометрия

9.
При нормальном падении света с длиной волны  нм на дифракционную
решeтку с периодом  нм
наблюдают серию дифракционных максимумов. При этом острый угол  (отсчитываемый от перпендикуляра к
решётке), под которым наблюдается максимум, и номер максимума  связаны
соотношением . Под каким
минимальным углом  (вградусах)
можно наблюдать третий максимум на решeтке с периодом, не превосходящим 2400
нм?

Запишем
условие задачи в виде неравенства. Заметим, что нам нужен третий максимум, то
есть номер максимума .

$sin varphi ge frac{1}{2}$

Поскольку
угол — острый, $varphi_{min}={30}^{{}^circ }$

Ответ:
30.

Это
была простая задача по тригонометрии. А закончим мы самыми сложными, какие
только могут встретиться в этой теме, — тригонометрическими неравенствами.

10.
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по
закону ,
где —
время в секундах. Кинетическая энергия груза, измеряемая в джоулях, вычисляется
по формуле $E=frac{mv^2}{2}$ ,
где —
масса груза (в кг), — скорость груза (в м/с). Определите, какую долю времени из
первой секунды после начала движения кинетическая энергия груза будет не менее
5 $cdot {10}^{-3}$ Дж.
Ответ выразите десятичной дробью, если нужно, округлите до сотых.

$E=frac{mv^2}{2}=frac{{sin}^2pi tcdot 0,08}{8}ge 5cdot {10}^{-3}$

${sin}^2pi tge 5cdot {10}^{-3}:{10}^{-2}$

${sin}^2pi tge frac{1}{2}$ . Применим формулу понижения
степени:

$frac{1-cos2pi t}{2}ge frac{1}{2}; , , cos2pi tle 0.$

Нарисуем
график функции при

Значения
этой функции не больше нуля ровно половину времени из первой секунды.

Ответ:
0,5.

11.
Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по
закону ,
где  —
время в секундах. Кинетическая энергия груза вычисляется по формуле $E=frac{mv^2}{2}$ , где  —
масса груза (вкг),  —
скорость груза (вм/с). Определите, какую долю времени из первой секунды после
начала движения кинетическая энергия груза будет не менее $2,4cdot {10}^{-1}$ Дж. Ответ выразите
десятичной дробью, если нужно, округлите до сотых.

$Ege 2,4cdot {10}^{-1};$

$frac{1}{8}cdot frac{{16}^2}{{10}^2}{cos}^2pi tge frac{2,4}{10};$

${cos}^2pi tge frac{3}{4};$

По
формуле понижения степени,

${cos}^2pi t=frac{cos2pi t+1}{2}.$ Отсюда

$cos2pi tge frac{1}{2}.$

Построим
график функции при

(при )

(при $t=frac{1}{2}$ )

$cosfrac{pi }{2}=0$ (при $t=frac{1}{4}$ )

$cosfrac{pi }{3}=frac{1}{2}$ (при $t=frac{1}{6}$ )

$cosfrac{5pi }{3}=frac{1}{2}$ (при $t=frac{5}{6}$ )

Найдем,
каждую часть из первой секунды выполняется неравенство $cos2pi tge frac{1}{2}.$

Получим,
что $cospi tge frac{1}{2}$ при на $0le tle frac{1}{6}$ и $frac{5}{6}le tle 1.$

Вместе
эти отрезки составляют $frac{1}{3}$ от первой секунды; $frac{1}{3}approx 0,33$

Ответ:
0,33.

Кому-то удобнее рисовать в этой задаче не график, а
тригонометрический круг. Это дело вкуса. Главное — не решать тригонометрические
неравенства в уме. И конечно, внимательно читать и анализировать условие.

Источник

Всего: 544 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Три свечи имеют одинаковую длину, но разную толщину. Третья свеча была зажжена на час раньше двух других, зажженных одновременно. В некоторый момент горения первая свеча и третья свечи стали одинаковой длины, а через 2 часа после этого одинаковой длины стали третья и вторая свечи. За сколько часов сгорает третья свеча, если вторая сгорает за 6 ч, а первая  — за 4 ч?

Источник: А. Ларин: Тренировочный вариант № 108.

В распоряжении прораба имеется бригада рабочих в составе 26 человек. Их нужно распределить на строительство двух частных домов, находящихся в разных городах. Если на строительстве первого дома работает t человек, то их суточная зарплата составляет д. е. Если на строительстве второго дома работает t человек, то их суточная зарплата составляет д. е. Дополнительные суточные накладные расходы (транспорт, питание и т. п.) обходятся в 4 д. е. в расчёте на одного рабочего при строительстве первого дома и в 3 д. е. при строительстве второго дома. Как нужно распределить на эти объекты рабочих бригады, чтобы все выплаты на их суточное содержание (т. е. суточная зарплата и суточные накладные расходы) оказались наименьшими? Сколько д. е. в сумме при таком распределении составят все суточные затраты (на зарплату и накладные расходы)?

Источник: А. Ларин. Тренировочный вариант № 271.

В распоряжении прораба имеется бригада рабочих в составе 28 человек. Их нужно распределить на строительство двух частных домов, находящихся в разных городах. Если на строительстве первого дома работает t человек, то их суточная зарплата составляет 5t² д. е. Если на строительстве второго дома работает t человек, то их суточная зарплата составляет 3t² д. е. Дополнительные суточные накладные расходы (транспорт, питание и т. п.) обходятся в 4 д. е. в расчёте на одного рабочего при строительстве первого дома и в 3 д. е. при строительстве второго дома. Как нужно распределить на эти объекты рабочих бригады, чтобы все выплаты на их суточное содержание (т. е. суточная зарплата и суточные накладные расходы) оказались наименьшими? Сколько д. е. в сумме при таком распределении составят все суточные затраты (на зарплату и накладные расходы)?

Источник: А. Ларин. Тренировочный вариант № 352.

Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, до видимой им линии горизонта вычисляется по формуле где  км  — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?

Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле где  км  — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 километров. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 10 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1.

В 8-литровой колбе находится смесь азота и кислорода, содержащая 32% кислорода. Из колбы выпустили некоторое количество смеси и добавили столько же азота, затем снова выпустили такое же, как и в первый раз, количество новой смеси и добавили столько же азота. В итоге процентное содержание кислорода в смеси составило 12,5%. Сколько литров смеси выпускали каждый раз?

Источник: А. Ларин: Тренировочный вариант № 98.

Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле где R = 6400 км  — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 3,2 км. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 15 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2.

В двух банках в конце года на каждый счет начисляется прибыль: в первом банке  — 60% к текущей сумме на счете, во втором  — 40% к текущей сумме на счете. Вкладчик в начале года часть имеющихся у него денег положил в первый банк, а остальные деньги – во второй банк, с таким расчетом, чтобы через два года суммарное количество денег на обоих счетах увеличилось на 150%. Сколько процентов денег вкладчик положил в первый банк?

Источник: А. Ларин: Тренировочный вариант № 107.

В начале года фирма «Жилстройсервис» выбирает банк для получения кредита среди нескольких банков, кредитующих под разные проценты. Полученным кредитом фирма фирма планирует распорядится следующим образом: 75% кредита направить на строительство коттеджей, а остальные 25% на оказание риэлтерских услуг населению. Первый проект может принести прибыль в размере от 36% до 44% годовых, а второй  — от 20% до 24% годовых. В конце года фирма должна вернуть кредит банку с процентами и при этом рассчитывает на чистую прибыль от указанных видов деятельности от не менее 13%, но и не более 21% годовых от всего полученного кредита. Какими должны быть наименьшая и наибольшая процентные ставки кредитования выбираемых банков, чтобы фирма гарантированно обеспечила себе указанный выше уровень прибыли.

Источник: А. Ларин: Тренировочный вариант № 157.

Имеется три пакета акций. Общее суммарное количество акций первых двух пакетов совпадает с общим количеством акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммарная стоимость первого и второго пакетов совпадает со стоимостью третьего пакета. Одна акция из второго пакета дороже одной акции из первого пакета на величину, заключенную в пределах от 16 тыс. руб. до 20 тыс. руб., а цена акции из третьего пакета не меньше 42 тыс. руб. и не больше 60 тыс. руб. Определите, какой наименьший и наибольший процент от общего количества акций может содержаться в первом пакете.

Источник: Варианты вступительных экзаменов в МГУ, экономический ф-т, 1997

Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% в проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y  — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.

Источник: А. Ларин. Тренировочный вариант № 366.

Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель − целое число от –2 до 2.

Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций  — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид

Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.

За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на Определите срок хранения вклада.

Источник: А. Ларин: Тренировочный вариант № 81.

Имеется три сплава. Первый содержит 30% меди и 70% олова, второй — 45% олова, 20% серебра и 35% меди, третий — 60% олова и 40% серебра. Из них необходимо составить новый сплав, содержащий 25% серебра. Какое наименьшее и наибольшее процентное содержание олова может быть в этом новом сплаве?

Источник: А. Ларин: Тренировочный вариант № 143.

Три станка‐автомата разной мощности должны изготовить по 800 деталей. Сначала запустили первый станок, спустя 20 мин.  — второй, а еще через 35 мин.  — третий. Каждый из них работал без сбоев и остановок, причем в ходе работы был момент, когда каждый станок выполнил одну и ту же часть задания. На сколько минут раньше второго станка закончил работу третий, если первый справился с заданием через 1 ч. 28 мин. после третьего?

Источник: А. Ларин: Тренировочный вариант № 164.

В два различных сосуда налиты растворы соли, причем в 1‐й сосуд налито 5 кг, а во второй  — 20 кг. При испарении воды процентное содержание соли в 1‐м сосуде увеличилось в p раз, а во втором  — в раз. О числах p и q известно, что pq=9. Какое наибольшее количество воды могло при этом испариться из обоих сосудов вместе?

Источник: А. Ларин. Тренировочный вариант № 266.

Курс доллара в течение двух месяцев увеличился на одно и то же число процентов ежемесячно, но не более, чем в 1,5 раза. За сумму, вырученную от продажи в начале первого месяца одного доллара, к концу второго месяца можно было купить на 9 центов меньше, чем в конце первого месяца. На сколько процентов уменьшился курс рубля за два месяца?

Источник: А. Ларин: Тренировочный вариант № 104.

За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на Определите срок хранения вклада.

Источник: А. Ларин: Тренировочный вариант № 81.

Всего: 544 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Задачи с физическим смыслом содержат физические и математические формулы, в которых необходимо отыскать неизвестную величину.

Основные правила выражения неизвестной из формул:

Все величины, кроме искомой, считаются известными данными.
Для выражения неизвестной величины пользуемся теми же правилами, что и в математике при решении уравнений.
Надо добиться того, чтобы неизвестная величина оказалась одна с левой стороны равенства, например:

Из формулы $h=vt-{gt^2}/{2}$ выразить $v$

Решение:

Поменяем части уравнения местами, так, чтобы неизвестная была с левой стороны

$vt-{gt^2}/{2}=h$

Далее избавим ее от известных величин, для этого перенесем ${gt^2}/{2}$ как известное слагаемое в правую сторону. При переносе через знак равно, знак слагаемого меняется на противоположный.

$vt=h+{gt^2}/{2}$

Неизвестной мешает только $t$. Так как $t$ умножается на неизвестную, делаем противоположное математическое действие: делим всю правую часть на $t$.

$v={h+{gt^2}/{2}}/{t}$.

Неизвестная величина осталась одна с левой стороны в равенстве, следовательно, мы ее выразили.

Полезным будет вспомнить единицы измерения физических величин их взаимосвязь:

Длины.

$мм⇄↙{·10}↖{:10}см⇄↙{·10}↖{:10}дм⇄↙{·10}↖{:10}м⇄↙{·1000}↖{:1000}км$

Массы.

$гр⇄↙{·1000}↖{:1000}кг⇄↙{·100}↖{:100}центнер⇄↙{·10}↖{:10}тонна$

Площади.

$мм^2⇄↙{·10}↖{:10}см^2⇄↙{·10}↖{:10}дм^2⇄↙{·100}↖{:100}м^2⇄↙{·1000000}↖{:1000000}км^2$

Чтобы перейти из км/ч в м/с необходимо величину разделить на $3.6$.

Пример:

При температуре 0℃ рельс имеет длину $l_0=14м$. При увеличении температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $l(t)=l_0(1+αt)$, где $α=1.2·10^{-5}(℃^{-1})$ — коэффициент теплового расширения, $t$ — температура в градусах Цельсия. При какой температуре рельс удлинится на $2.1$ мм? Ответ выразите в градусах.

Решение:

Чтобы упорядочить приведенные величины, запишем их в дано:

Дано: $l_0=14$м

$t_0=0℃$

$∆l=2.1$мм$=0.0021$м

$α=1.2·10^{-5}(℃^{-1})$

$t-?$

В дано сразу видим, что начальная длинна и разность длин $(∆l)$ имеют разные единицы измерения. Необходимо миллиметры перевести в метры, для этого число надо поделить на тысячу.

$2.1мм =0.0021м$

Далее запишем формулу

$l(t)=l_0(1+αt)$ и выразим из нее температуру $(t)$.

Для этого необходимо раскрыть скобки

$l(t)=l_0+l_{0}αt$

Поменяем части уравнения местами, так, чтобы неизвестная величина оказалась в левой части (так привычнее для решения)

$l_0+l_{0}αt=l(t)$

Перенесем $l_0$ в правую часть уравнения, так как это известная величина, при переносе через равно меняем знак на противоположный.

$l_{0}αt=l(t)-l_0$, где $l(t)-l_0=∆l$

$l_{0}αt=∆l$

Чтобы выразить t надо правую часть уравнения поделить на $l_{0}α$

$t={∆l}/{l_{0}α}$

Теперь подставим числовые значения в выраженную формулу

$t={∆l}/{l_{0}α}={0.0021}/{14·1.2·10^{-5}}$

Домножим дробь на $100000$, чтобы числа было легче считать

$t={∆l}/{l_{0}α}={0.0021}/{14·1.2·10^{-5}}={210}/{14·1.2}=12.5℃$

Ответ: $12.5$

Для успешного решения задач можно не выражать неизвестную величину из буквенной формулы, а сразу подставить в буквенную формулу все соответствующие числовые значения и найти неизвестную величину. Чтобы облегчить решение задач, лучше упорядочить приведенную информацию: записать в дано все известные величины с их единицами измерения и численными значениями. Проверить единицы измерения. Записать отдельно формулу. Все задачи далее можно разделить на:

Сводящиеся к уравнениям (линейным, квадратным, иррациональным, рациональным, логарифмическим, тригонометрическим).
Сводящиеся к неравенствам (линейным, квадратным, иррациональным, рациональным, логарифмическим).

Пример:

Автомобиль, движущийся с начальной скоростью $v_0=20$м/с, начал торможение с постоянным ускорением $а=5$м/с. За $t$ секунд после начала торможения он прошел путь $S=v_{0}t-{at^2}/{2}$(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал $30$м. Ответ дайте в секундах.

Решение:

Запишем дано: $v_0=20$м/с

$а=5$м/с

$S=30$м

$t-?$

Запишем формулу $S=v_{0}t-{at^2}/{2}$. Из формулы видно, что неизвестная у нас встречается несколько раз. В таких случаях проще сразу заменить буквы на их числовые значения

$30=20t-{5t^2}/{2}$

Получили квадратное уравнение, теперь его немного упростим: для этого перенесем все слагаемые в левую часть и домножим уравнение на ${2}/{5}$, чтобы получить целочисленные коэффициенты.

$t^2-8t+12=0$

По теореме Виета

$t_1+t_2=8$

$t_1·t_2=12$

Нам подходят $t_1=6$ и $t_2=2$

Из двух вариантов выбираем $t=2$, так как этого времени достаточно, чтобы автомобиль полностью остановился.

Ответ: $2$

Теперь разберем задачи, в которых получаются неравенства. Для решения таких задач так же кратко записываем дано и формулу. В дальнейшем подставляем известные данные в формулу и оцениваем, какое получается неравенство. В большинстве случаев получаются квадратные или линейные неравенства.

Пример:

Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением $T(t)=T_0+bt+at^2$, где $t$ – время в минутах, $T_0=1400К$, $a=-10$К/мин, $b=200$К/мин. Известно, что при температуре нагревателя свыше $1760$К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.

Решение:

Записываем дано: $T_0=1400$К

$a=-10$К/мин

$b=200$К/мин

$T(t)≤1760$K (Так как свыше этой температуры прибор сгорит).

$t-?$

$T(t)=T_0+bt+at^2$

Так как $T(t)≤1760$K, то и выражение $T_0+bt+at^2≤1760$K

Подставим числовые значения и получим квадратное неравенство

$1400+200t-10t^2≤1760$

В квадратном неравенстве необходимо все значения перенести в левую сторону и расставить слагаемые в порядке убывания степеней у неизвестного

$-10t^2+200t+1400-1760≤0$

$-10t^2+200t-360≤0$

Разделим все неравенство на $(-10)$. Важно помнить, что при делении или умножении неравенства на отрицательное значение, знак неравенства меняется на противоположный.

$t^2-20t+36≥0$

Решим данное неравенство методом интервалов: для этого надо найти корни выражения и разложить его на множители.

$t^2-20t+36=0$

$t_1=2$

$t_2=18$

$(t-2)(t-18)≥0$

Расставим корни на числовой оси.

Определим знак правой крайней области, для этого в разложенное уравнение вместо t надо подставить число, которое больше корней.

$(100-2)(100-18)$ результат будет положительным числом, следовательно, в крайней правой области на числовой ось знак плюс, а далее знаки чередуются.

Решение неравенства $(-∞;2]∪[8;+∞)$

Через $2$ минуты после включения прибор нагреется до $1760$К, и при дальнейшем нагревании может испортиться. Таким образом, прибор нужно выключить через $2$ минуты.

Ответ: $2$

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Прикладные задачи»

Открытый банк заданий по теме прикладные задачи. Задания B10 из ЕГЭ по математике (профильный уровень)

Задание №1092

Условие

Скорость колеблющегося на пружине груза меняется по закону v=4sinpi t (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения груза превышала 2 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Показать решение

Решение

Заметим, что в течение первой секунды, то есть при 0leqslant tleqslant1 выполняется неравенство 0leqslantpi tleqslantpi. Из этого неравенства следует, что: sinpi tgeqslant0.

Тогда 4sinpi tgeqslant2,

sinpi tgeqslantfrac12,

frac{pi}{6}leqslantpi tleqslantfrac{5pi}{6} (см. рис.),

frac16leqslant tleqslantfrac56.

Значит, на первой секунде скорость движения превышала 2 см/с на протяжении frac56-frac16=frac23approx 0,67 секунды.

Ответ

0,67

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1091

Условие

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и вычисляет расстояние до воды по формуле h=5t^2, где h — расстояние в метрах, t — время падения в секундах. Время падения камешков до дождя составляло 0,4 с. Определите, насколько должен подняться уровень воды в колодце после дождя, чтобы измеряемое время изменилось на 0,1 с? Ответ выразите в метрах.

Показать решение

Решение

Пусть h_0 — расстояние до воды до дождя, h — после дождя (в метрах). После дождя время падения t уменьшится и станет равно 0,4-0,1=0,3 с. Тогда h_0-h= 5(t_0^2-t^2)= 5(0,4^2-0,3^2)= 0,35.

Ответ

0,35

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1090

Условие

Груз массой 0,4 кг колеблется на пружине. Его скорость меняется по закону v=v_0cosfrac{2pi t}{T}, где t — время с момента начала колебаний, T=2 с — период колебаний, v_0=0,3 м/с. Кинетическая энергия E груза измеряется в джоулях и определяется формулой E=frac{mv^2}{2}, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 3 секунды после начала колебаний. Ответ дайте в джоулях.

Показать решение

Решение

E=frac{mleft(v_0cosdfrac{2pi t}{T}right)^2}{2},

E=frac{0,4left(0,3cosdfrac{2picdot3}{2}right)^2}{2}= 0,2cdot0,09= 0,018.

Кинетическая энергия груза через 3 секунды после начала колебаний равна 0,018 Дж.

Ответ

0,018

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1089

Условие

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=6 кг и радиусом R=12 см и двух боковых с массами M=2 кг и радиусами R+h. Момент инерции катушки относительно своей оси вращения, определяется формулой I=frac{(m+2M)R^2}{2}+M(2Rh+h^2) и выражается в кг · см². Определите, при каком наибольшем значении h момент инерции катушки не превышает предельного значения 770 кг · см²? Ответ выразите в сантиметрах.

Показать решение

Решение

Решим неравенство Ileqslant770 относительно h, учитывая, что m=6, R=12, M=2.

frac{(6+2cdot2)cdot12^2}{2},+ 2(2cdot12h+h^2)leqslant770,

720+48h+2h^2leqslant770,

h^2+24h-25leqslant0,

откуда -25leqslant hleqslant1.

Максимальное значение h равно 1 сантиметру.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1088

Условие

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a км/ч². Скорость v определяется формулой v=sqrt{2la}, где l — пройденный автомобилем путь. С каким ускорением должен двигаться автомобиль, чтобы, преодолев расстояние 0,7 километра, он приобрел бы скорость 98 км/ч. Ответ выразите в км/ч².

Показать решение

Решение

v=sqrt{2la}, v^2=2la, a=frac{v^2}{2l}.

Подставляем в эту формулу l=0,7, v=98:

Получаем: a=frac{98^2}{2cdot0,7}=6860.

Итак, ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,7 километра, приобрести скорость 98 км/ч, равно 6860 км/ч².

Ответ

6860

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1087

Условие

Автомобиль, масса которого равна m=1100 кг, начинает двигаться с ускорением, которое в течение t секунд остаётся неизменным, и за это время преодолевает расстояние S = 600 метров. Сила (в ньютонах), приложенная к автомобилю в это время, равна F=frac{2mS}{t^2}. Найдите наибольшее время за которое автомобиль преодолеет указанный путь после начала движения, если известно, что сила F, приложенная к нему, не меньше 3300 H. Ответ выразите в секундах.

Показать решение

Решение

Решим неравенство Fgeqslant3300.

frac{2mS}{t^2}geqslant3300,

frac{2cdot1100cdot600}{t^2}geqslant 3300,

frac{2cdot100cdot2}{t^2}geqslant 1.

t^2leqslant 400,

-20leqslant tleqslant 20.

Наибольшее время после начала движения автомобиля, за которое он пройдёт 600 метров, равно 20 секундам.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №937

Условие

Автомобиль, движущийся в начальный момент времени со скоростью v_0 = 12 м/с, начал торможение с постоянным ускорением a = 4 м/с². После начала торможения за t секунд автомобиль преодолел расстояние S=v_0t-frac{at^2}{2} (м). Сколько секунд прошло с момента начала торможения, если за это время автомобиль проехал 16 метров?

Показать решение

Решение

Подставим данные задачи в формулу S=v_0t-frac{at^2}{2}.

16=12t-frac{4t^2}{2},

t^2-6t+8=0,

t_1=4,,t^2=2.

С помощью формулы скорости при равнозамедленном движении v=v_0-at найдём время движения автомобиля до остановки: v=0, v_0=12 м/с, a=4 м/с²; 0=12-4t, откуда t=3. Итак, автомобиль остановится через 3 секунды после начала торможения.

Учитывая, что tleqslant3, получим, что от момента начала торможения прошло 2 секунды.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №936

Условие

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I=frac{varepsilon}{R+r}, где varepsilon — ЭДС источника (в вольтах), r = 2 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 40% от силы тока короткого замыкания I_кз = frac{varepsilon}{r}? Ответ выразите в омах.

Показать решение

Решение

Решим неравенство Ileqslant0,4cdot I_кз при условии, что r=2 Ом.

frac{varepsilon}{R+r}leqslant0,4cdotfrac{varepsilon}{r},

frac{1}{R+2}leqslantfrac{4}{10cdot2},

frac{1}{R+2}leqslantfrac15,

Rgeqslant3.

Итак, наименьшее сопротивление цепи, при котором сила тока будет составлять не более 40% от силы тока короткого замыкания, равно 3 Ом.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №935

Условие

Перед отправкой тепловоз издал гудок с частотой f_0 = 280 Гц. Чуть позже гудок издал подъезжающий к платформе тепловоз. В следствие движения тепловоза, частота второго гудка оказалась больше первого (эффект Доплера). Она зависит от скорости источника сигнала по закону: f(v)=frac{f_0}{1-dfrac vc} (Гц), где c — скорость звука (в м/с). Сигналист, стоящий на платформе, следит за движением тепловоза и успешно распознает сигналы, если они отличаются не менее чем на 7 Гц. Найдите наименьшую скорость приближающегося к платформе тепловоза, если сигналист смог различить издаваемые сигналы, а скорость звука равна 328 м/с. Ответ выразите в м/с.

Показать решение

Решение

Решим неравенство f(v)-f_0geqslant7, используя условие v<328.

frac{f_0}{1-dfrac vc}-f_0geqslant7,

frac{280}{1-dfrac{v}{328}}-280geqslant7,

frac{1}{1-dfrac{v}{328}}-1geqslantfrac{1}{40},

frac{1}{1-dfrac{v}{328}}geqslantfrac{41}{40},

1-frac{v}{328}leqslantfrac{40}{41},

frac{v}{328}geqslantfrac{1}{41},

vgeqslant8.

Следовательно, минимальная скорость тепловоза равна 8 м/с.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №934

Условие

Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1+8t-5t^2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?

Показать решение

Решение

Решим относительно t неравенство h(t)geqslant4.

-5t^2+8t+1geqslant4,

5t^2-8t-1leqslant-4,

5t^2-8t+3leqslant0.

Найдем корни уравнения 5t^2-8t+3=0:

Вычислим дискриминант: D=b^2-4ac= -8^2-4cdot5cdot3= 64-60=4,

t_{1,2}= frac{-bpmsqrt D}{2a}= frac{8pmsqrt4}{2cdot5}= frac{8pm2}{10},

t_1=frac35,,t_2=1;

5left ( t-frac35 right ) left ( t-1 right )leqslant0, откуда frac35leqslant tleqslant1. Мяч будет находиться на высоте не мене четырех метров в течение 1-frac35=frac25=0,4 секунды.

Ответ

0,4

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Задачи с прикладным содержанием

Разбор самых нетривиальных задач с прикладным содержанием (подстановкой в формулу)

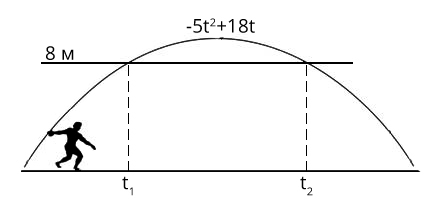
1) Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t) = -5t² + 18t (h — высота в метрах, t – время в секундах, прошедшее с момента броска). Найдите, сколько секунд камень находился на высоте не менее 9 метров.

Нарисуем данную ситуацию:

Полет камня задается уравнением: h = -5t² + 18t, то есть, подставив, например, вместо t ноль получим, что камень находился на высоте 0 метров. А в момент времени 3 секунды получим h = -5·3²+18·3 = 9 метров

Теперь, вспомнив 7-8 класс, когда мы строили графики и находили точку пересечения, сделаем здесь то же самое.

Приравняем -5t² + 18t = 9

После нескольких преобразований получим t = 0,6; t = 3 — абциссы точек пересечения двух графиков на рисунке (t₁ и t₂).

Ага, значит, камень находится выше 9 метров (параболла выше прямой) на промежутке от 0,6 секунды до 3 секунд.

Ответ: 2,4

2) Груз массой 0,7 кг колеблется на пружине. Его скорость υ меняется по закону υ = υ₀·sin(2·π·t /T) (*), где t — время с момента начала колебаний, T = 24 с — период колебаний, υ₀ = 0,6 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = m·υ²/2 (**), где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.

Тут сразу две формулы! Давайте разбираться постепенно, нужно найти кинетическую энергию. Она выражена в (**) формуле, но чтобы ее найти, сначала нужно найти скорость в момент времени 10 секунд по (*) формуле.

Без ментальных знаний тригонометрии тут не обойтись, но мы попытаемся!

Подставим время и период в (*):

5·π/6 можно разложить как π-π/6, так ведь? 5/6 = 1-1/6

sin(π-π/6) можно разложить по формуле разности синуса или по формуле приведения

Получается, что υ = 0,6/2 = 0,3 м/с

Тогда энергия:

Ответ: 0,0315

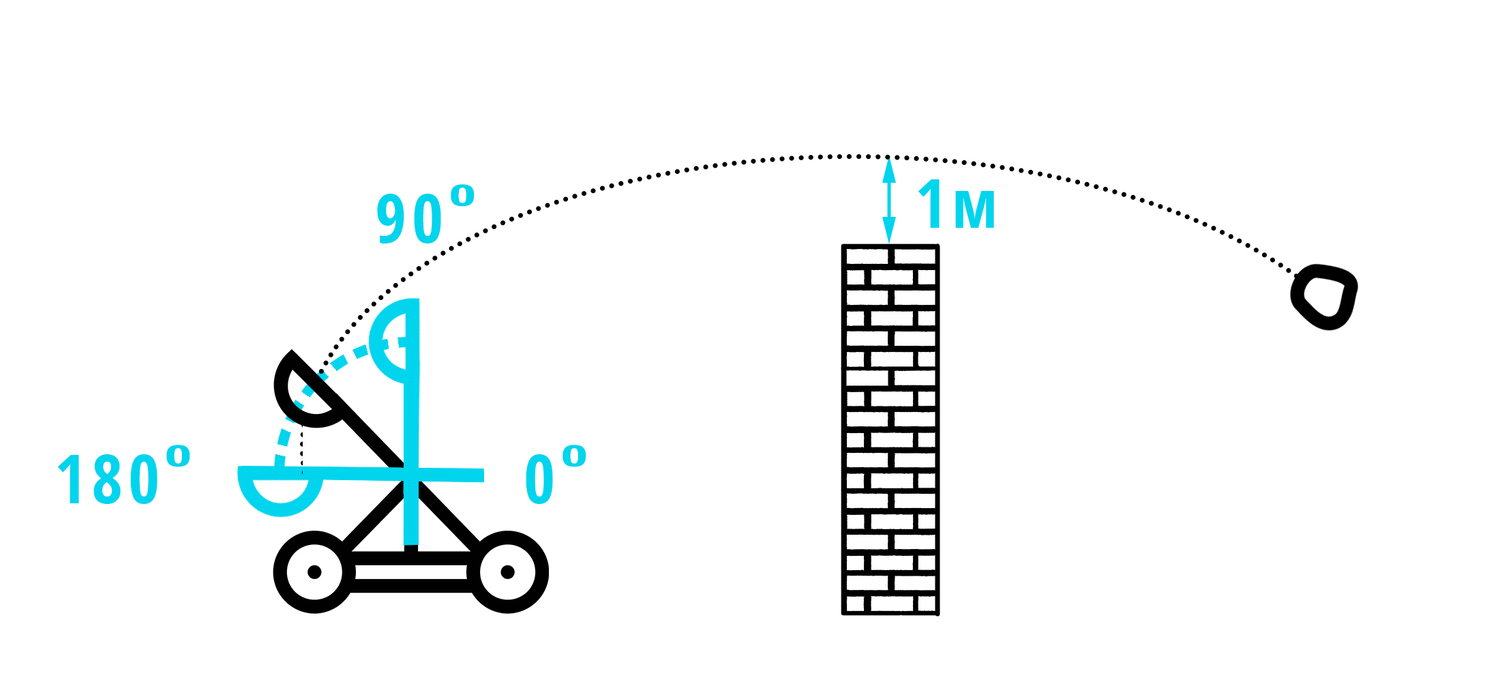
3) Снаряд бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полeта снаряда, выраженная в метрах, определяется формулой H=υ²·(1-cos2α)/4g, где υ = 22 м/с — начальная скорость, а g — ускорение свободного падения (считайте м/с). При каком наименьшем значении угла (в градусах) снаряд пролетит над стеной высотой 11,1 м на расстоянии 1 м?

Вопрос для правильного ответ: какая высота будет в формуле H?

Мячу нужно быть выше стены, которая высотой 11,1 метра, на 1 метр, тогда H = 12,1 метра, логично?

Все не так плохо, всего одна формула. Но нужно найти угол, и опять без тригонометрии не обойтись, но для начала выразим косинус:

Угол у нас должен быть острый, то есть в промежутке от 0 до 90°, по-другому камень не перелетит через стену.

Косинус равен нулю, когда α = 90 для нашего случая.

Угол нужен максимальный.

Ответ: 45

Теперь вы можете управлять осадой замка, а вдруг пригодится в XXI веке!

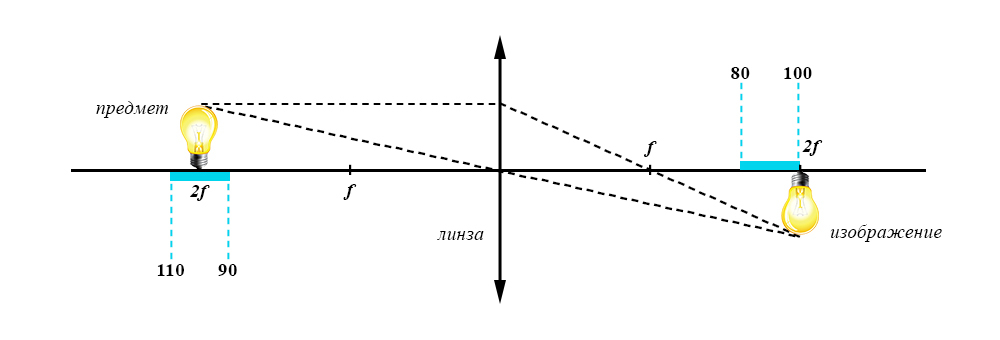
4) Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 50 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 90 до 110 см, а d₂ расстояние от линзы до экрана — в пределах от 80 до 100 см. Изображение на экране будет четким, если выполнено соотношение 1/d₁+1/d₂=1/f. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

Одна из составляющих наших глаз — хрусталик, который представляет из себя собирающую линзу.

Наш глаз так же, как и линза, имеет расстояние, на котором он сможет сфокусироваться.

В задаче используется собирающая линза (это «двойной вектор» по середине). Фокусное расстояние обозначено f и показывает расстояние от линзы до точки фокусировки.

Требуется найти наименьшее расстояние от линзы до лампочки — d₁.

Если мы берем наименьшее d₁, тогда дробь 1/d₁ будет наибольшей (Сравните дроби 1/5 и 1/10, чем меньше знаменталь, тем больше будет дробь).

Получается, что разность тоже должна быть как можно больше (1/50-1/d₂).

Значение f постоянно, а вот d₂ мы вольны выбирать из диапазона. Тогда дробь 1/d₂ возьмем как можно меньше (чтобы 1/50-1/d₂ было как можно больше). Для этого d₂ возьмем как можно больше из заданного диапазона — 100 см.

Данное значение попадает в диапазон. Изображение будет четким, а расстояние наименьшим.

Ответ: 100

5) Уравнение процесса, в котором участвовал газ, записывается в виде p·Vⁿ = const, где p (Па) — давление в газе, V — объeм газа в кубических метрах, n — положительная константа. При каком наименьшем значении константы n уменьшение в 9 раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 3 раза?

Начнем с интересного слова «const»: оно означает, что данное выражение должно всегда оставаться постоянной (6·4, уменьшив 6 в 2 раза, а 4 увеличив в 2 раза получим 3·8 = 6·4). То же самое происходит здесь:

p₁·V₁ⁿ = p₂·V₂ⁿ

Сказано, что объем уменьшается в 9 раз, то есть начальный объем был V₁, а стал V₁/9.

Не нравятся неизвестные? Пусть V₁ = 1, тогда V₂ = 1/9 ( главное, чтобы разница был в 9 раз).

То же самое с давлением p₁ и 3p₁ (или p₁ = 1, тогда p₂ = 3).

Единица в любой степени всегда останется единицей:

Ответ: 0,5

Будь в курсе новых статеек, видео и легкого математического юмора.

Источник

ЕГЭ профильный уровень

Задание №10 (новое)

Задачи с прикладным содержанием

Использовались материалы сайта http://self-edu.ru

Энергия катушки в идеальном колебательном контуре определяется формулой , где Гн, а сила тока I меняется по закону и измеряется в амперах. Вычислите энергию катушки в момент времени t=3 секунды.

Решение.

Сначала найдем значение силы тока в момент t=3, имеем:

Подставим эту величину в формулу энергии катушки, получим:

Дж.

Ответ: 0,18.

Предприниматель делает наценку на продаваемый товар в размере p рублей. Было замечено, что месячный объем N реализуемого товара зависит от наценки p по формуле:

единиц

При этом прибыль, которую получает предприниматель за месяц, равна

рублей

Найдите наибольшую наценку p, при которой доход предпринимателя в месяц составит 26000 рублей.

Решение.

Из формулы расчета прибыли выразим величину N, получим:

Подставим вместо N значение S/p, придет к формуле:

Умножаем обе части выражения на 100p, имеем:

Решаем квадратное уравнение, получаем два корня:

То есть, наибольшая наценка составляет 26 рублей.

Ответ: 26.

Энергия конденсатора в идеальном колебательном контуре определяется по формуле , где Ф – емкость конденсатора, а U – напряжение на его обкладках, которое меняется по закону

Колебательный процесс начался в момент времени t=0 секунд. Найдите ближайший момент времени, при котором энергия на конденсаторе достигнет своего максимума. Ответ дайте в секундах.

Решение.

Из формулы энергии конденсатора следует, что ее максимум достигается при достижении максимального по модулю значения напряжения. Из закона изменения напряжения видно, что максимум модуля напряжения будет наблюдаться, когда косинус равен 1 или -1. И ближайшее значение косинуса -1 будет достигнуто при угле π радиан:

то есть, при t=2 секунды получим ближайший максимум энергии на обкладках конденсатора.

Ответ: 2.

Мяч подбрасывают вертикально вверх. Известно, что максимальная высота его подъема h зависит от начальной скорости мяча по формуле , где g=10 м/с2 – ускорение свободного падения. Вычислите начальную скорость мяча, если максимальная высота его полета составила 5 метров. Ответ дайте в м/с.

Решение.

Сначала выразим начальную скорость мяча из формулы высоты, получим:

Затем, подставим числовые значения и найдем начальную скорость:

м/с

Ответ: 10.

Поисковая система Mail определяет релевантность результатов поиска по формуле:

где L – число ссылок на страницу сайта; C – объем контента страницы сайта (число символов); K – число встречающихся ключевых слов из запроса.

Определите релевантность страницы сайта, на которую ссылаются 8 других сайтов. Общий объем контента составляет 5643 символов и с 6 ключевыми словами, соответствующими запросу.

Решение.

Вычислим релевантность страницы сайта поисковому запросу при L=8, C=5643 и K=6:

Ответ: 6191.

Автомат выстреливает теннисные мячи, которые должны перелетать через сетку высотой 1,5 метра. Высота полета мячей от уровня теннисного корта определяется по закону . На каком минимальном расстоянии от сетки нужно поставить автомат, чтобы мячи перелетали через сетку? Ответ дайте в метрах.

Решение.

Мячи будут перелетать через сетку, если выполнено условие:

Решаем квадратное уравнение, получаем два корня:

Получаем минимальное расстояние x=3 м.

Ответ: 3.

Сопротивление R проводника определяется по формуле , где Ом/(м∙мм2) – удельное сопротивление проводника; S – площадь его поперечного сечения (в мм2); м – длина проводника. Найдите сопротивление проводника, если его поперечное сечение представляет собой круг с радиусом мм. Ответ дайте в Омах.

Решение.

Найдем площадь поперечного сечения проводника:

мм2.

И сопротивление, равно:

Ом.

Ответ: 400.

На тело, погруженное в жидкость, действует выталкивающая сила, равная , где ρ – плотность жидкости (кг/м3); g = 10 м/с2 – ускорение свободного падения; V – объем погруженной в жидкость части тела (м3). Найдите плотность жидкости ρ, если известно, что при погружении прямоугольного параллелепипеда с площадью основания 3 см2 на глубину 2 см выталкивающая сила составила 0,048 Н. Ответ дайте в кг/м3.

Решение.

Сначала вычислим объем погруженной в жидкость части тела, зная площадь основания м2 и высоту м:

м3.

Затем, из формулы выталкивающей силы выразим плотность жидкости:

кг/м3

Ответ: 800.

Имеется электрическая цепь, состоящая из трех параллельно соединенных сопротивлений с номиналами: R1=1 Ом, R2=2 Ом, R3=6 Ом. Известно, что общее сопротивление R такой цепи связано с сопротивлениями R1, R2, R3 выражением:

Найдите сопротивление цепи R. Ответ дайте в Омах.

Решение.

Вычислим величину 1/R, получим:

Ом.

Ответ: 0,6.

Нитяной маятник с грузом массой m=0,5 кг совершает гармонические колебания. Скорость движения груза определяется формулой . Кинетическая энергия такого маятника определяется формулой . Найдите значение кинетической энергии в момент времени t=2.

Решение.

Вычислим скорость груза в момент времени t=2, получим:

м/с.

Подставим это значение в формулу кинетической энергии, получим:

Дж.

Ответ: 2,25.

Источник