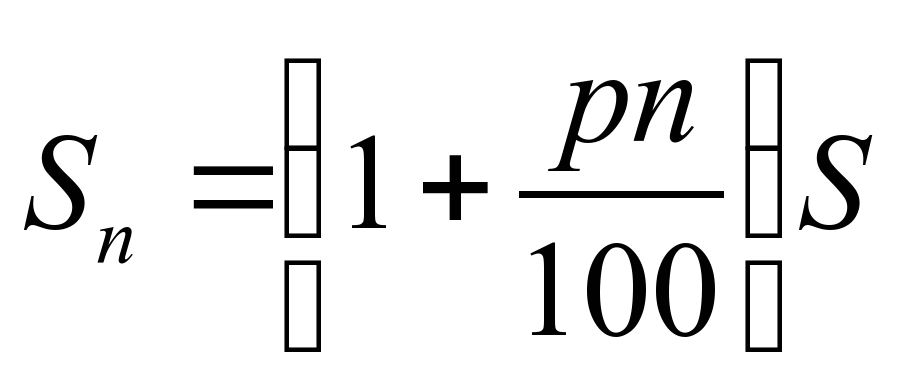Задачи с процентами егэ профиль как решать

Задачи на проценты из вариантов ЕГЭ по математике

Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.

Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за  мы принимаем ту величину, с которой сравниваем.

Мы также вывели полезные формулы:

если величину увеличить на процентов, получим
если величину уменьшить на процентов, получим
если величину увеличить на процентов, а затем уменьшить на , получим

если величину дважды увеличить на процентов, получим
если величину дважды уменьшить на процентов, получим

Воспользуемся ими для решения задач.

---

. В  году в городском квартале проживало  человек. В  году в результате строительства новых домов число жителей выросло на , а в  году — на  по сравнению с  годом. Сколько человек стало проживать в квартале в  году?

По условию, в  году число жителей выросло на , то есть стало равно  человек.

А в  году число жителей выросло на , теперь уже по сравнению с  годом. Получаем, что в  году в квартале стало проживать  жителей.

Следующая задача предлагалась на пробном ЕГЭ по математике в декабре  года. Она проста, но справились с ней немногие.

---

. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на  дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили  рублей. К вечеру понедельника они подорожали на  и стали стоить . Теперь уже эта величина принимается за , и к вечеру вторника акции подешевели на  по сравнению этой величиной. Соберем данные в таблицу:

По условию, акции в итоге подешевели на 

Получаем, что

Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения:

По смыслу задачи, величина положительна.
Получаем, что .

---

. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за  рублей, через два года был продан за  рублей.

Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил  рублей. Его цена два раза уменьшилась на , и теперь она равна:

---

. Четыре рубашки дешевле куртки на . На сколько процентов пять рубашек дороже куртки?

Пусть стоимость рубашки равна , стоимость куртки . Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет  от цены куртки, то есть .

Стоимость одной рубашки — в  раза меньше:

А стоимость пяти рубашек:

Получили, что пять рубашек на  дороже куртки.

Ответ: .

---

. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на . Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на  Сколько процентов от общего дохода семьи составляет зарплата жены?

Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась…») назовем «ситуация » и «ситуация ».

	муж	жена	дочь	Общий доход
В реальности
Ситуация
Ситуация

Осталось записать систему уравнений:

Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти , и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму .

Получим:

Это значит, что зарплата мужа составляет  от общего дохода семьи.

Во втором уравнении мы тоже вычтем из обеих частей выражение , упростим и получим, что

Значит, стипендия дочки составляет  от общего дохода семьи. Тогда зарплата жены составляет  общего дохода.

Ответ:

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Муниципальное бюджетное образовательное учреждение

Средняя общеобразовательная школа №41

Научное общество учащихся

XXIV научно-практическая
конференция «Шаг в будущее»

Решение задач на проценты из второй части ЕГЭ

Получение универсальной формулы.

Выполнил:Оганесян Лев,

Ученик 11 «А» класса

Научные руководители:

Данилина М.Ю.,

Ручина Л.Г.

учитель математики

Н.Новгород, 2015

Содержание:

Введение…………………………………………………………………………1

Методы
исследований…………………………………………………………2-4

Задача 1…………………………………………………………………………5-6

Получение
формы для решения задач на проценты………………………..7

Решение
задачи на проценты, где нужно найти размер выплаты, то есть X.

Задача 2………………………………………………………………………….8-9

Задача 3…………………………………………………………………………..10

Задача 4………………………………………………………………………11-12

Решение
задачи на проценты, где нужно найти размер кредита,

 то есть S.

Задача 5………………………………………………………………………13-14

Задача 6………………………………………………………………………15-16

Задача 7………………………………………………………………………17-18

Решение
задачи на проценты, где нужно найти количество лет ,

 то есть n.

Задача 8………………………………………………………………………19-20

Задача 9………………………………………………………………………21-22

Задача 10……………………………………………………………………..23-24

Решение
задачи на проценты, где нужно найти процентную ставку,

 то есть а.

Задача 11…………………………………………………………………………25

Задача 12…………………………………………………………………………26

Задача
13…………………………………………………………………….27-28

Заключение………………………………………………………………………29

Список
литературы…………………………………………………………….30

Введение

В современном
мире, где главную роль играет информация, люди стремятся к упрощению жизни, к
усовершенствованию старого во всех областях. Математика также не является
исключением. Несмотря на то, что в ней было достигнуто огромно число
разнообразных целей, совершенно колоссальное количество открытий, она не
перестает развиваться.

Открытие для
себя решил совершить и я. В этот мне помогло изменение структуры Единого
Государственного Экзамена  по математике. Как многим известно, в этом году во
второй части появилось новое задание на проценты.  Сама по себе задача
несложная, затруднение представляют вычисления, к тому же, за нее можно
получить достаточно много баллов. Чаще всего ошибка появляется из-за
невнимательного подсчета ответа.  Поэтому в своей работе я захотел найти такой
способ решения, который позволил бы получать ответ гораздо быстрее и легче.

Я считаю свою
работу актуальной, потому что с этого года для всей части населения,
сдающей в одиннадцатом классе экзамен по математике, будет полезно узнать
способ решения этой задачи на проценты, который обязательно поможет при сдаче
ЕГЭ.

Цель моей
работы- найти такой
способ решения задачи на проценты из второй части Единого Государственного
Экзамена, который позволил бы существенно сэкономить время, затраченное на
задание, и  получить абсолютно правильный ответ.

В ходе
изучения были поставлены следующие задачи:

1.    
Найти такой
способ решения задания на проценты.

2.    
Доказать его
справедливость.

3.    
Проверить
этот способ при решении заданий на проценты всех четырех типов( поиск размера
выплаты, размера кредита, процентной ставки и количества выплат).

4.    
Сравнить
обычное решение задач с новым способом.

Методы
исследований:

1.    
Метод построения
математической модели.

2.    
Метод
математической логики и упрощения решений.

3.    
Метод решения
логических задач.

4.    
Метод
математической индукции.                                                         (1)

Методы
исследований:

1.Метод построения математической модели.

Можно
выделить следующие основные этапы построения математической модели:

Определение
цели, т. е. чего хотят добиться, решая поставленную задачу.

Определение
параметров  модели, т.е. заранее известных фиксированных факторов, на значения
которых исследователь не влияет.

Формирование
управляющих переменных, изменяя значение которых можно приближаться к
поставленной цели. Значения управляющих переменных являются решениями задачи.

Определение
области допустимых решений, т.е. тех ограничений, которым должны удовлетворять
управляющие переменные.

Выявление
неизвестных факторов, т.е. величин, которые могут изменяться случайным или
неопределенным образом.

Выражение
цели через управляющие переменные, параметры и неизвестные факторы, т.e.
формирование целевой функции, называемой также критерием эффективности или
критерием оптимальности задачи.

2.Метод математической логики и упрощения
решений.                                                                                                                                       

Математическая логика — современная форма
логики, опирающаяся на формальные математические методы.

Основные объекты логики — высказывания, то есть
предложения, которые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опытный) и
логический. При эмпирическом подходе истинность высказываний
устанавливается на основе наблюдений, экспериментов, документов и других
фактов. При логическом подходе истинность высказываний доказывается на основе
истинности других высказываний, то есть чисто формально, на основе рассуждений
без обращения к фактам.

3.Метод решения логических задач.

Логические задачи
обычно формулируются на естественном языке. Их можно решать тремя методами: 

1. При помощи
логического рассуждения,

2. С помощью
составления таблиц истинности для высказываний и с помощью сравнения значений
этих высказываний с условием

                                                                                                                                    
(2)                                                                                                                                                                                                                                                                                                     

3. Через представление
задачи на языке математической логики и упрощения полученных выражений.

Полученные логические
выражения необходимо упростить и проанализировать. Для этого иногда бывает
необходимо построить таблицу истинности для полученного логического выражения.

1. Решение логических
задач средствами алгебры логики

Обычно используется
следующая схема решения:

1. изучается условие
задачи;

2. вводится система
обозначений для логических высказываний;

3. конструируется
логическая формула, описывающая логические связи между всеми высказываниями
условия задачи;

4. определяются
значения истинности этой логической формулы;

5. из полученных
значений истинности формулы определяются значения истинности введѐнных
логических высказываний, на основании которых делается заключение о решении.

4.Метод математической
индукции.     

Одним
из самых важных методов математических доказательств по праву является метод математической индукции. Подавляющее большинство формул,
относящихся ко всем натуральным числам n, могут быть доказаны методом математической индукции (к примеру,
формула суммы n первых членов арифметической
прогрессии 

,
формула бинома Ньютона 

 и т.п.).

Индукцией называют
переход от частных утверждений к общим. Напротив, переход от общих утверждений
к частным называется дедукцией.

В
основе метода математической индукции лежит принцип
математической индукции.

Он
заключается в следующем: некоторое утверждение справедливо для всякого
натурального n, если

1.       оно
справедливо для n = 1 и

2.       из
справедливости утверждения для какого-либо произвольного натурального n
= kследует его справедливость для n
= k+1.

То
есть, доказательство по методу математической индукции проводится в три этапа:

                                                                                                                               
(3)

1.       во-первых,
проверятся справедливость утверждения для любого натурального числаn (обычно
проверку делают для n = 1);

2.       во-вторых,
предполагается справедливость утверждения при любом натуральномn=k;

3.       в-третьих,
доказывается справедливость утверждения для числа n=k+1,
отталкиваясь от предположения второго пункта.

                                                                                                                                       
(4)

1.    
На примере
обычной задачи на проценты попытаемся найти

закономерности и важные моменты, которые
пригодятся для получения более лаконичного и простого способа решения.

Задача 1. 31
декабря 2014 года Алексей взял в банке 6902000 рублей в кредит под 12,5%
годовых. Схема выплаты кредита  следующая – 31 декабря каждого следующего  года
банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на
12,5%), затем Алексей  переводит в банк X рублей.
Какой должна быть сумма X,  чтобы Алексей выплатил долг четырьмя равными
платежами ( то есть за четыре года)?

Решение:

Пусть сумма
кредита равна S, а годовые составляют a%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на
коэффициент 

b=1+0,01a.

После первой
выплаты сумма долга составит

S₁=Sb—X.

После второй
выплаты сумма долга составит

S₂=S₁b—X=(Sb—X)b—X=Sb²—Xb—X=Sb²-(b+1)X, и в свою
очередь b+1 можно представить как

  = откуда получаем

S₂= Sb²—X
После третьей выплаты сумма оставшегося долга равна

S₃=S₂b—X=(Sb²-(b+1)X)b—X=Sb³—Xb²—Xb—X=Sb³=Sb³-(b²+b+1)X, и в свою
очередь (b²+b+1) можно представить  как

 = откуда получаем

                                                                                                                               
(5)

S₃=Sb³— X

 После
четвертой выплаты сумма оставшегося долга равна

S₄=S₃b—X= (Sb³-(b²+b+1)X)b—X=Sb⁴—Xb³—Xb²—Xb—X=Sb⁴-(b³+b²+b+1)X, попытаемся
представить  b³+b²+b+1 как

b³+b²+b+1===, следовательно

S₄=Sb⁴—X

По условию
четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 

Sb⁴—X=0,

Откуда

X=.

При S=6902000 и a=12,5, получаем: b=1,125 и

X==2296350(рублей).

Ответ:
2296350.

(6)                   

2.    
Получение
формы для решения задач на проценты.

При решение
предыдущей задачи мы замечаем, что

S₂= Sb²—X; S₃=Sb³—  X; S₄=Sb⁴— X.

А будет ли
формула верна и для 5 или 6 лет выплат?

Что бы это
доказать обратимся к Методу математической индукции.

Для этого нам
нужно доказать, что S_n= Sbⁿ—X верно при любых n.

1)    n=1

S₁= Sb¹— X

S₁=Sb—X – верно(было получено при решении Задачи 1).

2)  Пусть формула верна при n=k,  S_k=Sb^k—X. Докажем, что она верна при n=k+1, то есть

S_k+1=Sb^k+1—X;

S_k+1=S_kb—X= (Sb^k—X)b—X=Sb^k*b—Xb—X=Sb^k+1-(b+1)X=

Sb^k+1-( + )X= Sb^k+1-( )X= Sb^k+1—= S_k+1.

Следовательно,
S_n= Sbⁿ—X верно при любых n. Таким
образом, мы получаем уравнение для решения задач на проценты из второй части
Единого Государственного Экзамена.

Теперь
проверим формула при решение задач. Решим сначала обычным способом, а затем с
помощью формулы.

(7)

3.Решение задачи на проценты, где нужно найти
размер выплаты, то есть X.

Задача 2.

31 декабря
2014 года Алексей взял в банке 9 282 000 рублей в кредит под 10%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Алексей переводит в банк X рублей.
Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными
платежами (то есть за четыре года)?

Обычный
способ:

1)    9282000+0,1*9282000-X= 9282000+928200-X= 10210200-X  — сумма,
оставшаяся после первой выплаты.

2)    10210200-X +(10210200-X )*0,1-X=

=10210200-X+1021020-0,1X—X=11231220-2,1X   — сумма, оставшаяся после второй выплаты.

3)    11231220-2,1X+(11231220-2,1)*0,1-X=

=11231220-2,1X+1123122-0,21X—X=12354342-3,31X   -сумма, оставшаяся после третей выплаты.

4)    12354342-3,31X-(12354342-3,31X)*0,1-X=

=12354342-3,31X+1235434,2-0,331X—X=13589776,2-4,641X –сумма после четвертой выплаты равная 0.

13589776,2-4,641X=0

4,641X=13589776,2

X=13589776,2/4,641

X=2928200 рублей.

Ответ: 2928200 рублей.

  С помощью формулы:

S_n= Sbⁿ—X,

И так как Алексей выплатит долг за 4 года, то n=4, тогда S₄=0, b=1,1;

                                                                                                                               
(8)                                                                                                                                                               

X=  ;

X=

X=.

X=2928200
рублей.

Ответ: 2928200 рублей.

Результаты обоих решений оказались одинаковыми.

(9)

Задача 3.

31 декабря
2014 года Иван взял в банке 4 230 000 рублей в кредит под 11,5%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
11,5%), затем Иван переводит в банк X рублей.
Какой должна быть сумма X, чтобы Иван выплатил долг двумя равными
платежами (то есть за два года)?

Обычное
решение:

1.    
4230000+4230000*0,115-X=4230000+486450-X=4716450-X  
—

Сумма, которая останется после первой выплаты.

2.    
4716450-X+(4716450-X )*0,115-X= 4716450-X+542391,75-0,115X-X=

= 5258841,75-2,115X – сумма после второй выплаты равная 0.

5258841,75-2,115X=0

2,115X=5258841,75

X=5258841,75/2,115

X=2486450 рублей.

Ответ:
2486450 рублей.

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Иван выплатит долг за 2 года, то n=2, S₂=0, b=1,115.

X= ;

X= ;

X= .

X=2486450
рублей.

Ответ:
2486450 рублей.

Результаты обоих решений оказались одинаковыми.                        

                                                                                                                       
 (10)

Задача 4.

31 декабря
2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга( то есть увеличивает долг на
20%), затем Тимофей переводит в банк платеж. Весь долг Тимофей выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных  платежа?

Обычный
способ:

1)    7007000+0,2*7007000-X= 8408400-X – сумма, оставшаяся после первой выплаты.

2)    8408400-X+(8408400-X)*0,2-X=8408400-X+1681680-0,2X—X=

10090080-2,2X – сумма, оставшаяся после второй выплаты.

3)    Но если погасить кредит за два года, то

10090080-2,2X₁=0

2,2X₁=10090080

X₁=10090080/2,2

X₁=4586400 рублей- размер выплаты кредита, при условии, что он
будет погашен за 2 года.

4)    10090080-2,2X+(10090080-2,2X)*0,2-X=

=10090080-2,2X+2018016-0,44X—X=12108096-3,64X – сумма после третей выплаты равной 0.

12108096-3,64X=0

3,64X=12108096

X=12108096/3,64

X=3326400 рублей- размер выплаты кредита, при
условии, что он будет погашен за 3 года.

5)    3*X-2*X₁  — сэкономленные
деньги, которые мог бы получить Тимофей, если бы смог погасить кредит за 2
года.

3326400*3 -4586400*2= 9979200-9172800=806400 рублей- сэкономленные
деньги, которые мог бы получить Тимофей, если бы смог погасить кредит за 2
года.

Ответ: 806400
рублей.

                                                                                                                             
(11)

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Тимофей выплатит долг за 3 года, то n=3, S₃=0, b=1,2.

X= ;

X= ;

X=  ;

X=3326400
рублей- размер
выплаты кредита, при условии, что он будет погашен за 3 года.

Также Тимофей мог погасить кредит за 2 года, тогда n=2, S₂=0,b=1,2.

X₁= ;

X₁= ;

X₁= ;

X₁=4586400 рублей-  размер выплаты кредита, при условии, что он
будет погашен за 2 года.

3*X-2*X₁  — сэкономленные деньги, которые мог бы получить Тимофей,
если бы смог погасить кредит за 2 года.

3326400*3
-4586400*2= 9979200-9172800=806400 рублей- сэкономленные деньги, которые мог бы
получить Тимофей, если бы смог погасить кредит за 2 года.

Ответ: 806400
рублей.

Результаты обоих решений оказались одинаковыми.

   (12)

4.Решение
задачи на проценты, где нужно найти размер кредита,

 то есть S.

Задача 5.

31 декабря
2014 года Сергей взял в банке некоторую сумму в кредит под 12% годовых. Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 12%), затем Сергей
переводит в банк 3 512 320 рублей. Какую сумму взял Сергей в банке,
если он выплатил долг тремя равными платежами (то есть за три года)?

Обычный
способ:

      1)S+0,12*S-3512320= 1,12*S-3512320 
— сумма, оставшаяся от долга после первой выплаты.

2)1,12*S-3512320+(1,12*S-3512320)*0,12-3512320=

=1,12*S-3512320+0,1344*S-421478,4-3512320=

  =1,2544*S-7446118,4 –сумма, оставшаяся от долга после
второй выплаты.

3)1,2544*S-7446118,4+(1,2544*S-7446118,4)*0,12-3512320=

=1,2544*S-7446118,4+0,150528*S-893534,208-3512320=

=1,404928*S-11851972,608- сумма равная 0, то есть после
третей выплаты.

1,404928*S-11851972,608=0

1,404928*S=11851972,608

S=11851972,608/1,404928

S=8436000 рублей.

Ответ: S=8436000 рублей.

С помощью
формулы:

S_n= Sbⁿ—X;

(13)

И так как
Сергей выплатит долг за 3 года, то n=3, S₃=0, b=1,12.

S=;

S=*;

S= *=3,3744*2500000=8436000 рублей.

Ответ: S=8436000 рублей.

Результаты обоих решений оказались одинаковыми.

(14)

Задача 6.

31 декабря
2014 года Владимир взял в банке некоторую сумму в кредит под 10% годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты
на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Владимир
переводит в банк 3 025 000 рублей. Какую сумму взял Владимир в банке, если
он выплатил долг двумя равными платежами (то есть за два года)?

Обычное
решение:

1)S+0,1*S-3025000=1,1*S-3025000 –
сумма, которая останется после первой выплаты.

      2) 1,1*S-3025000+(1,1*S-3025000)*0,1-3025000=

=1,1*S-3025000+0,11*S-302500-3025000=1,21*S-6352500 – долг равный 0 после второй выплаты.

1,21*S-6352500=0

      1,21*S=6352500

      S=6352500/1,21

S=5250000 рублей.

Ответ: S=5250000 рублей.

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Владимир выплатит долг за 2 года, то n=2, S₂=0, b=1,1.

S=;

S=;

S=;

                                                                                                                             
(15)

S=2,1*25000000= 5250000 рублей.

Ответ: S=5250000 рублей.

Результаты обоих решений оказались одинаковыми.

(16)

Задача 7.

31 декабря
2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых.
Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Ярослав
переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если
он выплатил долг четырьмя равными платежами (то есть за четыре года)?

Обычный способ:

1)    S+0,125*S-2132325=1,125*S-2132325-
размер долга, который остался после первой выплаты.

2)    1,125*S-2132325+(1,125*S-2132325)*0,125-2132325=

=1,125*S-2132325+0,140625*S-266540,625-2132325=

=1,265625*S-4531190,625- размер долга, который остался после
второй выплаты.

3)    1,265625*S-4531190,625+(1,265625*S-4531190,625)*0,125-2132325=

=1,265625*S-4531190,625+0,158203125*S-566398,828125-2132325=

=1,423828125*S-7229914,45313– размер долга, который остался
после третей выплаты.

4)    1,423828125*S-7229914,45313+(1,423828125*S-7229914,45313)*0,125-

2132325=1,423828125*S-7229914,45313+0,17797851562*S-903739,306641—

2132325=1,60180664062*S-10265978,7598
–размер долга равный 0 после четвертой выплаты.

1,60180664062*S-10265978,7598=0

1,60180664062*S=10265978,7598

S=10265978,7598/1,60180664062

S=6409000 рублей.

Ответ:
6409000 рублей.

                                                                                                                         
    (17)

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Владимир выплатит долг за 4 года, то n=4, S₄=0, b=1,125.

S=;

S=;

S=;

S=4,81445312496*1331200;

S=6409000 рублей.

Ответ: 6409000
рублей

Результаты обоих решений оказались одинаковыми.

                                                                                                                             
(18)

5.Решение
задачи на проценты, где нужно найти количество лет ,

 то есть n.

Задача 8.

Максим хочет
взять в кредит 1,5 млн рублей. Погашение кредита происходит раз в год равными
суммами (кроме, может быть, последней) после начисления процентов. Ставка
процентов 10%годовых. На какое минимальное количество лет может Максим взять
кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей? 

Обычный
способ:

1.    
1500000+0,1*1500000-350000=1500000+150000-350000=1300000-
величина кредит, которая останется после первого года.

2.    
1300000+1300000*0,1-350000=1080000-
величина кредит, которая останется после второго года.

3.    
1080000+0,1*1080000-350000=838000
— величина кредит, которая останется после третьего года.

4.    
838000+0,1*838000-350000=571800-
величина кредит, которая останется после четвертого года.

5.    
571800+0,1*571800-350000=278980
— величина кредит, которая останется после пятого года.

6.    
278980+0,1*278980-350000=306878-350000
– последняя выплата за кредит, 6 год.

Ответ: 6 лет.

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Максим  взял в банке 1500000, b=1,1.

Sbⁿ= X.

1500000*1,1ⁿ= *350000.

                                                                                                                             
(19)

1,1ⁿ-1=

1,1ⁿ-1=0,43*1,1ⁿ.

1,1ⁿ-0,43*1,1ⁿ=1.

1,1ⁿ*(1-0,43)=1.

1,1ⁿ=1/(1-0,43).

1,1ⁿ=1,75.

n=6.

Ответ: 6 лет.

Результаты обоих решений оказались одинаковыми.

(20)

Задача 9.

Родион хочет
взять в кредит 1,2 млн рублей. Погашение кредита происходит раз в год равными
суммами (кроме, может быть, последней) после начисления процентов. Ставка
процентов 10%годовых. На какое минимальное количество лет может Родион взять
кредит, чтобы ежегодные выплаты были не более 320 тысяч рублей? 

Обычный
способ:

1.    
1200000+0,1*1200000-320000=1000000-
величина кредита, оставшаяся после первого года.

2.    
1000000+0,1*1000000-320000=780000-
величина кредита, оставшаяся после второго года.

3.    
780000+0,1*780000-320000=538000
– величина кредита, оставшаяся после третьего года.

4.    
538000+0,1*538000-320000=271800-
величина кредита, оставшаяся после четвертого года.

5.    
271800+0,1*271800-320000=298980-298980=0 
—  последняя выплата за кредит, 5 год.

Ответ: 5 лет.

С помощью формулы:

S_n= Sbⁿ—X;

И так как
Родион  взял в банке 1200000, b=1,1.

Sbⁿ= X.

1200000*1,1ⁿ= *320000.

1,1ⁿ= *.

1,1ⁿ=2,7*1,1ⁿ-2,7.

2,7*1,1ⁿ-1,1ⁿ=2,7.

                                                                                                                             
(21)

1,1ⁿ*(2,7-1)=2,7.

1,1ⁿ=1,61.

n=5.

Ответ: 5 лет.

Результаты обоих решений оказались одинаковыми.

(22)

Задача 10.

1 января 2015
года Александр Дмитриевич взял в банке 1,1 млн рублей в кредит. Схема выплаты
кредита следующая: 1 числа каждого следующего месяца банк начисляет 2 процента
на оставшуюся сумму долга(то есть увеличивает долг на 2%), затем Александр
Дмитриевич переводит в банк платеж. На какое минимальное количество месяцев 
Александр Дмитриевич может взять кредит, чтобы ежемесячные выплаты были не
более 275 тыс. рублей?

Обычный
способ:

1.    
1100000+1100000*0,02-275000=847000
– величина кредита, оставшаяся после первого месяца.

2.    
847000+847000*0,02-275000=588940
— величина кредита, оставшаяся после второго месяца.

3.    
588940+588940*0,02-275000=325718,8-
величина кредита, оставшаяся после третьего месяца.

4.    
325718,8+325718,8*0,02-275000=57233,176
— величина кредита, оставшаяся после четвертого месяца.

5.57233,176 +57233,176
*0,02-275000=58377,83952-58377,83952=0-  последняя выплата за кредит, 5 год.

Ответ: 5 лет.

С помощью
формулы:

S_n= Sbⁿ—X;

И так как
Александр Дмитриевич  взял в банке 1100000, b=1,02.

Sbⁿ= X.

1100000*1,02ⁿ=*275000.

1,02ⁿ= *.

(23)

1,02ⁿ=12,5*1,02ⁿ-12,5.

12,5*1,02ⁿ-1,02ⁿ=12,5.

1,02ⁿ*(12,5-1)=12,5.

1,02ⁿ=1,1.

n=5.

Ответ: 5 лет.

Результаты обоих решений оказались одинаковыми.

(24)

6.Решение
задачи на проценты, где нужно найти процентную ставку,

 то есть а.

Задача 11.

31 декабря 2014 года Борис взял в банке
1млн рублей в кредит. Схема выплаты кредит следующая: 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму долга (то есть
увеличивает долг на определенное количество процентов), затем Борис переводит
очередной транш. Борис выплатил кредит за два транша, переведя в первый раз 560
тыс. рублей, во второй – 644,1 тыс. рублей. Под какой процентов банк выдал
кредит Борису?

Обычный способ:

1.     1000000+a*1000000-560000=
440000+ a*1000000-
размер кредита, оставшаяся после первого года.

2.    
440000+ a*1000000+a*(440000+
a*1000000)-644100

=1000000*a²+1440000*a−204100-
кредит, погашенный за два транша.

1000000*a²+1440000*a−204100=0

D=1440000²-4*1000000*(-204100)=
1700000²

X₁=(-1440000+1700000)/2*1000000=0,13X₂—
не подходит.

Ответ: 13 процентов.

С помощью
формулы:

S_n= Sbⁿ—X;

Задачу тяжело
решить таким способом.

  (25)

Задача 12.

31 декабря 2014 года Арсений взял в банке
1млн рублей в кредит. Схема выплаты кредит следующая: 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму долга (то есть
увеличивает долг на определенное количество процентов), затем Арсений переводит
очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз
550 тыс. рублей, во второй – 638,4 тыс. рублей. Под какой процентов банк выдал
кредит Арсению?

Обычный способ:

1.1000000+1000000*a-550000=450000+1000000*a
— размер кредита, оставшаяся после первого года.

2. 450000+1000000*a+(450000+1000000*a)*a-638400=

=1000000*a²+1450000*a−188400-
кредит, погашенный за два транша.

1000000*a²+1450000*a−188400=0

D=1450000²-4*1000000*(−188400)=
1690000².

X₁=(-1450000+1690000)/2*1000000=0,12 
X₂—
не подходит.

Ответ: 12 процентов.

С помощью
формулы:

S_n= Sbⁿ—X;

Задачу тяжело
решить таким способом.

  (26)

Задача 13.

31 декабря 2014 года Петр взял в банке
некоторые сумму в кредит под некоторый процент годовых. Схема выплаты кредита
следующая – 31декабря каждого следующего года банк начисляет проценты на
оставшуюся сумму долга (то есть увеличивает долг на a%),
затем Петр переводит очередной транш. Если бы он будет платить каждый год по
2 592 000 рублей, то выплатит долг за 4 года. Если по
4 392 000, то за 2 года. Под какой процент Петр взял деньги в банке?

Обычный способ:

Таким способом решить задачу достаточно
тяжело.

С помощью
формулы:

Петр взял в
кредит S рублей, x₁=2592000 при n=4, x₂=4392000 при n=2.

S_n= Sbⁿ— X;

Sb²= X₂,

Sb⁴— X₁=0

 X₂*b²— X₁=0

(b²-1)*x₂*b²-(b⁴-1)*x₁=0
и
b≠1.

b²*(b²-1)* x₂-(b²-1)*(b²+1)*x₁=0

(b²-1)( b²* x₂-(b²+1)*x₁)=0

1.     b²-1=0

b≠1 и b=-1
(не подходит по условию задачи).

2.     b²*
x₂-(b²+1)*x₁=0

4392000*b²—2592000*b²—2592000=0

(27)

1800000* b²=2592000

b²=2592000/1800000

b=1,2  и b=-1,2
( не подходит по условию задачи).

b=1,2; тогда a=(b-1)*100=20%.

Ответ: 20 процентов.

                                                                                                                             
(28)

Заключение.

Итак, в ходе
своей работы я получил универсальную формулу для нахождения данных в задачах на
проценты из Единого Государственного Экзамена и доказал ее работоспособность
при любых n. Тем самым, я могу считать цели своей работы
полностью достигнутой; все задачи, для достижения этой цели были выполнены.

S_n= Sbⁿ—X;

Формулу
действительно можно считать универсальной, но, к сожалению, не всегда
прибегнуть к ней будет легче, что было показано решение предыдущих задач. Если
неизвестными  в задаче являются размер кредита или размер ежегодной выплаты, то
новый способ отлично подходит для решения задачи. Он существенно сэкономит
время и уменьшит шанс совершения ошибки при вычислении. Если же необходимо
найти процентную ставку, то легче решить задачу по шагам, то есть обычным
способом.  В задачах, где неизвестной является количество годов, при разных
размерах транша также легче обратиться к обычному способу, но если же размер
выплаты одинаковый или есть несколько условий сразу, то разумнее обратиться к формуле.

Не стоит
забывать, что при решении задачи в ЕГЭ необходимо самостоятельно вывести эту
формулу, иначе можно потерять баллы.

В заключении,
хотелось бы сказать, что я считаю свою работу актуально, так как она
действительно в некоторых случаях позволяет сэкономить время и получить
правильныйответ, что очень важно при сдаче Единого Государственного Экзамена.

                                                                                                                             
(29)

Список
литературы:

1.    
Интернет-сайты.

http://videouroki.net/filecom.php?fileid=98661787(Методы
решения логических задач)

http://scorcher.ru/adaptologiya/minimization_efforts/minimization_efforts5.php

(Упрощение
логических формул)

 

http://revolution.allbest.ru/finance/00310055_0.html(Основы
финансовой математики.Основные понятия математических методов исследования
экономики и математического программирования экономических процессов)

http://www.kazedu.kz/referat/6072(Математические
модели и методы их расчета)

http://www.cleverstudents.ru/articles/induction.html(Метод математической индукции.)

2.Книги.

«Типовые
экзаменационные варианты под редакцией И.В. Ященко. 36 вариантов 2015 год.»

«О
математической индукции. Наука» Илья Самойлович Соминский,
Лидия Ивановна Головина, Исаак Моисеевич Яглом. 1974 год.

Алгебра
и математический анализ, 10 класс: учебник для углубленного изучения математики
в общеобразовательных учреждениях/Н.Я. Виленкин, О.С. Ивашев-Мусатов,
С.И.Шварцбурд,-13 издание- М.: Мнемозине, 2006.

   (30)

Решение задач по теме: «ПРОЦЕНТЫ»

на ЕГЭ по математике

( профильный уровень)

Из опыта работы

учителя

математики

МОУ СОШ №1

р.п. Новые Бурасы

Новобурасского района

Саратовской области

Коротковой

Натальи Александровны

Понимание процентов и умение производить процентные расчеты в настоящее время необходимо каждому человеку, это способствует «вхождению» в современную информационно-экономическую среду и, в конечном счете, облегчает социализацию.

Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки, бытовые и производственные сферы жизни. Обучающиеся встречаются с процентами на уроках физики, химии, чтении газет, просмотре телепередач. Умением грамотно и экономно проводить элементарные процентные вычисления обладают далеко не все люди. Практика показывает, что очень многие окончившие школу не только не имеют прочных навыков обращения с процентами в повседневной жизни, но даже не понимают смысла процентов, как доли от некоторой заданной величины. Происходит это потому, что проценты изучаются на первом этапе основной школы, в 5-6 классах, когда учащиеся в силу возрастных особенностей еще не могут получить полноценные представления о процентах, об их роли в повседневной жизни.

В последнее время экзамен по математике проводится в форме ЕГЭ, и в контрольно-измерительных материалах ЕГЭ (профильный уровень) и ЕГЭ ( базовый уровень) присутствуют задачи на проценты. Специфика темы такова, что значительное позитивное влияние на знания и умения учащихся оказывает последующее обучение, причем не математике, а химии, где процентные расчеты являются существенным элементом содержания обучения, об этом свидетельствуют и приемы решения задач, и способы записи их решения.

Как подготовить учащихся 11 классов к правильному решению задач ЕГЭ на проценты?

I

Сначала надо систематизировать знания и умения по теме «Проценты», полученные в 5 и 6 классах.

Учащиеся должны уметь:

• преобразовывать десятичные и обыкновенные дроби,

• представлять проценты — в виде дроби и дробь – в виде процентов;

• находить проценты от величины, величину по ее проценту;

• выражать отношения в процентах;

• применять полученные математические знания в решении жизненных задач;

тест по теме «Проценты»

1. Найдите 25% от 56.

А) 14 Б) 22,04 В) 20 Г) 25

1. Найдите число, если 1% его равен 75.

А) 0,75 Б) 7,5 В) 7500 Г) 750

1. Клубника содержит 6% сахара. Сколько килограммов сахара в 27 кг клубники?

А) 1,82 кг Б) 1,62 кг В) 2,24 кг Г) 2,42 кг

1. Книга стоила 25 р. После повышения цены она стоит 30,25 р. На сколько процентов возросла стоимость книги?

А) на 21% Б) на 20% В) на 24% Г) на 25%

1. Найдите число, 34% которого равны 170.

А) 57,8 Б) 500 В) 56,5 Г) 510

1. На математической олимпиаде 32% участников получили грамоты. Сколько школьников приняло участие в олимпиаде, если наградили 416 человек?

А) 932 Б) 1300 В) 133,1 Г) 1340

1. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?

А) 330% Б) 30% В) 125% Г) 45%

1. Число уменьшили на 20%. На сколько процентов надо увеличить полученное число, чтобы получить данное число?

А) на 20% Б) на 40% В) на 25% Г) на 30%

1. Число 56 составляет 80% от некоторого числа. Найдите среднее арифметическое этих чисел.

А) 63 Б) 44,8 В) 126 Г) 56

1. Сторону квадрата уменьшили на 20%. На сколько процентов уменьшилась его площадь?

А) на 20% Б) на 36% В) на 10% Г) на 40%

Задания представлены в виде текстовых задач.

1. Квартирная плата повысилась на 20%. За прошлый месяц заплачено 120рублей. Сколько надо заплатить за текущий месяц?

2. В референдуме приняли участие 18 тыс. человек, что составило 60% всех жителей города, имеющих право голоса. Сколько жителей имеют право голоса?

3. В 5 тысячах из выпущенных 20 тысяч коробочек с жевательной резинкой находится сюрприз. Сколько процентов составили коробочки с сюрпризами?

4. Банком установлен тариф на пролонгацию аккредитива в размере 0,2% за квартал от суммы аккредитива. Вычислите размер комиссионных за пролонгацию аккредитива на сумму 100000 рублей за один квартал?

5. В первом квартале литр молока стоил 10 рублей. Во втором квартале цена на молоко повысилась на 20%, а в третьем еще на 50%. Сколько стал стоить литр молока?

6. Фирма платит разносчикам рекламных изданий за первую партию 10 тыс. рублей, а за каждую следующую в тот же день – на 5% больше по сравнению с предыдущей. Сколько получит человек, если в течение одного дня он разнес 4 партии изданий?

7. 15% жителей города ежегодно слушают ВВС, 45% — радио «Свобода» и 40% — «Голос Америки». Можно ли сказать, что все жители города ежедневно слушают передачи западного радио?

8. Себестоимость товара 30 тыс. рублей. В магазине этот товар продается по цене 90 тыс. руб. Сколько процентов от себестоимости составляет розничная цена.

9. Валовой национальный продукт государства составил 33 млрд. долларов, что соответствует 75% от планировавшегося бюджетом. Найдите плановую величину НВП этого государства.

10. Подоходный налог установлен в размере 13%. До вычета подоходного налога 1% заработной платы отчисляется в пенсионный фонд. Работнику начислено 5420 рублей. Сколько он получит после указанных вычетов?

11. Инфляция составляет 10% каждый месяц. Сколько процентов составила инфляция за два месяца?

12. В результате мелиоративных мероприятий посевные площади увеличились на 150% по сравнению с прошлым годом. Найдите величину посевных площадей этого года, если в прошлом году она была 60 га

II

Затем необходимо развивать и углублять общеучебные навыки и умения за счет: решения дополнительных задач (на процентное содержание, процентный раствор и концентрацию); новых способов их решения (уравнение, система уравнений, геометрически, старинный способ); решения задач с практической ориентацией.

ЗАДАНИЯ ИЗ ВАРИАНТОВ ЕГЭ

1. Смешали 160 г раствора, содержащего 60% соли, и 240 г раствора, содержащего 40% соли. Сколько процентов соли в получившемся растворе?

2. В январе пакет акций стоил на 10% меньше, чем в феврале. В феврале этот же пакет акций стоил на 20% меньше, чем в марте. На сколько процентов меньше стоимость акций в январе, чем в марте?

3. Предприятие уменьшило выпуск продукции на 20%. На сколько процентов необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?

4. Зарплату повысили на р%. Затем новую зарплату повысили на 2р%. В результате двух повышений зарплата увеличилась в 1,32 раза. На сколько процентов зарплата была повышена во второй раз?

ПРОЦЕНТНОЕ СОДЕРЖАНИЕ, ПРОЦЕНТНЫЙ РАСТВОР

Тип задач на составление уравнений и систем уравнений – задачи на сплавы и смеси, решение которых связано с понятиями «концентрация», «процентное содержание», «проба», «влажность».

Процентное содержание вещества в растворе, иногда называют %-м раствором, например, 15%-й раствор соли.

1. Сколько кг соли в 10 кг соленой воды, если %-е содержание соли 15%?

Решение: 10∙0,15 = 1,5(кг).

Ответ: 1,5 кг.

Процентное содержание вещества в сплаве – это часть, которую составляет вес данного вещества от веса всего сплава.

2. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?

Решение:

1) 10 + 15 = 25(кг) сплав;

2) 10: 25 ∙ 100% = 40% процентное содержание олова в сплаве.

3) 15: 25 ∙ 100% = 60% процентное содержание цинка в сплаве.

Ответ: 40%, 60%.

КОНЦЕНТРАЦИЯ, СМЕСИ И СПЛАВЫ

Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.

Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 300∙0,87 = 261 г.

В этом примере концентрация вещества выражена в процентах.

Отношение объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.

Сумма концентраций всех компонент, составляющих смесь, равна 1. В этом случае концентрация – безразмерная величина.

Если известно процентное содержание вещества, то его концентрация находится по формуле: к = р : 100%,

к – концентрация вещества;

р – процентное содержание вещества (в процентах).

Задача 1. Имеется два сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго слава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?

Решение (с помощью уравнения): Пусть к 20 кг первого сплава нужно добавить Х кг второго сплава. Тогда получим (20+Х) кг нового сплава. В 20 кг первого сплава содержится 0,4∙20 = 8 (кг) серебра, а в (20+Х) кг нового сплава содержится 0, 32∙(20+Х) кг серебра. Составим уравнение: 8+0,2Х = 0,32(20+Х), Х=13 1/3.

Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.

Задача 2. При смешивании 5%-ного раствора кислоты с 40%-ным раствором кислоты получили 140 г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?

Решение (с помощью системы уравнений):

Проследим за содержанием кислоты в растворах. Возьмем для смешивания Х г 5%-ного раствора кислоты (или 0,05Х г) и Υ г 40%-ного раствора (или 0,4Υ г). Так как в 140 г нового раствора кислоты стало содержаться 30%, т. е. 0,3∙140 г, то получаем следующее уравнение 0,05Х + 0,4Υ = 0,3∙140. Кроме того Х + Υ = 140.

Таким образом, приходим к следующей системе уравнений:

0,05Х + 40Υ = 30∙140,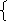

Х + Υ = 140.

Из этой системы находим Х = 40, Υ = 100. Итак, 5%-ного раствора кислоты следует взять 40 г, а 40%-ного раствора – 100 г.

Ответ: 40 г, 100 г.

Таким образом, задачи для старшеклассников содержат прагматическую ориентацию, их формулировки имеют практическое применение, представляют конкретные интересы.

Задача 1.

Стоимость компьютера 1250 долларов. Какова будет его стоимость после снижения цены на 20%?

Задача 2.

Торт стоил 100 рублей. Сначала цену повысили на 10%, а затем снизили на 10% (от новой цены). Сколько теперь стоит торт?

III

В первую очередь изучению – на основной или старшей ступени – подлежат «сложные» проценты. Понятия «простых» и «сложных» процентов, при условии достаточного овладения учащимися этими понятиями, могут послужить мощным источником мотивации введения многих математических понятий. Основой для введения арифметической и геометрической прогрессий.

Приведу в качестве примера три задачи.

Задача 3.

Скорость тела, движущегося равноускоренно, каждую секунду увеличивается на 10%. В данный момент его скорость10,00 м/сек. Какова будет его скорость через три секунды?

Задача 4.

При внесении квартирной платы на один день позже установленного срока начисляется пеня в размере 0,1% от суммы платежа. Сколько придется заплатить в случае задержки квартирной платы на три месяца, если квартирная плата составила 100 рублей?

Задача 5.

Банком установлена процентная ставка из расчета 3% в месяц. Сколько денег должен получить гражданин, вложивший в этот банк 100 рублей на 3 месяца?

Следует заметить, что самые естественные примеры могут служить «материальным» доказательством сравнения скорости роста арифметической и геометрической прогрессий. Этот факт оказывается, таким образом, не чисто математическим, причем достаточно сложным «изысканием», а совершенно очевидным «на практике» утверждением.

Задача 6.

Выгодно ли гражданину задержать на три месяца внесение квартирной платы (задача 4), вложив эти 100 рублей в банк (задача 5)?

IV

Решение задач с помощью уравнения

Проблема заключается в том, что даже при решении несложных задач, возникают затруднения при переводе текста задачи на язык уравнений.

Систематизируем знания по данному вопросу.

Неизвестную величину обозначим через Х, тогда

• чтобы найти 20% от нее, надо 0,2Х;

• чтобы увеличить ее, например, на 10%, надо Х+0,1Х=1,1Х;

• чтобы уменьшить ее, например, на 30%, надо Х-0,3Х=0,7Х,

• в общем виде: если 0

• чтобы найти Р% от Х, надо 0,РХ;

• чтобы увеличить ее на Р%, надо Х+0,РХ=1,РХ;

• чтобы уменьшить ее на Р%, надо Х-0,РХ=(1-0,Р)Х, далее составляем уравнение, соответствующее условию задачи.

Задача

В двух школах поселка было 1500 учащихся. Через год число учащихся первой школы увеличилось на 10%, а второй – на 20%, и в результате общее число стало равным 1720. Сколько учащихся было в каждой школе первоначально?

Решение:

Пусть Х учащихся было в первой школе, тогда (1500-Х) учащихся было во второй школе. После увеличения на 10% учащихся первой школы их стало Х+0,1Х=1,1Х, а во второй школе стало (1500-Х)+0,2(1500-Х)=1500-Х+300-0,2Х=1800-1,2Х учащихся. В результате их общее число стало равным 1720. Составим уравнение

1,1Х+1800-1,2Х=1720

-0,1Х=-80

Х=800

Таким образом получили, что 800 учащихся было в первой школе, тогда 700 учащихся было во второй школе первоначально.

Ответ: 800 и 700 учащихся.

V

Решение с помощью системы уравнений

Когда в условии задачи неизвестными являются две величины, то можно решить задачу с помощью системы уравнений. Решим предыдущую задачу с помощью системы уравнений.

Решение:

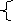
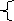
Пусть Х учащихся было в первой школе, тогда Υ учащихся было во второй школе. В двух школах поселка было 1500 учащихся. После увеличения учащихся первой школы их стало 1,1Х, а во второй стало 1,2Υ учащихся, в результате их общее число стало равным 1720. Составим систему уравнений и решим ее способом подстановки

Х+Υ=1500, Х=1500-Υ, Х=1500-Υ, Х=800,

1,1Х+1,2Υ=1720; 1,1(1500-Υ)+1,2Υ=1720; Υ=700; Υ=700.

Ответ: 800 и 700 учащихся.

Задачи из открытого банка заданий ЕГЭ

Задача 1. Одной машинистке на перепечатку рукописи требуется на 12 ч больше, чем другой. Если 25% рукописи перепечатает первая машинистка, а затем к ней присоединится вторая машинистка, то на перепечатку рукописи им понадобиться 35 ч, считая от момента начала работы первой машинистки. За сколько часов могла бы перепечатать рукопись каждая машинистка, работая отдельно?

Решение: Пусть на перепечатку рукописи первой машинистке требуется ч, тогда второй потребуется ч. На перепечатку 25% рукописи первая машинистка затратит ч. Выясним теперь, сколько времени потребуется двум машинисткам на перепечатку оставшихся 75% рукописи. Первая машинистка перепечатывает за один час часть рукописи, вторая – часть рукописи, а вместе за час они перепечатывают часть рукописи. На перепечатку рукописи им потребуется ч, т.е. ч. Отсюда получаем уравнение:

Решив это уравнение, найдем, что оно имеет два корня: и .

Второй корень не соответствует условию задачи.

Ответ: первой машинистке на перепечатку рукописи требуется 60 ч, а второй – 48 ч.

Задача 2. Положив в банк деньги, вкладчик получил через год прибыль в 240 тысяч рублей. Однако он не стал забирать деньги из банка, а, добавив к ним еще 60 тысяч, снова оставил деньги на год. В результате спустя еще год он получил в банке 1 миллион 100 тысяч рублей. Какая сумма была положена в банк первоначально и какой процент прибыли в год давал банк?

Решение: Допустим, что первоначальный вклад составляет тысяч рублей. Тогда процент прибыли за год равен . Сумма вклада, положенного в банк через год, составила тысяч рублей, т.е. тысяч рублей. Этот вклад принес доход, равный тысячам рублей. Всего вкладчик получил 1100 тысяч рублей.

Получаем уравнение:

Решив его, найдем, что это уравнение имеет два корня: , Выполнив расчеты, можно убедиться, что оба корня соответствуют условию задачи.

Ответ: задача имеет два решения: вкладчик вложил первоначально 200 тысяч рублей и получил доход 120% в год или вкладчик вложил первоначально 360 тысяч рублей и получил доход в год.

Задача 3. Имелось два слитка меди. Процент содержания меди в первом слитке был на 40 меньше, чем процент содержания меди во втором. После того как оба слитка сплавили, получили слиток, содержащий 36% меди. Найдите процентное содержание меди в первом и во втором слитках, если в первом слитке было 6 кг меди, а во втором – 12 кг.

Решение: Обозначим за массу первого слитка в кг, за массу второго слитка в кг, получим систему уравнений:

В результате получим: х=30, у=20.

Ответ: 30 кг, 20 кг

Задача 4. Для определения оптимального режима снижения цен социологи предложили фирме с 1 января снижать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 10%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо снижать цену товара через каждые два месяца во втором магазине?

Решение: Пусть руб. — стоимость товара, — число процентов. Тогда,

I магазин

Февраль

Март

……………………………………

Июль

II магазин

Март

Май

Июль

По условию задачи через полгода (1 июля) цены снова стали одинаковые, составляем уравнение:

Ответ: на 21%.

Задача 5. В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала повышать сотруднику зарплату на 3%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько процентов фирма должна повышать зарплату каждые полгода, чтобы 1 января следующего года зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренной договором.

Решение: Пусть руб. — зарплата, — процент повышения зарплаты. Тогда,

По плану: I квартал руб.

……………………………

IV квартал руб.

Фактически

I полугодие руб.

II полугодие руб.

По условию задачи зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренного договором, составляем уравнение:

Ответ: на 6,09 %.

Задача 6. На заводе было введено рационализаторское предложение. В результате время, необходимое для изготовления рабочими некоторой детали, уменьшилось на 20%. На сколько процентов возросла производительность труда этого рабочего?

Решение: Пусть — производительность труда, а — весь объем работы. Тогда работа будет выполнена за время . В результате роста производительности труда время на изготовление детали стало равно , соответственно производительность , или . Соответственно рост производительности труда составил:

Ответ: 25%

Задача 7. Из жителей города одни говорят только на украинском, другие – только на русском, третьи – на обоих языках. По-украински говорят 85% всех жителей, а по-русски – 75%. Сколько процентов всех жителей этого города говорят на обоих языках?

Решение:

100%-85%=15% — не говорят на украинском;

100%-75%=25% — не говорят на русском;

100%-15%-25%=60% — говорят на обоих языках.

Ответ: 60%

VI

Задачи «на банковские проценты» — в большинстве случаев являются экономическими задачами, в которых идёт речь о вкладах в банк с тем или иным процентом. При их решении надо помнить, что процент есть сотая доля числа. Решение задач этого типа тесно связано с тремя алгоритмами: нахождения части от целого, восстановление целого по его известной части, нахождение процентного прироста. Рассмотрим эти алгоритмы.

1. Пусть известна некоторая величина А, надо найти а % этой величины.

Если считать, что А есть 100%, а неизвестная часть х это а %, то из пропорции A/100=x/a

имеем x=Aa/100.

1. Пусть известно, что некоторое число b составляет а % от неизвестной величины А. Требуется найти А.

Рассуждая аналогично, из пропорции получаем   A=100b/a.

1. Пусть некоторая переменная величина А, зависящая от времени t, в начальный момент t₀ имеет значение А₀, а в моментt₁ – значение А₁.

Тогда абсолютный прирост величины А за время t₁–t₀ будет равен А₁–А₀; относительный прирост этой величины вычисляется по формуле       (A₁-A₀)/A₀, а процентный прирост по формуле   ((A₁-A₀)/A₀)100%.

Задача №1.

Известно, что вклад, находящийся в банке, с начала года возрастает к концу года на определённый процент (свой для каждого банка). В начале года 5/6 некоторого количества денег положили в первый банк. К концу года сумма этих вкладов стала равной 670 у.е., а к концу второго года – 749 у.е. Было подсчитано, что если бы первоначально исходного количества денег положили во второй банк, то по истечении одного года сумма вкладов в эти банки стала бы равной 710 у.е. В предложении, что исходное количество денег первоначально целиком положено в первый банк, определить величину вклада по истечении двух лет.

Решение.

Обозначим через x первоначальную сумму денег. Тогда через а обозначим процент, на который возрастает сумма за год в первом банке, а через b – во втором банке. К концу первого года сумму вклада в I банке стала равной (5x/6)(1+a/100), во II банке (x/6)(1+b/100), а к концу второго года(5x/6)(1+a/100)² и (x/6)(1+b/100)². По условию задачи сумма вкладов  в конце первого года составляет 670 у.е., а к концу второго года – 749 у.е., поэтому можно составить два уравнения:

(5x/6)(1+a/100)+(x/6)(1+b/100)=670 (1)

(5x/6)(1+a/100)²+(x/6)(1+b/100)²=749 (2)

Если во второй банк положить 5x/6  у.е., а в первый – x/6 у.е, то сумма вкладов к концу года составила бы:

(5x/6)(1+b/100)+(x/6)(1+a/100),

что равнялось бы 710 у.е. Поэтому получим третье уравнение:

(5x/6)(1+b/100)+(x/6)(1+a/100)=710 (3)

Для нахождения известного х составим систему уравнений из (1) и (3) и решим её:

1+a/100=660/x

1+b/100=720/x

Подставляя 660/x вместо 1+a/100 и 720/x вместо 1+b/100 в уравнение (2), приходим к уравнению (5x/6)(660/x)²+(x/6)(720/x)²=749, имеющему один корень: x=660, но тогда: 1+a/100=660/600=1,1

Если исходное количество денег положить на два года, то к концу второго года величина вклада составит 726 у.е.

Ответ 726 у.е.

Задача №6.

Рабочий положил на хранение в сберегательный банк 5000 руб.  По истечении одного года к его вкладу были причислены процентные деньги, и в то же время он увеличил свой вклад ещё на 5000 руб., а по истечении ещё одного года попросил выдать ему накопленные процентные деньги. Сколько процентов в год начисляет сбербанк, если рабочий получил 1232 руб. процентных денег, оставив вклад в 10 000 руб. на новый срок?

Решение.

Пусть x% в год начисляет сбербанк, а y% — процент за 2 года. x+x+y —  весь начисленный процент. По условию задачи 2x+y=1232 (руб.)

За I и II начисленный процент равен 5000?0,01x=50x, а процент за оба года равен 0,01x?(5000+50x).

Составим уравнение:

50x+50x+0,01x?(5000+50x)=1232

Решив это уравнение 50x+50x+0,01x(5000+50x)=1232

100x+50x+0,5x²-1232=0

0,5x²+150x-1232=0

D=b²-4ac=150²-4?0,5?(-1232)=24964, D0, два корня.

x₁=-308

x₂=8

Найдём два значения для х: х₁=-308 – не удовлетворяет условию задачи, х₂=8. Значит, сбербанк начисляет в год 8%.

Ответ: 8%

Проценты в банковской системе.

Простой процентный рост.

Если человек не вносит своевременную плату за квартиру, то на него налагается штраф, который называется «пеня». Так в Москве пеня составляет 1% от суммы квартплаты за каждый день просрочки. Поэтому, например, за 19 дней просрочки, сумма составит 19% от суммы квартплаты, и в месте , скажем, со 100 руб. квартплаты человек должен будет внести пеню 0,19 * 100 = 19 руб., а всего 119 руб.

Ясно, что в разных городах и у разных людей, квартплата, размер пани и время просрочки разные. Поэтому имеет смысл, составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S – ежемесячная кварт плата, пеня составляет p% квартплаты за каждый день просрочки, а n – число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.

Тогда за n дней просрочки, пеня составит pn% от S , или , а всего придётся заплатить .Таким образом,

Задача 1. Сколько надо заплатить москвичу, если его квартплата составляет 100 руб. и просрочена на 5 дней?

Решение.

Подставляя в формулу значение p = 1 и значения n = 5 * 4, получим:

(1 + ) * 100 = 1,05 * 100 = 105 (руб.)

Ответ: через 5 дней – 105 руб.

Таким образом, установленная формула позволяет быстро рассчитывать необходимые значения выплат за квартиру.

Рассмотрим еще одну ситуацию. Банк выплачивает вкладчикам каждый месяц p% от внесенной суммы. Поэтому, если клиент внес сумму S, то через n месяцев на его счете будет ()S, и мы вновь получаем, что

S_n=(1+) S

Мы получили в точности ту же самую формулу, что и в примере с квартплатой, хотя буквы в этих двух примерах имеют разный смысл: в первом примере n – число дней, а во втором примере n — число месяцев, в первом примере S – величина квартплаты, а во втором S – сумма, внесенная в банк. Такая же формула будет получаться и во всех иных случаях, когда некоторая величина увеличивается на постоянное число процентов за каждый фиксированный период времени. Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Задача 2. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?

Решение.

Для решения задачи достаточно подставить в формулу величину процентной ставки p = 2, числа месяцев n = 6 и первоначального вклада S = 500:

(1 + ) * 500 = 1,12 * 500 = 560 (руб.)

Ответ: через полгода на вкладе будет 560 руб.

Сложный процентный рост.

В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется 40% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют.

Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года 40% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк1000 руб. и ни разу не будет брать деньги со счета:

40% от 1000 руб. составляют 0,4 * 1000 = 400 руб., и следовательно, через год на его счете будет

1000 + 400 = 1400 (руб.)

40% от новой суммы 1400 руб. составляют 0,4 * 1400 = 560 руб., и следовательно, через 2 года на его счете будет

1400 + 560 = 1960 (руб.)

40% от новой суммы 1960 руб. составляют 0,4 * 1960 = 784 руб., и следовательно, через 3 года на его счете будет

1960 + 784 = 2744 (руб.)

Нетрудно представить себе, сколько при таком непосредственном , «лобовом» подсчёте понадобилось бы времени для нахождения суммы вклада через 10 лет. Между тем, подсчёт можно вести значительно проще.

Именно через год начальная сумма увеличится на 40%, то есть составит 140% от начальной, или, другими словами, увеличится в 1,4 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 40%. Следовательно, через 2 года начальная сумма увеличится в 1,4 * 1,4 = 1,4² раза.

Еще через один год и эта сумма увеличится в 1,4 раза, так что начальная сумма увеличится в 1,4 * 1,4² = 1,4³ раза. При таком способе рассуждения получаем решение нашей задачи значительно более простое:

1,4³ * 1000 = 2,744 * 1000 = 2744 (руб.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет p% годовых, внесённая сумма равна S рублей, а сумма, которая будет на счёте через n лет, равна S_n рублей.

p% от S составляют S рублей, и через год на счёте окажется сумма

S₁ = S

то есть начальная сумма увеличится в 1 + раза.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счёте будет сумма

S₂ = (1 +) S₁ = (1 +) (1+) S =(1 + )² S.

Аналогично, S₃ =(1 + )³ S и так далее. Другими словами, справедливо равенство

S_n = (1 + ) ³ S.

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Задача 1. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?

Решение.

Подставим в формулу значения процентной ставки p = 10, количество лет n = 4 и величину первоначального вклада S = 2000, получим:

(1 + )⁴ * 2000 = 1,1⁴ * 2000 = 1,4641 * 2000 = 2928,2 (рублей).

Ответ: через 4 года на счёте будет сумма 2928,2 рубля.

Банковский процент.

Предположим, что вы хотите положить в банк 10 000 рублей, чтобы на них «росли проценты». В Сбербанке вам предложат 120% годовых, если вы кладёте деньги на 3 месяца, 130% годовых, если положите на 6 месяцев, и 150% годовых при вкладе на год.

В банке «Триумф» вам предложат 200% годовых при вкладе на год. Подсчитаем, сколько вы получите через 5 лет. Поскольку каждый год вы будете получать 200% годовых, то за 5 лет вы получите в 5 раз больше – 1000%, т.е. 100 000 рублей к своим 10 тысячам рублей. Но это не так!

Считать следует иначе! За год ваш вклад утраивается, т.е. через год у вас будет 30 тысяч рублей, а за второй год он еще утроится и составит 90 000 рублей. То же самое буде происходить после третьего, четвёртого и пятого года. Поэтому после третьего года у вас будет уже 270 000 рублей, после четвёртого 810 000 рублей, а после пятого – 2 430 000 рублей, а не 110 000 рублей, как мы предполагали сначала. Теперь стоит выбрать способ вложения денег: на 3 месяца, на 5 месяцев или на год.

Казалось бы, лучше всего положить на год, что даёт самый высокий процент годовых – 150%. Но, наученные расчётами с другими банками, давайте проверим.

Если положить на полгода из расчёта 130% годовых, то через полгода получим доход в 65% от вложенной суммы, т.е. сумма увеличится в 1,65 раз. Если затем еще раз положить на полгода все полученные деньги, то сумма возрастёт в 1,65 * 1,65 = 2,7225 раза, то есть на 172,25%, что существенно больше 150-ти процентов при вкладе сразу на год.

А если положить деньги на три месяца, потом еще на три, и еще, и еще раз на три месяца? В первый раз прибыль составит четверть от 120%, т.е. 30% от вложенной суммы. Это значит, что вклад увеличится в 1,3 раза. В следующий месяц он увеличится еще в 1,3 раза, что даст увеличение первоначальной суммы в 1,69 раза. Через следующие три месяца увеличение составит 2,197 раза, а к концу года получим увеличение в 2,8561 раза. Таким образом, получаем 185,61% годовых. Правда, при этом нужно приходить в банк каждые три месяца, чтобы забирать вклад и снова класть его на три месяца.

Но есть ещё форма вклада под 100% годовых с правом снять вклад в любое время с получением соответствующей доли прибыли. Вот, наверное, золотая жила! Ведь мы убедились, что чем чаще кладёшь и берёшь вклад, тем больше оказывается прибыль.

Если ходить в Сбербанк каждый день, то каждый раз вклад будет увеличиваться в 1+ , а за год увеличение составит (1 +)³⁶⁵ раза.

Величина числа (1 +)ⁿ действительно увеличивается с увеличением n, но не может превзойти числа е= 2,71828… и стремится к этому числу с увеличением n.

Число е названо так в честь Леонардо Эйлера. Оно играет важную роль во многих разделах математики.

Итак, даже бегая в Сбербанк каждый час, нам не удастся получить доход больше 172% годовых, если мы примем эту форму вложения денег.

Ипотеки.

Ипотека — это заем, который предоставляет нам бан­ковское учреждение для того, чтобы мы могли опла­тить стоимость жилья. Когда банк одалживает нам деньги, мы должны вернуть ему эту сумму плюс соот­ветствующие проценты. Возвращение ипотечного кре­дита осуществляется не в конце договорного срока, а ежегодными частями. Например, Эдуард купил себе квартиру, но так как у него не было для этого достаточно денег, он обратился в банк за ипотечным кредитом в один миллион рублей со сро­ком погашения 20 лет. Тип годового процента является фиксированным: 4%. Какую сумму должен возвращать Эдуард банку ежегодно? Возвращаемая сумма называ­ется годовым погашением и рассчитывается следую­щим образом:

рубля

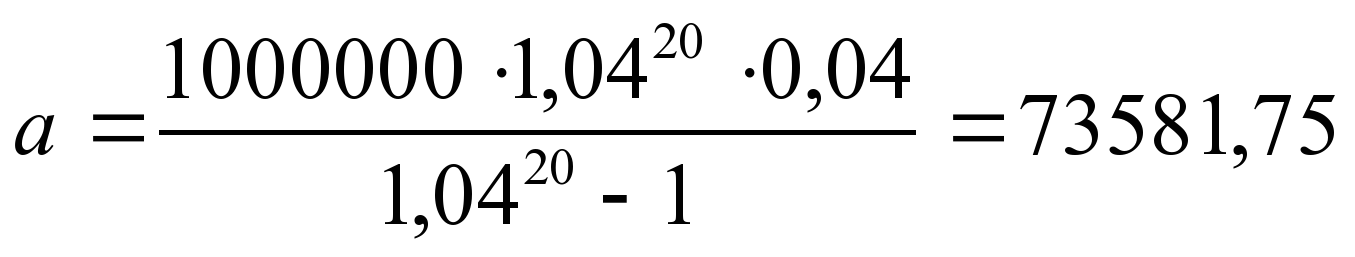
Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Интенсивная математизация различных областей человеческой деятельности особенно усилилась с внедрением современных информационных технологий, требующих математической грамотности человека буквально на каждом рабочем месте. Понятие «проценты» вошло в нашу жизнь не только с уроками в средней школе и с проведением сложных научно-исследовательских работ, не только с выпечкой кулинарных изделий и приготовлением лакомств, солений и варений, оно буквально атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, кредитов, инфляций, девальваций. «Брать ссуду в банке или купить в кредит? Может быть выгоднее накопить денег для покупки дорогостоящей вещи?» Чтобы ответить на эти вопросы, требуется умение решать задачи по теме «Проценты».

Ресурсы:

1. http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege

Открытый банк заданий ЕГЭ-2016

2. http://www.prosv ru

– сайт издательства, Просвещение,рубрика ,,математика,,/;

3. http://www.edu.ru-//www.edu.ru -Центральный образовательный портал, содержит нормативвные документы Министерства, стандарты;

4. http://www.pedsovet.su/;

5. http://nsportal.ru/shkola/obshchepedagogicheskie—tekhnologii/library/2015/03/04/;

6. ОГЭ 2015. Математика. Тем. тест. задания_Глазков, Варшавский и др_2015 -112с.pdf;

7. Математика. Тем. тесты для подг ЕГЭ( профильный уровень)-2015_ред. Лысенко_2015 -320с.pdf;

8. http://math-prosto.ru/?page=pages/percent/percent3.php