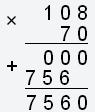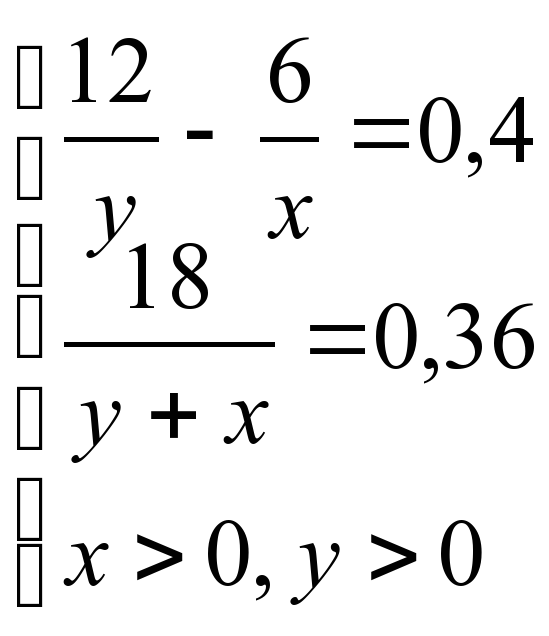Задачи с процентами как решать 11 класс егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Задачи на проценты из вариантов ЕГЭ по математике

Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.

Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за  мы принимаем ту величину, с которой сравниваем.

Мы также вывели полезные формулы:

если величину увеличить на процентов, получим
если величину уменьшить на процентов, получим
если величину увеличить на процентов, а затем уменьшить на , получим

если величину дважды увеличить на процентов, получим
если величину дважды уменьшить на процентов, получим

Воспользуемся ими для решения задач.

---

. В  году в городском квартале проживало  человек. В  году в результате строительства новых домов число жителей выросло на , а в  году — на  по сравнению с  годом. Сколько человек стало проживать в квартале в  году?

По условию, в  году число жителей выросло на , то есть стало равно  человек.

А в  году число жителей выросло на , теперь уже по сравнению с  годом. Получаем, что в  году в квартале стало проживать  жителей.

Следующая задача предлагалась на пробном ЕГЭ по математике в декабре  года. Она проста, но справились с ней немногие.

---

. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на  дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили  рублей. К вечеру понедельника они подорожали на  и стали стоить . Теперь уже эта величина принимается за , и к вечеру вторника акции подешевели на  по сравнению этой величиной. Соберем данные в таблицу:

По условию, акции в итоге подешевели на 

Получаем, что

Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения:

По смыслу задачи, величина положительна.
Получаем, что .

---

. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за  рублей, через два года был продан за  рублей.

Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил  рублей. Его цена два раза уменьшилась на , и теперь она равна:

---

. Четыре рубашки дешевле куртки на . На сколько процентов пять рубашек дороже куртки?

Пусть стоимость рубашки равна , стоимость куртки . Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет  от цены куртки, то есть .

Стоимость одной рубашки — в  раза меньше:

А стоимость пяти рубашек:

Получили, что пять рубашек на  дороже куртки.

Ответ: .

---

. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на . Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на  Сколько процентов от общего дохода семьи составляет зарплата жены?

Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась…») назовем «ситуация » и «ситуация ».

	муж	жена	дочь	Общий доход
В реальности
Ситуация
Ситуация

Осталось записать систему уравнений:

Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти , и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму .

Получим:

Это значит, что зарплата мужа составляет  от общего дохода семьи.

Во втором уравнении мы тоже вычтем из обеих частей выражение , упростим и получим, что

Значит, стипендия дочки составляет  от общего дохода семьи. Тогда зарплата жены составляет  общего дохода.

Ответ:

---

Задачи на проценты

---

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №3 ЕГЭ по математике нам предстоит решить простую задачу на проценты или часть от целого. Данные задачи в большинстве случаев интуитивно понятны, так как взяты из реальных жизненных ситуаций, тем не менее необходимо быть внимательным при их выполнении.

Тематика заданий: часть от целого, доли, проценты

Бал: 1 из 20

Сложность задания: ♦♦◊

Примерное время выполнения: 3 мин.

[/su_box]

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

---

Вариант 3МБ1

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 8% годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 108% от 7000, получим:

1. 7000 : 100 = 70(рублей) – составит 1 %.
2. 70 · 108 = 7560(рублей) – составит вклад через год.

• Вариант 2.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь(разделить на сто), затем умножит число на полученную десятичную дробь.

108% = 108 : 100 = 1,08

7000 · 1,08 или

.

Выполнив умножение столбиком, имеем:

Ответ: 7560.

---

Вариант 3МБ2

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 7 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 107% от 3000, получим:

1. 3000 : 100 = 30(рублей) – составит 1 %.
2. 30 · 107 = 3210(рублей) – составит вклад через год.

• Вариант 2.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь (разделить на сто), затем умножит число на полученную десятичную дробь.

107% = 107 : 100 = 1,07

3000 · 1,07 или

Ответ: 3210.

---

Вариант 3МБ3

[su_note note_color=”#defae6″]

В сентябре 1 кг слив стоил 40 рублей, в октябре сливы подорожали на 40%, а в ноябре ещё на 15%. Сколько рублей стоил 1 кг слив после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Решение с пояснениями:

Найдем сколько составляет один процент от начальной стоимости:

40 : 100 = 0,4 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 40 = 140 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

140 · 0,4 = 56 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

56 : 100 = 0,56 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 15 = 115 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

115 · 0,56 = 64,4 (рубля) – конечная стоимость.

Решение в общем виде:

Подорожание на 40% означает увеличение стоимости на 140%, то есть, 40 рублей становятся равными

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 15%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 40+15=55% и вычислять 155% от 40 рублей! Это будет приводить к неверным решениям.

Ответ: 64,4.

---

Вариант 3МБ4

[su_note note_color=”#defae6″]

В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20 %, а в ноябре ещё на 25 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Подробный разбор:

Найдем сколько составляет один процент от начальной стоимости:

90 : 100 = 0,9 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 20 = 120 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

120 · 0,9 = 108 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

108 : 100 = 1,08 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 25 = 125 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

125 · 1,08 = 135 (рублей) – конечная стоимость.

Решение в общем виде:

Подорожание на 20% означает увеличение стоимости на 120%, то есть, для 90 рублей имеем:

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 25%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 20+25=45% и вычислять 145% от 90 рублей! Это будет приводить к неверным решениям.

Ответ: 135.

---

Вариант 3МБ5

[su_note note_color=”#defae6″]

Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доход физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Вычесть из 100% налог в процентах.
2. Найти 1% от начальной суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Вычесть из 100% налог в процентах.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вычтем из 100% налог в процентах.

100 – 13 = 87 (%) – получит Иван Кузьмич после вычета налога.

Найдем 1 % от начальной суммы.

20000 : 100 = 200 (рублей) – составит 1%.

Найдем 87% от 20000.

87 · 200 = 17400 (рублей) – получит Иван Кузьмич.

• Вариант 2.

Вычтем из 100% налог в процентах. 100 – 13 = 87 (%)

Полученные проценты переведем в десятичную дробь (разделить на сто). 87 : 100 = 0,87

Найдем процент от числа (число умножить на полученную десятичную дробь).

20000 · 0,87 = 17400 (рублей)

Ответ: 17400 рублей получит Иван Кузьмич.

---

Вариант 3МБ6

[su_note note_color=”#defae6″]

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

[/su_note]

Решение:

Нам известно, что количество учеников, сдававших ЕГЭ по физике равно 25, и это составляет 1/3 от общего числа выпускников. Значит 25 – это 1/3, тогда общее число учеников:

25 • 3 = 75

Количество учеников, не сдававших ЕГЭ по физике, равно:

75 – 25 = 50

Ответ: 50

---

Вариант 3МБ7

[su_note note_color=”#defae6″]

Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена стоимость футболки?

[/su_note]

Алгоритм выполнения

1. От 800 отнимаем 680. Узнаем, сколько рублей составило снижение.
2. Делим результат вычитания на 800. Это даст нам долю, которую составляет скидка от первоначальной стоимости.
3. Полученное число умножаем на 100. Получаем снижение в процентах.

Решение:

800 – 680 = 120 (руб.) – составляет снижение

120 : 800 = 0,15 – доля скидки

0,15 ·100 = 15 %

Ответ: 15

---

Вариант 3МБ8

[su_note note_color=”#defae6″]

В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 3500 рублей (наверное, это было очень давно – прим. ред. 🙂 ) Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько составляет 5% от стоимости мебели. Для этого 3500 делит на 100 и умножаем на 5.
2. К 3500 прибавляем полученное число.

Решение:

3500 : 100 · 5 = 175 (руб.) – стоимость сборки мебели

3500 + 175 = 3675 (руб.) стоит мебель со сборкой

Ответ: 3675

---

Вариант 3МБ9

[su_note note_color=”#defae6″]

Товар на распродаже уценили на 40%, при этом он стал стоить 840 рублей. Сколько рублей стоит товар до распродажи?

[/su_note]

Алгоритм выполнения

1. От 100 % вычитаем 40%, чтобы найти, сколько процентов составляет уцененная стоимость. Получим 60 %.
2. Воспользуемся правилом нахождения целого по его части. Для этого 840 разделим на 60 и умножим на 100.

Решение:

100 – 40 = 60 % – составляет цена товара после его уценки.

840 : 60 · 100 = 1400 (руб.)

1400

---

Вариант 3МБ10

[su_note note_color=”#defae6″]

Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 14 рублей 40 копеек (грандиозная скидка – прим. ред. 😉 ) Сколько процентов составила скидка для пенсионера?

[/su_note]

Алгоритм выполнения

1. От 15 руб. отнимаем 14 руб.40 коп. Так найдем сумму скидки. Выразим эту сумму в рублях.
2. Полученное число разделим на 15 и умножим на 100 %.

Решение:

15 руб. – 14 руб.40 коп. = 60 коп. = 0,6 руб.

0,6 : 15 ·100 % = 4 %.

Ответ: 4

---

Вариант 3МБ11

[su_note note_color=”#defae6″]

Число хвойных деревьев в парке относится к числу лиственных как 93:7. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

[/su_note]

Алгоритм выполнения

1. Суммируем 93 и 7, чтобы найти общее кол-во деревьев в парке.
2. Кол-во лиственных деревьев (7) делим на общее кол-во деревьев и умножаем на 100 %.

Решение:

93 + 7 = 100 (шт.) – деревьев всего в парке.

7 : 100 ·100 = 7 %

Ответ: 7

---

Вариант 3МБ12

[su_note note_color=”#defae6″]

Городской бюджет составляет 48 млн. рублей, а расходы на одну из его статей составили 40%. Сколько миллионов рублей потрачены на эту статью бюджета?

[/su_note]

Алгоритм выполнения

Нужно применить правило нахождения части от целого по ее проценту. Для этого целое делится на 100 и умножается на кол-во процентов.

Решение:

48 : 100 · 40 = 19,2 (млн.руб.)

Ответ: 19,2

---

Вариант 3МБ13

[su_note note_color=”#defae6″]

Поступивший в продажу в феврале мобильный телефон стоил 1800 рублей. В июне он стал стоить 1530 рублей. На сколько процентов снизилась цена мобильного телефона в период с февраля по июнь?

[/su_note]

Алгоритм выполнения

1. Из 1800 вычитаем 1530. Определяем, сколько рублей составила скидка.
2. Полученное число делим на первоначальную цену и умножаем на 100 %.

Решение:

1800 – 1530 = 270 (руб.) – скидка

270 : 1800 · 100 = 15 %

Ответ: 15

---

Вариант 3МБ14

[su_note note_color=”#defae6″]

В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 25%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько (в руб.) составляет 10 % от стоимости чайника. Для этого 1600 делим на 100 и умножаем на 10.
2. От первоначальной стоимости отнимаем сумму скидки, составляющей 10 %.
3. Полученную цену со скидкой делим на 100 и умножаем на 25. Так найдем величину скидки (в руб.) после второго снижения цены.
4. От числа, полученного в п.2 отнимаем число, полученное в п.3.

Решение:

1600 : 100 · 10 = 160 (руб.) – составляет скидка в 10 %

1600 – 160 = 1440 (руб.) – стал стоить чайник после понижения цены на 10 %

1440 : 100 · 25 = 360 (руб.) составляет скидка в 25 %

1440 – 360 = 1080 (руб.)

Ответ: 1080

---

Вариант 3МБ15

[su_note note_color=”#defae6″]

Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продает с наценкой 30%. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько рублей составляет наценка в 30 %. Для этого закупочную стоимость делим на 100 и умножаем на 30.
2. К закупочной стоимости прибавляет сумму наценки.
3. Полученное число умножаем на 4.

Решение:

110 : 100 · 30 = 33 (руб.) – равна наценка

110 + 33 = 143 (руб.) – стоит погремушка в магазине

143 · 4 = 572 (руб.) – стоят 4 погремушки

Ответ: 572

---

Вариант 3МБ16

[su_note note_color=”#defae6″]

Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

[/su_note]

Алгоритм выполнения

1. Обозначим число больных через х. Тогда кол-во больных через месяц станет равным х/2.
2. х/2 делим на х и умножаем на 100 %. Так найдем кол-во процентов, которое составит число больных через месяц по отношению к первоначальному их кол-ву. В процессе вычисления х сократится.

Решение:

х / 2 : х · 100 % = х / 2· 1 / х· 100 % =1 / 2 · 100 % = 0,5 · 100 % = 50 %

Ответ: 50

Даниил Романович | Просмотров: 14.5k

                  Д
Е П А Р Т А М Е Н Т     О Б Р А З О В А Н И Я     г. М О С К В Ы

Юго
– Западное окружное управление образования Государственное бюджетное
образовательное учреждение города Москвы

 средняя общеобразовательная школа № 1101

Ул. Академика Варги, 34                                                              8(495)339-77-39

КУРСОВАЯ РАБОТА

по теме: «Решение задач на проценты»

Учитель:
Федорова С.В. 

2018
– 2019 уч. год

План работы

1.     Основные
задачи на проценты, тренировочные задачи …………………………… 2

2.     Задачи
на смеси и сплавы

I.        
к смеси или сплаву добавляют вещество
…………………………………………….. 4

II.     
две смеси (сплава) смешали в одну (один сплав)
……………………………….. 7

III.  
разборка задач
………………………………………………………………………………..
12

3.    
Задачи с последовательным повышением (понижением) процента,
разбор- ка задач
………………………………………………………………………………………………..
14

4.     Задачи
на высушивание ягод, грибов, винограда ………………………………….
18

5.     Интересные
задачи «из жизни торговли»
……………………………………………… 20

6.     Литература…
……………………………………………………………………………………….24

1. Основные
задачи на проценты, тренировочные задачи.

I.         Нахождение процента от
числа. Найти p% от числа а

правило	пропорция
Чтобы найти процент от числа, надо это число умножить на десятичную дробь, соответствую- щую проценту, т.е. p  a 100	a −100% b(?) − p% b =  p  a 100

Примеры:

✓  8%
от 6 кг.

8

8% =                                   = 0,08, т.е. 0,08 6 = 0,48кг. 100

✓  0,4%
от 0,25 с.        

                         0,4                      

     0,4% =
= 0,004 , т.е. 0,004  0,25 = 0,001с.

100

✓  20%
от 15,25

15,25 −
100%               15,25 
20

                                              b =   = 3,05

        b(?) − 20%                      100

 Примечание: хорошо, если ученики понимают, что 5%
от числа а это

   ⁵   
a = ¹  a = a : 20 ; 10%
от а это ¹ 
a = a :10
 и т.д.

      100
       20                                       10

✓ 12% от а  

     a −
100%              a 12

                                      b = = 0,12a

     b(?)
−12%              100

✓  75%
от 80%

      (процент)    (число)

3

0,75 80
= 80 = 60%

4

Подборка задач:

Что больше: а) 15% от 17 или 17%
от 15; б) 1,2% от 48 или 12% от 480;

в) 147% от 621 или 125% от 549;
г) 72% от 150 или 70% от 152; д) 80% от а или 40% от 2а; е) 36% от 2,5b или
1,5% от 80b?

             II.      Нахождение числа по его
проценту.

Найти число, если p%
от него равно b

правило	пропорция
Чтобы найти число по его проценту, надо часть числа разделить на десятичную дробь, соответ- p ствующую проценту, т.е. a = b :   100	a(?) −100% b − p% a = 100 b p

Примеры:

✓  От
какой величины 7% составляют 7 руб.

7 : 0,07 = 700 : 7 =100 р.

✓ 
12% от ? составляют 36 экземпляров 36 : 0,12 = 3600 :12 = 300 экз.

1

✓ 
25% от ? составляют 10г. (или  от ? равно 10 г.) 4

     a −
100%         a
= 10 100 = 40 г.

10 −
25%                          25

✓  300%
от ? равны b ?

     a(?) −100%
             b 100
  b  

 a = =  . b − 300% 300 3

Подборка задач:

Сравнить величины, если:

а) 40% первой составляют 300
руб., а 30% второй составляют 400 руб.;

б) 150% первой составляют 120
руб., а 120% второй составляют 90 руб.;

в) 50% первой составляют 0,5а
руб., а 20% второй составляют 0,2а руб.;

г) 12,5% первой составляют b
руб., а 30% второй составляют 3b руб.?

             III.
    Нахождение процентного отношения двух чисел.

правило	пропорция
Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разде- лить на второе и результат умножить на 100.	a   −100% b   − p (?)% b p% = 100 a

Примеры: сколько процентов составляют

✓  16с
от 50с?

16

 100
= 32%

50

✓  15
г от 1 кг?

15

                                                100 =
1,5%

1000

✓  1,2
от 0,15?  

     0,15 −
100%         p%
= ^{1,2 100} ₌
800%

                                               1,2
− p%       0,15

✓  2а
от 8а?

8a −100% 2a 100 
p% =
 = 25% . 2a
− p%  8a

Подборка задач:

№1. В каком случае процентное
отношение больше:

а) 8 отличников из 40 учащихся
или 9 отличников из 50 учащихся;

б) 6 разбитых
лампочек из 20 или 7 разбитых лампочек из 30? № 2. Какое изменение более
значительно:

а) подорожание с 400 руб. до 500
руб. или с 500 руб. до 600 руб.;

б) похудание со 100 кг до 90 кг
или с 50 кг до 40 кг?

2. Задачи на смеси
и сплавы.

             I.       К смеси или сплаву
добавляют вещество.

В этих задачах нужно:

1)       
отделить вещество в смеси (сплаве) по массе от всей смеси
(сплава), поль- зуясь правилом I или пропорцией.

2)       
понимать, что при добавлении вещества оно прибавляется, по массе,
ко всей смеси (сплаву) и к конкретному веществу

вода + вода

соль
+ соль золото + золото Пример: К 40% раствору серной кислоты добавили 50 г
чистой серной ки- слоты, после чего концентрация раствора стала равна 60%.
Найти первона- чальный вес раствора.

Пусть х (г) – первоначальный вес
раствора, тогда, если кислота составляет 40%, то ее масса 0,4х (г).

Составляем пропорцию:

x +
50 − 100%

                                               ;                          

0,4x +
50 − 60% 

Получаем:                                        

                   100(0,4x + 50) = 60(x + 50)    / :10

10(0,4x +
50) = 6(x + 50)

4x +
500 = 6x + 300

2x =
200 x =
100

Ответ: 100 г.

Пример: К раствору, содержащему 30
г соли, добавили 400 г воды, после че- го концентрация соли уменьшилась на 10%.
Найти первоначальную концен- трацию соли в растворе.

Пусть х (г) – вес первоначального раствора, тогда
процентное содержание

 соли
в нем: 30 100 = 3000 .

                                        x
              x

По условию задачи составляем пропорцию:

^{x + 400 − 100%}   p% =
3000  (измененный процент соли в
новом рас-

      30 −
p%                              x +
400

творе).

По условию задачи процентное содержание соли в растворе
уменьшилось на

10%. Составим и решим уравнение:

3000  3000

      −                                                                = 10 / :10

           x      x + 400

          300  300
        

      −            =

x   x + 400 x = 200

200 (г) – вес первоначального раствора, процентное
содержание соли в нем

      3000    3000            

                    =         = 15%

           x
       200

Ответ: 15%

Пример: В 5 кг сплава олова и цинка содержится 80% цинка.
Сколько кг оло- ва надо добавить к сплаву, чтобы процентное содержание цинка
стало вдвое

меньше?

 

0,8 5 = 4,0 (кг) – чистый цинк

2) Пусть
х кг олова добавили к сплаву, тогда

5 +
x − 100%

4 −
80% : 2 = 40%

Получаем уравнение:

40(5 +
x) = 100  4 5 + x = 10 x = 5

Ответ: 5 кг олова Подборка задач:

№ 1. Имеется кусок сплава меди с
оловом общей массой 24 кг, содержащий 45% меди. Сколько чистого олова надо
прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40 %
меди? Ответ: 3

№ 2. Сплав меди с цинком,
содержащий 5 кг цинка, сплавили с 15 кг цинка. В результате содержание меди в
сплаве понизилось по сравнению с первона- чальным на 30%. Какова была
первоначальная масса сплава, если известно, что она была меньше 20 кг? Ответ:
10

№ 3. Сплав золота с серебром,
содержащий 80 г золота, сплавили со 100 г чистого золота. В результате
содержание золота в сплаве повысилось по сравнению с первоначальным на 20%.
Сколько серебра в сплаве? Ответ: 120 № 4. Если к раствору кислоты добавить 50 г
воды, то его концентрация станет равной 15%. Если же к первоначальному раствору
добавить 50 г ки- слоты, то его концентрация станет равной 40%. Найти
первоначальную концентрацию раствора. Ответ: 16

             II.      Две смеси (сплава) смешали
в одну (один сплав).

В этих задачах нужно:

1)  Отделить вещество от
всей смеси (сплава)

2)  Когда
получается смесь, то массы исходный растворов (сплавов) склады- ваются.

медь + медь

соль + соль золото
+ золото

Пример: Имеется два сплава меди и свинца. Один сплав содержит
15% меди, а другой – 65% меди. Сколько нужно взять каждого сплава, чтобы
получить 200 г сплава, содержащего 30% меди?

Эту задачу можно решать с одной переменной, но удобнее
ввести две.

Пусть х (г) – вес первого сплава, а у (г) –
вес второго сплава.

Отделим медь от каждого сплава. В первом 15% от х – 0,15х
(чистая медь), во втором 65% от у – 0,65у (чистая медь).

При сплавлении первого и второго сплавов получаем: x
+ y − 100%

 30(x + y) =100(0,15x + 0,65y) 0,15x
+ 0,65y − 30%

Составим и решим систему:

    x +
y = 200                 x + y = 200    x = 140

     
                                ; 
                   ; 

30x
+ 30 y = 15x + 65y 15x − 35y = 0  y = 60

Ответ: 140 г и 60 г.

Пример: Имеется два разных сплава меди,
процент содержания меди в пер- вом сплаве на 40% меньше, чем во втором. Когда
оба сплава сплавили вме- сте, то новый сплав стал содержать 36% меди. Известно,
что в первом сплаве было 6 кг меди, а во втором вдвое больше. Каково процентное
содержание меди в обоих сплавах?

+ =

Пусть х (кг) – вес первого сплава, а у (кг)
– вес второго сплава.

                            6           600

p%(I ) =   100 =      x x

                               12           1200

p%(II ) =        100 =  y       y

По условию задачи процент содержания меди
в первом сплаве на 40% мень- ше, чем во втором, тогда:

1200 − 600 = 40 / : 20 y        x

      60    30       

              −     = 2

        y      x

Пропорция, соответствующая сумме двух
сплавов, выглядит следующим об- разом:

x + y −
100%



     6
+12 − 36%          

x +
y = 18 100 ;

36

x + y =
50

Составим и решим систему уравнений:

     60
   30       

                         −     =
2



      
y      x

^x + y = 50

Эту задачу можно решать, составив другую
модель, приняв за х и у процент- ное содержание меди в каждом из
сплавов. Тогда

1   _сплав: m1 −100%     _
m1 ₌
600 6 − x%
  x

                            m2  −100%
             1200

2   сплав:  m 2=   12 −
y%       y

600  + 1200  −
100%

1 + 2 сплав:        x         y                     

6 +12
− 36%

      600    1200   18 100 

                 +         =             ;

          x         y          36

600 + 1200 = 50 / : 50; x       y

      12    24       

             +     = 1

        x      y

Составим и решим систему:

  y − x = 40  x  = 20

     12  +
24  ₌
1; y ₌ 60

    
x    y        

Эта модель удобнее тем, что полученные величины являются
ответом к задаче.

Ответ: 20% и 60%.

Пример: В какой пропорции нужно смешать
10% и 35% растворы аммиачной селитры, чтобы приготовить 15%-ный раствор?

Пусть х (г) – весь первый раствор, у (г) –
весь второй раствор. Найти х : у.

                                                                                                 x
+ y − 100%              _

0,1x
+ 0,35y − 15%

15(x
+ y) = 100( 0,1x
+ 0,35)

15x
+ 15 y = 10x + 35 y

5x = 20 y

x                     
4 y x = 4 y  =      = 4 :1

y                     
y

Ответ: 4 : 1.

Пример: Если два раствора кислоты смешать
в отношении 1 : 4, то получится раствор, содержащий 38% кислоты. Если же эти
растворы смешать в отно- шении 4 : 1, то получится раствор, содержащий 32%
кислоты. Найти про- центное содержание кислоты во втором растворе.

Проиллюстрируем первое предложение условия задачи:

         Каждый из
растворов имеет свою концентрацию p₁ и p₂.

Тогда                      p1  

Первой кислоты по массе p₁% от х,
т.е.   x ; 100      p2

Второй кислоты по массе p₂%
от 4х, т.е. ^{ 4x .} 100 x + 4x − 100%

Составляем
пропорцию для нового раствора:       p₁ x +
4 p₂ x
− 38%

                                                         100
   100

Получаем первое
уравнение системы: p¹                       4
p₂   /:
x  0

   5x 
38 = 100x(
    ₊
)

                                         100
   100

190 =
p₁ + 4 p₂

Проиллюстрируем второе предложение условия задачи:

 

Процентное
содержание растворов осталось p₁ и p₂.

p1

Первой кислоты по массе p₁%
от 4у, т.е.          ^{ 4 y ;} 100            p2  

Второй кислоты по массе p₂% от у,
т.е.            y .

100 

4                
y + y −
100%  Составляем
пропорцию для нового раствора: 100p₁   
4 y + 100p_{2 } 
y ₋
32%

Получаем второе уравнение системы:

                                         p¹                               p²

5                
y  32 =
100(        
4 y +         
y)

                                      100
        100

160 y = p₁  4 y + p₂  y / : y  0

160 =
4 p₁ + p₂

Составим и решим систему уравнений:

 
p₁  + 4 p₂  = 190 ; _
 p₁ = 30

4
p1   + p2 = 160 
p2 = 40

Ответ: 40%

             III.    Разборка задач

Пример: Сплавляя два одинаковых по весу
слитка, состоящих только из зо- лота и серебра, с разным содержанием золота,
получили сплав, в котором со- держится 3 кг золота. Если бы второй слиток был в
два раза тяжелее, то в сплаве содержалось бы 11 кг серебра. Известно, что
процентное содержание золота в первом слитке было на 20% больше, чем во втором.
Сколько кило- граммов серебра содержится в полученном сплаве?

Проиллюстрируем первое предложение задачи:

Отделим золото от каж- дого
из сплавов.

                                                                                   p
+ 20

Масса чистого золота в первом куске —    ^{ x (кг)} 100            p         

Масса чистого золота во втором куске —         ^{ x} (кг).

100

По условию задачи в новом сплаве
содержится 3 кг чистого золота, получаем уравнение:

      p +
20        p

    
x +                          x =
3;

  x100
p +  20 ₊  100p  _
= 3;

         
                 


100     100  p
+ 10

 x = 3 (*) 50

Находясь в условиях второго предложения
«Если бы…», получаем следую- щую математическую модель:

Масса чистого золота в первом куске — p ⁺
20  2x (кг)
100    p         

Масса чистого золота во втором куске —         ^{ x} (кг).

100

По условию задачи новый сплав содержал бы
11 кг чистого серебра. Его вес получим, вычитая из веса всего сплава вес
чистого золота:

3x − p ^{+ 20}  2x −
 ^p   x = 11

                   100            100

     x 300 − 2 p − 40 − p  ₌ 11

      ^          100          ^
 

    160 − 3 p            

 x = 11 (**) 100

Разделим уравнение (**) на (*), понимая, что x  0.

     160 −
3 p     

   100 ^{ x}₌
11;   p + 10  x 3

              50        

160 −
3 p  50           11

     =       ;

            100      p + 10    3

     160 − 3 p    11

=  ;

480 −
9 p = 22 p
+ 220;

13 p = 260; p = 20

Таким образом, получаем, что в первом
сплаве чистого золота 40 %, а во вто- ром – 20%.

Читаем внимательно
вопрос задачи: «Сколько кг серебра содержится в по- лученном сплаве?». Делаем
вывод, что в первом сплаве чистого серебра 60%, а во втором – 80%. Т.е.

В первом сплаве чистого серебра по массе
– 0,6х (кг), во втором – 0,8х (кг), в новом сплаве – 1,4х (кг).

Нам известно, что в новом сплаве содержится 3 кг чистого
золота, поэтому

0,4x +
0,2x = 3
0,6x = 3 x
= 5

Тогда 1,4x =1,4  5 = 7(кг) Ответ: 7 кг.

Подборка задач:

№1. Смешали 30%-ный раствор
соляной кислоты с 10%-ным и получили 600 г 15%-го раствора. Сколько граммов
10%-го раствора было взято? Ответ: 450

№2. Два сосуда с раствором щелочи
разных концентраций (по объему) содержат вме- сте 20 л раствора. Первый сосуд
содержит 4 л щелочи, а второй – 6 л. Сколько процен- тов щелочи содержит первый
сосуд, если второй содержит щелочи на 40% меньше пер- вого? Ответ: 80

№3. Имеется два раствора кислоты.
Первый раствор состоит из 1056 г кислоты и 44 г воды, а второй – из 756 г
кислоты и 1344 г воды. Из этих растворов нужно получить 1500 г нового раствора,
содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для
этого взять? Ответ: 100

№4. Имеется два достаточно
больших слитка сплава золота с медью. Первый слиток содержит 92% золота, а
второй – 80% золота. Из этих слитков надо получить 600 г сплава, содержание
золота в котором 85%. Определите массу куска, который для этого необходимо
взять от первого слитка. Ответ: 250

3. Задачи
с последовательным понижением, повышением процента. Основная ошибка,
которую допускают учащиеся при решении задач этого типа, это сложение и
вычитание процентов, которое категорически нельзя допускать, т.к. проценты
берутся от разных величин.

Пример: В двух магазинах были одинаковые
цены. В одном магазине их сначала пони- зили на 15%, а потом повысили на 10%, а
в другом – сначала повысили на 10%, а потом понизили на 15%. Как изменились
цены в этих магазинах по сравнению с первоначаль- ной? В каком из них выгоднее
покупать товар?

1   магазин:

Эту запись можно прочесть как 93,5% от х
(0,935 – десятичная дробь, соот- ветствующая проценту), т.е. по сравнению с
первоначальной ценой в этом магазине она понизилась на 6,5%.

2   магазин:

                                                             ,
т.е. 93,5% от х. Как мы видим, цены в магазинах не стали разными, но так
бывает не всегда! Пример: Цена первого товара поднялась на 40%, а потом еще на
25%. Цена второго товара поднялась на 30%, после чего оказалось, что цена
первого то- вара на 40% выше второго. На сколько процентов первоначальная цена
пер- вого товара была больше цены второго товара?

1   товар:

                                                                       
, т.е.

175% от х.

2   товар:

После чего оказалось, что цена первого товара на 40% выше
цены второго. Внимание! С какой величиной происходит сравнение (второй товар),
ту цену и принимаем за 100%, т.е.

             

Эту запись читаем: х составляет 104% от у, т.е.
104% — 100%= 4% — на столь- ко процентов первоначальная цена первого товара
была больше первона- чальной цены второго товара.

Ответ: на 4%

 Замечание: если бы вопрос звучал
«На сколько процентов цена второго това- ра была ниже цены первого товара?», то
ответ не был бы, конечно, 4%, т.к. сравнение производится с ценой первого
товара, поэтому p% ₌ (x − y) 100 x

      x − 100%                       (1,04 y)
100

                                                p% =                      

      (x
− y) − p%                        1,04
y

                                                                          4
y      400      11     

                                                       p%
=         _{=
       =}
3    %

                                                                     1,04
y    104      13

Пример: Цена первого товара на 10% больше
цены второго товара. На второй товар цена вначале поднялась на 21%, а потом еще
раз поднялась на 25%. На сколько процентов требуется поднять цену первого
товара, чтобы цены обо- их товаров стали одинаковыми?

1 товар: 1,1х, т.к. цена первого товара на 10%
больше цены второго.

1 товар: х – 100%

Покажем изменение цены второго товара:

                  +21% om x                                                                      +25%om 1,21x

x⎯1⎯00%⎯+21%⎯=12⎯1%=1⎯,21→1,21x⎯1⎯00%⎯+25%⎯=12⎯5%=1⎯,25→1,251,21x =1,5125x,  
т.е.   151,25% от х.

По условию задачи нужно поднять цену
первого товара, чтобы цены стали одинаковыми, т.е.

1,1x −
100%         p%
= 1,25 1,21x 100 = 125 1,1 = 137,5%

1,5125x
− p%                                1,1x

Значит,
137,5% −100% = 37,5%

Ответ: на 37,5%

Пример: Товар стоил 4000 руб. После двух
последовательных повышений цены он стал стоить 4830 руб. Какова была цены
товара после первого по- вышения, если процент повышения во второй раз был на
10% больше, чем в первый раз?

  4000   _100%+
  +
p %                  ^100
+ p  4000 = (100 + p)  40^ + p %₁₀₀+10_%%+ _p om_%(100+₁₀+_% p = )40

                 ⎯⎯⎯p %⎯=(10⎯0+ p )⎯:100→ ^ 100                                                                                                                                          _^
 ⎯⎯⎯(11⎯0+ p )⎯:100 ⎯⎯→

_

^{110 + p}  (100 + p)  40 = 4830^

     
100                                  

Составим и решим уравнение:

(110 +
p)(100 + p)
 2  / 5  ₌
4830

                              5                               2

(110 +
p)(100 + p)
= 12075

После раскрытия скобок и упрощения получаем:

p² +
210 p −1075
= 0 p = 5

По условию задачи нужно узнать цену
товара после первого повышения це- ны, т.е. (100 +
p)  40 =105 40 = 4200

Ответ: 4200 руб.

Подборка задач:

№1. Как изменилась величина, если
она:

а) сначала увеличилась на 20%, а
потом увеличилась на 25%;

б) сначала увеличилась на 20%, а
потом уменьшилась на 25%;

в) сначала уменьшилась на 20%, а
потом уменьшилась на 25%;

г) сначала уменьшилась на 20%, а
потом увеличилась на 25%? №2. Как изменилась температура воздуха, если она:

а) сначала увеличилась на 25%, а
потом уменьшилась на 40%;

б) сначала уменьшилась на 60%, а
потом увеличилась на 80%;

в) сначала увеличилась на 5%, а
потом на 20%;

г) сначала уменьшилась на 10%, а
потом на 30%?

№ 3. В двух магазинах цены были
одинаковые. В одном магазине их сначала понизили на 40%, а потом повысили на
40%, а в другом – сначала повысили на 50%, но зато потом понизили на 50%. Как
изменились цены в этих мага- зинах по сравнению с первоначальной?

№ 4. а) Одну сторону
прямоугольника увеличили на 20%, а другую – на 25%. На сколько процентов
увеличилась площадь прямоугольника?

б) Одну сторону прямоугольника
увеличили на 60%, а другую уменьшили на 60%. Как изменилась площадь
прямоугольника и на сколько процентов?

в) Длина прямоугольника в 3 раза
больше ширины. Длину уменьшили на 20%, а ширину уменьшили на 40%. На сколько
процентов уменьшился периметр прямоугольника?

г) Ширина прямоугольника в 4 раза
меньше длины. Длину увеличили на 10%, а ширину уменьшили на 20%. Как и на
сколько процентов изменился периметр прямоугольника?

№ 5. После двух последовательных
повышений размер пенсии был увеличен на 56%. На сколько процентов повысили
пенсию в первый раз, если второе повышение было в полтора раза больше первого
(в процентном отношении)? Ответ: 20

№ 6. За два года количество
безработных в регионе снизилось на 60%. На сколько процентов снизилась
безработица за первый год, если во второй год снижение было в два с половиной
раза больше, чем в предыдущем (в про- центном отношении)? Ответ: 20

№ 7. Расценки на грузоперевозки
по железной дороге увеличивались за год дважды: на 20% в первый раз, и на 10% —
во второй. Определите, на сколько процентов возрастут расходы почтовой фирмы на
железнодорожный транспорт, если объем перевозимой ею по железной дороге почты
вырос на 30%. Ответ: 71,6

4. Задачи на
высушивание ягод, грибов, винограда

Этот класс задач учащиеся решают очень
плохо, хотя они решаются доволь- но просто. Главное, представлять себе, что
виноград, ягоды, грибы состоят из:

Клеточное вещество остается
неизменимым как в свежем, так и в засушенном виде.

Пример: Свежие грибы содержат 90% воды, а
сухие 12% воды. Сколько ки- лограммов сухих грибов получится из 33 килограмм
свежих?

По условию имеем 33 кг свежих грибов,
отделим от них клеточное вещество, т.е. 0,1 33 = 3,3 кг.

Переходим к сухим грибам, помним, что те же 3,3 кг клеточного
вещества остается в них от свежих грибов. а (кг) – 100 %        3,3100

                                                       a =                  a = 3,75

3,3 (кг) – 88 %                        ⁸⁸

Ответ: 3,75 кг.

Пример: Из 10 кг свежих фруктов получают
3,5 сушеных фруктов, содержа- щих 20% воды. Каково процентное содержание воды в
свежих фруктах?

Отделим в сухих фруктах клеточное вещество от влаги:

80% от 3,5 кг – это              
(кг), это масса клеточного вещества содер- жится и в свежих фруктах.

Сразу получим процентное содержание влаги:

Ответ: 72%

 Примечание: задачи об обогащении
руды имеют тот же смысл, только вместо клеточного вещества думаем о чистой
руде, вместо воды представляем при- меси.

Пример: Руда содержит 40% примесей, а
выплавленный из нее металл со- держит 4% примесей. Сколько тонн руды необходимо
взять, чтобы выпла- вить из нее 15 тонн металла?

Отделим чистую руду от примесей в
15 тоннах металла:               (т) Сколько же чистой руды содержится в руде с
40% примесей. Составим про- порцию:

       
                                   (т)

Ответ: 24 тонны.

Подборка задач:

№1. Свежие грибы содержат по массе 90% воды, а сухие –
20%. Сколько надо собрать свежих грибов, чтобы из них получить 4,5 кг сухих
грибов? Ответ:36 кг.

№2. Собрали 100 кг грибов.
Оказалось, что их влажность 99%. Когда их подсушили, то влажность снизилась до
98%. Какой стала масса этих гри- бов после того, как их подсушили? Ответ: 50
кг.

№3. Собрали 42 кг свежих грибов,
содержащих по массе 95% воды. Когда их подсушили, они стали весить 3 кг. Каков
процент содержания воды по массе в сухих грибах? Ответ: 30 кг.

№4. Только что добытый каменный
уголь содержит 2% воды, а после двух- недельного пребывания на воздухе он
содержит 20% воды. На сколько кг увеличилась масса добытой тонны угля после
того, как уголь две недели по- лежал на воздухе? Ответ:225 кг.

5. Интересные задачи из «жизни
торговли»

Очень интересные задачи, для решения
которых нужно понимать некоторые ключевые моменты:

•      Когда
продают что-либо, то основным показателем являются, цена, ко- личество,
стоимость;

•      Когда
получают прибыль от продажи партии товара, то она складыва- ется из тех же
показателей, что и выше, только цена является разницей между закупочной ценой и
ценой с наценкой (реализации);

•      Нужно
очень внимательно читать условие задачи, оформлять которое проще в виде
таблицы;

•     
Не бояться вводить более двух переменных.

Пример: Ювелирное изделие состоит из серебра и золота. В
начале года се- ребро дорожает на 5%, а золото – на 20% по сравнению с
предыдущим го- дом, в результате чего стоимость ювелирного изделия
увеличивается на 15%. Какую часть ювелирного изделия составляет золото, если в
предыдущем году 1 г золота стоил в 18 раз дороже 1 г серебра? (ответ дать в
виде десятичной дроби)

		Цена за 1 г	Кол-во в г	Стоимость
До подорожания	Золото	18х	m	18xm
Серебро	х	n	xn
После подорожания	Золото		m	21,6xm
Серебро	1,05x	n	1,05xn

Составим пропорцию:

Получаем уравнение:

                                                      
(по условию задачи)

      
Золото составляет   часть всего изделия, значит   

Ответ: 0,1

Пример: Салон модной одежды выставил на
продажу новую коллекцию, сде- лав наценку 140% от закупочной цены. После
продажи 0,85 все коллекции салон распродал оставшуюся часть с одинаковой
скидкой от продажной цены (в процентном отношении) на все элементы коллекции.
Сколько процентов составила эта скидка, если прибыль салона от продажи всей
коллекции со- ставила 113% от закупочной цены?

Внимание! Наценка 140% от закупочной цены означает, что                          от
закупочной цены, т.е. 2,4х – цена продажи в салоне. Прибыль салона
составила 113% от закупочной цены. Это значит, что

                  
Составим таблицу:

	Закупочная цена	Цена с наценкой	Количество	Стоимость
покупка	х	—	а	ха
продажа	х	2,4х	0,85а
х	*	0,15a

 *Скидка
в p% от цены 2,4х вычисляется:           

Составим пропорцию:

  (2xa
,4−   0,85100xa%
+  2,4  0,15xa^1− p ) ₋
213%

                                                                              

                                                                        100  

Получаем, что

                                           p  

213 = 2,485 + 151 − 100 



     213 ₌               15 p _


                2,485 + 15 −     

                                       100 

213 = 240 − 24 ^{15 p}

1000

     24 15 p        

= 27

 

p = 75

Ответ: 75%

Пример: Магазин получил партию товара и
продал 30% этого товара с при- былью 20%, а 50% оставшегося товара – с прибылью
40%. Какую прибыль получил магазин от реализации товара, оставшегося после двух
распродаж, если общая прибыль от продажи всей партии товара составила 27%.

	цена	количество	стоимость
партия	x	a	xa
1 продажа	1,2x	0,3a	0,36xa
2 продажа	1,4x	0,5(a − 0,3a) = 0,35a	1,4x  0,35a = 0,49xa
остаток	x 1 + p  * 100                    	a − 0,3a − 0,35a = 0,35a p	0,35xa 1+ p   100  p             

* повышение цены х (руб) на p%, т.е. x +         x = ^x1+     ^

                                                                                                                                                   

                                                                                                                   100
           100  

По условию задачи прибыль составила 27%, т.е. 100% + 27% =127%.

Составим и решим пропорцию:

  0xa
,85−xa
100 +
%0,35 xa^1+
p _
− 127%

                                                      

                                                100  

Получаем, что

       85 +  ₊  p ^_ = 127

35_1   
100  

35 p

 = 127 −120 100

      35 p                   7 100                                         Ответ:
20%

       = 7  p =                 p = 20%

      100                         35

Подборка задач:

№ 1.
Антикварный магазин, купив портсигар и статуэтку, продал их, полу- чив 40%
прибыли. Во сколько раз портсигар обошелся дороже магазина, чем статуэтка, если
на портсигаре было получено 35% прибыли, а на статуэт- ке – 60%? Ответ: 4

№ 2. Кондитерская фабрика
производит 20 видов шоколада. В новом году 5 из этих видов будут производить на
10% больше, а другие 7 видов – на 20% больше. На сколько процентов увеличится
выпуск шоколада на фабрике, если в старом году все виды шоколада производились
в одинаковом количестве?

Ответ: 9,5

№ 3. Молокозавод планирует
увеличить выпуск продукции на 10%. На сколь- ко процентов увеличится чистая
прибыль завода, если отпускная цена на его продукцию возросла на 15%, а ее
себестоимость для завода, которая до этого составляла ¾ отпускной цены,
увеличилась на 20%. Ответ: 10 № 4. В результате расширения компании сотовой
связи и одновременного снижения тарифов на 50% ежемесячный объем продаж ее
услуг вырос в 3 раза. Через сколько месяцев дополнительная прибыль, получаемая
компани- ей, компенсирует затраты на расширение, если они составили половину
прежнего годового дохода компании? Ответ: 12

Литература:

1.     Дорофеев
Г.В., Петерсон Л.Г., Математика. 6 класс. Часть 1. – М.: «Ба- ласс», «Ювента»,
2004. – 112 с.: ил.

2.     П.А.
Андриянов, В.И. Ермаков, Сборник задач по математике. Для подготовительных
курсов. Издание пятое, — М.: Издательство «Менед- жер», 2005. – 160 с.

3.     Лысенков,
Сборник задач для подготовки к ЕГЭ, — М.: издательство «Легион», — 2013.

Решение задач по теме: «ПРОЦЕНТЫ»

на ЕГЭ по математике

( профильный уровень)

Из опыта работы

учителя

математики

МОУ СОШ №1

р.п. Новые Бурасы

Новобурасского района

Саратовской области

Коротковой

Натальи Александровны

Понимание процентов и умение производить процентные расчеты в настоящее время необходимо каждому человеку, это способствует «вхождению» в современную информационно-экономическую среду и, в конечном счете, облегчает социализацию.

Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки, бытовые и производственные сферы жизни. Обучающиеся встречаются с процентами на уроках физики, химии, чтении газет, просмотре телепередач. Умением грамотно и экономно проводить элементарные процентные вычисления обладают далеко не все люди. Практика показывает, что очень многие окончившие школу не только не имеют прочных навыков обращения с процентами в повседневной жизни, но даже не понимают смысла процентов, как доли от некоторой заданной величины. Происходит это потому, что проценты изучаются на первом этапе основной школы, в 5-6 классах, когда учащиеся в силу возрастных особенностей еще не могут получить полноценные представления о процентах, об их роли в повседневной жизни.

В последнее время экзамен по математике проводится в форме ЕГЭ, и в контрольно-измерительных материалах ЕГЭ (профильный уровень) и ЕГЭ ( базовый уровень) присутствуют задачи на проценты. Специфика темы такова, что значительное позитивное влияние на знания и умения учащихся оказывает последующее обучение, причем не математике, а химии, где процентные расчеты являются существенным элементом содержания обучения, об этом свидетельствуют и приемы решения задач, и способы записи их решения.

Как подготовить учащихся 11 классов к правильному решению задач ЕГЭ на проценты?

I

Сначала надо систематизировать знания и умения по теме «Проценты», полученные в 5 и 6 классах.

Учащиеся должны уметь:

• преобразовывать десятичные и обыкновенные дроби,

• представлять проценты — в виде дроби и дробь – в виде процентов;

• находить проценты от величины, величину по ее проценту;

• выражать отношения в процентах;

• применять полученные математические знания в решении жизненных задач;

тест по теме «Проценты»

1. Найдите 25% от 56.

А) 14 Б) 22,04 В) 20 Г) 25

1. Найдите число, если 1% его равен 75.

А) 0,75 Б) 7,5 В) 7500 Г) 750

1. Клубника содержит 6% сахара. Сколько килограммов сахара в 27 кг клубники?

А) 1,82 кг Б) 1,62 кг В) 2,24 кг Г) 2,42 кг

1. Книга стоила 25 р. После повышения цены она стоит 30,25 р. На сколько процентов возросла стоимость книги?

А) на 21% Б) на 20% В) на 24% Г) на 25%

1. Найдите число, 34% которого равны 170.

А) 57,8 Б) 500 В) 56,5 Г) 510

1. На математической олимпиаде 32% участников получили грамоты. Сколько школьников приняло участие в олимпиаде, если наградили 416 человек?

А) 932 Б) 1300 В) 133,1 Г) 1340

1. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?

А) 330% Б) 30% В) 125% Г) 45%

1. Число уменьшили на 20%. На сколько процентов надо увеличить полученное число, чтобы получить данное число?

А) на 20% Б) на 40% В) на 25% Г) на 30%

1. Число 56 составляет 80% от некоторого числа. Найдите среднее арифметическое этих чисел.

А) 63 Б) 44,8 В) 126 Г) 56

1. Сторону квадрата уменьшили на 20%. На сколько процентов уменьшилась его площадь?

А) на 20% Б) на 36% В) на 10% Г) на 40%

Задания представлены в виде текстовых задач.

1. Квартирная плата повысилась на 20%. За прошлый месяц заплачено 120рублей. Сколько надо заплатить за текущий месяц?

2. В референдуме приняли участие 18 тыс. человек, что составило 60% всех жителей города, имеющих право голоса. Сколько жителей имеют право голоса?

3. В 5 тысячах из выпущенных 20 тысяч коробочек с жевательной резинкой находится сюрприз. Сколько процентов составили коробочки с сюрпризами?

4. Банком установлен тариф на пролонгацию аккредитива в размере 0,2% за квартал от суммы аккредитива. Вычислите размер комиссионных за пролонгацию аккредитива на сумму 100000 рублей за один квартал?

5. В первом квартале литр молока стоил 10 рублей. Во втором квартале цена на молоко повысилась на 20%, а в третьем еще на 50%. Сколько стал стоить литр молока?

6. Фирма платит разносчикам рекламных изданий за первую партию 10 тыс. рублей, а за каждую следующую в тот же день – на 5% больше по сравнению с предыдущей. Сколько получит человек, если в течение одного дня он разнес 4 партии изданий?

7. 15% жителей города ежегодно слушают ВВС, 45% — радио «Свобода» и 40% — «Голос Америки». Можно ли сказать, что все жители города ежедневно слушают передачи западного радио?

8. Себестоимость товара 30 тыс. рублей. В магазине этот товар продается по цене 90 тыс. руб. Сколько процентов от себестоимости составляет розничная цена.

9. Валовой национальный продукт государства составил 33 млрд. долларов, что соответствует 75% от планировавшегося бюджетом. Найдите плановую величину НВП этого государства.

10. Подоходный налог установлен в размере 13%. До вычета подоходного налога 1% заработной платы отчисляется в пенсионный фонд. Работнику начислено 5420 рублей. Сколько он получит после указанных вычетов?

11. Инфляция составляет 10% каждый месяц. Сколько процентов составила инфляция за два месяца?

12. В результате мелиоративных мероприятий посевные площади увеличились на 150% по сравнению с прошлым годом. Найдите величину посевных площадей этого года, если в прошлом году она была 60 га

II

Затем необходимо развивать и углублять общеучебные навыки и умения за счет: решения дополнительных задач (на процентное содержание, процентный раствор и концентрацию); новых способов их решения (уравнение, система уравнений, геометрически, старинный способ); решения задач с практической ориентацией.

ЗАДАНИЯ ИЗ ВАРИАНТОВ ЕГЭ

1. Смешали 160 г раствора, содержащего 60% соли, и 240 г раствора, содержащего 40% соли. Сколько процентов соли в получившемся растворе?

2. В январе пакет акций стоил на 10% меньше, чем в феврале. В феврале этот же пакет акций стоил на 20% меньше, чем в марте. На сколько процентов меньше стоимость акций в январе, чем в марте?

3. Предприятие уменьшило выпуск продукции на 20%. На сколько процентов необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?

4. Зарплату повысили на р%. Затем новую зарплату повысили на 2р%. В результате двух повышений зарплата увеличилась в 1,32 раза. На сколько процентов зарплата была повышена во второй раз?

ПРОЦЕНТНОЕ СОДЕРЖАНИЕ, ПРОЦЕНТНЫЙ РАСТВОР

Тип задач на составление уравнений и систем уравнений – задачи на сплавы и смеси, решение которых связано с понятиями «концентрация», «процентное содержание», «проба», «влажность».

Процентное содержание вещества в растворе, иногда называют %-м раствором, например, 15%-й раствор соли.

1. Сколько кг соли в 10 кг соленой воды, если %-е содержание соли 15%?

Решение: 10∙0,15 = 1,5(кг).

Ответ: 1,5 кг.

Процентное содержание вещества в сплаве – это часть, которую составляет вес данного вещества от веса всего сплава.

2. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?

Решение:

1) 10 + 15 = 25(кг) сплав;

2) 10: 25 ∙ 100% = 40% процентное содержание олова в сплаве.

3) 15: 25 ∙ 100% = 60% процентное содержание цинка в сплаве.

Ответ: 40%, 60%.

КОНЦЕНТРАЦИЯ, СМЕСИ И СПЛАВЫ

Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.

Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 300∙0,87 = 261 г.

В этом примере концентрация вещества выражена в процентах.

Отношение объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.

Сумма концентраций всех компонент, составляющих смесь, равна 1. В этом случае концентрация – безразмерная величина.

Если известно процентное содержание вещества, то его концентрация находится по формуле: к = р : 100%,

к – концентрация вещества;

р – процентное содержание вещества (в процентах).

Задача 1. Имеется два сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго слава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?

Решение (с помощью уравнения): Пусть к 20 кг первого сплава нужно добавить Х кг второго сплава. Тогда получим (20+Х) кг нового сплава. В 20 кг первого сплава содержится 0,4∙20 = 8 (кг) серебра, а в (20+Х) кг нового сплава содержится 0, 32∙(20+Х) кг серебра. Составим уравнение: 8+0,2Х = 0,32(20+Х), Х=13 1/3.

Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.

Задача 2. При смешивании 5%-ного раствора кислоты с 40%-ным раствором кислоты получили 140 г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?

Решение (с помощью системы уравнений):

Проследим за содержанием кислоты в растворах. Возьмем для смешивания Х г 5%-ного раствора кислоты (или 0,05Х г) и Υ г 40%-ного раствора (или 0,4Υ г). Так как в 140 г нового раствора кислоты стало содержаться 30%, т. е. 0,3∙140 г, то получаем следующее уравнение 0,05Х + 0,4Υ = 0,3∙140. Кроме того Х + Υ = 140.

Таким образом, приходим к следующей системе уравнений:

0,05Х + 40Υ = 30∙140,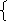

Х + Υ = 140.

Из этой системы находим Х = 40, Υ = 100. Итак, 5%-ного раствора кислоты следует взять 40 г, а 40%-ного раствора – 100 г.

Ответ: 40 г, 100 г.

Таким образом, задачи для старшеклассников содержат прагматическую ориентацию, их формулировки имеют практическое применение, представляют конкретные интересы.

Задача 1.

Стоимость компьютера 1250 долларов. Какова будет его стоимость после снижения цены на 20%?

Задача 2.

Торт стоил 100 рублей. Сначала цену повысили на 10%, а затем снизили на 10% (от новой цены). Сколько теперь стоит торт?

III

В первую очередь изучению – на основной или старшей ступени – подлежат «сложные» проценты. Понятия «простых» и «сложных» процентов, при условии достаточного овладения учащимися этими понятиями, могут послужить мощным источником мотивации введения многих математических понятий. Основой для введения арифметической и геометрической прогрессий.

Приведу в качестве примера три задачи.

Задача 3.

Скорость тела, движущегося равноускоренно, каждую секунду увеличивается на 10%. В данный момент его скорость10,00 м/сек. Какова будет его скорость через три секунды?

Задача 4.

При внесении квартирной платы на один день позже установленного срока начисляется пеня в размере 0,1% от суммы платежа. Сколько придется заплатить в случае задержки квартирной платы на три месяца, если квартирная плата составила 100 рублей?

Задача 5.

Банком установлена процентная ставка из расчета 3% в месяц. Сколько денег должен получить гражданин, вложивший в этот банк 100 рублей на 3 месяца?

Следует заметить, что самые естественные примеры могут служить «материальным» доказательством сравнения скорости роста арифметической и геометрической прогрессий. Этот факт оказывается, таким образом, не чисто математическим, причем достаточно сложным «изысканием», а совершенно очевидным «на практике» утверждением.

Задача 6.

Выгодно ли гражданину задержать на три месяца внесение квартирной платы (задача 4), вложив эти 100 рублей в банк (задача 5)?

IV

Решение задач с помощью уравнения

Проблема заключается в том, что даже при решении несложных задач, возникают затруднения при переводе текста задачи на язык уравнений.

Систематизируем знания по данному вопросу.

Неизвестную величину обозначим через Х, тогда

• чтобы найти 20% от нее, надо 0,2Х;

• чтобы увеличить ее, например, на 10%, надо Х+0,1Х=1,1Х;

• чтобы уменьшить ее, например, на 30%, надо Х-0,3Х=0,7Х,

• в общем виде: если 0

• чтобы найти Р% от Х, надо 0,РХ;

• чтобы увеличить ее на Р%, надо Х+0,РХ=1,РХ;

• чтобы уменьшить ее на Р%, надо Х-0,РХ=(1-0,Р)Х, далее составляем уравнение, соответствующее условию задачи.

Задача

В двух школах поселка было 1500 учащихся. Через год число учащихся первой школы увеличилось на 10%, а второй – на 20%, и в результате общее число стало равным 1720. Сколько учащихся было в каждой школе первоначально?

Решение:

Пусть Х учащихся было в первой школе, тогда (1500-Х) учащихся было во второй школе. После увеличения на 10% учащихся первой школы их стало Х+0,1Х=1,1Х, а во второй школе стало (1500-Х)+0,2(1500-Х)=1500-Х+300-0,2Х=1800-1,2Х учащихся. В результате их общее число стало равным 1720. Составим уравнение

1,1Х+1800-1,2Х=1720

-0,1Х=-80

Х=800

Таким образом получили, что 800 учащихся было в первой школе, тогда 700 учащихся было во второй школе первоначально.

Ответ: 800 и 700 учащихся.

V

Решение с помощью системы уравнений

Когда в условии задачи неизвестными являются две величины, то можно решить задачу с помощью системы уравнений. Решим предыдущую задачу с помощью системы уравнений.

Решение:

Пусть Х учащихся было в первой школе, тогда Υ учащихся было во второй школе. В двух школах поселка было 1500 учащихся. После увеличения учащихся первой школы их стало 1,1Х, а во второй стало 1,2Υ учащихся, в результате их общее число стало равным 1720. Составим систему уравнений и решим ее способом подстановки

Х+Υ=1500, Х=1500-Υ, Х=1500-Υ, Х=800,

1,1Х+1,2Υ=1720; 1,1(1500-Υ)+1,2Υ=1720; Υ=700; Υ=700.

Ответ: 800 и 700 учащихся.

Задачи из открытого банка заданий ЕГЭ

Задача 1. Одной машинистке на перепечатку рукописи требуется на 12 ч больше, чем другой. Если 25% рукописи перепечатает первая машинистка, а затем к ней присоединится вторая машинистка, то на перепечатку рукописи им понадобиться 35 ч, считая от момента начала работы первой машинистки. За сколько часов могла бы перепечатать рукопись каждая машинистка, работая отдельно?

Решение: Пусть на перепечатку рукописи первой машинистке требуется ч, тогда второй потребуется ч. На перепечатку 25% рукописи первая машинистка затратит ч. Выясним теперь, сколько времени потребуется двум машинисткам на перепечатку оставшихся 75% рукописи. Первая машинистка перепечатывает за один час часть рукописи, вторая – часть рукописи, а вместе за час они перепечатывают часть рукописи. На перепечатку рукописи им потребуется ч, т.е. ч. Отсюда получаем уравнение:

Решив это уравнение, найдем, что оно имеет два корня: и .

Второй корень не соответствует условию задачи.

Ответ: первой машинистке на перепечатку рукописи требуется 60 ч, а второй – 48 ч.

Задача 2. Положив в банк деньги, вкладчик получил через год прибыль в 240 тысяч рублей. Однако он не стал забирать деньги из банка, а, добавив к ним еще 60 тысяч, снова оставил деньги на год. В результате спустя еще год он получил в банке 1 миллион 100 тысяч рублей. Какая сумма была положена в банк первоначально и какой процент прибыли в год давал банк?

Решение: Допустим, что первоначальный вклад составляет тысяч рублей. Тогда процент прибыли за год равен . Сумма вклада, положенного в банк через год, составила тысяч рублей, т.е. тысяч рублей. Этот вклад принес доход, равный тысячам рублей. Всего вкладчик получил 1100 тысяч рублей.

Получаем уравнение:

Решив его, найдем, что это уравнение имеет два корня: , Выполнив расчеты, можно убедиться, что оба корня соответствуют условию задачи.

Ответ: задача имеет два решения: вкладчик вложил первоначально 200 тысяч рублей и получил доход 120% в год или вкладчик вложил первоначально 360 тысяч рублей и получил доход в год.

Задача 3. Имелось два слитка меди. Процент содержания меди в первом слитке был на 40 меньше, чем процент содержания меди во втором. После того как оба слитка сплавили, получили слиток, содержащий 36% меди. Найдите процентное содержание меди в первом и во втором слитках, если в первом слитке было 6 кг меди, а во втором – 12 кг.

Решение: Обозначим за массу первого слитка в кг, за массу второго слитка в кг, получим систему уравнений:

В результате получим: х=30, у=20.

Ответ: 30 кг, 20 кг

Задача 4. Для определения оптимального режима снижения цен социологи предложили фирме с 1 января снижать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 10%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо снижать цену товара через каждые два месяца во втором магазине?

Решение: Пусть руб. — стоимость товара, — число процентов. Тогда,

I магазин

Февраль

Март

……………………………………

Июль

II магазин

Март

Май

Июль

По условию задачи через полгода (1 июля) цены снова стали одинаковые, составляем уравнение:

Ответ: на 21%.

Задача 5. В соответствии с договором фирма с целью компенсации потерь от инфляции была обязана в начале каждого квартала повышать сотруднику зарплату на 3%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько процентов фирма должна повышать зарплату каждые полгода, чтобы 1 января следующего года зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренной договором.

Решение: Пусть руб. — зарплата, — процент повышения зарплаты. Тогда,

По плану: I квартал руб.

……………………………

IV квартал руб.

Фактически

I полугодие руб.

II полугодие руб.

По условию задачи зарплата сотрудника была равна той зарплате, которую он получил бы при режиме повышения, предусмотренного договором, составляем уравнение:

Ответ: на 6,09 %.

Задача 6. На заводе было введено рационализаторское предложение. В результате время, необходимое для изготовления рабочими некоторой детали, уменьшилось на 20%. На сколько процентов возросла производительность труда этого рабочего?

Решение: Пусть — производительность труда, а — весь объем работы. Тогда работа будет выполнена за время . В результате роста производительности труда время на изготовление детали стало равно , соответственно производительность , или . Соответственно рост производительности труда составил:

Ответ: 25%

Задача 7. Из жителей города одни говорят только на украинском, другие – только на русском, третьи – на обоих языках. По-украински говорят 85% всех жителей, а по-русски – 75%. Сколько процентов всех жителей этого города говорят на обоих языках?

Решение:

100%-85%=15% — не говорят на украинском;

100%-75%=25% — не говорят на русском;

100%-15%-25%=60% — говорят на обоих языках.

Ответ: 60%

VI

Задачи «на банковские проценты» — в большинстве случаев являются экономическими задачами, в которых идёт речь о вкладах в банк с тем или иным процентом. При их решении надо помнить, что процент есть сотая доля числа. Решение задач этого типа тесно связано с тремя алгоритмами: нахождения части от целого, восстановление целого по его известной части, нахождение процентного прироста. Рассмотрим эти алгоритмы.

1. Пусть известна некоторая величина А, надо найти а % этой величины.

Если считать, что А есть 100%, а неизвестная часть х это а %, то из пропорции A/100=x/a

имеем x=Aa/100.

1. Пусть известно, что некоторое число b составляет а % от неизвестной величины А. Требуется найти А.

Рассуждая аналогично, из пропорции получаем   A=100b/a.

1. Пусть некоторая переменная величина А, зависящая от времени t, в начальный момент t₀ имеет значение А₀, а в моментt₁ – значение А₁.

Тогда абсолютный прирост величины А за время t₁–t₀ будет равен А₁–А₀; относительный прирост этой величины вычисляется по формуле       (A₁-A₀)/A₀, а процентный прирост по формуле   ((A₁-A₀)/A₀)100%.

Задача №1.

Известно, что вклад, находящийся в банке, с начала года возрастает к концу года на определённый процент (свой для каждого банка). В начале года 5/6 некоторого количества денег положили в первый банк. К концу года сумма этих вкладов стала равной 670 у.е., а к концу второго года – 749 у.е. Было подсчитано, что если бы первоначально исходного количества денег положили во второй банк, то по истечении одного года сумма вкладов в эти банки стала бы равной 710 у.е. В предложении, что исходное количество денег первоначально целиком положено в первый банк, определить величину вклада по истечении двух лет.

Решение.

Обозначим через x первоначальную сумму денег. Тогда через а обозначим процент, на который возрастает сумма за год в первом банке, а через b – во втором банке. К концу первого года сумму вклада в I банке стала равной (5x/6)(1+a/100), во II банке (x/6)(1+b/100), а к концу второго года(5x/6)(1+a/100)² и (x/6)(1+b/100)². По условию задачи сумма вкладов  в конце первого года составляет 670 у.е., а к концу второго года – 749 у.е., поэтому можно составить два уравнения:

(5x/6)(1+a/100)+(x/6)(1+b/100)=670 (1)

(5x/6)(1+a/100)²+(x/6)(1+b/100)²=749 (2)

Если во второй банк положить 5x/6  у.е., а в первый – x/6 у.е, то сумма вкладов к концу года составила бы:

(5x/6)(1+b/100)+(x/6)(1+a/100),

что равнялось бы 710 у.е. Поэтому получим третье уравнение:

(5x/6)(1+b/100)+(x/6)(1+a/100)=710 (3)

Для нахождения известного х составим систему уравнений из (1) и (3) и решим её:

1+a/100=660/x

1+b/100=720/x

Подставляя 660/x вместо 1+a/100 и 720/x вместо 1+b/100 в уравнение (2), приходим к уравнению (5x/6)(660/x)²+(x/6)(720/x)²=749, имеющему один корень: x=660, но тогда: 1+a/100=660/600=1,1

Если исходное количество денег положить на два года, то к концу второго года величина вклада составит 726 у.е.

Ответ 726 у.е.

Задача №6.

Рабочий положил на хранение в сберегательный банк 5000 руб.  По истечении одного года к его вкладу были причислены процентные деньги, и в то же время он увеличил свой вклад ещё на 5000 руб., а по истечении ещё одного года попросил выдать ему накопленные процентные деньги. Сколько процентов в год начисляет сбербанк, если рабочий получил 1232 руб. процентных денег, оставив вклад в 10 000 руб. на новый срок?

Решение.

Пусть x% в год начисляет сбербанк, а y% — процент за 2 года. x+x+y —  весь начисленный процент. По условию задачи 2x+y=1232 (руб.)

За I и II начисленный процент равен 5000?0,01x=50x, а процент за оба года равен 0,01x?(5000+50x).

Составим уравнение:

50x+50x+0,01x?(5000+50x)=1232

Решив это уравнение 50x+50x+0,01x(5000+50x)=1232

100x+50x+0,5x²-1232=0

0,5x²+150x-1232=0

D=b²-4ac=150²-4?0,5?(-1232)=24964, D0, два корня.

x₁=-308

x₂=8

Найдём два значения для х: х₁=-308 – не удовлетворяет условию задачи, х₂=8. Значит, сбербанк начисляет в год 8%.

Ответ: 8%

Проценты в банковской системе.

Простой процентный рост.

Если человек не вносит своевременную плату за квартиру, то на него налагается штраф, который называется «пеня». Так в Москве пеня составляет 1% от суммы квартплаты за каждый день просрочки. Поэтому, например, за 19 дней просрочки, сумма составит 19% от суммы квартплаты, и в месте , скажем, со 100 руб. квартплаты человек должен будет внести пеню 0,19 * 100 = 19 руб., а всего 119 руб.

Ясно, что в разных городах и у разных людей, квартплата, размер пани и время просрочки разные. Поэтому имеет смысл, составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S – ежемесячная кварт плата, пеня составляет p% квартплаты за каждый день просрочки, а n – число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.

Тогда за n дней просрочки, пеня составит pn% от S , или , а всего придётся заплатить .Таким образом,

Задача 1. Сколько надо заплатить москвичу, если его квартплата составляет 100 руб. и просрочена на 5 дней?

Решение.

Подставляя в формулу значение p = 1 и значения n = 5 * 4, получим:

(1 + ) * 100 = 1,05 * 100 = 105 (руб.)

Ответ: через 5 дней – 105 руб.

Таким образом, установленная формула позволяет быстро рассчитывать необходимые значения выплат за квартиру.

Рассмотрим еще одну ситуацию. Банк выплачивает вкладчикам каждый месяц p% от внесенной суммы. Поэтому, если клиент внес сумму S, то через n месяцев на его счете будет ()S, и мы вновь получаем, что

S_n=(1+) S

Мы получили в точности ту же самую формулу, что и в примере с квартплатой, хотя буквы в этих двух примерах имеют разный смысл: в первом примере n – число дней, а во втором примере n — число месяцев, в первом примере S – величина квартплаты, а во втором S – сумма, внесенная в банк. Такая же формула будет получаться и во всех иных случаях, когда некоторая величина увеличивается на постоянное число процентов за каждый фиксированный период времени. Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Задача 2. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?

Решение.

Для решения задачи достаточно подставить в формулу величину процентной ставки p = 2, числа месяцев n = 6 и первоначального вклада S = 500:

(1 + ) * 500 = 1,12 * 500 = 560 (руб.)

Ответ: через полгода на вкладе будет 560 руб.

Сложный процентный рост.

В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется 40% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют.

Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года 40% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк1000 руб. и ни разу не будет брать деньги со счета:

40% от 1000 руб. составляют 0,4 * 1000 = 400 руб., и следовательно, через год на его счете будет

1000 + 400 = 1400 (руб.)

40% от новой суммы 1400 руб. составляют 0,4 * 1400 = 560 руб., и следовательно, через 2 года на его счете будет

1400 + 560 = 1960 (руб.)

40% от новой суммы 1960 руб. составляют 0,4 * 1960 = 784 руб., и следовательно, через 3 года на его счете будет

1960 + 784 = 2744 (руб.)

Нетрудно представить себе, сколько при таком непосредственном , «лобовом» подсчёте понадобилось бы времени для нахождения суммы вклада через 10 лет. Между тем, подсчёт можно вести значительно проще.

Именно через год начальная сумма увеличится на 40%, то есть составит 140% от начальной, или, другими словами, увеличится в 1,4 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 40%. Следовательно, через 2 года начальная сумма увеличится в 1,4 * 1,4 = 1,4² раза.

Еще через один год и эта сумма увеличится в 1,4 раза, так что начальная сумма увеличится в 1,4 * 1,4² = 1,4³ раза. При таком способе рассуждения получаем решение нашей задачи значительно более простое:

1,4³ * 1000 = 2,744 * 1000 = 2744 (руб.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет p% годовых, внесённая сумма равна S рублей, а сумма, которая будет на счёте через n лет, равна S_n рублей.

p% от S составляют S рублей, и через год на счёте окажется сумма

S₁ = S

то есть начальная сумма увеличится в 1 + раза.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счёте будет сумма

S₂ = (1 +) S₁ = (1 +) (1+) S =(1 + )² S.

Аналогично, S₃ =(1 + )³ S и так далее. Другими словами, справедливо равенство

S_n = (1 + ) ³ S.

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Задача 1. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?

Решение.

Подставим в формулу значения процентной ставки p = 10, количество лет n = 4 и величину первоначального вклада S = 2000, получим:

(1 + )⁴ * 2000 = 1,1⁴ * 2000 = 1,4641 * 2000 = 2928,2 (рублей).

Ответ: через 4 года на счёте будет сумма 2928,2 рубля.

Банковский процент.

Предположим, что вы хотите положить в банк 10 000 рублей, чтобы на них «росли проценты». В Сбербанке вам предложат 120% годовых, если вы кладёте деньги на 3 месяца, 130% годовых, если положите на 6 месяцев, и 150% годовых при вкладе на год.

В банке «Триумф» вам предложат 200% годовых при вкладе на год. Подсчитаем, сколько вы получите через 5 лет. Поскольку каждый год вы будете получать 200% годовых, то за 5 лет вы получите в 5 раз больше – 1000%, т.е. 100 000 рублей к своим 10 тысячам рублей. Но это не так!

Считать следует иначе! За год ваш вклад утраивается, т.е. через год у вас будет 30 тысяч рублей, а за второй год он еще утроится и составит 90 000 рублей. То же самое буде происходить после третьего, четвёртого и пятого года. Поэтому после третьего года у вас будет уже 270 000 рублей, после четвёртого 810 000 рублей, а после пятого – 2 430 000 рублей, а не 110 000 рублей, как мы предполагали сначала. Теперь стоит выбрать способ вложения денег: на 3 месяца, на 5 месяцев или на год.

Казалось бы, лучше всего положить на год, что даёт самый высокий процент годовых – 150%. Но, наученные расчётами с другими банками, давайте проверим.

Если положить на полгода из расчёта 130% годовых, то через полгода получим доход в 65% от вложенной суммы, т.е. сумма увеличится в 1,65 раз. Если затем еще раз положить на полгода все полученные деньги, то сумма возрастёт в 1,65 * 1,65 = 2,7225 раза, то есть на 172,25%, что существенно больше 150-ти процентов при вкладе сразу на год.

А если положить деньги на три месяца, потом еще на три, и еще, и еще раз на три месяца? В первый раз прибыль составит четверть от 120%, т.е. 30% от вложенной суммы. Это значит, что вклад увеличится в 1,3 раза. В следующий месяц он увеличится еще в 1,3 раза, что даст увеличение первоначальной суммы в 1,69 раза. Через следующие три месяца увеличение составит 2,197 раза, а к концу года получим увеличение в 2,8561 раза. Таким образом, получаем 185,61% годовых. Правда, при этом нужно приходить в банк каждые три месяца, чтобы забирать вклад и снова класть его на три месяца.

Но есть ещё форма вклада под 100% годовых с правом снять вклад в любое время с получением соответствующей доли прибыли. Вот, наверное, золотая жила! Ведь мы убедились, что чем чаще кладёшь и берёшь вклад, тем больше оказывается прибыль.

Если ходить в Сбербанк каждый день, то каждый раз вклад будет увеличиваться в 1+ , а за год увеличение составит (1 +)³⁶⁵ раза.

Величина числа (1 +)ⁿ действительно увеличивается с увеличением n, но не может превзойти числа е= 2,71828… и стремится к этому числу с увеличением n.

Число е названо так в честь Леонардо Эйлера. Оно играет важную роль во многих разделах математики.

Итак, даже бегая в Сбербанк каждый час, нам не удастся получить доход больше 172% годовых, если мы примем эту форму вложения денег.

Ипотеки.

Ипотека — это заем, который предоставляет нам бан­ковское учреждение для того, чтобы мы могли опла­тить стоимость жилья. Когда банк одалживает нам деньги, мы должны вернуть ему эту сумму плюс соот­ветствующие проценты. Возвращение ипотечного кре­дита осуществляется не в конце договорного срока, а ежегодными частями. Например, Эдуард купил себе квартиру, но так как у него не было для этого достаточно денег, он обратился в банк за ипотечным кредитом в один миллион рублей со сро­ком погашения 20 лет. Тип годового процента является фиксированным: 4%. Какую сумму должен возвращать Эдуард банку ежегодно? Возвращаемая сумма называ­ется годовым погашением и рассчитывается следую­щим образом:

рубля

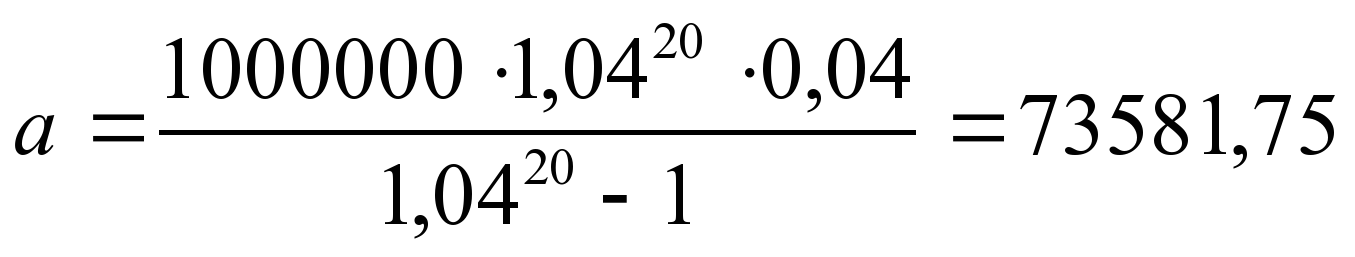
Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Интенсивная математизация различных областей человеческой деятельности особенно усилилась с внедрением современных информационных технологий, требующих математической грамотности человека буквально на каждом рабочем месте. Понятие «проценты» вошло в нашу жизнь не только с уроками в средней школе и с проведением сложных научно-исследовательских работ, не только с выпечкой кулинарных изделий и приготовлением лакомств, солений и варений, оно буквально атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, кредитов, инфляций, девальваций. «Брать ссуду в банке или купить в кредит? Может быть выгоднее накопить денег для покупки дорогостоящей вещи?» Чтобы ответить на эти вопросы, требуется умение решать задачи по теме «Проценты».

Ресурсы:

1. http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege

Открытый банк заданий ЕГЭ-2016

2. http://www.prosv ru

– сайт издательства, Просвещение,рубрика ,,математика,,/;

3. http://www.edu.ru-//www.edu.ru -Центральный образовательный портал, содержит нормативвные документы Министерства, стандарты;

4. http://www.pedsovet.su/;

5. http://nsportal.ru/shkola/obshchepedagogicheskie—tekhnologii/library/2015/03/04/;

6. ОГЭ 2015. Математика. Тем. тест. задания_Глазков, Варшавский и др_2015 -112с.pdf;

7. Математика. Тем. тесты для подг ЕГЭ( профильный уровень)-2015_ред. Лысенко_2015 -320с.pdf;

8. http://math-prosto.ru/?page=pages/percent/percent3.php