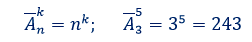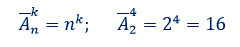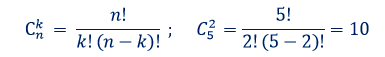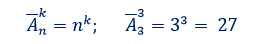Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Без метода (8 шт.)
Категория:
Версия для печати и копирования в MS Word
1
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
2
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
3
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
4
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
5
За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
Пройти тестирование по этим заданиям
Элементы
комбинаторики
Комбинаторика – это
раздел элементарной математики, связанный с изучением количества комбинаций,
подчинённых тем или иным условиям, которые можно составить из заданного
конечного множества элементов (безразлично, какой природы; это могут быть
буквы, цифры, какие-либо предметы и т.п.).
1. Непосредственные подсчеты
Для решения комбинаторных задач существуют различные
способы грамотного подсчета, исключающие возможность потери какой-либо
комбинации элементов.
Логический перебор: При
логическом переборе выписывают все комбинации элементов, придерживаясь
некоторого правила.
Пример 1. В случайном
эксперименте симметричную монету бросают: а) дважды; б) трижды. Определите все
возможные комбинации выпадения орла и решки.
Решение. Выпадение
орла обозначим буквой О, решки – буквой Р.
а)
Записываем на первом месте букву О: ОО, ОР. Теперь на первом месте записываем
букву Р: РО, РР. В итоге получаем 4 комбинации выпадения орла и решки: ОО, ОР,
РО, РР.
б)
В каждой комбинации, полученной в предыдущей задаче, добавляем слева букву О: ООО,
ООР, ОРО, ОРР. Аналогично слева приписываем букву Р: РОО, РОР, РРО, РРР.
В итоге получаем 8 комбинаций.
Ответ:
8.
Пример 2. Сколько четных
двузначных чисел можно составить из цифр 0, 1, 2, 5, 8, 9?
Решение. Составим
таблицу: слева от первого столбца таблицы поместим цифры десятков двузначных
чисел, выше первой строки – цифры единиц.
|
0 |
2 |
8 |
|
|
2 |
20 |
22 |
28 |
|
5 |
50 |
52 |
58 |
|
8 |
80 |
82 |
88 |
|
9 |
90 |
92 |
98 |
Искомых чисел будет столько же, сколько клеток в таблице,
то есть 5·3=15.
Ответ:15.
Иногда подсчет вариантов облегчают графы. Так
называют геометрические фигуры, состоящие из точек (их называют вершинами)
и соединяющих их отрезков (называемых ребрами графа). Для удобства
иллюстрации условия задачи с помощью графа его вершины-точки могут быть
заменены кругами или прямоугольниками, а ребра-отрезки – любыми линиями.
Полный граф: При
решении задач с помощью полного графа проводят все возможные ребра.
Пример 3. Андрей, Борис,
Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько
партий было сыграно?
Решение.
Рассмотрим полный граф с четырьмя вершинами, обозначенными по первым буквам
имен каждого из 4 мальчиков. Отрезки-ребра обозначают шахматные партии,
сыгранные каждой парой мальчиков. Из рисунка видно, что граф имеет 6 ребер,
следовательно, и партий было сыграно 6.
Ответ:
6.
Граф-дерево
При
решении некоторых задач удобно использовать граф, называемый деревом (за внешнее
сходство с деревом).
Пример 4. Антон, Борис и Василий
купили 3 билета на футбольный матч на 1, 2 и 3-е места первого ряда. Сколькими способами
они могут занять имеющиеся три места?
Решение. Изобразим
перебор способов с помощью графа-дерева, помещая в вершины графа первые буквы
имен друзей А, Б и В.
В
итоге получаем 6 способов.
Ответ: 6.
2. Правило умножения
Перебрать и подсчитать всевозможные комбинации из
данных элементов, используя наглядные средства, несложно, когда их количество
невелико. Однако при большом количестве элементов этот перебор затруднителен, и
тогда используют правила комбинаторики. Правило умножения (правило «и») — одно
из основных правил комбинаторики.
Согласно
ему, если элемент множества А может быть выбран m способами,
а элемент множества B — n способами,
то упорядоченная пара (A, B) может
быть составлена m•n способами. Правило
обобщается на произвольную длину последовательности.
Пример 5. Сколько
трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если:
а)
числа не повторяются;
б)
числа могут повторяться.
Решение.
а)
Первую цифру выбираем 5 способами, вторую цифру – 4 способами, третью – 3
способами. Всего 5•4•3 =60 трехзначных
чисел.
б)
Всего 5•5•5 =125
трехзначных чисел.
Ответ: а) 60;
б) 125.
3. Правило сложения
Правило
сложения (правило «или») – одно из основных правил комбинаторики, утверждающее,
что, если элемент множества A можно выбрать m способами,
элемент множества B можно выбрать n способами,
и множества A
и
B
не
имеют общих элементов, то выбор одного из элементов множеств A или B осуществляется
m+n способами.
Пример 6. На блюдце лежит 8
яблок и 6 груш. Сколькими способами можно
взять
плод с блюдца?
Решение. Всего
способов 6 +8 =14 .
Ответ: 14.
4. Перестановки
Перестановками называют
комбинации, состоящие из одних и тех же n различных
элементов
и отличающиеся только порядком их расположения. Число всех возможных
перестановок из n различных элементов Pn= n!, где n!=1•2 •3•…• (n —1) • n ; 1!11; 0!=0.
Например,
из трех элементов a, b и c можно
образовать 3!=1•2•3 = 6
перестановок: abc, acb, bac, bca, cab, cba.
Пример 7. Сколькими
способами можно обозначить вершины куба буквами A, B, C, D, E, F, G, K?
Решение. Число
способов обозначить восемь вершин куба данными различными буквами (которых
также восемь) равно P8 = 8!= 40320
Ответ:
40320.
5. Размещения
Размещениями называют
комбинации, составленные из n различных элементов по
m
элементов,
которые отличаются либо составом элементов, либо их порядком. Число всех
возможных размещений
В
частности, при m = n получаем = n!=Pn .
Например,
из четырех элементов a, b, c и d можно образовать
размещений по два элемента: ab, ba,
ac, ca, ad, da, bc, cb, bd, db,
cd, dc.
Пример 8. Сколько можно
составить сигналов из 6 флажков различного цвета,
взятых
по 2?
Решение.
Ответ:
30.
1.6. Сочетания
Сочетаниями называют
комбинации, составленные из n различных элементов по
m
элементов,
которые отличаются только составом элементов. Число всех возможных сочетаний
Например,
из пяти элементов a, b, c, d и e можно
образовать
сочетаний
по три элемента: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
Числа
размещений, перестановок и сочетаний связаны равенством
Пример 9. Сколькими способами
читатель может выбрать две книжки из пяти
имеющихся?
Решение.
Ответ:
10.
5 ноября 2020
В закладки
Обсудить
Жалоба
Задачи по комбинаторике
Подборка задач по комбинаторике с краткими пояснениями и ответами.
Комбинаторика — это наука, с который каждый встречается в повседневной жизни: сколько способов выбрать трёх дежурных для уборки класса или сколько способов составить слово из данных букв. В целом, комбинаторика позволяет вычислить, сколько различных комбинаций, согласно некоторым условиям, можно составить из заданных объектов (одинаковых или разных).
В ЕГЭ по математике базового уровня — задача №10.
komb.docx
komb.pdf
Задача 1: Сколькими способами можно составить список из 5 учеников?
Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?
Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.
Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?
Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?
Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?
Задача 8: В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими способами можно выбрать покупку из двух разных блокнотов и одной ручки?
Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?
Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?
Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?
Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?
Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?
Задача 16: Сколько существует различных семизначных телефонных номеров?
Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?
Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом?
Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?
Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?
Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?
Подготовка к ЕГЭ по математике (В4) Решение комбинаторных задач
Зарьянцева В.П.
Комбинаторика
Правило
Формулы
суммы
произведения
Перестановки
Размещения
Сочетания
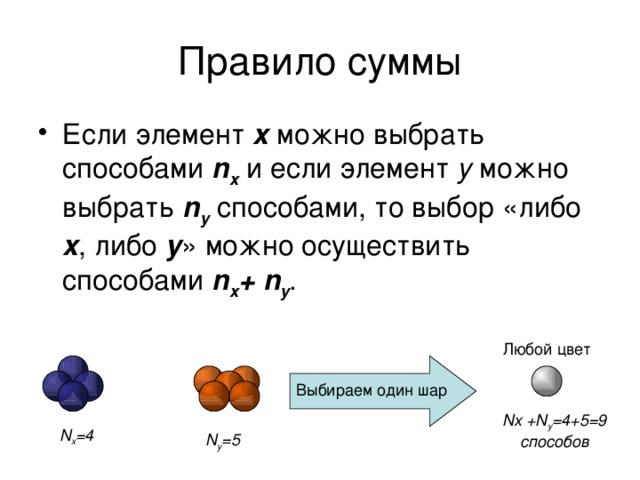
Правило суммы
- Если элемент x можно выбрать способами n x и если элемент y можно выбрать n y способами, то выбор «либо x , либо y » можно осуществить способами n x + n y .
Любой цвет
Выбираем один шар
Nx +N y =4+5=9 способов
N x =4
N y =5
Пример 1
- В коробке 10 тетрадей в клетку и 5 тетрадей в линию. Сколькими способами можно выбрать одну тетрадь?
- Решение: или – логическая сумма
- 10+5=15 (выбор неважен)
- Пример1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
- Решение:
- к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
- к1+к2 = 5+4 = 9
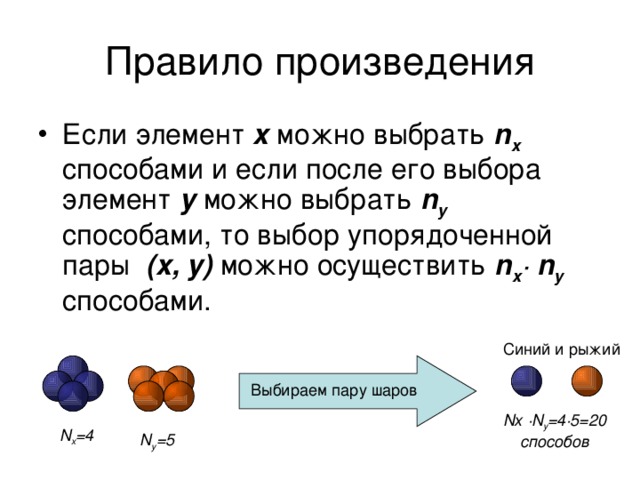
Правило произведения
- Если элемент x можно выбрать n x способами и если после его выбора элемент y можно выбрать n y способами, то выбор упорядоченной пары (x, y) можно осуществить n x ∙ n y способами.
Синий и рыжий
Выбираем пару шаров
Nx ∙N y =4∙5=20 способов
N x =4
N y =5
Пример 2
- В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
- 5*3=15
Пример 2. а) Сколько различных двузначных чисел можно составить из цифр 1,3,5,7,9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5 х1 =5
- Пример5 . Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
- а ) Сколько всего стран могут использовать такую символику?
- Решение : Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N= 4х3х2х1=24
- б ) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом?
- Решение : Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
- Пример7 . Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Коля и Оля оказались рядом?
- Решение : Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
- Пусть Коля сидит на краю. Место на краю можно выбрать 2 способами, после чего Олю можно посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
4х2х4х3х2х1=192 способами.
- По правилу сложения 48+192= 240 способов
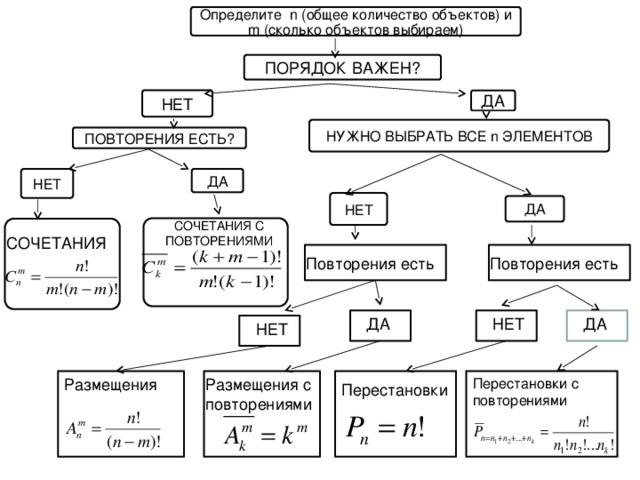
Определите n (общее количество объектов) и m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
НУЖНО ВЫБРАТЬ ВСЕ n ЭЛЕМЕНТОВ
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
НЕТ
ДА
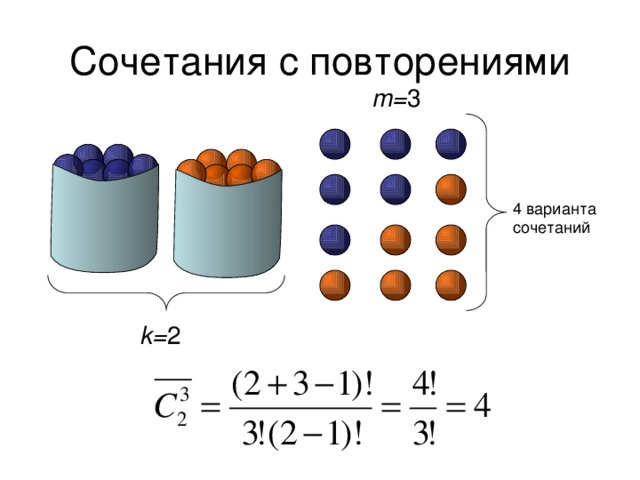
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
СОЧЕТАНИЯ
Повторения есть
Повторения есть
ДА
ДА
НЕТ
НЕТ
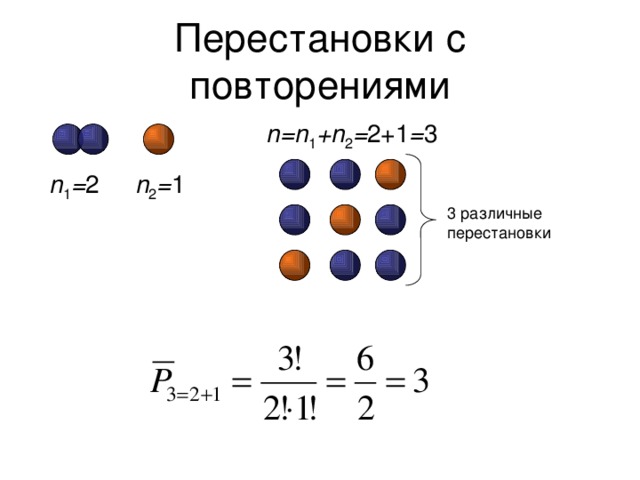
Перестановки с повторениями
Размещения с повторениями
Размещения
Перестановки
13
Перестановки
Перестановки без повторений
- Перестановками без повторений из n различных элементов называются все возможные последовательности этих n элементов. Число перестановок без повторений из n элементов равняется
по определению
Перестановки без повторений
6 различных перестановок
Сколькими способами 4 человека могут разместиться в четырехместном купе?
Задача 19 . Даны цифр: 1,2,3,4,5,6,7. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1234567, 2354167, 7546321 .
Перестановка-упорядоченное множество.
Число перестановок из n элементов вычисляют по формуле P n =n! .
По условию n=7
Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.
Перестановки с повторениями
- Перестановки с повторением из n элементов k типов
- число элементов 1-го типа n 1 ; число элементов 2-го типа n 2 ; …; число элементов k -го типа n k ,
- все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают
- подсчитывают так:
Перестановки с повторениями
n=n 1 +n 2 = 2+1 = 3
n 2 = 1
n 1 = 2
3 различные перестановки
Пример 4
- Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами это можно сделать, если в команде 11 человек?
Пример 5
- Сколько различных гирлянд можно сделать, если у нас 5 красных, 7 синих и 4 желтых светодиода?
Пример Даны цифр: 1,2,2,3,3,3,4,. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1223334, 4232331,2233314.
Некоторые числа при перестановке одинаковых цифр не меняются.
По условию n = 7, n1=2 , n2 =3
- Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
- Сколько различных гирлянд получится, если замкнуть гирлянду из предыдущей задачи в кольцо?
Размещения
(выборки)
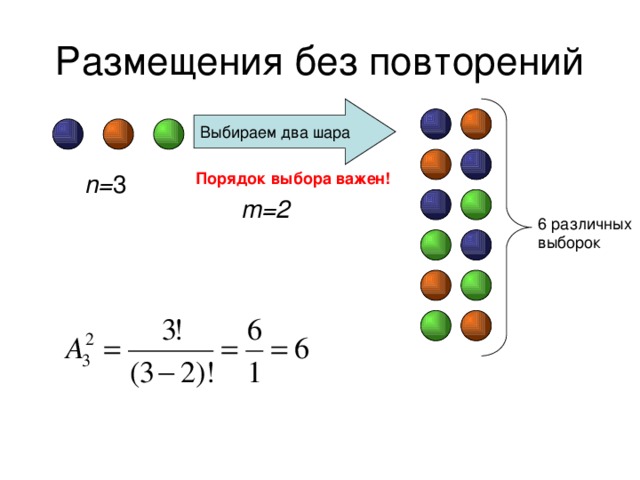
Размещения без повторений
- Размещениями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга или порядком следования элементов, или составом элементов.
- Число размещений без повторений из n элементов по m обозначается символом
Размещения без повторений
Выбираем два шара
n= 3
Порядок выбора важен!
m=2
6 различных выборок
Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин .
Пример
- Из группы в 15 человек выбирается 4 участника эстафеты 800+400+200+100. Сколькими способами можно расставить спортсменов по этапам эстафеты?
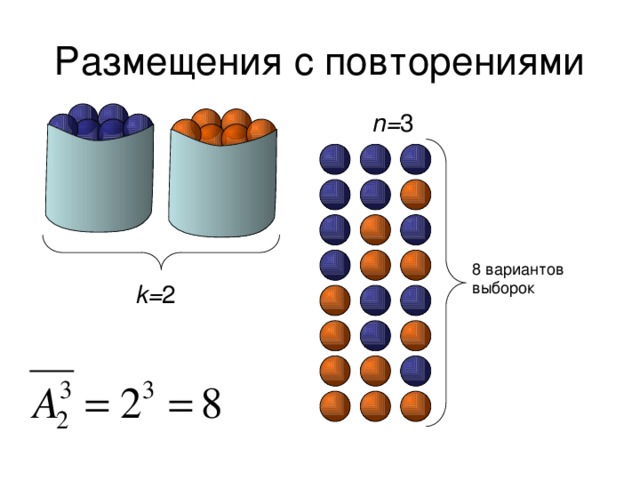
Размещения с повторениями
- Размещения с повторениями из элементов k типов по m элементов ( k и m могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличаются друг от друга или порядком следования элементов, или составом элементов.
Размещения с повторениями
n= 3
8 вариантов выборок
k= 2
Пример 8
- Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует четырехзначных «симпатичных» чисел?
- k=5 порядок важен
Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Сочетания
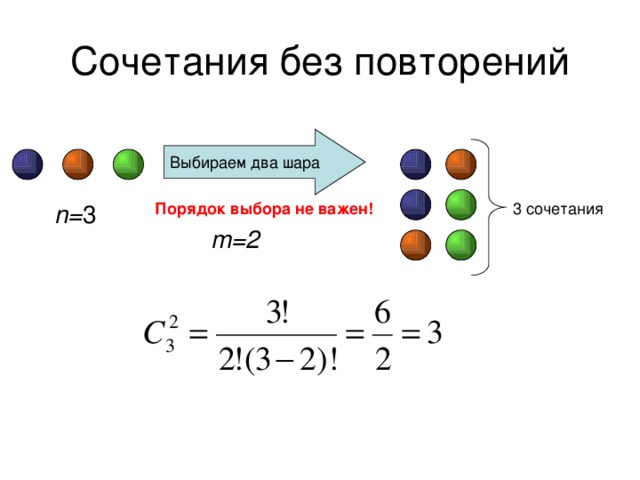
Сочетания без повторений
- Сочетаниями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга составом элементов.
Сочетания без повторений
Выбираем два шара
Порядок выбора не важен!
n= 3
3 сочетания
m=2
Пример 9
- Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков.
Сочетания с повторениями
- Сочетаниями с повторениями из элементов k типов по m элементов ( m и k могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличают друг от друга составом элементов.
Сочетания с повторениями
m= 3
4 варианта сочетаний
k= 2
Пример 10
В вазе стоят 10 красных и 4 розовых гвоздики. Все цветы на внешний вид одинаковы. Сколькими способами можно выбрать 3 цветка из вазы?
Решение Так как по условию задачи все цветы на внешний вид одинаковы, то мы получаем формулу без повторений. Вы выбираем цветы в букет, порядок выбора не важен, следовательно, мы получаем формулу сочетаний без повторений: два типа цветов, выбираем три цветка.
В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?
- Один выбор (анализ) элементов или несколько? Если один, то см. п.3
- Каким союзом варианты выбора (анализа) соединяются? «И» – правило произведения, «или» – правило суммы.
Для каждого выбора задаются следующие вопросы:
- Все элементы используются? Если «да», то это перестановки. Переходим к п. 5.
- Порядок выбора элементов важен? Если «да», то это размещения, «нет» – сочетания.
- Есть ли одинаковые элементы? Если «да» – то формула с повторениями, «нет» – без повторений.
Сколько различных гирлянд можно сделать из 10 светодиодов разного цвета?
При замыкании линии в кольцо перестановки, являющиеся циклическими сдвигами относительно друг друга, становятся одинаковыми. Возьмем, например, следующую перестановку и посмотрим, сколько других перестановок явлюяются ее циклическим сдвигом: 1. ккккксссссссжжжж 2. кккксссссссжжжжк 3. ккксссссссжжжжкк … 15. жжккккксссссссжж 16. жккккксссссссжжж Следовательно, все перестановки разбиваются на группы по 16 цепочек в группе. Итак, число кольцевых гирлянд будет
13
Пример 11
- Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?
- У людоеда в подвале томятся 25 пленников.
- а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин?
- б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?
Решение 25*24*23 = 13800 способов.
Заметим, что в предыдущем пункте каждую тройку пленников мы посчитали 3·2·1 = 6 раз. Поскольку теперь их порядок нам неважен, то ответом будет число 13800 : 6 = 2300.
Волонтеры разделились на две равные группы для розыска заблудившегося ребенка. Среди них только 4 знакомы с местностью. Каким числом способов они могут разделиться так, чтобы в каждую группу вошло 2 человека, знающих местность, если всего их 16 человек?
Решение Мы делим всех волонтеров на две равные группы, то есть выбираем участников первой группы, а все остальные переходят в другую группу. Один выбор. Теперь рассмотрим этот выбор первой группы. Выбор состоит из выбора волонтеров, знающих местность, и выбора волонтеров, незнающих местность. Следовательно, будем соединять эти два числа правилом произведения . Найдем число выборов волонтеров, знающих местность. Всего таких волонтеров 4 человека. Нам нужно 2. Порядок выбора не важен. Сочетания без повторений.
Найдем число выборов волонтеров, незнающих местность. Всего их 16-4=12 , выбираем шесть человек (ровно половину). Общее число выборов:
- Сколько существует натуральных чисел, меньших 256 10 , таких, что в записи каждого числа в двоичной системе счисления будет равное количество единиц и значащих нулей. В ответе укажите целое число.
Решение Переведем данное число из десятичной системы счисления в двоичную. 256 10 =100000000 2 Следовательно, числа меньше данного состоят из восьми, семи, шести, пяти, четырех, трех, двух и одного разряда.
1) Рассмотрим восьмиразрядные числа. 1ХХХХХХХ. Так как мы точно знаем сколько нулей и единиц, то мы используем формулу перестановки с повторениями.
2) Рассмотрим семиразрядные числа. Очевидно, что такие числа не удовлетворяют условию задачи, так как не могут состоять из одинакового числа единиц и нулей. Аналогичный вывод можно сделать о пятиразрядных, трехразрядных и одноразрядных числах.
3) Рассмотрим шестиразрядные числа. Рассуждая аналогично п.1 получаем:
4) Четырехразрядные числа.
5) Двухразрядное число только одно 10 2
Итак, у нас может быть или восьмиразрядное число, или шестиразрядное число, или четырехразрядное число, или двухразрядное число. Правило суммы.
Пример 15
- В коробке находятся 16 шариков – 4 красных, 4 синих и 8 черных. Из коробки наугад вынули два шарика. Какое из перечисленных сообщений несет в себе наибольший объем информации?
- Один из вынутых шариков – красного цвета, а другой – синего;
- Один из вынутых шариков – синего цвета, а другой – черного;
- Оба вынутых шарика красного цвета;
- Оба вынутых шарика черного цвета;
- Цвета вынутых шариков отличаются друг от друга;
- Вынуты шарики одного и того же цвета.
Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
Решение
В этой задаче нам обязательно нужно использовать цифры 2, 4 и 5. Но они могут стоять на разных местах и в разном порядке. У нас три «важные» и две «неважные» цифры в числе — два типа цифр. Это перестановки с повторениями.
Теперь посчитаем сколько различных перестановок «важных» цифр между собой. Это перестановки без повторений
Итак у нас 60 различных перестановок. Теперь посчитаем, сколько различных «неважных» цифр может быть в каждой из этих перестановок. Мы выбираем две «неважные» цифры из шести. Порядок выбора важен . Это размещения без повторений .
В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
- Решение:
- Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380.
- Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
19. Задачи на теорию чисел
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по комбинаторике
Задание
1
#2209
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (12). Сколько чисел выписал Боря?
Различные делители числа (12) – это (1), (2), (3), (4), (6), (12), то есть 6 чисел.
Ответ:
(6)
Задание
2
#2210
Уровень задания: Легче ЕГЭ
Шесть пчёлок прилетели опылять два разных цветочка. Они договорились, что один цветочек будет опылять ровно одна пчёлка. Им предстоит решить, кому достанутся эти два цветочка на опыление. Сколькими способами они могут распределить двух пчёлок по двум разным цветочкам?
На первый цветочек может претендовать любая из 6 пчёлок. Как только выбрана пчёлка, которая будет опылять первый цветочек, на второй цветочек может претендовать любая из 5 оставшихся пчёлок.
Какую бы пчёлку не назначили на первый цветочек, после этого назначения остаётся 5 различных возможных вариантов назначить пчёлку на второй цветочек. То есть каждый из 6 вариантов для первого цветочка даёт 5 различных вариантов для второго цветочка.
Получаем, что всего вариантов – “шесть раз по пять”( ), то есть (6cdot 5 = 30).
Ответ:
(30)
Задание
3
#2211
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (120). Сколько чисел выписал Боря?
Разложим (120) на простые множители: (120 = 2^3cdot 3cdot 5). Все делители числа (120) равны (2^acdot 3^bcdot 5^c), где
(a) может принимать значения (0, 1, 2) или (3),
(b) может принимать значения (0) или (1),
(c) может принимать значения (0) или (1).
При этом если тройки ((a_1, b_1, c_1)) и ((a_2, b_2, c_2)) не совпадают, то числа (2^{a_1}cdot 3^{b_1}cdot 5^{c_1}) и (2^{a_2}cdot 3^{b_2}cdot 5^{c_2}) – различны.
Таким образом, у числа (120) столько же различных делителей, сколько существует различных троек вида ((a, b, c)), где (a) принимает одно из четырёх значений, (b) принимает одно из двух значений, (c) принимает одно из двух значений, то есть количество подходящих троек равно (4cdot 2cdot 2 = 16).
Ответ:
(16)
Задание
4
#2212
Уровень задания: Легче ЕГЭ
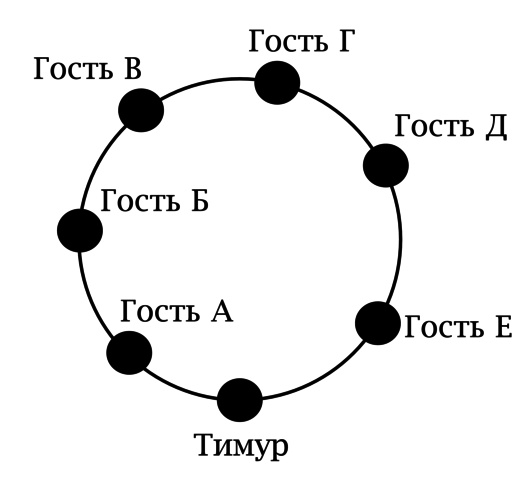
В честь своего дня рождения Тимур накрыл праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей, ведь у него имеется шесть разных гостевых стульев (которые уже стоят у стола и двигать их он не намерен). Сколькими способами он может это сделать?
Так как место Тимура за столом фиксировано, то можно считать, что его за столом не будет (ответ от этого не изменится).
Пусть Тимур как-то занумеровал стулья. Тогда на первый стул может претендовать любой из 6 гостей.
Какой бы из 6 гостей не занял первый стул, на второй стул может претендовать любой из оставшихся на этот момент 5 гостей. [dots]
На последний шестой стул будет претендовать один единственный гость.
В итоге: каждый из 6 вариантов для первого стула даёт пять различных вариантов для второго стула и т.д., то есть всего есть (6! = 1cdot 2cdot 3cdot 4cdot 5cdot 6 = 720) различных способов рассадить гостей.
Ответ:
(720)
Задание
5
#2213
Уровень задания: Легче ЕГЭ
Боря выписал все различные делители числа (2016). Сколько чисел выписал Боря?
Разложим (2016) на простые множители: (2016 = 2^5cdot 3^2cdot 7). Все делители числа (2016) равны (2^acdot 3^bcdot 7^c), где
(a) может принимать значения (0, 1, 2), (3), (4) или (5),
(b) может принимать значения (0), (1) или (2),
(c) может принимать значения (0) или (1).
При этом если тройки ((a_1, b_1, c_1)) и ((a_2, b_2, c_2)) не совпадают, то числа (2^{a_1}cdot 3^{b_1}cdot 7^{c_1}) и (2^{a_2}cdot 3^{b_2}cdot 7^{c_2}) – различны.
Таким образом, у числа (2016) столько же различных делителей, сколько существует различных троек вида ((a, b, c)), где (a) принимает одно из шести значений, (b) принимает одно из трёх значений, (c) принимает одно из двух значений, то есть количество подходящих троек равно (6cdot 3cdot 2 = 36).
Ответ:
(36)
Задание
6
#2214
Уровень задания: Легче ЕГЭ
В честь своего следующего дня рождения Тимур планирует накрыть праздничный стол на себя и шестерых гостей. Тимур хочет сесть во главе стола (его место фиксировано). Он думает, как ему рассадить гостей на шесть одинаковых гостевых стульев (ему не важно, на какой гостевой стул кто сядет, важно лишь кто будет соседями каждого гостя). Сколькими способами он может это сделать?
Справа от Тимура может сесть любой из 6 гостей. После того, как Тимур определится со своим правым соседом, на место справа от правого соседа Тимура может сесть любой из 5 гостей и т.д.
В итоге сосед, сидящий слева от Тимура будет, определён однозначно, то есть имеется (6! = 720) вариантов, но не все они различны.
Пусть Тимур зафиксировал гостя, который будет его соседом справа, зафиксировал и его соседа справа и т.д. Он получил некоторую последовательность, в которой он будет сажать гостей, двигаясь в одну сторону вдоль граничной окружности стола.
Но если он будет сажать гостей в той же последовательности, двигаясь в другую сторону вдоль окружности, то при этом для каждого гостя состав его соседей не изменится.
Таким образом, когда мы получили (6!) вариантов, каждый вариант рассадки мы учли ровно по два раза, следовательно, у Тимура есть (dfrac{6!}{2} = 360) способов рассадить гостей.
Ответ:
(360)
Задание
7
#2215
Уровень задания: Легче ЕГЭ
Белоснежка и семь гномов садятся за круглый стол. Известно, что Ворчун не хочет сидеть рядом с Весельчаком и Соней. Сколькими способами их можно рассадить за стол так, чтобы Ворчуна всё устраивало, если считать, что не важно, кто на какое место сядет, важно только, кто будет соседями каждого гнома и Белоснежки?
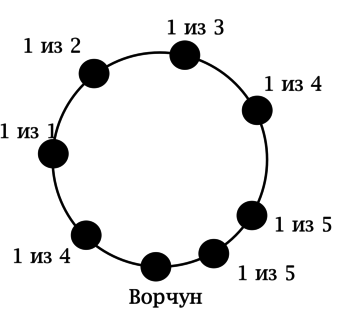
Ответ не зависит от того, в каком порядке мы будем сажать Белоснежку и гномов за стол. Пусть первым за стол садится всегда Ворчун. Тогда его правым соседом может быть один из 5 кандидатов. После того, как его правый сосед выбран, на роль левого соседа Ворчуна могут претендовать 4 кандидата.
Далее имеем ситуацию как на рисунке:
Таким образом, есть (1cdot 2cdot 3cdot 4cdot 4cdot 5cdot 5 = 2400) способов, но не все они различны. На самом деле каждый способ мы учли по два раза (если рассаживать кандидатов по часовой стрелке в определённой последовательности и если рассаживать их против часовой стрелки в той же последовательности, то рассадки будут одинаковыми).
В итоге есть (2400 : 2 = 1200) способов, которыми можно рассадить за стол гномов и Белоснежку так, чтобы Ворчуна всё устроило.
Ответ:
(1200)
При подготовке к сдаче Единого государственного экзамена по математике у большинства школьников возникают сложности с решением задач из раздела «Комбинаторика». Ученикам нелегко даются способы вычисления распределения элементов, поэтому стоит обратить на данную тему особое внимание.
Выбирайте образовательный портал «Школково» для качественной подготовки к аттестационному тестированию по математике!
Чтобы знать все необходимые формулы раздела «Комбинаторика» и быстро распределять элементы, воспользуйтесь нашим удобным онлайн-сервисом. На сайте вы найдете все необходимое для грамотной подготовки к ЕГЭ: правила, примеры с решениями и индивидуальные задания, которые постоянно обновляются и дополняются. Вся информация собрана преподавателями «Школково». Они систематизировали и изложили ее в максимально понятной форме, поэтому проблем даже с упражнениями сложного уровня у учеников не возникнет.
Мы предлагаем наиболее удобный метод повторения и усвоения информации по трудным тематикам. Для того, чтобы эффективно подготовиться к сдаче заключительного экзаменационного тестирования, рекомендуем начать с основ — легких задач по распределению элементов, постепенно переходя к сложным. Благодаря такому подходу каждый ученик сможет выявить для себя наиболее сложные типы упражнений и при подготовке уделить им больше времени.
Перед тем, как приступать к выполнению заданий, ознакомьтесь с формулами в разделе «Теоретическая справка». Потренируйтесь, решая типовые примеры, и переходите в раздел «Каталоги». В нем вы найдете большое количество упражнений различного уровня сложности и сможете выбрать подходящие для вас варианты.
При возникновении трудностей выпускник может отложить решение задачи по комбинаторике, добавив ее в «Избранное». Позже к ней можно вернуться для повторного изучения самостоятельно или уже с помощью преподавателя.
Если вы понимаете, что задания легкого и среднего уровня даются вам без проблем, смело пропускайте их и переходите к сложным упражнениям.
Начните готовиться к Единому государственному экзамену уже сейчас на портале «Школково»! Уделяйте достаточное количество времени выполнению заданий на нашем сайте, и результат не заставит себя ждать. С нашей помощью в скором времени вы сможете выполнять упражнения на сочетание чисел, с которыми ранее не справлялись.
Занятия на портале «Школково» совершенно бесплатны. Онлайн-сервисом могут пользоваться не только школьники из Москвы, но и других городов России. Просто зарегистрируйтесь на сайте для сохранения личных достижений и начинайте занятия! Желаем успехов в подготовке к ЕГЭ!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Комбинаторные задачи в ЕГЭ
Комбинаторные методы в ЕГЭ по информатике применяются для решения задачи №10 (бывшая В4). Рассмотрим решение типичных задач, с использованием комбинаторных приемов.
Решим задачу под номером В4 из демонстрационной версии ЕГЭ по информатике 2014 года.
Задача. Для передачи аварийных сигналов договорились использовать специальные цветные сигнальные ракеты, запускаемые последовательно. Одна последовательность ракет – один сигнал; в каком порядке идут цвета – существенно. Какое количество различных сигналов можно передать при помощи запуска ровно пяти таких сигнальных ракет, если в запасе имеются ракеты трёх различных цветов (ракет каждого вида неограниченное количество, цвет ракет в последовательности может повторяться)?
Решение.
Ракеты могут быть трех различных цветов, при этом в одной последовательности пять ракет. Значит, рассматривается выборка объема пять из трех элементов (n = 3, k = 5).
Определим комбинаторную схему. Два положения в условие задачи:
- «в каком порядке идут цвета – существенно»;
- «цвет ракет в последовательности может повторяться»;
указывают на то, что – это размещения с повторениями.
Ответ. 243
Решим задачу №10 из демоверсии ЕГЭ по информатике 2016 года.
Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует 5-буквенные слова, в которых есть только буквы П, И, Р, причём буква П появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?
Решение.
1) буква «П» появляется ровно 1 раз, значит она может находиться на одной из 5 позиций в слове.
2) буквы «И» и «Р» заполнят остальные 4 позиции. Рассмотрим выборки объема 4 из 2 элементов (k = 4, n = 2). Кодовые слова могут отличаться как порядком следования букв, так и составом, значит, комбинаторная схема – размещения с повторениями. Найдем число таких размещений:
3) применим правило произведения: 5 * 16 = 80
Ответ. 80
Типичная тренировочная задача №10 для подготовки к ЕГЭ по информатике.
Задача. Вася составляет 5-буквенные слова из четырехбуквенного алфавита {A, C, R, T}, причём буква А используется в каждом слове ровно 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом, считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Решение.
1) пронумеруем позиции в слове, тогда варианты расположений букв «А» можно представить в качестве неупорядоченного выбора двух цифр из пяти. Значит, комбинаторная схема — сочетания без повторений
2) остальные допустимые символы будут занимать 3 позиции. Эти выборки объемом 3 из 3 элементов будут отличаться как порядком следования, так и набором символов. Очевидно, комбинаторная схема – размещения с повторениями.
3) применим правило произведения: 27 * 10 = 270
Ответ. 270
Примеры решений задач по комбинаторике
Комбинаторика — это наука, с который каждый встречается в повседневной жизни: сколько способов выбрать 3 дежурных для уборки класса или сколько способов составить слово из данных букв. В целом, комбинаторика позволяет вычислить, сколько различных комбинаций, согласно некоторым условиям, можно составить из заданных объектов (одинаковых или разных).
Как наука комбинаторика возникла еще в 16 веке, а теперь ее изучает каждый студент (и зачастую даже школьник). Начинают изучение с понятий перестановок, размещений, сочетаний (с повторениями или без), на эти темы вы найдете задачи и ниже. Наиболее известные правила комбинаторики — правила суммы и произведения, которые чаще всего применяются в типовых комбинаторных задачах.
Ниже вы найдете несколько примеров задач с решениями на комбинаторные понятия и правила, которые позволят разобраться с типовыми заданиями. Если есть трудности с задачами — заказывайте контрольную по комбинаторике.
Не получается решить задачи? Поможем недорого!
Полезная страница? Сохрани или расскажи друзьям
Калькуляторы онлайн и примеры
|
|
Еще: Комбинаторика в Excel
Задачи по комбинаторике с решениями онлайн
Задача 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд
она выдает по одному фрукту. Сколькими способами это может быть сделано?
Задача 2. Предприятие может предоставить работу по одной специальности 4
женщинами, по другой — 6 мужчинам, по третьей — 3 работникам независимо от пола.
Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6
женщин и 8 мужчин?
Задача 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
Задача 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?
Задача 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.
Задача 6. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
Задача 7. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Задача 8. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?
Задача 9. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
Задача 10. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается?
Мы отлично умеем решать задачи по комбинаторике
Готовые примеры
Нужны решенные задачи по комбинаторике? Найди в решебнике: