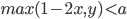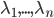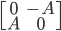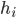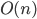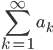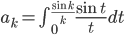ВСЕ ЭЛЕКТРОННЫЕ МАТЕРИАЛЫ ДЛЯ ПОДГОТОВКИ | ШАД ЯНДЕКСА
За время подготовки в ШАДу накопилось очень много материалов. Это и задачи с экзаменов с решениями, и задачи с собеседований, и все необходимые книги, конспекты, шпаргалки и прочее. Все это доступно по этой ссылке.
Что есть материалах по подготовке к ШАДу:
- 1_Online_Test – мои решение задач с теста на Питоне
- 2_Exams – задачи с экзаменов 2012-2018 и их решения. Еще советую посмотреть supershad – там формат поудобнее.
- 3_Interviews – задачи с интервью прошлых лет и их решения. Еще источник
- 4_Books – все книги, перечисленные в программе для поступления в ШАД, плюс еще много разных полезных книг, которыми я пользовался при подготовке
- 5_Formulae – различные конспекты, формулы и шпаргалки. Если нужно освежить в памяти отдельные темы или нет времени целиком прочитать книги
- 6_Problemsets – задачи, близкие к экзаменам и интервью в ШАД. Сейчас там лежат листки по теорверу ФКН Вышки. Добавлю еще материалы, если найду
- More_materials – дополнительные материалы по подготовке, на которые наткнулся в Интернете. Сам не успел ими воспользоваться, но подозреваю, что интересные задачи там найдутся
Папка большая (700 МВ), поэтому не знаю, сколько проживет ссылка. Пишите в комментах, постараемся ее оживлять.
Если еще не подписались на наш канал в YouTube, самое время это сделать вот здесь! В начале августа узнаем, к чем привела вся эта эпопея =)
Similar posts
Карьера
29.01.2018
Как попасть в инвестиционный банк. Личный опыт
Расскажу, как я подходил к отбору в инвестиционные локальные и Bulge Bracket банки, попал в ВТБ и Goldman Sachs, а также поделюсь материалами для подготовки. [Читать подробнее об курсе Investment Banking Interview Prep] О себе После окончания МГИМО получил оффер в IBD и Structuring департаменты банка VTB Capital. В итоге присоединился к команде Structuring, где занимался решениями в области сложных M&A / Private Equity сделок, а также структурным финансированием и управлением рисками на валютных, процентных и товарно-сырьевых рынках. Уже через …

CV | CL | Fit
17.10.2015
Why Consulting?
Нужен структурированный ответ, а не поток сознания Прежде чем отвечать на этот вопрос, стоит сделать небольшое исследование (поиск в интернете, общение с консультантами, профессиональная литература) и понять для себя, что представляет из себя работа в консалтинге и какие её аспекты тебе интересны больше всего и / или перекликаются с твоим предыдущим профессиональным или студенческим опытом. О том, что такое консалтинг, написано множество книг, и настоятельно рекомендую прочитать несколько из них, как минимум The McKinsey Approach to Problem-Solving (всего 27 страниц!). В целях …

MBA
01.11.2015
01. MBA: выбор программы, план подготовки
Первая статья из серии “Из Бутово в Стэнфорд” Ноябрь 2015. Я начинаю рассказ о поступлении на MBA в режиме (почти) реального времени! Сидя дома в Южном Бутово (отсюда название), по выходным буду последовательно готовить пакеты документов на программы Stanford GSB MBA и Wharton MBA 2016-2018 и параллельно рассказывать вам о всех деталях подготовки, трудностях, с которыми я буду сталкиваться, полезных материалах и идеях и прочих life hacks – и, конечно, о всех шишках, которые набью по дороге. В итоге из …

Привет! Меня зовут Азат, я студент 3 курса Факультета Компьютерных Наук ВШЭ. На днях ко мне обратился знакомый с Экономики ВШЭ и попросил помочь с решением задач вступительного экзамена в ШАД. Мы с однокурсником Даниилом посмотрели на задания, они показались нам довольно сложными, но очень интересными, захотелось поломать над ними голову. В итоге мы прорешали 1 из вариантов 2019 года и хотим показать наши решения миру.
Задача 1
Заполните третий столбец матрицы
если известно, что это матрица ортогональной проекции на некоторую плоскость.
Решение
Назовём эту матрицу
, воспользуемся свойством ортогональных проекторов:
и займёмся арифметикой:
Нам необязательно считать 2 и 3 столбец, информации в первом достаточно для решения, на экзамене так можно было бы сэкономить время.
Получаем тривиальную систему:
Таким образом, мы заполнили 3 столбец, получив в итоге матрицу
Задача 2
Что вы можете сказать о сходимости (абсолютной или условной) ряда
, если известно, что ряд
сходится (а) абсолютно, (б) условно?
Решение
Введём обозначения:
Докажем вспомогательное утверждение (1).
Ряд
сходится
сходится
.
Для этого представим второй ряд как
(кроме, может быть, выколотой точки -a).
Заметим, что ряд можно представь как
, где
. Отбросим члены до
, это не повлияет на сходимость. Тогда выполнены все условия признака Дирихле сходимости ряда. А именно:
1. Последовательность частичных сумм
ограничена, так как ряд
сходится.
2.
3.
Значит, ряд сходится. Хорошо, теперь приступим к заданию.
a) T сходится абсолютно, то есть ряд
сходится. Разобьём эту сумму:
Мы можем без влияния на сходимость заменить первые
элементов, тогда получим:
Отсюда, пользуясь утверждением (1), получаем что
сходится.
Выкинем первые
членов каждого из этих рядов (опять же, это не влияет на их сходимость) и рассмотрим разность:
А мы уже знаем, что ряд
сходится. Тогда получается, что ряд
— это сумма 2 сходящихся рядов. Ну значит и он сам сходящийся.
б)
сходится условно, то есть ряд
сходится, а ряд
— нет.
Докажем, что тогда ряд
тогда тоже сходится условно.
Опять же, из сходимости ряда
с помощью утверждения (1) следует сходимость ряда
. Из тех же соображений о разности, что и в предыдущем пункте, применённых теперь к
и
, получим, что ряд
сходится. Осталось лишь доказать, что ряд
не сходится.
Будем действовать от противного. Пусть
сходится. Тогда, отбросив первые
членов
и
, поймём, что:
так как
.
Но эти ряды положительные, поэтому если сходится больший из них, то сходится и меньший. Значит
сходится, противоречие.
Задача 3
Алёна очень любит алгебру. Каждый день, заходя на свой любимый алгебраический форум, она с вероятностью
находит там новую интересную задачу про группы, а с вероятностью
интересную задачку про кольца. С вероятностью
новых задач на форуме не окажется. Пусть
— это минимальное число дней, за которые у Алёны появится хотя бы одна новая задача про группы и хотя бы одна про кольца. Найдите распределение случайной величины
. В ответе должны участвовать только компактные выражения (не содержащие знаков суммирования, многоточий и пр.).
Решение
Нам нужно найти
. Для этого надо понять на пальцах, в каком случае
. Первый случай — когда в каждый из предыдущих
дней либо не было задач, либо были только про группы, а в
-ый попалась задача про кольца. Второй случай — когда в каждый из предыдущих
дней либо не было задач, либо были только про кольца, а в
-ый попалась задача про группы. На самом деле мы оба раза учли не подходящий случай, когда все предыдущие
дней задач не было вообще. С поправкой на это ответ будет таким:
Задача 4
Дан массив
вещественных чисел, отсортированный по возрастанию, а также числа
,
,
. Предложите алгоритм, строящий массив
, состоящий из чисел
, где
, также отсортированный по возрастанию. Ограничение по времени —
, по дополнительной памяти —
.
Решение
,
.
Сначала предположим, что
.
Изобразим нашу функцию.
Заметим, что:
1.
после применения
порядок остаётся прежним.
2.
после применения
порядок будет обратным.
То есть для «правой» части после применения к каждому значению функции
подпоследовательность остаётся правильно отсортированной, для левой части она становится отсортированной в обратном порядке.
Тогда бинпоиском за
найдём место в
, в котором массив делится на эти самые доли. Сделаем reverse левой части. Применим ко всем элементам функцию
. Получили 2 отсортированных массива. С помощью процедуры merge за
по времени и по памяти получим целиком отсортированный массив.
В случае
решим задачу для
, а затем сделаем reverse всего массива и домножим каждое значение
на -1. Получим правильный результат.
В случае
порядок зависит от знака
.
1.
2.
И построение в этом случае сводится к применению функции ко всем значениям. Только в случае
за
надо ещё сделать reverse. В случае когда
порядок уже правильный.
Задача 5
Вещественнозначная функция
определена на отрезке
и дифференцируема на нём. Докажите, что найдётся точка
, для которой
Решение
Давайте докажем от противного. Пусть
.
Сначала посмотрим, что будет происходить при равенстве:
Обозначим эту функцию как
. Заметим, что
. То есть мы пользуемся тем, что функция
растёт не менее быстро, получаем, что и разница с изначальной точкой будет не меньше, чем у
.
Функция
у нас имеет константу
. Примем значение этой константы таким, что
. Тогда:
Мы знаем, что
. Тогда на
существует хотя бы одна точка
такая, что
(потому что шаг
). В этой точке
. При этом мы знаем, что
.
Получили, что в какой-то из точек
функция уходит на бесконечность. А значит функция терпит разрыв, то есть не является непрерывной, а это дано нам в условии. Получили противоречие.
Задача 6
Квадратная вещественная матрица
такова, что
, где
— многочлен с ненулевым свободным членом. Докажите, что
обратима. Верно ли, что для любого оператора
найдётся многочлен
и некоторый базис, в котором матрица
удовлетворяет условию
?
Решение
В начале, покажем, что
, распишем подробно:
Отсюда можно получить, что
.
1. Будем доказывать от противного. Пусть матрица
необратима. Тогда существует вектор
такой, что
. Тогда ещё можно сказать, что
. Теперь распишем это:
Теперь пользуемся тем, что
:
Но мы знаем, что
. Получили противоречие.
2. Рассмотрим линейный оператор
с матрицей
в стандартном базисе.
Тогда в любом другом базисе матрица будет иметь вид
, где
— матрица перехода.
Заметим, что
, значит
. Тогда
.
Пусть
. Так как все степени выше 1 обнуляются,
.
При этом
, так как иначе, пользуясь первым пунктом, можем получить, что матрица
обратима, а это не так (т.к.
).
Вспомним, что
.
Распишем:
.
Теперь рассмотрим несколько случаев:
1.
:
Подставим в другое место:
Наша матрица размерности всего 2, поэтому вполне можем расписать поэлементно:
Но мы знаем что
. Распишем определитель:
.
Получили противоречие. Матрица оператора
в стандартном базисе ненулевая, она не может быть нулевой в другом базисе.
2.
:
Тогда после подстановки получаем
. Тогда
.
При этом
И снова получаем противоречие.
3.
.
Здесь тогда тоже получаем, что
.
Значит нет многочлена и базиса в котором матрица
оператора
представима, как
. Что и требовалось доказать.
Задача 7
Дан граф с
вершинами. Известно, что для любых
вершин в графе есть цикл длины
, содержащий эти вершины. Докажите, что найдётся
вершин, попарно соединённых рёбрами друг с другом.
Решение
Сначала покажем, что диаметр графа
.
Выберем 2 самые удалённые друг от друга вершины
и
и 3 произвольные. По условию дано, что любые 5 вершин составляют цикл. Значит есть и цикл, состоящий из этих 5 вершин. В этом цикле путь от
до
будет максимум 2 (видно на картинке). Значит
.
Теперь зафиксируем произвольную вершину
. Мы уже сделали вывод, что до любой другой вершины графа расстояние от
равно либо 1, либо 2. Покажем, что на «втором уровне» не больше
вершин:
Будем доказывать от противного. Пусть есть вершины
. Возьмём ещё одну произвольную вершину
. Снова, эти вершины составляют цикл. Но тогда, как бы мы ни разместили вершины в этом цикле, расстояние от
до хотя бы одной из вершин
,
или
будет равно 1, получили противоречие.
Получили,
, то есть каждая вершина имеет степень не меньше
.
Теперь попробуем с этой информацией найти клику (вершины, попарно соединённые рёбрами — то, что требуется в условии) длины 10. Найти клику размера 10 в графе
— это то же самое, что найти независимое множество (то есть вершины, между которыми вообще нет рёбер) того же размера 10 в обратном графе
.
Рассмотрим
. Если в изначальном графе
у нас степень вершины
, то в обратном
.
Тогда обратный граф состоит из набора «цепей» (1) и «циклов» (2). Другие структуры невозможны из-за жёсткого ограничения
.
В компонентах вида (1) можно найти независимое множество размера
, вида (2) —
.
Пусть
— общее количество компонент в обратном графе, а
— количество «цепочек». Тогда размер максимального независимого множества будет равен:
Понятно, что это число будет минимальным, если мы по возможности будем округлять вниз, при этом с наибольшими потерями. Этого можно добиться, например, взяв 10 компонент размера 3. Тогда получим нижнюю оценку.
То есть мы показали, что в обратном графе
максимальное независимое множество имеет размер 10 или больше, то есть в графе
существует клика размера 10 или больше. Что и требовалось доказать.
Задача 8
Найдите предел
Решение
Здесь нужно по виду формулы догадаться о теории вероятностей.
Введём случайную величину:
Пусть монетка неправильная — орёл выпадает с вероятностью
.
Тогда
это в точности значение под знаком суммирования:
— это количество возможных размещений
орлов (ещё 1 выпадает в конце).
— это вероятность выпадения орлов на выбранных позициях.
— это вероятность выпадения решек на оставшихся позициях.
Тогда наш предел превращается в
Заметим, что вероятность события
можно интерпретировать по-другому. Это вероятность того, что за
бросков выпадет
орлов.
Введём новую случайную величину:
При этом величину можно представить как сумму элементарных:
Тогда
Применим центральную предельную теорему к
. Получим:
Вспоминаем, что у нас нормальное распределение симметрично относительно матожидания и получаем итоговый ответ:
Заключение
В целом экзамен довольно сложный. Мой знакомый пожаловался, что подготовиться непросто. Это действительно так — нужно не только знать обширную математическую теорию, но и иметь навык решения олимпиадных задачек, в ШАДе дают именно такие. Поэтому для подготовки нужно много тренироваться, вспоминать теорию и набивать руку.
Если у вас есть другие идеи решения задач или какие-то замечания, смело пишите мне в телеграм @Azatik1000. Всегда рад ответить!
Азат Калмыков, куратор ШАД Helper
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Экзамены в ШАД — это серьёзная проверка и стресс даже для абитуриентов с хорошей подготовкой: нужно глубоко знать теорию математики, программировать и решать олимпиадные задачи. С наскока освоить такой объём информации не получится. Поэтому первым делом внимательно изучите программу на сайте и определите, какие темы вы знаете хорошо, а что нужно подтянуть.
Дисциплина — ключ к успеху
Начинайте готовиться сразу, как только определились с темами. Чётко распишите план подготовки, учитывая текущую загрузку, и обязательно сделайте скидку на то, что всё может пойти не так. Занимайтесь регулярно, но без фанатизма. Не нужно зубрить 24/7: в какой-то момент наступит перенасыщение знаниями и от подготовки не будет толка.
Хорошее самочувствие тоже часть подготовки. Не забывайте переключаться и делать передышки. Это поможет не перегореть и сохранить силы для поступления.
Выбор трека как стратегия
Есть разные подходы к подготовке в зависимости от выбранного трека, но база неизменна. Повторите все формулировки и определения из программы, откройте варианты и контесты прошлых лет — и решайте все задачи, которые с ходу не даются. Навыки программирования оттачивайте на LeetCode, Codeforces или TopCoder, а умение рассуждать — объясняя решение задач друзьям, далёким от математики. Тренируйтесь, пока не начнёте описывать выводы стройно и понятно, на собеседованиях, помимо знаний, оценивается умение излагать ход мыслей. Учитесь задавать вопросы по задаче, это поможет, если запутаетесь в решении.
Не злоупотребляйте готовыми разборами. Во-первых, в интернете многие задачи, особенно по теории вероятностей, разбираются неправильно. Во-вторых, заучивание готового не поможет на экзаменах. Лучше просидеть над задачей три дня, самостоятельно прийти к какому-то некрасивому решению и только после этого прочитать правильное. Так вы запомните его гораздо лучше и сможете объяснить.
— Михаил Берновский, студент 1-го курса ШАДа, альтернативный трек.
Насколько глубоко погружаться в каждую тему, зависит от того, на какой трек вы поступаете. Если на классическом треке ожидается, что вы понимаете связь между размерностью ядра, размерностью образа и кратностью нуля как собственного значения матрицы, то на альтернативном треке достаточно помнить, что для нахождения ядра нужно решить систему. Поступая на альтернативный трек, нужно понимать, как что-то посчитать, а поступая на классический — нужно уметь свободно рассуждать на тему решения и на близкие темы.
Но это не значит, что альтернативный трек — лёгкий способ попасть в ШАД. При поступлении на него требуется опыт в IT: промышленная разработка или исследования в области data science.
Классический трек и три математических столпа
Есть три больших области знаний, в которых надо ориентироваться: математический анализ, линейная алгебра и теория вероятностей. Хорошая стратегия — досконально изучить хотя бы две, а лучше все три.
Я поступала в ШАД на 4-м курсе мехмата, поэтому математику более-менее помнила. Из книг читала «Комбинаторику» Виленкина и «Основы теории вероятностей» Жуковского. Но это всё не помогает, пока не решишь минимум 100 задач на каждый жанр.
— Евгения Елистратова, выпускница ШАДа, разработчица в Яндекс Погоде.
В матанализе огромное количество теории, но для успешного прохождения экзаменов важнее решать задачи, очень много задач. Без умения хорошо считать не обойтись: нужно уметь брать интегралы, дифференцировать, находить минимумы и максимумы.
Линейная алгебра также нужна во многом на уровне языка. Теория пригодится ровно настолько, чтобы хорошо решать задачи. На практике важнее всего будет уметь работать с матрицами, но вы сильно выиграете, если сможете, глядя на абстрактные матричные выражения, вспомнить соответствующую теорию.
К экзамену по теории вероятностей, в отличие от матанализа и линейной алгебры, готовиться нужно намного основательнее. Есть много условий и ограничений в теоремах, которые важно повторить. Например, есть разные типы сходимости, и нужно помнить, какой из какого следует, какой — в центральной предельной теореме, а какой — в законе больших чисел. Желательно также повторить основные распределения и уметь с ними работать.
Альтернативный трек: алгоритмы и IT-опыт
Если вы выбрали альтернативный трек, то бóльшую часть математической теории можно опустить, максимально сосредоточившись на написании кода и алгоритмах.
Хотя совсем без математики не обойтись. Необходимо уметь объяснять математические задачи, а также знать базовые алгоритмы и определения из матанализа и линейной алгебры. Как минимум, дифференцировать точно нужно уметь.
Я поступал в ШАД через несколько лет после окончания вуза и понимал, что не конкурент свежим выпускникам мехмата. Поэтому сразу выбрал альтернативный трек. На всю программу по математике у меня времени не было, и я стал решать ШАДовские задачи с прошлых экзаменов. Параллельно читал разборы, чтобы освежить теорию.
— Леонид Курахтенков, студент 1-го курса ШАДа, альтернативный трек.
Задачи по теории вероятностей здесь будут немного проще, чем в классическом треке. Скорее всего, потребуется вычислить дискретную вероятность — решить «задачу с цветными шариками». Также нужно будет показать, что вы умеете рассуждать логически, не путаете причину и следствие и не считаете, что пример доказывает утверждение.
Повторите теорию алгоритмов и структур данных: сортировки, обходы графов, устройство хэш-таблиц и «жадные» алгоритмы. Рекомендуем пройти тренировки по алгоритмам: в них собрана хорошая база теории, а также задачи с разбором для прокачки практических навыков.
Что касается машинного обучения, то здесь достаточно разбираться в основах. Строить сложные модели, требующие больших вычислительных ресурсов, на экзамене не потребуется, но нужно уметь анализировать данные и понимать, как решаются нетривиальные задачи обучения с учителем и без.
Какой опыт необходим для поступления на альтернативный трек? В первую очередь, конечно, индустриальная разработка, ML и продуктовая аналитика. Если у вас есть исследовательский опыт или опубликованные научные статьи, расскажите об этом в своей анкете и на собеседовании.
Как определить мотивацию
Итак, вы прошли все этапы, осталось собеседование по мотивации. Как к нему подготовиться и о чём говорить с куратором? Сначала честно ответьте на вопрос: «Зачем вам ШАД». Вы хотите подняться на новый карьерный уровень, сменить профессиональный трек или углубиться в то направление, которое уже изучаете?
Если вы учитесь в вузе на математической специальности и ищете прикладное применение своим знаниям в IT, то ШАД поможет объединить теорию и практику.
ШАД — это хорошая возможность развиться в профессиональном плане как дата-саентист или разработчик машинного обучения. В университете я изучаю науку, а ШАД даёт этой базе конкретное практическое применение.
— Константин Гордеев, студент 1-го курса ШАДа, классический трек.
Сформулируйте мотивацию заранее, так вы поймёте, какие моменты подсветить на собеседовании, а что звучит не слишком убедительно. Обдумайте на берегу, готовы ли вы вкладываться в учёбу на 200%: важно показать, что вы не просто загорелись идеей поступить в ШАД, но и полны решимости трудиться два года. И если это так — дерзайте!
Полезные материалы
Здесь собран минимум, который пригодится для подготовки к экзаменам. Но, конечно, мы рассчитываем, что вы знакомы со всем списком рекомендуемой литературы.
1. Алгоритмы: построение и анализ (Т. Кормен, Ч. Лейзерсон, Р. Риверст, К. Штайн)
2. Задачи и теоремы линейной алгебры (В. Прасолов)
3. Основные понятия теории вероятностей (А. Колмогоров)
4. Курс теории вероятностей и математической статистики (Б. Севастьянов)
5. Курс комбинаторики А. М. Райгородского в YouTube
6. Тренажёры по написанию кода: Codeforces, LeetCode или TopCoder
7. Контесты прошлых лет
8. Задачи с экзаменов в ШАДе для классического и альтернативного треков
9. Тренировки Яндекса по алгоритмам
10. Разбор задач для поступления в ШАД
11. Архив олимпиады Putman Competition
Также рекомендуем почитать статью Виктора Рогуленко о том, как он готовился к поступлению в ШАД в 2019 году. Ждём ваших заявок и желаем удачи!
Вступительный экзамен в Школу анализа данных
3 июня 2017
Условия задач
- Пусть
и
— два ненулевых вектора из
. Верно ли, что найдется симметричная матрица
, для которой
?
- Непрерывная функция
такова, что
. Докажите, что для какого-то
имеет место равенство
.
- Из равномерного распределения на отрезке
независимо выбираются две точки
и
. При каких
события
и
независимы?
- В компании «Тындекс» у каждого сотрудника не менее 50 знакомых. Оказалось, что есть два сотрудника, знакомые друг с другом лишь через 9 рукопожатий (то есть кратчайшая соединяющая из цепочка из попарно знакомых людей содержит 8 промежуточных людей). Докажите, что в этой компании хотя бы 200 сотрудников.
- Квадратная матрица
размера nxn имеет различные собственные значения
. Найдите все собственные значения (в том числе комплексные) матрицы
.
- Вы — воин Света, и сегодня вам нужно победить толпу из
гоблинов, каждый из которых изначально имеет
единиц жизни (
,
). Боретесь с гоблинами вы с помощью специального магического посоха. Если ударить таким посохом по гоблину, тот сразу же теряет
единиц жизни, а все остальные гоблины в толпе теряют
единиц каждый (таковы магические свойства посоха). Гоблин считается побежденным, если после очередного удара его здоровье становится меньше или равно нулю. Обычная борьба с нечистью давно вам приелась, и чтобы внести разнообразие в сегодняшнюю битву, вы решили победить всех гоблинов, сделав минимально возможное число ударов посохом. Предложите алгоритм нахождения этого числа ударов. Ваш алгоритм должен иметь асимптотику по времени
, затраты по памяти —
.
- Пусть
и
— две случайных булевых матрицы nxn, у которых каждый элемент равен 1 с вероятностью
(значения различных элементов не зависят друг от друга). Сколько в среднем единиц будет в их произведении, если сложение и умножение происходят по модулю 2?
- Исследуйте на сходимость (абсолютную и условную) ряд
, где
Все материалы для подготовки
смотрите еще Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов







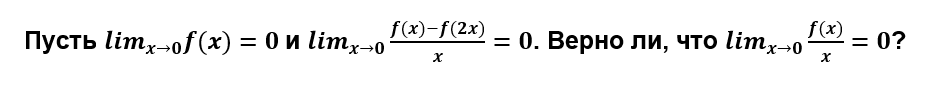
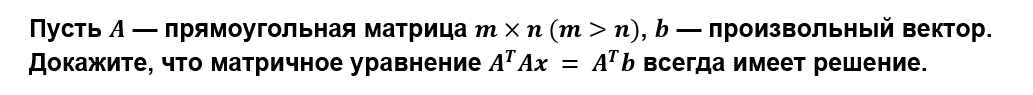



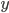
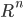
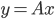
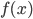
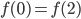
![xin[0;2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_f97a66d9bab80e30c2a40e05e2986e1d.gif)
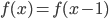
![[0;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b8b4326ebb88870f8cc97ab3f59a0867.gif)