Задание 10 егэ математика профильный уровень 2023 презентация - Помощь в подготовке к экзаменам и поступлению

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.

Источник

Презентация составлена в программе PowerPoint для подготовки выпускников к ЕГЭ-2023 по математике (профильный уровень) для отработки навыков решения задания №10 «Функции». Для выполнения задания нужно изучить основные элементарные функции, их свойства и графики. Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции. А также решать системы уравнений. Из открытого банка заданий ЕГЭ по математике представлены следующие темы:
Линейные функции
Кусочно-линейная функция
Параболы и гиперболы
Тригонометрические функции
Показательные и логарифмические функции
Комбинированные задачи

Светлана Васильевна Вебер

Понравилось? Сохраните и поделитесь:

Неограниченная бесплатная загрука материала «ЕГЭ-2023. Математика (профильный уровень). Прототип №10. Функции» доступна всем пользователям. Разработка находится в разделе «ЕГЭ по математике» и представляет собой: «повторение, систематизация».

Загрузка началась…

Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!

Подарок каждому подписчику!

Источник

ПРЕЗЕНТАЦИЯ «Разбор задания 10 ЕГЭ математика профиль»

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Разбор задание № 10 ЕГЭ математика профиль МКОУ Верхнекарачанская СОШ Учитель математики Табакова О.Н

Слайд 4

Квадратичная функция

По теме: методические разработки, презентации и конспекты

Варианты ЕГЭ математика (профиль), задания 1-12.

Варианты ЕГЭ математика (профиль), задания 1-12. Задания варианта соответствуют заданиям демоверсии ЕГЭ. При составлении вариантов использованы задания открытого банка заданий ЕГЭ. Ответы прилагаются….

Мне нравится

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Источник

Разбор задач с физическим содержанием в профильном ЕГЭ по математике

Аннотация:

Презентация является пособием для подготовки к профильному ЕГЭ по математике. Задание 10 » задачи с физическим содержанием» часто вызывают затруднения у учащихся. Длинный текст с описанием явления, физические параметры с единицами измерения, «скрытые» данные и длинная формула — этот уже повод для детей пропустить эту задачу. В работе представлены решения 15 задач из сборника «ЕГЭ, 4000 задач с ответами по математике, Все задания закрытый сегмент, Базовый и профильный уровни», Ященко И.В., Высоцкий И.Р., Забелин А.В., 2017г. Произведена подборка однотипных задач из сборника для самостоятельного решения.

Целевая аудитория: для 11 класса

Автор: Анисимова Оксана Михайловна
Место работы: ФГКВОУ ВИФК Кадетский корпус (спортивная школа) Санкт-Петербург
Добавил: Okcana

Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!

Всего комментариев: 0

Физкультминутки

Физкультминутки обеспечивают кратковременный отдых детей на уроке, а также способствуют переключению внимания с одного вида деятельности на другой.

В помощь учителю

Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.

Для добавления презентации на портал необходимо зарегистрироваться.

Конкурсы

Диплом и справка о публикации каждому участнику!

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

Презентация представляет собой сборник многовариантных задач.

Описание разработки

Как организовать время ученику выпускного класса, чтобы получить на ЕГЭ хорошие результаты? Какие задачи решить, чтобы не растеряться и увидеть «знакомые задания»? Эти вопросы волнуют всех выпускников. Особенно остро проблема стоит в период интенсивной подготовки к ЕГЭ.

Тренажёр представляет собой сборник многовариантных задач. Задачи для тренажеров подбирались из различных информационных ресурсов (печатные издания: газета «Математика», сборники для подготовки к ЕГЭ, открытый банк заданий ФИПИ, КИМы диагностических, тренировочных, экзаменационных работ по математике разных лет).

Характер задания.

Тип задания. Анализ практической ситуации, приводящей к решению неравенства или уравнения.

Характеристика задания. Текстовое задание, моделирующее реальную или близкую к реальной ситуацию (например, физические, химические и др. процессы).

Комментарий. По условию задачи требуется составить и решить линейное или квадратное неравенство, после чего в ответе записать искомую величину.

Особенности задания B10.

Задания этого блока проверяют умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

Трудные на первый взгляд задачи, как правило, сводятся к решению простых линейных или квадратных уравнений или неравенств.

Для решения задания В10 требуется применить умения извлекать информацию из зависимостей между величинами, решать уравнения и неравенства.

Алгоритм решения заданий B10.

1. Внимательно прочитать условие и, анализируя его, выявить искомую величину.

2. Выполнить подстановку данных из условия в заданную формулу.

3. Решить получившееся уравнение или неравенство относительно неизвестной величины.

4. Выбрать из полученных решений те, которые удовлетворяют условию задачи.

Содержимое разработки

Тренажер к заданию № 10 части В ЕГЭ по математике

Выполнил ученик 11 «А» класса МОУ «Гимназия №4»

Шиба Дмитрий

Руководитель:

Силиванец Светлана Валерьевна

Содержание

Характер задания
Особенности задания B10
Алгоритм решения заданий B10

Блоки заданий

1. Движение тела вертикально вверх под действием силы тяжести
2. Свободное падение камня в колодец
3. Движение по параболе
4. Тепловое линейное расширение
5. Нагревательный прибор
6. КПД теплового двигателя
7. Температура звезд
8. Закон Ома
9. Параллельное сопротивление проводников
10. Закон радиоактивного распада

Характер задания

Тип задания. Анализ практической ситуации, приводящей к решению неравенства или уравнения.
Характеристика задания. Текстовое задание, моделирующее реальную или близкую к реальной ситуацию (например, физические, химические и др. процессы).
Комментарий. По условию задачи требуется составить и решить линейное или квадратное неравенство, после чего в ответе записать искомую величину.

Особенности задания B10

Задания этого блока проверяют умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Трудные на первый взгляд задачи, как правило, сводятся к решению простых линейных или квадратных уравнений или неравенств.
Для решения задания В10 требуется применить умения извлекать информацию из зависимостей между величинами, решать уравнения и неравенства.

Алгоритм решения заданий B10

1. Внимательно прочитать условие и, анализируя его, выявить искомую величину.
2. Выполнить подстановку данных из условия в заданную формулу.
3. Решить получившееся уравнение или неравенство относительно неизвестной величины.
4. Выбрать из полученных решений те, которые удовлетворяют условию задачи.

Движение тела вертикально вверх под действием силы тяжести

Высоту над землей подброшенного вертикально вверх мяча вычисляют по формуле h(t) = -4 t 2 + 22t, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 м?
Рекомендации. Анализируя условие, заметим, что для ответа на вопрос необходимо найти промежуток времени, когда камень находился на высоте не менее 10 м, то есть те значения t, при которых h(t) ≥10.
Решая полученное неравенство -4t 2 + 22t ≥10, получаем t Є [0,5; 5]
Длина полученного промежутка равна 5-0,5 = = 4,5 секунд.
Ответ: 4.5 с.

Решите сами

Вариант 1

h(t) = -5t 2 + 18t h(м) не менее 9;
Ответ: t (с)= 2,4

Вариант 2

h(t) = 1 + 11t -5t 2 h(м) более 3
Ответ: t (с)= 1,8

Вариант 3

h(t) = 2 + 12t -5t 2 h(м) более 6
Ответ: t (с)= 1,6

Вариант 4

h(t) = 2 + 14t -5t 2 h(м) более 10
Ответ: t (с)= 1,2

Вариант 5

h{t) = 3 + 15t -6t 2 h(м) более 9
Ответ: t (с)= 1,5

Свободное падение камня в колодец

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время падения камешка в колодец и рассчитывает расстояние до воды по формуле h = 0,5t 2 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешка составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Рекомендации. Обратим внимание, что уровень поднятия воды — это не что иное, как разность высот при заданном времени падения.
Ответ: 0,1 м.

Решите сами

Вариант 1

t (c)= 0,8 Изменение t (c)= более чем на 0.1
Ответ: изменение h (м)= 0,75

Вариант 2

t (c)= 1 Изменение t (c)= более чем на 0.1
Ответ: изменение h (м)= 0,95

Вариант 3

t (c)= 1,2 Изменение t (c)= на 0.1
Ответ: изменение h (м)= 1,15

Вариант 4

t (c)= 1,2 Изменение t (c)= на 0.2
Ответ: изменение h (м)= 2,2

Вариант 5

t (c)= 1,4 Изменение t (c)= на 0.2
Ответ: изменение h (м)= 2,6

Движение по параболе

Камнеметательная машина выстреливает камни под определенным углом к горизонту с фиксированной начальной скоростью. Траектория полета камня описывается формулой
у = -ах 2 + bх, где , . На каком наибольшем расстоянии (в метрах) от крепостной стены высоты 9 м нужно расположить машину, чтобы камни перелетали через нее?
Рекомендации. Подставить значения параметров а, b и высоту стены у и найти корни получившегося уравнения.
Ответ: 900 м.

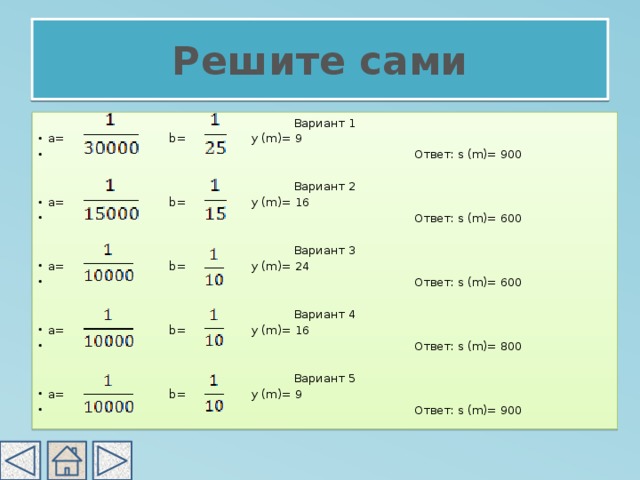
Решите сами

Вариант 1

a= b= y (m)= 9
Ответ: s (m)= 900

Вариант 2

a= b= y (m)= 16
Ответ: s (m)= 600

Вариант 3

a= b= y (m)= 24
Ответ: s (m)= 600

Вариант 4

a= b= y (m)= 16
Ответ: s (m)= 800

Вариант 5

a= b= y (m)= 9
Ответ: s (m)= 900

Тепловое линейное расширение

При температуре 0°С рельс имеет длину 1 0 = 12,5 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 1(t°) = = 1 0 (l + at 0 ), где а = 1,2 • 10 ‑5 — коэффициент теплового расширения в градусах Цельсия в минус первой степени, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.
Рекомендации. Получение ответа упрощается, если задачу решать в общем виде, как это принято на уроках физики: раскрыть скобки, выразить искомую величину, а потом подставить значения; учесть, что изменение длины рельса должно быть выражено в метрах.
Ответ: 40 °С.

Решите сами

Вариант 1

l 0 (м) = 20 Удлинение = 9
Ответ: t (°C) = 37,5

Вариант 2

l 0 (м) = 25 Удлинение = 12
Ответ: t (°C) = 40

Вариант 3

l 0 (м) = 20 Удлинение = 2,4
Ответ: t (°C) = 10

Вариант 4

l 0 (м) = 10 Удлинение =6
Ответ: t (°C) = 50

Вариант 5

l 0 (м) = 10 Удлинение = 4,5
Ответ: t (°C) = 37,5

Нагревательный прибор

Зависимость температуры (в Кельвинах) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально, и на исследуемом интервале температур задается выражением T(t) = Т 0 + at + bt 2 , где Т 0 = 200 К, а = 75 К/мин, b = -0,5 К/мин 2 . Известно, что при температурах нагревателя свыше 1500 К прибор может испортиться, поэтому его нужно отключить. Определите (в минутах), через какое наибольшее время после начала работы нужно отключить прибор.
Рекомендации. Подставить данные в уравнение и решить относительно t.
Ответ: 130 мин.

Решите сами

Вариант 1

T 0 (K) = 200 a (K/мин) = 75 b (K/мин 2 ) = -0,5
T max (K) = 1500
Ответ: t (мин) = 130

Вариант 2

T 0 (K) = 540 a (K/мин) = 56 b (K/мин 2 ) = -0,4
T max (K) = 1500
Ответ: t (мин) = 120

Вариант 3

T 0 (K) = 1200 a (K/мин) = 48 b (K/мин 2 ) = -0,4
T max (K) = 2000
Ответ: t (мин) = 100

Вариант 4

T 0 (K) = 1500 a (K/мин) = 100 b (K/мин 2 ) = -0,5
T max (K) = 4700
Ответ: t (мин) = 40

КПД теплового двигателя

Коэффициент полезного действия теплового двигателя определяется формулой При каких значениях температуры Т 1 нагревателя КПД этого двигателя будет больше 70%, если температура холодильника Т 2 = 300 К?
Рекомендации. Рациональное решение — сначала подставить данные, упростить, затем найти искомую величину.
Ответ: 1000 К.

Решите сами

Вариант 1

(%) = не менее 80 T 2 (К) = 400
Ответ: T 1 (К) = 2000

Вариант 2

(%) = не меньше 40 T 2 (К) = 300
Ответ: T 1 (К) = 500

Вариант 3

(%) = больше 30 T 2 (К) = 350
Ответ: T 1 (К) = 500

Вариант 4

(%) = более 70 T 2 (К) = 150
Ответ: T 1 (К) = 500

Вариант 5

(%) = больше 90 T 2 (К) = 100
Ответ: T 1 (К) = 1000

Температура звезд

Для определения эффективной температуры звезд используют закон Стефана—Больцмана, согласно которому мощность излучения нагретого тела вычисляется по формуле Р = aST 4 , где

а = 5,7 • 10 -8 Дж • с -1 • м -2 • К -4 , площадь поверхности S измеряется в квадратных метрах, температура Т — в Кельвинах, а мощность — в ваттах. Известно, что некоторая звезда

имеет площадь , а излучаемая ее мощность Р не менее 0,57 • 10 15 Вт. Определите наименьшую возможную температуру этой звезды (в Кельвинах).

Рекомендации. Вычисления упрощаются, если в данную формулу сначала подставить известные величины, упростить, а потом вычислить неизвестную величину.
Ответ: 200 К.

Решите сами

Вариант 1

P (Вт) = не менее 46,17•10 17 S =
Ответ: Наим. возм. темп. T (K) = 600

Вариант 2

P (Вт) = не менее 46,17•10 24 S =
Ответ: Наим. возм. темп. T (K) = 120000

Вариант 3

P (Вт) = не менее 9,12•10 10 S =
Ответ: Наим. возм. темп. T (K) = 400

Вариант 4

P (Вт) = не менее 0,57•10 15 S =
Ответ: Наим. возм. темп. T (K) = 300

Вариант 5

P (Вт) = не менее 9,12•10 15 S =
Ответ: Наим. возм. темп. T (K) = 800

Закон Ома

В электросеть включен предохранитель, рассчитанный на максимальную силу тока I. Какое максимальное сопротивление должно быть у электроприбора, подключаемого к розетке с подаваемым напряжением U, чтобы сеть продолжала работать. Сила тока и напряжение по закону Ома связаны соотношением , где R — сопротивление электроприбора в омах.

Вариант 1

I (A) = 16 U (B) = 220
Ответ: R max (Oм) = 13,75

Вариант 2

I (A) = 20 U (B) = 220
Ответ: R max (Oм) = 11

Вариант 3

I (A) = 8 U (B) = 220
Ответ: R max (Oм) = 27,5

Параллельное сопротивление проводников

В розетку электросети подключены приборы, общее сопротивление которых составляет 100 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите (в омах) наименьшее возможное сопротивление электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R 1 и R 2 их общее сопротивление задается формулой , а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 20 Ом.
Рекомендации. Оценивая достоверность результата, вспомните, что при параллельном соединении общее сопротивление всегда меньше меньшего сопротивления.
Ответ: 25 Ом.

Решите сами

Вариант 1

R общ (Ом) = не меньше 20 R 1 (Ом) = 100
Ответ: R 2 (Ом) = 25

Вариант 2

R общ (Ом) = не меньше 15 R 1 (Ом) = 90
Ответ: R 2 (Ом) = 18

Вариант 3

R общ (Ом) = не меньше 30 R 1 (Ом) = 90
Ответ: R 2 (Ом) = 45

Вариант 4

R общ (Ом) = не меньше 20 R 1 (Ом) = 70
Ответ: R 2 (Ом) = 28

Вариант 5

R общ (Ом) = не меньше 10 R 1 (Ом) = 60
Ответ: R 2 (Ом) = 12

Закон радиоактивного распада

Масса радиоактивного вещества уменьшается по закону , где m 0 — начальная масса изотопа, t — прошедшее от начального момента время (мин), Т — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m 0 = 40 мг изотопа, период полураспада которого Т = 10 мин. В течение какого времени t масса изотопа будет не меньше 5 мг?
Рекомендации. Рационально подставить числовые значения величин, упростить, а затем найти неизвестное.
Ответ: 30 мин.