ЕГЭ Профиль №13. Показательные уравнения
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 353 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 2021 года. Досрочная волна., Задания 13 ЕГЭ–2021
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 347.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 357.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
Источник: Избранные задания по математике из последних сборников ФИПИ
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 288.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 305. (Часть C)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 375.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 101., Задания 13 (С1) ЕГЭ 2013
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 08.05.2014. Досрочная волна, резервная волна. Вариант 2, Задания 13 (С1) ЕГЭ 2014
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2016 г.
Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 115.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2017. Задания С1., Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 6. (Часть C).
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017
а)Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017
а)Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 281.
Всего: 353 1–20 | 21–40 | 41–60 | 61–80 …
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Задание №13 ЕГЭ по математике профильного уровня
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем
Простейшие (Protozoa) — тип одноклеточных животных.
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
3. Делаем обратную замену:
Решаем эти уравнения:
Следовательно, получаем два семейства решений. Пункт б):
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
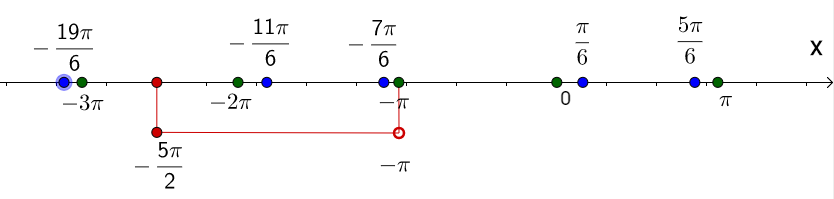
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
D=b 2 – c = 81 – 4∙4∙2 =49,
3. Возвращаемся к переменной х: 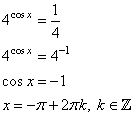
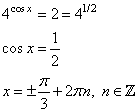
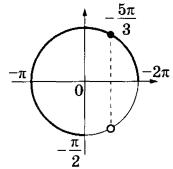
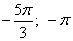
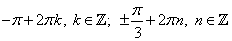
Третий вариант задания (из Ященко, № 6)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
- Решаем неравенства для каждого случая.
- Записываем ответ.
Задание № 13 ЕГЭ по математике — подборка задач с решениями
Подборка задач № 13 ЕГЭ по профильной математике с решениями.
Задание № 13. Уметь решать уравнения и неравенства
Из кодификатора на этой позиции могут встретиться темы:
Уравнения
Равносильность уравнений, систем уравнений
Простейшие системы уравнений с двумя неизвестными
Основные приёмы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
Использование свойств и графиков функций при решении уравнений
Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учёт реальных ограничений.
Неравенства
Системы линейных неравенств
Системы неравенств с одной переменной
Равносильность неравенств, систем неравенств
Использование свойств и графиков функций при решении неравенств
Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
источники:
http://spadilo.ru/zadanie-13-ege-po-matematike-profilnyj/
http://vpr-ege.ru/ege/matematika/706-zadanie-13-ege-po-matematike-podborka-zadach-s-resheniyami
Встречалось и такое:
а) Решите уравнение 2log32(2cos x) – 5log3(2cos x) + 2 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 5π/2].
Ответ: а) {π/6 + 2πk; -π/6 + 2πk, k∊Z} и б) 11π/6; 13π/6.
Во-вторых, изучение методов решения показательных и логарифмических уравнений является хорошей подготовкой к решению задачи № 15, так как в основных методах решения и уравнений, и неравенств фактически используются одни и те же математические идеи.
Основные методы решения показательных и логарифмических уравнений несложно запомнить, их всего пять: сведение к простейшему уравнению, использование равносильных переходов, введение новых неизвестных, логарифмирование и разложение на множители. Отдельно стоит метод использования свойств показательной, логарифмической и других функций при решении задач: иногда ключом к решению уравнения является область определения, область значений, неотрицательность, ограниченность, четность входящих в него функций.
Как правило, в задаче № 13 встречаются уравнения, требующие применения перечисленных выше пяти основных методов. Каждый из этих методов имеет свои особенности, которые необходимо знать, так как именно их незнание приводит к ошибкам при решении задач.
Какие типичные ошибки совершают экзаменуемые?
Нередко при решении уравнений, содержащих показательно-степенную функцию, школьники забывают рассмотреть один из случаев выполнения равенства. Как известно, уравнения такого вида равносильны совокупности двух систем условий (см. ниже), речь идет о случае, когда a(x) = 1
Данная ошибка связана с тем, что решая уравнение экзаменуемый формально использует определение показательной функции (y = ax, a>0, a ≠ 1): при а ≤ 0
показательная функция действительно не определена,
а вот при а = 1 определена, но не является показательной, так как единица в любой действительной степени тождественно равна самой себе. А значит если в рассматриваемом уравнении при а(x) = 1 возникает верное числовое равенство, то соответствующие значения переменной будут корнями уравнения.
Еще одна ошибка – применение свойств логарифмов без учета области допустимых значений. Например, хорошо знакомое многим свойство «логарифм произведения равен сумме логарифмов», оказывается, имеет обобщение:
loga(f(x)g(x)) = loga│f(x)│ + loga│g(x)│, при f(x)g(x) > 0, a > 0, a ≠ 1
Действительно, для того, чтобы было определено выражение в левой части этого равенства, достаточно, чтобы произведение функций f и g было положительным, но сами функции при этом могут быть как одновременно больше, так и одновременно меньше нуля, поэтому при применении данного свойства необходимо использовать понятие модуля.
И таких примеров можно привести немало. Поэтому для эффективного освоения методов решения показательных и логарифмических уравнений лучше всего воспользоваться услугами опытного преподавателя, который сумеет рассказать о подобных «подводных камнях» на примерах решения соответствующих экзаменационных задач.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
- Получить доступ ко всей теории и тренажерам задачи №13. Это стоит всего 990 рублей.
- Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 13 в экзамене ЕГЭ, задачи на логарифмы, ким ЕГЭ 2017, подготовка к ЕГЭ профиль математика, Математика профиль, решение уравнений и логарифмов, решение задач на показательные уравнения ЕГЭ, вычисление свойств логарифмов, показательно-степенная функция, задачи по математике профильного уровня, применение свойств логарифмов, решение задач на корни, задачи ЕГЭ 2017 по показательным уравнениям, подготовка к егэ выпускникам 11 класса в 2018 году, поступающим в технический вуз.
Уравнения, часть С
Теория к заданию 13 из ЕГЭ по математике (профильной)
Уравнения, часть $С$
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Схема решения сложных уравнений:
- Перед решением уравнения надо для него записать область допустимых значений (ОДЗ).
- Решить уравнение.
- Выбрать из полученных корней уравнения то, которые удовлетворяют ОДЗ.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
2. Подкоренное выражение, должно быть не отрицательным.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
Логарифмические уравнения
Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
4. При умножении двух логарифмов можно поменять местами их основания
6. Формула перехода к новому основанию
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
Можно выделить несколько основных видов логарифмических уравнений:
Представим обе части уравнения в виде логарифма по основанию $2$
Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.
Т.к. основания одинаковые, то приравниваем подлогарифмические выражения
Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые
Проверим найденные корни по условиям $table< x^2-3x-5>0; 7-2x>0;$
При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень
- Метод замены переменной.
В данном методе надо:
Решите уравнение $log_<2>√x+2log_<√x>2-3=0$
1. Запишем ОДЗ уравнения:
$table< х>0,text»так как стоит под знаком корня и логарифма»; √х≠1→х≠1;$
2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:
3. Далее сделаем замену переменной $log_<2>√x=t$
4. Получим дробно — рациональное уравнение относительно переменной t
Приведем все слагаемые к общему знаменателю $t$.
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
5. Решим полученное квадратное уравнение по теореме Виета:
6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:
Прологарифмируем правые части уравнений
Приравняем подлогарифмические выражения
Чтобы избавиться от корня, возведем обе части уравнения в квадрат
7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.
Первый корень удовлетворяет ОДЗ.
$<table 16 >0; 16≠1;$ Второй корень тоже удовлетворяет ОДЗ.
- Уравнения вида $log_x+log_x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.
Дробно рациональные уравнения
- Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
- Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые не удовлетворяют условию ОДЗ.
- Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения.
Показательные уравнения
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
4. При возведении в степень произведения в эту степень возводится каждый множитель
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
6. При возведении любого основания в нулевой показатель степени результат равен единице
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
8. Радикал (корень) можно представить в виде степени с дробным показателем
Виды показательных уравнений:
1. Простые показательные уравнения:
а) Вида $a^=a^$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.
b) Уравнение вида $a^=b, b>0$
Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается
2. Метод уравнивания оснований.
3. Метод разложения на множители и замены переменной.
- Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^$.
- Сделать замену переменной $a^=t, t > 0$.
- Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
- Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.
По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.
Сделаем замену переменной $2^x=t; t>0$
Получаем кубическое уравнение вида
Умножим все уравнение на $2$, чтобы избавиться от знаменателей
Разложим левую часть уравнения методом группировки
Вынесем из первой скобки общий множитель $2$, из второй $7t$
Дополнительно в первой скобке видим формулу разность кубов
Далее скобку $(t-1)$ как общий множитель вынесем вперед
Произведение равно нулю, когда хотя бы один из множителей равен нулю
Решим первое уравнение
Решим второе уравнение через дискриминант
Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения
4. Метод преобразования в квадратное уравнение
- Имеем уравнение вида $А·a^<2f(x)>+В·a^+С=0$, где $А, В$ и $С$ — коэффициенты.
- Делаем замену $a^=t, t > 0$.
- Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
- Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.
Способы разложения на множители:
- Вынесение общего множителя за скобки.
Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:
- Определить общий множитель.
- Разделить на него данный многочлен.
- Записать произведение общего множителя и полученного частного (заключив это частное в скобки).
Разложить на множители многочлен: $10a^<3>b-8a^<2>b^2+2a$.
Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:
Это и есть конечный результат разложения на множители.
Применение формул сокращенного умножения
1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.
2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.
3. Разность квадратов раскладывается на произведение разности чисел и их сумму.
4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.
5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.
6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.
7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.
Метод группировки
Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.
Разложить многочлен на множители $2a^3-a^2+4a-2$
Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками.
Далее из каждой группы вынесем общий множитель
После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.
Произведение данных скобок — это конечный результат разложения на множители.
С помощью формулы квадратного трехчлена.
Если имеется квадратный трехчлен вида $ax^2+bx+c$, то его можно разложить по формуле
$ax^2+bx+c=a(x-x_1)(x-x_2)$, где $x_1$ и $x_2$ — корни квадратного трехчлена
Задание №13 ЕГЭ по математике профильного уровня
Уравнения
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем
Простейшие (Protozoa) — тип одноклеточных животных.
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
3. Делаем обратную замену:
Решаем эти уравнения:
Следовательно, получаем два семейства решений. Пункт б):
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
D=b 2 – c = 81 – 4∙4∙2 =49,
3. Возвращаемся к переменной х: 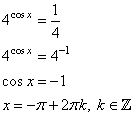
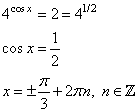

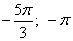
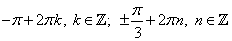
Третий вариант задания (из Ященко, № 6)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
- Решаем неравенства для каждого случая.
- Записываем ответ.
Задание 13. Уравнения
За правильное выполненное задание получишь 2 балла.
На решение отводится примерно 10 минут.
Чтобы решить задание 13 по математике профильного уровня нужно знать:
- Задание 13 в ЕГЭ подразделяется на несколько видов:
- логарифмические и показательные уравнения;
- тригонометрические уравнения;
- смешанные уравнения.
- Тригонометрические формулы:
- Основные тригонометрические тождества.
- Формулы приведения.
- Формулы сложения.
- Формулы двойного, тройного и т.д. угла.
- Формулы половинного угла.
- Формулы понижения степени.
- Формулы суммы и разности тригонометрических функций.
- Формулы произведения синусов, косинусов и синуса на косинус.
- Универсальная тригонометрическая подстановка.
Задачи для тренировки
a) Решите уравнение 2sin (x + frac < pi > < 3 >) + cos2x= sqrt <3>cos x+1
б) Укажите корни этого уравнения, принадлежащие отрезку [-3π; -frac < 3π > < 2 >)
источники:
http://spadilo.ru/zadanie-13-ege-po-matematike-profilnyj/
http://bingoschool.ru/ege/maths-profile/tasks/13/
Иррациональные уравнения на ЕГЭ прошлых лет
| 1 | а) Решите уравнение x — 3sqrt{x — 1} + 1 = 0 б) Найдите все корни этого уравнения, принадлежащие промежутку left[ sqrt{3}; sqrt{20} right] |
Смотреть видеоразбор |
| 2 | а) Решите уравнение sqrt{x^3 — 4x^2 — 10x + 29} = 3 — x б) Найдите все корни этого уравнения, принадлежащие промежутку left[ -sqrt{3}; sqrt{30} right] |
Смотреть видеоразбор |
Показательные уравнения на ЕГЭ прошлых лет
| 1 | а) Решите уравнение 8^x — 9 cdot 2^{x + 1} + 2^{5 — x} = 0 б) Найдите все корни этого уравнения, принадлежащие промежутку left[log_5 2; log_5 20 right] |
Смотреть видеоразбор |
Тригонометрические уравнения на ЕГЭ прошлых лет
| 1 | а) Решите уравнение dfrac{sin x}{sin^2dfrac{x}{2}} = 4cos^2dfrac{x}{2} б) Найдите все корни этого уравнения, принадлежащие промежутку left[ -dfrac{9pi}{2}; -3pi right] |
Смотреть видеоразбор |
| 2 | а) Решите уравнение cos 2x = 1 — cosleft(dfrac{pi}{2} — xright) б) Найдите все корни этого уравнения, принадлежащие промежутку left[ -dfrac{5pi}{2}; -pi right) |
Смотреть видеоразбор |
| 3 | а) Решите уравнение cos^2 (pi — x) — sin left( x + dfrac{3pi}{2} right) = 0 б) Найдите все корни этого уравнения, принадлежащие промежутку left[dfrac{5pi}{2}; 4pi right] |
Смотреть видеоразбор |
| 4 | а) Решите уравнение 8 sin^2 x + 2sqrt{3} cos left( dfrac{3pi}{2} — xright) = 9 б) Найдите все корни этого уравнения, принадлежащие промежутку left[- dfrac{5pi}{2}; -pi right] |
Смотреть видеоразбор |
| 5 | а) Решите уравнение sin x + left(cos dfrac{x}{2} — sin dfrac{x}{2}right)left(cos dfrac{x}{2} + sin dfrac{x}{2}right) = 0 б) Найдите все корни этого уравнения, принадлежащие промежутку left[pi; dfrac{5pi}{2}right] |
Смотреть видеоразбор |
Уравнения смешанного типа на ЕГЭ прошлых лет (логарифмические или показательные + тригонометрия)
| 1 | а) Решите уравнение 2log_3^2 (2 cos x) — 5log_3 (2 cos x) + 2 = 0 б) Найдите все корни этого уравнения, принадлежащие промежутку left[pi; dfrac{5pi}{2} right] |
Смотреть видеоразбор |
| 2 | а) Решите уравнение left( dfrac{1}{49} right)^{sin x} = 7^{2 sin 2x} б) Найдите все корни этого уравнения, принадлежащие промежутку left[dfrac{3pi}{2}; 3pi right] |
Смотреть видеоразбор |
| 3 | а) Решите уравнение log_4 (sin x + sin 2x + 16) = 2 б) Найдите все корни этого уравнения, принадлежащие промежутку left[ -4pi; -dfrac{5pi}{2} right] |
Смотреть видеоразбор |
За это задание ты можешь получить 3 балла. На решение дается около 20 минут. Уровень сложности: повышенный.
Средний процент выполнения: 5.6%
Ответом к заданию 13 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 13:
В задании требуется решить уравнение одного из видов: тригонометрическое, рациональное, показательное, логарифмическое, уравнение с радикалом или смешанное уравнение, которое может содержать в себе несколько видов, например, логарифмы и тригонометрию. После решения уравнения, часто необходимо отобрать корни, которые принадлежат определенному промежутку.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
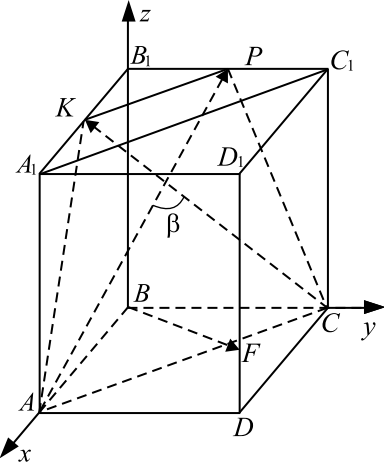
Дан куб $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $M$, причём $AM:MA_1=1:1$, на ребре $BB_1$ отмечена точка $N$,
причём $BN:NB_1=1:2$, на ребре $CC_1$ отмечена точка $K$, причём $CK:KC_1=1:3$.
а) В каком отношении, считая от точки $D$, плоскость $MNK$ делит ребро $DD_1$?
б) Найдите величину угла между плоскостями $MNK$ и $ABC$.
Решение
а) Пусть ребро куба равно $1$. Противоположные грани куба параллельны, поэтому плоскость $MNK$ пересекает их по параллельным отрезкам. Сечением куба плоскостью $MNK$ является параллелограмм $MNKF$, где $F$ — точка пересечения ребра $DD_1$ с плоскостью $MNK$. Рассмотрим проекцию куба на грань $CC_1D_1D$. $DM_1=AM$, $CN_1=BN$. Отрезки $M_1N_1$ и $FK$ параллельны, поэтому $N_1K={1} / {3}-{1} / {4}={1} / {12}$, и $FD=M_1D-M_1F={1} / {2}-{1} / {12}={5} / {12}$, значит, $DF:FD_1=5:7$. б) Прямая $FK$ пересекает плоскость основания куба в точке $L$, прямая $NK$ пересекает плоскость основания куба в точке $T$, поэтому плоскость $MNK$ пересекает плоскость $ABC$ по прямой $TL$. В прямоугольном треугольнике $CLT$ отрезок $CH$ — высота, по теореме о трёх перпендикулярах $KH⊥ TL$, поэтому линейный угол $CHK$ является углом между плоскостями $MNK$ и $ABC$. Треугольники $CLK$ и $DLF$ подобны, $CK={1} / {4}$, $FD={5} / {12}$, $DL=1+CL$, тогда из пропорции ${1} / {4}:{5} / {12}=CL:(1+CL)$, получим $CL={3} / {2}$. Аналогично из подобия треугольников $CTK$ и $BTN$ найдём $CT=3$. В прямоугольном треугольнике $CLT$ гипотенуза $LT$ вычисляется по теореме Пифагора:$LT={3√ 5} / {2}$, а высота $CH={CL⋅ CT} / {LT}={3} / {√ 5}$. В прямоугольном треугольнике $CHK$ вычисляем
$tg∠ CHK={CK} / {CH}={1} / {4}:{3} / {√ 5}={√ 5} / {12}$, значит, $∠ CHK=arctg{√ 5} / {12}$.
Ответ: begin{tabular}{c}а)$5:7$\б)$arctgfsm{sqrt5}{12}$end{tabular
Задача 2
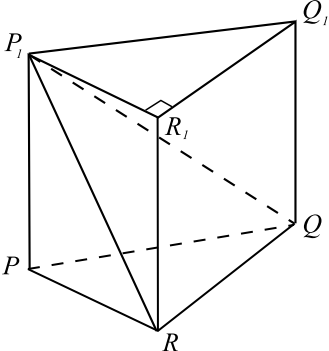
Основанием прямой треугольной призмы $PQRP_1Q_1R_1$ является прямоугольный треугольник $PQR$ с прямым углом $R$. Диагонали боковых граней $PP_1Q_1Q$ и $PP_1R_1R$ равны $17$ и $15$ соответственно, $PQ = 10$.
а) Докажите, что треугольник $P_1QR$ прямоугольный.
б) Найдите объём пирамиды $P_1QRR_1$.
Решение
По условию задачи сделаем чертёж.
а) Прямая $QR$ перпендикулярна плоскости $PP_1R_1R$, поскольку она перпендикулярна прямым $PR$ и $RR_1$. Значит, прямые $QR$ и $RP_1$ перпендикулярны, следовательно, в $△P_1QR$
$∠P_1RQ = 90°$.
б) Пусть $V$ — объём призмы $PQRP_1Q_1R_1$. Тогда объём треугольной пирамиды $PP_1QR$ равен ${V}/{3}$, поскольку её высота $PP_1$ и основание $PQR$ совпадают с высотой и основанием призмы соответственно. Аналогично, объём треугольной пирамиды $P_1Q_1R_1Q$ равен ${V}/{3}$. Призма $PQRP_1Q_1R_1$ составлена из трёх пирамид: $PP_1QR, P_1Q_1R_1Q$ и $P_1QRR_1$. Значит, объём пирамиды $P_1QRR_1$ равен ${V}/{3}$.
В призме $PQRP_1Q_1R_1 : QQ_1 = √{P_1Q^2 — P_1Q_1^2} = 3√21, QR = √{P_1Q^2 — P_1R^2} = 8, PR = √{PQ^2 — QR^2} = 6, V = PP_1 · {PR · QR}/{2} = 72√21$.
Таким образом, объём пирамиды $P_1QRR_1$ равен $24√21$.
Ответ: 24sqrt{21}
Задача 3
В правильной четырёхугольной пирамиде $SABCD$ боковое ребро $SA=12$, а высота равна $4$. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $E$, $F$ и $K$ соответственно, причём $BE=CF=12$, $AK=3$.
а) Докажите, что плоскости $SBC$ и $KEF$ параллельны.
б) Найдите объём пирамиды $KSBC$.
Решение
а) Докажем, что плоскости $SBC$ и $KEF$ параллельны.
Введём прямоугольную систему координат, учитывая, что в основании правильной пирамиды квадрат $ABCD$ и угол между диагоналями квадрата прямой .
1. Найдём координаты точек $S, B, C , K , E, F$. В прямоугольном треугольнике $SOA$ по теореме Пифагора $OA^2 = SA^2 — SO^2, OA = √{12^2 — 4^2} = 8√2. OC = OB = OD = OA = 8√2$, тогда сторона квадрата $AB = {OA}/{sin 45°} = {8√2}/{{1}/{√2}} = 16, AE = AB — BE = 16 — 12 = 4$.
Проведём $KN ‖ SO, SO ⊥ (ABC)$, тогда $KN ⊥ (ABC)$ и $KN ⊥ OA, △SAO ∼ △KAN$ по первому признаку подобия $(∠SOA = ∠KNA = 90°, ∠A$ — общий) ${AS}/{AK} = {SO}/{KN}, {12}/{3} = {4}/{KN}, KN = 1$.
В прямоугольном треугольнике $ANK$ по теореме Пифагора $AN^2 = AK^2 — KN^2, AN = √{3^2 — 1^2} = 2√2$, тогда $ON = OA — AN = 8√2 — 2√2 = 6√2. EN$ — проекция $KE$ на плоскость $ABC$, значит $△ANE$ прямоугольный и равнобедренный $EN = AN = 2√2$.
Получим $S(0; 0; 4), B(0; -8√2; 0), C (-8√2; 0; 0), K (6√2; 0; 1), E(6√2; -2√2; 0), F (-2√2; 6√2; 0)$.
2. Докажем, что векторы нормали к плоскостям $SBC$ и $KEF$ коллинеарны. Для плоскости $SBC$, вектор нормали ${n_1}↖{→}(a_1; b_1; c_1)$ перпендикулярен к обеим прямым $SB$ и $SC$, поэтому он должен быть перпендикулярен к векторам ${SB}↖{→}(0; -8√2; -4)$ и ${SC}↖{→}(-8√2; 0; -4)$.
Получим систему ${table {n_1}↖{→} · {SB}↖{→} = 0; {n_1}↖{→} ·{SC}↖{→} = 0;$ ${table · a_1 — 8√2 · b_1 — 4c_1 = 0; -8√2a_1 + 0 · b_1 — 4 · c_1 = 0;$ ${table-2√2b_1 — c_1 = 0; -2√2a_1 — c_1 = 0;$
Пусть $c_1 = -1$, тогда система примет вид ${table-2√2b_1 + 1 = 0; -2√2a_1 + 1 = 0;$
Её решение $a_1 = {√2}/{4}; b_1 = {√2}/{4}$.
${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $SBC$ .
Для плоскости $KEF$, вектор нормали ${n_2}↖{→}(a_2; b_2; c_2)$ перпендикулярен к обеим прямым $KE$ и $KF$, поэтому он должен быть перпендикулярен к векторам ${KE}↖{→}(0; -2√2; -1)$ и ${KF}↖{→}(-8√2; 6√2; -1)$.
Получим систему ${table {n_2}↖{→} · {KE}↖{→} = 0; {n_2}↖{→} · {KF}↖{→} = 0;$ ${table · a_2 — 2√2 · b_2 — 1 · c_2 = 0; -8√2a_2 + 6√2 · b_2 — 1 · c_2 = 0;$ ${table-2√2b_2 — c_2 = 0; -8√2a_2 + 6√2b_2 — c_2 = 0$.
Пусть $c_2 = -1$, тогда система примет вид ${table-2√2b_2 + 1 = 0; 8√2a_2 + 6√2b_2 + 1 = 0;$
Её решение $a_2 = {√2}/{4}; b_2 = {√2}/{4}$.${n_2}↖{→}({√2}/{4}; {√2}/{4}; -1)$ — вектор нормали плоскости $KEF$.
Векторы ${n_1}↖{→}$ и ${n_2}↖{→}$ равны, значит коллинеарны, следовательно плоскости $SBC$ и $KEF$ параллельны.
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь треугольника $SBC$, а высота пирамиды $h$ — это расстояние от точки $K$ до плоскости $SBC$.
1. $S = {1}/{2}SB · SC · sin α$, где $α$ — угол между прямыми $SB$ и $SC$. $cos α ={{SB}↖{→} · {SC}↖{→}}/{|{SB}↖{→}| · |{SC}↖{→}|} = {0 · (-8√2) + (-8√2) · 0 + (-4)(-4)}/{12 · 12} = {16}/{144} = {1}/{9}$.
$sin α = √{1 — cos^2α} = √{1 — {1}/{81}} = {4√5}/{9} · S = {1}/{2} · 12 · 12 · {4√5}/{9} = 32√5$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $SBC$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости. Согласно пункту а), один из векторов нормали ${n_1}↖{→}({√2}/{4}; {√2}/{4}; -1)$. Значит, уравнение имеет вид ${√2}/{4}x + {√2}/{4}y — z + d = 0$. Чтобы найти значение $d$ подставим координаты точки $S(0; 0; 4)$ в это уравнение, получим $-4 + d = 0, d = 4$, тогда ${√2}/{4}x + {√2}/{4}y — z + 4 = 0$ — уравнение плоскости $SBC$. Расстояние от точки $K(6√2; 0; 1)$ до плоскости $SBC$
$h = {|ax_0+ by_0 + z_0 + d|}/{√{a_2 + b_2 + z_2}} ={|{√2}/{4} · 6√2 + {√2}/{4} · 0 + (-1) · 1 + 4|}/{√{({√2}/{4})^2 + ({√2}/{4})^2 + (-1)^2}} = {12√5}/{5}$, где $x_0, y_0, z_0$ — координаты точки $K$.
3. $V = {1}/{3} · 32√5 · {12√5}/{5} = 128$.
Ответ: 128
Задача 4
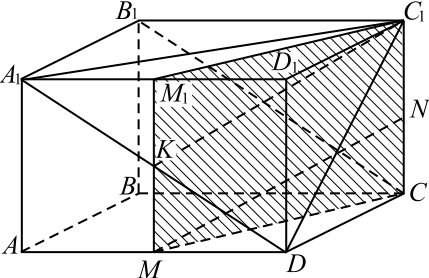
В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB=8√ {2}$, а боковое ребро $AA_1=16$. Точка $K$ — середина ребра $A_1B_1$. На ребре $DD_1$ отмечена точка $F$ так, что $DF=4$. Плоскость $α$ параллельна прямой $A_1C_1$ и содержит точки $K$ и $A$.
а) Докажите, что прямая $BF$ перпендикулярна плоскости $α$.
б) Найдите объём пирамиды, вершина которой точка $B$, а основание — сечение данной призмы плоскостью $α$.
Решение
1. Построим сечение призмы плоскостью $α$.
Грани $ABCD$ и $A_1 B_1 C_1 D_1$ параллельны, значит плоскость α пересекает их по параллельным прямым.
По условию плоскость α параллельна прямой $A_1 C_1$, то есть содержит прямую, параллельную $A_1 C_1$. Поэтому, проведя через точку $K$ прямую $KP (P ∈ B_1 C_1)$, параллельную прямой $A_1 C_1$, и через точку $A$ — прямую $AC$, параллельную прямой $A_1 C_1$ (прямая $AC$ содержит диагональ нижнего основания) получим трапецию $AKPC$ — искомое сечение.
2. Выберем прямоугольную систему координат, как показано на рисунке. Найдём координаты нужных точек: $B(0; 0; 0), F (8√2; 8√2; 4), A(8√2; 0; 0), C (0; 8√2; 0), K (4√2; 0; 16), P (0; 4√2; 16)$.
3. Рассмотрим векторы ${BF}↖{→} (8√2; 8√2; 4), {AP}↖{→} (-8√2; 4√2; 16)$ и ${CK}↖{→} (4√2; -8√2; 16)$.
Так как ${BF}↖{→}· {AP}↖{→} = 8√2(-8√2) + 8√2 · 4√2 + 16 · 4 = 0$, то ${BF}↖{→} ⊥ {AP}↖{→}$.
Так как ${BF}↖{→} · {CK}↖{→} = 8√2 · 4√2 + 8√2 · (-8√2) + 4 · 16 = 0$, то ${BF}↖{→} ⊥ {CK}↖{→}$.
Отсюда следует, что $BF ⊥ α$ по признаку перпендикулярности прямой и плоскости ($BF$ перпендикулярна двум пересекающимся прямым плоскости).
б) Искомый объём $V = {1}/{3}S · h$, где $S$ — площадь четырёхугольника $AKPC$, а высота $h$ — расстояние от точки $B$ до плоскости $α$.
1. $S_{AKPC} = {1}/{2}AP · CK sin β$, где $β$ — угол между диагоналями $AP$ и $CK$ четырёхугольника $AKPC$.
$cos β = {{AP}↖{→} · {CK}↖{→}}/{|{AP}↖{→}| · |{CK}↖{→}|} = {-8√2 · 4√2 + 4√2(-8√2) + 16 · 16}/{√{(-8√2)^2 + (4√2)^2 + 16^2} · √{(4√2)^2 + (-8√2)^2 + 16^2}} = {-64 — 64 + 256}/{416} = {128}/{416} = {4}/{13}; |{AP}↖{→}| = |{CK}↖{→}| = √{416}$.
$sin β = √{1 — cos^2β} = √{1 — {16}/{169}} = {3√17}/{13}$.
Таким образом $S = {1}/{2} · √{416} · √{416} · {3√17}/{13} = 48√{17}$.
2. Чтобы найти $h$ необходимо найти уравнение плоскости $α$. Оно имеет вид $ax + by + cz + d = 0$, где ${n}↖{→}(a; b; c)$ — вектор нормали этой плоскости.
Согласно пункту а) одним из векторов нормали является вектор ${BF}↖{→}(8√2; 8√2; 4)$.
Значит, уравнение плоскости имеет вид $8√2x + 8√2y + 4z + d = 0 (1)$.
Чтобы найти значение $d$ подставим координаты точки $A(8√2; 0; 0)$ в уравнение (1) и получим $8√2 · 8√2 + d = 0, d = -128$.
Уравнение плоскости $α$ примет вид $8√2x + 8√2y + 4z — 128 = 0$.
Найдём расстояние $h$ от точки $B(0; 0; 0)$ до плоскости сечения.
$h = {|ax_0+ by_0 + cz_0 + d|}/{√{a^2 + b^2 + c^2}} = {|8√2 · 0 + 8√2 · 0 + 4 · 0 — 128|}/{√{(8√2)^2 + (8√2)^2 + 16}} = {32}/{√17}$, где ($x_0 ; y_0 ; z_0$ ) — координаты точки $B$.
$V = {1}/{3} · S · h = {1}/{3} · 48√{17} · {32}/{√17} = 512$.
Ответ: 512
Задача 5
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ сторона $AB=AA_{1}=3$, $AD=6$. На рёбрах $AD$ и $CC_{1}$ взяты соответственно точки $M$ и $N$ — середины этих рёбер.
а) Постройте сечение параллелепипеда плоскостью, проходящей через вершину $D$, параллельно $MN$ и $B_{1}C$.
б) Найдите объём пирамиды, основание которой — построенное сечение, а вершина — точка $D_{1}$.
Решение
а) Искомое сечение проходит через вершину $D$ параллельно $B_1 C$, следовательно, пересекает грань $AA_1 D_1 D$ по диагонали $A_1 D$
Действительно, $A_1 D||B_1 C$ (плоскость пересекает две параллельные плоскости по параллельным прямым)
Рассмотрим прямоугольник $C C_1 M_1M$, где $M_1$ середина $A_1 D_1$
Проведём $C_1 K ||M N$. $K$ — середина отрезка $M M_1$ и середина отрезка $A_1 D$, значит, принадлежит искомому сечению, поэтому $C_1 K$ лежит в плоскости сечения
Таким образом, $A_1 C_1 D$ — искомое сечение.
б) Рассмотрим пирамиду $D_1A_1C_1D$ как пирамиду с основанием $D_1DC_1$ и высотой $A_1D_1 (A_1D_1 ⊥ D_1DC_1)$.
$V_{D_1A_1C_1D} = {1}/{3}S_{D_1DC_1} ·A_1D_1 = {1}/{3} · {1}/{2}D_1C_1 ·D_1D ·A_1D_1 = {1}/{6} ·3·3·6 = 9$.
Ответ: 9
Задача 6
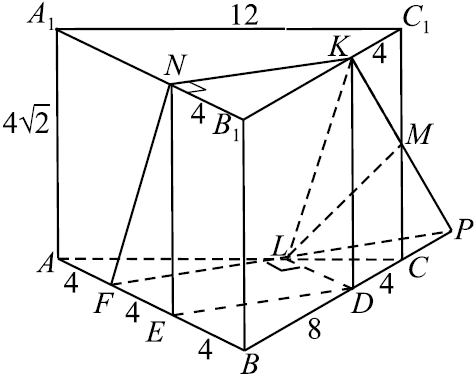
В правильной треугольной призме $ABCA_1 B_1 C_1$ сторона основания равна $12$, а боковое ребро равно $4√ {2}$. На рёбрах $AB$, $A_1 B_1$ и $B_1 C_1$ отмечены точки $F$, $N$ и $K$ соответственно, причём $AF=B_1 N=C_1 K =4$.
а) Пусть $L$ — точка пересечения плоскости $FNK$ с ребром $AC$. Докажите, что $FNKL$ — ромб.
б) Найдите площадь сечения призмы плоскостью $FNK$.
Решение
а) Докажем, что $FNKL$ — ромб.
1) Так как точка $L$ — точка пересечения плоскости $FNK$ с ребром $AC$, то (по свойству параллельных плоскостей) линии пересечения плоскости $FNK$ с основанием призмы параллельны, т.е $FL ‖ N K$.
2) В основаниях правильной треугольной призмы лежат правильные треугольники со стороной $12$.
В треугольнике $NB_1K$ $∠B1 = 60°, NB_1 = 4$ по условию, а $B_1 K = 12 — 4 = 8$. По теореме косинусов $N K = 4√3$, поэтому $N K^2 + NB_1^2 = KB_1^2$. Отсюда следует, что $∠N = 90°, ∠K = 30°$.
Значит, $N K ⊥ A_1B_1$ и $F L ⊥ AB$, т.к. $N K ‖ F L$, а $A_1B_1 ‖ AB$.
3) В $△AFL$ $∠A = 60°, ∠F = 90°, AF = 4$;
$AF$ в прямоугольном $△AFL$ лежит против $∠L = 30°$, следовательно, $AF = {1}/{2}AL, AL = AF · 2 = 4 · 2 = 8$;
$FL^2 = AL^2 — AF^2 = 8^2 — 4^2 = 64 — 16 = 48, F L = 4√3$.
Имеем $N K ‖ F L$ и $N K = F L$, следовательно $F N K L$ — параллелограмм.
Проведём $N E ⊥ F B$.
В $△NFE$ $∠E = 90°, N E = 4√2, F E = 12 — 8 = 4$.
$FN^2 = NE^2 + FE^2 = (4√2)^2 + 4^2 = 32 + 16 = 48$,
$FN = √48 = 4√3, KL = FN$ как противоположные стороны параллелограмма.
4) Имеем: $N K = K L = F N = F L$, следовательно, $F N K L$ — ромб.
б) $K N ⊥ A_1B_1 , K N ⊥ N E ⇒ K N ⊥ (AA_1B_1)$ и $K N ⊥ F N$, значит $K N F L$ — квадрат, $S_{KNFL} = FN^2 = 48$.
Построим сечение пирамиды плоскостью $FNK$ .
Продлим $FL$ до пересечения с $BC$, получим точку $P$.
Соединим точку $P$ с точкой $K$, $KP$ пересекает $CC_1$ в точке $M$. Соединим точку $M$ с точкой $L$.
Пятиугольник $F N K M L$ — искомое сечение.
В прямоугольном $△FBP$ $∠B = 60°$, значит $BP = 2FB = 16, PC = 16 — 12 = 4$.
$KC_1 = CP, ∠KC_1M = ∠MCP = 90°$, тогда $△KC_1M = △PCM$ и $C_1M = CM = 2√2. KM = √{4^2 + (2√2)^2} = √{24}$. В $△LMC$ $LM^2 = LC^2 + MC^2, LC = AC — AL = 12 — 8 = 4, MC = {1}/{2}CC_1 = 2√2, √{4^2 + (2√2)^2} = √{24}, K L = √{48}$, следовательно, $△KLM$ прямоугольный, $S_{KLM} = {1}/{2}(√{24})^2 = 12$.
$S_{сеч} = S_{KNFL} + S_{KLM} = 48 + 12 = 60$.
Ответ: 60
Задача 7
Дана четырёхугольная пирамида $SABCD$ с прямоугольником $ABCD$ в основании, $AB=6$, $BC=6√ {2}$. Высота пирамиды проектируется в точку пересечения диагоналей основания. Из вершин $A$ и $C$ на ребро $SB$ опущены перпендикуляры $AP$ и $CQ$.
а) Докажите, что точка $P$ является серединой отрезка $BQ$.
б) Найдите угол между плоскостями $SBA$ и $SBC$, если $SD=12$.
Решение
а) Пусть боковое ребро $SB$ равно $x$.
1) $△SHB∼△APB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${PB}/{BH} = {AB}/{SB}$. $H$ — середина $AB$. Тогда ${PB}/{3} = {6}/{x}; PB = {18}/{x}$.
2) $△SKB∼△CQB$ (прямоугольные с общим острым углом при вершине $B$). Тогда ${QB}/{BK} = {BC}/{SB}; {QB}/{3√2} = {6√2}/{x}; QB = {36}/{x}$.
3) Так как ${QB}/{PB} = {{36}/{x}}/{{18}/{x}} = 2$, то $PQ = PB$.
б) 1) Из пункта а) следует, что $PK$ — средняя линия $△BCQ$. Следовательно, $PK ‖ QC$. Но так как $QC ⊥ BS$, то и $PK ⊥ BS$. Значит, $∠APK$ — линейный угол двугранного угла между гранями $SBA$ и $SBC$. Пусть, $∠APK = α$.
2) $AK = √{AB^2 + BK^2} = √{6^2 + (3√2)^2} = 3√6$.
3) Так как по условию $SD = 12$ и $SB = SD$ (равным проекциям соответствуют равные наклонные), то $x = 12$, а $QB = {36}/{x} = {36}/{12}=3$.
Тогда $CQ = √{BC^2 — QB^2} = √{(6√2)^2 — 3^2} = 3√7$.
Так как $PK$ — средняя линия, то $PK = {1}/{2}CQ = {3√7}/{2}$.
4) $PB = {1}/{2}QB = {1}/{2}·3 = {3}/{2}$.
$AP = √{AB^2 — PB^2} = √{6^2 — ({3}/{2})^2} = {3}/{2}√{15}$.
5) По теореме косинусов для $△APK$:
$AK^2 = AP^2 + PK^2 — 2·AP·PK·cosα$;
$54 = {135}/{4} + {63}/{4} — 2·{3}/{2}√{15}·{3√7}/{2}·cosα$;
$cosα = — {1}/{√{105}}$;
Так как $cosα < 0$, то $α$ — тупой угол.
Значит, искомый угол между плоскостями $SBA$ и $SBC$ равен ($π-α$).
$cos(π-α) = -cosα = {1}/{√{105}}$.
Следовательно, искомый угол равен $arccos{1}/{√{105}}$.
Ответ:
Задача 8
Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали граней $AA_1B_1B$ и $BB_1C_1C$ равны $2√ {41}$ и $10$ соответственно, $AB=10$.
а) Докажите, что треугольник $A_1C_1B$ прямоугольный.
б) Найдите объём пирамиды $ACC_1B_1$.
Решение
а) Так как $A_1C_1 ⊥ B_1C_1$ и $A_1C_1 ⊥ CC_1$ по условию, то $A_1C_1 ⊥ BB_1C_1$ по признаку перпендикулярности прямой и плоскости.
Следовательно, $A_1C_1 ⊥ BC_1$, то есть треугольник $A_1C_1B$ прямоугольный.
б) 1) $AC = A_1C_1 = √{A_1B^2 — BC^2_1} = √{(2√{41})^2 — 10^2} = 8$.
2) $B_1C_1 = BC = √{AB^2 — AC^2} = √{10^2 — 8^2} = 6$.
3) $CC_1 = √{BC_1^2 — BC^2} = √{10^2 — 6^2} = 8$.
4) $V_{ACC_1B_1} = {1}/{3}·S_{ACC_1} ·B_1C_1 = {1}/{3} · {1}/{2} ·AC·CC_1 ·B_1C_1 = {1}/{6} ·8·8·6 = 64$.
Ответ: 64
Задача 9
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=3$, $BC=5$, $CD=4$, а высота пирамиды $PABCD$ равна $7$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) Обозначим $BK = x, CK = y$.
1) $△BKC∼ △AKD$, так как $AD ‖ BC$.
Тогда ${AK}/{BK} = {DK}/{CK}; {AB + BK}/{BK} = {CD + CK}/{CK}; {AB}/{BK} + 1 = {CD}/{CK} + 1; {AB}/{BK} = {CD}/{CK}; {3}/{x} = {4}/{y}; x = {3}/{4}y$.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; x^2 + y^2=5^2; ({3}/{4}y)^2+y^2=25; {25}/{16}y^2=25; y=4;x={3}/{4}y=3$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}·3 ·4= 6$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·6·7 = 14$.
Ответ: 14
Задача 10
В основании четырёхугольной пирамиды $PABCD$ лежит трапеция $ABCD$ с большим основанием $AD$. Известно, что сумма углов $BAD$ и $ADC$ равна $90^°$, плоскости $PAB$ и $PCD$ перпендикулярны основанию, прямые $AB$ и $CD$ пересекаются в точке $K$.
а) Докажите, что плоскость $PAB$ перпендикулярна плоскости $PDC$.
б) Найдите объём $PKBC$, если $AB=BC=CD=4$, а высота пирамиды $PABCD$ равна $9$.
Решение
а) 1) $∠AKD = 180° — (∠A + ∠D) = 180° — 90° = 90°$.
2) Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, так же перпендикулярной этой плоскости. Отсюда следует, что так как $PAB ⊥ ABC$ и $PCD ⊥ ABC$, то $PK ⊥ ABC$.
3) Так как $PK ⊥ ABC$, то $PK ⊥ KA$ и $PK ⊥ KD$.
Значит, $∠AKD$ — линейный угол двугранного угла между плоскостями $PAB$ и $PCD$. Следовательно, $PAB ⊥ PCD$.
б) 1) Так как $ABCD$ — равнобедренная трапеция, то $∠A = ∠D$. Так как $BC ‖ AD$, то $∠A = ∠KBC, ∠D = ∠KCB$ как соответственные. Значит, $∠KBC = ∠KCB$, то есть $△KBC$ равнобедренный.
2) По теореме Пифагора $BK^2 + CK^2 = BC^2; 2BK^2 = BC^2; BK^2 = {BC^2}/{2} = {4^2}/{2} = 8$.
3) $S_{KBC} = {1}/{2}BK·CK = {1}/{2}BK^2 = {1}/{2}·8 = 4$.
4) $V_{PKBC} = {1}/{3}S_{KBC}·PK = {1}/{3}·4·9 = 12$.
Ответ: 12
Задача 11
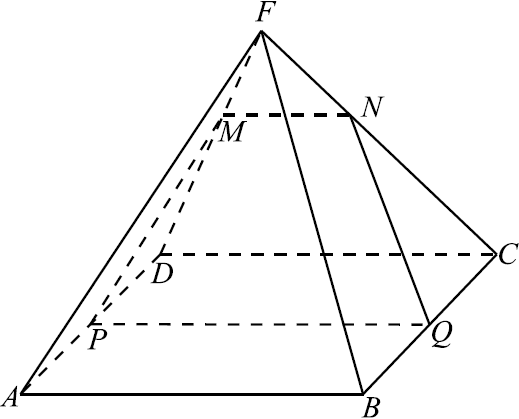
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=1:3$. Точки $P$и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN ‖ CD$.
Так как и $PQ ‖ CD$, то $MN ‖ PQ$. Следовательно, точки $M, N, P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$.
2) $△FMN ∼△FDC$ (так как $MN ‖ CD$, то $∠FNM = ∠FCD$ и $∠FMN = ∠FDC$ как соответственные). Так как $△FCD$ равнобедренный, то и $△FNM$ тоже равнобедренный. Тогда $FM = FN; NC = FC — FN = FD — FM = MD$.
Кроме того, $PD = {1}/{2}AD = {1}/{2}BC = QC$. Так как $△FAD = △FBC$, то $∠MDP = ∠NCQ$. Отсюда $△PDM = △QCN$ по двум сторонам и углу между ними. Следовательно, $PM = NQ$, то есть $MNQP$ — равнобедренная трапеция.
б) 1) Пусть $MR ⊥ PQ, MS ⊥ CD, NX ⊥ PQ, NY ⊥ CD$.
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1 = V_{PQCDMN} = V_{MRSNXY} + 2·V_{NXQCY}$ — объём первой части.
2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC = XY = RS = {a}/{2}; MN = {1}/{3}a; MO = {2}/{3}h(△FMN ∼△FDC$ и ${FM}/{FD} = {1}/{3}; QX = {PQ -MN}/{2} = {a -{1}/{3}a}/{2} = {1}/{3}a (MNQP$ — равнобедренная трапеция).
3) $S_{MRS} = {1}/{2}RS·MO = {1}/{2}·{a}/{2}·{2}/{3}h = {1}/{6}ah$. Объём прямой призмы $MRSNXY$ равен $V_{MRSNXY} = S_{MRS}·MN = {1}/{6}ah·{1}/{3}a = {1}/{18}a^2h$.
$V_{NXQCY} = {1}/{3}S_{XQCY}·MO = {1}/{3}·QX·QC·MO = {1}/{3}·{1}/{3}a·{a}/{2}·{2}/{3}h = {1}/{27}a^2h$.
$V_1 = V_{MRSNXY} + 2·V_{NXQCY} = {1}/{18}a^2h + 2·{1}/{27}a^2h = {7}/{54}a^2h$.
4) $V = V_{SABCD} = {1}/{3}S_{ABCD}·h = {1}/{3}a^2h$.
$V_2 = V — V_1 = ({1}/{3} — {7}/{54})a^2h = {11}/{54}a^2h$ — объём второй части.
5) ${V_1}/{V_2} ={{7}/{54}a^2h}/{{11}/{54}a^2h} = {7}/{11}$.
Ответ: 7:11
Задача 12
На боковом ребре $FD$ правильной четырёхугольной пирамиды ${FABCD}$ отмечена точка $M$ так, что $FM:FD=2:5$. Точки $P$ и $Q$ — середины рёбер $AD$ и $BC$ соответственно.
а) Докажите, что сечение пирамиды плоскостью $MPQ$ есть равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость $MPQ$ разбивает пирамиду.
Решение
а) 1) Построим $MN∥ CD$ (см. рис.).
Так как и $PQ∥ CD$, то $MN∥ PQ$. Следовательно, точки $M$, $N$, $P$ и $Q$ лежат в одной плоскости. Таким образом, трапеция $MNQP$ является сечением пирамиды плоскостью $MPQ$. 2) $▵ FMN∼ ▵ FDC$ (так как $MN∥ CD$, то $∠ FNM=∠ FCD$ и $∠ FMN=∠ FDC$ как соответственные). Так как $▵ FDC$ равнобедренный, то и $▵ FMN$ тоже равнобедренный. Тогда $FM=FN$; $NC=FC-FN=FD-FM=MD$. Кроме того, $PD={1} / {2}AD={1} / {2}BC=QC$. Так как $▵ FAD=▵ FBC$, то $∠ MDP=∠ NCQ$. Отсюда $▵ PDM=▵ QCN$ по двум сторонам и углу между ними. Следовательно, $PM=NQ$, то есть $MNQP$ — равнобедренная трапеция. б) 1) Пусть $MR⊥ PQ$, $MS⊥ CD$, $NX⊥ PQ$, $NY⊥ CD$ (см. рис.).
Так как $MNQP$ и $MNCD$ — равнобедренные трапеции, то $V_1=V_{PQCDMN}=V_{MRSNXY}+2⋅ V_{NXQCY}$ — объём первой части. 2) Пусть $a$ — сторона основания, $h$ — высота пирамиды. Тогда $QC=XY=RS={a} / {2}$; $MN={2} / {5}a$; $MO={3} / {5}h$ $(▵ FMN∼ ▵ FDC$ и ${FM} / {FD}={2} / {5})$; $QX={PQ-MN} / {2}={a-{2} / {5}a} / {2}={3} / {10}a$ ($MNQP$ — равнобедренная трапеция). 3) $S_{MRS}={1} / {2}RS⋅ MO={1} / {2}⋅ {a} / {2}⋅ {3} / {5}h={3} / {20}ah$. Объём прямой призмы $MRSNXY$ равен: $V_{MRSNXY}=S_{MRS}⋅ MN={3} / {20}ah⋅ {2} / {5}a={3} / {50}a^2h$. $V_{NXQCY}={1} / {3}S_{XQCY}⋅ MO={1} / {3}⋅ QX⋅ QC⋅ MO={1} / {3}⋅ {3} / {10}a⋅ {a} / {2}⋅ {3} / {5}h={3} / {100}a^2h$. $V_1=V_{MRSNXY}+2⋅ V_{NXQCY}={3} / {50}a^2h+2⋅ {3} / {100}a^2h={3} / {25}a^2h$. 4) $V=V_{SABCD}={1} / {3}S_{ABCD}⋅ h={1} / {3}a^2h$. $V_2=V-V_1=({1} / {3}-{3} / {25})a^2h={16} / {75}a^2h$ — объём второй части. 5) ${V_1} / {V_2}={{3} / {25}a^2h} / {{16} / {75}a^2h}={9} / {16}$.
Ответ: 9:16
Задача 13
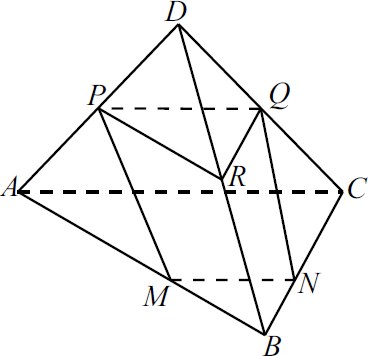
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=2:1$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны).
Значит $∠NMB = ∠CAB$. Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB$. Аналогично $QR ‖ BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {1}/{3}$, то $S_1 = ({1}/{3})^2·S = {S}/{9}$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({S}/{9} + √{{S}/{9}·{S}/{4}} + {S}/{4}) = {h}/{6}({S}/{9} + {S}/{6} + {S}/{4})= {19}/{216}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{216}Sh = {7}/{54}Sh. V_2 = V — V_1 = {1}/{3}Sh — {7}/{54}Sh = {11}/{54}Sh$.
5) ${V_1}/{V_2} = {{7}/{54}Sh}/{{11}/{54}Sh} = {7}/{11}$.
Ответ: 7:11
Задача 14
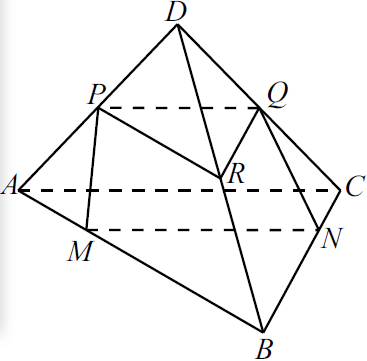
На рёбрах $AB$ и $BC$ треугольной пирамиды $DABC$ отмечены точки $M$ и $N$ так, что $AM:MB=CN:NB=1:3$. Точки $P$ и $Q$ — середины рёбер $DA$ и $DC$ соответственно.
а) Докажите, что точки $P$, $Q$, $M$ и $N$ лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость $PQM$ делит пирамиду.
Решение
а) 1) $△ABC ∼△MBN$ (угол $B$ общий, две пропорциональные стороны). $MB ={3}/{4}AB, BN ={3}/{4}BC$.
Следовательно, $MN ‖ AC$, так как равны соответствующие углы.
2) Так как $PQ$ — средняя линия $△ADC$, то $PQ ‖ AC$.
3) Так как $MN ‖ AC$ и $PQ ‖ AC$, то $MN ‖ PQ$. Следовательно, точки $P, Q, N$ и $M$ лежат в одной плоскости.
б) 1) Пусть $R$ — середина ребра $DB$. Тогда $PR$ — средняя линия $△ADB$. Следовательно, $PR ‖ AB, PR = {1}/{2}AB$. Аналогично $QR ‖ BC, QR = {1}/{2}BC$.
2) Обозначим через $V$ объём пирамиды $DABC, V_1 = V_{DPQR} + V_{MNBPQR}, V_2 = V — V_1, h$ — высота пирамиды $DABC, S$ — площадь $△ABC$.
Так как $△PQR∼ △ACB$ и ${PQ}/{AC} = {1}/{2}$, то $S_{PQR} ={S}/{4}$.
Так как ${DP}/{DA} = {1}/{2}$, то высота пирамиды $DPQR$ равна ${h}/{2}$.
Таким образом, $V_{DPQR} = {1}/{3}S_{PQR}· {h}/{2} = {1}/{3}· {S}/{4} ·{h}/{2} = {Sh}/{24}$.
3) Можно доказать, что $MNBPQR$ — усечёная пирамида. Её высота равна ${h}/{2}$.
Пусть $S_1 = S_{MNB}, S_2 = S_{PQR}$.
Так как $△BMN ∼ △BAC$ и ${BM}/{BA} = {3}/{4}$, то $S_1 = ({3}/{4})^2·S = {9}/{16}S$.
Тогда $V_{MNBPQR} = {1}/{3}·{h}/{2}·(S_1 + √{S_1·S_2} + S_2)= {h}/{6}·({9}/{16}S + √{{9}/{16}S·{S}/{4}} + {S}/{4}) = {h}/{6}({9}/{16}S + {3}/{8}S + {S}/{4})= {19}/{96}Sh$.
4) $V_1 = V_{DPQR} + V_{MNBPQR} = {Sh}/{24} + {19}/{96}Sh = {23}/{96}Sh. V_2 = V — V_1 = {1}/{3}Sh — {23}/{96}Sh = {3}/{32}Sh$.
5) ${V_1}/{V_2} = {{23}/{96}Sh}/{{3}/{32}Sh} = {23}/{9}$.
Ответ: 23:9
Задача 15
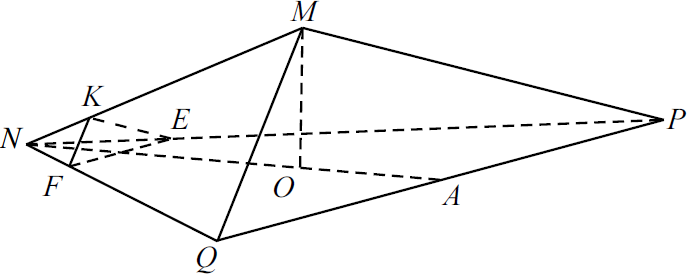
В правильной треугольной пирамиде $MNPQ$ с вершиной $M$ сторона основания равна $15$, высота равна $√ {6}$. На рёбрах $NP$, $NQ$ и $NM$ отмечены точки $E$, $F$, $K$ соответственно, причём $NE=NF=3$ и $NK={9} / {5}$. а) Докажите, что плоскости $EFK$ и $MPQ$ параллельны. б) Найдите расстояние от точки $K$ до плоскости $MPQ$.
Решение
а) Докажем, что $EFK ‖ MPQ$. Воспользуемся признаком параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
В плоскости $MPQ$ возьмём прямые $QP$ и $MQ$, а в плоскости $EFK$ — прямые $FE$ и $KF$. Пусть $O$ — центр основания.
В $△MNO: ∠NOM = 90°$ и по теореме Пифагора $NM = √{NO^2 +MO^2}$. Найдём $NO$: треугольник $NPQ$ — правильный, все его стороны равны, а высота $NA = {a√3}/{2}$, где $a$ — сторона треугольника $NPQ$. $NO = {2}/{3}NA = {2}/{3}·{a√3}/{2} = {a√3}/{3}$, то есть $NO = {15√3}/{3} = 5√3$. B $△NMO: ∠MON = 90°, NM = √{MO^2 + NO^2} = √{(5√3)^2 + 6} = √{75 + 6} = √{81} = 9$.
1) $△NKF∼△NMQ$, так как ${NK}/{NM} ={{9}/{5}}/{9} ={1}/{5}, {NF}/{NQ} = {3}/{15} = {1}/{5}$ и $∠MNQ$ — общий. Из подобия следует, что $∠NKF = ∠NMQ$. Это соответственные углы при прямых $KF$ и $MQ$ и секущей $NM$. Значит, $KF ‖ MQ$.
2) $△NEF∼△NPQ$, так как ${NE}/{NP} ={3}/{15} = {1}/{5}, {NF}/{NQ} ={3}/{15} = {1}/{5}$ и $∠PNQ$ — общий. Из подобия следует, что $∠NEF = ∠NPQ$. Это соответственные углы при прямых $EF$ и $PQ$ и секущей $NP$. Значит, $EF ‖ PQ$.
Итак, две пересекающейся прямые $KF$ и $FE$ плоскости $KFE$ соответственно параллельны двум пересекающимся прямым $MQ$ и $PQ$ плоскости $MPQ$, следовательно, $KFE ‖ MPQ$.
б) Найдём расстояние от точки $K$ до плоскости $MPQ$. Так как плоскость $KFE$ параллельна плоскости $MPQ$, то расстояние от точки $K$ до плоскости $MPQ$ равно расстоянию от точки $B$ до плоскости $MPQ$ и оно равно длине отрезка $BD$ ($BD$ — перпендикуляр к $AM$. Докажем это.
$NA ⊥ QP$ и $MA ⊥ QP$ (как высоты треугольников $NPQ$ и $MPQ$), значит, прямая $QP$ перпендикулярна плоскости $NMA$, и тогда прямая $PQ$ перпендикулярна любой прямой этой плоскости, в частности $BD$. С другой стороны $BD ⊥ AM$ по построению, значит, прямая $BD$ перпендикулярна двум пересекающимся прямым плоскости $MPQ$, и тогда отрезок $BD$ перпендикулярен плоскости $MPQ$ и равен расстоянию от $B$ до плоскости $MPQ$.
В $△BDA: ∠BDA = 90°; BD = BA · sin∠DAB; BA = NA — NB; NA = {15√3}/{2}; NB ={1}/{5}NA = {3√3}/{2}; BA = {15√3}/{2} — {3√3}/{2} = 6√3$.
Из $△MOA: sin∠MAO = sin∠DAB = {MO}/{MA} = {√6}/{√{MO^2 + OA^2}}={√6}/{√{6 +{75}/{4}}} = {√6·2}/{√{99}} = {2√6}/{3√{11}} ={2}/{3}√{{6}/{11}}$ (так как $AO ={1}/{3}NA = {5√3}/{2})$.
Из $△ABD:BD = AB·sin∠DAB = 6√3·{2}/{3}√{{6}/{11}} = 4√{{18}/{11}} = 12√{{2}/{11}} = {12√{22}}/{11}$.
Ответ:
Задача 16
В правильной треугольной пирамиде $DABC$ с вершиной $D$ сторона основания $AB$ равна $9$, высота равна $3$. На рёбрах $AB$, $AC$, $AD$ отмечены точки $P$, $K$, $F$ соответственно, причём $AP=AK=3$ и $AF=2$. а) Доказать, что плоскости $PKF$ и $DBC$ параллельны. б) Найти расстояние от точки $F$ до плоскости $DBC$.
Решение
Докажем, что плоскость $DBC$ параллельна плоскости $PKF$. Для этого в плоскости $PKF$ возьмём прямые $KP$ и $FP$, а в плоскости $DBC$ — прямые $CB$ и $DB$ (см. рис.). Пусть $O$ — центр основания.
В $▵ ADO$: $∠ DOA=90°$ и по теореме Пифагора $AD=√ {DO^2+AO^2}$. Найдём $AO$, треугольник $ABC$ — правильный, все его стороны равны, $AM$ — высота, $AM={a√ {3}} / {2}$, где $a$ — сторона $▵ ABC$, $AO={2} / {3} AM={2} / {3}⋅ {a√ {3}} / {2}={a√ {3}} / {3}$, то есть $AO={9√ {3}} / {3}=3√ {3}$, $AD=√ {3^2+(3√ {3})^2}=√ {9+27}=6$. $▵ APF∼ ▵ ABD$, так как ${AF} / {AD}={2} / {6}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ DAB$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ AFP=∠ ADB$. Это соответственные углы при прямых $FP$ и $DB$ и секущей $AD$. Значит, $FP∥ DB$. Аналогично рассуждая, получим, что $▵ AKP∼ ▵ ACB$, так как ${AK} / {AC}={3} / {9}={1} / {3}$, ${AP} / {AB}={3} / {9}={1} / {3}$ и $∠ BAC$ — общий, то есть две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Из подобия следует, что $∠ APK=∠ ABC$. Это соответственные углы при прямых $KP$ и $BC$ и секущей $AB$. Значит, $KP∥ BC$. Итак, две пересекающиеся прямые $KP$ и $FP$ плоскости $PKF$ соответственно параллельны двум пересекающимся прямым $CB$ и $BD$ плоскости $DBC$. Следовательно, плоскости $DBC$ и $PKF$ параллельны по признаку параллельности плоскостей. б) Найдём расстояние от точки $F$ до плоскости $DBC$. Так как плоскость $KFP$ параллельна плоскости $DBC$, то расстояние от точки $F$ до плоскости $DBC$ равно расстоянию от точки $L$ до плоскости $DBC$ и равно длине отрезка $LN$ (см. рис.), где $LN$ — перпендикуляр к $MD$ в плоскости $AMD$.
Докажем это. $AM ⊥ BC$ и $DM⊥ BC$ (как высоты треугольников $ABC$ и $DBC$), значит, $BC⊥ MDA$ и тогда $BC$ перпендикулярен любой прямой этой плоскости, в частности, $LN$. С другой стороны, $LN ⊥ MD$ по построению, значит, $LN$ перпендикулярен двум пересекающимся прямым плоскости $DBC$, и тогда отрезок $LN$ перпендикулярен плоскости $DBC$ и равен расстоянию от точки $L$ до плоскости $DBC$. В $▵ LNM$: $∠ LNM=90°$, $LN=LM⋅ sin ∠ NML$. $ML=AM-LA$; $AM={9√ {3}} / {2}$;
$LA={1} / {3}⋅ AM={9√ {3}} / {6}={3√ {3}} / {2}$. $ML={9√ {3}} / {2}-{3√ {3}} / {2}=3√ {3}$. $sin ∠ NML={DO} / {DM}$; $DO=3$ (по условию). Из $▵ MDB$ найдём $DM$: $∠ DMB=90°$,
$MD=√ {BD^2-MB^2}=√ {36-({9} / {2})^2}={3√ {7}} / {2}$. $sin ∠ NML={2} / {√ {7}}$. $LN=LM⋅ sin ∠ NML=3√ {3}⋅{2} / {√ {7}}=6√ {{3} / {7}}$.
Ответ: 6sqrt{fsm{3}{7}}
Задача 17
В правильной треугольной пирамиде $BMNK$ с основанием $MNK$ сторона основания равна $6$, а высота пирамиды равна $3$. На рёбрах $MN, MK$ и $MB$ соответственно отмечены точки $F, E$ и $P$, такие, что $MF = ME ={√{21}}/{2}$ и $MP ={7}/{4}$.
а) Докажите, что плоскости $FEP$ и $NBK$ параллельны.
б) Найдите расстояние от точки $P$ до плоскости $NBK$.
Решение
а) Пусть $BO -$ высота пирамиды. Чтобы доказать, что плоскости $FEP$ и $NKB$ параллельны, достаточно показать, что две пересекающиеся прямые $PF$ и $FE$ плоскости $FEP$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $BNK$. Покажем это.
Найдём боковое ребро $MB$ из треугольника $MBO$:
В $∆MKN:$ $MO_1 -$ высота, $MO_1 = {a√3}/{2}$, где $a -$ сторона $∆MNK$. $MO_1 = {6√3}/{2} = 3√3$.
$MO ={2}/{3} MO_1 = 2√3$,
$MB = √{OB^2 + OM^2} = √{3^2 + (2√3)^2} = √{21}$.
1. ${MP}/{MB} ={7}/{4·√{21}}={√{21}}/{12},{MF}/{MN} ={√{21}}/{2·6} = {√{21}}/{12}$. Отношения сторон равны. Используя условие, что $∠BMN$ общий, получим: $∆MPF∼∆MBN$. Из подобия треугольников следует, что $∠MPF = ∠MBN$. Эти углы — соответственные, образованные при пересечении двух прямых $PF$ и $BN$ прямой $MB$. Значит, $PF ‖ BN$.
2. Рассматривая треугольники $MEF$ и $MKN$, можно аналогично доказать, что $FE ‖ NK$.
Так как две пересекающиеся прямые $PF$ и $FE$ плоскости $PFE$ соответственно параллельны двум пересекающимся прямым $BN$ и $NK$ плоскости $NBK$, то эти плоскости параллельны.
б) Пусть $O_2$ — точка пересечения $MO_1$ и $FE$. Поскольку плоскость $PFE$ параллельна плоскости $BNK$, то расстояние от точки $P$ до плоскости $BNK$ равно расстоянию от точки $O_2$ до плоскости $BNK$, и оно равно длине отрезка $O_2H$, где точка $H$ лежит на $BO_1$ и $O_2H ⊥ BO_1$. Докажем, что $O_2H$ — расстояние от $O_2$ до плоскости $BNK$.
$NK ⊥ MO_1$ и $NK ⊥ BO_1$ ($MO_1$ и $BO_1$ — высоты $∆MNK$ и $∆NBK$), значит, $NK$ перпендикулярна плоскости $MBO_1$, и тогда $NK$ перпендикулярна любой прямой этой плоскости, в том числе $NK ⊥ O_2H$. По построению $O_2H ⊥ BO_1$. Прямая $O_2H$ перпендикулярна двум пересекающимся прямым плоскости $BNK$, значит, она перпендикулярна $BNK$, и отрезок $O_2H$ равен расстоянию от $O_2$ до плоскости $BNK$.
В треугольнике $O_2HO_1: O_2H = O_2O_1 sin∠HO_1O_2$.
$O_2O_1 = MO_1-MO_2$.
Из $∆MEO_2: ∠MO_2E = 90°, ∠EMO_2 = 30°$;
$MO_2 = MEcos30° = {√{21}}/{2}·{√3}/{2} = {3√7}/{4}$.
$O_2O_1 = 3√3 — {3√7}/{4} = {3(4√3 — √7)}/{4}$;
$sin ∠HO_1O_2 = {BO}/{BO_1} = {BO}/{√{BO^2 + OO_1^2}} = {3}/{√{3^2 + (√3)^2}} = {√3}/{2}$.
$O_2H = {3(4√3 — √7)}/{4}·{√3}/{2} = {3(12 — √{21})}/{8}$.
Ответ: ${3(12-√{21})}/{8}$
Задача 18
В прямоугольном параллелепипеде $ABCDA_{1}B_{1}C_{1}D_{1}$ стороны оснований $AB$ и $BC$ равны соответственно $8$ и $5$, а боковое ребро $AA_1$ равно $4$. На ребре $A_{1}B_1$ отмечена точка $K$, а на луче $BC$ — точка $F$, причём $A_{1}K = KB_1$ и $BF = AB$. Плоскость $AKF$ пересекает ребро $B_{1}C_1$ в точке $P$.
а) Докажите, что $B_{1}P : PC_1 = 4 : 1$.
б) Найдите площадь сечения параллелепипеда плоскостью $AKF$.
Решение
а) Построим сечение параллелепипеда плоскостью $AKF$.
$E$ — точка пересечения ребра $DC$ и отрезка $AF$.
$В$ плоскости $ABB_1$ проведём лучи $AK$ и $BB_1, AK$ пересекает $BB_1$ в точке $Q$. В плоскости $BCC_1$ проведём отрезок $FQ, FQ$ пересекает $B_1C_1$ в точке $P$, а $CC_1$ — в точке $R$. Пятиугольник $AKPRE$ — искомое сечение.
$KB_1 ‖ AB, KB_1 ={1}/{2}A_1B_1$, значит, $KB_1$ — средняя линия $△ABQ$, отсюда $BB_1 = QB_1$, а так как $BF ‖ B_1P$, то $B_1P$ — средняя линия $△FBQ, BF = 8, B_1P ={1}/{2}BF = 4. C_1P = B_1C_1 — B_1P = 5 — 4 = 1$, следовательно, $B_1P : PC_1 = 4 : 1$.
б) Прямоугольные треугольники $ABQ, FBQ$ и $ABF$ равны по двум катетам $AB = BF = BQ = 8$, отсюда $AQ = AF = QF = 8√2$. $S_{AQF} ={a^2√3}/{4}$ как площадь равностороннего треугольника со стороной $a$. $S_{AQF} = {(8√2)^2·√3}/{4} = 32√3, S_{KQP} ={1}/{4}S_{AQF}={32√3}/{4} = 8√3$.
$S_{AKPF} = S_{AQF} — S_{KQP} = 32√3 — 8√3 = 24√3$.
$△RCF~△RC_1P$ по первому признаку подобия $(∠C = ∠C_1 = 90°, ∠1 = ∠2$ как вертикальные). Из подобия следует ${CF}/{PC_1} ={FR}/{PR}$. По доказанному в а) $PC_1 = 1, BF = AB = 8$, тогда $CF = 8 — 5 = 3$ и ${FR}/{PR} ={3}/{1}$. Так как $KP$ средняя линия $△AQF$, то $PF ={1}/{2}QF = 4√2, FR = {3PF}/{4} = {4√2·3}/{4} = 3√2$.
В равнобедренном прямоугольном треугольнике $FCE$ $FC = EC = 3$, тогда $EF = 3√2$.
В $△REF$ $FR = EF = 3√2, ∠RFE = 60°$, отсюда $△REF$ — равносторонний. $S_{REF} ={(3√2)^2√3}/{4} = {9√3}/{2}$.
$S_{AKPRE} = S_{AKPF} — S_{REF} = 24√3 — {9√3}/{2} = {39√3}/{2}$.
Ответ: ${39√3}/{2}$

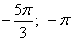
F(x).png)