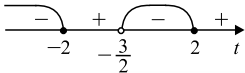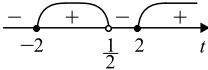ЕГЭ Профиль №14. Логарифмические неравенства
Прототипы задания №14 ЕГЭ по математике профильного уровня — неравенства. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №14 необходимо уметь решать уравнения и неравенства.
Практика
| time4math.ru | Скачать задания |
| math100.ru | Рациональные неравенства
Неравенства с модулями Показательные неравенства Логарифмические неравенства Логарифмические неравенства с переменным основанием |
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 15
Связанные страницы:
Задание 11 ЕГЭ по математике профильный уровень — наибольшее и наименьшее значение функций
Решение 17 задания ЕГЭ по профильной математике
Задание 5 ЕГЭ по математике профильный уровень — стереометрия
Задание 4 ЕГЭ по математике (профиль) — вычисления и преобразования
Задание 11 ЕГЭ 2022 по математике: «Наибольшее и наименьшее значения функции»
За это задание ты можешь получить 2 балла. На решение дается около 15 минут. Уровень сложности: повышенный.
Средний процент выполнения: 20.8%
Ответом к заданию 14 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Задачи для практики
Задача 1
Решите неравенство: $log_7^2(9-x^2)-10log_7(9-x^2)+21⩾ 0$.
Решение
$log_7^2(9 — x^2) — 10 log_7(9 — x^2) + 21 ≥ 0$.
Обозначим $log_7 (9 — x^2) = t$. Неравенство примет вид: $t^2 — 10t + 21 ≥ 0, (t — 3)(t — 7) ≥ 0$, отсюда $t ≤ 3, t ≥ 7$.
${tablelog_7 (9 — x^2) ≤ 3; 9 — x^2 ≥ 0;$ или ${tablelog_7 (9 — x^2) ≥ 7; 9 — x^2 ≥ 0;$ ${table9-x^2 ≤ 7^3; x^2
${tablex^2 ≥ 9 — 7^3; x^2
Отсюда $x ∈ (-3; 3)$.
Ответ: ($-3;3$)
Показать решение
Полный курс
Задача 2
Решите неравенство: ${4^{x}+16} / {4^x-16}+{4^x-16} / {4^x+16}⩾{4⋅ 4^{x+1}+480} / {16^x-256}$.
Решение
${4^x+16}/{4^x — 16} + {4^x — 16}/{4^x +16} ≥ {4·4^{x+1} + 480}/{16^x — 256}$;
${(4^x +16)^2 + (4^x — 16)^2}/{(4^x — 16)(4^x +16)} ≥ {4·4^{x+1} + 480}/{(4^x — 16)(4^x + 16)}$,
${4^{2x} +32 · 4^x + 256 + 4^{2x} — 32 · 4^x + 256-480-16· 4^x}/{(4^x — 16)(4^x +16)} ≥ 0$,
${4^{2x} — 8 · 4^x + 16}/{(4^x — 16)(4^x +16)} ≥ 0$,
${(4^x — 4)^2}/{(4^x — 16)(4^x +16)} ≥ 0$.
Обозначим $4^x = t, t > 0$ и найдём решения неравенства ${(t — 4)^2}/{(t — 16)(t +16)} ≥ 0$.
Числитель положительное число, либо равное нулю при $t = 4$, то есть $4^x = 4, x = 1$.
Знаменатель — положительное число при $t 16$.
А так как $t > 0$, то $t > 16$, то есть $4^x > 16, x > 2$.
Итак, $x ∈ {1}∪(2; +∞)$.
Ответ:
Показать решение
Полный курс
Задача 3
Решите неравенство: ${6} / {log_4x}-{log_4x} / {log_4{x} / {256}}⩾{15} / {log_4x^4-log_4^2x}$.
Решение
${6}/{log_4x} — {log_4x}/{log_4{x}/{256}} ≥ {15}/{log_4x^4-log_4^2x}$
ОДЗ: $x > 0, x ≠ 256, x ≠ 1$.
${6}/{log_4x} — {log_4x}/{log_4x-4} ≥ {15}/{4log_4x-log_4^2x}$;
${6}/{log_4x} — {log_4x}/{log_4x-4} ≥ {15}/{log_4x(4-log_4x)}$.
${6(log_4x-4)-log_4^2x}/{log_4x(log_4x-4)} ≥ {-15}/{log_4x(log_4x-4)}$.
${6log_4x-24-log_4^2x+15}/{log_4x(log_4x-4)} ≥ 0$
${log_4^2x-6log_4x+9}/{log_4x(log_4x-4)}≤ 0$
${(log_4x-3)^2}/{log_4x(log_4x-4)}≤ 0$
Обозначим $log_4 x = t$. Неравенство примет вид: ${(t — 3)^2}/{t(t — 4)} ≤ 0$.
Решим это неравенство методом интервалов.
Итак, $0
Ответ: (1;256)
Показать решение
Полный курс
Задача 4
Решите неравенство ${50⋅ 3^x-100+50⋅ 3^{-x}} / {3^x+3^{-x}+2}-{20+20⋅ 3^x} / {3^x+1}⩽ {3^{x+1}⋅ 5-15} / {3^x+1}$.
Решение
${50·3^x — 100 + 50 · 3^{-x}}/{3^x + 3^{-x} + 2} — {20 + 20 · 3^x}/{3^x + 1} ≤ {5· 3^{x+1} — 15}/{3^x + 1}$.
Выполним преобразования, обозначив $3^x = t, t > 0$.
${50t +{50}/{t} — 100}/{t + {1}/{t} + 2} — {20 + 20t}/{t + 1} ≤ {15t — 15}/{t + 1}$,
${50(t^2 — 2t + 1)}/{t^2 + 2t + 1} — {20(1 + t)}/{t + 1} ≤ {15(t — 1)}/{t + 1}$
Так как $t > 0$, то ${t^2 + 2t + 1}>0$ и ${t + 1}>0$
Значит мы можем привести неравенство к следующему виду
$50(t^2 — 2t + 1) — 20(t + 1)^2 — 15(t — 1)(t + 1) ≤ 0$,
$50t^2 — 100t + 50 — 20t^2 — 40t — 20 — 15t^2 + 15 ≤ 0$,
$15t^2 — 140t + 45 ≤ 0, 3t^2 — 28t + 9 ≤ 0$.
$3t^2 — 28t + 9 = 0, D = 28^2 — 27 · 4 = 676 = 26^2$.
$t_1 ={1}/{3}, t_2 = 9$.
Решением неравенства $3t^2 — 28t + 9 ≤ 0$ будет $t ∈ [{1}/{3}; 9]$.
Переходя к переменной $x$, получаем $3^x ∈ [{1}/{3}; 9], x ∈ [-1; 2]$.
Ответ: [$-1;2$]
Показать решение
Полный курс
Задача 5
Решите неравенство ${45⋅ 2^x-90+45⋅ 2^{-x}} / {2^x+2+2^{-x}}-{21⋅ 2^x+21} / {2^x+1}⩽{2^{x+3}-8} / {2^x+1}$.
Решение
${45(2^x+2^{-x}-2)} / {2^x+2^{-x}+2}-{21(2^x+1)} / {2^x+1}⩽ {2^3(2^x-1)} / {2^x+1}$
Выполним преобразования, обозначим $2^x=t$, $t>0$
Тогда неравенство примет вид: ${45(t+{1} / {t}-2)} / {t+{1} / {t}+2}-{21(t+1)} / {t+1}⩽ {8(t-1)} / {t+1}$, ${45⋅ (t-1)^2} / {(t+1)^2}-21⩽ {8(t-1)} / {t+1}$, ${45(t-1)^2} / {(t+1)^2}-{8(t-1)} / {t+1}-21⩽0$, ${45(t-1)^2-8(t^2-1)-21(t+1)^2} / {(t+1)^2}⩽ 0$; $(t+1)^2>0$
Cледовательно, $45(t-1)^2-8(t^2-1)-21(t+1)^2⩽ 0$, $45t^2-90t+45-8t^2+8-21t^2-42t-21⩽ 0$, $16t^2-132t+32⩽ 0$, $16t^2-132t+32=0$, $4t^2-33t+8=0$, $D=33^2-32⋅ 4=961=31^2$. $t_{1, 2}={33±31} / {8}$, $t_1=8$; $t_2={2} / {8}={1} / {4}$
Решением неравенства $4t^2-33t+8⩽ 0$ будет $t∈ [{1} / {4};8]$, то есть, переходя к переменной $x$, получаем $2^x∈ [{1} / {4};8]$, $x∈ [-2;3]$.
Ответ: [-2;3]
Показать решение
Полный курс
Задача 6
Решите неравенство ${3log_{9}x+1}/{2log_{9}x+3}≤3-log_{9}x$.
Решение
Преобразуем исходное неравенство: ${(3log_9x +1)- (3-log_9x)(2log_9x + 3)}/{2log_9x +3} ≤ 0$.
Обозначим $log_9x = t$.
Тогда неравенство примет вид: ${3t + 1- (3-t)(2t+3)}/{2t+3} ≤ 0$.
${2t^2 − 8}/{2t +3} ≤ 0, {(t − 2)(t + 2)}/{t +{3}/{2}} ≤ 0.$
Последнее неравенство решим методом интервалов.
$(t − 2)(t + 2) = 0, t = -2; t = 2.$
$t +{3}/{2} ≠ 0, t ≠-{3}/{2}.$
Получим $t ∈ (−∞; -2] ∪ (-{3}/{2}; 2].$
Вернёмся к исходной переменной.
$[table{{tablelog_9x >-{3}/{2}; log_9x ≤2;}; log_9x ≤-2;$ $[table{{tablex >(9^{{3}/{2}})^{-1};
$[table{{tablex >(27)^{-1}; {1}/{27};
Ответ: $(0;{1}/{81}]∪({1}/{27};81]$
Показать решение
Полный курс
Задача 7
Решите неравенство ${11log_{4}x-28}/{2log_{4}x-1}≥4-3log_{4}x$.
Решение
Преобразуем исходное неравенство: ${11log_4x − 28 + (3log_4x − 4)(2log_4x − 1)}/{2log_4x − 1} ≥ 0$.
Обозначим $log_4x = t$.
Тогда неравенство примет вид: ${11t − 28 + 6t^2 − 11t + 4}/{2t − 1} ≥ 0$.
${6t^2 − 24}/{2t − 1} ≥ 0, {(t − 2)(t + 2)}/{t −{1}/{2}} ≥ 0.$
Последнее неравенство решим методом интервалов.
$(t − 2)(t + 2) = 0, t = 2; t = −2.$
$t −{1}/{2} ≠ 0, t ≠{1}/{2}.$
Получим $t ∈ [−2; {1}/{2}) ∪ [2; +∞).$
Вернёмся к исходной переменной.
$[table{{tablelog_4x ≥-2; log_4x
$[table{{tablex ≥{1}/{16};
Ответ: $[{1}/{16};2)∪[16;+∞]$
Показать решение
Полный курс
Задача 8
Решите неравенство ${1}/{log_{x}0.5}+6≥16log_{4x}2$.
Решение
ОДЗ уравнения ${tablex > 0; x≠1; x≠{1}/{4};$.
Т.к. ${1}/{log_x0.5}=-{1}/{log_x2}=-log_2x$, а $log_{4x}2 = {1}/{{log_{2} x} + 2}$, то неравенство примет вид $-log_{2}x + 6 ≥ {16}/{{log_{2}x} + 2}$. Пусть $log_2x = t$, тогда ${16}/{t +2}+t-6 ≤ 0, {(t − 2)^2}/{t + 2} ≤ 0, t = 2$ или $t
$log_2x = 2$, откуда $x = 4$ или $log_2x
Ответ: $(0;{1}/{4}),4$
Показать решение
Полный курс
Задача 9
Решите неравенство $log_3(x — 1) ≤ 4 — 9 log_{9(x-1)}3$.
Решение
ОДЗ уравнения ${tablex-1 > 0; 9(x-1)≠1;$ то есть $x > 1, x ≠{10}/{9}$.
Используя формулу $log_ab ={log_cb}/{log_ca}$, получаем $log_{9(x−1)}3 = {1}/{log_3(x − 1) + 2}$.
Неравенство примет вид $log_3(x − 1) ≤ 4 − {9}/{log_3(x − 1) + 2}$. Пусть $log_3(x − 1) = t$, тогда $t − 4 + {9}/{t + 2} ≤ 0, {(t − 1)^2}/{t + 2} ≤ 0, t = 1$ или $t
$log_3(x − 1) = 1$, откуда $x − 1 = 3, x = 4$ или $log_3(x − 1)
Ответ: $(1;{10}/{9}),4$
Показать решение
Полный курс
Задача 10
Решите неравенство $2 log_{x}3 + 3log_{3x}3 ≤ 2$.
Решение
Заметим, что $x > 0, x ≠ {1}/{3}, x ≠ 1$.
Используя свойства логарифмов, преобразуем неравенство:
${2}/{log_{3}x} + {3}/{log_{3}3x} ≤ 2,$
${2}/{log_{3}x} + {3}/{log_{3}3 + log_{3}x} ≤ 2,$
${2}/{log_{3}x} + {3}/{1 + log_{3}x} ≤ 2$
Пусть $log_{3}x = t$, тогда получим неравенство, которое удобно решить методом интервалов:
${2}/{t} + {3}/{1 + t} ≤ 2$,
${2(1 + t) + 3t − 2t(1 + t)}/{t(1 + t)} ≤ 0$,
${2t^2 − 3t − 2}/{t(1 + t)} ≥ 0$,
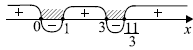
${(2t + 1)(t − 2)}/{t(t + 1)} ≥ 0.$

Получим два простых неравенства и одно двойное, решим их, возвращаясь к переменной $x$:
$t
$log_3x
$0
Так как найденные значения переменной удовлетворяют ОДЗ, то решение неравенства — $(0; {1}/{3})∪[{1}/{√3};1) ∪ [9; +∞)$.
Ответ: $(0;{1}/{3})∪[{1}/{√3};1)∪[9;+∞)$
Показать решение
Полный курс
Задача 11
Решите неравенство $(x^2+2x-3)log_{2x-1}(4x^2-11x+7)≤0$.
Решение
$(x^2 + 2x − 3) log_{2x−1}(4x^2 − 11x + 7) ≤ 0$
ОДЗ: ${table2x − 1 > 0; 2x − 1 ≠ 1; 4x^2 − 11x + 7 > 0;$ ${tablex > {1}/{2}; x ≠ 1; [tablex {7}/{4};$ $x ∈({1}/{2}; 1)∪({7}/{4}; +∞)$
Применяя метод рационализации, получим, что на ОДЗ исходное неравенство равносильно неравенству:
$(x^2 + 2x − 3)(2x − 1 − 1)(4x^2 − 11x + 7 − 1) ≤ 0;$
$(x − 1)(x + 3)(2x − 2)(4x^2 − 11x + 6) ≤ 0;$
$(x − 1)^2(x + 3)(x − 2)(x − {3}/{4})≤ 0.$
Из рисунка следует, что ${3}/{4}≤ x
Ответ: $[{3}/{4};1)∪({7}/{4};2]$
Показать решение
Полный курс
Задача 12
Решите неравенство $6^x√{15-x^2-2x}≥36√{15-x^2-2x}$.
Решение
Будем использовать метод интервалов, предварительно найдя ОДЗ и нули левой части неравенства. Преобразуем неравенство.
$(6^x-36)√{15 — x^2 — 2x} ≥ 0$
Найдём ОДЗ неравенства:
$-x^2 — 2x + 15 ≥ 0; x^2 + 2x — 15 ≤ 0; (x — 3)(x + 5) ≤ 0; x ∈ [-5; 3].$
Выражение $√{15 — x^2 — 2x}$ неотрицательно при любом допустимом значении $x$, значит неравенство выполняется при $6^x ≥ 36, 6^x ≥ 6^2, x ≥ 2$, а также если $√{15 — x^2 — 2x}=0; x^2 + 2x — 15 = 0; x_1 = -5, x_2 = 3$.
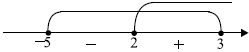
Учтём ОДЗ и найдём знаки левой части неравенства.
$x ∈ [2; 3] ∪$ {$-5$}.
Ответ: $[2;3]∪${-5}
Показать решение
Полный курс
Задача 13
Решите неравенство $log_{|x-2|}(4 + 7x — 2x^2)≥2$.
Решение
$log_{|x-2|}(4 + 7x−2x^2) ≥ 2$.
ОДЗ:
${table 4 + 7x−2x^2 > 0; x -2≠0; {|x -2|} ≠ 1;$
${table 2x^2 −7x−4
${table (x + 0.5)(x−4)
$x ∈ (−0.5;1)∪(1;2)∪(2;3)∪(3;4)$.
$log_{|x-2|}(4 + 7x−2x^2) ≥ log_{|x-2|}(x -2)^2$.
$log_{|x-2|}(4 + 7x−2x^2)−log_{|x-2|}(x -2)^2 ≥ 0$.
На ОДЗ заменим полученное неравенство равносильными неравенствами, применив дважды метод рационализации:
1) знак $log_{a}f −log_{a}g$ совпадает со знаком $(a−1)(f −g)$.
2) знак $|f|−|g|$ совпадает со знаком $(f − g)(f + g)$.
Применяем 1: $(|x -2|−1)(4 + 7x−2x^2 −x^2 +4x−4) ≥ 0, (|x -2|−1)(−3x^2 + 11x) ≥ 0$.
Разделим обе части неравенства на $−3$.
$(|x -2|−1)(x^2 −{11x}/{3}) ≤ 0$.
Применяем 2: $(x -2−1)(x -2 + 1)x(x−{11}/{3}) ≤ 0, x(x — 3)(x -1)(x−{11}/{3}) ≤ 0$.
$0 ≤ x ≤ 1, 3 ≤ x ≤ {11}/{3}$.
Учитывая ОДЗ, получим:
$0 ≤ x
Ответ: $[0;1)∪(3;{11}/{3}]$
Показать решение
Полный курс
Задача 14
Решите неравенство $log_{|x+4|}(16 + 14x — 2x^2) ≥ 2$.
Решение
$log_{|x+4|}(16 + 14x−2x^2) ≥ 2$.
ОДЗ:
${table 16 + 14x−2x^2 > 0; x + 4≠0; {|x + 4|} ≠ 1;$
${table x^2 −7x−8
${table (x + 1)(x−8)
$x ∈ (−1;8)$.
$log_{|x+4|}(16 + 14x−2x^2) ≥ log_{|x+4|}(x + 4)^2$.
$log_{|x+4|}(16 + 14x−2x^2)−log_{|x+4|}(x + 4)^2 ≥ 0$.
На ОДЗ заменим полученное неравенство равносильными неравенствами, применив дважды метод рационализации:
1) знак $log_{a}f −log_{a}g$ совпадает со знаком $(a−1)(f −g)$.
2) знак $|f|−|g|$ совпадает со знаком $(f − g)(f + g)$.
Согласно 1: $(|x + 4|−1)(16 + 14x−2x^2 −x^2 −8x−16) ≥ 0, (|x + 4|−1)(−3x^2 + 6x) ≥ 0$.
Разделим обе части неравенства на $−3$.
$(|x + 4|−1)(x^2 −2x) ≤ 0$.
Согласно 2: $(x + 4−1)(x + 4 + 1)x(x−2) ≤ 0, x(x + 3)(x + 5)(x−2) ≤ 0$.
$−5 ≤ x ≤ −3, 0 ≤ x ≤ 2$.
Учитывая ОДЗ, получим:
$0 ≤ x ≤ 2$.
Ответ: $[0;2]$
Показать решение
Полный курс
Задача 15
Решите неравенство ${35·3^x}/{4+10·3^x-6·3^{2x}}≥{3^x+2}/{3^{x+1}+1}-{3^{x+1}-1}/{3^x-2}$.
Решение
С помощью замены $3^x = t$, где $t > 0$ приведём неравенство к виду
${35t}/{4 + 10t — 6t^2} ≥ {t + 2}/{3t + 1}- {3t — 1}/{t — 2}$.
$-6t^2 + 10t + 4 = -2(3t^2 — 5t — 2) = -2(t — 2)(3t + 1)$.
${35t}/{-2(t — 2)(3t + 1)} ≥ {(t + 2)(t — 2) — (3t — 1)(3t + 1)}/{(3t + 1)(t — 2)}$
${35t}/{-2(t — 2)(3t + 1)} ≥ {(t^2 — 4) — (9t^2 — 1)}/{(3t + 1)(t — 2)}$
${35t}/{-2(t — 2)(3t + 1)} ≥ {-8t^2 — 3}/{(3t + 1)(t — 2)};$
${35t}/{(t — 2)(3t + 1)} ≤ {16t^2 + 6}/{(3t + 1)(t — 2)};$
${16t^2 — 35t + 6}/{(3t + 1)(t — 2)}≥ 0;$
${16(t — 2)(t — {3}/{16})}/{(3t + 1)(t — 2)}≥ 0;$
${(t — {3}/{16})}/{(3t + 1)} ≥ 0, t ≠ 2.$
$t 2$. С учётом условия $t > 0, {3}/{16} ≤ t 2$. Возвращаясь к переменной $x$, получим, что ${3}/{16} ≤ 3^x 2$, откуда $log_3{3}/{16} ≤ x log_{3}2$.
Ответ: $[log_{3}{3}/{16};log_{3}2)∪(log_{3}2;+∞)$
Показать решение
Полный курс
Задача 16
Решите неравенство ${4^{x}+27·2^{x}+18}/{2^{2x}+8·2^{x}+12}≥1+2^{x}-{2^{x}-3}/{2^{x}+6}$
Решение
${4^x + 27·2^x + 18}/{2^{2x} + 8·2^x + 12} ≥ 1 + 2^x — {2^x — 3}/{2^x + 6}$.
Обозначим $2^x = t, t > 0$. Неравенство примет вид:
${t^2 + 27t + 18}/{t^2 + 8t + 12} ≥ 1 + t — {t — 3}/{t + 6}$,
${t^2 + 8t + 12 + 19t + 6}/{t^2 + 8t + 12} ≥ 1 + t — {t — 3}/{t + 6}$,
$1 + {19t + 6}/{(t + 2)(t + 6)} ≥ 1 + t — {t — 3}/{t + 6}$,
${19t + 6}/{(t + 2)(t + 6)} — t + {t — 3}/{t + 6} ≥ 0$,
$-{t(t^2 + 7t — 6)}/{(t + 2)(t + 6)} ≥ 0$.
Полученное неравенство при условии $t > 0$ равносильно неравенству $t^2 + 7t — 6 ≤ 0$ (так как $t> 0, t + 2 > 0$ и $t + 6 > 0$),
$0
$0
$x ≤ log_2 {√{73} — 7}/{2}$.
Ответ: $(-∞;log_{2}{√{73}-7}/{2}]$
Показать решение
Полный курс
Задача 17
Решите неравенство ${3^{2x}+2·3^{x}+2}/{3^{2x}+2·3^{x}}≤4+{1}/{3^x}-{3·3^{x}+1}/{3^{x}-1}$.
Решение
${3^{2x} + 2·3^x + 2}/{3^{2x} + 2·3^x} ≤ 4 + {1}/{3^x}-{3·3^x + 1}/{3^x — 1}$.
Обозначим $3^x = t, t > 0$. Неравенство примет вид:
${t^2 + 2t + 2}/{t^2 + 2t}≤4 + {1}/{t}-{3t + 1}/{t — 1}$,
$1 + {2}/{t(t + 2)} — 4 — {1}/{t} + {3t + 1}/{t — 1} ≤ 0$,
${3(t + 3)t}/{t(t — 1)(t + 2)} ≤ 0$. Воспользуемся условием $t > 0$.
Так как при этом $t + 3 > 0$ и $t + 2> 0$, то неравенство верно при $t — 1
Ответ: $(-∞;0)$
Показать решение
Полный курс
Задача 18
Решите неравенство $(3x — 7) log_{5x-11}(x^{2} — 8x + 17) ≥ 0$.
Решение
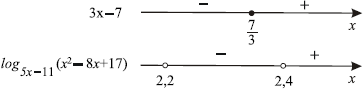
В правой части неравенства стоит $0$, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.
При $x ={7}/{3}$ выражение $3x — 7 = 0$, при $x > {7}/{3}$ выражение $3x — 7 > 0$, а при $x
Рассмотрим выражение $log_{5x-11}(x^2 — 8x + 17)$ и определим его знаки. Заметим, что $x^2 — 8x + 17 = (x — 4)^2 + 1 ≥ 1$ при любых значениях $x$. Значит, при $5x — 11 > 1$, то есть при $x > 2.4$, выражение $log_{5x-11}(x^2 — 8x + 17) > 0$; при $0
Удобно знаки сомножителей отметить на двух параллельных прямых.
Таким образом, решение исходного неравенства: ${11}/{5} 2.4$.
Ответ: $(2.2;2{1}/{3}];(2.4;)+∞)$
Показать решение
Полный курс
Задача 19
Решите неравенство $(7x — 10) log_{4x-3}(x^{2} — 4x + 9) ≥ 0$.
Решение
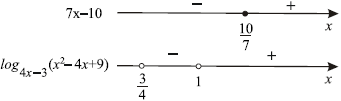
В правой части неравенства стоит $0$, в левой — произведение двух множителей. Определим знаки каждого из этих множителей.
При $x ={10}/{7}$ выражение $7x-10 = 0$, при $x > {10}/{7}$ выражение $7x-10 > 0$, а при $x
Рассмотрим выражение $log_{4x-3}(x^2 — 4x + 9)$. Заметим, что $x^2 — 4x + 9 = (x — 2)^2 + 5 ≥ 5$ при любых значениях $x$. Значит, при $4x — 3 > 1$, то есть при $x > 1$, выражение $log_{4x-3}(x^2 — 4x + 9) >0$, при $0
Удобно знаки сомножителей отметить на двух параллельных прямых.
Таким образом, решение исходного неравенства: ${3}/{4}
Ответ: $(0.75;1);∪[{10}/{7};+∞)$
Показать решение
Полный курс
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Уравнения и неравенства с модулем
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:
Сделаем замену
Тогда , а
Получим:
Решим неравенство относительно t методом интервалов:
Получим:
Вернемся к переменной x:
Ответ:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Ответ:
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством
тоже все просто. Но что делать с неравенством
? Ведь
Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда , и это значит, что
Значение
не достигается ни при каких х.
Но если и
, то
Мы получили:
Ответ:
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Ответ:
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
ОДЗ:
Замена
Ответ:
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Поскольку
Согласно методу замены множителя, выражение заменим на
Получим систему:
Решить ее легко.
Ответ: .
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
ОДЗ:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и
— монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при
значения этой функции меньше 4. Конечно, при этом
, то есть x принадлежит ОДЗ.
Ответ:
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Уравнения и неравенства с модулем
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:
Сделаем замену
Тогда , а
Получим:
Решим неравенство относительно t методом интервалов:
Получим:
Вернемся к переменной x:
Ответ:
Показательные неравенства
2. Решите неравенство
Сделаем замену Получим:
Умножим неравенство на
Дискриминант квадратного уравнения
Значит, корни этого уравнения:
Разложим квадратный трехчлен на множители.
. Вернемся к переменной x.
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Ответ:
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.
3. Решите неравенство
Сделаем замену Получим:
Вернемся к переменной
Первое неравенство решим легко: С неравенством
тоже все просто. Но что делать с неравенством
? Ведь
Представляете, как трудно будет выразить х?
Оценим Для этого рассмотрим функцию
Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Мы получили, что
Тогда , и это значит, что
Значение
не достигается ни при каких х.
Но если и
, то
Мы получили:
Ответ:
Логарифмические неравенства
4. Решите неравенство
Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.
Ответ:
Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!
5. Решите неравенство
ОДЗ:
Замена
Ответ:
А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.
6. Решите неравенство:
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Поскольку
Согласно методу замены множителя, выражение заменим на
Получим систему:
Решить ее легко.
Ответ: .
Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.
7. Решите неравенство:
ОДЗ:
Привести обе части к одному основанию не получается. Ищем другой способ.
Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.
Функции и
— монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.
Поскольку при x=9 значение монотонно возрастающей функции равно 4, при
значения этой функции меньше 4. Конечно, при этом
, то есть x принадлежит ОДЗ.
Ответ:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Прототипы задания №14 ЕГЭ по математике профильного уровня — неравенства. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №14 необходимо уметь решать уравнения и неравенства.
Практика
| time4math.ru | Скачать задания |
| math100.ru | Рациональные неравенства
Неравенства с модулями Показательные неравенства Логарифмические неравенства Логарифмические неравенства с переменным основанием |
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 15
Связанные страницы:
Задание 11 ЕГЭ по математике профильный уровень — наибольшее и наименьшее значение функций
Решение 17 задания ЕГЭ по профильной математике
Задание 5 ЕГЭ по математике профильный уровень — стереометрия
Задание 4 ЕГЭ по математике (профиль) — вычисления и преобразования
Задание 11 ЕГЭ 2022 по математике: «Наибольшее и наименьшее значения функции»
| 3640 | Решите неравенство 31^x+33 >= 11*(7-sqrt(18))^x+3*(7+sqrt(18))^x |
Решите неравенство 31^x + 33 >= 11(7-sqrt(18))^x + 3(7+sqrt(18))^x | |
| 3617 | Решите неравенство x^3+7x^2+(16x^2+5x-15)/(x-3)<=5 |
Решите неравенство x3 + 7×2 + 16×2+5x-15 / x-3 <= 5 ! Тренировочная работа №1 по математике 10 класс Статград 08-02-2023 Вариант МА2200109 Задание 14 | |
| 3614 | Решите неравенство: log_{2}(32x)/(log_{2}(x) -5)+ (log_{2}(x)-5)/ log_{2}(32x)>= (log_{2}(x^16)+18)/((log_{2}(x))^2-25) |
Решите неравенство: log2 (32x) / log2 x -5+ log2 x-5 / log2 (32x) >= log2 x16+18 / log2 2 x -25 | |
| 3597 | Решите неравенство: x^2*log_{64}(3-2x) >= log_{2}(4x^2-12x+9) |
Решите неравенство: x2 log64 (3-2x) >= log 2 (4×2 — 12x+9) ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 14 | |
| 3596 | Решите неравенство 4*9^(1-5/x)-91*12^(-5/x)+3*4^(2-10/x)>=0 |
Решите неравенство 4 9^(1-5/x)-91 12^(-5/x)+3 4^(2-10/x) >= 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 20 Задание 14 |
|
| 3586 | Решите неравенство: (log_{5}(x^4))^2-28log_{0.04}(x^2) <= 8 |
Решите неравенство: log2 5 x4 — 28log0,04 x2 <= 8 ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 14 | |
| 3579 | Решите неравенство: (log_{2}(x^4))^2-4log_{0.25}(x^2) >= 12 |
Решите неравенство: log2 2 (x4) -4log0.25 (x2) >= 12 ! 36 вариантов ФИПИ Ященко 2023 Вариант 17 Задание 14 | |
| 3569 | Решите неравенство (3x^3-18x^2+27x)*(x-3)^-1-. (6x^3-11x^2-44x-30)*(2x+3)^-1<=11 |
Решите неравенство (3x^3 — 18x^2 +27x)(x-3)^-1 -(6x^3 -11x^2 -44x -30) (2x+3)^-1 <=11 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 14 Вариант МА2210209 | |
| 3550 | Решите неравенство: 8^(lg(-1-x))<=(x^2-1)^(lg2) |
Решите неравенство: 8 lg(-1-x)<=(x2 — 1) lg2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 14 | |
| 3533 | Решите неравенство: 4log_{0.25}(1-4x) -log_{sqrt(2)}(-1-x)+. 4log_{4}(x^2-1) <= log_{2}(x^2). |
Решите неравенство: 4log 0,25 (1-4x) — log sqrt2 (-1-x) +4log4 (x2 -1) <= log2 x2 ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 14 | |
Курс ведёт: Андрей Юрьевич Иванов, кандидат технических наук, преподаватель ЧОУ «Школа Экспресс» Санкт-Петербурга.
Задание 14 в профильном ЕГЭ по математике 2022 года – это решение неравенств (соответствует заданию № 15 ЕГЭ 2021 года).
За это задание можно получить 2 балла. Уровень сложности: средний. Время решения 5-18 минут. Ответом к заданию является развернутый ответ (полная запись решения с обоснованием выполненных действий).
Решение неравенства с модулем. № 1(3)
Решение неравенства с модулем. № 2(4)
Решение неравенства с модулем. № 3(5)
Решение логарифмического неравенства с модулем. № 6
Решение логарифмического неравенства. № 7
Решение неравенства с модулем. № 8
Решение логарифмического неравенства. № 9
Решение комбинированного неравенства. № 10 (метод интервалов)
Решение комбинированного неравенства. № 11 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 12 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение показательного неравенства. № 13 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение показательного неравенства. № 14 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение логарифмического неравенства. № 15 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 16 (методика комплексного анализа и упрощения неравенств, методы интервалов и знакотождественных выражений)
Решение логарифмического неравенства. № 17 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 18 (метод интервалов, комплексного анализа и упрощения неравенств)
Решение логарифмического неравенства. № 19 (свойства логарифмов, метод комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 20 (метод интервалов, комплексного анализа и упрощения неравенств, свойства логарифмов, метод знакотождественных выражений)
Решение логарифмического неравенства. № 21 (свойства логарифмов, метод комплексного анализа и упрощения неравенств)
Решение логарифмического неравенства. № 22 (свойства логарифмов, метод комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 23 (метод интервалов, комплексного анализа и упрощения неравенств, свойства логарифмов, метод знакотождественных выражений)
Решение комбинированного неравенства. № 24 (метод интервалов, комплексного анализа и упрощения неравенств, свойства иррациональных функций и логарифмов)
Решение комбинированного неравенства. № 25 (метод интервалов, комплексного анализа и упрощения неравенств, свойства иррациональных и показательных функций)
Решение комбинированного неравенства. № 26 (свойства логарифмов, методика комплексного анализа и упрощения неравенств, метод знакотождественных выражений)
Решение комбинированного неравенства. № 27 (свойства логарифмов, свойства иррациональных и показательных функций, равносильные преобразования выражений, содержащих переменную под знаком модуля; методика комплексного анализа и упрощения неравенств, метод знакотождественных выражений, метод интервалов). Время решения 22-24 минуты
Решение показательного неравенства. № 28 (свойства показательных функций, методика комплексного анализа и упрощения неравенств, метод интервалов)
Решение логарифмического неравенства. № 29 (свойства логарифмов, метод комплексного анализа и упрощения неравенств)
Решение комбинированного неравенства. № 30 (свойства логарифмов и показательных функций, метод комплексного анализа и упрощения неравенств)