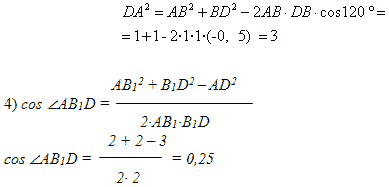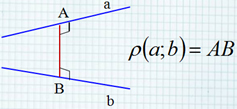Задание 14 егэ по математике профиль презентация

Слайд 1

Решение заданий №14 ЕГЭ профильного уровня (нахождение углов, расстояний, построение сечений)

Слайд 2

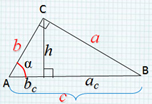
Соотношения между сторонами и углами прямоугольного треугольника Повторение. C A В a 2 + b 2 = c 2 c b a b c a c h α

Слайд 3

a 2 = B a A C c b Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними . b 2 + c 2 – 2bc cosA Теорема косинусов

Слайд 4

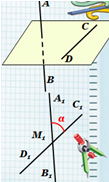
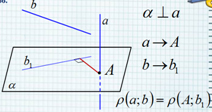
Угол между пересекающимися и скрещивающимися прямыми α 180 0 — α 0 0 < α 90 0 1. 2. Угол между скрещивающимися прямыми АВ и С D определяется как угол между пересекающимися прямыми А 1 В 1 и С 1 D 1 , при этом А 1 В 1 || АВ и С 1 D 1 || CD. А В D С А 1 В 1 С 1 D 1 α М 1

Слайд 5

A D C H ∠ ( (АСН); (СН D )) – это двугранный ∠ АСН D , где СН-общее ребро. Точки А и D лежат на гранях этого угла. AF⊥CH, FD⊥CH. F ∠ AFD – линейный угол двугранного ∠ А CHD Угол между плоскостями

Слайд 6

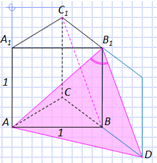
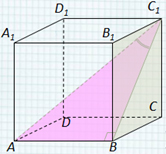
В правильной треугольной призме ABCA 1 B 1 C 1 , все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 . Задача № 1 1 А С В D А 1 С 1 В 1 1 3) из ∆ABD по теореме косинусов Продлим плоскость ВСС 1 , тогда ∠(AB 1 , ВС 1 ) = ∠(AB 1 , DВ 1 ) = ∠ AВ 1 D, т. к. C 1 В || B 1 D. Решение:

Слайд 7

В правильной треугольной призме ABCA 1 B 1 C 1 , все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 . Задача № 1 (продолжение) 1 А С В D А 1 С 1 В 1 1 Решение: 4) cos ∠ AB 1 D = AB 1 2 + B 1 D 2 – AD 2 2·AB 1 · B 1 D cos ∠ AB 1 D = = 2 + 2 – 3 1 2· 2 4 Ответ: 0,25 .

Слайд 8

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямой AC 1 и плоскостью ВС C 1 . Задача № 2 С В D А 1 С 1 В 1 D 1 А Решение: ВС 1 — проекция прямой АС 1 на плоскость(В C С 1 ), так как AB ⊥ (В C С 1 ) AB ⊥ ВС 1 ; ∠( AC 1 , ( В C С 1 ) ) = ∠( A С 1 ,С 1 В) = ∠ AC 1 B , т.е. ∆ АВC 1 – прямоугольный 3) tg ∠ AC 1 B = = = AB a 1 BC 1

Слайд 9

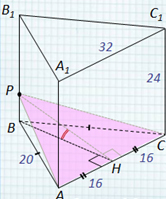
Основанием прямой треугольной призмы ABCA 1 B 1 C 1 , является равнобедренный треугольник АВС , в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру ВВ 1 , причем ВР : РВ 1 = 1 : 3. Найдите тангенс угла между плоскостями А 1 В 1 С 1 и АСР . 20 А С В А 1 С 1 В 1 24 Ответ: 0,5 . Задача № 3 Р Н 16 16 Решение: 1) Так как (АВС) ∥ (А 1 В 1 С 1 ), то ∠(( А 1 В 1 С 1 ) , (АСР)) = ∠( (АВС),(АСР)). 2) Т.к. ВН  АС (высота р / б ∆ ), то по теореме о трех перпендикулярах РН  АС. 3) Тогда ∠ РНВ – линейный угол двугранного ∠ РАСВ. Найдем его из прямоугольного ∆ РНВ. 4) РВ = ¼ ВВ 1 = ¼ · 24 = 6, 5) ВН 2 = АВ 2 – АН 2 (из ∆ A НВ) ВН 2 = 20 2 – 16 2 = 144, ВН = 12; 6) tg ∠ РНВ = PB / HB = 6 / 12 = 0,5. 32

Слайд 10

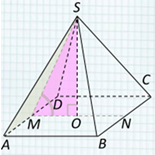
Решение: Так как ABCD – квадрат, то АВ ⊥ AD . Поэтому проекция AB на плоскость (SAD) будет ⊥ AD. Значит, искомый угол – двугранный угол при ребре основания AD. В правильной четырехугольной пирамиде S ABCD, все ребра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD . Задача № 4 С В D А S O M N 3) ∠ SMO – искомый угол, косинус которого найдем из прямоугольного ∆ SMO cos ∠ SMO = = = MO 0,5 1 SM

Слайд 11

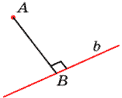
Расстояние от точки до прямой Определение. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, проведённого из данной точки к данной прямой. перпендикуляр Повторение.

Слайд 12

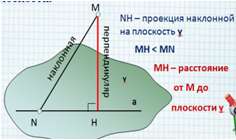
Расстояние от точки до плоскости Определение. Расстоянием от точки до плоскости является длина перпендикуляра, проведённого из данной точки к данной плоскости. перпендикуляр a ɣ M H N наклонная NH – проекция наклонной на плоскость ɣ MH < MN М H – расстояние от М до плоскости ɣ

Слайд 13

Общим перпендикуляром двух скрещивающихся прямых называют отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. a b A B Определение. Расстоянием между скрещивающимися прямыми называют длину их общего перпендикуляра. Расстояние между скрещивающимися прямыми

Слайд 14

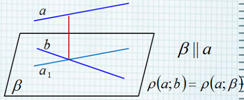
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой. 1 способ.

Слайд 15

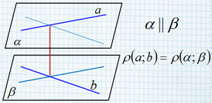
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые. 2 способ.

Слайд 16

Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между их проекциями на плоскость, перпендикулярную одной из них. 3 способ.

Слайд 17

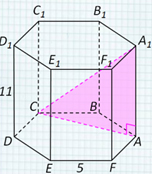
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1 . Задача № 5 Решение: 1)Так как ABCDEF – правильный шестиугольник, то C A ⊥ AF . C A ⊥ A 1 А по определению правильной призмы. C A ⊥(А A 1 F 1 ) по признаку перпендикулярности прямой и плоскости, т.е. СА –перпендикуляр к плоскости, C A 1 — наклонная , A 1 А – проекция наклонной, A 1 А ⊥ A 1 F 1 ; A 1 F 1 – прямая в плоскости. 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Тогда по теореме о трёх перпендикулярах CA 1 ⊥ A 1 F 1 , значит длина отрезка C A 1 равна искомому расстоянию .

Слайд 18

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1 . Задача № 5 (продолжение) Решение: 2) Из ∆ АВС (АВ=ВС=5, ) по теореме косинусов найдём СА: , , C A = . 3) Из ∆ CAA 1, по теореме Пифагора найдём CA 1 : CA 1 2 = 75 + 121 = 196 . CA 1 = 14 Ответ: 14 . 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Доказано, что C A 1 — искомое расстояние .

Слайд 19

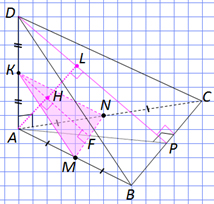
Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС . Найдите расстояние от А до плоскости, проходящей через середины ребер АВ , АС и А D , если А D = , АВ = АС = 10, ВС = . D C B A N F М К Р Искомое расстояние AH равно половине расстояния от вершины А до плоскости BCD , т.к. (KMN) ∥ (BCD) и KF – средняя линия ∆ ADP . L Н Задача № 6 Решение: Построим плоскость КМ N. Т. к. КМ – средняя линия ∆А D В, КМ∥ D В, MN — средняя линия ∆АВ C , М N ∥ C В, то (KMN) ∥ (BCD) по признаку ∥ плоскостей. АР–медиана и высота р/б , KF –медиана и высота р/б DP ⊥ BC по теореме о трёх перпендикулярах. ∆АВ C ∆ KMN . KF ∥ DP .

Слайд 20

Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС . Найдите расстояние от А до плоскости, проходящей через середины ребер АВ , АС и А D , если А D = , АВ = АС = 10, ВС = . D C B A N F М К Р Решение: Доказано, что AH — искомое расстояние. Найдём АР из ∆АВР по теореме Пифагора ( АВ= 10, ВР = ): AP 2 = AB 2 – BP 2 = 100 – 20 = = 80 ; АР= Найдём D Р из ∆А D Р по теореме Пифагора: DP 2 = AD 2 + AP 2 = = 20 + 80 = 100 ; DP = 10 . Тогда AL =( · ) : 10=4 Итак, АН = ½ AL = 2 . L Н Ответ: 2. Задача № 6 (продолжение). 2) ∆ LDA и ∆ ADP подобны по двум углам, LA:AP=AD:DP , тогда AL=(AP*AD):DP.

Слайд 21

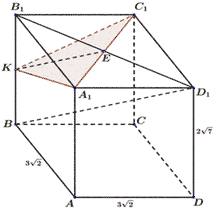
Задача № 7 В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F. Решение: а) 1) ВС 1 , BF, F Е 1 // С 1 B , Е 1 C 1 => Сечение – четырёхугольник BC 1 E 1 F с диагональю C 1 F. 4) Так как ∠ CBF=90°, то по теореме о трёх перпендикулярах, BF ⟘ BC 1 . Значит, сечение BC 1 E 1 F – прямоугольник. Диагональ прямоугольника C 1 F 2 =BF 2 +BC 1 2 ; C 1 F 2 =3+2=5.

Слайд 22

Задача № 7 (продолжение) Решение. б) Сечение – прямоугольник BC 1 E 1 F. ВК ⊥C 1 F, ВК – искомое расстояние от точки В до прямой C 1 F. Найдем ВК как высоту из ∆FBС 1 , Используя 2 формулы площади треугольника. В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F.

Слайд 23

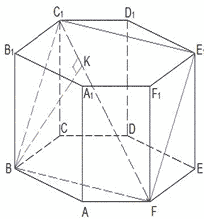
Задача №8 Основанием прямой четырехугольной призмы является квадрат ABCD со стороной , высота призмы равна . Точка K − середина ребра ВВ1. Через точки K и С1 проведена плоскость α, параллельная прямой BD1. а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. а) Для построения сечения призмы плоскостью α, проведём КЕ|| BD 1 , E € B 1 D 1 . Плоскость α проходит через точки К, С 1 и Е. Так как К – середина ВВ 1 и КЕ|| BD 1 , то Е – середина диагонали А 1 С 1 квадрата А 1 В 1 С 1 D 1 . Значит, плоскость α пересекает грань А 1 В 1 С 1 D 1 по диагонали А 1 С 1 . Соединив точки К, С 1 и А 1 , получаем ∆А 1 КС 1 — сечение призмы плоскостью α. ∆А 1 КВ 1 = ∆С 1 КВ 1 по двум сторонам и углу между ними (А 1 В 1 =С 1 В 1 ), В 1 К – общая сторона, . Из равенства треугольников следует, что А 1 К=С 1 К, значит ∆А 1 КС 1 — равнобедренный.

Слайд 24

Задача №8 (продолжение) Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является квадрат ABCD со стороной , высота призмы равна . Точка K − середина ребра ВВ 1 . Через точки K и С 1 проведена плоскость α, параллельная прямой BD 1 . а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. б)

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Метод координат
  в решении заданий 14 ЕГЭ (профильный уровень)

• 

  2 слайд

  Повторение. Метод координат на плоскости.
  Задача 1. Дана прямоугольная трапеция с основаниями a и b. Найдите расстояние между серединами ее диагоналей.
  Решение. 1. Введем систему координат как указано на рисунке 3. Тогда вершины трапеции будут иметь координаты: A(0,0), B(0,y), C(b,y) и D(a,0). (y – высота трапеции, АВ).
  2. Найдем координаты середин
  диагоналей. Для точки О, для точки О1:
  .
  По формуле найдем расстояние между точками О и О1:
  Ковалева Ирина Константиновна
  (0,0)
  (0,y)
  (b,y)
  (a,0)

• 

  3 слайд

  Ковалева Ирина Константиновна
  Задача 2. Медиана, проведенная к основанию равнобедренного треугольника, равна 160 см, а основание треугольника равно 80 см.
  Найдите две другие медианы этого треугольника.
  Решение. 1. Введем прямоугольную систему координат так, как показано на рисунке 4. В этой системе вершины треугольника будут иметь координаты:
  А(-40,0), В(0, 160), С(40,0), а точка М2(0,0).
  .
  Вычислим длины отрезков АМ1 и СМ3, используя формулу (6). Для АМ1 получим:
  .
  (-40,0)
  (0, 160)
  (40,0)
  (0,0)

• 

  4 слайд

  Ковалева Ирина Константиновна
  Задача 3. В прямоугольном равнобедренном треугольнике проведены медианы острых углов. Вычислите косинус угла между ними.
  Решение. 1. Введем систему координат так, как показано на рисунке. В этом случае вершины треугольника будут иметь координаты: С(0,0), А(а,0), В(0,а), а середины катетов (Здесь а – длина катета.):

  2. По формуле (4) вычислим координаты векторов
  (0,0)
  (а,0)
  0,а)

• 

  5 слайд

  Метод координат
  Приведём основные формулы.
  1. Расстояние между точками
  2. Координаты середины С отрезка АВ равны средним арифметическим соответствующих координат его концов:
  Координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
  3. Скалярным произведением векторов называется число

• 

  6 слайд

  4. Если — ненулевые векторы, а —угол между ними, то
  Векторы перпендикулярны (ортогональны) тогда и только тогда, когда а • b = 0, или
  5. Уравнение плоскости, проходящей через точку перпендикулярно ненулевому вектору ( вектору нормали плоскости), имеет вид
  Любое линейное уравнение с тремя неизвестными Ax + By + Cz + D = 0,
  где числа А, В и С одновременно не равны нулю, есть уравнение некоторой плоскости, причём п (А; В; С) — вектор нормали этой плоскости.
  6. (Уравнение плоскости в отрезках.) Если плоскость не проходит через начало координат, то её уравнение можно представить в виде
  где (р; 0; 0), (0; q; 0), (0; 0;r ) — точки пересечения плоскости с осями Ох, Оу и Oz соответственно.

• 

  7 слайд

  7. Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей этих плоскостей, т. е. если — угол между плоскостями, заданными уравнениями
  8. Параметрические уравнения прямой, проходящей через точку параллельно ненулевому вектору (направляющий вектор прямой), имеют вид
  9. Расстояние d от точки до плоскости, заданной уравнением Ах + By + Cz + D = 0, находится по формуле

• 

  8 слайд

  Если — угол между прямой с направляющим вектором и плоскостью Ах + Ву + Cz + D = 0 с вектором нормали
  то равен модулю косинуса угла между этими векторами, т. е.

• 

  9 слайд

  Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:
  Примеры выбора системы координат

• 

  10 слайд

  Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны 4):
  Очевидно, что координаты точки A (0;0;0) т. B — (4;0;0), т. G — (4;4;4) и т.д. (Рис. 1).

• 

  11 слайд

  Рассмотрим правильную пирамиду ABCD с ребром 4: т.A (0;0;0),
  координату x точки С можно получить, опустив перпендикуляр из т.С на ось OX. (Рис. 2), искомая координата 2.
  Координата y т.С  равна длине отрезка AF=CE. Найдем его по теореме Пифагора из треугольника AFC:

  Координата z точки C равна 0, потому что т.С лежит в плоскости XOY
  C(2;√12;0).
  E

• 

  12 слайд

  Найдем координаты вершины D. Координаты X и Y т.D совпадают с координатами X и Y т.H. Высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок EH=1/3CE=1/3∗√12 (медианы точкой пересечения делятся в отношении как 1:3) и равен координате т.D поY. Отрезок IH=2 координата т.D по X. А координата по оси Z равна высоте пирамиды:

• 

  13 слайд

  Угол между скрещивающимися прямыми
  И так, мы научились находить координаты точек, и при помощи них определять координаты векторов.

  { }
  { }

• 

  14 слайд

  Пример: Дан куб ABCDA1B1C1D1. Точка М — середина В1С1.
  Найдите угол между прямыми АС1 и ВМ.
  Пусть ребро куба равно 2. Найдём координаты точек: А(0; 0; 0),
  С1(2; 2; 2),
  В(0; 2; 0),
  М(1; 2; 2),
  Решение.
  Найдём координаты векторов

• 

  15 слайд

  Угол между плоскостями
  Иногда в задачах по стереометрии просят найти угол между плоскостями. В этом случае вам нужно найти уравнения этих плоскостей и воспользоваться формулой.
  Пусть даны два уравнения плоскостей:
  Тогда угол между этими плоскостями можно найти по формуле:
  Пример: Найдите угол между плоскостями, заданными уравнениями:
  Решение: исходя из данных уравнений: А=3; В=2; С=3
  А1=1; В1=-1; С1=2
  Подставим в формулу для нахождения угла между плоскостями:

• 

  16 слайд

  Уравнение плоскости
  В задачах №14 (С2) ЕГЭ часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: ,где A,B,C,D – какие-то числа. Если найти A,B,C,D, то мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
  Например, пусть даны три точки:
  Подставим координаты точек в общее уравнение плоскости:

  Получилась система из трех уравнений, но неизвестных 4: A,B,C,D.
  Если наша плоскость не проходит через начало координат, то мы можем D приравнять 1, если же проходит, то D=0. Объяснение этому простое: вы можете поделить каждое ваше уравнения на D, от этого уравнение не изменится, но вместо D будет стоять 1, а остальные коэффициенты будут в D раз меньше. Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

• 

  17 слайд

  Пример: Найти уравнение плоскости, проходящей через точки K(1;2;3); P(0;1;0); L(1;1;1).
  Получаем искомое уравнение плоскости:
  −0.5x−y+0.5z+1=0.

  Решение: Подставим координаты точек в уравнение плоскости D=1:
  K(1;2;3)
  P(0;1;0)
  L(1;1;1)

• 

  18 слайд

  Для составления уравнения плоскости можно использовать определитель
  третьего порядка, который можно просчитать правилом Саррюса.
  Пусть наша плоскость проходит через точки: М1(х1;у1;z1), М2(х2;у2;z2),
  М3(х3;у3;z3). Уравнение этой плоскости в координатной форме будет иметь вид:
  Теперь нам нужно найти многочлен от элементов квадратной матрицы
  с помощью специальных правил. Рассмотрим лишь один из способов –
  правило Саррюса. Для этого дополним наш определитель матрицей:

• 

• 

  20 слайд

  Пример 2. Найти уравнение плоскости, проходящей через точки K(1;2;3); P(0;1;0); L(1;1;1).
  Получаем искомое уравнение плоскости:

  Решение: Подставим координаты точек в определитель:
  K(1;2;3)
  P(0;1;0)
  L(1;1;1)
  х – 1 у – 2 z – 3
  0 – 1 1 – 2 0 – 3 = 0
  1 – 0 1 – 1 1 — 0
  Дополним определитель матрицей:
  х – 1 у – 2 z – 3 х – 1 у – 2
  0 – 1 1 – 2 0 – 3 0 – 1 1 – 2 =
  1 – 0 1 – 1 1 – 0 1 – 0 1 – 1
  4 5 6 + + +
  1 2 3 — — —
  =(х – 1)(1 -2)(1- 0)+(у – 2)(0 – 3)(1 – 0)+(z – 3)(0 – 1)(1 – 1) — (z – 3)(1 – 2)(1 – 0) –
  (х – 1)(0 -3)(1- 1) — (у – 2)(0 – 1)(1 – 0) = — х + 1 — 3у + 6 + z – 3 + у – 2=
  = — х – 2у + z + 2
  х – 2у + z + 2 = 0 / 2
  — 0,5х – у + 0,5z + 1 = 0

• 

  21 слайд

  Пример: Дан прямоугольный параллелепипед ABCDA1B1C1D1 с рёбрами АВ = 2, AD = 4, АА1 = 6. Найдите расстояние от середины ребра D1C1 до плоскости, проходящей через середины рёбер АВ, AD и ССг.
  Решение. Пусть К, L, М и Р — середины рёбер АВ, AD, СС1 и C1D1 соответственно. Введём прямоугольную систему координат, взяв за её начало вершину А. Найдём координаты следующих точек: L(2; 0; 0), К(0; 1; 0), М(4; 2;3), Р(4; 1; 6).
  Тогда уравнение плоскости KLM имеет вид
  Расстояние от точки Р (4; 1; 6) до плоскости равно

• 

  22 слайд

  Пример: В правильной четырехугольной пирамиде SАВСD сторона основания равна 2, а высота равна 1. Найдите угол между плоскостями SBС и MNP, где M — середина AB, N – середина ребра AD, P — середина SC.
  Решение. Выберем систему координат (рис.). Определим координаты точек:
  (-1;0;0)
  (0;0;1)
  (1;1;0)
  (1;-1;0)
  (0;-1;0)
  Запишем уравнение плоскости SBC:
  Запишем уравнение плоскости MNP:
  Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей этих плоскостей
  Cos (SBC;MNP)=ا-0,5ا = 0,5
  Ответ: 60º

• 

  23 слайд

  Пример: Дана правильная треугольная призма АВСА1В1С1 со стороной основания и боковым ребром . Точка М — середина ребра ВВ1. Найдите угол между плоскостями АМС и А1ВС1
  Решение. Пусть К и N — середины рёбер АС и А1С1 соответственно. На прямой, проходящей через вершину В параллельно АС, отметим точку Т.
  Введём прямоугольную систему координат, взяв за её начало вершину В, оси Вх, By и Bz по лучам ВК, ВТ и ВВ1 соответственно.
  Найдём координаты точек: В(0; 0; 0), K(√21; 0; 0), N(√21; 0; 2√15), М(0; 0; √15).
  Продолжить решение задачи самостоятельно

• 

  24 слайд

  Расстояние от точки до плоскости
  Зная координаты некоторой точки M(xM;yM;zM), легко найти расстояние до плоскости Ax+By+Cz+D=0:
  Пример: Найдите расстояние от т. H(1;2;0) до плоскости, заданной уравнением: 2∗x+3∗y−√2∗z+4=0.
  Решение: Из уравнения плоскости сразу находим коэффициенты:
  A=2, B=3, C=−√2, D=4.
  Подставим их в формулу для нахождения расстояния от точки до плоскости.

• 

  25 слайд

  Расстояние между скрещивающимися прямыми

  Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
  Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

• 

  26 слайд

  Решение:
  Решим задачу полностью методом координат. Нарисуем рисунок и выберем декартову систему координат. 

  Пример: Дана правильная треугольная призма ABCFDE, ребра которой равны 2.
  Точка G — середина ребра CE.
  а)Докажите, что прямые AD и BG перпендикулярны.
  б)Найдите расстояние между прямыми AD и BG.
  Определим координаты точек A, D, B и G. Координаты точки G по осям x и y совпадают с координатами точки C.
  Мы нашли координаты векторов. Теперь воспользуемся формулой для нахождения косинуса угла между скрещивающимися прямыми. Если косинус получится равен 0, это будет значить, что прямые перпендикулярны.

• 

  27 слайд

  Так как ADHE параллелограмм по построению, то DH=AB: H(4;0;2). Уравнение плоскости получим из системы уравнений, подставив в общее уравнение плоскости найденные координаты точек B, G и H.
  б)Для того, чтобы найти расстояние между скрещивающимися прямыми необходимо провести плоскость, проходящую через одну из прямых параллельно первой прямой.
  Выполним параллельный перенос прямой DA в точку B.  Получим прямую BН, где точка H лежит на продолжении ребра FD, потому что BH, очевидно, лежит в плоскости грани ABD, как прямая параллельная AD, и проходящая через точку B.
  Искомая плоскость, проходящая через прямую BG, и параллельная прямой AD, будет проходить через три точки: B, G и H. Найдем координаты точки H.
  , H(4;0;2)
  Из системы уравнений находим:
  Составляем уравнение плоскости:
  Найдем расстояние от любой точки на прямой AD до найденной плоскости, это и будет искомым расстоянием между прямыми AD и BG. На прямой AD удобно выбрать т. A(0;0;0).

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 779 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Организация маркетинга в туризме»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс повышения квалификации «Источники финансов»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»

• Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»

1. Повторение.

1.1.Соотношения между сторонами и углами
прямоугольного треугольника

Формулы: a² + b²= c²

1.2.Теорема косинусов

Квадрат стороны треугольника равен сумме
квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между
ними.

a² = b² + c²– 2bc·cosA

1.3. Угол между пересекающимися и
скрещивающимися прямыми.

За
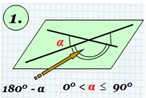
угол между пересекающимися прямыми принимают
острый угол, образованный этими прямыми.

 Угол между скрещивающимися прямыми АВ и СD
определяется как угол между пересекающимися
прямыми А₁В₁ и С₁D₁, при
этом А₁В₁|| АВ и С₁D₁|| CD.

1.4. Угол между плоскостями (АСН) и (СНD) – это
двугранный угол АСНD, где СН ребро.

Точки
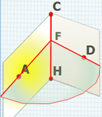
А и D лежат на гранях этого угла. AF CH, FD CH.

Угол AFD – линейный угол двугранного угла АCHD

2. Решение задач.

Задача №1.В правильной треугольной
призме ABCA₁B₁C₁, все рёбра которой
равны 1, найдите косинус угла между прямыми АВ₁
и ВС₁.

Решение:

1) Продлим плоскость ВСС₁, тогда (AB₁, ВС₁) = (AB₁, DВ₁) =
AВ₁D, т. к. C₁В || B₁D.

2) AB_{1 =} B₁D =из ABB_1.

3) из ABD по теореме
косинусов:

Ответ: 0,25.

Задача №2. В кубе ABCDA₁B₁C₁D₁
найдите угол между прямой AC₁ и плоскостью
ВСC₁.

Решение:

1) ВС₁ — проекция прямой АС₁ на
плоскость (ВCС₁), так как AB (ВCС₁), то AB ВС₁;

(AC₁, (ВCС₁))
= (AС₁,С₁В) = AC₁B, т.е. АВC₁ – прямоугольный.

2) Пусть АВ = а, тогда ВС₁ = а из C₁CB.

3) .

4) AC₁B = arctg .

Ответ: arctg .

Задача №3. Основанием прямой
треугольной призмы ABCA₁B₁C₁,
является равнобедренный треугольник АВС, в
котором АВ = ВС = 20, АС = 32. Боковое ребро
призмы равно 24. Точка Р принадлежит ребру ВВ₁,
причем ВР : РВ₁= 1 : 3. Найдите тангенс
угла между плоскостями А₁В₁С₁
и АСР.

Решение:

1) Так как (АВС) || (А₁В₁С₁), то (( А₁В₁С₁) ,
(АСР)) = ((АВС),(АСР)).

2) Т.к. ВН АС (высота
р/б ),то по теореме о
трех перпендикулярах РН АС.

3) Тогда РНВ –
линейный угол двугранного РАСВ. Найдем его из прямоугольного РНВ.

4) РВ = 1/4 ВВ₁ = 1/4 · 24 = 6,

5) ВН² = АВ² – АН² (из AНВ)

ВН² = 20² – 16² = 144, ВН = 12;

6) tg РНВ = PB/HB = 6/12 = 0,5.

Ответ: 0,5.

Задача №4. В правильной
четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите косинус угла между прямой AB и
плоскостью SAD.

Решение:

1) Так как ABCD – квадрат, то АВ AD. Поэтому проекция AB на плоскость (SAD)
будет AD. Значит,
искомый угол – двугранный угол при ребре
основания AD.

2) SM – высота грани SAD, SM =/2,
МО || АВ, МО = 0,5АВ = 0,5.

3) ?SMO – искомый угол, косинус которого найдем из
прямоугольного SMO.

сos ?SMO =
= =

Ответ :.

3. Повторение.

3.1. Расстояние от точки до прямой.

Определение. Расстоянием от
точки до прямой в пространстве называется длина
перпендикуляра, проведённого из данной точки к
данной прямой.

3.2. Расстояние от точки до плоскости.

Определение. Расстоянием от
точки до плоскости является длина
перпендикуляра, проведённого из данной точки к
данной плоскости.

3.3. Расстояние между скрещивающимися
прямыми.

Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.

Определение. Расстоянием между
скрещивающимися прямыми называют длину их
общего перпендикуляра.

• 1 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию от любой точки одной из
  этих прямых до плоскости, проходящей через
  вторую прямую параллельно первой прямой.

• 2 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию между двумя
  параллельными плоскостями, содержащими эти
  прямые.

• 3 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию между их проекциями на
  плоскость, перпендикулярную одной из них.

4. Решение задач.

Задача №5. В правильной шестиугольной
призме ABCDEFA₁B₁C₁D₁E₁F₁,
стороны основания которой равны 5, а боковые
рёбра равны 11, найдите расстояние от точки С
до прямой A₁F₁.

Решение:

1) Так как ABCDEF – правильный шестиугольник, то
прямые AC и AF перпендикулярны.

CA AFпо доказанному,

CA A₁А по
определению правильной призмы

CA (АA₁F₁)
по признаку перпендикулярности прямой и
плоскости, т.е.

СА – перпендикуляр к плоскости, CA₁ —
наклонная, A₁А – проекция наклонной,

A₁А A₁F₁;
A₁F₁ – прямая в плоскости.

Тогда по теореме о трёх перпендикулярах CA₁ A₁F₁, значит,
длина отрезка CA₁ равна искомому расстоянию.

2) Из АВС (АВ=ВС=5, B = 120^o)

по теореме косинусов найдём СА: , ,

3) Из CAA_1, по теореме
Пифагора найдём CA₁:

CA₁ ² = 75 + 121 = 196

CA₁ = 14

Ответ: 14.

Задача №6.

Ребро AD пирамиды DABC перпендикулярно
плоскости основания АВС. Найдите расстояние
от А до плоскости, проходящей через середины
ребер АВ, АС и АD, если АD = 2, АВ = АС = 10, ВС
= 4.

Решение:

1) Построим плоскость КМN.

Т. к. КМ – средняя линия АDВ,
КМ?DВ,

MN — средняя линия АВC, МN
||| CВ, то (KMN) || (BCD) по признаку

параллельности плоскостей. АР – медиана и
высота р/б АВC.

KF – медиана и высота р/б KMN.

DP BC по теореме о трёх
перпендикулярах, KF || DP.

Искомое расстояние AH равно половине расстояния
от вершины А до плоскости BCD, т.к. (KMN) || (BCD) и KF –
средняя линия ADP.

2) LDA и ADP подобны по двум углам, тогда LA:AP=AD:DP,
тогда AL = (AP*AD):DP.

Найдём АР из АВР по
теореме Пифагора (АВ=10, ВР = 2 ):

AP² = AB² – BP² = 100 – 20 = 80, АР= 4

Найдём DР из АDР по
теореме Пифагора: DP² = AD² + AP² = 20 +
80 = 100, DP = 10.

Тогда AL =( 4 · 2):10=4. Итак, АН = 1/2 AL =
2.

Ответ: 2.

Задача №7.

В правильной шестиугольной призме АВCDEFA₁B₁C₁D₁E₁F₁ все
рёбра равны 1.

а) Постройте сечение призмы плоскостью,
проходящей через точки B, С₁ и F.

б) Найдите расстояние от точки В до прямой C₁F.

Решение.

а) Сечение – четырёхугольник BC₁E₁F с
диагональю C₁F.

Сторона ВC₁= — диагональ квадрата ВВ1С1С со
стороной 1.

Сторону BF найдём из ABF по
теореме косинусов:

BF²=AB²+AF²-2 * AB * AF * cosBAF;

BF²=AB²+AF²-2 * AB * AF * cos120⁰ = 3.

Тогда

Так как CBF=90°, то по
теореме о трёх перпендикулярах, BF BC₁.

Значит,
сечение BC₁E₁F – прямоугольник.
Диагональ прямоугольника C₁F²=BF²+BC₁²;
C₁F²=3+2=5.

Отсюда

б) Сечение – прямоугольник BC₁E₁F.

ВК C₁F, ВК –
искомое расстояние от точки В до прямой C₁F.

Найдем ВК как высоту из FBС₁, 

Используя 2 формулы площади треугольника.

Задача №8.

Основанием прямой четырехугольной призмы
является квадрат ABCD со стороной , высота призмы равна . Точка K — середина ребра ВВ1.
Через точки K и С₁ проведена плоскость a,
параллельная прямой BD₁.

а) Докажите, что сечение призмы плоскостью a
является равнобедренным треугольником.

б) Найдите периметр треугольника, являющегося
сечением призмы плоскостью a.

Решение.

а) Для построения сечения призмы плоскостью a,
проведём КЕ || BD₁, E € B₁ D₁.

Плоскость a проходит через точки К, С₁ и
Е.

Так как К – середина ВВ₁ и КЕ || BD₁, то
Е – середина диагонали А₁ С₁ квадрата
А₁ В₁ С₁ Д₁. Значит,
плоскость a пересекает

грань А₁ В₁ С₁ Д₁ по
диагонали А₁ С₁ .

Соединив точки К, С₁ и А₁, получаем А₁ КС₁ — сечение
призмы плоскостью a.

А₁КВ₁ = С₁ КВ₁ по двум
сторонам и углу между ними (А₁ В₁ = С ₁В₁
, , В₁ К –
общая сторона).

Из равенства треугольников следует, что А₁К
= С₁К, значит А₁
КС₁ — равнобедренный.

5. Задачи для самостоятельного решения.

На ребре AA₁ прямоугольного
параллелепипеда ABCDA₁B₁C₁D₁
взята точка E так, что A₁E : EA = 2:5, на ребре BB₁
— точка F так, что B₁F : FB =1: 6, а точка Т —
середина ребра B₁ C₁. Известно, что AB = 5,
AD = 6 , AA₁ =14.

а) Докажите, что плоскость EFT проходит через
вершину D₁ .

б) Найдите угол между плоскостью EFT и плоскостью
AA₁B₁ .

Ответ. б) arctg .

2) Дана правильная треугольная призма ABCA₁B₁C₁,
все рёбра которой равны 4.

Через точки A, С₁ и середину T ребра
А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной
плоскостью является прямоугольным
треугольником.

б) Найдите угол между плоскостью сечения и
плоскостью ABC .

Ответ. б) arctg 2.

3) В правильной шестиугольной призме А…F₁
все рёбра равны 2.

а) Докажите, что плоскость ВВ₁F
перпендикулярна прямой В₁С_1.

б) Найдите расстояние от точки В до плоскости F В₁С_1.

Ответ. б) .

4) В пирамиде DАВС известны длины ребер
АВ=АС=DВ=DС=13, DА =6, ВС=24.

а) Постройте прямую, перпендикулярную прямым DА
и ВС.

б) Найдите расстояние между прямыми DА и ВС.

Ответ. б) 4.

5) Высота правильной треугольной пирамиды равна
20, а медиана её основания равна 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через её вершину и перпендикулярной
ребру основания.

б) Найдите тангенс угла, который образует
боковое ребро с плоскостью основания.

Ответ. б) 5.

6) В правильной четырёхугольной пирамиде МАВСD с
вершиной М сторона основания равна 3, а боковое
ребро равно 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через точку С и середину ребра МА
параллельно прямой ВD.

б) Найдите площадь этого сечения.

Ответ. б) 6.

Презентация.

Используемая литература.

1) И.В. Ященко, С.А. Шестаков, А.С. Трепалин
“Подготовка к ЕГЭ по математике 2016, профильный
уровень”, Москва, издательство МЦНМО, 2016.

2) Интернет-ресурсы:

• http://www.fipi.ru/
• http://mathege.ru/or/ege/Main
• https://math-ege.sdamgia.ru/
• http://alexlarin.net/
• https://ege-ok.ru/

Слайды и текст этой презентации

1.

МБОУ «Ергачинская СОШ»
Решение заданий 14 (С2)
по материалам ЕГЭ
профильного уровня
(нахождение углов,
расстояний, построение сечений)

2.

Соотношения между сторонами и
углами прямоугольного треугольника
Повторение.
C
b
A
α
bc
a
h
c
h bc ac
a2 + b2 = c2
ac
a ac c
a
sin
c
В
b
cos
c
a
tg
b
b bc c

3.

Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других
сторон минус удвоенное произведение этих сторон на косинус угла
сумме квадратов двух других сторон
между ними.
минус удвоенное произведение этих сторон
на косинус угла между ними.
2
a
=
2
b
+
2
c
– 2bc cosA
C
b
A
a
c
B

4.

Угол между пересекающимися и
скрещивающимися прямымиА
1.
С
α
D
1800 — α
00 < α
900
В
2.
Угол между скрещивающимися
прямыми АВ и СD определяется
как угол между пересекающимися
М1
прямыми А1В1 и С1D1, при
D1
этом А1В1|| АВ и С1D1|| CD.
В1
А1
α
С1

5.

Угол между плоскостями
C
F
D
A
H
∠ ((АСН); (СНD))
– это двугранный
∠ АСНD, где СНобщее ребро.
Точки А и D лежат
на гранях этого
угла.
AF⊥CH, FD⊥CH.
∠ AFD – линейный угол двугранного ∠ АCHD

6.

Задача № 1
В правильной треугольной призме ABCA1B1C1,
все рёбра которой равны 1, найдите косинус угла
между прямыми АВ1 и ВС1.
С1
Решение:
1) Продлим плоскость ВСС1,
В1
тогда ∠(AB1, ВС1) =
∠(AB1, DВ1) = ∠ AВ1D,
т. к. C1В || B1D.
А1
1
А
С
1
В
3) из ∆ABD по теореме
косинусов
DА2 AВ 2 ВD 2 2 AВ DВ cos120
1 1 — 2·1·1·(-0, 5) 3
D

7.

Задача № 1 (продолжение)
В правильной треугольной призме ABCA1B1C1, все
рёбра которой равны 1, найдите косинус угла
между прямыми АВ1 и ВС1.
С1
Решение:
А1
В1
4) cos∠AB1D =
1
А
2·AB1·B1D
2+2–3
cos∠AB1D =
2· 2
С
1
AB12 + B1D2 – AD2
В
Ответ: 0,25 .
D
1
=
4

8.

Задача № 2
В кубе ABCDA1B1C1D1 найдите угол между
прямой AC1 и плоскостью ВСC1.
Решение:
1) ВС1- проекция
С1
D1
прямой АС1 на
плоскость(ВCС1),
А1
В1
так как AB⊥(ВCС1)
AB⊥ВС1;
∠(AC1, (ВCС1)) =
∠(AС1,С1В) = ∠ AC1B,
С т.е. ∆АВC1 –
прямоугольный
D
А
В
3) tg∠AC1B =
AB
=
BC1
a
=
1

9.

Задача № 3
Основанием прямой треугольной призмы ABCA1B1C1,
является равнобедренный треугольник АВС, в котором
АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24.
Точка Р принадлежит ребру ВВ1, причем ВР : РВ1 = 1 : 3.
Найдите тангенс угла между плоскостями А1В1С1 и АСР.
Решение:
В1
С1 1) Так как (АВС)∥(А1В1С1), то
∠(( А1В1С1) , (АСР)) =
∠((АВС),(АСР)).
32
2) Т.к. ВН АС (высота р/б ∆),
А1
24 то по теореме о трех
Р
перпендикулярах РН АС.
3) Тогда ∠РНВ – линейный угол
двугранного ∠ РАСВ. Найдем его
В
С из прямоугольного ∆РНВ.
16 4) РВ = ¼ ВВ1 = ¼ · 24 = 6,
20
Н
5) ВН2 = АВ2 – АН2 (из ∆AНВ)
16
ВН2 = 202 – 162 = 144, ВН = 12;
А
6) tg∠РНВ = PB/HB = 6/12 = 0,5.
Ответ: 0,5 .

10.

Задача № 4
В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, найдите
косинус угла между прямой AB и плоскостью
SAD.
Решение:
1) Так как ABCD – квадрат,
S
то АВ ⊥ AD. Поэтому
проекция AB на плоскость
(SAD) будет ⊥ AD.
Значит, искомый угол –
С двугранный угол при ребре
основания AD.
D
M
O
N
В
А 3) ∠SMO – искомый
угол, косинус которого
найдем из прямоугольного ∆SMO
MO
0,5
1
cos∠SMO =
=
=
SM

11.

Повторение.
Расстояние от точки до прямой
Определение. Расстоянием от точки до
прямой в пространстве называется
длина перпендикуляра, проведённого из
данной точки к данной прямой.

12.

Расстояние от точки до плоскости
Определение. Расстоянием от точки до
плоскости является длина перпендикуляра,
проведённого из данной точки к данной
плоскости.
M
перпендикуляр
N
H
NH – проекция наклонной
на плоскость ɣ
MH < MN
МH – расстояние
ɣ
от М до
a
плоскости ɣ

13.

Расстояние между
скрещивающимися прямыми
Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.
A
a
а; b AB
B
b
Определение.
Расстоянием
между
скрещивающимися прямыми называют
длину их общего перпендикуляра.

14.

Способы вычисления расстояния между
скрещивающимися прямыми
1 способ.
а
b
|| a
а1
a; b a;
Расстояние между скрещивающимися прямыми
равно расстоянию от любой точки одной из этих
прямых до плоскости, проходящей через вторую
прямую параллельно первой прямой.

15.

Способы вычисления расстояния между
скрещивающимися прямыми
2 способ.
а
||
a; b ;
b
Расстояние между скрещивающимися прямыми
равно расстоянию между двумя параллельными
плоскостями, содержащими эти прямые.

16.

Способы вычисления расстояния между
скрещивающимися прямыми
3 способ.
b
b1
а
а
А
а А
b b1
a; b A; b1
Расстояние между скрещивающимися прямыми
равно расстоянию между их проекциями на
плоскость, перпендикулярную одной из них.

17.

Задача № 5
В
правильной
шестиугольной
призме
ABCDEFA1B1C1D1E1F1, стороны основания которой равны
5, а боковые рёбра равны 11, найдите расстояние от точки С
Решение:
до прямой A1F1.
1)Так как ABCDEF – правильный
С1
В1
шестиугольник, то
CA⊥AF.
А1 CA⊥A1А по определению
D1
правильной призмы.
E1
F1
CA⊥(АA1F1) по признаку
перпендикулярности прямой
и плоскости, т.е.
11
СА –перпендикуляр к плоскости,
С
В
CA1 — наклонная ,
A1А – проекция наклонной,
1F1 ;
D
А AA1АF ⊥A
1 1 – прямая в плоскости.
E
5
F
Тогда по теореме о трёх перпендикулярах CA1⊥A1F1, значит
длина отрезка CA1 равна искомому расстоянию.

18.

Задача № 5
(продолжение)
В
правильной
шестиугольной
призме
ABCDEFA1B1C1D1E1F1, стороны основания которой равны
5, а боковые рёбра равны 11, найдите расстояние от точки С
до прямой A1F1.
Решение:
С1
В1
1) Доказано, что
CA1 — искомое расстояние.
А1
D1
E1
2) Из ∆ АВС (АВ=ВС=5, В 120 0 )
по теореме косинусов найдём СА:
F1
СА2 СВ 2 ВА 2 2СВ АВ соs В ,
11
С
cos1200 cos 600 0,5 ,
В
D
А
CA =5 3 .
0
3) Из ∆CAA1, А 90 по
теореме Пифагора найдём CA1:
СА1 СА2 АА1
2
E
5
Ответ: 14.
F
2
CA1 2 = 75 + 121 = 196.
CA1 = 14

19.

Задача № 6
Ребро AD пирамиды DABC
перпендикулярно
плоскости основания АВС. Найдите расстояние от А
до плоскости, проходящей через середины ребер АВ,
АС и АD, если АD = 2 5 , АВ = АС = 10, ВС = 4 5 .
D
L
К
Н
A
N
F
М
Решение:
1) Построим плоскость КМN.
Т. к. КМ – средняя линия ∆АDВ, КМ∥DВ,
MN — средняя линия ∆АВC, МN∥CВ, то
(KMN)∥(BCD) по признаку ∥
плоскостей. АР–медиана и
C высота р/б ∆АВC ,
KF–медиана и высота
р/б ∆KMN.
DP⊥BC по теореме о трёх
Р перпендикулярах. KF ∥ DP.
Искомое расстояние AH
равно половине расстояния
от вершины А до плоскости
B
BCD, т.к. (KMN)∥(BCD) и
KF – средняя линия ∆ ADP.

20.

Задача № 6 (продолжение).
Ребро AD пирамиды DABC
перпендикулярно
плоскости основания АВС. Найдите расстояние от А
до плоскости, проходящей через середины ребер АВ,
АС и АD, если АD = 2 5 , АВ = АС = 10, ВС = 4 5 .
Решение:
D
К
A
1) Доказано, что
AH — искомое расстояние.
2) ∆LDA и ∆ADP подобны по двум углам,
L
LA:AP=AD:DP, тогда AL=(AP*AD):DP.
C Найдём АР из ∆АВР по теореме
Н
Пифагора (АВ=10, ВР = 2 5 ):
N
AP2 = AB2 – BP2 = 100 – 20 =
= 80; АР= 4 5
Найдём DР из ∆АDР
F
Р по теореме Пифагора:
М
DP2 = AD2 + AP2 =
= 20 + 80 = 100; DP = 10.
B
Тогда AL =(4 5 ·2 5 ):10=4
Итак, АН = ½ AL = 2.
Ответ: 2.

21.

Задача № 7
В правильной шестиугольной призме АВCDEFA1B1C1D1E1F1
все рёбра равны 1.
а) Постройте сечение призмы плоскостью, проходящей через
точки B, С1 и F.
б) Найдите расстояние от точки В до прямой C1F.
Решение:
а) 1) ВС1, BF, FЕ1 // С1B , Е1C1 =>
Сечение – четырёхугольник
BC1E1F с диагональю C1F.
4) Так как ∠CBF=90°, то по теореме о трёх перпендикулярах,
BF⟘BC1. Значит, сечение BC1E1F – прямоугольник. Диагональ
прямоугольника C1F2=BF2+BC12; C1F2=3+2=5.

22.

Задача № 7 (продолжение)
В правильной шестиугольной призме
АВCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Постройте сечение призмы плоскостью, проходящей через
точки B, С1 и F.
б) Найдите расстояние от точки В до прямой C1F.
Решение.
б) Сечение – прямоугольник BC1E1F.
ВК ⊥C1F, ВК – искомое расстояние
от точки В до прямой C1F.
Найдем ВК как высоту из ∆FBС1,
Используя 2 формулы площади
треугольника.

23.

Задача №8
Основанием прямой четырехугольной призмы АВСDА1В1С1D1
является квадрат ABCD со стороной 3 2 , высота призмы равна
2 7 . Точка K − середина ребра ВВ1. Через точки K и С1
проведена плоскость α, параллельная прямой BD1.
а) Докажите, что сечение призмы плоскостью α является
равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением
призмы плоскостью α. Решение.
а) Для построения сечения призмы
плоскостью α, проведём КЕ||BD1, E € B1D1.
Плоскость α проходит через точки К, С1 и Е.
Так как К – середина ВВ1 и КЕ||BD1, то
Е – середина диагонали А1С1 квадрата
А1В1С1D1. Значит, плоскость α пересекает
грань А1В1С1D1 по диагонали А1С1.
Соединив точки К, С1 и А1, получаем
∆А1КС1- сечение призмы плоскостью α.
∆А1КВ1= ∆С1КВ1 по двум сторонам
и углу между ними (А1В1=С1В1),
0
В1К – общая сторона, А1В1К С1В1К 90 .
Из равенства треугольников следует, что А1К=С1К, значит
∆А1КС1 — равнобедренный.

24.

Задача №8
(продолжение)
Основанием прямой четырехугольной призмы ABCDA1B1C1D1
является квадрат ABCD со стороной 3 2 , высота призмы равна
2 7 . Точка K − середина ребра ВВ1. Через точки K и С1
проведена плоскость α, параллельная прямой BD1.
а) Докажите, что сечение призмы плоскостью α является
равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением
призмы плоскостью α. Решение.
б)

25.

Задачи для самостоятельного решения
1) На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1
взята точка E так, что A1E : EA = 2:5, на ребре BB1 — точка F
так, что B1F : FB =1: 6, а точка Т — середина ребра B1 C1 .
Известно, что AB = 5, AD = 6 , AA1 =14 .
а) Докажите, что плоскость EFT проходит через вершину D1 .
б) Найдите угол между плоскостью EFT и плоскостью AA1B1 .
2) Дана правильная треугольная призма ABCA1B1C1, все рёбра
которой равны 4.
Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является
прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC .
Ответ: б) arctg 2.

26.

Задачи для самостоятельного решения
3) В правильной шестиугольной призме А…F1 все рёбра равны 2.
а) Докажите, что плоскость ВВ1F перпендикулярна прямой В1С1.
б) Найдите расстояние от точки В до плоскости F В1С1.
4) В пирамиде DАВС известны длины ребер АВ=АС=DВ=DС=13,
DА =6, ВС=24.
а) Постройте прямую, перпендикулярную прямым DА и ВС.
б) Найдите расстояние между прямыми DА и ВС.
Ответ: б) 4.

27.

Задачи для самостоятельного решения
5) Высота правильной треугольной пирамиды равна 20, а медиана
её основания равна 6.
а) Постройте сечение пирамиды плоскостью, проходящей через её
вершину и перпендикулярной ребру основания.
б) Найдите тангенс угла, который образует боковое ребро с
плоскостью основания.
Ответ: б) 5.
6) В правильной четырёхугольной пирамиде МАВСD с вершиной
М сторона основания равна 3, а боковое ребро равно 6.
а) Постройте сечение пирамиды плоскостью, проходящей через
точку С и середину ребра МА параллельно прямой ВD.
б) Найдите площадь этого сечения.
Ответ: б) 6.

28.

Используемая литература:
1) И. В. Ященко, С.А. Шестаков, А. С.
Трепалин «Подготовка к ЕГЭ по математике
2016,
профильный
уровень»,
Москва,
издательство МЦНМО, 2016.
2) Интернет-ресурсы:
http://www.fipi.ru/
http://mathege.ru/or/ege/Main
https://math-ege.sdamgia.ru/
http://alexlarin.net/
https://ege-ok.ru/
3) Шаблон презентации сайт http://pedsovet.su/ ,
автор Фокина Л. П.

  Скачать сертификат о публикации— как получить такой сертификат