Описание презентации по отдельным слайдам:
-
1 слайд
Задание №9 в КИМах ЕГЭ по математике профильного уровня
(2022 год)Решение задач по теме
«График дробно-линейной функции»
Презентация подготовлена
учителем математики
МАОУ «Гимназия №1 Октябрьского района г. Саратова»
Гришиной Ириной Владимировной -
2 слайд
Задача (по материалам сайта prof.mathege.ru).
На рисунке изображён график функции
f(x) = 𝑘𝑥+𝑎 𝑥+𝑏 . Найдите значения коэффициентов 𝑏, 𝑘 и 𝑎. -
3 слайд
Решение.
Прежде всего заметим, что функция
f(x) = 𝑘𝑥+𝑎 𝑥+𝑏 не определена в точке 𝑥=−𝑏,
так как при 𝑥=−𝑏 знаменатель дроби равен нулю. -
4 слайд
Решение (стр. 2)
По рисунку мы видим, что заданная функция не определена при х = − 4, так как график имеет вертикальную асимптоту – прямую с уравнением
х = − 4.
Значит, −𝑏 = −4,
то есть 𝑏 = 4. -
5 слайд
Решение (стр. 3)
Таким образом, формула функции приобретает вид
f(x) = 𝑘𝑥+𝑎 𝑥+4 .Остаётся найти коэффициенты 𝑘 и 𝑎.
-
6 слайд
Решение (стр. 4)
Обратим внимание на то, что составители задач выделили на заданном графике две точки с целыми координатами. Назовём точки А и В.
Определяем координаты точек: А(-3; 6), В(1;2). -
7 слайд
Решение (стр. 5)
Так как точки А(-3; 6) и В(1;2) принадлежат графику функции
f(x) = 𝑘𝑥+𝑎 𝑥+4 , то подстановка их координат в эту формулу должна приводить к верным числовым равенствам.
Подставим координаты
А и В в формулу
у = 𝑘𝑥+𝑎 𝑥+4 . -
8 слайд
Решение (стр. 6)
Подставляем координаты точки А(-3; 6) :
6 = 𝑘 −3 +𝑎 −3+4 ,6 = −3𝑘+𝑎 1 , то есть −3𝑘+𝑎 = 6. (1)
Подставляем координаты точки В(1;2) :
2 = 𝑘∙1+𝑎 1+4 ,2 = 𝑘+𝑎 5 , то есть 𝑘+𝑎 = 10. (2)
Из равенств (1) и (2) составим систему уравнений и решим её. -
9 слайд
Решение (стр. 7)
−3𝑘+𝑎=6, 𝑘+𝑎=10; вычтем из второго равенства первое
4𝑘=4, 𝑘+𝑎=10; 𝑘=1, 𝑎=9.
Таким образом, все три коэффициента найдены.
Ответ. b = 4,на данном рисунке, имеет вид f(x) = 𝑥+9 𝑥+4 .
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Слайд 1Задачи планиметрии
Профильный уровень
Учитель математики
МАОУ «Обдорская гимназия»
г. Салехард
ЯНАО
Е.И. Гусак

Слайд 2Треугольники в ЕГЭ по математике ЗАДАЧА № 16

Слайд 3Ключевая задача
Доказать, что если медиана, проведенная к гипотенузе,
равна ее половине, то треугольник прямоугольный.

Слайд 4
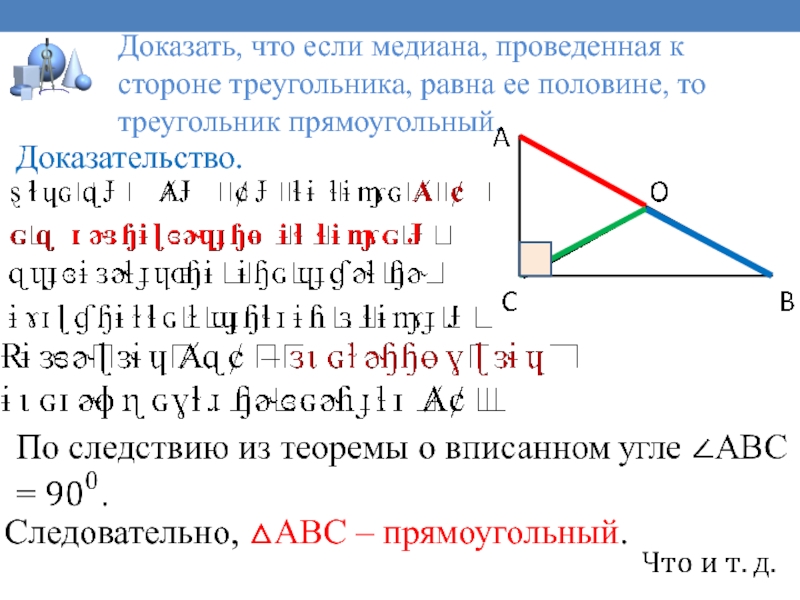
Доказать, что если медиана, проведенная к стороне треугольника, равна
ее половине, то треугольник прямоугольный.
Доказательство.
Следовательно, △АВС – прямоугольный.
Слайд 8Ключевая задача
Вычислите длину биссектрисы угла А △АВС со сторонами
АВ = 18, ВС = 15, АС = 12.

Слайд 9Вычислите длину биссектрисы угла А △АВС со сторонами АВ
= 18, ВС = 15, АС = 12.
А
С В
К

Слайд 14Ключевая задача
Найти медиану прямоугольного треугольника, проведенную из прямого угла,
если гипотенуза равна 12.

Слайд 15
Найти медиану прямоугольного треугольника, проведенную из прямого угла, если
гипотенуза равна 12.
Решение.
По свойству медианы:
медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы.
Следовательно, медиана равна 6.
Ответ: 6.
вспомним

Слайд 16Ключевая задача
Найти площадь треугольника, две медианы которого перпендикулярны и
равны 3 и 6.

Слайд 17
Найти площадь треугольника, две медианы которого перпендикулярны и равны
3 и 6.

Слайд 18Задача профильного уровня
Окружность с центром в точке О касается
боковой стороны АВ равнобедренного треугольника АВС, продолжения боковой стороны АС
и основания ВС в точке N. Точка М – середина ВС.
a)Доказать, что AN = ОМ.
б)Найти ОМ, если АВ = 13, ВС = 24.

Слайд 19
Окружность с центром в точке О касается боковой стороны
АВ равнобедренного треугольника АВС, продолжения боковой стороны АС и основания
ВС в точке N. Точка М – середина ВС.
a)Доказать, что AN = ОМ.
б)Найти ОМ, если АВ = 13, ВС = 24.

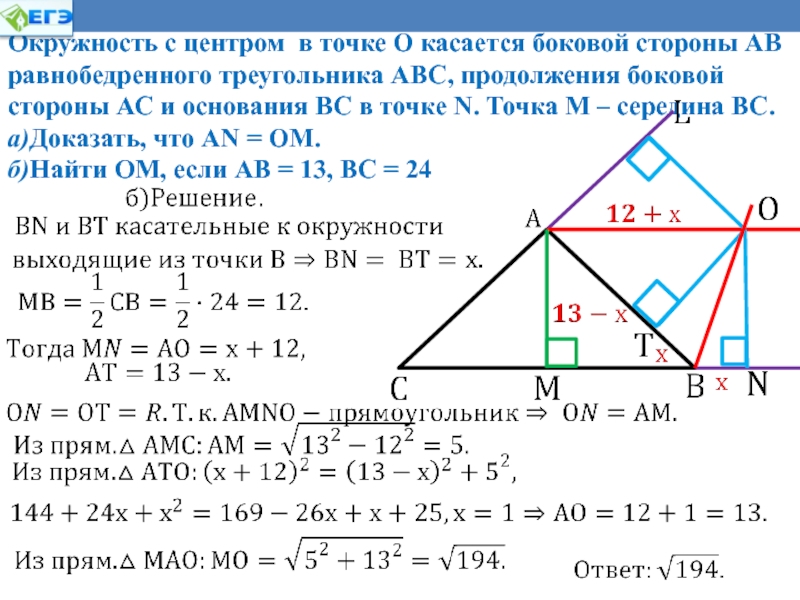
Слайд 20Окружность с центром в точке О касается боковой стороны
АВ равнобедренного треугольника АВС, продолжения боковой стороны АС и основания
ВС в точке N. Точка М – середина ВС.
a)Доказать, что AN = ОМ.
б)Найти ОМ, если АВ = 13, ВС = 24
Слайд 23Ключевая задача
На отрезке АС, равном 10, взяты точки М
и К так , что АК = 8, СМ =
6. Найти МК.

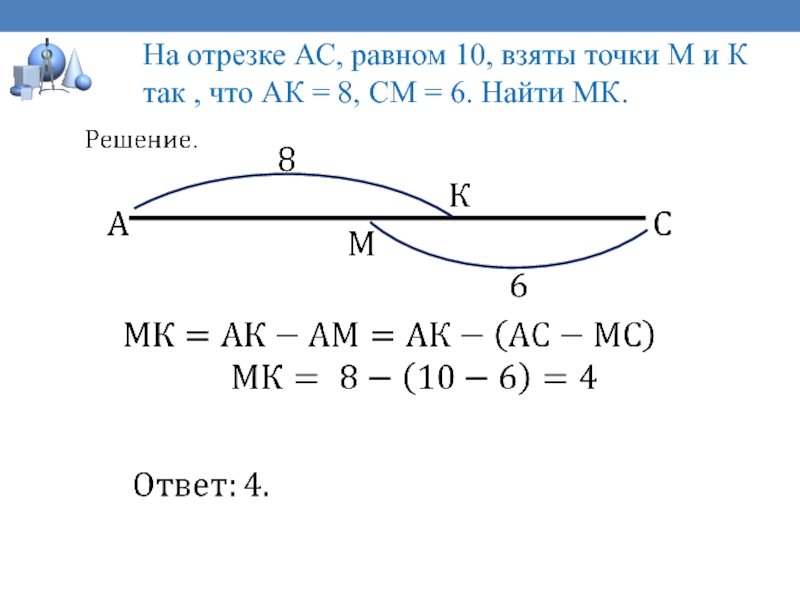
Слайд 24На отрезке АС, равном 10, взяты точки М и
К так , что АК = 8, СМ = 6.
Найти МК.
Слайд 25Ключевая задача
На серединах сторон АВ и ВС △АВС взяты
точки М и К соответственно. Найти площадь △ВМК, если площадь
△АВС равна 24.

Слайд 26
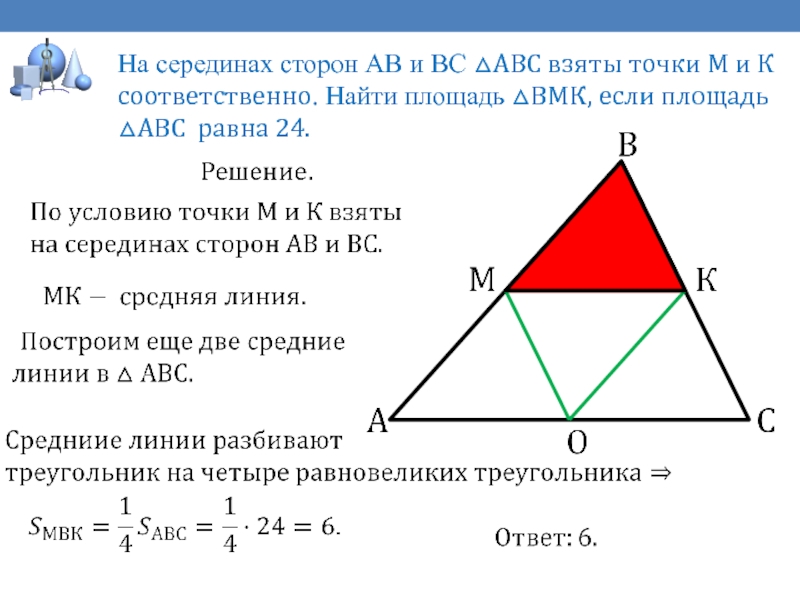
На серединах сторон АВ и ВС △АВС взяты точки
М и К соответственно. Найти площадь △ВМК, если площадь △АВС
равна 24.
Слайд 30Ключевая задача
В треугольнике АВС проведена биссектриса ВМ. АВ =
2, ВС = 3, АС = 3. Найти АМ, МС.

Слайд 31
В треугольнике АВС проведена биссектриса ВМ. АВ = 2,
ВС = 3, АС = 3. Найти АМ, МС.

Слайд 32Ключевая задача
В треугольнике АВС прямая МК пересекает стороны АС
и ВС так, что СК = 6, КВ = 3,
СМ = 4, МА = 2.
Докажите, что прямая МК параллельна АВ.

Слайд 33
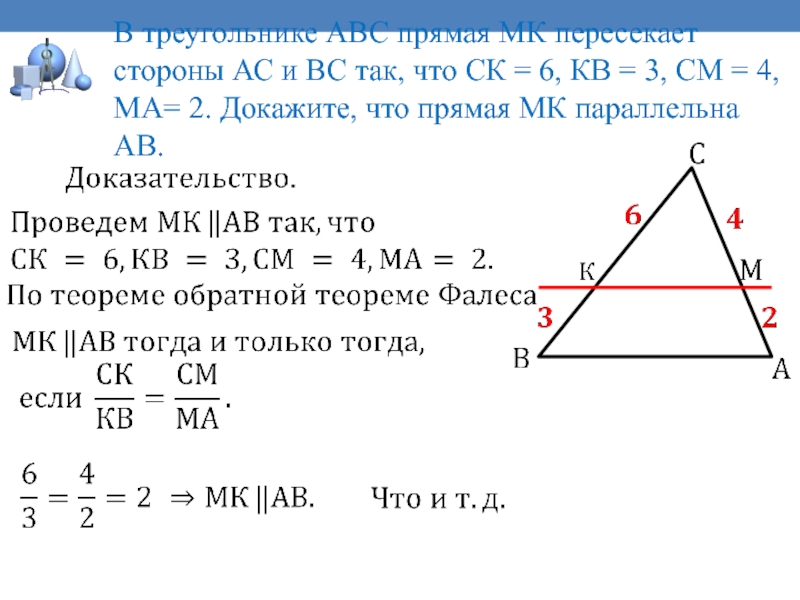
В треугольнике АВС прямая МК пересекает стороны АС и
ВС так, что СК = 6, КВ = 3, СМ
= 4, МА= 2. Докажите, что прямая МК параллельна АВ.
Слайд 39Спасибо за внимание!
Удачи на ЕГЭ.

Слайд 40Вспомним!!!
Теорема, обратная теореме Фалеса.
Если прямые, пересекающие стороны угла, отсекают
на одной и на другой стороне угла равные (или пропорциональные)
между собой отрезки, начиная от вершины, то такие прямые параллельны.
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
назад

Слайд 41Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы
1) В
прямоугольном △ АВС из вершины прямого угла С проведем к
гипотенузе AB отрезок CO так, чтобы CO=OA.
2) ∆ AOC — равнобедренный с основанием AC ⇒ ∠OAC=∠OCA=α.
3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в △АВС ∠B=90º- α.
4) Так как ∠BCA=90º (по условию), то ∠BCO=90º- ∠OCA=90º-α.
5) Рассмотрим треугольник BOC.
∠BCO=90º-α, ∠B=90º- α, следовательно, ∠BCO=∠B ⇒ BOC — равнобедренный с основанием BC. Отсюда BO=CO.
назад

B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Методика решения задач повышенного уровня сложности по планиметрии
(на примере задания №16 ЕГЭ)
Подготовила учитель математики
МКОУ СОШ№1 г. Дигора
Боциева А.А.
Подготовка к ЕГЭ-2020
по математике
Профильный уровень
планиметрия
Основные этапы плана
Специфика экзамена
Требования к результатам
Структура заданий
Подготовка к ЕГЭ
Базовый уровень
Профильный уовень
Получене аттестата
Получение аттестата
Для поступления
в ВУЗ нужна математика
Перевод первичных баллов в школьные оценки и тестовую шкалу 100 баллов выглядит примерно так:
0 – 6 – отметка «2»; 0-26 тестовых балла;
7 — 12 – отметка «3»; 27-50 баллов;
12 — 20 – отметка «4»; 50-75 баллов;
20 — 32 – отметка «5»; 75-100 баллов.
Минимальный порог профильного уровня устанавливается ближе к экзамену.
В прошлом году он составлял 27 тестовых баллов.
Что поможет подготовке?
- Неоднократная репетиция ситуации экзамена, формирование адекватной оценки, позитивный настрой на экзамен;
- Тренинг по совершенствованию вычислительных навыков;
- Регулярное проведение уроков обобщения;
- Своевременная систематизация материала на этапах повторения;
- Проведение в течение года диагностических работ, глубокий анализ результатов и работа по коррекции.
Работа учителя с учащимися
- Обеспечение учащихся достоверной и своевременной информацией о нормативных документах
- Консультативная поддержка уч-ся
- Индивидуальная и групповая работа по подготовке к ЕГЭ на уроках
- Обеспечение учащихся КИМами
Пробный вариант ЕГЭ по математике
Задание 16
Прямые, содержащие катеты AC и CB прямоугольного треугольника АВС, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.
Досрочный вариант ЕГЭ
Задание 16
Задача 16 (Основная волна, 29.05.2019)
Спасибо
за внимание и понимание!









