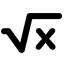Задание 17 егэ 2020 основная волна резервный день - Помощь в подготовке к экзаменам и поступлению


2386	Найти все значения параметра a, при каждом из которых система уравнений {(x^2+y^2=2x+2y), (x^2+y^2=2(1+a)x+2(1-a)y-2a^2):} имеет ровно два различных решения Решение График	Найти все значения параметра a, при каждом из которых система уравнений {(x^2 +y^2 = 2x +2y), (x^2 +y^2 =2(1 +a)x + 2(1-a)y -2a^2) :} имеет ровно два различных решения ! Задача 18 система из ЕГЭ 25.07.2020 резервный день # Два способа решения # 1 Решение — Елены Ильиничны Хажинской

2385	Биссектриса прямого угла прямоугольного треугольника ABC вторично пересекает окружность, описанную около этого треугольника, в точке L. Прямая, проходящая через точку L и середину N гипотенузы AB, пересекает катет BC в точке M. a) Докажите, что /_BML=/_BAC. б) Найдите площадь треугольника ABC, если AB=20 и CM=3sqrt5 Решение	Биссектриса прямого угла прямоугольного треугольника ABC вторично пересекает окружность ! Задача 16 на окружность из ЕГЭ 25.07.2020 резервный день

2384	В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 8, а боковое ребро AA1 равно 7. На ребре CC1 отмечена точка M, причем СМ=1 a) Точки О и O1 – центры окружностей, описанных около треугольников ABC и A1B1C1 соответственно. Докажите, что прямая OO1 содержит точку пересечения медиан треугольника ABM . б) Найдите расстояние от точки A1 до плоскости ABM Решение	В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 8, а боковое ребро AA1 равно 7 ! Задача 14 на треугольную призму — ЕГЭ резервный день 25.07.2020

2382	Решите неравенство 2745^x-27^(x+1)-1215^x+12*9^x+5^x-3^x<=0 Решение График	Решите неравенство 2745^x — 27^(x + 1) — 1215^x + 12*9^x + 5^x — 3^x <= 0 ! ЕГЭ по математике 25-07-2020 резервный день Задание 15

2381	а) Решите уравнение 1/(sin(x))^2+1/sin(x)-2=0 б) Укажите корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. Решение График	Решите уравнение 1/sin^2(x)+ 1/sin(x)-2 = 0 ! ЕГЭ по математике 25-07-2020 резервный день Задание 13

1517	Решите неравенство log_{11}(8x^2+7)-log_{11}(x^2+x+1)>=log_{11}(x/(x+5)+7) Решение График	Решите неравенство log_{11}(8x^2 +7) — log_{11}(x^2+ x+1) >= log_{11}(x/(x+5)+7) ! Задание 15 Демонстрационного варианта КИМ ФИПИ ЕГЭ 2021 # Задача 14 Критерии ЕГЭ 2022 ФИПИ # Пробный ЕГЭ 16-03-2019 Задание 15

Clear

Hide

Источник

Условие задачи

В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7.5 млн рублей?

Решение

S = 5 млн руб;

n лет;

p = 20%;

B = 7,5 млн. руб.

По формуле для величины переплаты по кредиту:

П = $frac{n+1}{2}cdot frac{p}{100}cdot S$ .

Здесь П — переплата, П = В — S;

П = 7,5 — 5 = 2,5 млн. руб.;

$2,5 = frac{n+1}{2}cdot frac{20}{100}cdot 5$ ;

$(n+1)cdot frac{1}{5}=1$ ;

n+1=5 ;

n=4.

Выведем формулу для величины переплаты. Пусть n — количество платёжных периодов, p — процент банка, S — сумма кредита, $k=1+frac{p}{100}$ .

Схема погашения кредита при равномерном уменьшении суммы долга:

Запишем, чему равны выплаты:

1 выплата: $Z_1 = scdot k - S cdot frac{n-1}{n};$

2 выплата: $Z_2 = S cdot frac{n-1}{n}cdot k - S cdot frac{n-2}{n};$

…

n-ая выплата: $Z_n = S cdot frac{1}{n} cdot k.$

Сумма всех выплат:

$B = S cdot k cdot (1+frac{n-1}{n}+frac{n-2}{2}+ dots +frac{1}{n}) - S (frac{n-1}{n}+frac{n-2}{n}+ dots +frac{1}{n})=$

$= S cdot k cdot (frac{1+frac{1}{n}}{2} cdot n) - S cdot (frac{1+n-1}{2 cdot n}(n-1))$

(воспользовались формулой суммы арифметической прогрессии),

$B = S cdot k cdot (frac{n+1}{2}) - S cdot (frac{n-1}{2})$ .

Так как $k = 1+ frac{p}{100}$ , получим:

$B = S cdot frac{n+1}{2} + S cdot frac{p}{100} cdot frac{n+1}{2} - S cdot frac{n-1}{2}=$

$=S + S cdot frac{p}{100} cdot frac{n+1}{2} = S+$ П, где П= $frac{n+1}{2}cdot frac{p}{100} cdot S$ .

Ответ:

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Решение. Задание 17. Досрочный ЕГЭ-2020» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник

№ 30178
Скачать
Формулы
Ответы
Решения
Критерии
Демо
Обсуждения

Просмотр

Если НЕ ОТОБРАЗИЛИСЬ материалы, то
ОБНОВИТЕ СТРАНИЦУ
или СКАЧАЙТЕ ИХ!

Образцы заданий ПОЛУЧЕНЫ ИЗ ОТКРЫТЫХ ИСТОЧНИКОВ в Интернете и

ПУБЛИКУЮТСЯ ПОСЛЕ окончания ЭКЗАМЕНА в ознакомительных целях!

Решения

Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

ВХОД	РЕГИСТРАЦИЯ
*бесплатно, в один клик!

Источник

: ЕГЭ по математике профиль

Образцы заданий № 17 реальных вариантов профильного ЕГЭ-2020 по математике.

Источник: alexlarin.net

Примеры реальных заданий:

17.1 В июле 2026 года планируется взять кредит на пять лет в размере S тыс.рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— в июле 2027, 2028 и 2029 годов долг остается равным S тыс. рублей;

— выплаты в 2030 и 2031 годах равны по 338 тыс.рублей;

— к июлю 2031 года долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

17.2 В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

Определите сумму кредита, если известно, что кредит будет выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78 030 рублей больше суммы, взятой в кредит.

Решение смотрите здесь

Связанные страницы:

Источник