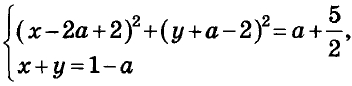Задание 1
Найдите корень уравнения $$(frac{1}{4}^{x-2,5})=frac{1}{8}.$$
Ответ: 4
Скрыть
$$(frac{1}{4}^{x-2,5})=frac{1}{8}$$
$$(2^{-2})^{x-2,5}=2^{-3}$$
$$2^{-2x+5}=2^{-3}$$
$$-2x+5=-3$$
$$-2x=-8$$
$$x=4$$
Задание 2
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Результат округлите до сотых.
Ответ: 0,14
Скрыть
m — число благоприятствующих этому событию исходов, то есть число исходов, когда выпадет 6 очков.
В эксперименте бросают две игральных кости, которые имеют 6 граней. Каждая грань имеет своё значение от 1 до 6. Нам необходимо, чтобы выпало 6 очков, а это возможно тогда, когда выпадет следующее сочетание чисел на гранях этих костей: 3 х 3, 4 х 2, 2 х 4, 1 х 5, 5 х 1, то есть получается, что m = 5, так как возможно 5 вариант выпадения 6 очков;
n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть на кубиках. Кидая первый кубик, может выпасть 6 вариантов, при бросании второго – тоже 6. Получается, что
$$n=6cdot6=36$$
Осталось найти вероятность выпадения 5 очков:
$$Р(А)=m/n=5/36=0,138888…$$
Нам нужно ответ округлить до сотых, поэтому
$$Р(А)=0,14$$
Задание 3
Градусная мера дуги АВ окружности, не содержащей точку D, равна 106°. Градусная мера дуги DE окружности, не содержащей точку А, равна 48°. Найдите угол АСВ. Ответ дайте в градусах

Ответ: 29
Скрыть
Рассмотрим вписанный угол BDA, который опирается на дугу AB с градусной мерой 106°, следовательно:
$$angle BDA=frac{106^{circ}}{2}=53^{circ}$$
По аналогии находим вписанный угол
$$angle DAE=frac{DE}{2}=frac{48^{circ}}{2}=24^{circ}$$
Рассмотрим развернутый угол BDC, из которой следует, что
$$angle ADC=180^{circ}-angle BDA=180^{circ}-53^{circ}$$
Из треугольника ADC получаем значение угла ACB:
$$angle ACB=180^{circ}-angle DAE=angle ADC$$
$$angle ACB=180^{circ}-180^{circ}+53^{circ}-24^{circ}=29^{circ}$$
Задание 4
Найдите значение выражения $$4cos4alpha,$$ если $$sin 2alpha=-0,4.$$
Ответ: 2,72
Скрыть
$$4cos4 alpha=4cdot(cos^2 2alpha–sin^2 2alpha)=4cdot(1–sin^2 2alpha–sin^2 2alpha)=$$
$$=4cdot(1–2sin^2 2alpha)=4cdot(1–2cdot(–0,4)^2)=4cdot(1–2cdot0,16)=$$
$$=4cdot(1–0,32)=2,72$$
Задание 5
В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ: 315
Скрыть
Высота всего конуса в 4 раза больше высоты жидкости (малого конуса). Следовательно, линейные размеры большого конуса также в 4 раза больше соответствующих линейных размеров малого конуса, а объем в $$4^3=64$$ раза больше и составляет:
$$V_1=64cdot V_2=64cdot5$$ мл
Следовательно, нужно долить:
$$V_1-V_2=64cdot5-5=63cdot5=315$$ мл
Задание 6
На рисунке изображён график $$y = f(x)$$ — производной функции f(x). На оси абсцисс отмечены 10 точек: $$x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}.$$ Сколько из этих точек лежит на промежутках убывания функции f(x)?
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Ор и объективности Tr публикаций. Каждый отдельный показатель — целое число от -1 до 1. Составители рейтинга считают, что информативность публикаций ценится вчетверо, а объективность — вдвое дороже, чем оперативность, то есть
$$R=frac{4In+Op+2Tr}{A}$$
Найдите, каким должно быть число А, чтобы издание, у которого все показатели максимальны, получило рейтинг 1.
Ответ: 7
Скрыть
Выразим из формулы рейтинга величину $$A,$$ получим:
$$A=frac{4In+Op+2Tr}{R}$$
Подставим сюда максимальные значения $$1$$ и $$R=1,$$ получим величину $$A:$$
$$A=frac{4cdot1+1+2cdot1}{1}=7$$
Задание 8
Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 63 км/ч, а вторую половину пути — со скоростью, большей скорости первого на 22 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Ответ: 77
Скрыть
Обозначим через x скорость первого автомобиля. Через S половину пути между пунктами A и B. Тогда время в пути первого автомобиля будет равно $$frac{2S}{x}.$$ Второй автомобиль первую половину пути ехал со скоростью 63 км/ч, а вторую половину пути со скоростью на 22 км/ч больше первого, то есть со скоростью $$x+22$$ км/ч. Следовательно, второй автомобиль затратил на весь путь время равное $$frac{S}{63}+frac{S}{x+22}.$$ Известно, что оба автомобиля приехали в пункт B одновременно, т.е. на весь путь затратили одно и то же время. Получим уравнение:
$$frac{2S}{x}=frac{S}{63}+frac{S}{x+22}$$
Пусть, условно $$S=1,$$ тогда:
$$frac{2}{x}=frac{1}{63}+frac{1}{x+22}$$
Отсюда найдем скорость первого автомобиля, имеем:
$$2cdot(63x+22cdot63)=xcdot(63+x+22)$$
$$126x+2772=63x+x^2+22x$$
$$x^2-41x-2772=0$$
$$D=1681+11088=12769=113^2$$
$$x_1=frac{41+113}{2}=77$$
$$x_2=frac{41-113}{2}<0$$
Имеем скорость первого автомобиля 77 км/ч.
Задание 9
На рисунке изображён график функции $$f(x)=a^x+b.$$ Найдите $$f(4).$$
Ответ: 76
Скрыть
Точки $$A(0;-4)$$ и $$B(1;-2)$$ принадлежат графику функции, тогда:
$$left{begin{matrix} -4=a^0+b\ -2=a^1+b end{matrix}right.Leftrightarrowleft{begin{matrix} -4=1+b\ -2=a+b end{matrix}right.Leftrightarrowleft{begin{matrix} b=-5\ a=-2+5=3 end{matrix}right.$$
Тогда:
$$f(4)=3^4-5=81-5=76$$
Задание 10
По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет- магазинов. Вероятность того, что нужный товар доставят вовремя из магазина А, равна 0,8. Вероятность того, что этот товар доставят вовремя из магазина Б, равна 0,85. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар вовремя.
Ответ: 0,03
Скрыть
Выделим два события: A – товар не доставлен из первого магазина; B – товар не доставлен из второго магазина. Вероятность события A равна
$$P(A)=1-0,8=0,2$$,
вероятность события B, равна
$$P(B)=1-0,85=0,15$$.
Так как магазины работают независимо друг от друга, то вероятность того, что товар не будет доставлен ни из первого, ни из второго магазина равна
$$P(AB)=0,2cdot0,15=0,03$$.
Задание 11
Найдите точку минимума функции $$у=11х-ln(х+4)^{11}-3. $$
Ответ: -3
Скрыть
$$y=11x-ln (x+4)^11-3=11x-11ln (x+4)-3$$
Найдём $$y’:$$
$$y’=11-11frac{1}{x+4}-0=11-11frac{1}{x+4}$$
Найдём нули производной функции:
$$y’=0$$
$$11-11frac{1}{x+4}=0$$
$$11=11frac{1}{x+4}$$ $$|:11$$
$$1=frac{1}{x+4}$$
$$x+4=1$$
$$x=-3$$
Задание 12
а) Решите уравнение $${sin left(2x+frac{2pi }{3}right) }{cos left(4x+frac{pi }{3}right) }-cos 2x=frac{{{sin }^2 x }}{{rm cos}(-frac{pi }{3})}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-2pi ; frac{3pi }{2}]$$
Ответ: а) $$-frac{pi}{12}+pi k, k in Z$$; б) $$-frac{13pi}{12}; -frac{pi}{12}; frac{11pi}{12}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
В правильной четырёхугольной призме $$ABCDA_1B_1C_1D_1$$ сторона основания $$АВ$$ равна $$2sqrt{3},$$ а боковое ребро $$АА_1$$ равно $$3.$$ На рёбрах $$A_1D_1$$ и $$DD_1$$ отмечены соответственно точки $$К$$ и $$М$$ так, что $$А_1К=KD_1,$$ a $$DM:MD_1=2:1.$$
а) Докажите, что прямые $$МК$$ и $$ВК$$ перпендикулярны.
б) Найдите угол между плоскостями $$ВМК$$ и $$ВСС_1.$$
Ответ: 45 градусов
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
Решите неравенство $$frac{6cdot 5^x-11}{{25}^{x+0,5}-6cdot 5^x+1}ge 0,25$$
Ответ: $$(-1;0); log_{5}3$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 15
Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Ответ: 54925
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
На сторонах $$АС, АВ$$ и $$ВС$$ прямоугольного треугольника $$АВС$$ с прямым углом $$С$$ вне треугольника $$АВС$$ построены равнобедренные прямоугольные треугольники $$АКС, ALB$$ и $$ВМС$$ с прямыми углами $$К, L$$ и $$М$$ соответственно.
а) Докажите, что $$LC$$ — высота треугольника $$KLM.$$
б) Найдите площадь треугольника $$KLM,$$ если $$LC=4.$$
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 17
Найдите, при каких неотрицательных значениях а функция $$f(х)=Зах^4-8х^3+Зх^2-7$$ на отрезке $$[-1; 1]$$ имеет ровно одну точку минимума.
Ответ: $$[0;1,5);[2;+infty)$$
Скрыть
Найдём производную функции:
$$f'(x)=12ax^3-24x^2+6x$$
$$12ax^3-24x^2+6x=0$$
$$6xcdot(2ax^2-4x+1)=0$$
В точке $$x=0$$ производная меняет знак с «-» на «+», поэтому точка $$x=0$$ является точкой минимума.
Функция $$f(x)=3ax^4-8x^3+3x^2-7$$ может иметь ещё точку минимума, если уравнение $$2ax^2-4x+1=0$$ имеет два корня, а значит, при $$a<2.$$
а) При $$a=0$$ уравнение имеет два корня:
$$x=0;$$ $$x=frac{1}{4}$$
Точка $$x=frac{1}{4}$$ является точкой максимума.
б) При $$ain (0;2)$$ уравнение имеет три различных корня:
$$x_1=0$$
$$x_2=frac{2-sqrt{4-2a}}{2a}$$
$$x_3=frac{2+sqrt{4-2a}}{2a}$$
где $$x_1<x_2<x_3.$$ Точка $$x_2$$ является точкой максимума, а точки $$x_1$$ и $$x_3$$ – точками минимума. Точка $$x_3$$ лежит на отрезке $$[-1; 1],$$ если $$frac{2+sqrt{4-2a}}{2a}leq1,$$ а это выполнено при всех $$ageq1,5.$$
Получили: функция $$f(x)=3ax^4-8x^3+3x^2-7$$ на отрезке $$[-1; 1]$$ имеет одну точку минимума при $$ain [0;1,5)$$ и $$a>2.$$
Задание 18
Для каждого натурального числа $$n$$ обозначим через $$n!$$ произведение первых $$n$$ натуральных чисел $$(1!=1).$$
а) Существует ли такое натуральное число $$n,$$ что десятичная запись числа $$n!$$ оканчивается ровно 9 нулями?
б) Существует ли такое натуральное число $$n,$$ что десятичная запись числа $$n!$$ оканчивается ровно 23 нулями?
в) Сколько существует натуральных чисел $$n,$$ меньших 100, для каждого из которых десятичная запись числа $$n!cdot(100-n)!$$ оканчивается ровно 23 нулями?
Ответ: а) да; б) нет; в) 16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Решение и ответы заданий Варианта №17 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
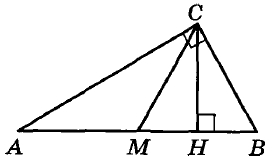
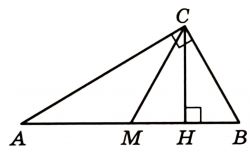
Острый угол В прямоугольного треугольника равен 50°. Найдите угол между высотой СН и медианой СМ, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Задание 2.
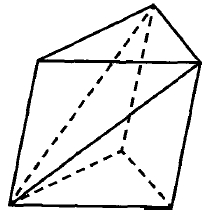
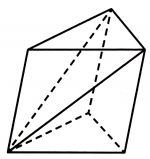
От треугольной призмы, объём которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объём оставшейся части.
Задание 3.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 спортсмена из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России.
Задание 4.
Игральный кубик бросают дважды. Известно, что в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.
Задание 5.
Найдите корень уравнения log9 32x+9 = 2.
Задание 6.
Найдите значение выражения frac{a^{5,96}cdot a^{2,4} }{a^{5,36}} при а = 6.
Задание 7.
Прямая у = 5х + 11 является касательной к графику функции у = х3 + 4х2 + 9х + 11. Найдите абсциссу точки касания.
Задание 8.
Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=sqrt{frac{Rh}{500}}, где 𝑅 = 6400 км – радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 24 километров. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 32 километров?
Задание 9.
Первый садовый насос перекачивает 8 литров воды за 4 минуты, второй насос перекачивает тот же объём воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 60 литров воды?
Задание 10.
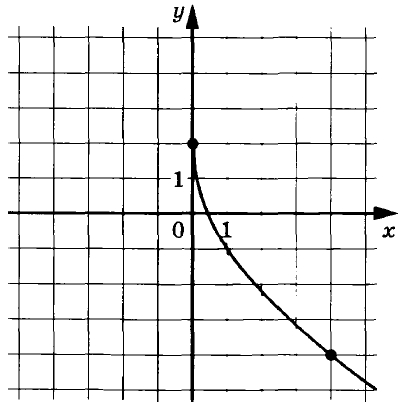
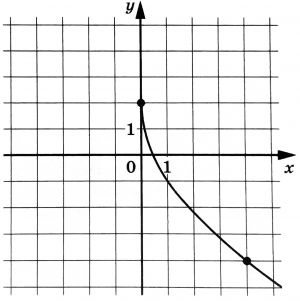
На рисунке изображён график функции f(x) = k√x + p. Найдите значение х, при котором f(х) = –10.
Задание 11.
Найдите точку максимума функции у = ln(х + 25)11 – 11х + 5.
Задание 12.
а) Решите уравнение 5sinx – 4sin3x = 2sin2x.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; -2pi ].
Задание 13.
Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В.
а) Докажите, что середина ребра SA равноудалена от вершин В и С.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = AC.
Задание 14.
Решите неравенство log22(x4) – 4log0,25 (x2) ≥ 12.
Задание 15.
Производство х тыс. единиц продукции обходится в q = 2х2 + 5х + 10 млн рублей в год. При цене р тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет рх – q. При каком наименьшем значении р через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении х?
Задание 16.
Точки A1, B1, С1 – середины сторон соответственно ВС, АС и АВ остроугольного треугольника АВС.
а) Докажите, что окружности, описанные около треугольников А1СВ1, А1ВС1 и В1АС1 пересекаются в одной точке.
б) Известно, что АВ = АС = 13 и ВС = 10. Найдите радиус окружности, вписанной в треугольник, вершины которого – центры окружностей, описанных около треугольников А1СВ1, А1ВС1 и В1АС1.
Задание 17.
Найдите все значения а, при каждом из которых система уравнений
имеет единственное решение.
Задание 18.
Для действительного числа х обозначим через [х] наибольшее целое число, не превосходящее х. Например, [frac{11}{4}] = 2, так как 2≤frac{11}{4}<3.
а) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{4}]+[frac{n}{7}]=n?
б) Существует ли такое натуральное число n, что [frac{n}{2}]+[frac{n}{3}]+[frac{n}{4}]=n+2?
в) Сколько существует различных натуральных n, для которых [frac{n}{2}]+[frac{n}{3}]+[frac{n}{9}]+[frac{n}{17}]=n+1945?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 3644 | При каких значениях параметра a уравнение (a^2-6a+8)*x^2+(a^2-4)*x+10-3a-a^2=0 имеет более двух корней |
При каких значениях параметра a уравнение (a2-6a+8)x2 +(a2-4)x + 10-3a-a2 =0 имеет более двух корней | |
| 3591 | Найдите все значения a при каждом из которых уравнение a(a+3)x^2+(2a+6)x-3a-9=0 имеет более одного корня |
Найдите все значения a при каждом из которых уравнение a(a+3)x2 +(2a+6)x -3a -9 =0 имеет более одного корня | |
| 3585 | Найдите все значения a при каждом из которых уравнение 2sqrt(x^4+(a-3)^4)=abs(x+a-3)+abs(x-a+3) имеет единственное решение |
Найдите все значения a при каждом из которых уравнение 2sqrt(x4 +(a-3)4) = abs(x+a-3) +abs(x-a+3) имеет единственное решение ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 17 Вариант МА2210209 #Задачи — аналоги 621 104 | |
| 3544 | Найдите все значения a, при которых система уравнений {(abs(y+x^3)-abs(y+3x)=2y+x^3+3x), (abs(-y-3x+1)-abs(y+x^3-a)=), (= -3y-6x-x^3+a+2) :} имеет единственное решение |
Найдите все значения a, при которых система уравнений {|y+x^3|-|y+3x| = 2y+x^3+3x), |-y-3x+1| -|y+x^3-a| =-3y-6x-x3+a+2 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 6 Задание 17 |
|
| 3434 | Найдите все значения параметра a, b при которых неравенство a^3x^4+2ax^3+b <= 2bx^2+b^3x+a выполняется для всех x из отрезка [0; 1] |
Найдите все значения параметра a, b при которых неравенство выполняется для всех x из отрезка [0; 1] ! ДВИ в МГУ 2022 — 5 поток, Вариант 225 Задание 6 # Решение Натальи Яковлевны Захаровой youtube видео разбор | |
| 3405 | Найдите все значения a, при которых система уравнений {(abs(y+1/2x^3)-abs(y+3/2x)=2y+1/2x^3+3/2x), (abs(-y-3/2x+1)-abs(y+1/2x^3-a)=), (-4 y-9/2x-1/2x^3+a+3) :}. имеет единственное решение |
Найдите все значения a, при которых система уравнений { |y+1/2×3| -|y+3/2x| = 2y + 1/2×3 +3/2x |-y-3/2x+1| — |y+1/2×3 -a| = -4y -9/2x -1/2×3 +a +3 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 8 Задание 17 # Ошибка в ответе пособия у Ященко ? : color{red}{a > -1 ?} |
|
| 3404 | Найдите все значения параметра a, при которых уравнение x^2+(1-a+root(4)(abs(x)))^2=a^2/4. имеет ровно три решения |
Найдите все значения параметра a, при которых уравнение x2 + (1-a+ корень 4 степени из |x|) 2 = a 2/4 имеет ровно три решения ! ДВИ в МГУ 2022 — 1 поток, Вариант 1 Задание 6 | |
| 3391 | Найдите все значения параметра a, при каждом из которых уравнение sqrt(15x^2+6ax+9)=x^2+ax+3 имеет три различных решения |
Найдите все значения параметра a, при каждом из которых уравнение корень из 15×2 +6ax+9 =x2 +ax+3 имеет три различных решения ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 17 | |
| 3379 | Найдите все значения параметра a, при каждом из которых уравнение x^2+a^2+2x-4a=abs(4x+2a). имеет более двух различных корней |
Найдите все значения параметра a, при каждом из которых уравнение x2 +a2 +2x -4a = |4x+2a| имеет более двух различных корней ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 17 Санкт-Петербург | |
| 3368 | Оценки экспертов решений задания 17 ЕГЭ по математике профильного уровня. Задание № 17 — это уравнение, неравенство или их системы с параметром. Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространёнными из них являются: – чисто алгебраический способ решения; – способ решения, основанный на построении и исследовании геометрической модели данной задачи; – функциональный способ, в котором могут быть и алгебраические, и геометрические элементы, но базовым является исследование некоторой функции. Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трёх перечисленных способов |
Критерии оценивания решений задания 17 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку | |

Показана страница 1 из 55
Задание 17. Вариант 7 ЕГЭ 2022 профиль Ященко
Задание 17. Найдите все значения a, при каждом из которых система уравнений
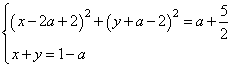
имеет единственное решение.
Решение.
Выразим из второго уравнения и подставим в первое:
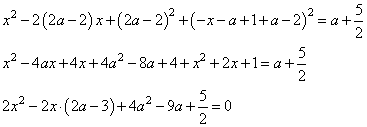
Поскольку y однозначно выражается через x, каждому корню этого уравнения будет соответствовать единственное решение исходной системы. Значит, система имеет единственное решение тогда и только тогда, когда дискриминант равен нулю:
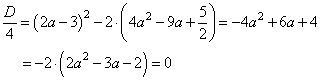
Получаем, что или
.
Ответ: -1/2; 2
ЕГЭ Профиль №17. Задачи, сводящиеся к исследованию квадратного трехчлена
Решение 17 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
Острый угол B прямоугольного треугольника равен 50°. Найдите угол между высотой CH и медианой CM, проведёнными из вершины прямого угла. Ответ дайте в градусах.
От треугольной призмы, объём которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объём оставшейся части.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 спортсмена из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России.
Игральный кубик бросают дважды. Известно, что в сумме выпало 6 очков. Найдите вероятность того, что в первый раз выпало 2 очка.
Найдите корень уравнения (log_9{3^{2x+9}}=2).
Найдите значение выражения (dfrac{a^{5{,}96}cdot a^{2{,}4}}{a^{5{,}36}}) при (a=6).
Прямая (y=5x+11) является касательной к графику (y=x^3+4x^2+9x+11). Найдите абсциссу точки касания.
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400, км) − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 24 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 32 км?
Первый садовый насос перекачивает 8 литров воды за 4 минуты, второй насос перекачивает тот же объём воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 60 литров воды?
На рисунке изображен график функции (f(x)=ksqrt{x}+p). Найдите значение (x), при котором (f(x)=-10).
Найдите точку максимума функции (y=lnleft(x+25right)^{11}-11x+5).
а) Решите уравнение (5sin{x}-4sin^3{x}=2sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{7pi}{2};-2piright] )
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол (в градусах) между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=AC.
Решите неравенство (log^2_{2}{left(x^4right)}-4log_{0{,}25}{left(x^2right)}geqslant 12).
Производство (x) тыс. единиц продуктции обходится в (q=2x^2+5x+10) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через 12 лет суммарная прибыль может составить не менее 744 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB = AC = 13 и BC = 10. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-2a+2right)^2+left(y+a-2right)^2=a+dfrac{5}{2}, \ x+y=1-a end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{4}right]+left[dfrac{n}{7}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{4}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]+left[dfrac{n}{17}right]=n+1945)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.