Продолжаем решать демоверсию ЕГЭ по информатике 2023.
Условия задач были взяты с сайта: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
В этой статье разберём задания 16-21 из демоверсии ЕГЭ по информатике 2023.
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
Задание 16
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
Решение:
Если мы просто перепечатаем функцию, как мы делали на экзамене в 2022 году, то программа откажится это вычислять. Здесь слишком большая глубина рекурсии.
Тогда посмотрим внимательно на функцию. Оказывается это функция факториала. Это действие означает n! = 1*2*3*…*n.
F(2023) / F(2020) = (2023 * 2022 * 2021 * 2020!) / 2020! = 2023 * 2022 * 2021
Выражение 2020! просто сокращается. В ответе напишем 2023 * 2022 * 2021 = 8266912626.
Ответ: 8266912626
Задание 17
В файле содержится последовательность целых чисел. Элементы
последовательности могут принимать целые значения от –10 000 до 10 000
включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары
не меньше квадрата максимального элемента последовательности,
оканчивающегося на 3. В ответе запишите два числа: сначала количество
найденных пар, затем максимальную из сумм квадратов элементов таких
пар. В данной задаче под парой подразумевается два идущих подряд
элемента последовательности.
Решение:
В начале нужно найти максимальное число последовательности, оканчивающегося на 3.
f=open('17.txt') mx=-10000 for s in f.readlines(): x=int(s) if abs(x)%10==3: mx = max(mx, x) print(mx)
Получается число 9973.
Напишем основную программу:
f=open('17.txt') k=0 mx=0 n1=int(f.readline()) for s in f.readlines(): n2=int(s) if ((abs(n1)%10==3) != (abs(n2)%10==3)) and (n1**2 + n2**2 >= 9973**2): k=k+1 mx = max(mx, n1**2 + n2**2) n1=n2 print(k, mx)
Как решать подобные задачи было рассказано в видеокурсе.
Здесь нужно помнить, что числа отрицательные. Поэтому при нахождении последней цифры, нужно использовать функцию модуля abs.
Так же здесь интересное логическое выражение «в которых только одно число оканчивается на 3». Это операция xor — отрицание равносильности.
Ответ:
Задание 18
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
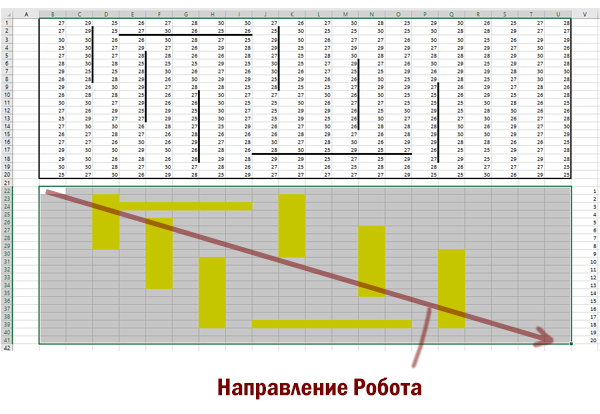
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Решение:
Открываем файл в программе Excel.
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
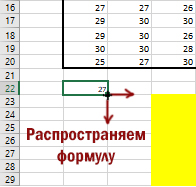
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
Распространим формулу на всё пространство, не трогая закрашенные клетки.
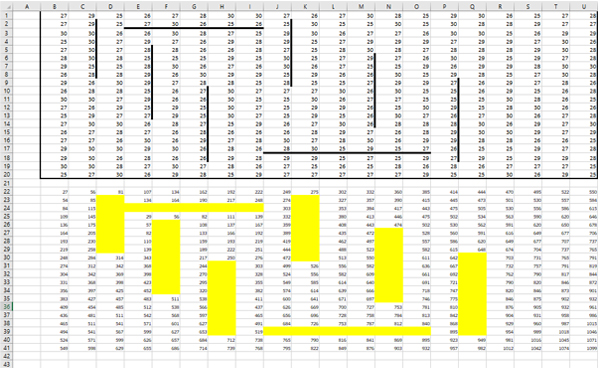
Получается такая картина:
Для вертикальных подкрашенных полосок, Робот может попасть только сверху! Поэтому пишем формулу для ячейки, к примеру, для D23:
=D22+D2
Распространяем формулу по всему закрашенному столбцу. Аналогично делаем для всех вертикальны подкрашенных полосок.
В ячейки для горизонтально подкрашенных полосок, Робот может попасть только слева! Поэтому пишем формулу, к примеру, для ячейки E24:
=D24+E3
Распространяем формулу по всей закрашенной строчке. Алагоично делаем со всеми горизонтальными полосками.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 1099.
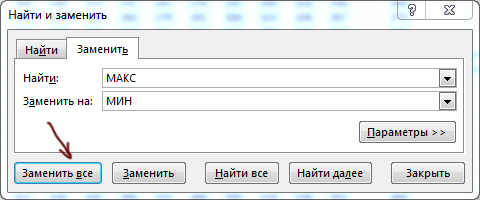
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 1026.
Ответ:
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход
игрок может добавить в кучу один камень или увеличить количество камней
в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть
неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится
не менее 129. Победителем считается игрок, сделавший последний ход,
т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128.
Будем говорить, что игрок имеет выигрышную стратегию, если он может
выиграть при любых ходах противника. Описать стратегию игрока – значит
описать, какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т.е. не являющиеся
выигрышными независимо от игры противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход,
но при любом ходе Пети Ваня может выиграть своим первым ходом.
Решение:
Решим задачу с помощью шаблона на языке программирования Python. Если хотите ознакомится с аналитическим решением задач на теорию игр, можете посмотреть мои статьи по 19 Заданию, 20 Заданию, 21 Заданию. Но с помощью шаблонов на экзамене решать быстрее и легче. Об этом подходе можете найти в видеокурсе.
Введём параметр p, который будет олицетворять позицию игры (ход).
| Начальная позиция | Ход Пети | Ход Вани | Ход Пети | Ход Вани | Ход Пети | |
| p | 1 | 2 | 3 | 4 | 5 | 6 |
def F(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Заводим функцию F. Т.к. у нас одна куча, то она принимает параметры: x — количество камней в куче, p-позиция игры.
Дальше описываем победу. Если x>=29 и позиция равна 3 (1 Ход Вани), то возвращаем True, что означает победу.
Если, позиция уже равна 3, но камней меньше, чем должно быть для победы, то возвращаем False (проигрыш).
Третье условие. Если кто-то выиграл, но на первых двух условиях мы не вышли из функции, то, значит, выиграл не тот, кто нам нужен, следовательно, возвращаем Fasle.
Если мы не вышли на первых трёх условиях, то, значит, продолжаем прокручивать ходы, рекурсивно запускаем функцию F.
Для нечётных p (это ходы Вани), возвращаем разные ходы через and, т.к. он должен побеждать в любом случае. При этом увеличиваем на 1 значение p.
Для чётных p (это ходы Пети), возвращаем ходы через or.
В конце перебираем все возможные значения для s через цикл for, ищём те значения, которые подходят по условию задачи.
Ответ: 64
Задание 20
Для игры, описанной в задании 19, найдите два наименьших таких значения S, при
которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
Задача точно такая же, как и в 19 задании, только теперь обязательно должен побежать Петя на своём втором ходу (p=4), при любой игре Вани.
Пишем тот же шаблон, немного отредактировав его.
def F(x, p): if x>=129 and p==4: return True if x<129 and p==4: return False if x>=129: return False if p%2==0: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s)
Получается 32 и 63.
Ответ:
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором
одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Решение:
Опять используем прошлый шаблон, но немного модернизируем.
def F(x, p): if x>=129 and (p==3 or p==5): return True if x<129 and p==5: return False if x>=129: return False if p%2==1: return F(x+1, p+1) and F(x*2, p+1) else: return F(x+1, p+1) or F(x*2, p+1) def F1(x, p): if x>=129 and p==3: return True if x<129 and p==3: return False if x>=129: return False if p%2==1: return F1(x+1, p+1) and F1(x*2, p+1) else: return F1(x+1, p+1) or F1(x*2, p+1) for s in range(1, 129): if F(s, 1): print(s) print() for s in range(1, 129): if F1(s, 1): print(s)
Здесь Ваня должен выигрывать либо на первом своём ходе (p=3), либо на втором своём ходе (p=5).
Т.к. Ваня не должен гарантированно выиграть своим первым ходом, то мы создаём ещё одну функцию F1, похожую на основную функцию F, которая вычисляет, когда Ваня именно гарантированно выигрывает на своём первом ходе (p=3). И, затем, мы из тех чисел, которые получились в первой функции F, исключаем числа, которые получились во второй функции F1.
В первой функции получилось 62,64, а во второй 64. Получается ответ 62.
Ответ: 62
Демоверсия ЕГЭ по информатике 2023 (Задания 1-5)
Демоверсия ЕГЭ по информатике 2023 (Задания 6-10)
Демоверсия ЕГЭ по информатике 2023 (Задания 11-15)
Демоверсия ЕГЭ по информатике 2023 (Задания 22-27)
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 18 задания. Объясняется тема об обработке числовой информации в электронных таблицах.
Содержание:
- ЕГЭ по информатике 18 задание объяснение
- Решение 18 задания ЕГЭ
- Исполнитель Робот
18-е задание: «Обработка числовой информации в электронных таблицах»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать вещественные выражения в электронных таблицах
Решение 18 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Исполнитель Робот
18 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:

Ответ: 1204 | 502
Решение подобного задания смотрите в следующем ниже разборе.
📹 YouTube здесь
Видеорешение на RuTube здесь
18_1:
Задание выполняется с использованием прилагаемых файлов
Исходные данные записаны в файле (выше) в виде электронной таблицы прямоугольной формы.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — верхняя правая ячейка
J12результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
=J1
J12 Робот мог, либо двигаясь из ячейки I12, либо из J13. I12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка I1). Ну и поскольку дальше он попадет только в ячейку J12, то необходимо прибавить значение этой ячейки. Поскольку значение уже просчитано для результирующей таблицы, то мы и будем его брать именно с результирующей таблицы. То есть введите формулу для ячейки I12:=I1+J12
I12, будет такой же и для всех оставшихся ячеек верхней строки.I12 в диапазон ячеек A12:H12:J13. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — J2) и добавим значение ячейки, в которую он пойдет дальше — ячейка J12 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=J2+J12
J13 подходит для всех ячеек данного столбца.J13 в диапазон ячеек J14:J21:I12 и J13 Робот мог попасть, также двигаясь из ячейки I13. Рассмотрим ее.I13 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I2), и затем у него альтернатива движения: либо в ячейку I12, либо в J13. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Для этого надо выбрать максимум из I12 и J13 и добавить к текущему значению. Введите формулу в I13:
=I2+МАКС(I12;J13)
I13, использовав маркер копирования, во все оставшиеся ячейки таблицы:I13 на =I2+МИН(I12;J13).Ответ: 1133 | 522
18_2:
Задание выполняется с использованием прилагаемых файлов
При попытке зайти на клетку со стеной Робот разрушается. Исходные данные записаны в файле в виде электронной таблицы прямоугольной формы. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю, не разрушившись. Известно, что такой путь существует. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
L25результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке исходной таблицы —L12. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
формула для L25:
=L12
L12 Робот мог, либо двигаясь из ячейки K12, либо из L11. К12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка K12). Ну и поскольку дальше он попадет только в ячейку L12, то необходимо прибавить значение этой ячейки.K25:=ЕСЛИ(И(L25>0;ИЛИ(K12<=100;K12>=500));K12+L25;0)
Если выполняются одновременно два условия: L25>0 И либо K12<=100 либо K12>=500, то собираем монету с текущей ячейки (K12) и добавляем монету с L25, так как там нет стены (L25>0)
K25 будет такой же и для всех оставшихся ячеек строки.K25 в диапазон ячеек A25:J25.L24. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — L11) и добавим значение ячейки, в которую он пойдет дальше — ячейка L25 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=ЕСЛИ(И(L25>0;ИЛИ(L11<=100;L11>=500));L11+L25;0)
Если выполняются одновременно два условия: L25>0 И либо L11<=100 либо L11>=500, то собираем монету с текущей ячейки (L11) и добавляем монету с L25, так как там нет стены (L25>0)
L24 в диапазон ячеек L14:L23.K24 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — K11), и затем у него альтернатива движения: либо в ячейку L24, либо в K25. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки, нет ли там стены. Для этого введите формулу в K24:=ЕСЛИ(И(K11>100;K11<500);0;ЕСЛИ(И(L24=0;K25=0);0;ЕСЛИ(L24=0;K11+K25; ЕСЛИ(K25=0;K11+L24;K11+МИН(L24;K25)))))
Здесь логика формулы следующая: если текущее значение ячейки соответствует стене, то записываем 0; ИНАЧЕ — если обе ячейки, в которые может двигаться Робот, — стены, то записываем в текущую ячейку 0; ИНАЧЕ — если ячейка справа — стена, то двигаемся вниз, собирая по пути монеты; ИНАЧЕ — если ячейка снизу — стена, то двигаемся вправо, собирая по пути монеты; ИНАЧЕ — выбираем минимальное значение из соседних ячеек и собираем монеты.
K24, использовав маркер копирования, во все оставшиеся ячейки таблицы:МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.
Ответ: 1492 640
18_3:
Задание выполняется с использованием прилагаемых файлов
Робот может двигаться только вниз и вправо. Для сбора денег у Робота есть контейнеры вместимостью 8 монет каждый. С каждой клетки Робот забирает наибольшее количество контейнеров, полностью заполненных монетами. Если контейнер не заполнен до конца, а монеты в клетке кончились, робот высыпает из него монеты перед переходом в следующую клетку. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
J21результирующей таблицы. Робот просто соберет монеты, которые находится в этой ячейке исходной таблицы —J10, если наберется целое число контейнеров (значение кратное 8). Если целое число контейнеров не набирается, — то робот забирает только то, что набралось в контейнеры (8* ЧАСТНОЕ от деления монет на 8). Поэтому для ячейки возьмем значение из исходной таблицы, проверяя его на кратность 8. Введите формулу:
формула для J21:
=ЕСЛИ(ОСТАТ(J10;8)=0;J10;8*ЧАСТНОЕ(J10;8))
J20. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка J9). При этом будем проверять значение на кратность 8 и действовать так же, как описано в предыдущем пункте. Ну и поскольку дальше Робот попадет только в ячейку J21, то необходимо прибавить значение этой ячейки.формула для J20: =ЕСЛИ(ОСТАТ(J9;8)=0;J9+J21;8*ЧАСТНОЕ(J9;8)+J21)
J20 будет такой же и для всех оставшихся ячеек столбца.J20 в диапазон ячеек J12:J19.I21. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — I10). Проверим заполненность контейнеров, и добавим значение ячейки, в которую Робот пойдет дальше — ячейка J21 (берем значение из результирующей таблицы, поскольку оно уже просчитано):формула для I21:
=ЕСЛИ(ОСТАТ(I10;8)=0;I10+J21;8*ЧАСТНОЕ(I10;8)+J21)
I21 в диапазон ячеек A21:H21.I20 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I9), проверяя заполненность контейнеров, и затем у него альтернатива движения: либо в ячейку J20, либо в I21. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки на заполненность контейнеров. Для этого введите формулу в I20:формула для I20:
=ЕСЛИ(ОСТАТ(I9;8)=0;I9+МАКС(J20;I21);8*ЧАСТНОЕ(I9;8)+МАКС(J20;I21))
I20, использовав маркер копирования, во все оставшиеся ячейки таблицы.МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.Ответ: 1144 448
Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!
В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.
Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.
Всех желающих — приглашаю ниже!
Быстрый перевод из системы в систему
В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:
bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…
Давайте посмотрим и на них:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
n = n // 2 #Целочисленное деление
print(b) #ВыводДанная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
if (n % 21) > 9: #Если остаток от деления больше 9...
if n % 21 == 10: #... и равен 10...
b = 'A' + b #... запишем слева A
elif n % 21 == 11:#... и равен 11...
b = 'B' + b#... запишем слева B
'''
И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)
'''
elif n % 21 == 11:
b = 'B' + b
elif n % 21 == 12:
b = 'C' + b
elif n % 21 == 13:
b = 'D' + b
elif n % 21 == 14:
b = 'E' + b
elif n % 21 == 15:
b = 'F' + b
elif n % 21 == 16:
b = 'G' + b
elif n % 21 == 17:
b = 'H' + b
elif n % 21 == 18:
b = 'I' + b
elif n % 21 == 19:
b = 'J' + b
elif n % 21 == 20:
b = 'K' + b
else: #Иначе (остаток меньше 10)
b = str(n % 21) + b #Остатот от деления записываем слева
n = n // 21 #Целочисленное деление
print(b) #ВыводСпособ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:
def convert_base(num, to_base=10, from_base=10):
# Перевод в десятичную систему
if isinstance(num, str): # Если число - строка, то ...
n = int(num, from_base) # ... переводим его в нужную систему счисления
else: # Если же ввели число, то ...
n = int(num) # ... просто воспринять его как число
# Перевод десятичной в 'to_base' систему
alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
if n < to_base: # Если число меньше системы счисления в которую переводить...
return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
else: # Иначе...
return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остаткаВызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).
Задача 2
Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.
Решение данной задачи совсем простое: банальный перебор.
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
print(x, y, z, F) #Выводим результатРезультат:
Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
if not F:
print(x, y, z, F) #Выводим результатРезультат:
Далее — простой анализ.
Задача 5
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:
Задача 6
Перепечатали и получили ответ:
s = 0
k = 1
while s < 66:
k += 3
s += k
print(k)Задача 12
В очередной раз, просто заменим слова на код:
a = '9' * 1000
while '999' in a or '888' in a:
if '888' in a:
a = a.replace('888', '9', 1)
else:
a = a.replace('999', '8', 1)
print(a)Задача 14
Компьютер железный, он всё посчитает:
a = 4 ** 2020 + 2 ** 2017 - 15
k = 0
while a > 0:
if a % 2 == 1:
k += 1
a = a // 2
print(k)Задача 16
Опять же, просто дублируем программу в python:
def F(n):
if n > 0:
F(n // 4)
print(n)
F (n - 1)
print(F(5))Результат:
Задача 17
Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!
with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)
k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...
for i in range(len(a)): #Обходим все элементы массива
if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
k += 1 #Счётчик
if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
m = int(a[i - 1]) + int(a[i])
print(k, m) #ВыводНемного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.
Задача 19, 20 и 21
Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:
Пишем рекурсивную функцию и цикл перебора S:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
breakНемного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:
|
Игра |
Петя |
Ваня |
Петя |
Ваня |
Петя |
|
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
Далее — всё по условию задачи.
Вторая задача на теорию игр:
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2 != 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Отличия:
-
Выиграл Петя, соответственно, позиция 4
-
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
-
Убрали break, так как нам нужны все S, а не единственный
Последняя вариация задачи:
Сразу код:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 5: #Условия завершения игры
return p == 3 or p == 5
if p % 2 == 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Ну и всего лишь 2 отличия:
-
Позиции 3 или 5, а не 4, так как выиграл Ваня
-
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.
Задача 22
Ctrl+C, Ctrl+V — наше всё! 
for i in range(1, 100000):
x = i
L = 0
M = 0
while x > 0 :
L = L+1
if (x % 2) != 0:
M = M + x % 8
x = x // 8
if L == 3 and M == 6:
print(i)Задача 23
Итак, код:
def f(x, y):
if x > y: #Перегнали цель
return 0
if x == y: #Догнали цель
return 1
if x < y: #Догоняем цель тремя методами
return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)
print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.
Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.
Ссылка на репозиторий со всеми программами:
Надеюсь, что смог помочь в своей статье выпускникам и готовящимся 
Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.
Всем удачи!
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Делаю разбор второй части?
Проголосовали 106 пользователей.
Воздержались 15 пользователей.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (888)
ЕСЛИ нашлось (222)
ТО заменить (222, 
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Источник: Демонстрационная версия ЕГЭ—2016 по информатике.
2
Исполнитель Редактор получает на вход строку цифр и преобразует её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 127 идущих подряд цифр «9»? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (999)
ЕСЛИ нашлось (333)
ТО заменить (333, 9)
ИНАЧЕ заменить (999, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
3
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из цифры 1, за которой следуют 80 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (18) ИЛИ нашлось (288) ИЛИ нашлось (3888)
ЕСЛИ нашлось (18)
ТО заменить (18, 2)
ИНАЧЕ ЕСЛИ нашлось (288)
ТО заменить (288, 3)
ИНАЧЕ заменить (3888, 1)
КОНЕЦ ЕСЛИ
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
4
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 125 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (888)
ЕСЛИ нашлось (333)
ТО заменить (333, 
ИНАЧЕ заменить (888, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
5
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Ниже приведена программа для исполнителя Редактор.
НАЧАЛО
ПОКА нашлось (722) ИЛИ нашлось (557)
ЕСЛИ нашлось (722)
ТО заменить (722, 57)
ИНАЧЕ заменить (557, 72)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход этой программе подается строка, состоящая из 55 цифр; последняя цифра в строке — цифра 7, а остальные цифры — пятёрки. Какая строка получится в результате применения программы к этой строке? В ответе запишите полученную строку.
Пройти тестирование по этим заданиям
ЕГЭ информатика 18 задание разбор, теория, как решать.
Динамическое программирование в электронных таблицах. Робот-сборщик монет, (П) — 1 балл
Е18.16 Определите максимальную и минимальную денежные суммы
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут …
Читать далее
Е18.20 количество недоступных клеток, в которые робот не сможет попасть из-за нехватки энергии
Робот с тоит в левом н ижнем углу прямоугольного поля, в каждой клетке которого записано целое число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вверх. Выходить за пределы поля робот не может. Числа показывают изменение запаса энергии робота при прохождении соответствующей клетки. Если число отрицательно, запас энергии уменьшается …
Читать далее
Е18.19 Посетив клетку, Робот забирает монету с собой
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут …
Читать далее
Е18.18 Определите количество способов, которыми Робот может попасть из левой верхней клетки в правую нижнюю.
Квадрат разлинован на МхМ клеток (1 < N < 20). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке пересечь границы квадрата (внутренние, обозначенные жирной линией, или внешние) Робот …
Читать далее
Е18.17 Проходя через клетку, Сборщик собирает все монеты, лежащие на ней
Квадрат разлинован на N×N клеток (2 < N < 21). В каждой клетке записано целое положительное число – количество монет. Исполнитель Сборщик имеет две команды ВПРАВО и ВВЕРХ, которые, соответственно, перемещают его на одну клетку вправо или на одну клетку вверх. Проходя через клетку, Сборщик собирает все монеты, лежащие на ней. На поле существуют стены, …
Читать далее
Е18.16 включается в сумму, если оно больше числа в предыдущей клетке на пути робота
Дан квадрат 15×15 клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы квадрата робот не может. При этом ведётся подсчёт суммы по следующим правилам: число в очередной клетке, через которую проходит …
Читать далее
Е18.15 Между соседними клетками квадрата также могут быть внутренние стены.
Между соседними клетками квадрата также могут быть внутренние стены. Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат …
Читать далее
Е18.14 За посещение клетки A взимается плата 1 монета
За посещение клетки A взимается плата 1 монета Квадрат разлинован на N x N клеток (1 < N < 20). Исполнитель Буквоед может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Буквоед перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке …
Читать далее
Е18.13 каждое следующее число отличалось от предыдущего не более чем на 10
каждое следующее число отличалось от предыдущего не более чем на 10 Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 10. Какую максимальную сумму могут иметь выбранные числа? В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана …
Читать далее
Е18.12 Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля.
Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля. Квадрат разлинован на N×N клеток (2 < N < 20), N – нечетное число. В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 1. Два исполнителя – ПРАВО и ЛЕВО – существуют в рамках одного поля. …
Читать далее
№1

f=open(’17_1.txt’)
a=[int(x) for x in f]
minimum=min(a)
k=0
max_summa=0
s1=0
k1=0
for i in range(len(a)):
if a[i]%4==0:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (a[i]%minimum==0 and a[i]+a[i+1]or (a[i+1]%minimum==0 and a[i]+a[i+1] k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)
Ответ: 1428 829
№2

f=open(’17_2.txt’)
a=[int(x) for x in f]
maximum=max(a)
k=0
min_summa=10000000000000
s1=0
k1=0
for i in range(len(a)):
if a[i]%10==3:
s1+=a[i]
k1+=1
sr_ar=s1/k1
for i in range(len(a)-1):
if (maximum%a[i]==0 and a[i]+a[i+1]sr_ar) or (maximum%a[i+1]==0 and a[i]+a[i+1]sr_ar):
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)
Ответ: 72 795
№3

f=open(’17_3.txt’)
a=[int(x) for x in f]
k=0
max_summa=0
for i in range(len(a)-1):
if a[i]%5==0 and a[i+1]%5==0:
k=k+1
max_summa=max(max_summa,a[i]+a[i+1])
print(k,max_summa)
Ответ: 213 965
№4

f=open(’17_4.txt’)
a=[int(x) for x in f]
k=0
min_summa=10000000000000
for i in range(len(a)-1):
if a[i]%20 or a[i+1]%20:
k=k+1
min_summa=min(min_summa,a[i]+a[i+1])
print(k,min_summa)
Ответ: 3741 -973
№5


def h(ch):
k6 = 0
while ch0:
ost=ch%10
if ost==6:
k6=k6+1
ch=ch//10
return k6
f=open(’17_5.txt’)
a=[int(x) for x in f]
k=0
m=1000000000000000
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=min(a[i],m)
print(k,m)
Ответ: 935 -496
№6


def h(ch):
k4 = 0
while ch0:
ost=ch%10
if ost==4:
k4=k4+1
ch=ch//10
return k4
f=open(’17_6.txt’)
a=[int(x) for x in f]
k=0
m=0
for i in range(len(a)):
if h(abs(a[i]))0:
k=k+1
m=max(a[i],m)
print(k,m)
Ответ: 1753 499
№7

f=open(’17_7.txt’)
a=[int(x) for x in f]
k=0
max_razn=0
for i in range(len(a)-1):
if a[i]a[i+1]:
k=k+1
max_razn=max(max_razn,a[i]-a[i+1])
print(k,max_razn)
Ответ: 2514 963
№8

f=open(’17_8.txt’)
a=[int(x) for x in f]
k=0
min_razn_kv=100000000000
for i in range(len(a)-1):
if a[i]0 and a[i+1]0 and a[i+1]a[i]:
k=k+1
min_razn_kv=min(min_razn_kv,a[i+1]**2-a[i]**2)
print(k,min_razn_kv)
Ответ: 670 171
№9

f=open(’17_9.txt’)
a=[int(x) for x in f]
m=0
k=0
for i in range(len(a)):
if a[i]%4==0 and a[i]%5!=0 and a[i]%8!=0 and a[i]%31!=0 and a[i]%41!=0:
k=k+1
m=max(m,a[i])
print(m,k)
Ответ: 9572 381
№10

f=open(’17_10.txt’)
a=[int(x) for x in f]
m=100000000000
k=0
for i in range(len(a)):
if a[i]%7==0 and a[i]%5==0 and a[i]%2!=0 and a[i]%11!=0 and a[i]%91!=0:
k=k+1
m=min(m,a[i])
print(m,k)
Ответ: -8785 43
№11

f=open(’17_11.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%2==0 and a[i]%30:
k=k+1
b.append(a[i])
b.sort(reverse=True)
print(k,b[1])
Ответ: 1299 9664
№12

f=open(’17_12.txt’)
a=[int(x) for x in f]
k=0
b=[]
for i in range(len(a)):
if a[i]%3==0 and a[i]%20:
k=k+1
b.append(a[i])
b.sort()
print(k,b[1])
Ответ: 669 -9777
№13


f=open(’17_13.txt’)
a=[int(x) for x in f]
k=0
m=100000000000000000
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]a[i] and a[i+1]a[i+2]:
k=k+1
m=min(m,a[i+1])
print(k,m)
Ответ: 1335 -8615
№14


f=open(’17_14.txt’)
a=[int(x) for x in f]
k=0
m=0
a=a[1:]
a=a[:-1]
for i in range(len(a)-2):
if a[i+1]or a[i+1]2] or a[i+1]and a[i+1]2]:
k=k+1
m=max(m,a[i+1])
print(k,m)
Ответ: 2661 9435
Public user contributions licensed under
cc-wiki license with attribution required