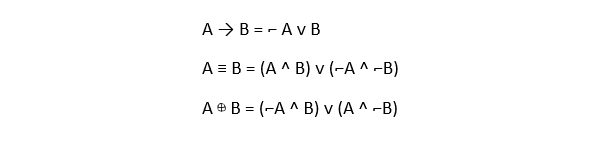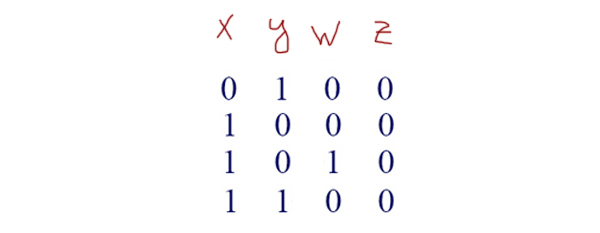На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
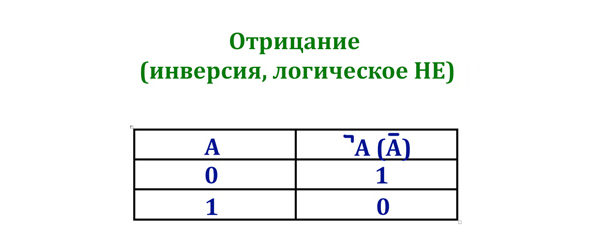
Отрицание (НЕ):
Таблица истинности операции НЕ
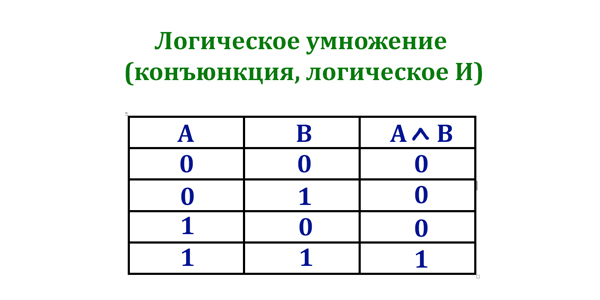
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
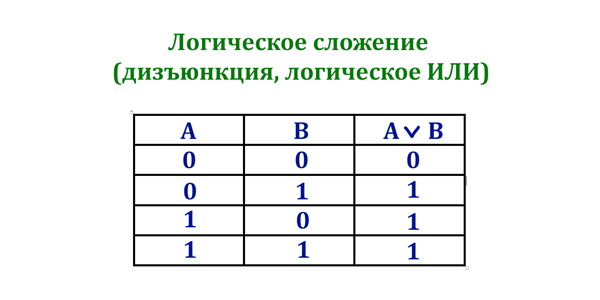
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
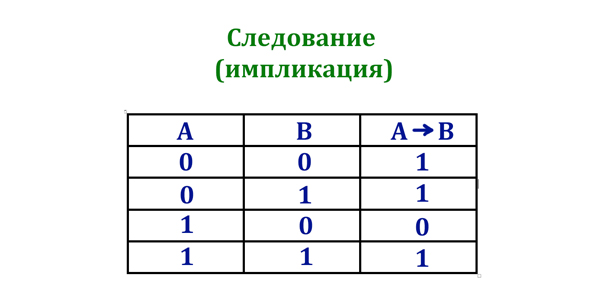
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
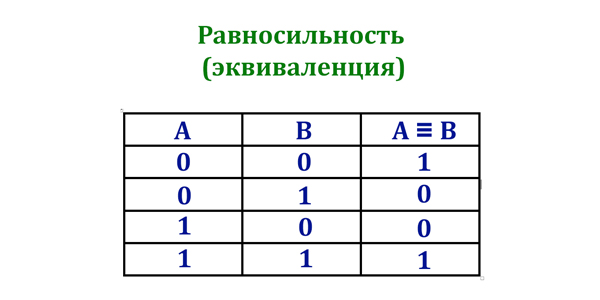
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
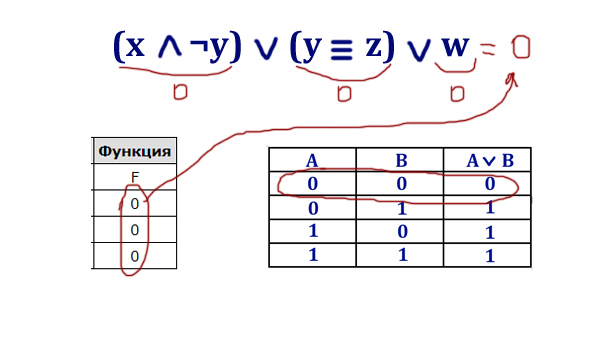
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
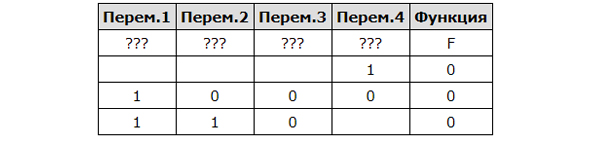
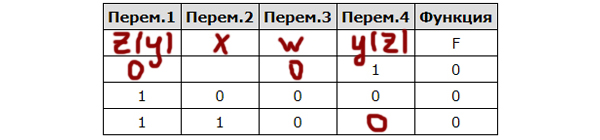
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
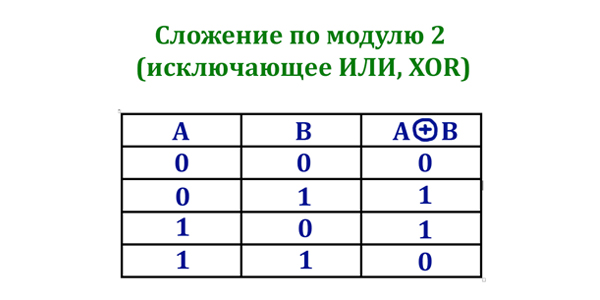
- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Так же на ЕГЭ по информатике будет полезно знать логические формулы :
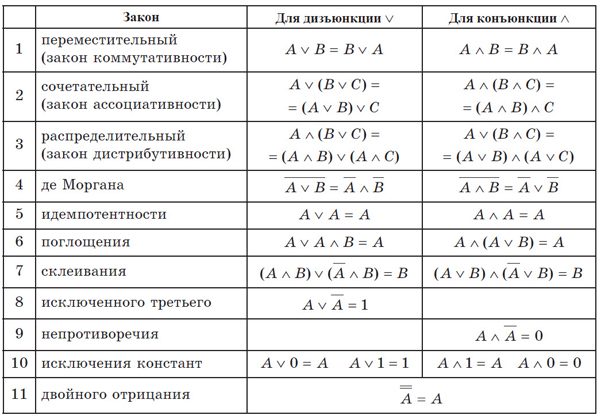
Передём к решению задач из ЕГЭ по информатике
Задача 1 (лёгкая)
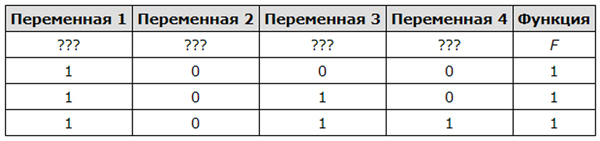
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
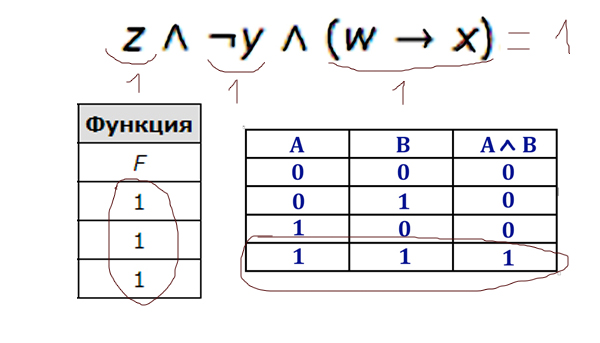
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Ответ: zyxw
Задача 2 (средний уровень)
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
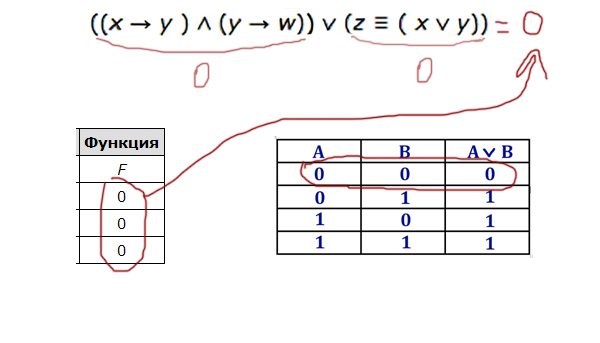
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 24).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Пока!
В спецификации написано, что эту задачу нужно решать без компьютера. Тем более её решить совсем не сложно с помощью «Мощнейшего метода».
Да ужметод. На простых заданиях разбирать можно
14688 информатика егэ
Информатика является вступительным экзаменом более чем для 60 специальностей российских вузов. Некоторые из них, причем, имеют лишь косвенное отношение к этому предмету, как сельское хозяйство, но баллы по информатике считают внимательно. Кстати, подход у всех разных, хотя экзамен для всех един.
Каждый вуз, куда требуется аттестат с данными ЕГЭ по информатике, по-разному оценивает баллы. Например, те заведения, где данный предмет является одной из ключевых наук, даже не смотрят на работы с результатом ниже 65-75 пунктов, хотя та же «Бауманка» довольствуется проходным баллом в 50-65 пунктов. Самый низкий проходной балл в МИИТ. Здесь он составляет всего 37 пунктов. Самый высокий — в МГУ. Минимальная граница здесь 79 баллов.
Таким образом, нужно понимать, что для МГУ подготовка к ЕГЭ по информатике будет максимально кропотливой и вдумчивой. Впрочем, без такой работы трудно будет даже в МИИТ поступить — задания по предмету имеют разные уровни сложности и меняются из года в год, равно как пересматриваются КИМы для оценки знаний учащихся. Так что нужно быть готовым ко всему.
Вся трудность экзамена в том, что он сдается письменно без компьютера. Казалось бы! Сейчас, правда, обсуждается необходимость внедрения электронного тестирования, но до реального воплощения этих задумок пройдет ещё год-два. Однако те, кто готовится к экзамену в ближайшем будущем, должен уже знать, что при подготовке к ЕГЭ по информатике ему придется больше внимания уделять программированию.
Из чего состоит ЕГЭ по информатике?
ЕГЭ по информатике состоит из трех частей. Первая предлагает выбор правильного ответа из нескольких предложенных вариантов, вторая и третья — это уже самостоятельное решение задачи, причем в последней части зачастую встречаются задания с подвохом.
Оценка правильных ответов по утвержденным КИМам осуществляется следующим образом: первая часть (А) — 1 балл за верное решение, вторая часть (В) — 1 балл, третья часть (С) — 2-4 балла в зависимости от сложности задачи. Таким образом, максимальный балл, который можно заработать по тесту — 40 пунктов. Они соответствуют итоговым 100 баллам.
Что нужно решить на 3, 4 или 5?
Чтобы заработать минимальный балл достаточно ответить на половину заданий группы А, даже скорее на 2/3. Но это поможет вам только сдать ЕГЭ и будет совершенно бесполезно при поступлении. То же касается «троечников». Для честной и твердой оценки «три» хватит правильных ответов на задания первой части теста. А вот дальше уже сложнее.
Для проходного балла в 50-60 пунктов придется дать верные ответы на вопросы из части А и решить половину и даже чуть больше задач из группы B. Третья часть теста больше нужна тем, кто собирается поступать в МГУ или аналогичные заведения, где проходной балл не ниже 70-75 пунктов. Для такого результата надо правильно ответить практически на все вопросы.
В чем сложность при подготовке к ЕГЭ по информатике?
Главная трудность заключается в том, что до сих пор некоторые школы не имеют достаточной материально-технической базы для качественного обучения. Отсюда возникает необходимость обращаться за помощью к специалистам: курсы, репетиторы и т. п. Если подобное решение принято, то даже не стоит откладывать его в долгий ящик.
Лучше начинать подготовку к ЕГЭ за год-полтора. Причем в индивидуальной работе с репетитором вам будет проще набить руку на решение задач группы C, что уже нельзя сказать со всей уверенностью про групповые занятия. Безусловно, там тоже хорошая подготовка, но разноуровневый состав учащихся не позволяет индивидуализировать работу и много времени уходит на то, чтобы довести задачу, формулу, уравнение до понимания всей группы. Такая подготовка больше подойдет для тех, кому важно получить просто положительный результат либо дотянуть до четверки.
Некоторые чувствуют в себе достаточно сил, чтобы заниматься самостоятельно. Однако даже им бывает не под силу решение каких-то задач и помощь специалиста будет весьма кстати.
Таким образом, подготовка к ЕГЭ по информатике должна начинаться заранее и учитывать тот уровень, который вы стремитесь достичь.
Смотрите также:
На страницах этого Интернет-портала можно найти словари и учебники, тесты, оценивающие степень подготовленности к ЕГЭ и уровень полученных знаний.
Однако те, кто готовится к экзамену в ближайшем будущем, должен уже знать, что при подготовке к ЕГЭ по информатике ему придется больше внимания уделять программированию.
Bibliotekar. ru
01.01.2018 12:24:44
2018-01-01 12:24:44
Источники:
Http://bibliotekar. ru/media/312.htm
ЕГЭ–2022, информатика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 14688 информатика егэ
14688 информатика егэ
14688 информатика егэ
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 2 № 14688
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий Неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных X, Y, Z.
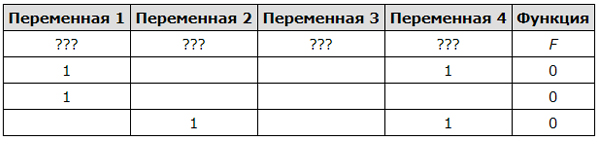
Переменная 1Переменная 2Переменная 3Функция
| . | . | . | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы X, Y, Z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение X → y, зависящее от двух переменных X и Y, и фрагмент таблицы истинности:
Переменная 1Переменная 2Функция
Тогда первому столбцу соответствует переменная Y, а второму столбцу соответствует переменная X. В ответе нужно написать: Yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ∨ y) → (z ≡ x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке Х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной X, и в первом столбце первой строки стоит 1.
Второй столбец таблицы может соответствовать только переменной Z, поскольку переменная Y принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной Y.
—>
Задание 2 № 14688
Составим таблицу истинности для выражения x y z x и выпишем те наборы переменных, при которых данное выражение равно 0.
Inf. reshuege. ru
10.03.2020 8:53:24
2020-03-10 08:53:24
Источники:
Http://inf. reshuege. ru/test? pid=14688
Тренировочные варианты ЕГЭ 2021 по информатике » /> » /> .keyword { color: red; } 14688 информатика егэ
Тренировочные варианты ЕГЭ 2021 по информатике
Тренировочные варианты ЕГЭ 2021 по информатике
Подборка вариантов ЕГЭ 2021 по информатике для 11 класса в формате ЕГЭ 2021.
Составлены в соответствии с демоверсией 2021 года.
Тренировочные варианты ЕГЭ 2021 по информатике
| На основе реального варианта (основная волна, Сибирь) | ||
| 24 июня, Сибирь | Скачать | Доп. файлы |
| ЕГЭ 100 баллов (с решениями) | ||
| Тренировочный вариант 1 | Скачать | Доп. файлы |
| Тренировочный вариант 2 | Скачать | Доп. файлы |
| Тренировочный вариант 4 | Скачать | Доп. файлы |
| Тренировочный вариант 5 | Скачать | Доп. файлы |
| Тренировочный вариант 6 | Скачать | Доп. файлы |
| Тренировочный вариант 6 | Скачать | Доп. файлы |
| СтатГрад (ответы + критерии оценивания) | ||
| Вариант 1-2 | Скачать |
В 2021 г. ЕГЭ по информатике и ИКТ проводится в компьютерной форме. Компьютерное предъявление КИМ позволило включить в работу задания на практическое программирование (составление и отладка программы в выбранной участником среде программирования), работу с электронными таблицами и информационный поиск.
Таких заданий в работе 9, т. е. треть от общего количества заданий.
Остальные 18 заданий сохраняют преемственность с КИМ ЕГЭ прошлых лет (экзамена в бланковой форме). При этом они адаптированы к новым условиям сдачи экзамена, в тех случаях, когда это необходимо.
Так, например, задание 6 КИМ 2021 г. является преемником задания 8 модели КИМ предыдущих лет.
В заданиях этой линии нужно было выполнить фрагмент программы вручную, что в условиях доступности компьютера со средами программирования делает задание тривиальным.
Поэтому, при сохранении тематики задания, была скорректирована постановка вопроса в сторону анализа соответствия исходных данных программы заданному результату её работы.
В отличие от бланковой модели экзамена, в 2021 г. выполнение заданий по программированию допускается на языках программирования (семействах языков) С++, Java, C#, Pascal, Python, Школьный алгоритмический язык.
Из примеров фрагментов кода в заданиях в связи с невостребованностью исключены примеры на Бейсике/
Выполнение заданий по программированию допускается на языках программирования семействах языков С, Java, C, Pascal, Python, Школьный алгоритмический язык.
Vpr-ege. ru
16.12.2020 19:50:37
2020-12-16 19:50:37
Источники:
Http://vpr-ege. ru/ege/informatika/1020-trenirovochnye-varianty-ege-2021-po-informatike
Автор материалов — Лада Борисовна Есакова.
В компьютере вся информация представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Собственно, и цифр как таковых у компьютера нет, а есть электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, который может принимать значения “высокий уровень электрического напряжения” (принимаемый нами за 1) и “низкий уровень электрического напряжения” (принимаемый за 0). Для различных действий над этими нулями и единичками нам необходимы специальные операции, которые работают с двоичными переменными. Такие операции называются логическими операциями.
Логические операции и их аргументы принимают только два значения: 1 (“истина”) и 0 (“ложь”).
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных.
Количество строк в таблице истинности выражения от N переменных равно 2N.
Основные логические операции:
1). Логическое умножение (конъюнкция, логическое И). Обозначается: AND, &, /.
Таблица истинности:
|
A |
B |
А&В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
2). Логическое сложение (дизъюнкция, логическое ИЛИ). Обозначается: OR, |, /.
Таблица истинности:
|
A |
B |
A / B |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
3). Логическое отрицание (инверсия, логическое НЕ). Обозначается: NOT, ¬, .
Таблица истинности:
4). Логическое следование (импликация). Обозначается: →.
Таблица истинности:
|
A |
B |
A → B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
5). Логическое равенство (эквивалентность). Обозначается: ↔, ~.
Таблица истинности:
|
A |
B |
A ~ B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Порядок (приоритет) выполнения логических операций:
Если в выражении нет скобок, то операции выполняются в следующем порядке:
— Логическое отрицание (инверсия, логическое НЕ);
— Логическое умножение (конъюнкция, логическое И);
— Логическое сложение (дизъюнкция, логическое ИЛИ);
— Логическое следование (импликация);
— Логическое равенство (эквивалентность).
Выбор выражения по таблице истинности
Пример 1.
Дан фрагмент таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Решение:
Все представленные варианты ответа — дизъюнкции трёх конъюнкций. Все значения F в таблице равны нулю. Дизъюнкция равна нулю, когда все слагаемые равны нулю.
Рассмотри поочерёдно все четыре выражения.
1) В первой строке таблицы x1=1 и x2=1, значит x1∧x2=1. Выражение не подходит.
2) Во второй строке таблицы x1=1 и x3=1, значит x1∧x3=1. Выражение не подходит.
3) Подставим в третье выражение поочередно значения всех строк таблицы:
Первая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (1 ∧ 0) ∨ (0 ∧ 0) ∨ (0 ∧ 1) = 0 ∨ 0 ∨ 0 = 0
Вторая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 0) ∨ (0 ∧ 1) ∨ (1 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Третья строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 1) ∨ (1 ∧ 0) ∨ (0 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Выражение подходит.
4) В третьей строке таблицы x1=1 и x4=1, значит x1∧x4=1. Выражение не подходит.
Ответ:3
Пример 2.
Для таблицы истинности функции F известны значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
0 |
1 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Решение:
Рассмотри поочерёдно все четыре выражения.
1) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. В первой строке x6 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
2) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. Подставим во второе выражение поочередно значения всех строк таблицы:
Первая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ 0 ∨ ¬x7 может принимать значение 1, если хотя бы один из операндов равен 1.
Вторая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 1 ∨ ¬x5 ∨ x6 ∨ 1 = 1
Третья строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ x6 ∨ ¬x7 может принимать значение 0, если все остальные операнды равны 0.
3) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. Во второй строке x4 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
4) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. В третьей строке x4 = 1, значит и все выражение F равно 1, что не соответствует таблице истинности.
Ответ:2
Пример 3.
Логическая функция F задаётся выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
|
Перем. 1 |
Перем. 2 |
Перем. 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
Выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций:
((¬z) ∧ x) ∨ (x ∧ y) . В обеих конъюнкциях присутствует x. Т. е. при x = 0 все выражение равно 0. Это выполняется только при Перем.3 = x.
Выражение равно 1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.
Ответ: zyx
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №2. Построение таблиц истинности логических выражений. Выбор выражения, соответствующего условию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023