На уроке рассмотрен разбор 23 задания ЕГЭ по информатике: дается подробное объяснение и решение заданий демоверсий и досрочных вариантов разных годов
23-е задание: «Динамическое программирование и анализ работы алгоритма»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 8 минут.
Проверяемые элементы содержания: Умение анализировать результат исполнения алгоритма
До ЕГЭ 2021 года — это было задание № 22 ЕГЭ
Рекомендации по выполнению:
«Один из распространенных способов выполнения этого задания – выписать последовательность
рекуррентных формул, определяющих, сколькими способами можно получить текущее число из ближайших предшественников, одновременно производя вычисления по этим формулам. «Ближайших» в данном случае означает тех, из которых текущее число получается в результате применения программы, состоящей из одной команды. Когда текущее число сравняется с заданным, количество таких способов и будет искомым числом программ»
Типичные ошибки и рекомендации по их предотвращению:
«Не стоит пытаться перечислить все пути в явном виде, это слишком трудоёмко и, скорее всего, в итоге приведёт к ошибке. Распространённая ошибка – экзаменуемые в процессе рекуррентных вычислений забывают о том, что траектория обязана содержать или не содержать указанные в условии числа»
ФГБНУ «Федеральный институт педагогических измерений»
Объяснение темы «Динамическое программирование»
- Динамическое программирование – это способ или техника решения сложных задач путем приведения их к более простым подзадачам того же типа.
- Динамическое программирование позволяет решать задачи, которые требуют полного перебора вариантов. Задание может звучать так:
- «подсчитайте количество способов…»;
- «как оптимально распределить…»;
- «найдите оптимальный маршрут…».
- Динамическое программирование позволяет увеличить скорость выполнения программы за счет эффективного использования памяти; полный перебор всех вариантов не требуется, поскольку запоминаются и используются решения всех подзадач с меньшими значениями параметров.
Более подробное знакомство с динамическим программированием доступно по ссылке.
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
23_4: Разбор досрочного ЕГЭ по информатике 2019:
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
Сколько существует программ, для которых при исходном числе 3 результатом является число 37 и при этом траектория вычислений содержит число 18?
✍ Решение:
📹 Подробный разбор смотрите на видео:
📹 YouTube здесь📹 Видеорешение на RuTube здесь
23_2:
У исполнителя Увеличитель две команды, которым присвоены номера:
- прибавь 1
- умножь на 4
Первая из них увеличивает число на экране на 1, вторая умножает его на 4.
Программа для Увеличителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 44?
✍ Решение:
- Возьмем такое наименьшее число, находящееся в интервале от 3 до 44, для которого применима только одна команда:
12 к нему применима только команда - прибавь 1 12 * 4 = 48 - это больше, чем 44
Пояснение: Красным цветом будем выделять количество команд для получения конкретного числа, а в круг обводить итоговое суммарное количество команд.
Пояснение: поскольку это задача динамического программирования, то полученные промежуточные результаты, используются для дальнейших вычислений:
- для 11 взят результат, полученный для 12 (1);
- для 10 взят результат, полученный для числа 11 (2);
- для 9 взят результат, полученный для 10 (3);
- и т.д.
Результат: 10
📹 Предлагаем посмотреть видео с решением данного 23 задания (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретический способ)
23_3: Демоверсия ЕГЭ 2018 информатика:
Исполнитель М17 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд.
Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 24, 26.
✍ Решение:
- Изобразим траекторию в виде луча, на котором отложим отрезки:
- Поскольку 8 и 10 обязательно должны содержаться в расчете, то для поиска общего количества программ необходимо найти произведение количества программ отдельных отрезков:
1 * 2 * 3 или (2 -> 8) * (8 -> 10) * (10 -> 12)
2 -> 8 = 157 7 + 1 = 8 7 + 2 = 9 - нельзя, вне интервала
8 -> 10 = 210 -> 12 = 215 * 2 * 2 = 60
Результат: 60
📹 Подробное решение 23 (теоретическое) задания демоверсии ЕГЭ 2018 доступно на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Здравствуйте! Сегодня речь пойдёт о 23 задании из ЕГЭ по информатике 2023.
Двадцать третье задание является последним заданием из первой части ЕГЭ по информатике 2023.
Давайте познакомимся с примерными задачами 23 задания из ЕГЭ по информатике 2023.
Задача (классическая)
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавить 3,
2. умножить на 2.
Первая из них увеличивает число на экране на 3, вторая — удваивает его.
Программа для Удвоителя — это последовательность команд.
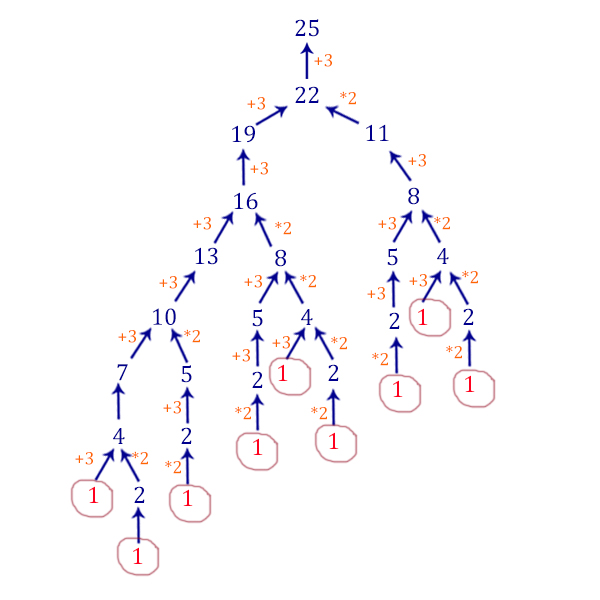
Сколько есть программ, которые число 1 преобразуют в число 25 ?
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+3, y) + F(x*2, y) print(F(1, 25))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
Ответ получается равен 9.
2 Способ (графический, для понимания)
Начинаем рассматривать задачку с конца. Если число нечётное, то оно может быть получено только с помощью первой команды. Если число чётное, то оно может быть получено с помощью двух команд.
Видим, что количество программ получается 9!
3 Способ (С помощью таблицы)
Некоторое число i можно получить только двумя способами: либо c помощью первой команды, либо с помощью второй команды. Тогда количество программ для некоторого числа i будет складываться из двух чисел: количества программ для числа i-3 и количества программ для числа i / 2 (Если i — чётное).
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| *2 | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 |
| Кол. Прог. |
1 | 1 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 3 |
| Числа | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| +3 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| *2 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | — |
| Кол. Прог. |
3 | 0 | 3 | 5 | 0 | 6 | 5 | 0 | 6 | 8 | 0 | 9 | 8 | 0 | 9 |
В первой строке пишутся числа от 1 до 25 (до того числа, которое нужно получить).
Во второй строке пишутся числа, которые в сумме с 3 (тройкой) дают числа, написанные в первой строке. (Прим. начиная с 4, числа идут по порядку.)
В третьей строке пишутся числа, которые при умножении на 2 дают числа, написанные в первой строке. (Прим. числа так же идут по порядку через одну пустую ячейку.)
В четвёртой строке для единицы ставим 1. Для остальных ячеек: смотрим, какие числа участвуют во второй и третьей строке для конкретной ячейки. Затем, эти числа ищем в первой строке и пишем сумму количеств программ для этих чисел (Т.е. пишем сумму уже известных значений из четвёртой строки для этих чисел).
Таким образом, основная идея 23 задания из ЕГЭ по информатике заключается в том, что результат каждого шага опирается на результаты предыдущих шагов!
Получаем ответ 9!
Ответ: 9
Задача (с избегаемым узлом)
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ — это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y or x==24: return 0 if x < y: return F(x+1, y) + F(x*2+1, y) print(F(1, 25))
Здесь на нельзя получать число 24, поэтому, если x будет равен 24, то мы возвращаем ноль.
Ответ получается равен 10.
2 способ (Решение с помощью таблицы).
Мы не может получать число 24! Значит, единственным способом добраться до числа 25 будет вторая команда.
Получается, что сначала нужно получить число 12, тогда 2 * 12 + 1 = 25 (2x+1). Это единственный путь!
Каждое число можем получить только 2 способами (Либо с помощью первой команды, либо с помощью второй команды). Поэтому количество программ для некоторого числа i будет равно сумме количеств команд для числа i-1 и для числа (i — 1) / 2 (Если число нечётное.) Если число i — чётное, то до числа i можно добраться единственным способом (с помощью первой команды).
Если записать с помощью массива:
A[i]=A[i-1] — если i — четное.
A[i]=A[i-1] + A[(i-1)/2] — если i нечетное;
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2x+1 | — | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол. Прог. |
1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 7 | 7 | 10 | 10 |
Ответ: 10
Задача (ЕГЭ по информатике, Москва, 2019)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает его на 2.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит число 9 и число 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(2, 9)*F(9, 11)*F(11, 12))
У нас числа 9 и 1 обязательные, поэтому разбиваем функцию следующим образом F(2, 9)*F(9, 11)*F(11, 12), через умножение. Это и будет ответ. Получается 50.
2 способ (с помощью таблицы).
От числа 11 до числа 12 можно добраться единственным путём (11 + 1 = 12).
От числа 9 до числа 11 можно добраться двумя способами (9 + 1 + 1 = 11, 9 + 2 = 11).
Найдём сколькими способами можно попасть от числа 2 до числа 9.
| Числа | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| +1 | — | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| *3 | — | — | — | — | 2 | — | — | 3 |
| +2 | — | — | 2 | 3 | 4 | 5 | 6 | 7 |
| Кол-во программ |
1 | 1 | 2 | 3 | 6 | 9 | 15 | 25 |
Учитывая, что от 9 до 11 двумя способами можно добраться, то 25 * 2 = 50 — это и будет ответ.
Ответ: 50
Задача ( ЕГЭ по информатике, Москва, 2020)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает на 2.
Сколько существует программ, которые преобразуют исходное число 3 в число 14 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(3, 9)*F(9, 14))
Ответ получается 112.
2 способ (с помощью таблицы).
Последней командой для получении любого числа из траектории программы может быть одна из трёх выше указанных команд!
Значит, количество программ для некоторого числа будет складываться из количества программ для тех чисел, из которых это число может быть получено.
Получается, что мы будем использовать основной принцип 23 задания из ЕГЭ по информатике: результат для некоторого числа опирается на результаты предыдущих чисел. Т.к. траектория вычислений программ обязательно должна проходить через число 9, то при вычислении результата для чисел больших 9, мы не можем опираться на результаты для чисел меньших 9 (Иначе мы пропустим число 9).
| Числа | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| +1 | — | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| *3 | — | — | — | — | — | — | 3 | — | — | — | — | — |
| +2 | — | — | 3 | 4 | 5 | 6 | 7 | — | 9 | 10 | 11 | 12 |
| Кол-во программ |
1 | 1 | 2 | 3 | 5 | 8 | 14 | 14 | 28 | 42 | 70 | 112 |
Ответ: 112
Посмотрим следующую задачу из 23 задания ЕГЭ по информатике 2023
Задача (с обязательным узлом, закрепление)
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x+3, y) print(F(1, 9)*F(9, 17))
Ответ получается 169.
2 способ (с помощью таблицы).
Любое число может получится в результате двух команд! Тогда количество программ для числа i будет складываться из количеств команд для числа i — 1 и для числа i — 3.
Если написать на языке массива
A[i] := A[i-1] + A[i-3], при i > 3.
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | — | — | 9 | 10 | 11 | 12 | 13 | 14 |
| Кол-во программ |
1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 13 | 13 | 26 | 39 | 52 | 78 | 117 | 169 |
При составлении значения для числа 10, мы не имеем право «заглядывать» за число 9, иначе число 9 будет пропущено! Поэтому для следующих трёх чисел (9, 9 + 1, 9 + 1 + 1), начиная с 9, будет 13 программ.
Для числа 17 получается ответ 169.
Ответ: 169
За это задание ты можешь получить 1 балл. На решение дается около 10 минут. Уровень сложности: высокий.
Средний процент выполнения: 25.4%
Ответом к заданию 23 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 47, причём траектория вычислений проходит через число 14? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Из числа 3 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число, т.к. нечётное +2 = нечётное и нечётное *3 = нечётное. Следовательно, число 14 получить невозможно. Тогда никакая траектория из числа 3 в число 47 не пройдёт через число 14.
Ответ: 0.
Ответ: 0
Задача 2
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 58?
Решение
Из числа 1 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число, т.к. нечётное +2 = нечётное и нечётное *3 = нечётное. Следовательно, число 58 получить невозможно.
Ответ: 0.
Ответ: 0
Задача 3
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 49?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Из числа 3 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число. Значит, чётные числа можно не писать.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 |
| Кол-во программ | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 |
| Число | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 | 49 |
| Кол-во программ | 6 | 6 | 6 | 8 | 8 | 8 | 10 | 10 | 10 | 13 | 13 | 13 |
Ответ: 13.
Ответ: 13
Задача 4
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь предыдущее
3. Прибавь следующее
Первая из них увеличивает число на экране на 1, вторая — прибавляет к текущему числу на единицу меньшее натуральное число, третья — прибавляет к текущему числу на единицу большее натуральное число. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 33, причём траектория вычислений не проходит через число 7 и 14, но проходит через число 12? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Кол-во программ | 1 | 1 | 3 | 3 | 7 | 7 | 0 | 0 | 10 | 10 | 24 | 24 |
После числа 12 нельзя пользоваться теми значениями, которые были до числа 12. Поэтому дальнейшая таблица имеет вид:
| Число | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| Кол-во программ | 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 24 | 72 | 72 | 96 | 96 | 96 | 96 | 96 | 96 | 96 |
Вычисление результата при помощи программы на С++:
#include <iostream>
using namespace std;int main(){
const int n0 = 1, nk = 33;
int arr[nk + 1];
for (int i = 0; i < nk + 1; ++i) arr[i] = 0;
arr[n0] = 1;
for (int n = n0 + 1; n <= nk; ++n) {
arr[n] = arr[n - 1]; // Kn-1
if (n % 2 != 0 && (n - 1) / 2 >= n0) //K(n - 1)/2
arr[n] += arr[(n - 1) / 2];
if (n % 2 != 0 && (n + 1) / 2 >= n0) //K(n + 1)/2
arr[n] += arr[(n + 1) / 2];
if (n == 7 || n == 14)
arr[n] = 0;
if (n == 12)
for (int i = n - 1; i >=0 ; --i)
arr[i] = 0;
}
cout << arr[nk];
return 0;
}
Ответ: 96.
Ответ: 96
Задача 5
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Сделай чётное
3. Сделай нечётное
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 2 раза и прибавляет единицу. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 2 преобразуют в число 30, траектория которых проходит через число 9 и не проходит через число 16? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Кол-во программ | 1 | 1 | 2 | 3 | 4 | 5 | 7 | 9 |
После числа 9 нельзя пользоваться теми значениями, которые были до числа 9. Поэтому дальнейшая таблица имеет вид:
| Число | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Кол-во программ | 9 | 9 | 9 | 9 | 9 | 9 | 0 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 |
Поиск ответа при помощи программы на С++:
#include <iostream>
using namespace std;int main(){
const int n0 = 2, nk = 30;
int arr[nk + 1];
for (int i = 0; i < nk + 1; ++i) arr[i] = 0;
arr[n0] = 1;
for (int n = n0 + 1; n <= nk; ++n) {
arr[n] = arr[n - 1]; // Kn-1
if (n % 2 != 0 && (n - 1) / 2 >= n0) //K(n - 1)/2 - сделай нечётное
arr[n] += arr[(n - 1) / 2];
if (n % 2 == 0 && n / 2 >= n0) //Kn/2 - сделай чётное
arr[n] += arr[n / 2];
if (n == 16)
arr[n] = 0;
if (n == 9)
for (int i = n - 1; i >=0 ; --i)
arr[i] = 0;
}
cout << arr[nk];
return 0;
}
Ответ: 117.
Ответ: 117
Задача 6
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Сделай чётное
3. Сделай нечётное
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 2 раза и прибавляет единицу. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 30?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Кол-во программ | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Число | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Кол-во программ | 11 | 13 | 15 | 18 | 21 | 25 | 29 | 34 | 39 | 45 | 51 | 58 |
Ответ: 58.
Ответ: 58
Задача 7
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 34?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Кол-во программ | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 6 | 6 |
| Число | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
| Кол-во программ | 8 | 8 | 10 | 11 | 13 | 13 | 17 | 17 | 20 | 21 | 25 | 25 | 32 | 32 | 38 | 40 | 46 |
Ответ: 46.
Ответ: 46
Задача 8
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 26?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Кол-во программ | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 8 | 8 |
| Число | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Кол-во программ | 10 | 11 | 14 | 14 | 20 | 20 | 25 | 27 | 32 | 32 | 43 | 43 | 51 |
Ответ: 51.
Ответ: 51
Задача 9
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
Первая из них увеличивает число на экране на 1, вторая — в 2 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 20, траектория вычислений которых не проходит через число 9? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кол-во программ | 1 | 2 | 2 | 4 | 4 | 6 | 6 | 10 | 0 | 4 | 4 | 10 | 10 | 16 | 16 | 26 | 26 | 26 | 26 | 30 |
Ответ: 30
Ответ: 30
Задача 10
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
Первая из них увеличивает число на экране на 1, вторая — в 2 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 26, у которых траектория вычислений проходит через число 10? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Кол-во программ | 1 | 2 | 2 | 4 | 4 | 6 | 6 | 10 | 10 | 14 |
После числа 10 нельзя пользоваться теми значениями, которые были до числа 10. Поэтому дальнейшая таблица имеет вид:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Кол-во программ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 28 | 28 | 42 | 42 | 56 | 56 | 70 |
Ответ: 70.
Ответ: 70
Задача 11
У исполнителя A2M5 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 5
Первая из них увеличивает данное число на 2, вторая — увеличивает его в 5 раз. Программа для исполнителя A2M5 — это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 31.
Решение
Заметим, что все числа, получаемые с помощью заданных команд из числа 1, нечётные. Будем решать поставленную задачу последовательно для чисел 1, 3, 5, . . . , 31 (то есть для каждого нечётного числа определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Будем считать, что R(1) = 1. Для каждого следующего числа рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число не делится на 5, то оно может быть получено только из предыдущего с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для предыдущего числа: R(i) = R(i — 2), i — нечётное. Если число на 5 делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда R(i) = R(i-2)+R(i=5), i — нечётное. Заполним соответствующую таблицу по приведённым формулам слева направо:
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 5 | 5 |
| 29 | 31 | ||||||||||||
| 5 | 5 |
Ответ: 5.
Ответ: 5
Задача 12
У исполнителя X123 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — на 2, а третья — в 3 раза. Программа для исполнителя X123 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 10?
Решение
Будем решать поставленную задачу последовательно для чисел 1, 2, 3, . . . , 10 (то есть для каждого из чисел определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Число 2 из числа 1 можно получить с помощью команды 1 (также будем считать, что R(1) = 1). Для каждого следующего числа i рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число i не делится на 3, то оно может быть получено либо из i — 1-го с помощью команды прибавь 1, либо из числа i — 2-го с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для i-1-го и i-2-го чисел:R(i) = R(i-1)+R(i-2). Если число на 3 делится, то вариантов последней команды три: прибавь 1, прибавь 2 и умножь на 3, следовательно, R(i) = R(i-1)+R(i-2)+R(i/3). Заполним соответствующую таблицу по приведенным формулам слева направо:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 3 | 4 | 7 | 12 | 19 | 31 | 53 | 84 |
Ответ: 84.
Ответ: 84
Задача 13
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 5.
Первая из них увеличивает данное число на 2, вторая — увеличивает его в 5 раз. Программа для исполнителя Удвоитель — это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 37.
Решение
Заметим, что все числа, получаемые с помощью заданных команд из числа 1, — нечётные. Будем решать поставленную задачу последовательно для чисел 1, 3, 5, . . . , 37 (то есть для каждого нечётного числа определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Будем считать, что R(1) = 1. Для каждого следующего числа рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число не делится на 5, то оно может быть получено только из предыдущего с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для предыдущего числа: R(i) = R(i − 2), i — нечётное. Если число на 5 делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда R(i) = R(i−2)+R(i/5), i — нечётное. Заполним соответствующую таблицу по приведенным формулам слева направо:
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 5 | 5 |
| 29 | 31 | 33 | 35 | 37 | |||||||||
| 5 | 5 | 5 | 7 | 7 |
Ответ: 7
Задача 14
У исполнителя X157 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 5
3. Умножь на 7
Первая из них увеличивает число на экране на 1, вторая — на 5, а третья — в 7 раз. Программа для исполнителя X157 — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Задача 15
У исполнителя X13 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 3 раза. Программа для исполнителя X13 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 35, причём траектория вычислений содержит число 13?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 1211 при исходном числе 2 траектория будет состоять из чисел 3; 9; 10; 11.
Задача 16
У исполнителя X157 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 5
3. Умножь на 7
Первая из них увеличивает число на экране на 1, вторая — на 5, а третья — в 7 раз. Программа для исполнителя X157 — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Задача 17
У исполнителя X135 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 3
3. Умножь на 5
Первая из них увеличивает число на экране на 1, вторая — на 3, а третья — в 5 раз. Программа для исполнителя X135 — это последовательность команд. Сколько существует программ, которые число 1 преобразуют в число 14?
Задача 18
У исполнителя Увеличитель две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — увеличивает его в 3 раза. Программа для исполнителя Увеличитель—это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 37.
Задача 19
У исполнителя X17 две команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 7
Первая из них увеличивает число на экране на 1, вторая — на 7. Программа для исполнителя X17—это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 26, и при этом траектория вычислений содержит число 12?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы.Например, для программы 1221 при исходном числе 3 траектория будет состоять из чисел 4, 11, 18, 19.
Задача 20
У исполнителя X125 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 5
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, а третья — в 5 раз. Программа для исполнителя X125 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 38, и при этом траектория вычислений содержит числа 10 и 20? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 2231 при исходном числе 5 траектория будет состоять из чисел 10, 20, 100, 101.
Рекомендуемые курсы подготовки
Еще один способ решения данного задания – написание программы.
На примере первой задачи посмотрим несколько способов решения.
Задание 1
У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Сколько есть программ, которые число 1 преобразуют в число 20?
В решении электронными таблицами мы получили формулы для расчетов:
Если число n НЕ делится на 3, количество программ для него
kn = kn-1
Если же число делится на 3, то
kn = kn-1 + kn / 3
их мы и будем использовать в данном задании.
1 способ решения. Заполнение списка.
Необходимые навыки:
- работа со списками
- условный оператор
- цикл for
# +1 *3 1->20
a = [0] * 21 # создаем список из такого количества
# элементов, чтобы нам хватило индексов от 0 до 20
a[1] = 1 # заполняем элемент с индексом стартового числа
for i in range(2, 20 + 1): # перебираем остальные числа от 2 до 20
if i % 3 == 0: # если кратно 3, добавляем предыдущее и / 3
a[i] = a[i – 1] + a[ i // 3]
else: # если не кратно 3, добавляем только предыдущее
a[i] = a[i – 1]
print(a[20]) # выводим на экран значение конечного числа
Данное решение является самым частным и не всегда получится им хорошо решить. Потребуются дополнительные условия когда могут получаться отрицательные индексы.
2 вариант решения без инверсии команд
# +1 *3 1->20 a = [0] * 100 # создаем список из такого количества # элементов, чтобы нам хватило индексов от 0 до 20 * 3 (я взял сильно с запасом) a[20] = 1 # заполняем элемент с индексом стартового числа for i in range(19, 0, -1): # перебираем остальные числа от 2 до 20 a[i] = a[i + 1] + a[i * 3] print(a[1]) # выводим на экран значение конечного числа
При таком решении не требуется условный оператор, но размер списка надо предусмотреть в 3 раза больше.
3 вариант решения. Рекурсивная функция
# +1 *3 1->20 def f(n): if n > 20: # перепрыгнули 20 return 0 if n == 20: # попали в 20 return 1 return f(n + 1) + f(n * 3) # число до 20
print(f(1))
Задача 2. Все варианты решения
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 40 и при этом траектория вычислений содержит число 20 и не содержит число 8?
Разобьем решение со списком на два этапа
# +1 *2 2->40 v20 x8 a = [0] * 100
a[20] = 1 # заполняем элемент с индексом стартового числа a[40] = 1 for i in range(19, 2 - 1, -1): if i != 8: a[i] = a[i + 1] + a[i * 2] for i in range(39, 20 - 1, -1): a[i] = a[i + 1] + a[i * 2] print(a[2] * a[20]) # выводим на экран значение конечного числа
Усовершенствуем рекурсивный алгоритм: добавим в функцию еще один параметр. Теперь их два: из какого числа считаем и в какое.
# +1 *2 2->40 v20 x8 def f(n, finish): if n == finish: return 1 if n > finish or n == 8: return 0 return f(n + 1, finish) + f(n * 2, finish) print(f(2, 20) * f(20, 40))
Решение задания программированием наиболее кратко получается с использованием рекурсивной функции. В целом, написание кода занимает время примерно равное решению в электронных таблицах, за исключением случаев когда дан большой диапазон чисел.
Следует рассматривать такой вариант решения как средство для проверки ручного решения.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Исполнитель А16 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает его на 2.
Программа для исполнителя А16 – это последовательность команд.
Сколько существует таких программ, которые исходное число 3 преобразуют в число 12 и при этом траектория вычислений программы содержит число 10?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 16, 18.
Источник: Демонстрационная версия ЕГЭ—2017 по информатике.
2
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203
3
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10204
4
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 4.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 4.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10103
5
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 3.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104
Пройти тестирование по этим заданиям
Задание 23 в ЕГЭ – это одно из заданий, проверяющих умение анализировать результат исполнения алгоритма, содержащего ветвление и цикл. Как правило, это задание не очень сложное и поэтому на него рекомендуется, на наш взгляд, обращать внимание всем учащимся, сдающим ЕГЭ по предмету «Информатика».
Основные способы решения задания 23 ЕГЭ по информатике.
1. Аналитический (с помощью дерева вариантов или таблицы)
2. Программный (рекурсия или динамическое программирование)
Рассмотрим пример задания.
Исполнитель преобразует число на экране.
У него две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая из них увеличивает число на экране на 1, а вторая – в два раза.
Программа исполнителя – это последовательность команд.
Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 1221 при исходном числе 5 траектория будет состоять из чисел 6, 12, 24, 25.
Сколько существует программ, которые число 2 преобразуют в число 32, причём траектория вычислений содержит число 10?
По сути, необходимо ответить на два вопроса.
А) Сколько существует программ, которые преобразуют число 2 в число 10?
Б) Сколько существует программ, которые преобразуют число 10 в число 32?
Для ответа на вопрос исходной задачи необходимо перемножить ответы на эти два вопроса, так как каждому способу получить из числа 2 число 10 может соответствовать любой из способов получения числа 32 из числа 10.
Приведём примеры решения задания выше.
1. Аналитический.
А) С помощью дерева вариантов посчитаем количество способов получения из числа 2 числа 10. Таких способов 7 (по числу обведённых в кружочек конечных результатов).
Б) С помощью дерева вариантов посчитаем количество способов получения из числа 10 числа 32. Таких способов 8 (по числу обведённых в кружочек конечных результатов).
Итого 7 * 8 = 56 различных программ.
2. Программный способ (рекурсия). Пример решения дадим на языке Pascal (легко можно перенести решение на нужный вам язык). Число a – начальное, b – число после работы программы из условия задачи. На каждом шаге анализируем, какие числа можем получить за 1 ход из числа a.
function func(a, b : integer) : integer;
begin
if (b < a) then
result := 0
else if (b = a) then result := 1
else result := func(a+1, b) + func(2*a, b)
end;
begin
writeln ( func(2,10) * func(10,32) );
end.
Замечание. Рассмотрим другой возможный вопрос в задаче.
Сколько существует программ, которые число 2 преобразует в число 32, причём траектория не содержит число 10?
Необходимо найти общее число программ, преобразующих число 2 в число 32, и вычесть количество программ, содержащих число 10, то есть вычислить результат по формуле func(2,32) — func(2,10)*func(10,32).
3*. Программный способ решения (с помощью динамического программирования). Последовательно вычисляем элементы в массиве элементы с индексами от a до b. В i-м элементе массива будет храниться число способов получить из начального числа a число i. Для каждого числа (индекса массива) смотрим, какие числа можно из него получить описанными операциями. Пример на языке Pascal (легко можно перенести решение на нужный вам язык).
var dp : array[ 1..32 ] of integer;
function func2 ( const a, b : integer) : integer;
var i: integer;
begin
dp [ a ] := 1;
for i := (a+1) to b do
dp[ i ] := 0;
for i:= a to b do
begin
if ( 2 * i <= b) then
dp [2 * i ] := dp [2 * i] + dp [ i ];
if (i + 1 <= b) then
dp [i + 1] := dp [i + 1] + dp [ i ];
end;
func2 := dp [b];
end;
begin
writeln ( func2(2,10) * func2(10,32) );
end.
Надеемся, что приведенные примеры помогут вам решить задание 23 в ЕГЭ по информатике и овладеть такими понятиями, как рекурсия, динамическое программирование, дерево вариантов.
РЕКОМЕНДУЕМЫЕ ТОВАРЫ
Информатика. ЕГЭ
Задания для подготовки
Задачи разных лет из реальных экзаменов, демо-вариантов, сборников задач и других источников
Задание 23. Информатика. Статград-22-1-1
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
- Прибавить (1)
- Умножить на (3)
Первая команда увеличивает число на экране на (1), вторая умножает его на (3).
Программа для исполнителя — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число (2) в число (90), и при этом траектория вычислений содержит число (28)?
Траектория вычисления — это последовательность результатов выполнения всех команд программы. Например, для программы (212) при исходном числе (4) траектория будет состоять из чисел (12), (13), (39).
Показать решение…
Задание 23. Информатика. Статград-22-1-2
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
- Прибавить (1)
- Умножить на (3)
Первая команда увеличивает число на экране на (1), вторая умножает его на (3).
Программа для исполнителя — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число (2) в число (87), и при этом траектория вычислений содержит число (26)?
Траектория вычисления — это последовательность результатов выполнения всех команд программы. Например, для программы (212) при исходном числе (4) траектория будет состоять из чисел (12), (13), (39).
Показать решение…
Задание 23. Информатика. Статград-22-2-1
Исполнитель преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
- Прибавить (1)
- Прибавить (2)
- Умножить на (3)
Первая команда увеличивает число на экране на (1), вторая увеличивает его на (2), третья — умножает на (3).
Программа для исполнителя — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число (1) в число (15), и при этом траектория вычислений содержит число (8)?
Траектория вычисления — это последовательность результатов выполнения всех команд программы. Например, для программы (231) при исходном числе (4) траектория будет состоять из чисел (6), (18), (19).
Показать решение…
Задание 23. Информатика. Статград-22-2-2
Исполнитель преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
- Прибавить (1)
- Прибавить (2)
- Умножить на (3)
Первая команда увеличивает число на экране на (1), вторая увеличивает его на (2), третья — умножает на (3).
Программа для исполнителя — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число (1) в число (15), и при этом траектория вычислений содержит число (10)?
Траектория вычисления — это последовательность результатов выполнения всех команд программы. Например, для программы (231) при исходном числе (4) траектория будет состоять из чисел (6), (18), (19).
Показать решение…
Задание 23. Информатика. Статград-22-3-1
Исполнитель преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
- Прибавить (1)
- Прибавить (2)
- Умножить на (2)
Первая команда увеличивает число на экране на (1), вторая увеличивает его на (2), третья — умножает на (2).
Программа для исполнителя — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число (1) в число (11), и при этом не содержат двух команд умножения подряд?
Показать решение…