На уроке рассмотрен разбор 23 задания ЕГЭ по информатике: дается подробное объяснение и решение заданий демоверсий и досрочных вариантов разных годов
23-е задание: «Динамическое программирование и анализ работы алгоритма»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 8 минут.
Проверяемые элементы содержания: Умение анализировать результат исполнения алгоритма
До ЕГЭ 2021 года — это было задание № 22 ЕГЭ
Рекомендации по выполнению:
«Один из распространенных способов выполнения этого задания – выписать последовательность
рекуррентных формул, определяющих, сколькими способами можно получить текущее число из ближайших предшественников, одновременно производя вычисления по этим формулам. «Ближайших» в данном случае означает тех, из которых текущее число получается в результате применения программы, состоящей из одной команды. Когда текущее число сравняется с заданным, количество таких способов и будет искомым числом программ»
Типичные ошибки и рекомендации по их предотвращению:
«Не стоит пытаться перечислить все пути в явном виде, это слишком трудоёмко и, скорее всего, в итоге приведёт к ошибке. Распространённая ошибка – экзаменуемые в процессе рекуррентных вычислений забывают о том, что траектория обязана содержать или не содержать указанные в условии числа»
ФГБНУ «Федеральный институт педагогических измерений»
Объяснение темы «Динамическое программирование»
- Динамическое программирование – это способ или техника решения сложных задач путем приведения их к более простым подзадачам того же типа.
- Динамическое программирование позволяет решать задачи, которые требуют полного перебора вариантов. Задание может звучать так:
- «подсчитайте количество способов…»;
- «как оптимально распределить…»;
- «найдите оптимальный маршрут…».
- Динамическое программирование позволяет увеличить скорость выполнения программы за счет эффективного использования памяти; полный перебор всех вариантов не требуется, поскольку запоминаются и используются решения всех подзадач с меньшими значениями параметров.
Более подробное знакомство с динамическим программированием доступно по ссылке.
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
23_4: Разбор досрочного ЕГЭ по информатике 2019:
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
Сколько существует программ, для которых при исходном числе 3 результатом является число 37 и при этом траектория вычислений содержит число 18?
✍ Решение:
📹 Подробный разбор смотрите на видео:
📹 YouTube здесь📹 Видеорешение на RuTube здесь
23_2:
У исполнителя Увеличитель две команды, которым присвоены номера:
- прибавь 1
- умножь на 4
Первая из них увеличивает число на экране на 1, вторая умножает его на 4.
Программа для Увеличителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 44?
✍ Решение:
- Возьмем такое наименьшее число, находящееся в интервале от 3 до 44, для которого применима только одна команда:
12 к нему применима только команда - прибавь 1 12 * 4 = 48 - это больше, чем 44
Пояснение: Красным цветом будем выделять количество команд для получения конкретного числа, а в круг обводить итоговое суммарное количество команд.
Пояснение: поскольку это задача динамического программирования, то полученные промежуточные результаты, используются для дальнейших вычислений:
- для 11 взят результат, полученный для 12 (1);
- для 10 взят результат, полученный для числа 11 (2);
- для 9 взят результат, полученный для 10 (3);
- и т.д.
Результат: 10
📹 Предлагаем посмотреть видео с решением данного 23 задания (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретический способ)
23_3: Демоверсия ЕГЭ 2018 информатика:
Исполнитель М17 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд.
Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 24, 26.
✍ Решение:
- Изобразим траекторию в виде луча, на котором отложим отрезки:
- Поскольку 8 и 10 обязательно должны содержаться в расчете, то для поиска общего количества программ необходимо найти произведение количества программ отдельных отрезков:
1 * 2 * 3 или (2 -> 8) * (8 -> 10) * (10 -> 12)
2 -> 8 = 157 7 + 1 = 8 7 + 2 = 9 - нельзя, вне интервала
8 -> 10 = 210 -> 12 = 215 * 2 * 2 = 60
Результат: 60
📹 Подробное решение 23 (теоретическое) задания демоверсии ЕГЭ 2018 доступно на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Здравствуйте! Сегодня речь пойдёт о 23 задании из ЕГЭ по информатике 2023.
Двадцать третье задание является последним заданием из первой части ЕГЭ по информатике 2023.
Давайте познакомимся с примерными задачами 23 задания из ЕГЭ по информатике 2023.
Задача (классическая)
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавить 3,
2. умножить на 2.
Первая из них увеличивает число на экране на 3, вторая — удваивает его.
Программа для Удвоителя — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 25 ?
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+3, y) + F(x*2, y) print(F(1, 25))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
Ответ получается равен 9.
2 Способ (графический, для понимания)
Начинаем рассматривать задачку с конца. Если число нечётное, то оно может быть получено только с помощью первой команды. Если число чётное, то оно может быть получено с помощью двух команд.
Видим, что количество программ получается 9!
3 Способ (С помощью таблицы)
Некоторое число i можно получить только двумя способами: либо c помощью первой команды, либо с помощью второй команды. Тогда количество программ для некоторого числа i будет складываться из двух чисел: количества программ для числа i-3 и количества программ для числа i / 2 (Если i — чётное).
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| *2 | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 |
| Кол. Прог. |
1 | 1 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 3 |
| Числа | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| +3 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| *2 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | — |
| Кол. Прог. |
3 | 0 | 3 | 5 | 0 | 6 | 5 | 0 | 6 | 8 | 0 | 9 | 8 | 0 | 9 |
В первой строке пишутся числа от 1 до 25 (до того числа, которое нужно получить).
Во второй строке пишутся числа, которые в сумме с 3 (тройкой) дают числа, написанные в первой строке. (Прим. начиная с 4, числа идут по порядку.)
В третьей строке пишутся числа, которые при умножении на 2 дают числа, написанные в первой строке. (Прим. числа так же идут по порядку через одну пустую ячейку.)
В четвёртой строке для единицы ставим 1. Для остальных ячеек: смотрим, какие числа участвуют во второй и третьей строке для конкретной ячейки. Затем, эти числа ищем в первой строке и пишем сумму количеств программ для этих чисел (Т.е. пишем сумму уже известных значений из четвёртой строки для этих чисел).
Таким образом, основная идея 23 задания из ЕГЭ по информатике заключается в том, что результат каждого шага опирается на результаты предыдущих шагов!
Получаем ответ 9!
Ответ: 9
Задача (с избегаемым узлом)
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ — это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y or x==24: return 0 if x < y: return F(x+1, y) + F(x*2+1, y) print(F(1, 25))
Здесь на нельзя получать число 24, поэтому, если x будет равен 24, то мы возвращаем ноль.
Ответ получается равен 10.
2 способ (Решение с помощью таблицы).
Мы не может получать число 24! Значит, единственным способом добраться до числа 25 будет вторая команда.
Получается, что сначала нужно получить число 12, тогда 2 * 12 + 1 = 25 (2x+1). Это единственный путь!
Каждое число можем получить только 2 способами (Либо с помощью первой команды, либо с помощью второй команды). Поэтому количество программ для некоторого числа i будет равно сумме количеств команд для числа i-1 и для числа (i — 1) / 2 (Если число нечётное.) Если число i — чётное, то до числа i можно добраться единственным способом (с помощью первой команды).
Если записать с помощью массива:
A[i]=A[i-1] — если i — четное.
A[i]=A[i-1] + A[(i-1)/2] — если i нечетное;
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2x+1 | — | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол. Прог. |
1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 7 | 7 | 10 | 10 |
Ответ: 10
Задача (ЕГЭ по информатике, Москва, 2019)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает его на 2.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит число 9 и число 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(2, 9)*F(9, 11)*F(11, 12))
У нас числа 9 и 1 обязательные, поэтому разбиваем функцию следующим образом F(2, 9)*F(9, 11)*F(11, 12), через умножение. Это и будет ответ. Получается 50.
2 способ (с помощью таблицы).
От числа 11 до числа 12 можно добраться единственным путём (11 + 1 = 12).
От числа 9 до числа 11 можно добраться двумя способами (9 + 1 + 1 = 11, 9 + 2 = 11).
Найдём сколькими способами можно попасть от числа 2 до числа 9.
| Числа | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| +1 | — | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| *3 | — | — | — | — | 2 | — | — | 3 |
| +2 | — | — | 2 | 3 | 4 | 5 | 6 | 7 |
| Кол-во программ |
1 | 1 | 2 | 3 | 6 | 9 | 15 | 25 |
Учитывая, что от 9 до 11 двумя способами можно добраться, то 25 * 2 = 50 — это и будет ответ.
Ответ: 50
Задача ( ЕГЭ по информатике, Москва, 2020)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает на 2.
Сколько существует программ, которые преобразуют исходное число 3 в число 14 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(3, 9)*F(9, 14))
Ответ получается 112.
2 способ (с помощью таблицы).
Последней командой для получении любого числа из траектории программы может быть одна из трёх выше указанных команд!
Значит, количество программ для некоторого числа будет складываться из количества программ для тех чисел, из которых это число может быть получено.
Получается, что мы будем использовать основной принцип 23 задания из ЕГЭ по информатике: результат для некоторого числа опирается на результаты предыдущих чисел. Т.к. траектория вычислений программ обязательно должна проходить через число 9, то при вычислении результата для чисел больших 9, мы не можем опираться на результаты для чисел меньших 9 (Иначе мы пропустим число 9).
| Числа | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| +1 | — | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| *3 | — | — | — | — | — | — | 3 | — | — | — | — | — |
| +2 | — | — | 3 | 4 | 5 | 6 | 7 | — | 9 | 10 | 11 | 12 |
| Кол-во программ |
1 | 1 | 2 | 3 | 5 | 8 | 14 | 14 | 28 | 42 | 70 | 112 |
Ответ: 112
Посмотрим следующую задачу из 23 задания ЕГЭ по информатике 2023
Задача (с обязательным узлом, закрепление)
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x+3, y) print(F(1, 9)*F(9, 17))
Ответ получается 169.
2 способ (с помощью таблицы).
Любое число может получится в результате двух команд! Тогда количество программ для числа i будет складываться из количеств команд для числа i — 1 и для числа i — 3.
Если написать на языке массива
A[i] := A[i-1] + A[i-3], при i > 3.
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | — | — | 9 | 10 | 11 | 12 | 13 | 14 |
| Кол-во программ |
1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 13 | 13 | 26 | 39 | 52 | 78 | 117 | 169 |
При составлении значения для числа 10, мы не имеем право «заглядывать» за число 9, иначе число 9 будет пропущено! Поэтому для следующих трёх чисел (9, 9 + 1, 9 + 1 + 1), начиная с 9, будет 13 программ.
Для числа 17 получается ответ 169.
Ответ: 169
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
| Бейсик | Python |
|---|---|
|
SUB F(n) PRINT n IF n < 5 THEN F(n + 1) F(n + 3) END IF END SUB |
def F(n): print(n) if n < 5: F(n + 1) F(n + 3) |
| Паскаль | Алгоритмический язык |
|
procedure F(n: integer); begin writeln(n); if n < 5 then begin F(n + 1); F(n + 3) end end |
алг F(цел n) нач вывод n, нс если n < 5 то F(n + 1) F(n + 3) все кон |
| С++ | |
|
void F(int n) { cout << n << endl; if (n < 5) { F(n + 1); F(n + 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(1)?
Источник: Демонстрационная версия ЕГЭ—2015 по информатике.
2
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
| Бейсик | Python |
|---|---|
|
SUB F(n) PRINT n IF n > 0 THEN F(n — 1) F(n — 3) END IF END SUB |
def F(n): print(n) if n > 0: F(n — 1) F(n — 3) |
| Паскаль | Алгоритмический язык |
|
procedure F(n: integer); begin writeln(n); if n > 0 then begin F(n — 1); F(n — 3) end end |
алг F(цел n) нач вывод n, нс если n > 0 то F(n — 1) F(n — 3) все кон |
| Си | |
|
void F(int n) { cout << n; if (n > 0) { F(n — 1); F(n — 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(5)?
3
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
| Бейсик | Python |
|---|---|
|
SUB F(n) PRINT n IF n > 1 THEN F(n — 1) F(n — 3) END IF END SUB |
def F(n): print(n) if n > 1: F(n — 1) F(n — 3) |
| Паскаль | Алгоритмический язык |
|
procedure F(n: integer); begin writeln(n); if n > 1 then begin F(n — 1); F(n — 3) end end |
алг F(цел n) нач вывод n, нс если n > 1 то F(n — 1) F(n — 3) все кон |
| C++ | |
|
void F(int n) { cout << n; if (n > 1) { F(n — 1); F(n — 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(6)?
4
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
| Бейсик | Python |
|---|---|
|
SUB F(n) PRINT n IF n < 5 THEN F(n + 1) F(n + 2) END IF END SUB |
def F(n): print(n) if n < 5: F(n + 1) F(n + 2) |
| Алгоритмический язык | Паскаль |
|
алг F(цел n) нач вывод n, нс если n < 5 то F(n + 1) F(n + 2) все кон |
procedure F(n: integer); begin writeln(n); if n < 5 then begin F(n + 1); F(n + 2) end end |
| Си | |
|
void F(int n) { cout << n; if (n < 5) { F(n + 1); F(n + 2); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(2)?
5
Ниже на пяти языках программирования записан рекурсивный алгоритм F.
| Бейсик | Python |
|---|---|
|
SUB F(n) PRINT n IF n < 4 THEN F(n + 1) F(n + 3) END IF END SUB |
def F(n): print(n) if n < 4: F(n + 1) F(n + 3) |
| Алгоритмический язык | Паскаль |
|
алг F(цел n) нач вывод n, нс если n < 4 то F(n + 1) F(n + 3) все кон |
procedure F(n: integer); begin writeln(n); if n < 4 then begin F(n + 1); F(n + 3) end end |
| Си | |
|
void F(int n) { cout << n; if (n < 4) { F(n + 1); F(n + 3); } } |
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(1)?
Пройти тестирование по этим заданиям
Задание 23 в ЕГЭ – это одно из заданий, проверяющих умение анализировать результат исполнения алгоритма, содержащего ветвление и цикл. Как правило, это задание не очень сложное и поэтому на него рекомендуется, на наш взгляд, обращать внимание всем учащимся, сдающим ЕГЭ по предмету «Информатика».
Основные способы решения задания 23 ЕГЭ по информатике.
1. Аналитический (с помощью дерева вариантов или таблицы)
2. Программный (рекурсия или динамическое программирование)
Рассмотрим пример задания.
Исполнитель преобразует число на экране.
У него две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая из них увеличивает число на экране на 1, а вторая – в два раза.
Программа исполнителя – это последовательность команд.
Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 1221 при исходном числе 5 траектория будет состоять из чисел 6, 12, 24, 25.
Сколько существует программ, которые число 2 преобразуют в число 32, причём траектория вычислений содержит число 10?
По сути, необходимо ответить на два вопроса.
А) Сколько существует программ, которые преобразуют число 2 в число 10?
Б) Сколько существует программ, которые преобразуют число 10 в число 32?
Для ответа на вопрос исходной задачи необходимо перемножить ответы на эти два вопроса, так как каждому способу получить из числа 2 число 10 может соответствовать любой из способов получения числа 32 из числа 10.
Приведём примеры решения задания выше.
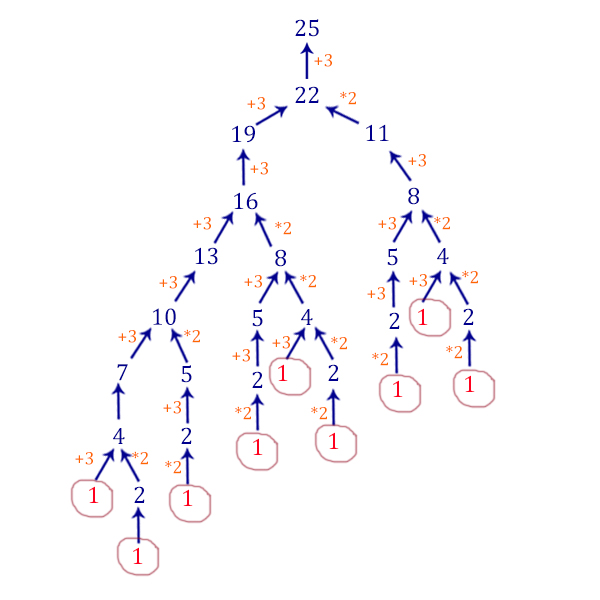
1. Аналитический.
А) С помощью дерева вариантов посчитаем количество способов получения из числа 2 числа 10. Таких способов 7 (по числу обведённых в кружочек конечных результатов).
Б) С помощью дерева вариантов посчитаем количество способов получения из числа 10 числа 32. Таких способов 8 (по числу обведённых в кружочек конечных результатов).
Итого 7 * 8 = 56 различных программ.
2. Программный способ (рекурсия). Пример решения дадим на языке Pascal (легко можно перенести решение на нужный вам язык). Число a – начальное, b – число после работы программы из условия задачи. На каждом шаге анализируем, какие числа можем получить за 1 ход из числа a.
function func(a, b : integer) : integer;
begin
if (b < a) then
result := 0
else if (b = a) then result := 1
else result := func(a+1, b) + func(2*a, b)
end;
begin
writeln ( func(2,10) * func(10,32) );
end.
Замечание. Рассмотрим другой возможный вопрос в задаче.
Сколько существует программ, которые число 2 преобразует в число 32, причём траектория не содержит число 10?
Необходимо найти общее число программ, преобразующих число 2 в число 32, и вычесть количество программ, содержащих число 10, то есть вычислить результат по формуле func(2,32) — func(2,10)*func(10,32).
3*. Программный способ решения (с помощью динамического программирования). Последовательно вычисляем элементы в массиве элементы с индексами от a до b. В i-м элементе массива будет храниться число способов получить из начального числа a число i. Для каждого числа (индекса массива) смотрим, какие числа можно из него получить описанными операциями. Пример на языке Pascal (легко можно перенести решение на нужный вам язык).
var dp : array[ 1..32 ] of integer;
function func2 ( const a, b : integer) : integer;
var i: integer;
begin
dp [ a ] := 1;
for i := (a+1) to b do
dp[ i ] := 0;
for i:= a to b do
begin
if ( 2 * i <= b) then
dp [2 * i ] := dp [2 * i] + dp [ i ];
if (i + 1 <= b) then
dp [i + 1] := dp [i + 1] + dp [ i ];
end;
func2 := dp [b];
end;
begin
writeln ( func2(2,10) * func2(10,32) );
end.
Надеемся, что приведенные примеры помогут вам решить задание 23 в ЕГЭ по информатике и овладеть такими понятиями, как рекурсия, динамическое программирование, дерево вариантов.
РЕКОМЕНДУЕМЫЕ ТОВАРЫ
Хотите готовиться со мной к ЕГЭ?
Пишите: ydkras@mail.ru
Немного обо мне.
В задаче 23 ЕГЭ по информатике описывается исполнитель, который может выполнять несколько команд (чаще всего две), например, прибавить 1 или прибавить 3. Требуется найти количество программ, которые преобразуют одно число (исходное) в другое (цель). Например, из числа 2 нужно получить число 15, используя две описанные выше команды.
Такая задача решается вручную, но нас здесь интересует программый способ её решения. Получить искомое число программ можно с помощью несложной рекурсивной функции.
Для каждого числа менее цели количество программ, требуемых для её достижения — это сумма числа программ, получаемых с помощью каждой из команд исполнителя.
Заметим, что каждая команда увеличивает число. Поэтому если команда дает результат, превышающий целевое число, то в дальнейшем мы никогда не получим целевого числа. Если текущее число равно целевому, то мы, очевидно, достигли цели.
Наша рекурсивная функция на языке Питон может выглядеть, например, так:
def ways(n, goal):
if n>goal: return 0
if n==goal: return 1
return ways(n+1,goal)+ways(n+3,goal)
Чтобы получить ответ для описанной выше задачи, нужно найти результат вычисления функции с параметрами 2 и 15:
print(ways(2,15))
Таким образом, задача решена с помошью всего лишь пяти строк кода на Питоне.
Если команды исполнителя не увеличивают число, а уменьшают его, то нужно изменить операцию сравнения: вместо «больше» написать «меньше». Так, для задачи получения числа 2 из числа 22 с помощью операций «вычти 2» и «вычти 5» можно написать такую программу:
def ways(n, goal):
if n<goal: return 0
if n==goal: return 1
return ways(n-2,goal)+ways(n-5,goal)
print(ways(22,2))
Программы с обязательным этапом
В более сложных вариантах данной задачи требуется либо найти число программ, в которых траектория вычислений либо должна содержать определенное число, либо же, напротив, не должна содержать какого-то числа.
Рассмотрим вначале программы с обязательным этапом. Типичная задача — получить из числа 3 число 12, причем разрешается использовать три операции: и «умножь на 2», а на одном из промежуточных этапов должно получиться число 10.
Решается задача просто: подсчитывается число программ первого этапа (сколько существует способов получить из числа 3 число 10) и способов второго этапа (получить из число 10 число 12). Так как любую программу первого этапа можно комбинировать с любой программой первого этапа, то ответ на задачу — это произведение числа споcобов первого этапа на число способов второго этапа.
Программа для решений этой задачи может выглядеть так:
def ways(n, goal):
if n>goal: return 0
if n==goal: return 1
return ways(n+1,goal)+ways(n+2,goal)+ways(n*2,goal)
print(ways(3,10)*ways(10,12))
Программы с избегаемым этапом
Если нам запрещают получать в ходе вычислений какое-то число, то нашу функцию придется немного изменить: она должна возвращать 0 для «запрещенных» чисел.
Пример задачи — получить из числа 3 число 13, причем разрешается использовать две операции: «прибавь 1» и «прибавь 2», а в процессе вычислений не должно получаться числа 8.
Введем в нашу функцию ешё один параметр — массив zapret, который содержит числа, которых мы должны избегать. Зачем массив? Для случаев, когда «запрещенных» чисел более одного. (Ниже мы столкнемся с ситуацией, когда это потребуется.)
Вот программа, решающая данную задачу:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n+2,goal,zapret)
print(ways(3,13,[8]))
Так как в нашем случае «запрещенное» число всего одно, то в функцию передается массив, состоящий из одного элемента.
Крест-накрест: обязательный этап вместо избегаемого и наоборот
Вначале — очень простая мысль: общее число программ — это сумма числа программ, треактория вычислений которых проходит через некое число, и числа программ, траектория которых через это число не проходит.
Таким образом, мы можем решать задачи с обязательным этапом, пользуясь методикой для избегаемого, и наоборот. Например, чтобы найти число программ с обязательным этапом, следует вычесть из общего числа программ число программ с избегаемым этапом.
Так, рассмотренную в разделе «Программы с обязательным этапом» задачу можно решить так:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal, zapret)+ways(n+2,goal, zapret)+ways(n*2,goal, zapret)
print(ways(3,10,[])*ways(10,12,[]))
print(ways(3,12,[])-ways(3,12,[10]))
(Когда у нас нет «запрещенных» чисел, тогда в функцию передается пустой массив.)
Мы решили задачу двумя способами: рассмотренным ранее перемножением числа вариантов первого этапа (3-10) и числа вариантов второго этапа (10-12), а также вычитанием из общего числа программ числа тех программ, траектория которых не содержит числа 10. В обоих случаях получается одинаковый результат (как и следовало ожидать).
Аналогичным образом можно решить задачу на запрещенный этап, используя метод обязательного этапа:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n+2,goal,zapret)
print(ways(3,13,[8]))
print(ways(3,13,[])-ways(3,8,[])*ways(8,13,[]))
Эта идея позволяет легко решать задачи вроде следующей: получить из числа 11 число 29, пользуясь операциями «прибавь 1» и «прибавь 2», причем траектория вычислений должна содержать либо число 17, либо число 23, либо оба этих числа одновременно.
Решение можно найти, если из общего числа программ вычесть число таких программ, траектория которых не содержит ни числа 17, ни числа 23:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n+2,goal,zapret)
print(ways(11,29,[])-ways(11,29,[17,23]))
Программы с обязательным и избегаемым этапами
Часто встречаются задачи, в которых сочетаются обязательный и избегаемый этап. Например, требуется получить из числа 2 число 29, при этом разрешены операции «прибавить 1» и «умножить на 2», а траектория вычислений должна содержать число 14 и не должна содержать числа 25.
Эту задачу можно решить двумя способами. Можно подсчитать число способов получить из числа 2 число 14, а из числа 14 — число 29 и перемножить эти числа (разумеется, нужно учитывать запрет на число 25). Можно также подсчитать число способов получить из числа 2 число 29 с запретом на число 25, а затем вычесть из него количество программ, которые не проходят ни через число 14, ни через число 25 — так мы получим количество программ, которые не проходят число 25, но обязательно пройдут через число 14.
Оба эти способа иллюстрирует такая программа:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n*2,goal,zapret)
print(ways(2,14,[25])*ways(14,29,[25]))
print(ways(2,29,[25])-ways(2,29,[14,25]))
В некоторых задачах число обязательных и/или избегаемых этапов более одного. Рассмотрим задачу, в которой траектория вычислений должна содержать число 8 и не должна содержать чисел 10 и 11, в ней требуется из числа 1 получить число 28, а используемые операции — «прибавь 1», «прибавь 2» и «умножь на три».
Задача решается следующей программой (в ней опять-таки показаны два возможных способа решения):
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n+2,goal,zapret)+ways(n*3,goal,zapret)
print(ways(1,8,[10,11])*ways(8,28,[10,11]))
print(ways(1,28,[10,11])-ways(1,28,[8,10,11]))
Если количество «обязательных» чисел более одного, то нам надо разбить путь не на два этапа, а более. Например, в одной из задач нужно получить из числа 2 число 15, пользуясь операциями «прибавь 1», «прибавь 2» и «умножь на три», а траектория вычислений должна содержать числа 4 и 11.
Разбиваем путь на три этапа: 2-4, 4-11, 11-15. Программа для решения жтой задачи следующая:
def ways(n, goal, zapret):
if n>goal: return 0
if n in zapret: return 0
if n==goal: return 1
return ways(n+1,goal,zapret)+ways(n+2,goal,zapret)+ways(n*3,goal,zapret)
print(ways(2,4,[])*ways(4,11,[])*ways(11,15,[]))
Ограничение на число команд программы или требования к командам
В некоторых задачах выдвигаютсыя особые требования к программе исполнителя. Например, программа должна состоять из определенного числа команд. Рассмотрим одну из подобных задач.
Имеются две операции:
1. Прибавить 1
2. Прибавить 2
Сколько существует программ, для которых при исходном числе 4 результатом является число 14, а предпоследней командой которых является команда «1»?
Очевидно, нам надо знать последовательность команд, с помощью которых был получен результат, и подсчитывать только те решения, которые удовлетворяют условию задачи.
Добавим в нашу рекурсивную функцию ways дополнительный параметр prog: строку, содержащую цепочку команд, выполненных прелылущими операциями. При выполнении операции 1 будем приписывать к этой строке цифру 1, а при выполнении операции 2 — цифру 2. Когда цель будет достигнута, проверим, что предпоследний символ нашей строки равен 1. (Напомним, что в Питоне s[-1] — это последний символ строки, s[-2] — предпоследний и т.д.) Если это не так, то не учитываем такое решение.
При вызове этой функции из основной программы в качестве параметра prog задаем пустую строку.
Вот программа целиком:
def ways(n, goal, prog):
if n>goal: return 0
if n==goal:
if prog[-2]==’1′: return 1
else: return 0
return ways(n+1,goal,prog+’1′)+ways(n+2,goal,prog+’2′)
print(ways(4,14,»))
Подобным же образом можно решить задачу, в которой имеется ограничение на число команд в программе исполнителя. Вот пример такой задачи.
Допустимые операции исполнителя следующие:
1. Прибавить 1
2. Прибавить 4
3. Умножить на 2
Требуется получить из числа 3 число 27, причем программа должна содержать ровно 7 команд.
Можно было бы передавать при вызовах строку команд, как в предыдущем примере, и при достижении цели проверять её длину. Но так как нам требуется лишь число команд, то можно использовать целую переменную, которую будем увеличивать на единицу при последующий вызовах. При достижении цели проверим, равно ли число команд требуемому. Если это условие выполнено, функция вернет 1, в противном случае — 0.
Приведем программу, решающую эту задачу:
def ways(n, goal, lprog):
if n>goal: return 0
if n==goal:
if lprog==7: return 1
else: return 0
return ways(n+1,goal,lprog+1)+ways(n+4,goal,lprog+1)+ways(n*2,goal,lprog+1)
print(ways(3,27,0))
Количество результатов программы, состоящей из определенного числа команд
Разновидность данной задачи требует найти количество чисел, которое получается при выполнении всех возможный программ для исполнителя, состоящих из некоторого фиксированного числа команд.
Задачу можно решить методом «грубой силы» — выполнив все возможные программы, состоящие из требуемого числа команд, и подсчитав количество полученных результатов.
Количество всех программ сравнительно велико. Так, если допустимо n команд, а длина программы — k команд, то число всех возможных программ — это n**k (операция ** — это возведение в степень).
Рассмотрим конкретную задачу. Пусть у исполнителя есть две допустимые команды: «прибавить 1» и «умножить на 2 и вычесть 3». Требуется начать с числа 3 и подсчитать количество различных результатов, которые дадут все программы, состоящие ровно из 12 команд.
Вначале решим задачу без применения рекурсии. Первый этап — генерация всех возможных программ для исполнителя. Программа — это строка символов, в которых символ «0» обозначает первую команду, а «1» — вторую. Такую строку можно получить, перебрав все числа от 0 до 2**12-1 и преобразовав эти числа в двоичную запись. Это делается следующим фрагментом программы:
k=12
for i in range(2**k):
prog=bin(i)[2:]
if len(prog)<k: prog=’0’*(k-len(prog)) + prog
Выражение bin(i)[2:] работает так: функция bin(i) преобразует целое число в его двоичное представление, которое начинается с символов «0b». Чтобы отрезать эти символы, используем операцию выделения подстроки [2:], которая удалаяет первые два символа. Если длина нашей строки prog менее k, мы приписываем к ней слева такое количество нулей, чтобы её длина было ровно k символов.
Теперь выполним полученную программу. Выбираем из строки символы по очереди. Если символ — «0», то выполняем операцию «прибавить 1», в противном случае — операцию «умножить на 2 и вычесть 3». Соответствующий фрагмент программы вышлядит так:
n=start
for j in range(k):
if prog[j]==’0′: n += 1
else: n=2*n-3
После завешения этого цивла переменная n будет содержать результат выполнения текущей программы из k команд.
Чтобы полсчитать число различных резудьтатов, будем использовать массив a (изначально пустой). Если данное число не содержится в нём — добавим это число в массив:
if not n in a: a.append(n)
Когда закончится внешний цикл, то в массиве a будут содержаться все возможные результаты выполнения — под одному разу каждый. Всё, что осталось сделать — вывести количество элементов массива a:
print(len(a))
Приведем программу полностью:
k=12
start=3
a=[]
for i in range(2**k):
prog=bin(i)[2:]
if len(prog)<k: prog=’0’*(k-len(prog)) + prog
n=start
for j in range(k):
if prog[j]==’0′: n += 1
else: n=2*n-3
if not n in a: a.append(n)
print(len(a))
Теперь решим ту же самую задачу с использованием рекурсии. Для этого напишем рекурсивную функцию f:
def f(n,l,k):
if l==k:
if not n in a: a.append(n)
return
f(n+1,l+1,k)
f(2*n-3,l+1,k)
return
Параметры функции следующие: n — текущее число, с которым работает исполнитель, l — текущее число команд, k — длина программ, которые требуется выполнять.
Если l равно k, это означает, что мы выполнили программу из k команд. Проверяем, содержится ли данный результат в массиве a, если нет — добавляем его в массив. После этого выходим из программы.
Если же требуемое количество команд ещё не выполнено, вызываем функцию два раза, первый — увеличив значение n на 1, второй — со значением 2*n-3. В обоих случаях увеличиваем l на 1, т.к. мы выполнили ещё одну команду.
Основная программа очень короткая: в ней переменной a присваивается пустой массив, вызывается функция f с параметром l, равным 0 (мы её не выполнили ни одноё команды), а после её завершения печатается количество элементов в массиве a.
Вот программа полностью:
def f(n,l,k):
if l==k:
if not n in a: a.append(n)
return
f(n+1,l+1,k)
f(2*n-3,l+1,k)
return
k=12
start=3
a=[]
f(start,0,k)
print(len(a))
Вообще говоря, рекурсивный вариант должен выполняться немного быстрее, т.к. нерекурсивном варианте дерево команд проходится каждый раз от когня до конца, а в рекурсивном осуществляются возвраты вверх по ветвям. Разница во времени выполнения должна быть примерно двукратной. Но оба варианта выполняются практически мгновенно, поэтому это несущественно.
Некоторые «хитрые» операции
В ряде задач встречаются «хитрые» операции получения следующего числа. Рассмотрим некоторые из них.
«Сделай нечётное». Если число чётное, к нему прибавляется 1, а если чётное, то 2. Результат достигается с помощью выражения n+n%2+1.
«Дописать справа 0» и «дописать справа 1». К десятичной записи числа справа приписывается ноль или единица. Такой результат дают выражения 10*n и 10*n+1 соответственно.
«Прибавить предыдущее» и «прибавить следующее». В первом случае к числу прибавляется число, меньшее на 1 (так, из числа 5 получается число 5+4, т.е. 9), во втором — на единицу большее. Соответствующие выражения — 2*n-1 и 2*n+1.
«Обнулить младший разряд». Операция обнуляет младший разряд в троичной записи числа. Соответствующее выражение — (n//3)*3. Внимание, тут есть подвох! Если последняя цифра числа в троичной записи — ноль (например, число 6 в троичной записи выглядит как 20), то число не изменяется и рекурсия зациклится. Поэтому надо проверять эту ситуацию и в случае, когда последняя цифра — ноль, не вызывать функцию. Для операций «отнять 2» и «обнулить младший разряд» функция ways может выглядеть так:
def ways(n, goal, zapret):
if n<goal: return 0
if n in zapret: return 0
if n==goal: return 1
if n%3==0: return ways(n-2,goal,zapret)
else: return ways(n-2,goal,zapret)+ways((n//3)*3,goal,zapret)
(Обратите внимание: так как операции уменьшают число, то во второй строке функции используется операция сравнения «меньше», а не «больше».)
«Добавить слева 1». Операция приписывает к двоичной записи числа единицу слева. Это можно сделать, например, с помощью выражения int(‘1’+bin(n)[2:],2).
«Убрать последнюю цифру справа». Удаляется последняя цифра справа в десятичной записи числа. Это можно сделать целочисленным делением на 10: n//10.
«Обнулить». Первая слева цифра числа в двоичной записи не изменяется, а остальные заменяются нулями. Возможное выражение — n-int(bin(n)[3:],2). Тут тоже возможны неприятности, аналогичные упомянутым в операции «обнулить младший разряд» (см. выше).
«Прибавить следующее четное». К числу прибавляется минимальное четное число, превосходящее данное. Так, к числу 2 прибавляется 4, а к числу 5 — 6. Это можно сделать при помощи выражения 2*n+1+(n+1)%2.
«Сделать простое». Требуется получить простое число, большее, чем данное, и ближайшее в нему. Так, для числа 8 результатом должно быть число 11. Тут придется написать функцию, которая будет последовательно перебирать числа n+1, n+2 и т.д., пока не найдет простое число. Функция может выглядеть, например, так:
def makeprime(n):
n += 1
while True:
k=2
prime=True
while k*k<=n:
if n%k==0:
prime=False
break
k += 1
if prime: return n
n += 1
(О простых числах и способах проверки «на простоту» я писал ранее.)
Задачи ЕГЭ 23 и 13 — по сути одна задача
Данная задача является подсчетом числа путей в ориентированном графе. Вершинами графа являются числа, а правила перехода от одного числа к другому задаются разрешенными в задаче операциями. Поэтому данная задача аналогична задаче ЕГЭ № 13, в которой рисуется схема дорог между городами и задается вопрос вроде: «Сколько существует различных путей из города А в город Н?»
Возникает вопрос: а можно ли решать программным путем и задачу 13? Разумеется, можно! Самая большая сложность — представить граф из задачи 13 в форме, удобной для компьютерной обработки. Впрочем, сложность эта вполне преодолима. Но более подробный рассказ об этом — тема для отдельной заметки.
Использованные выше задачи взяты с сайта «Решу ЕГЭ» (информатика) и с сайта К.Ю.Полякова.
(c) Ю.Д.Красильников, 2022 г.
За это задание ты можешь получить 1 балл. На решение дается около 10 минут. Уровень сложности: высокий.
Средний процент выполнения: 25.4%
Ответом к заданию 23 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 47, причём траектория вычислений проходит через число 14? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Из числа 3 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число, т.к. нечётное +2 = нечётное и нечётное *3 = нечётное. Следовательно, число 14 получить невозможно. Тогда никакая траектория из числа 3 в число 47 не пройдёт через число 14.
Ответ: 0.
Ответ: 0
Задача 2
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 58?
Решение
Из числа 1 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число, т.к. нечётное +2 = нечётное и нечётное *3 = нечётное. Следовательно, число 58 получить невозможно.
Ответ: 0.
Ответ: 0
Задача 3
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 49?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Из числа 3 с помощью команд «Прибавь 2» и «Умножь на 3» невозможно получить чётное число. Значит, чётные числа можно не писать.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 |
| Кол-во программ | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 |
| Число | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 | 49 |
| Кол-во программ | 6 | 6 | 6 | 8 | 8 | 8 | 10 | 10 | 10 | 13 | 13 | 13 |
Ответ: 13.
Ответ: 13
Задача 4
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь предыдущее
3. Прибавь следующее
Первая из них увеличивает число на экране на 1, вторая — прибавляет к текущему числу на единицу меньшее натуральное число, третья — прибавляет к текущему числу на единицу большее натуральное число. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 33, причём траектория вычислений не проходит через число 7 и 14, но проходит через число 12? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Кол-во программ | 1 | 1 | 3 | 3 | 7 | 7 | 0 | 0 | 10 | 10 | 24 | 24 |
После числа 12 нельзя пользоваться теми значениями, которые были до числа 12. Поэтому дальнейшая таблица имеет вид:
| Число | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| Кол-во программ | 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 24 | 72 | 72 | 96 | 96 | 96 | 96 | 96 | 96 | 96 |
Вычисление результата при помощи программы на С++:
#include <iostream>
using namespace std;int main(){
const int n0 = 1, nk = 33;
int arr[nk + 1];
for (int i = 0; i < nk + 1; ++i) arr[i] = 0;
arr[n0] = 1;
for (int n = n0 + 1; n <= nk; ++n) {
arr[n] = arr[n - 1]; // Kn-1
if (n % 2 != 0 && (n - 1) / 2 >= n0) //K(n - 1)/2
arr[n] += arr[(n - 1) / 2];
if (n % 2 != 0 && (n + 1) / 2 >= n0) //K(n + 1)/2
arr[n] += arr[(n + 1) / 2];
if (n == 7 || n == 14)
arr[n] = 0;
if (n == 12)
for (int i = n - 1; i >=0 ; --i)
arr[i] = 0;
}
cout << arr[nk];
return 0;
}
Ответ: 96.
Ответ: 96
Задача 5
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Сделай чётное
3. Сделай нечётное
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 2 раза и прибавляет единицу. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 2 преобразуют в число 30, траектория которых проходит через число 9 и не проходит через число 16? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Кол-во программ | 1 | 1 | 2 | 3 | 4 | 5 | 7 | 9 |
После числа 9 нельзя пользоваться теми значениями, которые были до числа 9. Поэтому дальнейшая таблица имеет вид:
| Число | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Кол-во программ | 9 | 9 | 9 | 9 | 9 | 9 | 0 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 |
Поиск ответа при помощи программы на С++:
#include <iostream>
using namespace std;int main(){
const int n0 = 2, nk = 30;
int arr[nk + 1];
for (int i = 0; i < nk + 1; ++i) arr[i] = 0;
arr[n0] = 1;
for (int n = n0 + 1; n <= nk; ++n) {
arr[n] = arr[n - 1]; // Kn-1
if (n % 2 != 0 && (n - 1) / 2 >= n0) //K(n - 1)/2 - сделай нечётное
arr[n] += arr[(n - 1) / 2];
if (n % 2 == 0 && n / 2 >= n0) //Kn/2 - сделай чётное
arr[n] += arr[n / 2];
if (n == 16)
arr[n] = 0;
if (n == 9)
for (int i = n - 1; i >=0 ; --i)
arr[i] = 0;
}
cout << arr[nk];
return 0;
}
Ответ: 117.
Ответ: 117
Задача 6
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Сделай чётное
3. Сделай нечётное
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 2 раза и прибавляет единицу. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 30?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Кол-во программ | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Число | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Кол-во программ | 11 | 13 | 15 | 18 | 21 | 25 | 29 | 34 | 39 | 45 | 51 | 58 |
Ответ: 58.
Ответ: 58
Задача 7
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 34?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Кол-во программ | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 6 | 6 |
| Число | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
| Кол-во программ | 8 | 8 | 10 | 11 | 13 | 13 | 17 | 17 | 20 | 21 | 25 | 25 | 32 | 32 | 38 | 40 | 46 |
Ответ: 46.
Ответ: 46
Задача 8
У исполнителя Считатель-1 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, третья — в 3 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 26?
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Кол-во программ | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 8 | 8 |
| Число | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Кол-во программ | 10 | 11 | 14 | 14 | 20 | 20 | 25 | 27 | 32 | 32 | 43 | 43 | 51 |
Ответ: 51.
Ответ: 51
Задача 9
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
Первая из них увеличивает число на экране на 1, вторая — в 2 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 20, траектория вычислений которых не проходит через число 9? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кол-во программ | 1 | 2 | 2 | 4 | 4 | 6 | 6 | 10 | 0 | 4 | 4 | 10 | 10 | 16 | 16 | 26 | 26 | 26 | 26 | 30 |
Ответ: 30
Ответ: 30
Задача 10
У исполнителя Считатель-1 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
Первая из них увеличивает число на экране на 1, вторая — в 2 раза. Программа для исполнителя Считатель-1 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 26, у которых траектория вычислений проходит через число 10? Траектория вычислений — множество чисел, через которые проходила конкретная программа для получения одного числа из другого.
Решение
Будем считать количество программ постепенно для каждого числа слева направо по следующему принципу:
Если число А можно получить с помощью X программ из начального значения, число B можно получить с помощью Y программ из начального значения, а с помощью одной любой команды из условия число C можно получить только из чисел A и B, то количество программ, с помощью которых можно получить число C из начального значения, равно X + Y.
Таблица, отображающая количество программ для каждого отдельного числа, вычисленная по данному правилу:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Кол-во программ | 1 | 2 | 2 | 4 | 4 | 6 | 6 | 10 | 10 | 14 |
После числа 10 нельзя пользоваться теми значениями, которые были до числа 10. Поэтому дальнейшая таблица имеет вид:
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Кол-во программ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 28 | 28 | 42 | 42 | 56 | 56 | 70 |
Ответ: 70.
Ответ: 70
Задача 11
У исполнителя A2M5 две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 5
Первая из них увеличивает данное число на 2, вторая — увеличивает его в 5 раз. Программа для исполнителя A2M5 — это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 31.
Решение
Заметим, что все числа, получаемые с помощью заданных команд из числа 1, нечётные. Будем решать поставленную задачу последовательно для чисел 1, 3, 5, . . . , 31 (то есть для каждого нечётного числа определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Будем считать, что R(1) = 1. Для каждого следующего числа рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число не делится на 5, то оно может быть получено только из предыдущего с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для предыдущего числа: R(i) = R(i — 2), i — нечётное. Если число на 5 делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда R(i) = R(i-2)+R(i=5), i — нечётное. Заполним соответствующую таблицу по приведённым формулам слева направо:
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 5 | 5 |
| 29 | 31 | ||||||||||||
| 5 | 5 |
Ответ: 5.
Ответ: 5
Задача 12
У исполнителя X123 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 2
3. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — на 2, а третья — в 3 раза. Программа для исполнителя X123 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 10?
Решение
Будем решать поставленную задачу последовательно для чисел 1, 2, 3, . . . , 10 (то есть для каждого из чисел определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Число 2 из числа 1 можно получить с помощью команды 1 (также будем считать, что R(1) = 1). Для каждого следующего числа i рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число i не делится на 3, то оно может быть получено либо из i — 1-го с помощью команды прибавь 1, либо из числа i — 2-го с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для i-1-го и i-2-го чисел:R(i) = R(i-1)+R(i-2). Если число на 3 делится, то вариантов последней команды три: прибавь 1, прибавь 2 и умножь на 3, следовательно, R(i) = R(i-1)+R(i-2)+R(i/3). Заполним соответствующую таблицу по приведенным формулам слева направо:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 3 | 4 | 7 | 12 | 19 | 31 | 53 | 84 |
Ответ: 84.
Ответ: 84
Задача 13
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 5.
Первая из них увеличивает данное число на 2, вторая — увеличивает его в 5 раз. Программа для исполнителя Удвоитель — это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 37.
Решение
Заметим, что все числа, получаемые с помощью заданных команд из числа 1, — нечётные. Будем решать поставленную задачу последовательно для чисел 1, 3, 5, . . . , 37 (то есть для каждого нечётного числа определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Будем считать, что R(1) = 1. Для каждого следующего числа рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число не делится на 5, то оно может быть получено только из предыдущего с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для предыдущего числа: R(i) = R(i − 2), i — нечётное. Если число на 5 делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда R(i) = R(i−2)+R(i/5), i — нечётное. Заполним соответствующую таблицу по приведенным формулам слева направо:
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 5 | 5 |
| 29 | 31 | 33 | 35 | 37 | |||||||||
| 5 | 5 | 5 | 7 | 7 |
Ответ: 7
Задача 14
У исполнителя X157 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 5
3. Умножь на 7
Первая из них увеличивает число на экране на 1, вторая — на 5, а третья — в 7 раз. Программа для исполнителя X157 — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Задача 15
У исполнителя X13 две команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 3
Первая из них увеличивает число на экране на 1, вторая — в 3 раза. Программа для исполнителя X13 — это последовательность команд.
Сколько существует программ, которые число 3 преобразуют в число 35, причём траектория вычислений содержит число 13?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 1211 при исходном числе 2 траектория будет состоять из чисел 3; 9; 10; 11.
Задача 16
У исполнителя X157 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 5
3. Умножь на 7
Первая из них увеличивает число на экране на 1, вторая — на 5, а третья — в 7 раз. Программа для исполнителя X157 — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Задача 17
У исполнителя X135 три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 3
3. Умножь на 5
Первая из них увеличивает число на экране на 1, вторая — на 3, а третья — в 5 раз. Программа для исполнителя X135 — это последовательность команд. Сколько существует программ, которые число 1 преобразуют в число 14?
Задача 18
У исполнителя Увеличитель две команды, которым присвоены номера:
1. Прибавь 2
2. Умножь на 3
Первая из них увеличивает число на экране на 2, вторая — увеличивает его в 3 раза. Программа для исполнителя Увеличитель—это последовательность команд.
Определите количество программ, которые число 1 преобразуют в число 37.
Задача 19
У исполнителя X17 две команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 7
Первая из них увеличивает число на экране на 1, вторая — на 7. Программа для исполнителя X17—это последовательность команд.
Сколько существует программ, которые число 5 преобразуют в число 26, и при этом траектория вычислений содержит число 12?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы.Например, для программы 1221 при исходном числе 3 траектория будет состоять из чисел 4, 11, 18, 19.
Задача 20
У исполнителя X125 три команды, которым присвоены номера:
1. Прибавь 1
2. Умножь на 2
3. Умножь на 5
Первая из них увеличивает число на экране на 1, вторая — в 2 раза, а третья — в 5 раз. Программа для исполнителя X125 — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 38, и при этом траектория вычислений содержит числа 10 и 20? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 2231 при исходном числе 5 траектория будет состоять из чисел 10, 20, 100, 101.
Рекомендуемые курсы подготовки
Еще один способ решения данного задания – написание программы.
На примере первой задачи посмотрим несколько способов решения.
Задание 1
У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Сколько есть программ, которые число 1 преобразуют в число 20?
В решении электронными таблицами мы получили формулы для расчетов:
Если число n НЕ делится на 3, количество программ для него
kn = kn-1
Если же число делится на 3, то
kn = kn-1 + kn / 3
их мы и будем использовать в данном задании.
1 способ решения. Заполнение списка.
Необходимые навыки:
- работа со списками
- условный оператор
- цикл for
# +1 *3 1->20
a = [0] * 21 # создаем список из такого количества
# элементов, чтобы нам хватило индексов от 0 до 20
a[1] = 1 # заполняем элемент с индексом стартового числа
for i in range(2, 20 + 1): # перебираем остальные числа от 2 до 20
if i % 3 == 0: # если кратно 3, добавляем предыдущее и / 3
a[i] = a[i – 1] + a[ i // 3]
else: # если не кратно 3, добавляем только предыдущее
a[i] = a[i – 1]
print(a[20]) # выводим на экран значение конечного числа
Данное решение является самым частным и не всегда получится им хорошо решить. Потребуются дополнительные условия когда могут получаться отрицательные индексы.
2 вариант решения без инверсии команд
# +1 *3 1->20 a = [0] * 100 # создаем список из такого количества # элементов, чтобы нам хватило индексов от 0 до 20 * 3 (я взял сильно с запасом) a[20] = 1 # заполняем элемент с индексом стартового числа for i in range(19, 0, -1): # перебираем остальные числа от 2 до 20 a[i] = a[i + 1] + a[i * 3] print(a[1]) # выводим на экран значение конечного числа
При таком решении не требуется условный оператор, но размер списка надо предусмотреть в 3 раза больше.
3 вариант решения. Рекурсивная функция
# +1 *3 1->20 def f(n): if n > 20: # перепрыгнули 20 return 0 if n == 20: # попали в 20 return 1 return f(n + 1) + f(n * 3) # число до 20
print(f(1))
Задача 2. Все варианты решения
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 40 и при этом траектория вычислений содержит число 20 и не содержит число 8?
Разобьем решение со списком на два этапа
# +1 *2 2->40 v20 x8 a = [0] * 100
a[20] = 1 # заполняем элемент с индексом стартового числа a[40] = 1 for i in range(19, 2 - 1, -1): if i != 8: a[i] = a[i + 1] + a[i * 2] for i in range(39, 20 - 1, -1): a[i] = a[i + 1] + a[i * 2] print(a[2] * a[20]) # выводим на экран значение конечного числа
Усовершенствуем рекурсивный алгоритм: добавим в функцию еще один параметр. Теперь их два: из какого числа считаем и в какое.
# +1 *2 2->40 v20 x8 def f(n, finish): if n == finish: return 1 if n > finish or n == 8: return 0 return f(n + 1, finish) + f(n * 2, finish) print(f(2, 20) * f(20, 40))
Решение задания программированием наиболее кратко получается с использованием рекурсивной функции. В целом, написание кода занимает время примерно равное решению в электронных таблицах, за исключением случаев когда дан большой диапазон чисел.
Следует рассматривать такой вариант решения как средство для проверки ручного решения.