Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Спрятать решение
Решение.
Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания a и боковое ребро H формулой Подставим значения a и S:
откуда находим, что
Ответ: 12.
Найдите боковое ребро правильной четырехугольной
Дата: 2022-01-13
204
Категория: Стерео Призма
Метка: ЕГЭ-№2
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
27063 решу егэ математика
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Работа выполняется позже назначенного срока, оценка будет снижена.
Версия для печати и копирования в MS Word
—>
Выставленные учителем баллы отобразятся в вашей статистике.
Math-ege. sdamgia. ru
12.01.2018 6:11:07
2018-01-12 06:11:07
Источники:
Https://math-ege. sdamgia. ru/test? id=44414984
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 27063 решу егэ математика
27063 решу егэ математика
27063 решу егэ математика
—>
Д. Д. Гущин Готовимся к ЕГЭ по профильной математике
Определите желаемый балл. (Будьте скромнее. Потом можно изменить.) Укажите дни, когда вы будете заниматься. (Понадобится 2−3 раза в неделю по 1−2 часа.) Пройдите входное тестирование. (Будет построен ваш индивидуальный образовательный маршрут.) Изучайте указанные темы, следуя расписанию занятий. (Можно опережать.) Сдав контрольную работу, переходите на следующий уровень.
Математика это сложно, получить больше 85 баллов трудно. Но если серьёзно относиться к делу, то к концу года можно получить прибавку в 27 баллов к начальному уровню. #математиканедлявсех #математикаэтосложно
Вы можете узнать свой текущий уровень прямо сейчас. Пройдите входное тестирование по заданиям из открытого банка ЕГЭ.
—>
Д. Д. Гущин Готовимся к ЕГЭ по профильной математике
Изучайте указанные темы, следуя расписанию занятий.
Ege. sdamgia. ru
13.06.2019 15:42:35
2019-06-13 15:42:35
Источники:
Https://ege. sdamgia. ru/lesson
Решу егэ профиль математика 27506 — Математика и Английский » /> » /> .keyword { color: red; } 27063 решу егэ математика
Решу егэ профиль математика 27506
Решу егэ профиль математика 27506
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задания Д2 № 9627
На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−4; 6), B (−4; 4), C (4; 4). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
Задания Д2 № 9627
Задания Д2 9627.
Источники:
Задание 6 ЕГЭ по математике (профиль) | » /> » /> .keyword < color: red; >Решу егэ профиль математика 27506
Задание 6 ЕГЭ по математике (профиль)
Задание 6 ЕГЭ по математике (профиль)
Открытый банк заданий mathege. ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege. ru.
Использование свойств производной для исследования функций
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12. В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
Геометрический смысл производной
27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x 2 + 6x — 8. Найдите абсциссу точки касания.
27486. Прямая y = -4x — 11 является касательной к графику функции y = x 3 + 7x 2 + 7x — 6. Найдите абсциссу точки касания.
27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27505. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.
40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
119972. Прямая y = 3x +1 является касательной к графику функции ax 2 + 2x + 3. Найдите a.
119973. Прямая y = -5x + 8 является касательной к графику функции 28x 2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
119974. Прямая y = 3x + 4 является касательной к графику функции 3x 2 — 3x + c. Найдите c.
317543. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» /> [/su_expand]
Физический смысл производной
119975. Материальная точка движется прямолинейно по закону x(t) = 6t 2 — 48t +17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 с.
119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t 3 — 3t 2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
119977. Материальная точка движется прямолинейно по закону x(t) = — t 4 + 6t 3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
119978. Материальная точка движется прямолинейно по закону x(t) = t 2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t 3 — 3t 2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Первообразная
323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x 3 + 30x 2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= — x 3 — 27x 2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Задание 6 ЕГЭ по математике (профиль)
Открытый банк заданий mathege. ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege. ru.
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12. В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
Материальная точка движется прямолинейно по закону x t 6t 2 48t 17, где x расстояние от точки отсчета в метрах, t время в секундах, измеренное с начала движения.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 27506
Решу егэ профиль математика 27506
Решу егэ профиль математика 27506
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 6 № 27506
На рисунке изображён график функции и касательная к нему в точке с абсциссой X0. Найдите значение производной функции F(x) в точке X0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
Источники:
Задание 6 ЕГЭ по математике (профиль) | » /> » /> .keyword < color: red; >Решу егэ профиль математика 27506
Открытый банк заданий mathege. ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege. ru.
На рисунке изображён график y f x производной функции f x.
Dankonoy. com
25.03.2019 10:05:40
2019-03-25 10:05:40
Источники:
Https://dankonoy. com/ege/ege12/archives/4734
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 2 № 27148
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Спрятать решение
Решение.
Сторона ромба a выражается через его диагонали и
как
Площадь ромба
Тогда боковое ребро найдем из выражения для площади поверхности:
Ответ: 10.
Аналоги к заданию № 27148: 75963 75965 75967 75969 75971 75973 75975 75977 75979 75981 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Классификатор стереометрии: Площадь поверхности призмы
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение площади поверхности объемных фигур. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Площади поверхности
Многогранники
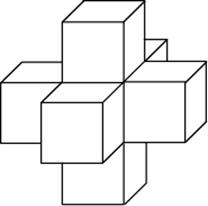
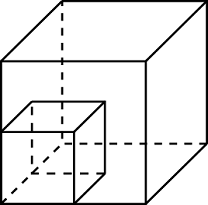
27158. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27215. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Куб
27055. Площадь поверхности куба равна 18. Найдите его диагональ.
27056. Объем куба равен 8. Найдите площадь его поверхности.
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
27130. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?
27168. Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Призма
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Пирамида
27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Цилиндр
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
245358. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
284361. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна 2π, а высота — 1. Найдите диаметр основания.
Конус
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Шар
27072. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Элементы 71—80 из 166.
Задача №:
27148. Прототип №: 27148
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27151. Прототип №: 27151
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27153. Прототип №: 27153
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27158. Прототип №: 27158
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27161. Прототип №: 27161
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27162. Прототип №: 27162
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ:
Показать/скрыть правильный ответ
Задача №:
27163. Прототип №: 27163
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27168. Прототип №: 27168
Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Ответ:
Показать/скрыть правильный ответ

Меню
-
HomeГлавная страница -
ОбразованиеПроблемы и решения-
Домашнее обучение -
Как учиться -
Будущее образования -
Математическое образование -
Школьное образование -
Разное
-
-
ЕГЭПодготовка к экзамену

Элементарные задания
Меню
-
Элементарные заданияВ1, В2, В3, В4 -
Практико-ориентированные задачи -
Графики -
Выбор варианта
Алгебра +
Меню
-
Алгебра +В7, В11 -
Уравнения -
Преобразования
Производная
Меню
-
ПроизводнаяВ9, В15 -
Анализ графиков, касательная, скорость, первообразная -
Вычисление производной
Задачи
Меню
-
ЗадачиB6, B12, B14 -
Работа, движение, растворы, прогрессии -
Построение мат. моделей в физике и технике -
Теория вероятности, комбинаторика и статистика
Геометрия
Меню
-
Углы и треугольники -
4х-угольники. Многоугольники и окружности -
Площади. Вектора. Координаты -
Многогранники -
Тела вращения
Вход/Регистрация
Логин
Пароль
Запомнить меня
- Забыли пароль?
- Забыли логин?
- Регистрация

Проверить аттестат
Наверх
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение площади поверхности объемных фигур. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Площади поверхности
Многогранники
27158. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27215. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Куб
27055. Площадь поверхности куба равна 18. Найдите его диагональ.
27056. Объем куба равен 8. Найдите площадь его поверхности.
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
27130. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?
27168. Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Призма
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Пирамида
27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Цилиндр
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
245358. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
284361. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна 2π, а высота — 1. Найдите диаметр основания.
Конус
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Шар
27072. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
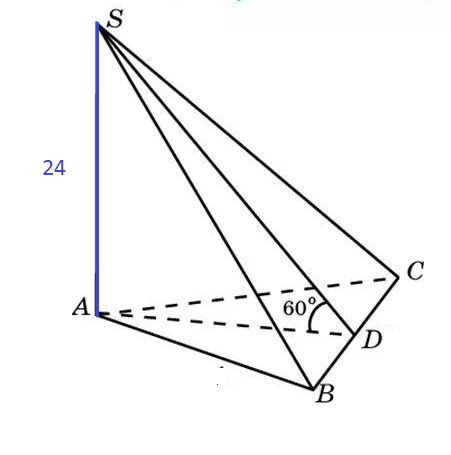
Задача 27063 Рисунки к задачам,пожалуйста…
Условие

Рисунки к задачам,пожалуйста

математика 10-11 класс
709
Решение
★
1.
Из прямоугольного треугольника SAD
tg∠ADS=AS/AD
AD=AS/tg60^(o)=24*2/sqrt(3)=16sqrt(3)
SD=32sqrt(3)
катет против угла в 30 градусов равен половине гипотенузы, значит гипотенуза в два раза больше катета.
В равностороннем треугольнике АВС
AD=16sqrt(3)
AB=BC=AC=32
S=S( ΔABC)+S(ΔSAB)+S(ΔSAC)+S(ΔSBC)=
=(32*sqrt(3)/4)+2*(1/2)32*24+(1/2)*12*32sqrt(3)=
=200 sqrt(3)+786
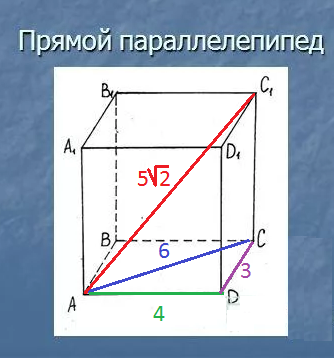
2.В основании прямого параллелепипеда — параллелограмм АВСD
По формуле
АС^2+BD^2=2*AB^2+2CD^2
находим ВD
BD=sqrt(14)
H^2=(5sqrt(2))^2-6^2=14
H=sqrt(14)
S(BDD1B1)=BD*H=14