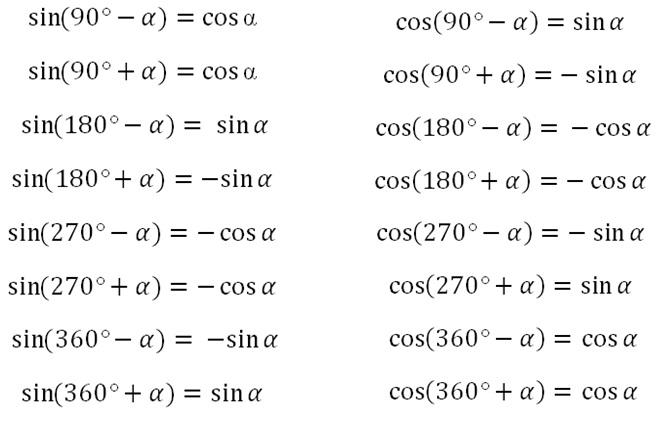Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
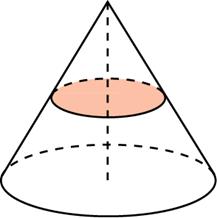
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
Спрятать решение
Решение.
Площадь боковой поверхности конуса равна где C — длина окружности основания, а l — образующая. При увеличении образующей в 3 раза площадь боковой поверхности конуса увеличится в 3 раза.
Ответ: 3.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2013-03-04

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Решу егэ математика 27136
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв слов или цифр.
Ege. sdamgia. ru
07.02.2018 10:25:57
2018-02-07 10:25:57
Источники:
Https://ege. sdamgia. ru/test? id=45021622
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 27136
Решу егэ математика 27136
Решу егэ математика 27136
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
—>
Единицы измерений писать не нужно.
Ege. sdamgia. ru
09.07.2019 19:57:25
2019-07-09 19:57:25
Источники:
Https://ege. sdamgia. ru/test? id=46445704
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 27136
Решу егэ математика 27136
Решу егэ математика 27136
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите
Единицы измерений писать не нужно.
Ege. sdamgia. ru
15.11.2018 21:23:10
2018-11-15 21:23:10
Источники:
Https://ege. sdamgia. ru/test? id=46465764
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 2 № 27148
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Спрятать решение
Решение.
Сторона ромба a выражается через его диагонали и
как
Площадь ромба
Тогда боковое ребро найдем из выражения для площади поверхности:
Ответ: 10.
Аналоги к заданию № 27148: 75963 75965 75967 75969 75971 75973 75975 75977 75979 75981 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Классификатор стереометрии: Площадь поверхности призмы
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение площади поверхности объемных фигур. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Площади поверхности
Многогранники
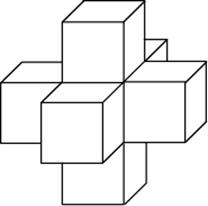
27158. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27215. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Куб
27055. Площадь поверхности куба равна 18. Найдите его диагональ.
27056. Объем куба равен 8. Найдите площадь его поверхности.
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
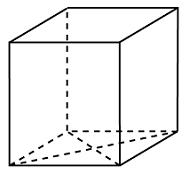
27130. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?
27168. Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Призма
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
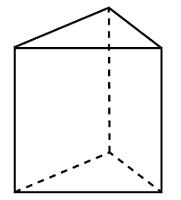
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Пирамида
27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Цилиндр
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
245358. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
284361. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна 2π, а высота — 1. Найдите диаметр основания.
Конус
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Шар
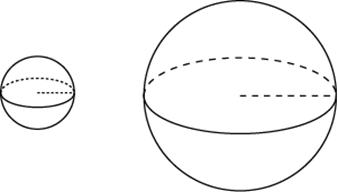
27072. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Элементы 71—80 из 166.
Задача №:
27148. Прототип №: 27148
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27151. Прототип №: 27151
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27153. Прототип №: 27153
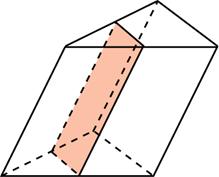
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27158. Прототип №: 27158
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27161. Прототип №: 27161
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27162. Прототип №: 27162
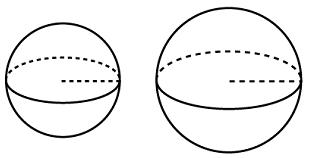
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Ответ:
Показать/скрыть правильный ответ
Задача №:
27163. Прототип №: 27163
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27168. Прототип №: 27168
Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Ответ:
Показать/скрыть правильный ответ

Меню
-
HomeГлавная страница -
ОбразованиеПроблемы и решения-
Домашнее обучение -
Как учиться -
Будущее образования -
Математическое образование -
Школьное образование -
Разное
-
-
ЕГЭПодготовка к экзамену

Элементарные задания
Меню
-
Элементарные заданияВ1, В2, В3, В4 -
Практико-ориентированные задачи -
Графики -
Выбор варианта
Алгебра +
Меню
-
Алгебра +В7, В11 -
Уравнения -
Преобразования
Производная
Меню
-
ПроизводнаяВ9, В15 -
Анализ графиков, касательная, скорость, первообразная -
Вычисление производной
Задачи
Меню
-
ЗадачиB6, B12, B14 -
Работа, движение, растворы, прогрессии -
Построение мат. моделей в физике и технике -
Теория вероятности, комбинаторика и статистика
Геометрия
Меню
-
Углы и треугольники -
4х-угольники. Многоугольники и окружности -
Площади. Вектора. Координаты -
Многогранники -
Тела вращения
Вход/Регистрация
Логин
Пароль
Запомнить меня
- Забыли пароль?
- Забыли логин?
- Регистрация

Проверить аттестат
Наверх
Подборка задач № 13 ЕГЭ по профильной математике с решениями.
→ скачать задания и решения
Задание № 13. Уметь решать уравнения и неравенства
Из кодификатора на этой позиции могут встретиться темы:
Уравнения
Квадратные уравнения
Рациональные уравнения
Иррациональные уравнения
Тригонометрические уравнения
Показательные уравнения
Логарифмические уравнения
Равносильность уравнений, систем уравнений
Простейшие системы уравнений с двумя неизвестными
Основные приёмы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
Использование свойств и графиков функций при решении уравнений
Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учёт реальных ограничений.
Неравенства
Квадратные неравенства
Рациональные неравенства
Показательные неравенства
Логарифмические неравенства
Системы линейных неравенств
Системы неравенств с одной переменной
Равносильность неравенств, систем неравенств
Использование свойств и графиков функций при решении неравенств
Метод интервалов
Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
Связанные страницы:
Консультация по английскому языку
Английский | Сегодня, 10:14
Разработчики экзаменационных материалов, учителя и выпускники, расскажут, как подготовиться к экзамену, об особенностях заданий в ЕГЭ и ответят на вопросы старшеклассников.
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
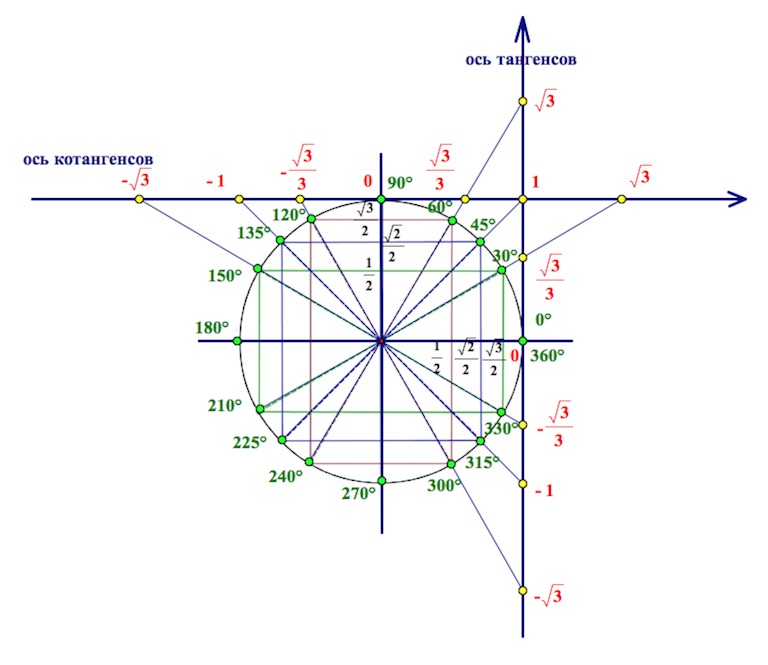
Линия тангенсов
Реальный ЕГЭ 26го июня 2018, задание 13
Найти корни между Подберем вручную корень, подходит: Поделим в столбик многочлен на , получим , т.е. Через дискриминант найдем корни Итого Ответ: a) , b)
Реальный ЕГЭ 29 мая 2019, задание 13
a) Решите уравнение b) Укажите корни, принадлежащие отрезку Пункт b: Спустимся на пару этажей вниз:
Решение задания 13, вариант 7, Ященко 36 вариантов, ЕГЭ-2019 (видео)
а) Решите уравнение 6) Найдите все корни этого уравнения, принадлежащие отрезку . Напишем ОДЗ: Когда произведение равно нулю? Когда либо одно, либо другое равно нулю: Решим первое уравнение: Читать далее …
Задача 15
Здесь нужно воспользоваться формулой Тогда получится квадратное уравнение. Свойства функций и смотрите здесь
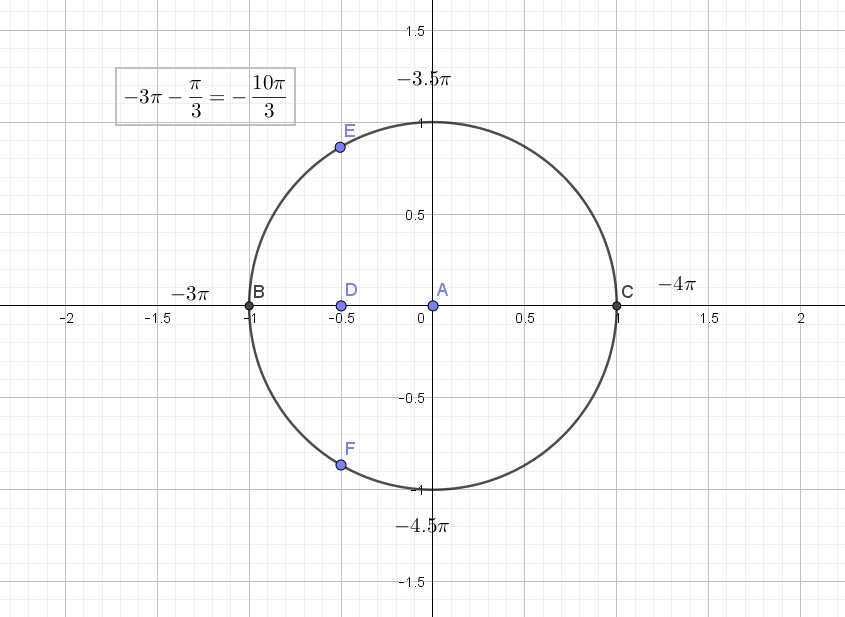
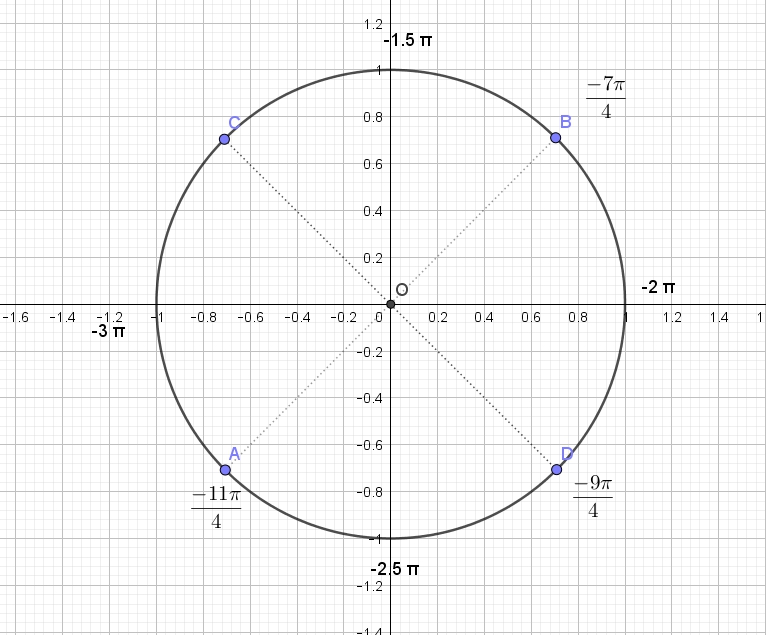
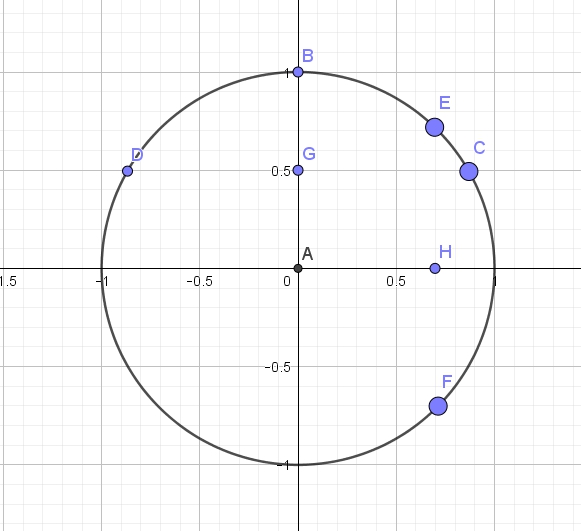
Числовая окружность
Формулы тригонометрии
Формулы приведения
Мотивация
Если вы откроете список всех задач по Планиметрии №16, которые встречались на ЕГЭ по Профилю за всё время его существования, вы удивитесь тому, как сильно она усложнилась, и на сегодняшний день на этой позиции стоит достаточно содержательная геометрическая задача с действительно порой навороченными конструкциями, которые вводят в ступор, начинающих её решать школьников. Всё это еще приправлено тем, что из года в год, на фоне эволюции этой задачи, или из-за этого, процент учеников школ решающих геометрию в ЕГЭ весьма низкий:
Хуже решается только задача по Стереометрии №13. Отсюда комом накатывается мнение, что «№16 решать дано не всем», «лучше меньше баллов, зато точно решу №12», «я нарисовал треугольник, а что делать не вижу дальше» и куча других деструктивных мыслей, которые точно не помогают вам в подготовке к ЕГЭ. По факту, из моего личного опыта, задачи по Геометрии что в ЕГЭ, что в ОГЭ, очень плохо решаются в силу отсутствия какого-то четкого алгоритма действий(как это есть в параметрах, уравнениях и неравенствах, финансовой математике), которые бы точно приводили к конкретным результатам — делай раз, делай два…
Всё правда, нам нужен не просто набор теории и формул с фактами, этого недостаточно. Нам нужна практика, опыт решения задач и стараться чувствовать эту логику при решении задач. И тут я не открою странных лайфхаков, секретных методик, будистких тайн и введьминых приколов. Будем честны, нужно время, конкретная структура и понятный набор ресурсов.
В рамках этой статьи я вложу весь свой преподавательский опыт и свои знания, как человека, который не перестаёт учиться и осваивать новые знания, чтобы помочь вам забрать на экзамене баллы за одну из самых сложных задач.
Начинаем с азов
Давайте представим, что ваша задача поднять с нуля ваши знания по геометрии на приемлемый для ЕГЭ и выше уровень. Нам не обойтись без основ и фундамента, с которым вы встречались со времен 7 класса. Что делаем? Берем учебник Атанасяна, и тут у многих расширятся зрачки и волна ужаса пройдет ледяной лавиной от бровей до мизинцев. На самом деле прошу не пугаться, нам нужен какой-то подробный школьный учебник, в котором будет изложена вся структурированная теория, необходимая и та, что мы можем применять для решения задач. Если у вас есть альтернативный — без проблем, используйте его.
Схема работы следующая: открываем со второй главы и для каждого параграфа нас будут интересовать все доказанные теоремы, а вернее не просто сухой факт, а то откуда он берется и как его доказать. Сначала пробуем сами как-то к этому придти, если не получается, то смотрим на то, какое доказательство приводит автор.
Важно! Мы не сидим тупо перед книжкой, развивая геморрой, мы берем ручку и листочек, и сидим выписываем, конспектируем и пробуем доказывать все указанные теоремы. А после просматриваем задачи в конце, решать все не нужно, только те, которые вам покажутся реально сложными и с наскока не понятными как решать.
Что нам это даст? Мы учимся воспринимать конструкции, понимать логику построения доказательства в геометрии того или иного утверждения, а также мы сами того не подозревая запоминаем всю нужную информацию, которую мы будем применять позже для решения задач №16 на ЕГЭ!
Подумайте сами, математика — это про структуру, логику, и сколько вам нужно времени чтобы зазубрить строчку предложения? 5 ? 10 минут? А на сколько вас хватит держать это всё в голове? Вы забудете при первой же возможности. Нам нужна логика доказательства этого факта, благодаря которой наш мозг будет обучаться новому подходу в мышлении и все что связанно с геометрическими фактами вы запомните намного лучше, если будете реально пытаться доказать простейшие факты из учебника. А также на самом экзамене, уровень стресса которого пробивает все возможные значения, вы будете 100% уверены, что используемый вами факт при решении задачи не вымысел возбужденного воображения.
Сколько нужно на это времени? Если идти со скоростью две главы в день, то около недели.
Как закрепить полученный результат на практике?
Теперь, друг, ты — мощь и сила! Но без практики нам не обойтись поэтому все полученные навыки начинаем применять для решения конкретных задач. Тут нам поможет книга Гордина «Планиметрия».
Схема работы с ней следующая: можете кратко просмотреть задачи данные в качестве разобранных в начале каждой главы, попробовать решить самостоятельно и потом сравнить с данным решением. Далее, переходим на отработку задач первого уровня, тут прям всё решать нет большого смысла, хоть и страшно полезно, но в режиме ограниченного времени сразу смотрим на задачи второго уровня и пытаемся прорешать максимальное количество в каждом разделе. После того как разобрались со вторым уровнем стараемся решить задачи из третьего, но тут уже можно прыгать с задачи на задачу, так как местами именно в третий уровень уже включены задачи чуть сложнее ЕГЭ. И ещё: главы про симметрии, вектора, координаты и повороты можете пропускать, если чувствуете нехватку сил, времени и вдохновения.
Кабанеем
Если со всем предыдущими пунктами справились — Glückwünsch! Поздравляю! У нас как раз есть время чтобы порешать сложные задачи и разобрать другие методы для планиметрии Прасолова. Это поможет вам разобраться с самыми разнообразными методами, которые могут повстречаться вам при решении геометрических задач. Плюс, будет реально посмотреть эту книгу и книгу Ткачука при подготовке уже к ДВИ МГУ, но это совсем другая история))
Уровень: Убийца планиметрии
На этом мы выходим на финальный этап и раз наша цель именно ЕГЭ, то дальше делаем следующее:
Открываем все задачи ЕГЭ с 2014 года и планомерно их прорешиваем. Такая процедура даст нам понимание того, что такое реальные ЕГЭшные задачи, а не Статград, от которого порой хочется сбежать. Плюс нарабатывается навык решения задачи за ограниченное время и правильное оформление всего что вы нарешали.
На этом всё?
На этом этапе я всегда даю себе время на подумать, потому что хочется что-то ещё добавить и впихнуть максимальное количество пользы. Но в данном случае, я в одной статье уместил годы опыта и сотни учеников. Схема рабочая, пользуйтесь.
Всегда рад отзывам и комментариям!
С Пламенной любовью,
Никита Салливан из Умскул.
Клиент взял в банке кредит $60000$ рублей на год под $18 %$. Он должен погашать кре…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 2 мин. 16 сек.
ЕГЭ по математике (база) 2023 задание 14: номер 34 | 1j9b3 | Клиент взял в банке кредит 60…
35
Клиент взял в банке кредит $60000$ рублей на год под $18 %$. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Найдите значение выражения $5{1}/{5} + 3{2}/{7} · 2.1$.
Найдите значение выражения $0.18 : {3}/{4} + 3$.
Найдите значение выражения ${1}/{{1}/{8}-{1}/{12}}$.
Найдите значение выражения $8.5 · 3.2 : 0.8$.