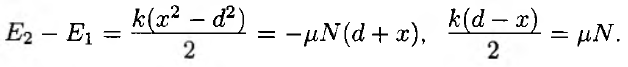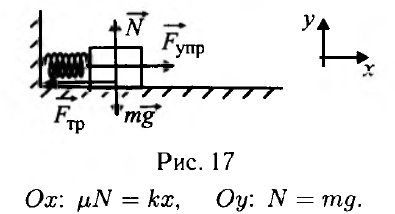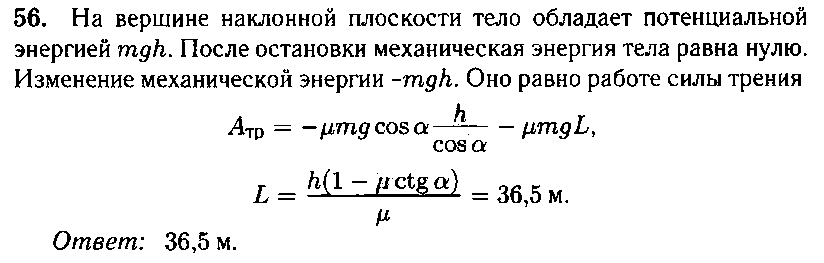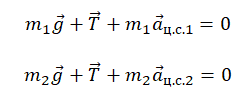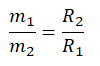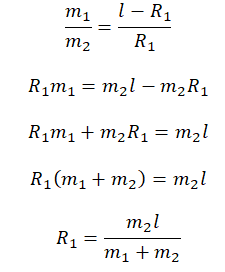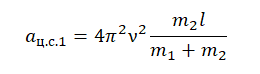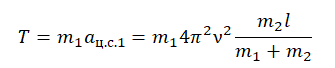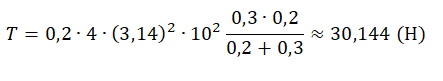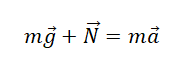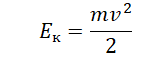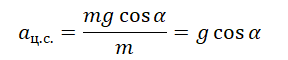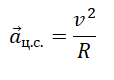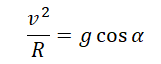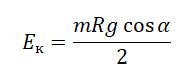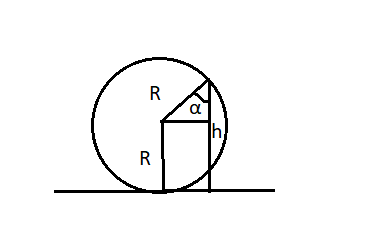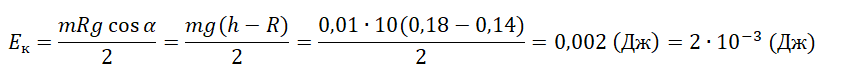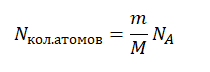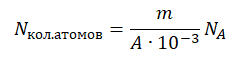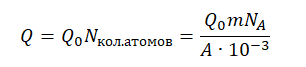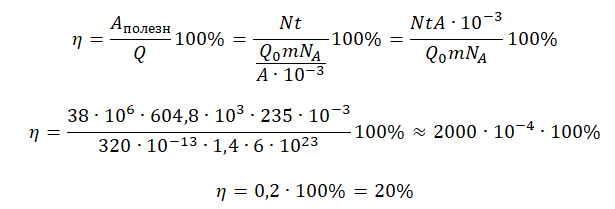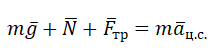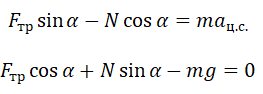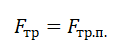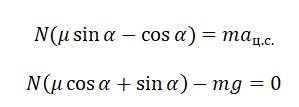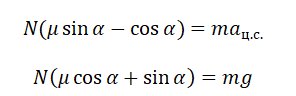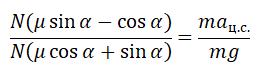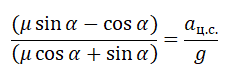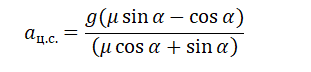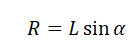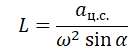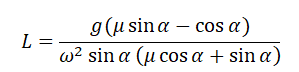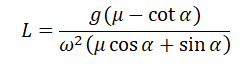Задание 29 егэ по физике представляет собой - Помощь в подготовке к экзаменам и поступлению

Подготовка к ЕГЭ по физике. Задания высокого уровня сложности с развернутыми ответами. ЗАДАНИЕ № 29 (с решениями). Расчетная задача. Максимальная оценка 3 балла.

Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.

ЕГЭ по физике. ЗАДАНИЕ № 29

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно. Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

Один из вариантов решения

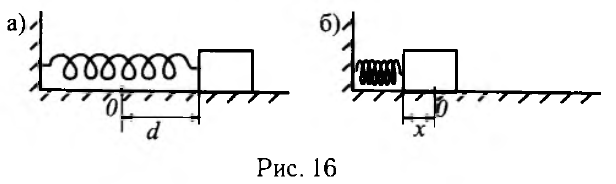
Сделаем поясняющий чертёж.

В начальный момент времени (см. рис. 16а) пружина была растянута на величину d, следовательно, её потенциальная энергия была равна E₁ = kd²/2 (k — коэффициент жёсткости пружины). Когда груз отпустили, пружина начала сжиматься, а сам груз — двигаться в сторону закреплённого конца пружины. В некоторый момент движение груза прекратилось, пружина при этом сжалась на величину х (см. рис. 16б). Соответственно в момент остановки груза потенциальная энергия пружины была равна Е₂ = kx²/2.

Изменение механической энергии системы равно работе сил трения.
А = –F_тр • S = –F_тр • (d + х) = – μN • (d + x).
Здесь S — пройденный грузом путь, μ — коэффициент трения, N — сила реакции опоры.

Кинетические энергии груза и в начальном положении, и в конечном равны нулю, следовательно:

Рассмотрим силы, действующие на груз в момент остановки — силу трения, силу упругости со стороны пружины, силу тяжести и силу реакции опоры (см. рис. 17). Груз покоится, значит, равнодействующая этих сил равна нулю. Запишем проекции сил на оси Ох и Оу:

Выразим из этих двух уравнений величину сжатия пружины х: х = μN/k = μmg/k

Отсюда k/2 • (d – μmg/k) = μN. Выразим массу тела: m = kd/2μg = 2,5 (кг).

Ответ: m = 2,5 кг.

Решение № 1 (на 3 балла)

Комментарий: Здесь в полном соответствии с пунктом 2 в критериях оценки указана на рисунке вновь введённая автором решения величина d₁.

Решение № 2 (на 2 балла)

Комментарий: К недостаткам работы следует отнести отсутствие рисунка с указанием вновь вводимых обозначений. Кроме того, замечены ошибки в математических преобразованиях; однако недостатки решения, каждый из которых приводит к снижению оценки на 1 балл, не суммируются. Оценка 2 балла.

Решение № 3 (на 2 балла)

Комментарий: Такие же замечания, как и в предыдущей работе, и та же оценка.

Решение № 4 (на 2 балла)

Комментарий: Здесь получен правильный ответ, т.к. как ошибки в расчётах сил сопротивления компенсировались ошибками в математических преобразованиях. Оценка 2 балла.

Решение № 5 (на 0 баллов)

Комментарий: Оценка 0 баллов, т.к. неверно записаны исходные формулы.

Образцы заданий № 29 (с решениями)

Часть 1. Кинематика

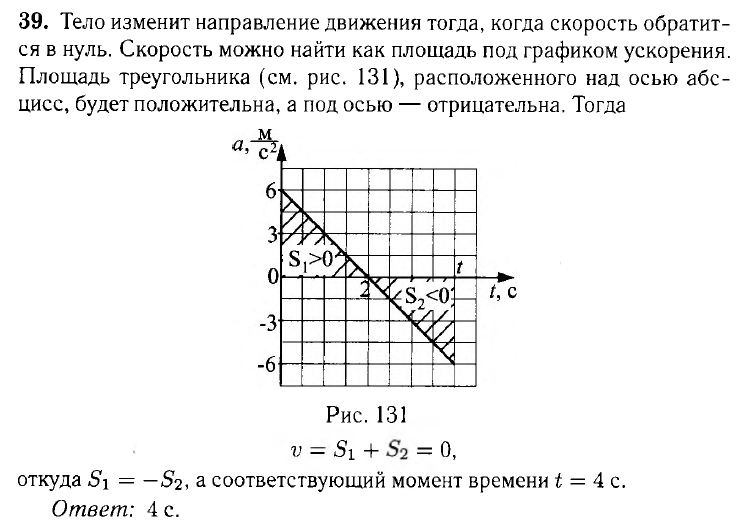
1.1. На рисунке 18 представлена зависимость ускорения материальной точки от времени. Начальная скорость точки равна 0. В какой момент времени точка изменит направление движения?

Смотреть решение и ответ

1.2. Тело брошено под углом α к горизонту с начальной скоростью υ₀. При этом на тело действует попутный горизонтальный ветер, сообщая ему постоянное ускорение а. Найдите время полёта, наибольшую высоту и наибольшую дальность полёта.

Смотреть решение и ответ

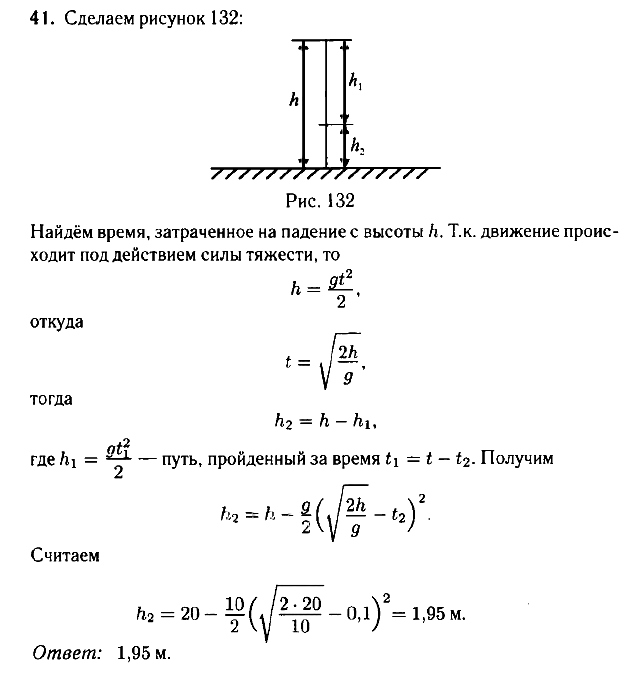
1.3. Тело брошено с высоты 20 м. Какой путь пройдёт тело за последние 0,1 с своего движения? Начальная скорость тела равна нулю.

Смотреть решение и ответ

1.4. Из некоторой точки одновременно бросают два тела с одинаковой скоростью 25 м/с: одно — вертикально верх, другое — вертикально вниз. На каком расстоянии друг от друга будут эти тела через 2 с?

Смотреть решение и ответ

1.5. Из поднимающегося вертикально вверх вертолёта со скоростью υ на высоте Н вылетает тело. Через сколько времени оно упадёт на Землю? Какой будет скорость у тела? Сопротивления воздуха нет.

Смотреть решение и ответ

1.6. Жонглёр бросает вертикально вверх шарики с одинаковой скоростью через равные промежутки времени. При этом пятый шарик жонглёр бросает в тот момент, когда первый шарик возвращается в точку бросания. Найдите максимальное расстояние S_max между первым и вторым шариками, если начальная скорость шариков υ₀ = 5 м/с. Ускорение свободного падения принять равным g = 10 м/с². Сопротивлением воздуха пренебречь.

Смотреть решение и ответ

Часть 2. Динамика

2.1. Диск вращается в горизонтальной плоскости с угловой скоростью 3 рад/с. На расстоянии 30 см от центра диска лежит небольшое тело. При каком минимальном значении коэффициента трения тело будет удерживаться на диске?

Смотреть решение и ответ

2.2. С наклонной плоскости длиной 4 м и углом наклона 30° соскальзывает тело массой 2 кг, после чего проходит некоторое расстояние по горизонтали. Коэффициент трения на всём пути 0,05. Найдите расстояние, пройденное телом по горизонтали.

Смотреть решение и ответ

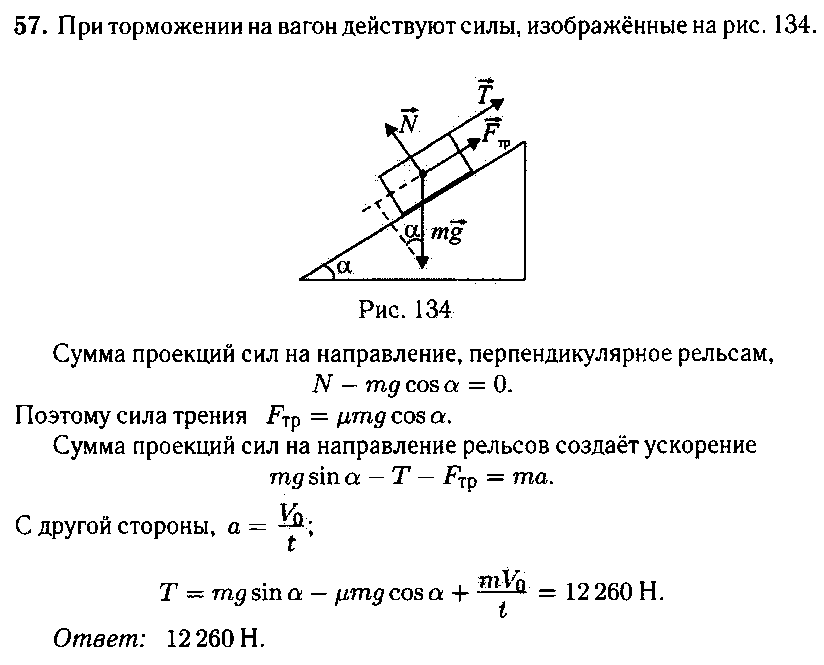
2.3. По рельсам фуникулёра, проложенным под углом 30° к горизонту, спускается вагон массой 2 т. Скорость вагона на всём пути рана 10 м/с, время торможения перед остановкой 5 с. Найдите силу натяжения каната при торможении. Коэффициент трения между колёсами и рельсами 0,1.

Смотреть решение и ответ

2.4. Лётчик массой 70 кг совершает мёртвую петлю в вертикальной плоскости с включённым двигателем, поддерживая постоянную по модулю скорость. Насколько вес лётчика в верхней точке траектории меньше, чем в нижней?

Смотреть решение и ответ

2.5. Катер массой 1 т плывёт под действием трёх сил: силы тяги двигателя 1,5 кН, силы ветра 1 кН и силы сопротивления 0,5 кН, причём сила тяги и сила ветра перпендикулярны друг другу. Каково ускорение катера?

Смотреть решение и ответ

2.6. На расстоянии r = 25 см от центра шероховатого диска покоится тело. Диск начали раскручивать, увеличивая его угловую скорость вращения. Чему равен коэффициент трения тела о диск, если тело начинает скользить по диску при угловой скорости ω = 4,5 рад/с?

Смотреть решение и ответ

Подготовка к ЕГЭ по физике. Задания высокого уровня сложности с развернутыми ответами. ЗАДАНИЕ № 29 (с решениями). Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.

Источник

Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.

Задание EF18920

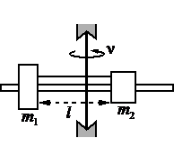
На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m₁ = 200 г и m₂ = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.

Алгоритм решения

1.Записать исходные данные. Перевести их в СИ.

2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.

3.Записать второй закон Ньютона в векторной форме для каждого из тел.

4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.

5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.

6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.

Решение

Запишем исходные данные, сразу переведя их в СИ:

• Масса первого груза m₁ = 200 г = 0,2 кг.

• Масса первого груза m₂ = 300 г = 0,3 кг.

• Длина нити l = 20 см = 0,2 м.

• Натяжение нити с обеих сторон одинаково, следовательно: T₁= T₂= T.

• Частота вращения штанги ν = 600 об./мин. = 10 об./с.

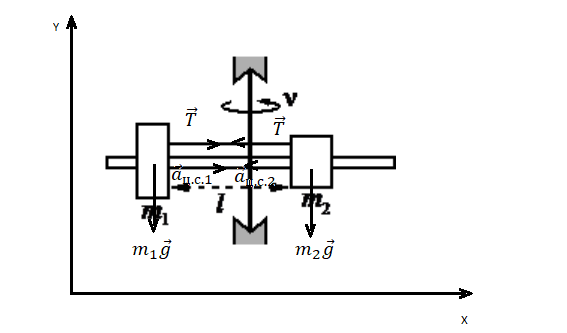
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.

Запишем второй закон Ньютона для первого и второго груза соответственно:

Запишем проекции на ось ОХ для каждого из тел:

T = m₁a_ц.с.1

T = m₂a_ц.с.2

Центростремительное ускорение также определяется формулой:

a_ц.с. = ω²R

Угловая скорость определяется формулой:

ω = 2πν

Следовательно, центростремительное ускорение равно:

a_ц.с. = 4π²ν²R

Применим эту формулу для обоих грузов:

a_ц.с.1 = 4π²ν²R₁

a_ц.с.2 = 4π²ν²R₂

Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:

R₁ + R₂ = l

Выразим радиус окружности, по которой вращается второй груз:

R₂ = l – R₁

Так как грузы связаны между собой, и ни один из них не перевешивает другой:

m₁gR₁ = m₂gR₂

Ускорение свободного падения взаимоуничтожается. Получаем:

Подставим радиус второй окружности и выразим радиус первой окружности:

Следовательно, центростремительное ускорение первого груза равно:

Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:

Подставим известные данные и вычислим силу натяжения нити:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18982

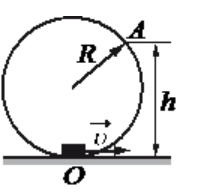
Небольшая шайба массой m=10 г, начав движение из нижней точки закреплённого вертикального гладкого кольца радиусом R=0,14 м, скользит по его внутренней поверхности. На высоте h=0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? Сделайте рисунок с указанием сил, действующих на шайбу в точке А.

Алгоритм решения

1.Записать исходные данные. Перевести единицы измерения величин в СИ.

2.Сделать чертеж и указать все силы, действующие на шайбу в точке А. Указать их направление и выбрать систему координат.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций на ось ОХ.

5.Записать формулу, определяющую кинетическую энергию тела.

6.Применить геометрические законы для нахождения величины радиуса кольца и формулу центростремительного ускорения для нахождения скорости тела.

7.Записать решение в общем виде, подставить исходные данные и произвести вычисления.

Решение

Запишем исходные данные:

• Масса шайбы m = 10 г = 0,01 кг.

• Радиус кольца, по которому перемещалась шайба, составляет R = 0,14 м.

• Высота, с которой шайба упала, равна h = 0,18 м.

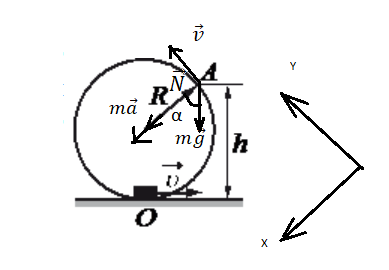
Сделаем чертеж. Выберем систему координат такую, чтобы направление линейной скорости шайбы в точке совпадала с направлением оси ОУ.

Запишем второй закон Ньютона в векторной форме:

Под ускорением в этой записи понимается полное ускорение, составляющими которого является центростремительное и тангенциальное ускорение, направленное касательно к окружности (на рисунке мы его не обозначили, так как оно нам не понадобится).

Запишем проекцию на ось ОХ. Учтем, что в точке А шайба отрывается от кольца и падает. Следовательно, нормальная реакции опоры равна нулю:

mg cosα = ma_ц.с.

Кинетическая энергия тела определяется формулой:

Выразим центростремительное ускорение из проекции на ось ОХ:

Но центростремительное ускорение также определяется формулой:

Приравняем правые части уравнений и получим:

Квадрат скорости будет равен:

Следовательно, кинетическая энергия равна:

Чтобы избавиться от неизвестных величин, обратимся к геометрии:

Из рисунка видно, что высота h есть сумма радиуса окружности и произведения радиуса на косинус угла α:

h = R + Rcosα

Отсюда следует, что:

Rcosα = h – R

Подставим это выражение в формулу кинетической энергии и выполним вычисления:

Отсюда следует, что кинетическая энергия шарика в начале движения равна 2 мДж.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18271

Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.

Алгоритм решения

1.Записать исходные данные и перевести их в СИ.

2.Записать формулу для определения КПД атомной электростанции.

3.Решить задачу в общем виде.

4.Подставить известные данные и вычислить искомую величину.

5.Массовое число: A = 235.

6.Зарядовое число: Z = 92.

Решение

Запишем исходные данные:

• Энергия, выделяемая при делении одного ядра урана-235: Q₀ = 200 МэВ.

• Масса урана-235: m = 1,4 кг.

• Время, в течение которого происходит деление: t = 1 неделя.

• Мощность атомной электростанции: N = 38 МВт.

Переведем все единицы измерения в СИ:

1 эВ = 1,6∙10^–19 Дж

200 МэВ = 200∙10⁶∙1,6∙10^–19 Дж = 320∙10^–13 Дж

1 неделя = 7∙24∙60∙60 с = 604,8∙10³с

38 МВт = 38∙10⁶ Вт

КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:

η=AполезнQ100%

Полезную работу мы можем вычислить по формуле:

A=Nt

Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.

Количество атомов равно произведению количество молей на постоянную Авогадро:

N_{кол.атомов} = νN_A

Количество молей равно отношения массы вещества к его молярной массе, следовательно:

Молярная масса численно равна массовому числу в граммах на моль. Следовательно:

M = A (г/моль) = A∙10^–3 (кг/моль)

Отсюда количество атомов равно:

Энергия, выделенная всеми атомами, равна:

Теперь можем вычислить КПД:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17562

С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.

Алгоритм решения

1.Записать исходные данные.

2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.

3.Выбрать нулевой уровень для определения потенциальной энергии.

4.Записать закон сохранения энергии.

5.Решить задачу в общем виде.

6.Подставить числовые значения и произвести вычисления.

Решение

Запишем исходные данные:

• Время падения стального шарика: t = 0,4 c.

• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.

• Угол наклона плиты: α = 30^о.

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p

Потенциальная энергия шарика в точке А равна:

E_pA = mgH

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

EpB=mgl1

Перед ударом кинетическая энергия шарика равна:

EkB=mv22

Согласно закону сохранения энергии:

EpA=EpB+EkB

mgH=mgl1+mv22

Отсюда высота H равна:

H=mgl1mg+mv22mg=l1+v22g

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h−l1=v2sin2β2g=v2sin2(90−2α)o2g

Отсюда:

l1=h−v2sin2(90−2α)o2g

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

v=gt

Следовательно:

H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g

H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)

H=1,4−10·0,422(sin2(90−60)o−1)

H=1,4−5·0,16(sin230o−1)

H=1,4−0,8((12)2−1)=1,4−0,8(14−1)

H=1,4+0,6=2 (м)

Ответ: 20

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18127

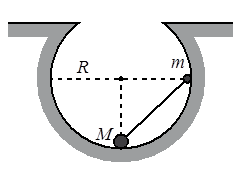
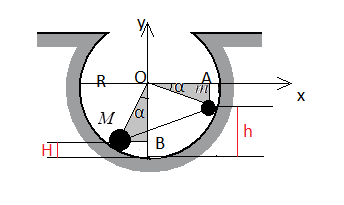
Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.

В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.

3.Записать закон сохранения энергии.

4.Выполнить общее решение задачи.

5.Подставить известные данные и выполнить вычисление искомой величины.

Решение

Запишем исходные величины:

• Масса первого шарика: m = 30 г.

• Масса второго шарика: M = 60 г.

• Максимальная высота подъема шарика М: H = 12 см.

Переведем единицы измерения величин в СИ:

30 г = 0,03 кг

60 г = 0,06 кг

12 см = 0,12 м

Выполним чертеж:

Нулевой уровень — нижняя точка выемки.

Запишем закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p= const

В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:

E_p0m= mgR

Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:

E_pm= mgh

E_pM= MgH

Поэтому закон сохранения энергии применительно к задаче примет вид:

mgR = mgh + MgH

Преобразуем выражение и получим:

mgR−mgh=MgH

R−h=MgHmg=MHm

При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:

MB = mA = R – h

OA = OB = R – H

OM = Om = R

Это дает нам право воспользоваться теоремой Пифагора:

(R−h)2=R2−OA2=R2−(R−H)2

Следовательно:

(R−h)2=R2−(R2−2RH+H2)=2RH−H2

Подставим в это выражение правую часть ранее полученного выражения:

R−h=MHm

(MHm)2=2RH−H2

Теперь можем выразить и вычислить радиус:

2RH=(MHm)2+H2

R=(MHm)2+H22H

R=(Mm)2H2+H2=(0,060,03)20,122+0,122=0,3 (м)

Ответ: 0,3

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18057

На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ₁ = 400 кг/м³ и ρ₂ = 2ρ₁, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?

Алгоритм решения

1.Записать исходные данные.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в проекции на ось ординат.

5.Выполнить общее решение.

6.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

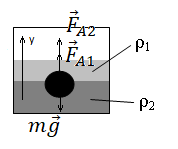
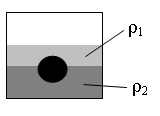
• Плотность первой жидкости: ρ₁ = 400 кг/м³.

• Плотность второй жидкости: ρ₂ = 2ρ₁.

• Объем шарика выше границы раздела двух жидкостей: V₁ = V/4.

• Объем шарика выше границы раздела двух жидкостей: V₂ = 3V/4.

Построим рисунок и укажем все силы, действующие на шарик:

Запишем второй закон Ньютона в векторном виде:

m→g+→FA1+→FA2=0

Запишем второй закон Ньютона в виде проекции на ось ординат:

mg=FA1+FA2

Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:

ρVg=ρ1gV1+ρ2gV2

Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:

ρV=ρ1V4+2ρ13V4

Объемы сокращаются. Остается:

ρ=ρ14+2ρ134=7ρ14=7·4004=700 (кгм3)

Ответ: 700

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17513

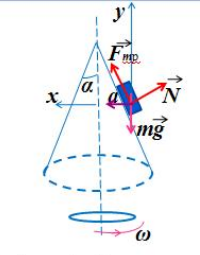
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.

Алгоритм решения

1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.

2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.

3.Записать второй закон Ньютона в виде проекций на оси.

4.Через систему уравнений вывести искомую величину.

Решение

Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.

Второй закон Ньютона в векторном виде выглядит следующим образом:

Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:

Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:

Максимальное значение силы трения равно:

Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:

Запишем систему уравнение в следующем виде:

Поделим первое уравнение на второе и получим:

Сделаем сокращения и получим:

Отсюда центростремительное ускорение равно:

Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:

Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:

Отсюда центростремительное ускорение равно:

Выразим искомую величину L:

Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:

Поделим числитель на синус угла α, чтобы упростить выражение, и получим:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

26 октября 2015

В закладки

Обсудить

Жалоба

Задачи по физике повышенной сложности

Задания по 4 разделам: механика, молекулярная физика, электростатика, электродинамика.

Часть заданий с подробными решениями, остальные с ответами.

Автор: Гойхман Григорий Семёнович.

4fizika.rar

Физика ЕГЭ 2020. Подробный разбор заданий повышенного и высокого уровня сложности для отработки навыков выполнения самых сложных заданий ЕГЭ по физике, правильное решение которых практически гарантирует высокий результат на экзамене. Даётся методика решения задач высокого уровня сложности, обращается внимание на особенности оформления решений.

Часть 2 варианта ЕГЭ по физике содержит 8 заданий, объединённых общим видом деятельности — решением задач, из них 3 задания с кратким ответом и 5 заданий, для которых необходимо привести развёрнутый ответ. Среди этих пяти заданий есть одно качественное задание повышенного уровня сложности и 4 расчётных задания высокого уровня сложности.

Качественные задания направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. Четыре последних задания части 2 (29-32) являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в изменённой или новой ситуации. Выполнение таких заданий требует применения знаний сразу из нескольких разделов физики.

Разбор самых сложных заданий:

Задание № 28. Механика, квантовая физика (качественная задача).

Задание № 29. Механика (расчётная задача)

Задание № 30. Молекулярная физика (расчётная задача).

Задание № 31. Электродинамика (расчётная задача)

Задание № 32. Электродинамика, квантовая физика (расчётная задача).

При подготовке к решению качественных задач №28 прежде всего следует обратить особое внимание на то, что эти задания оцениваются по шкале от 0 до 3 баллов. Учащемуся следует тщательно изучить требования к развёрнутому ответу.

Критерии оценивания выполнения задания № 28

Критерии	Баллы
Приведено полное решение, включающее следующие элементы: Приведено полное правильное решение, включающее правильный ответ и исчерпывающие верные рассуждения с прямым указанием наблюдаемых явлений и законов	3
Дан правильный ответ и приведено объяснение, но в решении имеются один или несколько из следующих недостатков. В объяснении не указано или не используется одно из физических явлений, свойств, определений или один из законов (формул), необходимых для полного верного объяснения. (Утверждение, лежащее в основе объяснения, не подкреплено соответствующим законом, свойством, явлением, определением и т.п.). И (ИЛИ) Указаны все необходимые для объяснения явления и законы, закономерности, но в них содержится один логический недочёт. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.). И (ИЛИ) В решении имеется неточность в указании на одно из физических явлений, свойств, определений, законов (формул), необходимых для полного верного объяснения	2
Представлено решение, соответствующее одному из следующих случаев. Дан правильный ответ на вопрос задания и приведено объяснение, но в нём не указаны два явления или физических закона, необходимых для полного верного объяснения. ИЛИ Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся рассуждения, направленные на получение ответа на вопрос задания, не доведены до конца. ИЛИ Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся рассуждения, приводящие к ответу, содержат ошибки. ИЛИ Указаны не все необходимые для объяснения явления и законы, закономерности, но имеются верные рассуждения, направленные на решение задачи	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла	0
Максимальный балл	3

Надо внимательно вчитаться в условие задания и тщательно прочитать вопрос к нему.

Критерии оценивания выполнения заданий №№ 29-32

Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.

При ручной проверке этих задач по критериям оценивания ФИПИ 3 балла выставляются в следующем случае: Приведено полное решение, включающее следующие элементы:

записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае перечисляются законы и формулы). В качестве исходных принимаются формулы, указанные в кодификаторе элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по физике.;
описаны все вновь вводимые в решение буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов). Стандартными считаются обозначения физических величин, принятые в кодификаторе элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по физике;
проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
представлен правильный ответ с указанием единиц измерения искомой величины.

Очень важно обратить внимание на эти примечания:

Критерии	Баллы
Приведено полное решение, включающее следующие элементы: 1) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; 2) описаны все вновь вводимые в решение буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); 3) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); 4) представлен правильный ответ с указанием единиц измерения искомой величины	3
Правильно записаны все необходимые положения теории, физические законы, закономерности и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту 2, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т.п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт 4, или в нём допущена ошибка (в том числе в записи единиц измерения величины)	2
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла	0
Максимальный балл	3

Материалы для подготовки к ЕГЭ по физике. Подробный разбор заданий повышенного и высокого уровня сложности для отработки навыков выполнения самых сложных заданий ЕГЭ по физике, правильное решение которых практически гарантирует высокий результат на экзамене. Даётся методика решения задач высокого уровня сложности, обращается внимание на особенности оформления решений.

Главная » ЕГЭ » Физика. Задания высокой и повышенной сложности — Лях В.В.

Перед вами пособие по решению задач высокой и повышенной сложности в формате ЕГЭ по физике. Это не просто сборник интересных и сложных задач. Книга-репетитор, книга путеводитель от школьной «четверки» до 100 баллов — вот что это такое. Здесь есть все: необходимая и достаточная теория, справочные материалы, тесты, репетиторские хитрости, секреты и рекомендации. И конечно, сами задачи — с решениями и образцовым оформлением. Ориентиром по уровню сложности задач в книге послужили задания части 2 ЕГЭ. Пособие предназначено для абитуриентов, учителей и репетиторов.

Рубрика: ЕГЭ / ЕГЭ по Физике
Автор: Лях В.В.
Год: 2020
Для учеников: 11 класс
Язык учебника: Русский
Формат: PDF
Страниц: 200

ЕГЭ 2020, Физика, Задания высокой и повышенной сложности, Лях В.В.

Перед вами пособие по решению задач высокой и повышенной сложности в формате ЕГЭ по физике. Это не просто сборник интересных и сложных задач. Книга-репетитор, книга- путеводитель от школьной «четверки» до 100 баллов — вот что это такое. Здесь есть все: необходимая и достаточная теория, справочные материалы, тесты, репетиторские хитрости, секреты и рекомендации. И конечно, сами задачи — с решениями и образцовым оформлением. Ориентиром по уровню сложности задач в книге послужили задания части 2 ЕГЭ. Пособие предназначено для абитуриентов, учителей и репетиторов.

Как пользоваться книгой.
Для получения большей пользы от изучения книги очень советую сначала внимательно изучить теорию, а затем разобраться с приведенными в параграфе задачами, после чего постараться решить их самостоятельно, не подсматривая в решение, и только потом переходить к самостоятельным работам. Задачи в самостоятельных работах подобраны для закрепления теоретического материала и подготовки к решению сложных задач из контрольных работ. В конце книги, перед итоговой контрольной работой, приведены все задачи, которые разбирались в тексте книги. Очень советую перерешать их перед итоговой контрольной работой и за пару недель до экзамена, чтобы еще раз повторить весь материал.

Оглавление.
От автора.
Как пользоваться книгой.
Рекомендации по решению задач.
Раздел 1.Механика.
Глава 1.Кинематика.
Глава 2.Динамика.
Глава 3.Статика.
Глава 4.Импульс. Работа. Энергия.
Глава 5.Гидростатика.
Раздел 2.МКТ. Газовые законы. Термодинамика.
Глава 1.МКТ.
Глава 2.Газовые законы.
Глава 3.Термодинамика.
Глава 4.Влажность. Насыщенный пар.
Раздел 3.Электродинамика.
Глава 1.Электростатика.
Глава 2.Законы постоянного тока.
Глава 3.Магнитное поле.
Раздел 4.Колебания и волны. Оптика.
Глава 1.Механические колебания.
Глава 2.Электромагнитные колебания.
Глава 3.Геометрическая оптика.
Глава 4.Волны.
Раздел 5.Квантовая физика.
Задачи на повторение.
Итоговая контрольная работа.
Приложения.
Ответы к самостоятельным и контрольным работам.
Литература.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу ЕГЭ 2020, Физика, Задания высокой и повышенной сложности, Лях В.В. — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— pdf — Яндекс.Диск.

Дата публикации: 24.12.2019 06:41 UTC

Теги:

Лях :: подготовка к ЕГЭ :: ЕГЭ по физике :: задачи по физике :: физика :: 2020 :: 11 класс

Следующие учебники и книги:

ЕГЭ 2020, Физика, Сборник заданий, 600 заданий с ответами, Ханнанов Н.К., Никифоров Г.Г., Орлов В.А., 2019
ЕГЭ 2020, тренажёр, физика, Лукашева Е.В., Чистякова Н.И., 2020
ЕГЭ, Высший балл, Физика, Задания высокой и повышенной сложности, Лях В.В., 2020
ЕГЭ 2020, банк заданий, физика, 1000 задач, все задания частей 1 и 2, Демидова М.Ю., 2020

Предыдущие статьи:

ЕГЭ 2020, 100 баллов, Физика, Практическое руководство, Никулова Г.А., Москалев А.Н.
ЕГЭ 2020, Физика, 32 варианта, Типовые варианты экзаменационных заданий, Лукашева Е.В., Чистякова Н.И.
ЕГЭ 2020, Физика, Эксперт в ЕГЭ, Громцева О.И., Бобошина С.Б.
ЕГЭ 2020, Физика, 14 вариантов, Типовые варианты экзаменационных заданий, Демидова М.Ю., Грибов В.А., Гиголо А.И.

Скачать материал

Сейчас обучается 140 человек из 50 регионов

Сейчас обучается 63 человека из 37 регионов

Описание презентации по отдельным слайдам:

1 слайд

«РЕШЕНИЕ задач повышенной трудности егэ ПО ФИЗИКЕ»

Алисова Любовь Анатольевна
МБОУ «Обоянская СОШ №2»
учитель физики
без квалификационной категории
2 слайд

Цели урока:

— формирование умений и навыков решения вычислительных задач повышенной трудности и умений обосновывать свой вариант решения;

— развитие у школьников теоретического, творческого мышления, формирование операционного мышления, направленного на выбор оптимальных решений;

— систематизация практических умений, необходимых для успешной сдачи ЕГЭ по физике.
3 слайд

Задание №29 относится к высокому уровню сложности.

Тематика этого номера – механика.

Задача требует полного оформления:
Запись «Дано».
Перевод единиц измерения в систему «СИ».
Необходимый чертеж или рисунок.
Построение и описание физической модели.
Запись всех необходимых для решения задачи законов и формул.
Проведение математических преобразований и расчётов.
Получение ответа.

При выполнении всех указанных требований задача оценивается тремя баллами.
4 слайд

Два небольших шара массами 0,2 кг и 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рисунок). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень – шары».
5 слайд

Укажем все силы,
действующие на систему тел «стержень – шары» (см. рисунок).
6 слайд

Запишем условия равновесия с учетом равенства нулю геометрической суммы сил и алгебраической суммы моментов сил.
7 слайд

Это уравнение в проекциях на ось OY будет иметь вид:
8 слайд

C учетом 𝑁 2 𝑁 1 = 2, запишем:
9 слайд

Для моментов сил относительно точки А справедливо соотношение:

Здесь учтено, что плечо силы относительно точки А равно нулю, соответственно, момент силы также равен нулю.
11 слайд

Проведем промежуточный расчет силы 𝑁 1
13 слайд

Из уравнения (3) выразим искомую величину – длину стержня L.
14 слайд

Подставим численные значения и проведем расчет длины стержня.
15 слайд

Таким образом, ответ в данной задаче 1м.

Секрет решения. В этой задаче требуется глубокое понимание и умение применять условия равновесия твердого тела (системы тел). Еще раз надо обратить внимание на понятие плеча силы – кратчайшего расстояния от линии действия силы до выбранной точки. При записи алгебраической суммы моментов сил надо правильно расставить знаки «+» или «-», в зависимости от того, куда стремится повернуть сила твердое тело: по часовой или против часовой стрелки.
Общепринято считать момент силы положительным, если сила стремится повернуть тело против часовой стрелки относительно выбранной точки и наоборот.
16 слайд

В этой задаче правило моментов записывалось относительно точки А, но в тоже время, можно было его записать и относительно точек С и D.
Это зависит от того, какие физические величины известны по условию, сколько неизвестных величин в полученных уравнениях. Прежде чем тратить силы и время на решение системы уравнений, надо убедиться, что число неизвестных равно числу независимых уравнений.
Тогда остается только выбрать наиболее рациональный метод решения системы уравнений.

phys-ege.sdamgia.ru
17 слайд

Задание №30. Это задание также относится к высокому уровню сложности.
Как правило, тематика этого задания «МКТ» и «Термодинамика».
Какие-то задачи требуют только формульного решения, какие-то необходимо сопровождать графическими пояснениями термодинамических процессов.
В любом случае, теоретический материал полностью соответствует кодификатору элементов содержания и спецификации контрольных измерительных материалов.
18 слайд

В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол
при температуре кипения

При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень.

Удельная теплота парообразования бензола

его молярная масса

Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы?

Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.
19 слайд

Запишем первый закон термодинамики для изобарного процесса:
20 слайд

Выразим из этого равенства изменение внутренней энергии
21 слайд

Работу газа в изобарном процессе можно рассчитать по формуле:
22 слайд

с учетом уравнения Менделеева-Клапейрона получим:
23 слайд

При совершении работы давление бензола не изменяется, так как поршень в цилиндре легкоподвижный. Давление бензола все время остается равным атмосферному.

При этом
— это масса бензола, превратившегося в газообразное состояние.
24 слайд

Количество теплоты, которое идет на превращение бензола в это состояние можно рассчитать по формуле:
25 слайд

Выражение для работы бензола (2) и количества теплоты (3) подставим в уравнение
26 слайд

После сокращения на получим искомую формулу:
27 слайд

Подставим численные значения и проведем расчет
28 слайд

Секрет решения. На первый взгляд задача кажется несложной, но в ней «спрятаны» несколько искусственных приемов, до которых додуматься достаточно сложно.

Первый прием – выражение

Это математический ход, который сразу подсказывает, что конкретно надо находить в этой задаче.

phys-ege.sdamgia.ru
29 слайд

Второй прием – получение равенства, используя уравнения Менделеева-Клапейрона

Здесь надо придерживаться следующих рассуждений: если в левой части уравнения есть переменная величина (в этой задаче ), то и в правой части должна изменяться какая-то физическая величина (в этой задаче ).
Можно сказать еще проще: если в левой части равенства есть знак дельта » «, то и в правой части он должен обязательно появиться.
30 слайд

В крайнем случае, можно «перебрать» все величины из правой части: температура не может изменяться, так как при парообразовании она всегда постоянна; молярная масса также неизменна, потому что речь идет об одном и том же газе; R – табличная величина.

Остается только

Эти рассуждения помогут понять ситуацию, описанную в задаче и правильно ее решить.

phys-ege.sdamgia.ru
31 слайд

В цепи, изображённой на рисунке, сопротивление диода
в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением, потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась
равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.
32 слайд

Если при подключении батареи потенциал точки А оказывается выше, чем потенциал точки В, то ток через диод не течёт, и эквивалентная схема цепи имеет вид, изображённый на рис. 1. Потребляемую мощность можно рассчитать по формуле:
33 слайд

При изменении полярности подключения батареи диод открывается и подключает резистор параллельно резистору Эквивалентная схема цепи в этом случае изображена на рис.2

При этом потребляемая мощность увеличивается:
Эта формула для расчета мощности с учетом того, что резисторы R_{1} и R_{2} во втором случае соединены параллельно. Общая мощность, выделяемая в цепи, равна сумме мощностей на каждом из резисторов.
34 слайд

Выразим из формулы (2) сопротивление резистора 𝑅 1

Подставим численные значения и проведем расчет.
35 слайд

Список источников основного содержания:

phys-ege.sdamgia.ru
36 слайд

Список иллюстраций:

images.yandex.ru

phys-ege.sdamgia.ru

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 726 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

15.04.2021
200
4

15.04.2021
202
0

15.04.2021
365
4

15.04.2021
362
10

14.04.2021
109
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
Курс повышения квалификации «Экономика: инструменты контроллинга»
Курс повышения квалификации «Страхование и актуарные расчеты»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс повышения квалификации «Методы и инструменты современного моделирования»
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
Курс профессиональной переподготовки «Управление качеством»
Курс профессиональной переподготовки «Стандартизация и метрология»

Укажите регион, чтобы мы точнее рассчитали условия доставки

Начните вводить название города, страны, индекс, а мы подскажем

Например:
Москва,
Санкт-Петербург,
Новосибирск,
Екатеринбург,
Нижний Новгород,
Краснодар,
Челябинск,
Кемерово,
Тюмень,
Красноярск,
Казань,
Пермь,
Ростов-на-Дону,
Самара,
Омск

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д29 C2 № 2950

Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время а такой же последний  — за время Найдите полное время падения тела t, если его начальная скорость равна нулю.

Задания Д29 C2 № 2951

Тело, свободно падающее с некоторой высоты из состояния покоя, за время после начала движения проходит путь в n=5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

Задания Д29 C2 № 2953

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Задания Д29 C2 № 3070

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью под углом к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 1.

Пройти тестирование по этим заданиям

Источник

Статьи

Среднее общее образование

Физика

Предлагаем вашему вниманию разбор 29 задания ЕГЭ-2018 по физике. Мы подготовили пояснения и подробный алгоритм решения, а также рекомендации по использованию справочников и пособий, которые могут понадобиться при подготовке к ЕГЭ.

20 марта 2018

Задание 29

Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см². В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T.

Решение


Рис. 1		Рис. 2

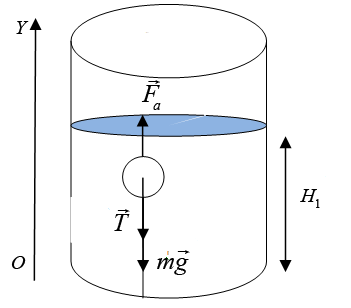
Первоначально деревянный шар привязан нитью ко дну цилиндрического сосуда площадью дна S = 100 см² = 0,01 м² и полностью погружен в воду. На шар действуют три силы: сила тяжести со стороны Земли, – сила Архимеда со стороны жидкости, – сила натяжения нити, результат взаимодействия шара и нити. По условию равновесия шара в первом случае геометрическая сумма всех действующих на шарик сил, должна быть равна нулю:

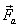
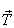
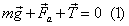
ЕГЭ-2018. Физика. Сдаем без проблем!

В книге содержатся материалы для успешной сдачи ЕГЭ по физике: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену. Издание содержит задания разных типов по всем темам, проверяемым на ЕГЭ по физике, а также решение задач повышенного уровня сложности.

Купить

Выберем координатную ось OY и направим ее вверх. Тогда с учетом проекции уравнение (1) запишем:

F_a₁ = T + mg (2).

Распишем силу Архимеда:

F_a₁ = ρ · V₁g (3),

где V₁ – объем части шара погруженной в воду, в первом это объем всего шара, m – масса шара , ρ – плотность воды. Условие равновесия во втором случае

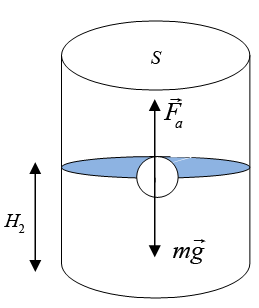
F_a₂ = mg (4)

Распишем силу Архимеда в этом случае:

F_a₂ = ρ · V₂g (5),

где V₂ – объем части шара, погруженной в жидкость во втором случае.

Поработаем с уравнениями (2) и (4) . Можно использовать метод подстановки или вычесть из (2) – (4), тогда F_a₁ – F_a₂ = T, используя формулы (3) и (5) получим ρ · V₁g – ρ · V₂g = T;

ρg (V₁ – V₂) = T (6)

Учитывая, что

V₁ – V₂ = S ·h (7),

где h = H₁ – H₂; получим

T = ρ · g · S · h (8)

Подставим числовые значения

T = 1000	кг	· 10	м	· 5 · 10^–2 м = 5 Н
м³	с²

Ответ: 5 Н.

ЕГЭ-2018. Физика. 30 тренировочных вариантов экзаменационных работ

Издание содержит:
• 30 тренировочных вариантов ЕГЭ
• инструкцию по выполнению и критерии оценивания
• ответы ко всем заданиям
Тренировочные варианты помогут учителю организовать подготовку к ЕГЭ, а учащимся – самостоятельно проверить свои знания и готовность к сдаче выпускного экзамена.

Купить

Источник

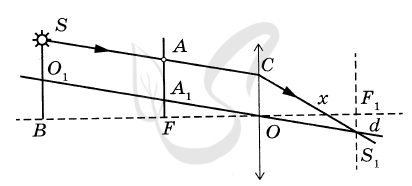
15977. Главная оптическая ось тонкой собирающей линзы с оптической силой D = 5 дптр и точечный источник света S находятся в плоскости рисунка. Точка S находится на расстоянии b = 70 см от плоскости линзы и на расстоянии H = 10 см от её главной оптической оси. В левой фокальной плоскости линзы лежит тонкий непрозрачный экран с маленьким отверстием A, находящимся в плоскости рисунка на расстоянии h от главной оптической оси линзы. Определите расстояние h, если известно, что луч SA от точечного источника, пройдя через отверстие в экране и линзу, пересечёт её главную оптическую ось на расстоянии x = 18 см от плоскости линзы. Дифракцией света пренебречь. Постройте рисунок, показывающий ход луча через линзу.

1. Известно, что оптическая сила линзы D связана с её фокусным расстоянием F: ( F = frac{1}{D} = frac{1}{5} = 0,2 ) м = 20 см.

2. Построим ход луча SACS₁, прошедшего через экран и собирающую линзу, используя основные свойства тонкой линзы: параллельный пучок лучей, падающих на линзу, собирается в её фокальной плоскости; луч O₁OS₁, прошедший через оптический центр линзы (точку O), не преломляется.

3. Луч SAC, принадлежащий параллельному пучку лучей SA и O₁A₁, после преломления пересечёт луч O₁OS₁ в фокальной плоскости линзы в точке S₁ на расстоянии d от главной оптической оси BO. Так как расстояние от фокальных плоскостей AF и S₁F₁, до плоскости линзы одинаково, то A₁F = F₁S₁ = d, OC = AA₁ = O₁S = h — d, O₁B = H — (h — d).

4. Луч CS₁ пересечёт главную оптическую ось на расстоянии x от линзы, которое определяется из подобия треугольников ΔOCx и ΔxF₁S₁. Из пропорции ( frac{x}{{h — d}} = frac{{F — x}}{d} ) получаем: ( x = Fleft( {1 — frac{d}{h}} right) ).

Для определения d воспользуемся подобием треугольников ΔO₁BO и ΔA₁FO и составим пропорцию ( frac{{H — left( {h — d} right)}}{b} = frac{d}{F} ), откуда: ( d = frac{{H — h}}{{b — F}}F ). После подстановки получаем:

( h = frac{{{F^2}H}}{{Fleft( {b + x} right) — bx}} = frac{{{{20}^2} cdot 10}}{{20 cdot (70 + 18) — 70 cdot 18}} ) = 8 см.

Ответ: h = 8 см.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15977.

15947. Главная оптическая ось тонкой собирающей линзы с фокусным расстоянием F = 20 см и точечный источник света S находятся в плоскости рисунка. Точка S находится на расстоянии b = 70 см от плоскости линзы и на расстоянии H = 5 см от её главной оптической оси. В левой фокальной плоскости линзы лежит тонкий непрозрачный экран с маленьким отверстием A, находящимся в плоскости рисунка на расстоянии h = 4 см от главной оптической оси линзы. На каком расстоянии x от плоскости линзы луч SA от точечного источника, пройдя через отверстие в экране и линзу, пересечёт её главную оптическую ось? Дифракцией света пренебречь. Постройте рисунок, показывающий ход луча через линзу.

1. Построим ход луча SACS₁, прошедшего через экран и собирающую линзу, используя основные свойства тонкой линзы: параллельный пучок лучей, падающих на линзу, собирается в её фокальной плоскости; луч O₁OS₁, прошедший через оптический центр линзы (точку O), не преломляется.

2. Луч SAC, принадлежащий параллельному пучку лучей SA и O₁A₁, после преломления пересечёт луч O₁OS₁ в фокальной плоскости линзы в точке S₁ на расстоянии d от главной оптической оси BO. Так как расстояние от фокальных плоскостей AF и S₁F₁, до плоскости линзы одинаково, то A₁F = F₁S₁ = d, OC = AA₁ = O₁S = h — d, O₁B = H — (h — d).

3. Луч CS₁ пересечёт главную оптическую ось на расстоянии x от линзы, которое определяется из подобия треугольников ΔOCx и ΔxF₁S₁. Из пропорции ( frac{x}{{h — d}} = frac{{F — x}}{d} ) получаем: ( x = Fleft( {1 — frac{d}{h}} right) ).

( x = frac{F}{h}frac{{bh — FH}}{{b — F}} = frac{{20}}{4} cdot 3,6 = ) 18 см.

Ответ: x = 18 см.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15947.

15917. В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности радиуса r = 8 см с частотой v = 30 об/мин движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе.

1. Построим изображение источника света в линзе. Изображением светящейся точки A в некоторый момент времени будет точка A₁ Введём обозначения: радиус окружности по которой движется источник света, r = AB; радиус окружности, по которой движется изображение источника света, R = A₁B₁; расстояние OB = d; расстояние OB₁ = ( f ); фокусное расстояние линзы OF = F.

2. Из формулы тонкой линзы ( frac{1}{F} = frac{1}{d} + frac{1}{f} ) при ( d = frac{{3F}}{2} ) получим: ( f = 3F ).

3. Из подобия треугольников AOB и A₁OB₁, следует, что: ( frac{d}{f} = frac{r}{R} = frac{1}{2} Rightarrow R = 2r ).

4. Угловая скорость источника света равна угловой скорости его изображения: ( omega = 2pi nu ), т.к. в любой момент времени источник света и его изображение лежат в одной плоскости с главной оптической осью линзы.

5. Тогда скорость движения изображения точечного источника света:

( upsilon ‘ = omega R = 2pi nu cdot 2r = 2 cdot 3,14 cdot 0,5 cdot 2 cdot 0,08 ) ≈ 0,5 м/с.

Ответ: ( {upsilon ‘} ) = 0,5 м/с.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15917.

15887. В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью υ = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе.

1. Построим изображение источника света в линзе. Изображением светящейся точки A в некоторый момент времени будет точка A₁. Введём обозначения: радиус окружности по которой движется источник света, r = AB; радиус окружности, по которой движется изображение источника света, R = A₁B₁; расстояние OB = d; расстояние OB₁ = ( f ); фокусное расстояние линзы OF = F.

2. Из формулы тонкой линзы ( frac{1}{F} = frac{1}{d} + frac{1}{f} ) при ( d = frac{{3F}}{2} ) получим: ( f = 3F ).

3. Из подобия треугольников AOB и A₁OB₁, следует, что: ( frac{d}{f} = frac{r}{R} = frac{1}{2} ).

4. Угловая скорость источника света равна угловой скорости его изображения: ( omega = frac{upsilon }{r} ), т.к. в любой момент времени источник света и его изображение лежат в одной плоскости с главной оптической осью линзы.

5. Тогда скорость движения изображения точечного источника света:
( upsilon ‘ = omega R = frac{{upsilon R}}{r} = 2upsilon = 2 cdot 5 = 10 ) м/с.

Ответ: ( {upsilon ‘} ) = 10 м/с.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15887.

15857. В дно водоёма глубиной 3 м вертикально вбита свая высотой 2,5 м, целиком скрытая под водой. Угол падения солнечных лучей на поверхность воды равен 30°. Какой длины тень отбрасывает свая на дно водоёма? Постройте ход лучей, определяющих тень от сваи на дне. Показатель преломления воды n = 4/3.

Согласно рисунку длина тени ( L ) определяется высотой сваи ( h ) и углом ( gamma ) между сваей и скользящим по её вершине лучом света: ( L = h cdot tggamma ). Этот угол ( gamma ) является и углом преломления солнечных лучей на поверхности воды.

Согласно закону преломления ( frac{{sin alpha }}{{sin gamma }} = n ), ( sin gamma = frac{{sin alpha }}{n} = frac{1}{{2n}} ), ( tggamma = frac{{sin gamma }}{{sqrt {1 — {{sin }^2}gamma } }} = frac{1}{{sqrt {4{n^2} — 1} }} ).

Следовательно, ( L = frac{h}{{sqrt {4{n^2} — 1} }} = frac{{2,5}}{{sqrt {4 cdot {{left( {frac{4}{3}} right)}^2} — 1} }} ) ≈ 1 м.

Ответ: L ≈ 1 м.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15857.

15827. В дно водоёма глубиной 3 м вертикально вбита свая, целиком скрытая под водой. Угол падения солнечных лучей на поверхность воды равен 30°. Свая отбрасывает на дно водоёма тень длиной 0,75 м. Постройте ход лучей, определяющих тень от сваи на дне, и определите высоту сваи. Показатель преломления воды n = 4/3.

Следовательно, ( h = Lsqrt {4{n^2} — 1} = 0,75sqrt {4frac{{16}}{9} — 1} ) ≈ 1,85 м.

Ответ: h ≈ 1,85 м.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15827.

15797. Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит дальше от центра линзы, чем вершина острого угла A. Расстояние от центра линзы до точки А равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Длину х горизонтального катета ( A’C’ ) изображения находим по формуле линзы:

( frac{1}{{2F + a}} + frac{1}{{2F — x}} = frac{1}{F} ), откуда ( x = frac{{aF}}{{F + a}} = frac{a}{{1 + aD}} )

Длину ( y ) вертикального катета ( B’C’ ) изображения находим из подобия:

( y = a cdot frac{{2F — x}}{{2F + a}} = frac{{aF}}{{F + a}} = frac{a}{{1 + aD}} = x )

Площадь изображения

( {S_1} = frac{1}{2}A’C’ cdot B’C’ )( = frac{{{a^2}}}{{2{{left( {1 + aD} right)}^2}}} = frac{{{{0,04}^2}}}{{2{{left( {1 + 0,04 cdot 2,5} right)}^2}}} ) ≈ 6,6 см²

Ответ: S₁ ≈ 6,6 см²

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15797.

15767. Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки А равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Длину х горизонтального катета ( A’C’ ) изображения находим по формуле линзы:

( frac{1}{{2F — a}} + frac{1}{{2F + x}} = frac{1}{F} ), откуда ( x = frac{{aF}}{{F — a}} = frac{a}{{1 — aD}} )

Длину ( y ) вертикального катета ( B’C’ ) изображения находим из подобия:

( y = a cdot frac{{2F + x}}{{2F — a}} = frac{{aF}}{{F — a}} = frac{a}{{1 — aD}} = x )

Площадь изображения

( {S_1} = frac{1}{2}A’C’ cdot B’C’ = )( frac{{{a^2}}}{{2{{left( {1 — aD} right)}^2}}} = frac{{{{0,04}^2}}}{{2{{left( {1 — 0,04 cdot 2,5} right)}^2}}} ) ≈ 9,9 см²

Ответ: S₁ ≈ 9,9 см²

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15767.

15737. Фотоэлектроны, выбитые монохроматическим светом частотой ν ≈ 7,4 ⋅ 10¹⁴ Гц из металла с работой выхода A_вых = 2,4 эВ, попадают в однородное электрическое поле Е = 250 В/м. Какова длина тормозного пути у фотоэлектронов, чья начальная скорость максимальна и направлена вдоль линий напряжённости поля ( {vec E} )?

Уравнение Эйнштейна для фотоэффекта:

( hnu = {A_{вых}} + frac{{mupsilon _{max }^2}}{2} ) (1)

Фотоэлектроны, влетевшие в электрическое поле ( {vec E} ), будут тормозиться им и, пройдя тормозной путь d, остановятся, затем начнут двигаться обратно.

Закон сохранения энергии для вылетевшего фотоэлектрона: ( frac{{mupsilon _{max }^2}}{2} — e{varphi _1} = — e{varphi _2} ), откуда с учётом ( {varphi _2} — {varphi _1} = — U < 0 ) получаем:

( frac{{mupsilon _{max }^2}}{2} = eU = eEd ), (2)

где e — модуль заряда электрона.

Объединяя (1) и (2), имеем:

( d = frac{{hnu — {A_{вых}}}}{{eE}} = )( frac{{6,6 cdot {{10}^{ — 34}} cdot 7,4 cdot {{10}^{14}} — 2,4 cdot 1,6 cdot {{10}^{ — 19}}}}{{1,6 cdot {{10}^{ — 19}} cdot 250}} ) ≈ 2,6 ⋅ 10^-3 м = 2,6 мм

Ответ: d ≈ 2,6 мм

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15737.

15707. Фотоэлектроны, выбитые монохроматическим светом из металла с работой выхода A_вых = 1,89 эВ, попадают в однородное электрическое поле E = 100 В/м. Какова частота света ν, если длина тормозного пути у фотоэлектронов, чья начальная скорость максимальна и направлена вдоль линий напряжённости поля, составляет d = 8,7 мм?

Уравнение Эйнштейна для фотоэффекта:

( hnu = {A_{вых}} + frac{{mupsilon _{max }^2}}{2} ) (1)

( frac{{mupsilon _{max }^2}}{2} = eU = eEd ), (2)

где e — модуль заряда электрона.

Объединяя (1) и (2), имеем:

( nu = frac{{{A_{вых}} + eEd}}{h} = )( frac{{1,89 cdot 1,6 cdot {{10}^{ — 19}} + 1,6 cdot {{10}^{ — 19}} cdot 100 cdot 8,7 cdot {{10}^{ — 3}}}}{{6,6 cdot {{10}^{ — 34}}}} ) ≈ 6,7 ⋅ 10¹⁴ Гц

Ответ: ν ≈ 6,7 ⋅ 10¹⁴ Гц

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15707.

Для вас приятно генерировать тесты, создавайте их почаще

Источник