ЕГЭ Профиль №3. Квадрат, прямоугольник, параллелограмм, ромб
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Квадрат, прямоугольник, параллелограмм, ромб
| Задача 1. В параллелограмме ABCD (AB = 3,;;AD = 21,;;sin A = frac{6}{7}.) Найдите большую высоту параллелограмма.
Ответ
ОТВЕТ: 18. |
| Задача 2. Найдите площадь квадрата, если его диагональ равна 1.
Ответ
ОТВЕТ: 0,5. |
| Задача 3. Найдите диагональ квадрата, если его площадь равна 2.
Ответ
ОТВЕТ: 2. |
| Задача 4. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Ответ
ОТВЕТ: 18. |
| Задача 5. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Ответ
ОТВЕТ: 6. |
| Задача 6. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Ответ
ОТВЕТ: 18. |
| Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Ответ
ОТВЕТ: 18. |
| Задача 8. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Ответ
ОТВЕТ: 14. |
| Задача 9. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Ответ
ОТВЕТ: 48. |
| Задача 10. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
Ответ
ОТВЕТ: 13. |
| Задача 11. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
Ответ
ОТВЕТ: 48. |
| Задача 12. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Ответ
ОТВЕТ: 2. |
| Задача 13. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Ответ
ОТВЕТ: 30. |
| Задача 14. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Ответ
ОТВЕТ: 6. |
| Задача 15. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Ответ
ОТВЕТ: 8. |
| Задача 16. Найдите площадь ромба, если его высота равна 2, а острый угол ({30^ circ }).
Ответ
ОТВЕТ: 8. |
| Задача 17. Найдите площадь ромба, если его диагонали равны 4 и 12.
Ответ
ОТВЕТ: 24. |
| Задача 18. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Ответ
ОТВЕТ: 3. |
| Задача 19. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Ответ
ОТВЕТ: 2. |
| Задача 20. Сумма двух углов параллелограмма равна 100°. Найдите один из оставшихся углов. Ответ дайте в градусах.
Ответ
ОТВЕТ: 130. |
| Задача 21. Один угол параллелограмма больше другого на 70°. Найдите больший угол. Ответ дайте в градусах.
Ответ
ОТВЕТ: 125. |
| Задача 22. Диагональ параллелограмма образует с двумя его сторонами углы ({26^ circ }) и ({34^ circ }). Найдите больший угол параллелограмма. Ответ дайте в градусах.
Ответ
ОТВЕТ: 120. |
| Задача 23. Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.
Ответ
ОТВЕТ: 10. |
| Задача 24. Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, который образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.
Ответ
ОТВЕТ: 60. |
| Задача 25. Найдите высоту ромба, сторона которого равна (sqrt 3 ), а острый угол равен ({60^ circ }).
Ответ
ОТВЕТ: 1,5. |
| Задача 26. Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах.
Ответ
ОТВЕТ: 126. |
| Задача 27. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Ответ
ОТВЕТ: 90. |
| Задача 28. Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма.
Ответ
ОТВЕТ:20 . |
| Задача 29. Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
Ответ
ОТВЕТ: 20. |
| Задача 30. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Ответ
ОТВЕТ: 28. |
| Задача 31. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Ответ
ОТВЕТ: 10. |
| Задача 32. Найдите большую диагональ ромба, сторона которого равна (sqrt 3 ), а острый угол равен 60°.
Ответ
ОТВЕТ: 3. |
| Задача 33. Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Ответ
ОТВЕТ: 48. |
| Задача 34. В ромбе ABCD угол ABC равен ({122^ circ }). Найдите угол ACD. Ответ дайте в градусах.
Ответ
ОТВЕТ: 29. |
| Задача 35. В ромбе ABCD угол ACD равен ({43^ circ }). Найдите угол ABC. Ответ дайте в градусах.
Ответ
ОТВЕТ: 94. |
| Задача 36. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Ответ
ОТВЕТ: 141,75. |
| Задача 37. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.
Ответ
ОТВЕТ: 76,5. |
| Задача 38. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.
Ответ
ОТВЕТ: 44. |
| Задача 39. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Ответ
ОТВЕТ: 9. |
ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 3
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).
Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.
Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:
- треугольники:
- четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
- многоугольники, в частности правильные многоугольники;
- окружность и круг, описанные и вписанные в многоугольник окружности;
- площади треугольника, параллелограмма, трапеции, круга, сектора.
План выполнения:
- Внимательно прочитайте задачу.
- При необходимости выполните на чертеже дополнительные построения.
- Выполните арифметические вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на Прямоугольные треугольники
При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.
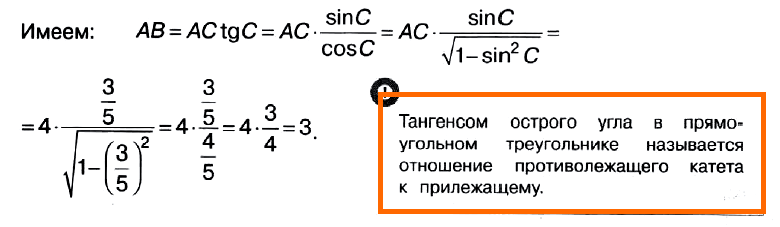
Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.
Решение:
Ответ: 3.
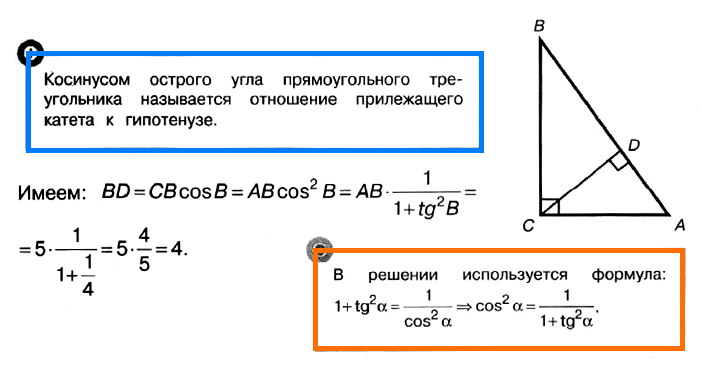
Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.
Решение:
Ответ: 4.
Задачи на Равнобедренные треугольники
Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.
Решение:
Ответ: 16.
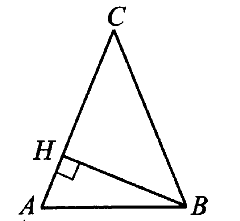
Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.
Решение:
Ответ: 24.
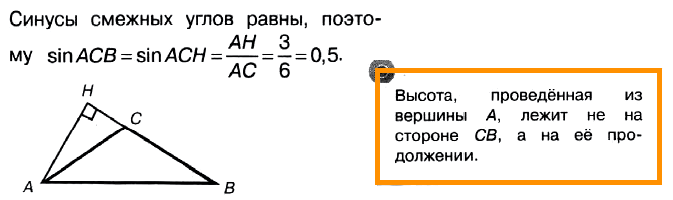
Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.
Решение:
Ответ: 0,5.
Задачи на Разносторонние треугольники
Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.
Решение:
Ответ: 2.
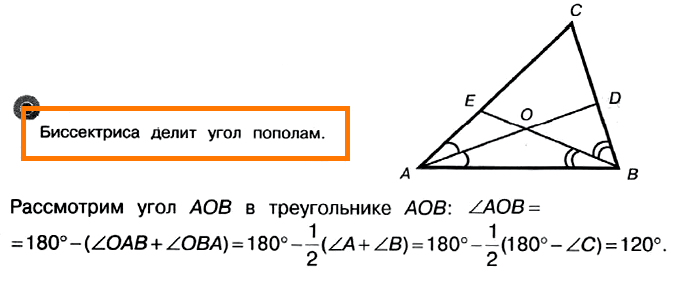
Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
Решение:
Ответ: 120.
Задачи на Параллелограммы
Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Решение:
Ответ: 6.
Задачи на Трапецию
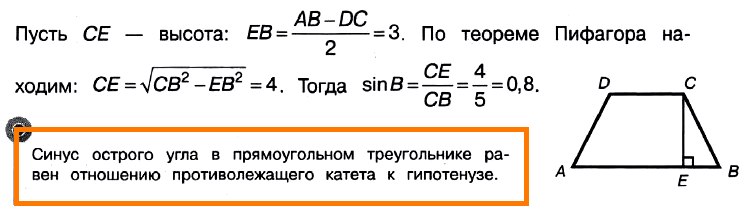
Задача № 3 (9).
Решение:
Ответ: 0,8.
Задачи на Центральные и вписанные углы
При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.
Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.
Решение:
Ответ: 60.
Задачи на Вписанные и описанные окружности
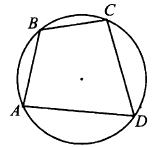
Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.
Решение:
Ответ: 20.
Задача № 3 (12).
Решение:
Ответ: 1.
Тренировочные задания с самопроверкой
№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.
Открыть ОТВЕТ
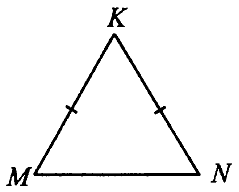
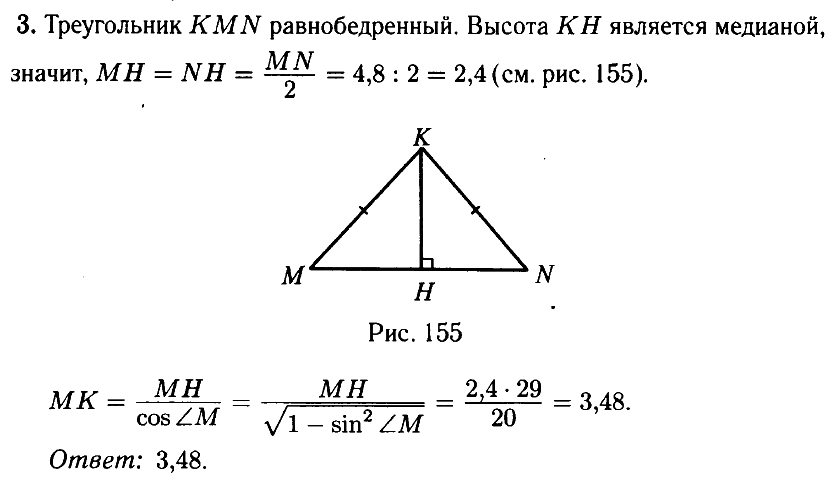
№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК.
Открыть ОТВЕТ
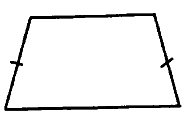
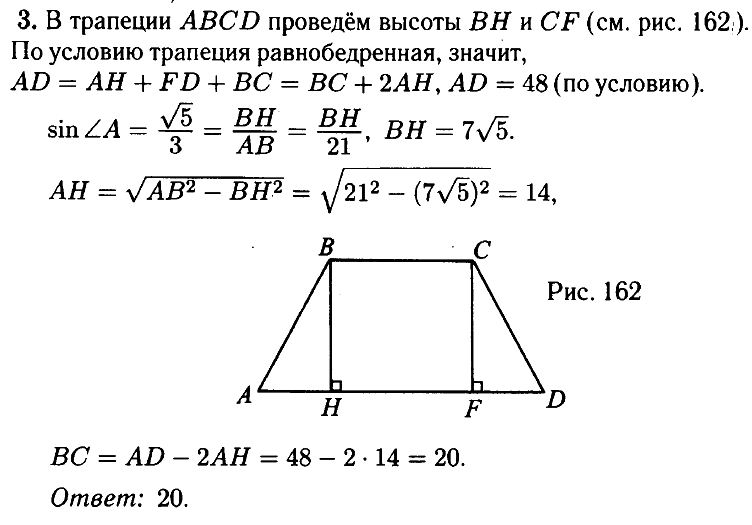
№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание.
Открыть ОТВЕТ
№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС.
Открыть ОТВЕТ
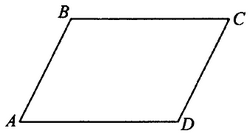
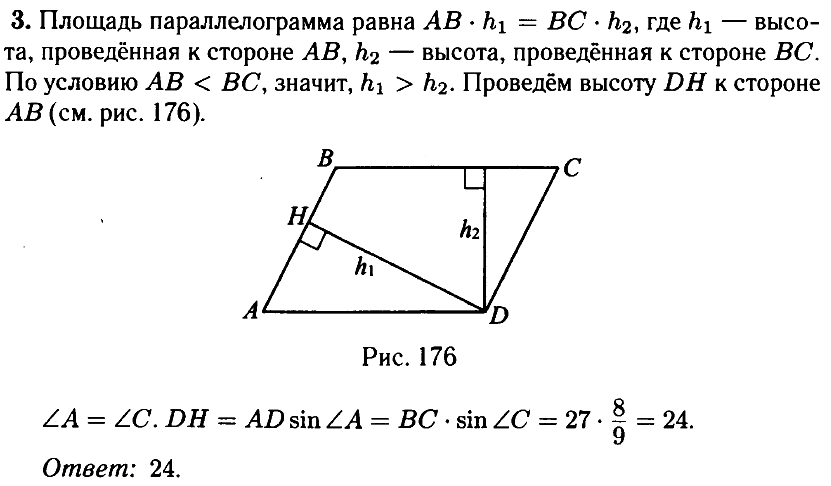
№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
18 271
Задание 3 Профильного ЕГЭ по математике. Планиметрия
Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.
Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?
Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №3 являются схемами для решения более сложных геометрических задач.
Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №3 Профильного ЕГЭ по математике.
Тригонометрия в прямоугольном треугольнике
1. B треугольнике ABC угол C равен , BC = 15, . Найдите AC.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:
2. B треугольнике ABC угол C равен . Найдите AB.
По определению косинуса угла,
Найдем косинус угла A с помощью формулы:
Треугольники. Формулы площади треугольника.
3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.
По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен
4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
По формуле площади треугольника, . Получим:
Элементы треугольника: высоты, медианы, биссектрисы
5. B треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда
Углы ACD и DCB в сумме дают . Отсюда
6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O . Найдите угол DOE. Ответ дайте в градусах.
B треугольниках ACE и OCD угол C — общий, углы A и D равны . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен
7. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.
8. B треугольнике ABC угол A равен угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Найдем третий угол треугольника ABC — угол C. Он равен
Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть и
Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть
9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
По условию, треугольники ADC и ADB — равнобедренные.
Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.
Обозначим угол BAD за х.
Из равнобедренного треугольника ABD угол ABD равен .
C другой стороны, этот угол равен углу BAC, то есть
Параллелограмм
10. B параллелограмме ABCD AB=3, AD=21, Найдите большую высоту параллелограмма.
Большая высота параллелограмма проведена к его меньшей стороне.
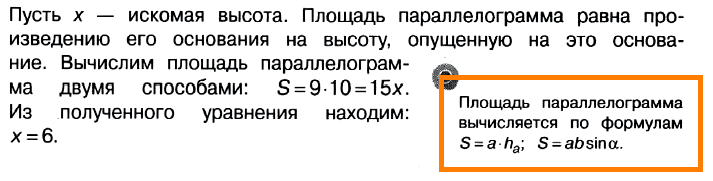
11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.
Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна
Прямоугольник
12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
Обозначим длины сторон а и b. Тогда периметр равен , его площадь равна ab, а квадрат диагонали равен
По формуле квадрата суммы,
Отсюда квадрат диагонали , и длина диагонали
13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит,
Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны Тогда HGFE — ромб, и его периметр равен .
Трапеция и ее свойства
14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Отрезок AН равен полуразности оснований трапеции:
Из прямоугольного треугольника ADH найдем высоту трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту:
15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим центр окружности и соединим его с точками A, B, C и D.
Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.
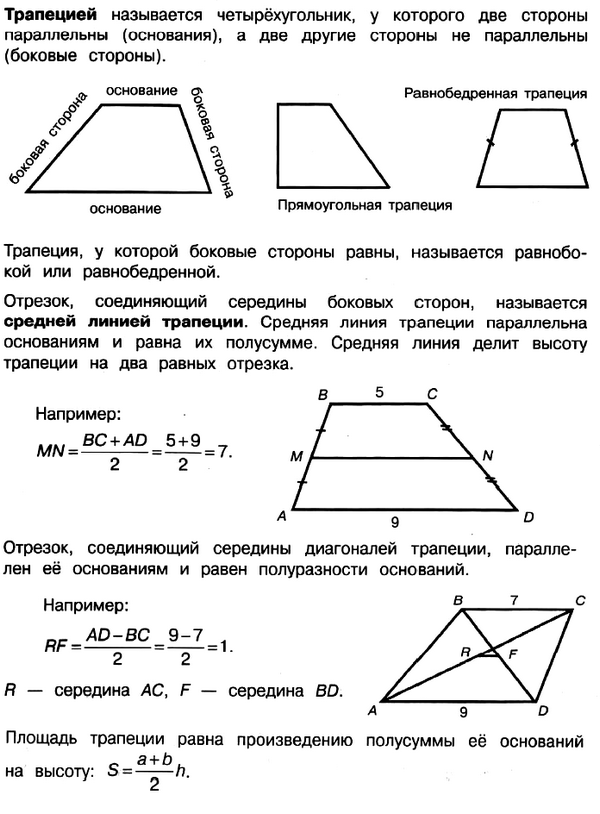
16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.
Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
PM — средняя линия треугольника ABC, значит, PM = 1.
NQ — средняя линия треугольника BCD, значит, NQ = 1.
17. Диагонали равнобедренной трапеции диагонали перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.
Треугольники AOE и FOC — прямоугольные и равнобедренные,
Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.
Центральные и вписанные углы
18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру . Найдите вписанный угол ACB. Ответ дайте в градусах.
Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть
19. Угол ACB равен Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.
Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.
Тогда угол ADB равен — как вписанный, опирающийся на дугу AB.
Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.
Касательная, хорда, секущая
20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен , и тогда угол ОBA равен Угол ОAB также равен , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен
Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна
21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен
Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна
Bписанные и описанные треугольники
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Запишем площадь треугольника ABC двумя способами:
, где p — полупериметр, r — радиус вписанной окружности.
По формуле Герона, площадь треугольника
23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.
Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна
24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.
По теореме синусов, Тогда
Угол C может быть равен или — ведь синусы этих углов равны Однако по рисунку угол C — острый, значит, он равен
25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
По теореме синусов, Тогда
По условию, угол C — тупой. Значит, он равен
26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
Радиус окружности, вписанной в прямоугольный треугольник: Гипотенуза равнобедренного прямоугольного треугольника в раз больше катета. Получим:
Bписанные и описанные четырехугольники
27. B четырёхугольник ABCD вписана окружность, , Найдите периметр четырёхугольника ABCD.
B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,
Тогда периметр четырехугольника равен
28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен
C четырехугольником справились. A с n-угольником?
Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен Найдите n.
Задание 3 ЕГЭ математика (профильный уровень)
За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.
Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты
В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.
При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки – надо внимательно читать задание.
По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.
Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.
При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.
Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.
Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.
Большинство задач можно решить несколькими способами.
Пример №1
Найдите большую диагональ ромба.
Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.
Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.
Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.
Пример №2
Найдите площадь треугольника.
Решение:
1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24
2) Найдем площади «лишних» прямоугольных треугольников
(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)
3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8
Эту же задачу можно решить другим способом.
1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.
2) Катеты найдем из прямоугольных треугольников
Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)
3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8
Пример №3
Найдите площадь многоугольника
Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.
Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5
Эту задачу можно решить и вычитанием из площади прямоугольника.
Пример №4
Найти площадь многоугольника.
Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.
Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).
Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.
Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.
Пример № 5
Найдите градусную меру угла АВС.
Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.
Проведем радиусы в точки А и С.
По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.
Пример №6
Найдите тангенс угла.
Решение: Выделим смежный острый угол.
Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).
Тангенс смежного тупого угла противоположен по знаку.
В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.
Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.
Разбор заданий № 3 ЕГЭ по математике (профиль) — теория и практика
Задание №3 ЕГЭ-2021 (профильный уровень). Простейшая геометрия (задачи на клетчатой бумаге или координатной плоскости). Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы:
— формулы площадей фигур: треугольника, параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга;
— формулы длины окружности, длины дуги и площади сектора;
— формулы средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения.
К данному конспекту смотрите приложения, содержащие все необходимые формулы для решения задания 3 ЕГЭ по математике профильного уровня и о том, как быстро выучить формулы.
За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.
Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты
В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.
При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки — надо внимательно читать задание.
По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.
Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.
При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.
Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.
Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.
Большинство задач можно решить несколькими способами.
Пример №1
Найдите большую диагональ ромба.
Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.
Ответ: 4 см.
Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.
Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.
Пример №2
Найдите площадь треугольника.
Решение:
1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24
2) Найдем площади «лишних» прямоугольных треугольников
(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)
3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8
Ответ: 8.
Эту же задачу можно решить другим способом.
1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.
2) Катеты найдем из прямоугольных треугольников
Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)
3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8
Ответ: 8.
Пример №3
Найдите площадь многоугольника
Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.
Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5
Ответ: 7,5.
Эту задачу можно решить и вычитанием из площади прямоугольника.
Ответ: 7,5.
Пример №4
Найти площадь многоугольника.
Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.
Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).
Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.
7+9/2-1=10,5
Ответ: 10,5
Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.
Пример № 5
Найдите градусную меру угла АВС.
Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.
Проведем радиусы в точки А и С.
По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.
135/2=67,5
Ответ: 67,5.
Пример №6
Найдите тангенс угла.
Решение: Выделим смежный острый угол.
Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).
tgA=4/1=4
Тангенс смежного тупого угла противоположен по знаку.
Ответ: -4.
В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.
Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна
Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где
и
— диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны
и
. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
.
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
.
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна
.
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как
. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как
), а длина дуги данного сектора равна
, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть
градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть
круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в
раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023