Задание 3222 физика егэ - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

Тип 8 № 3222

Относительная влажность воздуха равна 42%, парциальное давление пара при температуре 20 °С равно 980 Па. Каково давление насыщенного пара при заданной температуре? (Ответ дать в паскалях, округлив до целых.)

Спрятать решение

Решение.

Относительная влажность воздуха связана с парциальным давлением пара при некоторой температуре и давлением насыщенных паров при той же температуре соотношением Отсюда находим давление насыщенного пара при :

Ответ: 2333.

Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.1.13 Насыщенные и ненасыщенные пары, 2.1.14 Влажность воздуха. Относительная влажность

Спрятать решение

Сообщить об ошибке · Помощь

Источник

2017-04-30

Оптическая система состоит из собирающей линзы с фокусным расстоянием $F$ и зеркального шара радиусом $R$, центр которого находится на оптической оси линзы на расстоянии $d > F$ от нее. На каком расстоянии от линзы нужно расположить источник света $S$ на оптической оси системы, чтобы его изображение совпало с самим источником?

Решение:

Рассмотрим случай, изображенный на рис., когда $d < R + F$. Если после преломления в лише луч будет падать на зеркальный шар по направлению его радиуса, то, отразившись от шара, он пройдет тем же путем, но в обратном направлении. Изображение источника света $S$ в системе, состоящей из линзы и шара, совпадет с источником. Итак, в этом случае изображение источника света в линзе будет находиться в точке О. Применяя формулу тонкой линзы, получаем $frac{1}{F} = frac{1}{x} + frac{1}{f}$, где $f = d$. Отсюда $x = frac{Ff}{f-F} = frac{Fd}{d-F}$.

Пусть $d > R + F$. На рис. изображен случай, аналогичный разобранному выше, из которого следует, что $x = frac{Fd}{d — F}$.

Однако, при $d > R + F$ возможен и другой вариант. В случае, представленном на рис., изображение источника света $S$ в линзе получается в точке А. В силу симметрии луч, который первоначально шел по пути SDA, после отражения от шара пойдет по пути ACS, а луч, который проходил путь SCA, отразившись от шара в точке А, пройдет путем ADS. Таким образом, в этом случае изображение источника света S в системе, состоящей из линзы и шара, совпадает с источником. Изображение источника $S$ в линзе будет находиться в точке А, если выполняется уравнение $frac{1}{F} = frac{1}{x} + frac{1}{f}$, где $f = d — R$. Отсюда находим, что $x = frac{Ff}{f — F} = frac{F(d-R)}{d — R — F}$.

Источник

Подборка тренировочных вариантов ЕГЭ 2023 по физике для 11 класса с ответами из различных источников.

Соответствуют демоверсии ЕГЭ 2023 по физике

→ варианты прошлого года

Тренировочные варианты ЕГЭ 2023 по физике

ЕГЭ 100 баллов (с ответами)
Вариант 1	скачать
Вариант 2	скачать
Вариант 3	скачать
Вариант 4	скачать
Вариант 5	скачать
Вариант 6	скачать
vk.com/shkolkovo_fiz
Вариант 1	ответы
Вариант 2	разбор
Вариант 3	ответы
easy-physic.ru
Вариант 110	ответы	разбор
Вариант 111	ответы	разбор
Вариант 112	ответы	разбор
Вариант 113	ответы	разбор
Вариант 114	ответы	разбор
Вариант 115	ответы	разбор
Вариант 116	ответы	разбор

Примеры заданий:

1. Цилиндрический сосуд разделён лёгким подвижным теплоизолирующим поршнем на две части. В одной части сосуда находится аргон, в другой – неон. Концентрация молекул газов одинакова. Определите отношение средней кинетической энергии теплового движения молекул аргона к средней кинетической энергии теплового движения молекул неона, когда поршень находится в равновесии.

2. Газ получил количество теплоты, равное 300 Дж, при этом внутренняя энергия газа уменьшилась на 100 Дж. Масса газа не менялась. Какую работу совершил газ в этом процессе?

3. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.

1) При увеличении длины нити математического маятника период его колебаний уменьшается.
2) Явление диффузии протекает в твёрдых телах значительно медленнее, чем в жидкостях.
3) Сила Лоренца отклоняет положительно и отрицательно заряженные частицы, влетающие под углом к линиям индукции однородного магнитного поля, в противоположные стороны.
4) Дифракция рентгеновских лучей невозможна.
5) В процессе фотоэффекта с поверхности вещества под действием падающего света вылетают электроны.

4. В запаянной с одного конца трубке находится влажный воздух, отделённый от атмосферы столбиком ртути длиной l = 76 мм. Когда трубка лежит горизонтально, относительная влажность воздуха ϕ1 в ней равна 80%. Какой станет относительная влажность этого воздуха ϕ2 , если трубку поставить вертикально, открытым концом вниз? Атмосферное давление равно 760 мм рт. ст. Температуру считать постоянно

5. Предмет расположен на главной оптической оси тонкой собирающей линзы. Оптическая сила линзы D = 5 дптр. Изображение предмета действительное, увеличение (отношение высоты изображения предмета к высоте самого предмета) k = 2. Найдите расстояние между предметом и его изображением.

Связанные страницы:

Источник

» Меню сайта

Главная страница

Учителю математики

Учителю физики

Ученикам

ГИА по физике

ЕГЭ по физике

Эксперименты

Олимпиады

Кл. руководителю

Родителям

Фотоальбомы

Форум

Гостевая книга

Обратная связь

Обо мне

» Категории раздела

Новости СЭДО [1]

Новости сайта [8]

Для учителей [1]

ЕГЭ [2]

» Подготовка к ЕГЭ

» Кнопка сайта

» Код кнопки сайта

Решение задач ЕГЭ части С

» Вход на сайт

» Статистика сайта

» Поиск

» Погода

Новосибирск — погода
https://world-weather.ru/pogoda/russia/kazan/

» Календарь

« Март 2023 »

Пн Вт Ср Чт Пт Сб Вс

1 2 3 4 5

6 7 8 9 10 11 12

13 14 15 16 17 18 19

20 21 22 23 24 25 26

27 28 29 30 31

Источник

За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 69.1%
Ответом к заданию 1 по физике может быть целое число или конечная десятичная дробь.

Алгоритм решения задания 1:

Первым делом определите, на какой вид движения задача (равномерное, равноускоренное и т.д).
Далее посмотрите, что вам необходимо найти. Обратите внимания на ключевые слова: МОДУЛЬ, ПРОЕКЦИЯ, ПУТЬ, ПЕРЕМЩЕНИЕ. Так как именно на этих словах вас хотят подловить.
Выбирайте наиболее подходящую для решения формулу.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Уравнение движения тела имеет вид x = 2t + 0,5t². Найдите, с каким ускорением двигалось тело. Ответ выразите в (м/с²).

Решение

Дано:

$x=2t+0.5t^2$

$a-?$

Решение:

Запишем уравнение движения в общем виде и сравнив с имеющимся: $x=2t+0.5t^2; x=υ_0t+{at^2}/{2}$, тогда ${at^2}/{2}=0.5t^2; a=0.5·2$ или $a=1м/с^2$.

Ответ: 1

Задача 2

Первую четверть пути поезд прошёл со скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С какой скоростью поезд двигался на оставшейся части пути? Ответ выразите в (км/ч).

Решение

Дано:

$υ_1=60$км/ч

$S_1={1}/{4}S$

$S_2={3S}/{4}$

$υ_{ср}=40$км/ч

$υ_2-?$

Решение:

Средняя скорость определяется выражением: $υ_{ср}={S_{общ}}/{t_{общ}}$(1), где $S_{общ}=S_1+S_2={S}/{4}+{3S}/{4}={4S}/{4}=S$(2), $t_{общ}=t_1+t_2={S_1}/{υ_1}+{S_2}/{υ_2}={S}/{4υ_1}+{3S}/{4υ_2}={Sυ_2+3Sυ_1}/{4υ_1υ_2}$(3).

Подставим выражения (2) и (3) в (1), получим: $υ_{ср}={S}/{1}:{S(3υ_1+υ_2)}/{4υ_1υ_2}={S}/{1}·{4υ_1υ_2}/{S(3υ_1+υ_2)}={4υ_1υ_2}/{(3υ_1+υ_2)}$(4). Из (4) выразим скорость $υ_2$: $υ_{ср}(3υ_1+υ_2)=4υ_1υ_2⇒3υ_1υ_{ср}+υ_{ср}υ_2=4υ_1υ_2⇒4υ_1υ_2-υ_{ср}υ_2=3υ_1υ_{ср}⇒υ_2(4υ_1-υ_{ср})=3υ_1υ_{ср}⇒υ_2={3υ_1υ_{ср}}/{(4υ_1-υ_{ср})}$(5). Подставим числовые значения в (5): $υ_2={3·60·40}/{4·60-40}={7200}/{200}=36км/ч$.

Ответ: 36

Задача 3

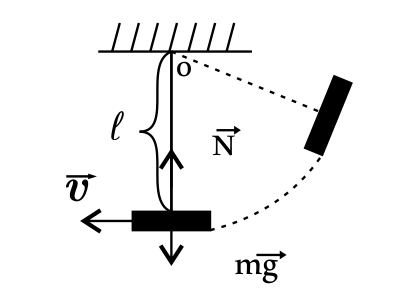
Цирковая гимнастка массой 50 кг качается на качелях с длиной верёвок 5 м. С какой силой она давит на сиденье при прохождении положения равновесия со скоростью 6 м/с? Ответ выразите в (Н). Ускорение свободного падения считать равным 10 м/с^2

Решение

Дано:

$m=50$кг

$g=10м/с^2$

$l=5$м

$υ=6$м/c

$N-?$

Решение:

При прохождении качелями среднего положения второй закон Ньютона в проекции на вертикальное направление иммет вид: $ma=N-mg$(1), здесь $a$ — ускорение гимнастики, совпадающее с центростремительным, $m$ — масса гимнастики, $N$ — сила реакции опоры (сиденья), равная по модулю, согласно третьему закону Ньютона, силе, с которой мальчик давит на сиденье. Так как центростремительное ускорение равно $a_{ц.с.}={υ^2}/{l}$(2), то сила, действующая на сиденье, равна: $N=ma+mg=m(a+g)=m({υ^2}/{l}+g)$(3). Подставим числовые значения в (3): $N=50·({36}/{5}+10)=50·17=860H$.

Ответ: 860

Задача 4

Из начала координат одновременно начинают движение две точки. Первая движется вдоль оси Ox со скоростью 3 м/с, а вторая — вдоль оси Oy со скоростью 4 м/с. (Оси перпендикулярны). С какой скоростью они будут удаляться друг от друга? Ответ выразите в (м/с).

Решение

Дано:

$υ_1=3$м/с

$υ_2=4$м/с

$υ_{отн}-?$

Решение:

Вектор относительной скорости $υ_{отн}$ есть разность векторов скоростей двух точек. По правилу вычитания векторов, вектор относительной скорости будет ижти от конца вектора скорости одной точки к концу векторая скорости другой точки. Так как скорости точек направлены перпендикулярно, длина вектора относительной скорости является гипотенузой прямоугольного треугольника и находится по теореме Пифагора: $υ_{отн}=√{υ_1^2+υ_2^2}=√{(3)^2+(4)^2}=√{9+16}=√{25}=5$м/с.

Ответ: 5

Задача 5

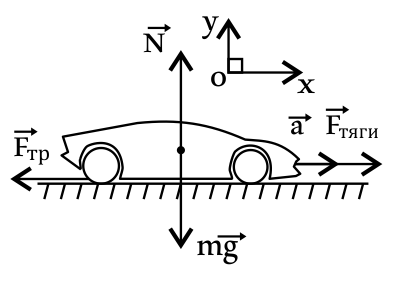
Автобус, масса которого 15 т, движется с ускорением 0,7 м/с². Чему равна сила тяги двигателя, если коэффициент сопротивления движению равен 0,03? Ответ выразите в (кН).

Решение

Дано:

$m=15·10^3$кг

$a=0.7м/с^2$

$μ=0.03$

$F_{тяги}-?$

Решение:

На автомобиль действуют силы: тяги, трения, тяжести и силы реакции опоры. Запишем второй закон Ньютона: $ma↖{→}={F_{тяги}}↖{→}+{F_{тр}}↖{→}+mg↖{→}+N↖{→}$(1).

В проекциях на оси координат имеем: $Ox:ma=F_{тяги}-F_{тр}$(2), откуда $F_{тяги}=ma+F_{тр}$(3). $Oy:O=N-mg$(4), откуда $N=mg$(5). Учитывая, что сила трения $F_{тр}=μN$, то с учетом (5) получим: $F_{тр}=μmg$(6). Подставим (6) в (3) и найдем $F_{тяги}:F_{тяги}=ma+μmg=m(a+μg)$(7), где $g≈10м/с^2$ — ускорение свободного падения.

Подставим числовые значения в (7), получим: $F_{тяги}=15·10^3·(0.7+0.03·10)=15·10^3·(0.7+0.3)=15·10^3·1=15·10^3=15$кН.

Ответ: 15

Задача 6

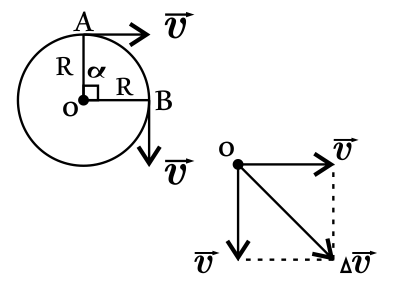
Тело движется по окружности равномерно. Радиус окружности 1 м. Найдите изменение вектора скорости при перемещении тела на угол 90◦. Период обращения 3,14 с. Ответ округлите до десятых. Ответ выразите в (м/с). Число ${π}$ принять равным 3,14

Решение

Дано:

$R=1$м

$α=90°$

$T=3.14$c

$∆υ-?$

Решение:

Изменение вектора скорости при перемещении тела на угол $90°$ равно по теореме Пифагора: $∆υ=√{υ^2+υ^2}=√{2υ^2}=√{2}υ$(1).

Найдем величину скорости $υ$: $υ={S}/{t}={2πR}/{T}={3.14·2·1}/{3.14}=2$м/с(2).

Подставим числовые значения в (1), получим: $∆υ=√2·υ=1.41·2=2.82=2.8$м/с.

Ответ: 2.8

Задача 7

Тело движется вдоль оси Ox. Чему равна проекция скорости тела v_x, координата x которого меняется с течением времени по закону x = 3 − 2t, где все величины выражены в системе СИ? Ответ выразите в (м/c).

Решение

Дано:

$x=3-2t$

$υ_х-?$

Решение:

Известно, что $υ_x=x'(t)$, тогда $x'(t)=-2·1=-2$.

Ответ: -2

Задача 8

Подъёмный кран поднимает груз вверх со скоростью 3 м/с. В некоторый момент времени трос обрывается и груз начинает падать вниз. Определите скорость груза в момент падения на землю, если время падения составляет 4 с. Ответ выразить в (м/с). Ускорение свободного падения принять равным $10м/с^2$

Решение

Дано:

$υ=3$м/с

$t=4$c

$υ_к-?$

Решение:

На тело действует сила тяжести и ускорение свободного падения $g=const=10м/с^2$

$g={υ_к-(-υ_0)}/{t}$, т.к. ускорение $g$ и $υ_0$ разнонаправлены. $υ_к=gt-υ_0=10·4-3=37$м/с.

Ответ: 37

Задача 9

Тело движется вдоль оси Ox. Чему равно перемещение тела за 10 с, координата x которого меняется с течением времени по закону x = 3 − 2t + t², где все величины выражены в системе СИ? Ответ выразить в (м).

Решение

Дано:

$t=10$c

$x=3-2t+t^2$

$x_0=3$

$r-?$

Решение:

$x=-20+100=80+3=83$

$r=x-x_0=83-3=80$м, т.к. изначально тело уже прошло 3м.

Ответ: 80

Задача 10

Планета имеет радиус в 2 раза меньший радиуса Земли. Найдите массу этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как и на Земле. Масса Земли 6 · 10²⁴ кг. Ответ выразить в (·10²⁴ кг).

Решение

Дано:

$R_n={R_3}/{2}$

$M_n-?$

$g_n=g_3$

$M_3=6·10^{24}$м

Решение:

${tableg_n=G{M_n}/{R_r^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{R_n^2}={M_3}/{R_3^2}; M_n=M_3·{R_n^2}/{R_3^2}=6·10^{24}·{1}/{4}=1.5·10^{24}$кг

Ответ: 1.5

Задача 11

Материальная точка движется по окружности радиусом ${1.5}/{π}$ м. Найдите перемещение точки за 2 полных оборота. Ответ выразить в (м).

Решение

Дано:

$R={1.5}{π}$

Решение:

Точка делает 2 полных оборота и возвращается в начальную точку, ее перемещение равно 0.

Ответ: 0

Задача 12

Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 10⁶ м. Ответ выразите в (км).

Решение

Дано:

$M_n={M_3}/{4}$

$R_n-?$

$g_n=g_3$

$R_3=6.4·10^6$м

Решение:

${tableg_n=G{M_n}/{R_n^2}; g_3=G{M_3}/{R_3^2};$ ${M_n}/{M_3}={R_n^2}/{R_3^2}; {1}/{2}={R_n}/{R_3}$

$R_n=3200$км

Ответ: 3200

Задача 13

Найдите, чему равно ускорение свободного падения на некоторой планете, если период колебаний секундного земного математического маятника на ней оказался равным 1,41 с. Ответ выразите в (м/с²).

Решение

Дано:

$g_n-?$

$T_n=1.41$с

$T_3=1c$

Решение:

${tableT_n=2π√{{l}/{g_n}}; T_3=2π√{{l}/{g_3}};$ ${T_n}/{T_3}=√{{g_3}/{g_n}}; {1.41^2}/{1}={10}/{g_n}$

$g_n=5м/с^2$

Ответ: 5

Задача 14

Мяч массой 800 г брошен под углом 90◦ к горизонту с начальной скоростью 5 м/с. Найдите модуль силы тяжести, действующей на мяч сразу после броска. Ответ выразите в (Н).

Решение

Дано:

$m=0.8$кг

$υ=5$м/с

$F_{тяж}-?$

Решение:

Модуль силы тяжести, равна: $m·g=0.8·10=8H$

Ответ: 8

Задача 15

Найдите значение ускорения свободного падения на некоторой планете, плотность которой в два раза меньше плотности Земли, если радиусы планет одинаковы. Ответ выразите в (м/с²). Ускорение свободного падения на Земле принять равным 10 м/с^2

Решение

Дано:

$R_n=R_3$

${ρ_3}/{2}=ρ_n$

$ρ_n-?$

Решение:

${tableg^3=G{M_3}/{r^2}; g_n=G{M_n}/{r_n^2};$

а $V={4}/{3}π·R^3$, то и $V_n=V_3$.

${g_3}/{g_n}={ρ_3·V_3·r_n^2}/{ρ_n·V_n·r_3^2}⇒g_3=2·g_n; g_n=5м/с^2$.

Ответ: 5

Задача 16

Висящий на пружинке груз массой 400 г растягивает её на 10 см. На сколько сантиметров растянется пружина, если груз заменить на другой, массой 300 г? Ускорение свободного падения принять равным $10 м/{с^2}$. Ответ выразите в (см).

Решение

Дано:

$m_1=0.4$кг

$m_2=0.3$кг

$x_1=10^{-1}$ м=10 см

$x_2-?$

Решение:

${tablem_1g=kx_1; m_2g=kx_2;$ $⇒x_2={m_2g}/{m_1g}·x_1={0.3}/{0.4}·10см=7.5$

Ответ: 7.5

Задача 17

Велосипедист за 30 мин проехал 4 км, затем полчаса отдыхал, а затем проехал ещё 4 км за 15 мин. Какой была его средняя скорость на всём пути? Ответ выразите в (км/ч).

Решение

Известно, $υ_{ср}={∆S}/{∆t}={4+0+4}/{30+30+15}={8}/{1.25}=6.4{км}/ч$.

Ответ: 6.4

Задача 18

Найдите жёсткость пружины, если под действием силы 2 Н она растянулась на 4 см. Ответ выразите в (Н/м).

Решение

Дано:

$А=2·H$

$∆x=4·10^{-2}$

$K-?$

Решение:

По закону Гука $K={F}/{∆x}={2}/{4·10^{-2}}=50Н/м$.

Ответ: 50

Задача 19

Материальная точка равномерно движется по окружности. Найдите отношение пути к модулю перемещения за половину периода. Ответ округлить до сотых.

Решение

Дано:

${L}/{|S↖{→}|}-?$

$t={T}/{2}$

Решение:

1) За полпериода тело проходит половину окружности, поэтому пройденный путь равен половине дуги окружности: $L=π·R$
2) Модуль перемещения равен длине прямой, соединяющей начальную и конечную точки: $|S↖{→}|=2·R$

3) ${L}/{|S↖{→}|}={π·R}/{2·R}=1.57$

Ответ: 1.57

Задача 20

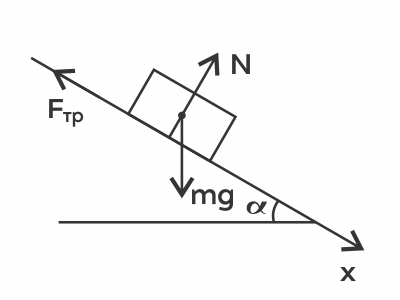
Брусок массой 2 кг покоится на наклонной плоскости с углом наклона 30◦ к горизонту. Определите силу трения, действующую на брусок, если коэффициент трения равен 0,7. Ответ выразите в (H). Ускорение свободного падения считать равным 10 $м/с^2$.

Решение

Дано:

$m=2$кг

$α=30°$

$μ=0.7$

Найти:$F_{тр}-?$

Решение:

Запишем 2-й закон Ньютона для тела: $ma↖{→}=mg↖{→}+N↖{→}+F_{тр}↖{→}=0$ (т.к. брусок покоится)

Направим ось х параллельно плоскости. 2-й закон Ньютона в проекции на ось х: $mg·sinα-F_{тр}=0⇒$

$F_{тр}=mgsinα=2·10·{1}/{2}=10Н$

Внимание! Многие при решении этой задачи используют неверную формулу $F_{тр}=μmgcosα$ — эта формула не может быть использована в этой задаче, потому что она описывает максимальную(!) силу трения покоя или силу трения скольжения. А в данной задаче тело покоится под действием силы трения, поэтому применять нужно формулы, указанные выше в решении.

Ответ: 10

Рекомендуемые курсы подготовки

Источник

В результате выполнения задания 25 ЕГЭ по физике проверяются следующие требования/умения:

Механика, молекулярная физика (расчетная задача)

Коды проверяемых требований к уровню подготовки (по кодификатору):

2.6 применять полученные знания для решения физических задач

Читать подробнее…

Коды проверяемых элементов содержания (по кодификатору):

1.1 КИНЕМАТИКА

1.2 ДИНАМИКА

1.3 СТАТИКА

1.4 ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

1.5 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

2.1 МОЛЕКУЛЯРНАЯ ФИЗИКА

2.2 ТЕРМОДИНАМИКА

Уровень сложности задания:

Повышенный

Максимальный балл за выполнение задания:

Примерное время выполнения задания выпускником, изучавшим предмет:

15-20

Идеальный газ получил количество теплоты 100 Дж, и при этом внутренняя энергия газа уменьшилась на 100 Дж. Чему равна работа, совершённая внешними силами над газом?

Скорость брошенного мяча непосредственно перед ударом о стену была вдвое больше его скорости сразу после удара. Какое количество теплоты выделилось при ударе, если перед ударом кинетическая энергия мяча была равна 20 Дж?

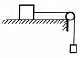
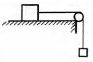
По горизонтальному столу движется брусок массой 0,7 кг, соединенный с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Определите ускорение бруска.

Идеальный газ отдал количество теплоты 100 Дж, и при этом внутренняя энергия газа уменьшилась на 100 Дж. Чему равна работа, совершённая газом?

Идеальный газ получил количество теплоты 300 Дж и совершил работу 100 Дж. Насколько увеличилась при этом внутренняя энергия газа?

Автомобиль, двигаясь по горизонтальной дороге совершает поворот по дуге окружности. Какой минимальный радиус окружности, при заданном коэффициенте трения шин о дорогу 0.4 и скорости автомобиля 10м/с , возможен без заноса.

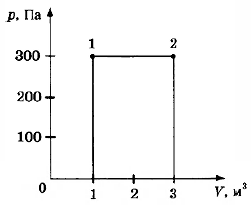
Какую работу совершил газ при переходе из состояния 1 в состояние 2 (см. рисунок)?

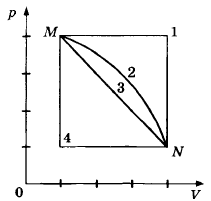
Переход газа из состояния М в состояние N (см. рисунок) совершается различными способами: 1, 2, 3, 4.

В каком случае работа газа максимальна?

Мальчик на санках скатился без трения с ледяной горки, а затем проехал до остановки по горизонтальной поверхности 30 м. Коэффициент трения при его движении по горизонтальной поверхности равен 0,2. Чему равна высота горки? Масса мальчика вместе с санями равна 50 кг.

По горизонтальному столу движется брусок массой 0,8 кг, соединенный с грузом массой 0,2 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок. Груз движется с ускорением 1,2 м/с2. Определите коэффициент трения бруска о поверхность стола.

Источник

Эксперт ЕГЭ Н. Л. Точильникова
Задача 32 на ЕГЭ по физике (по старой нумерации С6) – это расчетная задача, как правило, из раздела «квантовая физика» или волновая оптика. Но задача может быть и комбинированной: сразу на несколько тем. Или просто необычной.

Например, вот несложная задача на закон сохранения энергии:

1. Тренировочная работа № 3 от 11.04.2013

Радиоактивные источники излучения могут использоваться в космосе для обогрева оборудования космических аппаратов. Например, на советских «Луноходах» были установлены тепловыделяющие капсулы на основе полония-210. Реакция распада этого изотопа имеет вид: $vphantom{1}_{hphantom{i}84}^{210}Po rightarrow vphantom{1}_{hphantom{i}84}^{206}Po + alpha$ , где получающиеся alpha -частицы обладают кинетической энергией E=5,3 Мэв. Сколько атомов полония должно распасться в тепловыделяющей капсуле, чтобы с ее помощью можно было превратить в воду лед объемом V=10 см $vphantom{1}^3$ , находящийся при температуре $0^{circ}$ С? Плотность льда rho=900 кг/м $vphantom{1}^3$ , теплоемкостью стакана и капсулы, а также потерями теплоты можно пренебречь.

Дано:

E=5,3 Мэв
V=10 см $vphantom{1}^3$ $=10 cdot 10^{-6}$ м $vphantom{1}^3$ $= 10^{-5}$ м $vphantom{1}^3$
$t=0^{circ} C$
rho=900 кг/м $vphantom{1}^3$

Найти:

Решение:

1) Найдем количество теплоты, необходимое для того, чтобы превратить в воду лед объемом V=10 см $vphantom{1}^3$ , находящийся при температуре $0^{circ} C$ :

Где Дж/кг – удельная теплота плавления льда (табличная величина), а – масса льда.

Тогда:

$Q = lambda rho V= 3,3 cdot 10^5 cdot 900 cdot 10^{-5} = 2970$ Дж

2) Теперь запишем выражение для суммарной энергии alpha -частиц:

W=NE

3)По условию задачи энергии alpha -частиц полностью переходит в тепло: W=Q

То есть:

NE=Q

$N=genfrac{}{}{}{0}{Q}{E}=genfrac{}{}{}{0}{lambda rho V}{E}$

Энергия в Дж:

эВ $= 5,3 cdot 10^6 cdot 1,6 cdot 10^{-19}$ Дж $= 8,48 cdot 10^{-13}$ Дж,
где $e=1,6 cdot 10^{-19}$ Кл – заряд электрона.

Тогда:

$N=genfrac{}{}{}{0}{2970}{8,48 cdot 10^{-13}}=3,5 cdot 10^{15}$

Ответ: $N=3,5 cdot 10^{15}$ – число атомов полония, которые должны распасться.

А вот задача на радиоактивный распад, очень испугавшая абитуриентов своим медицинским содержанием, так что ее мало кто решил.

2. ЕГЭ-2012, Вар. 103

Пациенту ввели внутривенно дозу раствора, содержащего определённый изотоп натрия. Активность см $vphantom{1}^3$ этого раствора распадов в секунду. Период полураспада изотопа равен T=15,3 ч. Через t=3 ч мин активность см $vphantom{1}^3$ крови пациента стала a=0,28 распадов в секунду. Каков объём введённого раствора, если общий объём крови пациента V=6 л? Переходом ядер используемого изотопа натрия из крови в другие ткани организма пренебречь.

Дано:

расп. в секунду
a=0,28 расп. в секунду
V=6 л $= 6 cdot 10^{-3}$ м $vphantom{1}^3$
T=15,3 ч мин
t=3 ч мин мин

Найти:

Решение:

Активность всего объема крови пациента по прошествии времени , после введения препарата объемом cм $vphantom{1}^3$ , согласно закону радиоактивного распада, равна $a(t)=a_0 cdot 2^{genfrac{}{}{}{0}{-t}{T}}$ .

Пусть V_0 — начальный объем раствора, который на самом деле ввели пациенту.

Тогда активность образца крови в момент времени $t: a=a(t)genfrac{}{}{}{0}{V_0}{V}$ .

Отсюда $V_0=a cdot genfrac{}{}{}{0}{V}{a(t)}=genfrac{}{}{}{0}{a cdot V}{a_0 cdot 2^{genfrac{}{}{}{0}{-t}{T}}}=a cdot V cdot genfrac{}{}{}{0}{2^{genfrac{}{}{}{0}{t}{T}}}{a_0}$

$V_0=0,28 cdot 6 cdot 10^{-3} cdot genfrac{}{}{}{0}{2^{genfrac{}{}{}{0}{230}{918}}}{2000}= 10^{-6}$ м $vphantom{1}^3$

Ответ: см $vphantom{1}^3$ .

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача 32 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник