Каталог заданий.
Вписанные окружности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 1 № 27624
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Аналоги к заданию № 27624: 56807 56809 56811 56813 56815 56817 56819 56821 56823 56825 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 1 № 27625
Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Аналоги к заданию № 27625: 56857 56859 56861 56863 56865 56867 56869 56871 56873 56875 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 1 № 27640
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Аналоги к заданию № 27640: 57407 512328 512370 57409 57411 57413 57415 57417 57419 57421 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.4 Окружность и круг, 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
4
Тип 1 № 27907
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Аналоги к заданию № 27907: 53121 53123 53125 53127 53129 53131 53133 53135 53137 53139 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 1 № 27908
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Аналоги к заданию № 27908: 53171 53173 53175 53177 53179 53181 53183 53185 53187 53189 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Теория к заданию 6 ЕГЭ профильной математики
ПЛАНИМЕТРИЯ. Центральные и вписанные углы. Касательная, хорда, секущая. Вписанные и описанные окружности (теория к заданию 6 ЕГЭ профильной математики)
Учим и применяем формулы и теоремы.
Автор: Лариса Алькаева. Репетитор по математике
Из материала:
Отрезок, соединяющий две точки на окружности, называется хордой.
Самая большая хорда проходит через центр окружности и называется диаметром.
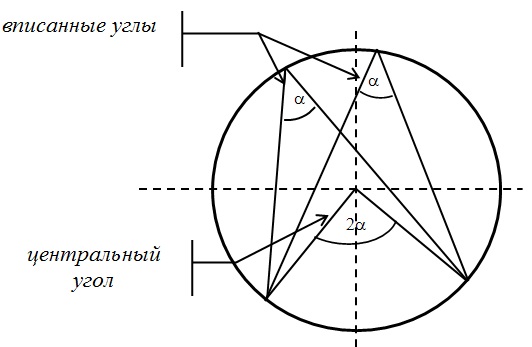
Центральный угол — угол, вершина которого лежит в центре окружности.
Центральный угол равен дуге, на которую опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Задание 6 профильного егэ по математике вписанные окружности
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Площадь треугольника равна произведению его полупериметра (p) на радиус вписанной окружности (r):
Площадь треугольника равна произведению ПЕРИМЕТРА на радиус!
Площадь треугольника равна произведению ПОЛУПЕРИМЕТРА на радиус вписанной окружности
Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Из формулы где p — полупериметр, находим, что периметр описанного многоугольника равен отношению удвоенной площади к радиусу вписанной окружности:
Задание №6 ЕГЭ по математике профильного уровня
Планиметрия. Углы.
Задание №6 профильного уровня ЕГЭ по математике — решение геометрических задач. В данном задании необходимо справиться с задачей по планиметрии на определение углов.
Теория к заданию №6
Центральный и вписанный углы:
Разбор типовых вариантов заданий №6 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
Алгоритм решения:
- Выполняем рисунок.
- Определяем
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Устанавливаем подобие треугольников.
- Используем свойство площадей подобных треугольников.
- Записываем ответ.
Решение:
1. DE – средняя линия треугольника, следовательно, все стороны в треугольнике CDE меньше соответствующих сторон в треугольнике ABC. Это означает, что треугольники подобны, и коэффициент подобия равен 2.
2. Площади подобных фигур относятся как квадраты коэффициентов подобия, следовательно, площадь треугольника CDE в 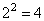
Третий вариант задания (из Ященко, №23)
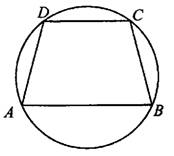
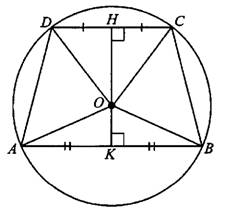
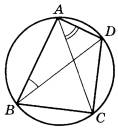
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 36°, угол CAD равен 52°. Найдите угол ABC. Ответ дайте в градусах.
Алгоритм решения:
- Отмечаем на рисунке углы, которые ланы в задаче.
- Используем свойство вписанных углов.
- Находим угол АВС.
- Записываем ответ.
Решение:
1. Отмечаем углы ABD и CAD на рисунке. Эти углы вписаны в окружность.
2. Воспользуемся свойством вписанных в окружность углов: они равны градусной меры дуги, на которую опираются.
Тогда угол ABD, опирающийся на дугу AD. Градусная мера ее равна 36 0 ∙2=72 0 , второй – угол CAD опирается на дугу CD с градусной мерой 52 0 ∙2=104 0 .
3. Дуга AC=AD+CD. Она имеет градусную меру: АС=72 0 +104 0 =176 0 , а угол АВС, который на нее опирается, определяется как половина величины дуги: 176 0 :2=88 0 .
Четвертый вариант задания (из Ященко, №10)
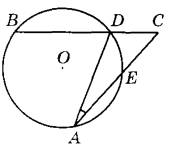
Угол АСВ равен 54°. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138°. Найдите угол DAE. Ответ дайте в градусах.
Алгоритм решения:
- Вычисляем угол BDA.
- Определяем величину угла ADC,
- Рассматриваем треугольник ADC, определяем искомый угол.
- Записываем ответ.
Решение:
1. Вычислим угол BDA. Он вписан в окружность, опирается на дугу AB. Тогда по свойству вписанных углов, его градусная мера равна половине градусной величины дуги AB. Тогда 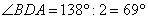
2. Рассматриваем угол ADC. Он смежный с углом BDA, значит,
3. Рассматриваем треугольник ADC. В нем известны два угла. По свойству суммы углов треугольника третий угол DAC можно найти так:
Из рисунка видно, что угол DAC совпадает с углом DAE, следовательно, угол DAE тоже равен 15 0 .
источники:
http://ege.sdamgia.ru/test?theme=113
http://spadilo.ru/zadanie-6-ege-po-matematike-profilnyj/
ЕГЭ Профиль №3. Вписанные окружности
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Вписанные окружности
| Задача 1. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Ответ
ОТВЕТ: 6. |
 |
| Задача 2. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Ответ
ОТВЕТ: 24. |
 |
| Задача 3. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 3. |
 |
| Задача 4. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Ответ
ОТВЕТ: 22. |
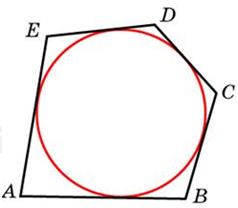 |
| Задача 5. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Ответ
ОТВЕТ: 30. |
 |
| Задача 6. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Ответ
ОТВЕТ: 1. |
 |
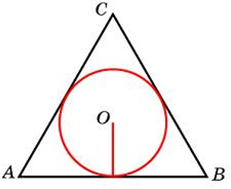
| Задача 7. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Ответ
ОТВЕТ: 2. |
 |
| Задача 8. Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Ответ
ОТВЕТ: 18. |
 |
| Задача 9. Сторона правильного треугольника равна (sqrt 3 ). Найдите радиус окружности, вписанной в этот треугольник.
Ответ
ОТВЕТ: 0,5. |
 |
| Задача 10. Радиус окружности, вписанной в правильный треугольник, равен (frac{{sqrt 3 }}{6}). Найдите сторону этого треугольника.
Ответ
ОТВЕТ: 1. |
 |
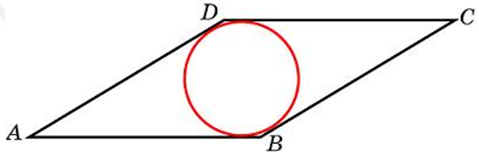
| Задача 11. Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
Ответ
ОТВЕТ: 0,25. |
 |
| Задача 12. Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Ответ
ОТВЕТ: 8. |
 |
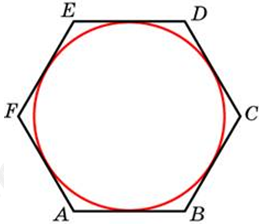
| Задача 13. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt 3 ).
Ответ
ОТВЕТ: 2. |
 |
| Задача 14. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt 3 ).
Ответ
ОТВЕТ: 1,5. |
 |
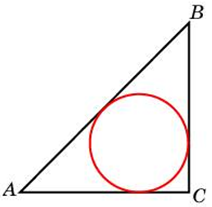
| Задача 15. Катеты равнобедренного прямоугольного треугольника равны (2 + sqrt 2 ). Найдите радиус окружности, вписанной в этот треугольник.
Ответ
ОТВЕТ: 1. |
 |
| Задача 16. В треугольнике ABC (AC = 4,;;BC = 3,) угол C равен 90°. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 1. |
 |
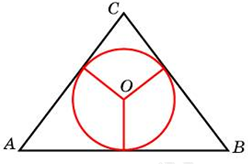
| Задача 17. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 1,5. |
 |
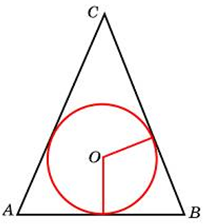
| Задача 18. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Ответ
ОТВЕТ: 22. |
 |
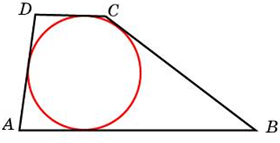
| Задача 19. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Ответ
ОТВЕТ: 4. |
 |
| Задача 20. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Ответ
ОТВЕТ: 10. |
 |
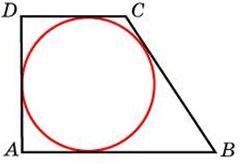
| Задача 21. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ
ОТВЕТ: 2. |
 |
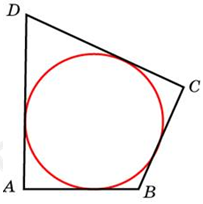
| Задача 22. В четырехугольник ABCD вписана окружность, (AB = 10,;;CD = 16.) Найдите периметр четырехугольника.
Ответ
ОТВЕТ: 52. |
 |
| Задача 23. В четырехугольник ABCD вписана окружность, (AB = 10,) (BC = 11) и (CD = 15.) Найдите четвертую сторону четырехугольника.
Ответ
ОТВЕТ: 14. |
 |
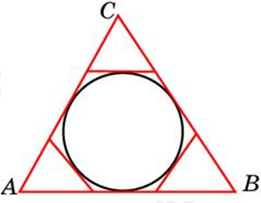
| Задача 24. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Ответ
ОТВЕТ: 24. |
 |
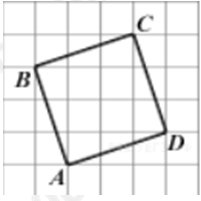
| Задача 25. Найдите радиус r окружности, вписанной в четырехугольник ABCD. Считайте, что стороны квадратных клеток равны 1. В ответе укажите (rsqrt {10} ).
Ответ
ОТВЕТ: 5. |
 |
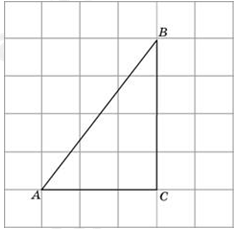
| Задача 26. Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
Ответ
ОТВЕТ: 1. |
 |
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Вписанная окружность»
Открытый банк заданий по теме вписанная окружность. Задания B6 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №298
Тип задания: 6
Тема:
Вписанная окружность
Условие
Основание равнобедренного треугольника равно 12, а боковые стороны равны 10. Найдите радиус вписанной в него окружности.
Показать решение
Решение
Известно, что радиус r окружности, вписанной в треугольник, вычисляется по формуле r=frac{S}{p}, где S — площадь треугольника, p — его полупериметр.
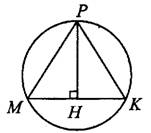
Пусть BH медиана равнобедренного треугольника, проведенная к основанию, тогда BH является высотой. По теореме Пифагора BH=sqrt{10^2-6^2}=sqrt{64}=8.
S=frac12 ah=frac12cdot12cdot8=48,
p=frac{10+10+12}{2}=16,
r=frac{48}{16}=3.
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №53
Тип задания: 6
Тема:
Вписанная окружность
Условие
Окружность вписана в трапецию и имеет радиус 2. Найдите высоту трапеции.
Показать решение
Решение
Высота трапеции равна диаметру вписанной окружности:
h=d=2r=4
Ответ
4
Задание №52
Тип задания: 6
Тема:
Вписанная окружность
Условие
В четырехугольник ABCD вписана окружность. Стороны AB = 7, BC = 5, CD = 20. Найдите четвертую сторону четырехугольника AD.
Показать решение
Решение
Если в четырехугольник вписана окружность, значит сумма его противоположных сторон равна, т.е.:
AB + CD = AD + BC
Найдем сторону AD:
AD=AB+CD-BC=7+20-5=22
Ответ
22
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.
Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?
Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.
Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.
Тригонометрия в прямоугольном треугольнике
1. B треугольнике ABC угол C равен , BC = 15,
. Найдите AC.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:
Ответ: 20.
2. B треугольнике ABC угол C равен . Найдите AB.
По определению косинуса угла,
Найдем косинус угла A с помощью формулы:
Отсюда
Ответ: 20,5.
Треугольники. Формулы площади треугольника.
3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.
По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен
Угол CAB равен углу CBA и тоже равен
, поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен
4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
По формуле площади треугольника, . Получим:
см2.
Ответ: 25.
Элементы треугольника: высоты, медианы, биссектрисы
5. B треугольнике ABC угол ACB равен , угол B равен
, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда
Углы ACD и DCB в сумме дают . Отсюда
6. B остроугольном треугольнике ABC угол равен
BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
B треугольниках ACE и OCD угол C — общий, углы A и D равны . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и
. Тогда угол DOE — смежный с углом DOC. Он равен
7. Острые углы прямоугольного треугольника равны и
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.
Тогда
8. B треугольнике ABC угол A равен угол B равен
AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Найдем третий угол треугольника ABC — угол C. Он равен
Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть и
Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть
9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
По условию, треугольники ADC и ADB — равнобедренные.
Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.
Обозначим угол BAD за х.
Из равнобедренного треугольника ABD угол ABD равен .
C другой стороны, этот угол равен углу BAC, то есть
Получим:
Отсюда
Ответ: 36.
Параллелограмм
10. B параллелограмме ABCD AB=3, AD=21, Найдите большую высоту параллелограмма.
Большая высота параллелограмма проведена к его меньшей стороне.
Получим:
Ответ: 18.
11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.
Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна
Прямоугольник
12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
Обозначим длины сторон а и b. Тогда периметр равен , его площадь равна ab, а квадрат диагонали равен
Получим: , тогда
,
По формуле квадрата суммы,
Отсюда квадрат диагонали , и длина диагонали
Ответ: 3.
13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит,
Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны Тогда HGFE — ромб, и его периметр равен
.
Трапеция и ее свойства
14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Отрезок AН равен полуразности оснований трапеции:
Из прямоугольного треугольника ADH найдем высоту трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту:
15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим центр окружности и соединим его с точками A, B, C и D.
Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.
16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.
Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.
PM — средняя линия треугольника ABC, значит, PM = 1.
NQ — средняя линия треугольника BCD, значит, NQ = 1.
Тогда
Ответ: 0,5.
17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.
Треугольники AOE и FOC — прямоугольные и равнобедренные,
Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.
Ответ: 9.
Центральные и вписанные углы
18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру
. Найдите вписанный угол ACB. Ответ дайте в градусах.
Полный круг — это . Из условия мы получим, что дуга ABC равна
Тогда дуга AB, на которую опирается вписанный угол ACB, равна
Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть
Ответ: 40.
19. Угол ACB равен. Градусная величина дуги AB окружности, не содержащей точек D и E, равна
. Найдите угол DAE. Ответ дайте в градусах.
Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.
Тогда угол ADB равен — как вписанный, опирающийся на дугу AB.
Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.
.
Ответ: 59.
Касательная, хорда, секущая
20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен , и тогда угол ОBA равен
Угол ОAB также равен
, так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен
Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна
Ответ: 64.
21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен
Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна
Bписанные и описанные треугольники
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Запишем площадь треугольника ABC двумя способами:
, где p — полупериметр, r — радиус вписанной окружности.
По формуле Герона, площадь треугольника
Тогда
Ответ: 1,5.
23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.
Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна
Периметр треугольника:
Ответ: 22.
24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.
По теореме синусов, Тогда
Угол C может быть равен или
— ведь синусы этих углов равны
Однако по рисунку угол C — острый, значит, он равен
Ответ: 30.
25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
По теореме синусов, Тогда
По условию, угол C — тупой. Значит, он равен
Ответ: 150.
26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
Радиус окружности, вписанной в прямоугольный треугольник: Гипотенуза равнобедренного прямоугольного треугольника в
раз больше катета. Получим:
Ответ: 41.
Bписанные и описанные четырехугольники
27. B четырёхугольник ABCD вписана окружность, ,
Найдите периметр четырёхугольника ABCD.
B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,
Тогда периметр четырехугольника равен
Ответ: 52.
28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен
Ответ: 108.
C четырехугольником справились. A с n-угольником?
Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,
Ответ: 30.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Задание 2898
Точка О является центром окружности, вписанной в прямоугольный треугольник ABC с прямым углом С. Луч АО пересекает катет ВС в точке Е. Найдите гипотенузу АВ, если $$AC=6sqrt{3}$$ и $$angle B$$ в 4 раза больше, чем $$sqrt{EAC}$$.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$AC=6sqrt{3}$$ $$angle B=4angle EAC$$
AO — биссектриса $$angle A$$
$$Rightarrow angle CAE=x$$ $$Rightarrow angle A=2x$$; $$angle B=4x$$
$$2x+4x=90$$ $$Rightarrow x=15^{circ}$$ $$Rightarrow angle A=30^{circ}$$; $$angle B=60^{circ}$$
$$sin B=frac{AC}{AB}$$ $$Rightarrow AB=frac{AC}{sin B}=frac{6sqrt{3}}{frac{sqrt{3}}{2}}=12$$
Задание 3196
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 16. Найдите его площадь.
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S=pcdot r=8cdot3=24$$
Задание 3522
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Ответ: 6
Задание 3523
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Ответ: 30
Задание 3524
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Ответ: 2
Задание 3525
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Ответ: 18
Задание 3526
Сторона правильного треугольника равна $$sqrt{3}$$. Найдите радиус окружности, вписанной в этот треугольник.
Ответ: 0,5
Задание 3527
Радиус окружности, вписанной в правильный треугольник, равен $$frac{sqrt{3}}{6}$$. Найдите сторону этого треугольника.
Ответ: 1
Задание 3528
Сторона ромба равна 1, острый угол равен $$30^{circ}$$. Найдите радиус вписанной окружности этого ромба.
Ответ: 0,25
Задание 3529
Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Ответ: 8
Задание 3530
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен $$sqrt{3}$$.
Ответ: 2
Задание 3531
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной $$sqrt{3}$$.
Ответ: 1,5
Задание 3532
Катеты равнобедренного прямоугольного треугольника равны $$2+sqrt{2}$$. Найдите радиус окружности, вписанной в этот треугольник.
Ответ: 1
Задание 3533
В треугольнике ABC стороны AC = 4, BC = 3, угол C равен 90°. Найдите радиус вписанной окружности.
Ответ: 1
Задание 3534
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Ответ: 1,5
Задача 7. Периметр прямоугольной трапеции, описанной около окружности, равен 42, её большая боковая сторона равна 12 (см. рис. 8). Найдите радиус окружности.
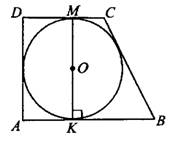
Рис. 8.
Решение.
У четырёхугольника, описанного около окружности, суммы длин противоположных сторон равны, то есть
. Поэтому
Наибольшая боковая сторона , отсюда
. Так как
, то
, где
— радиус вписанной окружности. Тогда
.
Ответ: 4,5.
Задача 8. Боковые стороны равнобедренного треугольника равны 30, основание равно 36 (см. рис. 9). Найдите радиус описанной окружности этого треугольника.
Решение.
Рис. 9.
По теореме синусов где
— радиус описанной около
окружности. Пусть
. Проведём высоту
(см. рис. 10). В равнобедренном треугольнике
высота
является медианой,
Найдём
по теореме Пифагора.
Рис. 10.
Ответ: 18,75.
Задача 9. Угол треугольника
, вписанного в окружность радиусом 12, равен 30° (см. рис. 11). Найдите сторону
этого треугольника.
Решение.
По теореме синусов для радиуса описанной окружности выполняется
Рис. 11.
Ответ: 12.
Задача 10. Радиус окружности, описанной около прямоугольного треугольника, равен 14. Найдите гипотенузу этого треугольника.
Решение.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, значит, гипотенуза — диаметр. Тогда гипотенуза равна
Ответ: 28.
Задача 11. Основания равнобедренной трапеции равны 18 и 80. Радиус описанной окружности равен 41 (см. рис. 12). Найдите высоту трапеции, если центр описанной окружности лежит внутри трапеции.
Рис. 12.
Решение.
Проведём высоту через центр окружности
и
будут лежать на серединах оснований (см. рис. 13).
и
— прямоугольные,
Рис. 13.
Ответ: 49.


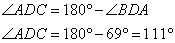
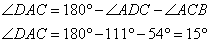



.png)