Задание 7 8299 егэ математика

Решу ЕГЭ задание №7 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки к экзамену, а также видео о том, как решать 7 задание профиля ЕГЭ 2022 по математике.

• Скачать задания рациональные уравнения и неравенства
• Скачать задания иррациональные уравнения и неравенства
• Скачать задания показательные и логарифмические уравнения
• Скачать задания тригонометрические уравнения
• Скачать задания разные типы

Задача 7 —это задания связаны с физикой. За правильное выполненное задание дают 1 балл. Ответом к заданию 7 по математике (профильной) может быть целое число или конечная десятичная дробь.

Тренажер задания 7 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 7 — задачи с физическим содержанием на линейные и квадратичные функции. Это задание на применение математических знаний при решении прикладных задач.

Рациональные уравнения и неравенства задание №7 ЕГЭ 2022 профиль задания и ответы:

Иррациональные уравнения и неравенства задание №7 ЕГЭ 2022 профиль задания и ответы:

Показательные и логарифмические уравнения и неравенства задание №7 ЕГЭ 2022 профиль задания и ответы:

Тригонометрические уравнения задание №7 ЕГЭ 2022 профиль задания и ответы:

Рациональные уравнения и неравенства задание №7 ЕГЭ 2022 профиль задания и ответы:

Как решать задание №7 ЕГЭ 2022 профиль по математике 11 класс?

1)При температуре 0 C рельс имеет длину 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

Правильный ответ: 25

2)Некоторая компания продает свою продукцию по цене pь500 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v 300 руб., постоянные расходы предприятия f 700 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π . Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300 000 руб.

Правильный ответ: 5000

3)После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле 2 h t  5 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.

Правильный ответ: 1

4)Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле . Определите наибольшую цену p, при которой месячная выручка составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

Правильный ответ: 6

5)Высота над землeй подброшенного вверх мяча меняется по закону 1,6 8 5 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?

Правильный ответ: 1,2

6)Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна 2 v P m g L , где m — масса воды в килограммах, v — скорость движения ведѐрка в м/с, L — длина верѐвки в метрах, g — ускорение свободного падения (считайте g 10 м/с2 ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.

Правильный ответ: 2

7)В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 2 2 0 0 2 2 g H t H gH k t k t , где t — время в секундах, прошедшее с момента открытия крана, 0 H 20 м — начальная высота столба воды, 1 50 k — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте g 10 м/с2 ). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

Правильный ответ: 50

8)В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 2 H t at bt H 0 , где 0 H 4 м — начальный уровень воды, 1 100 a м/мин2 , и 2 5 b м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

Правильный ответ: 20

9)Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой 2 y a x b x   , где 1 100 a   м -1 , b 1 — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?

Правильный ответ: 90

10)Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением   2 T t T bt at    0 , где t — время в минутах, 0 T 1400 К, a  10 К/мин2 , b  200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.

Правильный ответ: 2

11)Для сматывания кабеля на заводе используют лебедку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону 2 2 t t , где t — время в минутах,   20 / мин — начальная угловая скорость вращения катушки, а 2   4 / мин — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки  достигнет 1200 . Определите время после начала работы лебедки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.

Правильный ответ: 20

12)Мотоциклист, движущийся по городу со скоростью 0 v  57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a 12 км/ч2 . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 2 0 2 at S v t   . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.

Правильный ответ: 30

13)Автомобиль, движущийся в начальный момент времени со скоростью 0 v  20 м/с, начал торможение с постоянным ускорением a  5 м/с2 . За t секунд после начала торможения он прошёл путь 2 0 2 at S v t   (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.

Правильный ответ: 2

14)Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой m  8 кг и радиуса R 10 см, и двух боковых с массами M 1 кг и с радиусами R h  . При этом момент инерции катушки относительно оси вращения, выражаемый в 2 кг см  , задается формулой. При каком максимальном значении h момент инерции катушки не превышает предельного значения 2 625 кг см  ? Ответ выразите в сантиметрах

Правильный ответ: 5

15)На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: 3 F g l A   , где l — длина ребра куба в метрах, 3  1000кг м — плотность воды, а g — ускорение свободного падения (считайте g  9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78 400 Н? Ответ выразите в метрах.

Правильный ответ: 2

16)На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: 3 F g r A   , где   4,2 — постоянная, r — радиус аппарата в метрах, 3  1000кг м — плотность воды, а g — ускорение свободного падения (считайте g 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах

Правильный ответ: 2

17)Для определения эффективной температуры звезд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвѐртой степени температуры: — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь, а излучаемая ею мощность P не менее 25 9,12 10 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.

Правильный ответ: 4000

18)Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.

Правильный ответ: 36

19)Перед отправкой тепловоз издал гудок с частотой 0 f 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону (Гц), где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c 315 м/с. Ответ выразите в м/с.

Правильный ответ: 7

20)По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I R r , где — ЭДС источника (в вольтах), r 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания кз I r? (Ответ выразите в Омах.)

Правильный ответ: 4

21)Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: U I R , где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.

Правильный ответ: 55

22)Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч 2, вычисляется по формуле = корень из 2la. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.

Правильный ответ: 5000 

23)При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону , где 0 l 5 м — длина покоящейся ракеты, 5 c 3 10 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.

Правильный ответ: 180000

24)Расстояние от наблюдателя, находящегося на небольшой высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 500 Rh l , где R 6400 км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах

Правильный ответ: 1,25

25)Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 500 Rh l , где R 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?

Правильный ответ: 1,4

26)Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле 500 Rh l , где R 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?

Правильный ответ: 7

27)При адиабатическом процессе для идеального газа выполняется закон k pV const , где p — давление в газе в паскалях, V — объем газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него 5 3 k ) из начального состояния, в котором 5 5 const 10 Па м , газ начинают сжимать. Какой наибольший объем V может занимать газ при давлениях p не ниже 6 3,2 10 Па? Ответ выразите в кубических метрах.

Правильный ответ: 0,125

28)В ходе распада радиоактивного изотопа, его масса уменьшается по закону, где m0 — начальная масса изотопа, t (мин) — прошедшее от начального момента время, T — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени 0 m 40 мг изотопа Z, период полураспада которого T 10 мин. В течение скольких минут масса изотопа будет не меньше 5 мг?

Правильный ответ: 30

29)Уравнение процесса, в котором участвовал газ, записывается в виде a pV const , где p (Па) — давление в газе, V — объем газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объема газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?

Правильный ответ: 2

30)Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объѐм и давление связаны соотношением , где 1 p и 2 p — давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 — объѐм газа (в литрах) в начальном и конечном состояниях. Изначально объѐм газа равен 1,6 л, а давление газа равно одной атмосфере. До какого объѐма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах

Правильный ответ: 0,05

31)Eмкость высоковольтного конденсатора в телевизоре 6 C 2 10 Ф. Параллельно с конденсатором подключен резистор с сопротивлением 6 R 5 10 Ом. Во время работы телевизора напряжение на конденсаторе 0 U 16 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением 0,7 — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 21 с?

Правильный ответ: 2

32)Для обогрева помещения, температура в котором равна п T C 20 , через радиатор отопления, пропускают горячую воду температурой в T C 60 . Расход проходящей через трубу воды m  0,3 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры — теплоемкость воды, o Вт 21 м С — коэффициент теплообмена, а 0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 84 м?

Правильный ответ: 30

33)Водолазный колокол, содержащий в начальный момент времени 3 моля воздуха объемом 1 V 8 л, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха до конечного объема V2 . Работа, совершаемая водой при сжатии воздуха, определяется выражением 5,75 постоянная, а T 300 К — температура воздуха. Какой объем V2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?

Правильный ответ: 2

34)Мяч бросили под углом к плоской горизонтальной поверхности земли. Время полета мяча (в секундах) определяется по формуле 0 2 sin v t g . При каком наименьшем значении угла в градусах) время полета будет не меньше 3 секунд, если мяч бросают с начальной скоростью 0 v 30 м/с? Считайте, что ускорение свободного падения g 10 м/с2 .

Правильный ответ: 30

35)Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н м) определяется формулой 2A — сила тока в рамке, Тл — значение индукции магнитного поля, l 0,5 м — размер рамки, N 1000 — число витков провода в рамке, — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,75 Н м?

Правильный ответ: 30

36)Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону, где t — время в секундах, амплитуда 0 U 2 В, частота 120 / , c фаза 30 . Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Правильный ответ: 50

37)Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый показатель оценивается целыми числами от -2 до 2. Аналитик, составляющий формулу, считает, что объективность публикаций ценится втрое, а информативность — вдвое дороже, чем оперативность. В результате, формула примет вид . Каким должно быть число A, чтобы издание, у которого все показатели наибольшие, получило рейтинг 30?

Правильный ответ: 0,4

38)Рейтинг R интернет-магазина вычисляется по формуле , r — средняя оценка магазина покупателями, экс r — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.

Правильный ответ: 0,71

39)Катер должен пересечь реку шириной L=50 м и со скоростью течения u=2 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением t= L u ctgα, где α — острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом α (в градусах) нужно плыть, чтобы время в пути было не больше 25 с?

40)Груз массой 0,6 кг колеблется на пружине со скоростью, меняющейся по закону v=v0sin 2πt T , где t — время с момента начала колебаний, T=24 с — период колебаний, v0=1,4 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E= mv2 2 , где m — масса груза в килограммах, v — скорость груза (в м/с). Найдите кинетическую энергию груза через 2 секунды после начала колебаний. Ответ дайте в джоулях.

41)Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=√ Rh 500 , где R=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 2,4 км. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 4 километров?

42)Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле l=√ Rh 500 , где R=6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 3,2 км. К пляжу ведёт лестница, каждая ступенька которой имеет высоту 15 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 5,6 километров?

43)Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=25 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 10 до 80 см, а расстояние d2 от линзы до экрана — в пределах от 100 до 150 см. Изображение на экране будет чётким, если выполнено соотношение 1 d1 + 1 d2 = 1 f . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах.

44)Два тела, массой m=5 кг каждое, движутся с одинаковой скоростью v=30 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле Q=mv2sin2α, где m — масса в килограммах, v — скорость в м/с. Найдите, под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 3375 джоулей.

45)Плоский замкнутый контур площадью S=0,8 м2 находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой ϵi=aScosα, где α — острый угол между направлением магнитного поля и перпендикуляром к контуру, a=7,5⋅10−5 Тл/с — постоянная, S — площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать 3√3⋅10−5 В?

46)Рейтинг R интернет-магазина книг вычисляется по формуле R=rпок− rпок−rэкс (K+2)m , где m= 0,05K rпок+4,5 , rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 62, их средняя оценка равна 4,8, а оценка экспертов равна 3,2.

47)Рейтинг R интернет-магазина цифровой техники вычисляется по формуле R=rпок− rпок−rэкс (K+1)m , где m= 0,03K rпок+0,9 , rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 80, их средняя оценка равна 3,9, а оценка экспертов равна 2,1.

48)Для обогрева помещения, температура в котором поддерживается на уровне Tп=15°C, через радиатор отопления пропускают горячую воду температурой Tв=95°C. Расход проходящей через трубу радиатора воды m=0,3 кг/с. Проходя по трубе расстояние x м, вода охлаждается до температуры T, причём x=α cm γ log2 Tв−Tп T−Tп , где c=4200 Вт⋅с кг⋅°C — теплоёмкость воды, γ=35 Вт м⋅°C — коэффициент теплообмена, а α=2,5 — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 180 м.

49)В розетку электросети подключены приборы, общее сопротивление которых составляет R1=80 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление даётся формулой Rобщ= R1R2 R1+R2 (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 80 9 Ом. Ответ выразите в омах.

50)Очень лёгкий заряженный металлический шарик зарядом q=3,5⋅10−6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v=18 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол α с направлением движения шарика. Значение индукции поля B=5⋅10−3 Тл. При этом на шарик действует сила Лоренца, равная Fл=qvBsinα (Н) и направленная вверх, перпендикулярно плоскости. При каком наименьшем значении угла α∈[0°;180°] шарик оторвётся от поверхности, если для этого нужно, чтобы сила Fл была не менее чем 3,15⋅10−7 Н? Ответ дайте в градусах.

51)Водолазный колокол, содержащий в начальный момент времени υ=8 молей воздуха объёмом V1=80 л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V2. Работа, совершаемая водой при сжатии воздуха, определяется выражением A=αυTlog2 V1 V2 , где α=5,75 Дж моль⋅К — постоянная, а T=280 К — температура воздуха. Найдите, какой объём V2 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 51520 Дж.

52)Уравнение процесса, в котором участвовал газ, записывается в виде pVa=const, где p (Па) — давление в газе, V — объём газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение в пять раз объёма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 125 раз?

53)Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле P= 4mg πD2 , где m=2700 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g=10 м/с2, а π=3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 576000 Па. Ответ выразите в метрах.

54)Высота над землёй подброшенного вверх мяча меняется по закону h(t)=2,25+8t−4t2 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?

55)Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности Tr публикаций, а также качества Q сайта. Каждый отдельный показатель — целое число от −7 до 7. По решению составителей формула приняла вид: R= 4In+9Op+7Tr+3Q A . Если по всем четырём показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.

56)Независимое агентство намерено ввести рейтинг новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель — целое число от −4 до 4. По решению аналитиков формула приняла вид R= 2In+5Op+3Tr A . Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило бы рейтинг 50.

57)Некоторая компания продаёт свою продукцию по цене p=900 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v=400 руб., постоянные расходы предприятия f=800000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q)=q(p−v)−f. Определите месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 600000 руб.

58)На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA=ρgl3, где l — длина ребра куба в метрах, ρ=1000 кг/м3 плотность воды, а g — ускорение свободного падения (считайте g=9.8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 264600Н? Ответ выразите в метрах.

Тренировочные варианты ЕГЭ 2022 по математике профиль

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

ЕГЭ Профиль №7. Применение производной к исследованию функцийadmin2023-03-05T10:25:19+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №7. Применение производной к исследованию функций

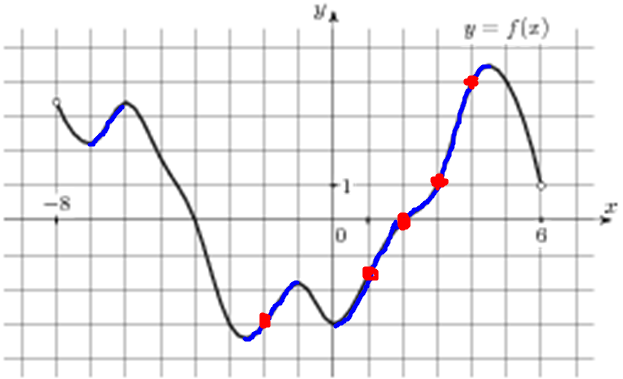
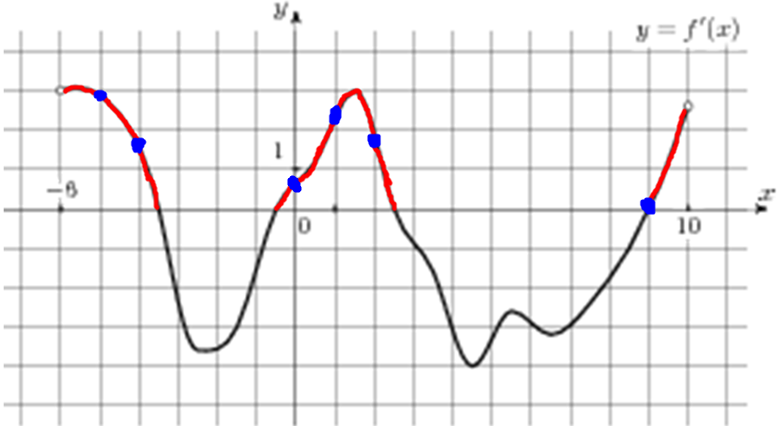
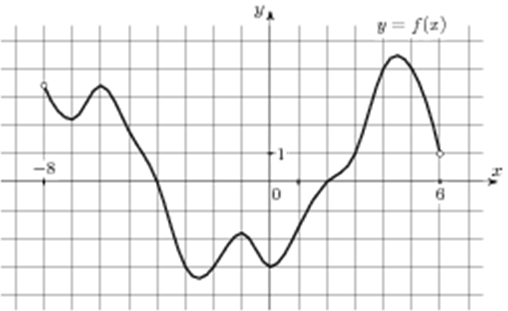
Задача 1. На рисунке изображен график функции  (y = fleft( x right)), определенной на интервале  (left( { — 8;6} right)). Определите количество целых точек, в которых производная функции (fleft( x right)) положительна. Ответ ОТВЕТ: 5. Решение Производная функции положительна в тех интервалах, на которых функция возрастает, то есть на интервалах (left( { — 7; — 6} right),,,,left( { — 2,5;, — 1} right))  и  (left( {0;,4,5} right).) Концы интервалов не включаем, так как они являются точками экстремума, а в них производная равна нулю. Интервалы возрастания выделены синим цветом (см. рисунок), а целые точки, входящие в эти интервалы -2, 1, 2, 3 и 4 выделены красным цветом и их количество равно 5. Ответ: 5.
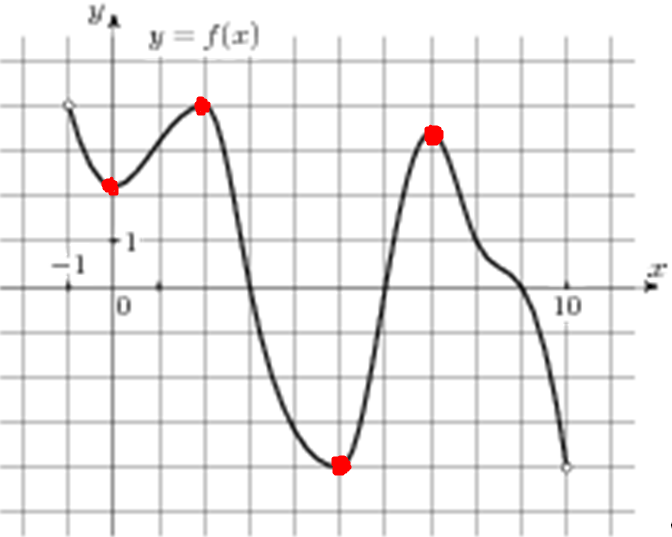
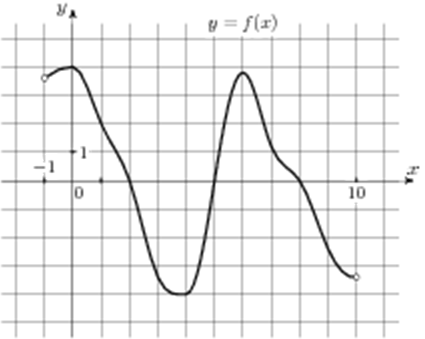
Задача 2. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале(left( { — 1;10} right)). Определите количество целых точек, в которых производная функции отрицательна. Ответ ОТВЕТ: 6. Решение Производная функции отрицательна в тех интервалах, на которых функция убывает, то есть на интервалах (left( {0;3,5} right))  и  (left( {6;,10} right).) Концы интервалов 0,  3,5  и  6 не включаем, так как они являются точками экстремума, а в них производная равна нулю. Интервалы убывания выделены синим цветом (см. рисунок), а целые точки, входящие в эти интервалы  1, 2, 3, 7, 8 и 9 выделены красным цветом и их количество равно 6. Ответ: 6.
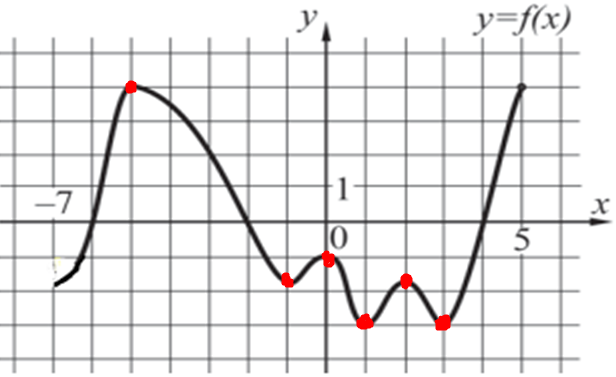
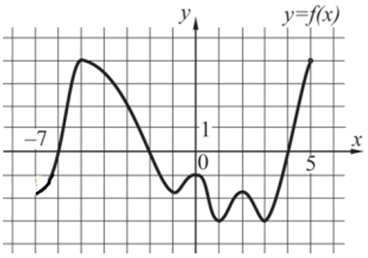
Задача 3. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале   (left( { — 7;5} right)). Найдите сумму точек экстремума функции (fleft( x right)). Ответ ОТВЕТ: 0. Решение Точки максимума и минимума объединяются общим термином – точки экстремума. Выделим на графике точки экстремума красным цветом. Они имеют следующие координаты по оси абсцисс:  -5,  -1,  0,  1,  2  и  3,  а их сумма равна  ( — 5 — 1 + 0 + 1 + 2 + 3 = 0). Ответ: 0.
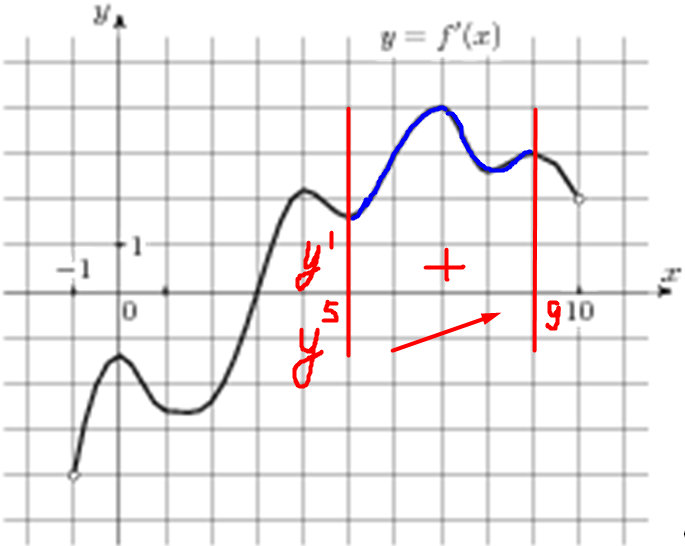
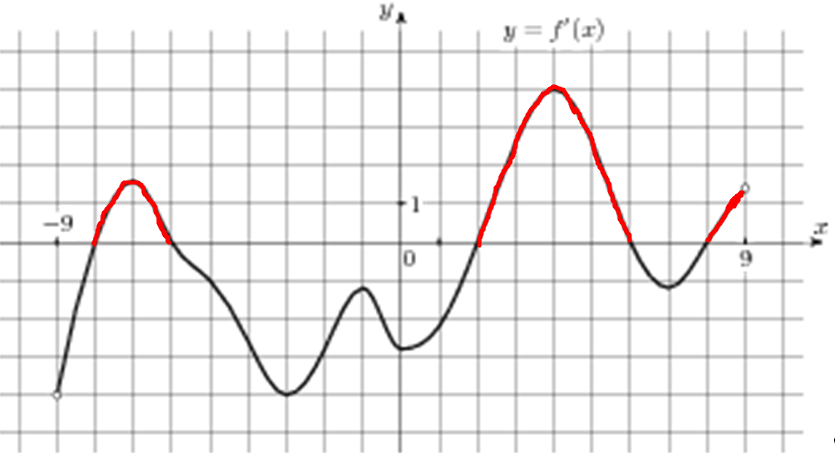
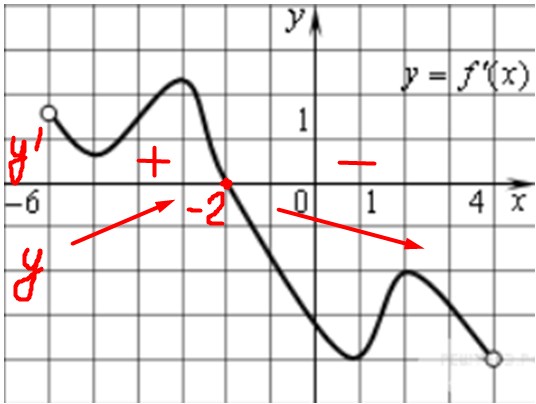
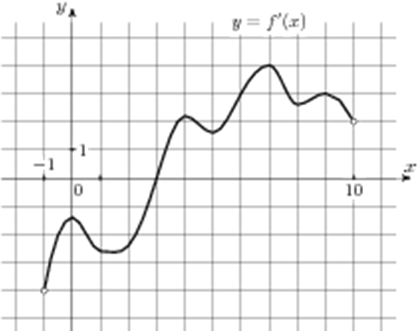
Задача 4. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 1;10} right)). В какой точке отрезка   (left[ {5;;9} right]) (fleft( x right)) принимает наибольшее значение? Ответ ОТВЕТ: 9. Решение На отрезке (left[ {5;,9} right]) график производной расположен выше оси Оx (см. рисунок), следовательно, производная принимает положительные значения, поэтому функция на этом отрезке возрастает и принимает наибольшее значение в правом конце отрезка, то есть в точке 9. Ответ: 9.
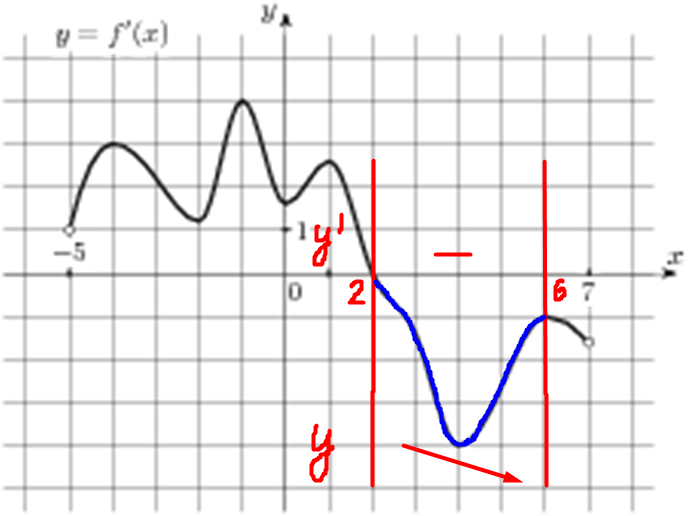
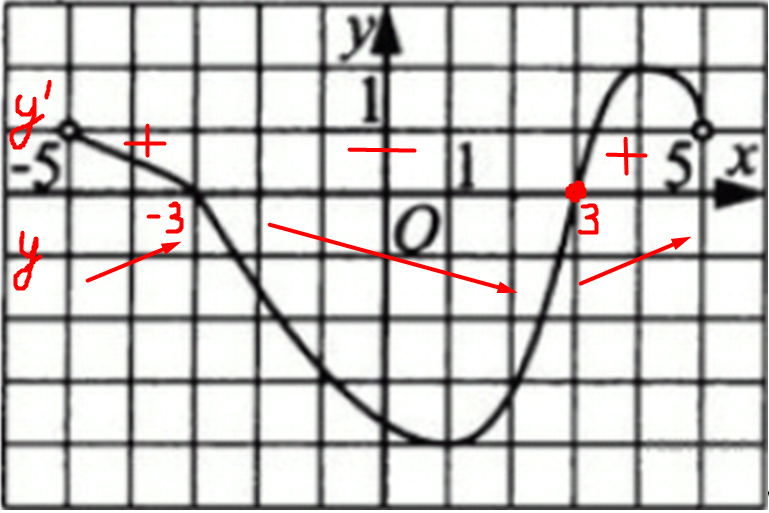
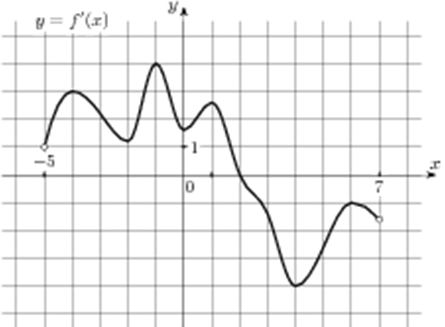
Задача 5. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 5;7} right)). В какой точке отрезка (left[ {2;;6} right]) (fleft( x right)) принимает наименьшее значение? Ответ ОТВЕТ: 6. Решение На отрезке (left[ {2;,6} right]) график производной расположен ниже оси Оx (см. рисунок), следовательно, производная принимает неположительные значения, поэтому функция на этом отрезке убывает и принимает наименьшее значение в правом конце отрезка, то есть в точке 6. Ответ: 6.
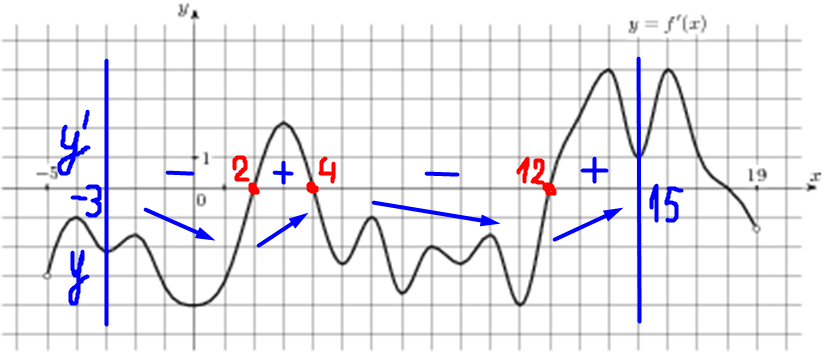
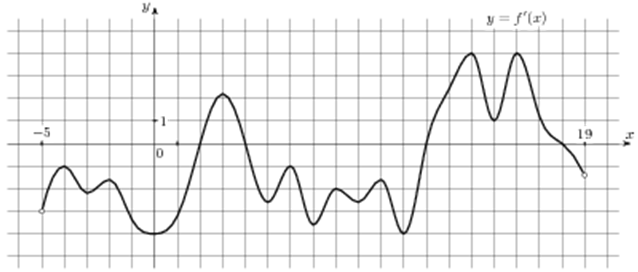
Задача 6. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 5;19} right)). Найдите количество точек максимума функции (fleft( x right)), принадлежащих отрезку    (left[ { — 3;;15} right]). Ответ ОТВЕТ: 1. Решение Значение производной (f’left( x right)) в точках максимума и минимума функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек максимума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется с «+» на «-». В данном случае на отрезке (left[ { — 3;,15} right]) производная равна нулю в точках (x = 2,,,x = 4,,,x = 12) (выделены красным цветом см. рисунок). На промежутках (left[ { — 3;,2} right]) и (left[ {4;,12} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ {2;,4} right]) и (left[ {12;,15} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак с «+» на «-» только при переходе через точку (x = 4), поэтому функция имеет 1 точку максимума. Ответ: 1.
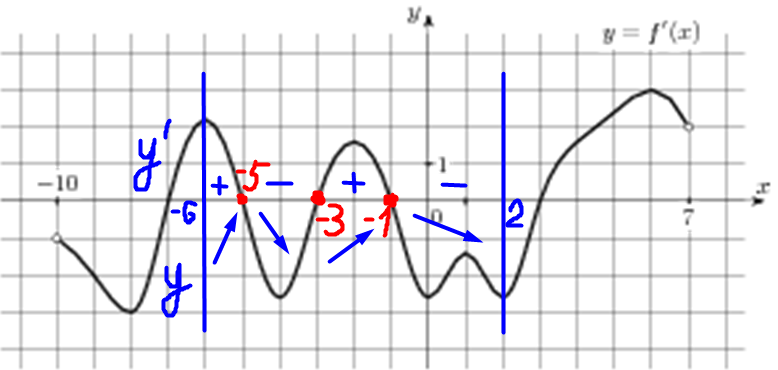
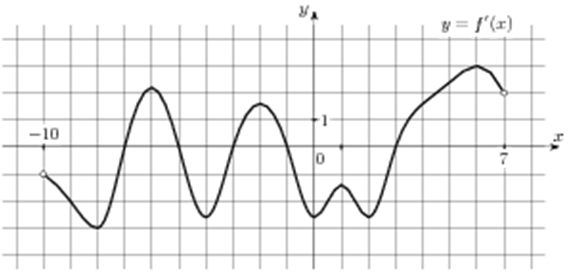
Задача 7. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 10;7} right)). Найдите количество точек минимума функции (fleft( x right)), принадлежащих отрезку (left[ { — 6;;2} right]). Ответ ОТВЕТ: 1. Решение Значение производной (f’left( x right)) в точках максимума и минимума функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек минимума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется с «-» на «+». В данном случае на отрезке (left[ { — 6;,2} right]) производная равна нулю в точках (x =  — 5,,,x =  — 3,,,x =  — 1) (выделены красным цветом см. рисунок). На промежутках (left[ { — 5;, — 3} right]) и (left[ { — 1;,2} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ { — 6;, — 5} right]) и (left[ { — 3;, — 1} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак с «-» на «+» только при переходе через точку (x =  — 3), поэтому функция имеет 1 точку минимума. Ответ: 1.
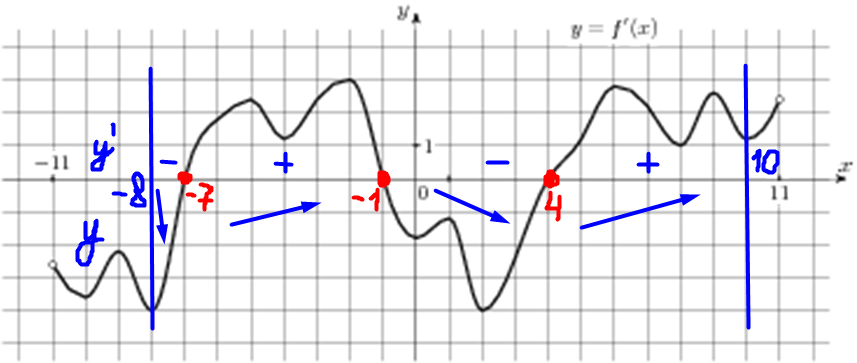
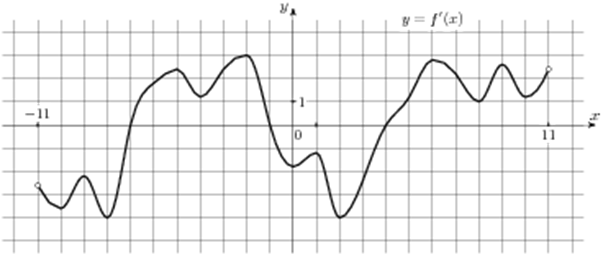
Задача 8. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 11;11} right)). Найдите количество точек экстремума функции (fleft( x right)), принадлежащих отрезку   (left[ { — 8;;10} right]). Ответ ОТВЕТ: 3. Решение Значение производной (f’left( x right)) в точках экстремума (в точках максимума и минимума) функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек экстремума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется. В данном случае на отрезке (left[ { — 8;,10} right]) производная равна нулю в точках (x =  — 7,,,x =  — 1,,,x = 4) (выделены красным цветом см. рисунок). На промежутках (left[ { — 8;, — 7} right]) и (left[ { — 1;,4} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ { — 7;, — 1} right]) и (left[ {4;,10} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак при переходе через точки (x =  — 7,,,x =  — 1,,,x = 4), поэтому функция имеет 3 точки экстремума. Ответ: 3.
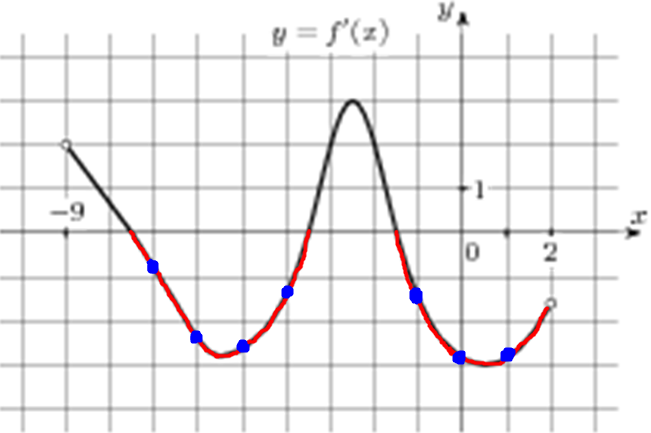
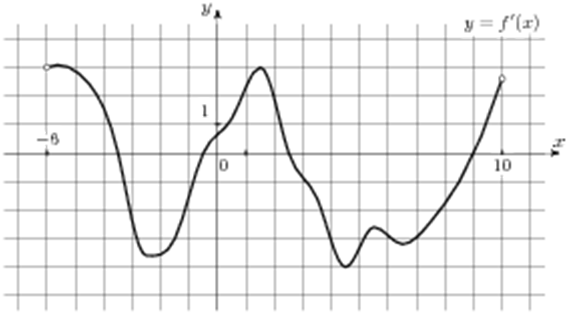
Задача 9. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 6;10} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ ОТВЕТ: 3. Решение На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае производная принимает неотрицательные значения на промежутках  (left( { — 6;, — 3,5} right],,,,left[ { — 0,5;,2,5} right]) и  (left[ {9;,10} right))  (выделены красным цветом см. рисунок), которые и являются промежутками возрастания функции (fleft( x right)). Целые точки, входящие в эти промежутки по оси абсцисс: ( — 5,,,, — 4,,,,0,,,,1,,,,2,,,,9)  (выделены синим цветом) и  их сумма равна  ( — 5 — 4 + 0 + 1 + 2 + 9 = 3.) Ответ: 3.
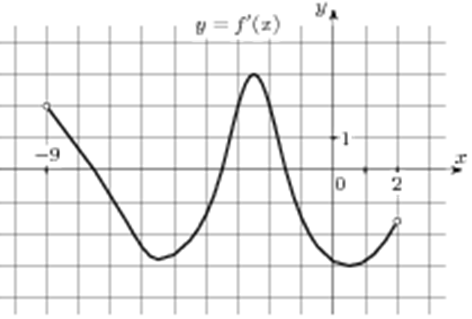
Задача 10. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;2} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ ОТВЕТ: — 22. Решение На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае производная принимает неположительные значения на промежутках (,left[ { — 7,5;, — 3,5} right]) и (left[ { — 1,5;,2} right)) (выделены красным цветом см. рисунок), которые и являются промежутками убывания функции (fleft( x right)). Целые точки, входящие в эти промежутки по оси абсцисс: ( — 7,,,, — 6,,,, — 5,,,, — 4,,,, — 1,,,,0,,,,1) (выделены синим цветом) и их сумма равна ( — 7 — 6 — 5 — 4 — 1 + 0 + 1 =  — 22.)    Ответ: –22.
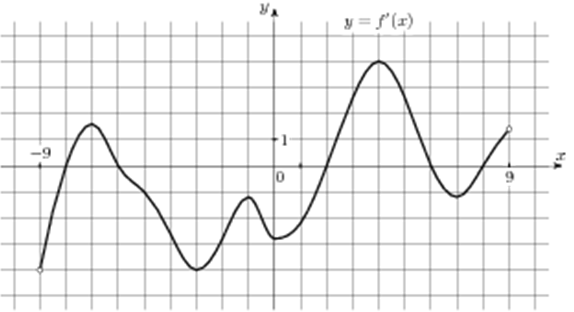
Задача 11. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;9} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите длину наибольшего из них. Ответ ОТВЕТ: 4. Решение На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае производная принимает неотрицательные значения на промежутках  (left[ { — 8;, — 6} right],,,,left[ {2;,6} right])  и  (left[ {8;,9} right))  (выделены красным цветом см. рисунок), которые являются промежутками возрастания функции (fleft( x right)). Длина первого промежутка равна  ( — 6 — left( { — 8} right) = 2,)  длина второго  (6 — 2 = 4,)  а длина третьего  (9 — 8 = 1.) Следовательно, длина наибольшего из них равна 4. Ответ: 4.

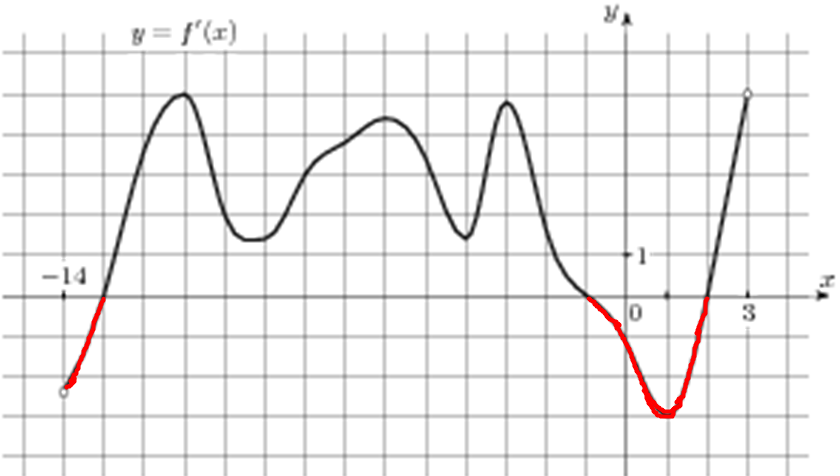
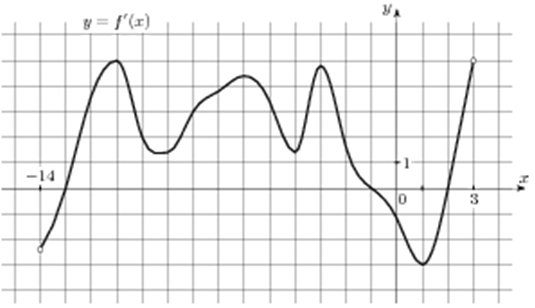
Задача 12. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 14;3} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите длину наибольшего из них. Ответ ОТВЕТ: 3. Решение На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае производная принимает неположительные значения на промежутках  (left( { — 14;, — 13} right])  и  (left[ { — 1;,2} right])  (выделены красным цветом см. рисунок), которые являются промежутками убывания функции (fleft( x right)). Длина первого промежутка равна  ( — 13 — left( { — 14} right) = 1,) а длина второго  (2 — left( { — 1} right) = 3.)  Следовательно, длина наибольшего из них равна 3. Ответ: 3.
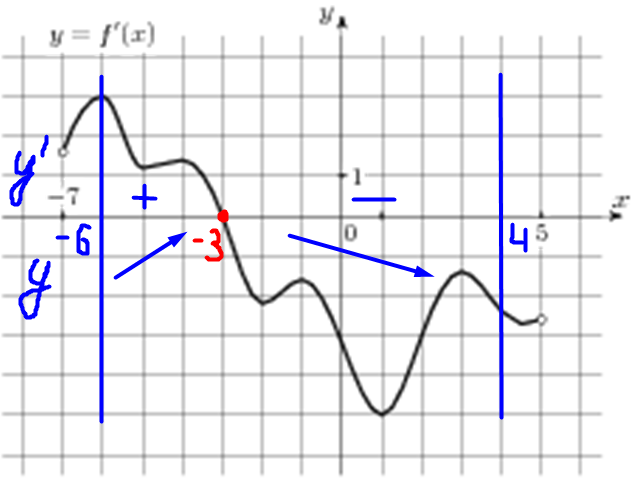
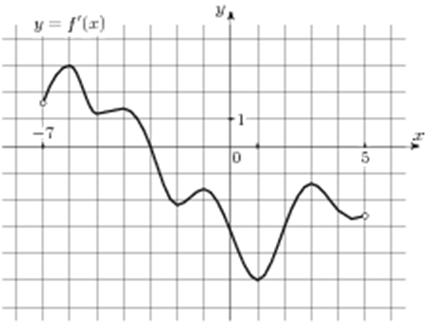
Задача 13. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале  (left( { — 7;5} right)). Найдите точку экстремума функции (fleft( x right)), принадлежащую отрезку (left[ { — 6;,4} right]). Ответ ОТВЕТ: — 3. Решение Значение производной (f’left( x right)) в точках экстремума (в точках максимума и минимума) функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения точки экстремума необходимо найти точку в которой производная равна нулю и при переходе через которую производная меняет знак. В данном случае на отрезке (left[ { — 6;,4} right]) производная равна нулю в точке (x =  — 3) (выделена красным цветом см. рисунок), при переходе через которую производная меняет знак с «+» на «-». Следовательно, точка (x =  — 3) является точкой экстремума. Ответ: –3.
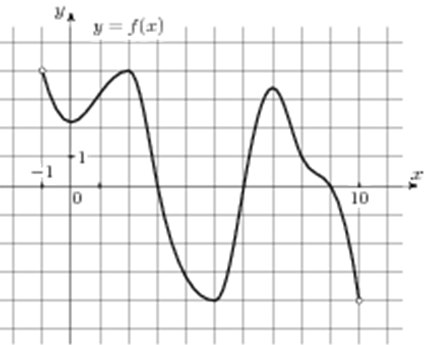
Задача 14. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале (left( { — 1;10} right)). Найдите количество точек, в которых производная функции (fleft( x right)) равна 0. Ответ ОТВЕТ: 4. Решение Производная функции (fleft( x right)) равна нулю в точках экстремума (точки максимума и минимума). Выделим их на графике красным цветом (см. рисунок). Всего таких точек 4. Ответ: 4.
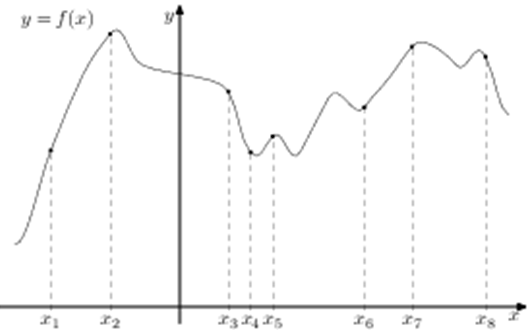
Задача 15. На рисунке изображён график функции (y = fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек производная функции (fleft( x right)) положительна? Ответ ОТВЕТ: 5. Решение Производная функции положительна в тех интервалах, на которых функция возрастает. В данном случае из 8 заданных точек функция возрастает в точках ({x_1},,,,{x_2},,,,{x_5},,,,{x_6},,,,{x_7},) то есть в 5 точках. Ответ: 5.
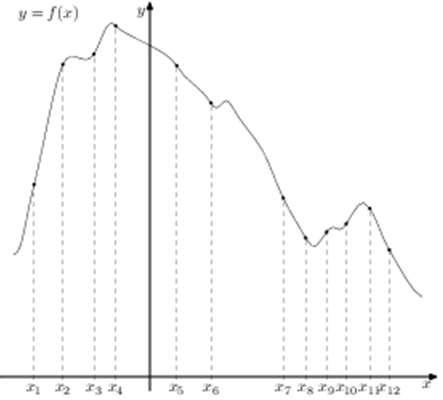
Задача 16. На рисунке изображён график функции (y = fleft( x right)) и двенадцать точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_{12}}.) В скольких из этих точек производная функции (fleft( x right)) отрицательна? Ответ ОТВЕТ: 7. Решение Производная функции отрицательна в тех интервалах, на которых функция убывает. В данном случае из 12 заданных точек функция убывает в точках ({x_4},,,,{x_5},,,,{x_6},,,,{x_7},,,,{x_8},,,,{x_{11}},,,,{x_{12}},) то есть в 7 точках. Ответ: 7.
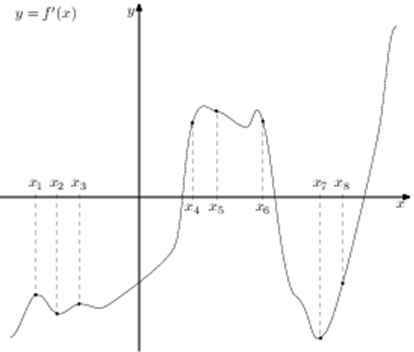
Задача 17. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) возрастает? Ответ ОТВЕТ: 3. Решение На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае из 8 заданных точек производная неотрицательная в точках ({x_4},,,,{x_5},,,,{x_6},) то есть в 3 точках. Ответ: 3.
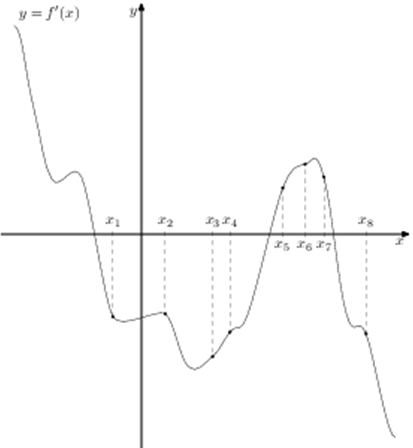
Задача 18. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс:  ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) убывает? Ответ ОТВЕТ: 5. Решение На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае из 8 заданных точек производная неположительная в точках ({x_1},,,,{x_2},,,,{x_3},,,,{x_4},,,,{x_8},) то есть в 5 точках. Ответ: 5.
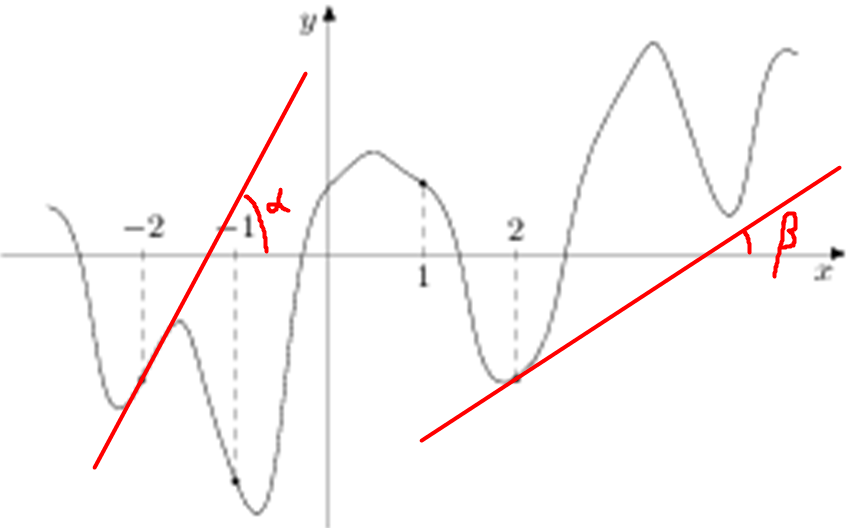
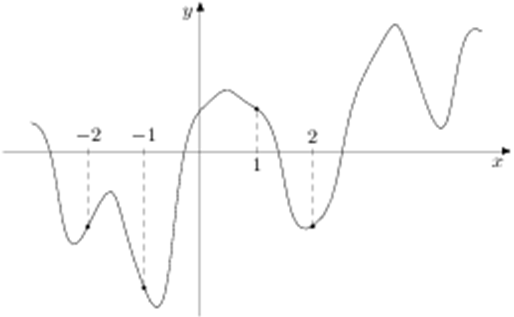
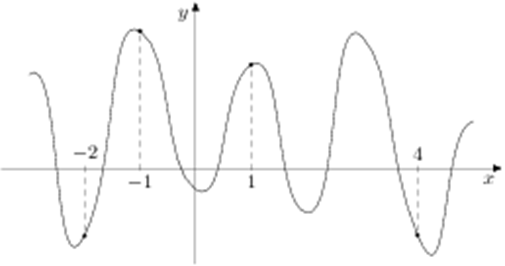
Задача 19. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки   ( — 2,; — 1,;1,;2). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку. Ответ ОТВЕТ: — 2. Решение Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках –1, 1 (так как в них функция убывает) и положительна в точках –2, 2 (так как в них функция возрастает). Следовательно, значение производной будет наибольшим либо в точке –2, либо в точке 2. В точке  –2  касательная образует угол наклона равный  ({rm{alpha }}), а в точке  2  угол ({rm{beta }}) (см. рисунок). Так как  ({rm{alpha }} > {rm{beta }})  и  ({rm{alpha }},,{rm{beta }} in left( {{0^ circ };,{{90}^ circ }} right)),  то  ({rm{tg}},{rm{alpha }} > {rm{tg}},{rm{beta }}), поэтому значение производной из 4 заданных точек в точке –2 будет наибольшим. Ответ: –2.
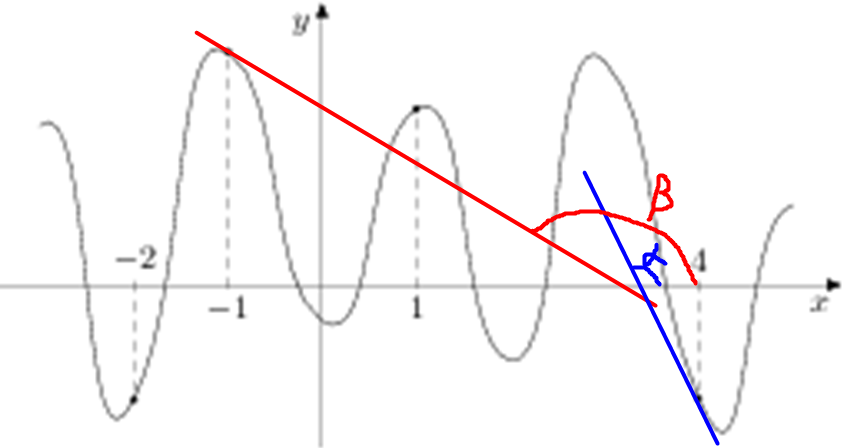
Задача 20. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки ( — 2,; — 1,;1,;4). В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. Ответ ОТВЕТ: 4. Решение Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках –1, 4 (так как в них функция убывает) и положительна в точках –2, 1 (так как в них функция возрастает). Следовательно, значение производной будет наименьшим либо в точке –1, либо в точке 4. В точке  4  касательная образует угол наклона равный  ({rm{alpha }}), а в точке  –1  угол ({rm{beta }}) (см. рисунок). Так как  ({rm{alpha }}, < ,{rm{beta }})  и  ({rm{alpha }},,{rm{beta }} in left( {{{90}^ circ };,{{180}^ circ }} right)),  то  ({rm{tg}},{rm{alpha }}, < ,{rm{tg}},{rm{beta }}), поэтому значение производной из 4 заданных точек в точке 4 будет наименьшим. Ответ: 4.
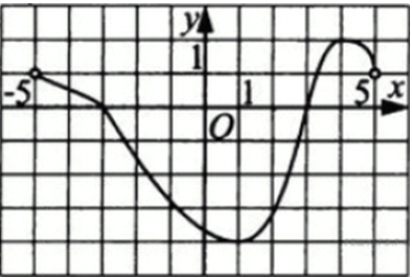
Задача 21. Функция (y = fleft( x right)) определена и непрерывна на отрезке (left[ { — 5;,5} right]). На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если   (fleft( { — 5} right) geqslant fleft( 5 right)). Ответ ОТВЕТ: 3. Решение На промежутках (left[ { — 5;, — 3} right]) и (left[ {3;,5} right]) производная принимает неотрицательные значения, следовательно, они являются промежутками возрастания функции (fleft( x right)), а на промежутке (left[ { — 3;3} right]) производная принимает неположительные значения, следовательно, он является промежутком убывания функции (fleft( x right)) (см. рисунок). Поэтому функция будет принимать наименьшее значения либо в точке –5, либо в точке 3. Так как по условию  (fleft( { — 5} right) ge fleft( 5 right)),  а  (fleft( 5 right) > fleft( 3 right)),  то (fleft( 3 right) < fleft( { — 5} right).)  Поэтому наименьшее значение функции (fleft( x right)) на отрезке (left[ { — 5;,5} right]) будет в точке 3. Ответ: 3.
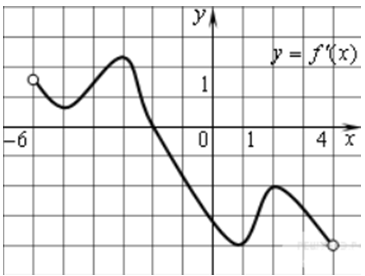
Задача 22. Функция (y = fleft( x right)) определена на промежутке (left( { — 6;,4} right)). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция (y = fleft( x right)) принимает наибольшее значение. Ответ ОТВЕТ: — 2. Решение На промежутке (left( { — 6;, — 2} right]) график производной расположен выше оси Оx, то есть значения производной неотрицательны, поэтому на этом промежутке функция (fleft( x right)) возрастает, а на промежутке (left[ { — 2;,4} right)) ниже оси Оx, то есть значения производной неположительны, поэтому на этом промежутке функция (fleft( x right)) убывает (см. рисунок). Следовательно, точка (x =  — 2) является точкой максимума и в ней на интервале (left( { — 6;,4} right)) функция будет принимать наибольшее значение. Ответ: –2.

Уважаемый посетитель!

Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в  30-дневный срок ответим на указанный вами адрес электронной почты

Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое

Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород

Тип обращения Вопрос Предложение Благодарность Жалоба

Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое

* Все поля обязательны для заполнения

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c  политикой конфиденциальности

Тренажер задания 7 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 7 — задачи на тригонометрические функции. Это задание на применение математических знаний при решении прикладных задач. Номер заданий соответствует номеру заданий в базе mathege.ru.

Тригонометрические функции

27998 Мяч бросили под углом α к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле:

.

При каком значении угла α (в градусах) время полeта составит 3 секунды, если мяч бросают с начальной скоростью v₀= 30 м/с? Считайте, что ускорение свободного падения g=10 м/с².

27999 Деталью некоторого прибора является квадратная рамка с намотанным на неe проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Нcdotм) определяется формулой где I = 2A — сила тока в рамке, B = 3 · 10^-3 Тл — значение индукции магнитного поля, l = 0,5 м — размер рамки, N = 1000 — число витков провода в рамке, α — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла α (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,75 Н · м?

28000 Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону:

где t — время в секундах, амплитуда U₀ = 2 В, частота ω = 120º/с, фаза φ = — 30º. Датчик настроен так, что если напряжение в нeм не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

28002 Очень лeгкий заряженный металлический шарик зарядом q = 2· 10^-6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет v = 5 м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол α с направлением движения шарика. Значение индукции поля B = 4 · 10^-3 Тл. При этом на шарик действует сила Лоренца, равная: (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла шарик оторвeтся от поверхности, если для этого нужно, чтобы сила F_л была не менее чем 2 · 10^-8 Н? Ответ дайте в градусах.

28003 Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой:

где v₀ = 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g = 10 м/с²). При каком наименьшем значении угла α (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?

28004 Небольшой мячик бросают под острым углом α к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле:

(м), где v₀ = 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с²). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 20 м?

28005 Плоский замкнутый контур площадью S = 0,5 м² находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой , где α — острый угол между направлением магнитного поля и перпендикуляром к контуру, a = 4 · 10^-4 Тл/с — постоянная, S — площадь замкнутого контура, находящегося в магнитном поле (в м²). При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать 10^-4 В?

28006 Трактор тащит сани с силой F = 80 кН, направленной под острым углом α к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScosα . При каком максимальном угле α (в градусах) совершeнная работа будет не менее 2000 кДж?

28007 Двигаясь со скоростью v = 3 м/с, трактор тащит сани с силой F = 50 кН, направленной под острым углом α к горизонту. Мощность, развиваемая трактором, вычисляется по формуле N = Fvcosα. Найдите, при каком угле α (в градусах) эта мощность будет равна 75 кВт (кВт — это ).

28008 При нормальном падении света с длиной волны λ = 400 нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением dsinφ = kλ. Под каким минимальным углом φ (в градусах) можно наблюдать второй максимум на решeтке с периодом, не превосходящим 1600 нм?

28009 Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле Q = mv²sin²α. Найдите, под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей.

28010 Катер должен пересечь реку шириной L = 100 м и со скоростью течения u = 0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением , где α — острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом α (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?

28011 Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью v = 3 м/с под острым углом α к рельсам. От толчка платформа начинает ехать со скоростью:

(м/с), где m = 80 кг — масса скейтбордиста со скейтом, а M = 400 кг — масса платформы. Под каким максимальным углом α (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?

28012 Груз массой 0,08 кг колеблется на пружине. Его скорость v меняется по закону:

где t — время с момента начала колебаний, T = 12 с — период колебаний, v₀ = 0,5 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = mv²/2, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.

28013 Груз массой 0,08 кг колеблется на пружине. Его скорость v меняется по закону:

где t — время с момента начала колебаний, T = 2 с — период колебаний, v₀ =0,5 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = mv²/2, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 1 секунду после начала колебаний. Ответ дайте в джоулях.

28014 Скорость колеблющегося на пружине груза меняется по закону v(t) = 5sinπt (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

ЕГЭ математика