На рисунке изображен график производной функции f(x), определенной на интервале (−8; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Спрятать решение
Решение.
Функция, дифференцируемая на отрезке [a; b], непрерывна на нем. Если функция непрерывна на отрезке [a; b], а её производная положительна (отрицательна) на интервале (a; b), то функция возрастает (убывает) на отрезке [a; b].
Поэтому промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции неотрицательна, то есть отрезкам [−7; −5] и [2; 5]. Наибольший из них — отрезок [2; 5], длина которого равна 3.
Ответ: 3.
ЕГЭ Профиль №7. Применение производной к исследованию функций
Скачать файл в формате pdf.
ЕГЭ Профиль №7. Применение производной к исследованию функций
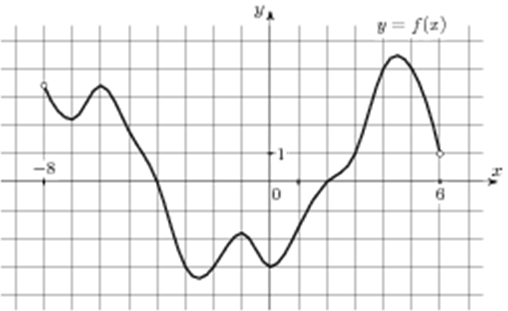
| Задача 1. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале (left( { — 8;6} right)). Определите количество целых точек, в которых производная функции (fleft( x right)) положительна.
Ответ
ОТВЕТ: 5. Решение
Производная функции положительна в тех интервалах, на которых функция возрастает, то есть на интервалах (left( { — 7; — 6} right),,,,left( { — 2,5;, — 1} right)) и (left( {0;,4,5} right).) Концы интервалов не включаем, так как они являются точками экстремума, а в них производная равна нулю. Интервалы возрастания выделены синим цветом (см. рисунок), а целые точки, входящие в эти интервалы -2, 1, 2, 3 и 4 выделены красным цветом и их количество равно 5. Ответ: 5. |
 |
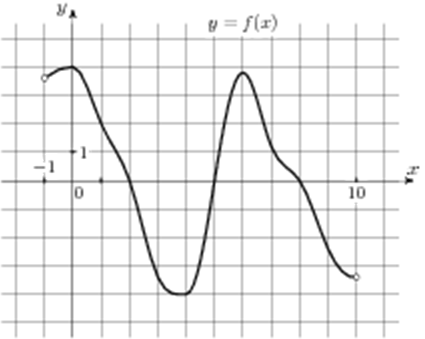
| Задача 2. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале(left( { — 1;10} right)). Определите количество целых точек, в которых производная функции отрицательна.
Ответ
ОТВЕТ: 6. Решение
Производная функции отрицательна в тех интервалах, на которых функция убывает, то есть на интервалах (left( {0;3,5} right)) и (left( {6;,10} right).) Концы интервалов 0, 3,5 и 6 не включаем, так как они являются точками экстремума, а в них производная равна нулю. Интервалы убывания выделены синим цветом (см. рисунок), а целые точки, входящие в эти интервалы 1, 2, 3, 7, 8 и 9 выделены красным цветом и их количество равно 6. Ответ: 6. |
 |
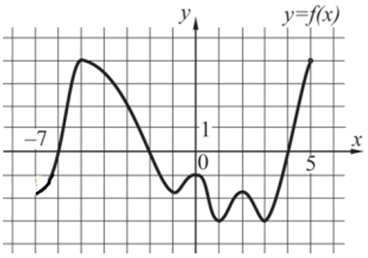
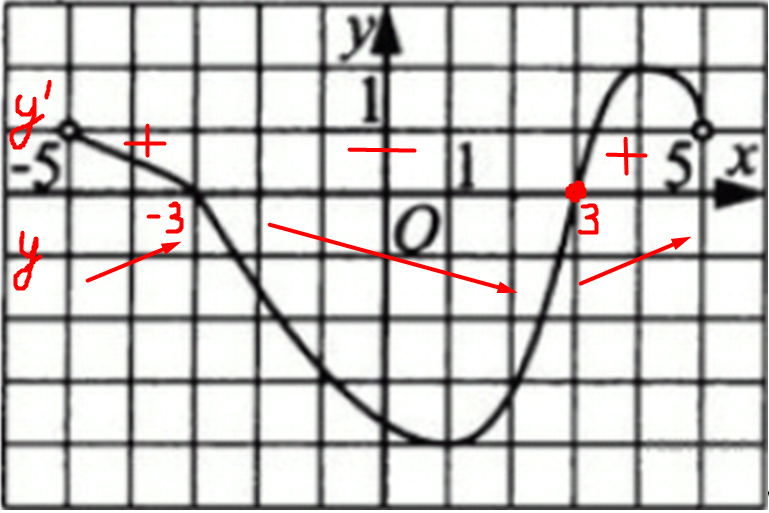
| Задача 3. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале (left( { — 7;5} right)). Найдите сумму точек экстремума функции (fleft( x right)).
Ответ
ОТВЕТ: 0. Решение
Точки максимума и минимума объединяются общим термином – точки экстремума. Выделим на графике точки экстремума красным цветом. Они имеют следующие координаты по оси абсцисс: -5, -1, 0, 1, 2 и 3, а их сумма равна ( — 5 — 1 + 0 + 1 + 2 + 3 = 0). Ответ: 0. |
 |
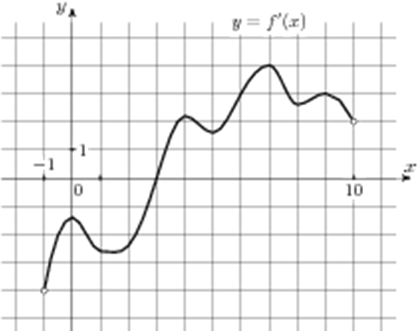
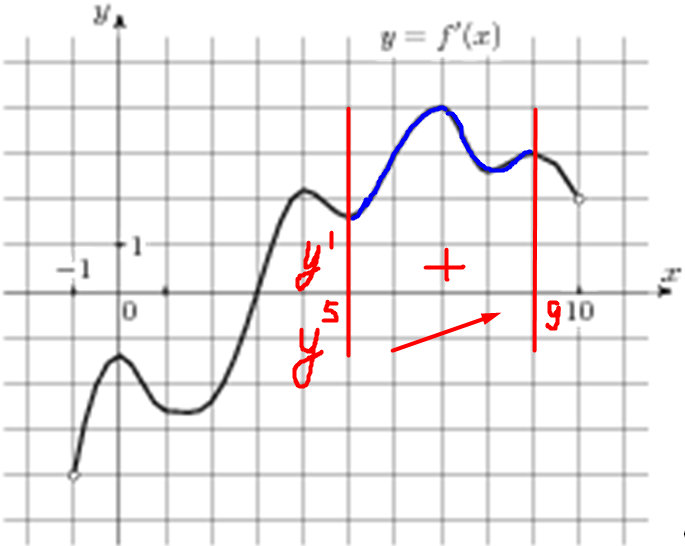
| Задача 4. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 1;10} right)). В какой точке отрезка (left[ {5;;9} right]) (fleft( x right)) принимает наибольшее значение?
Ответ
ОТВЕТ: 9. Решение
На отрезке (left[ {5;,9} right]) график производной расположен выше оси Оx (см. рисунок), следовательно, производная принимает положительные значения, поэтому функция на этом отрезке возрастает и принимает наибольшее значение в правом конце отрезка, то есть в точке 9. Ответ: 9. |
 |
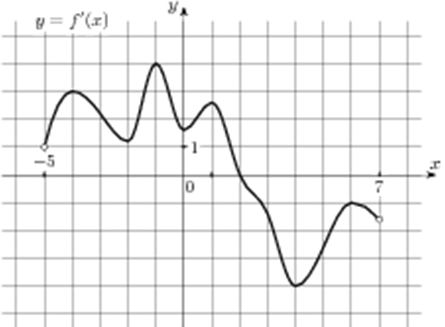
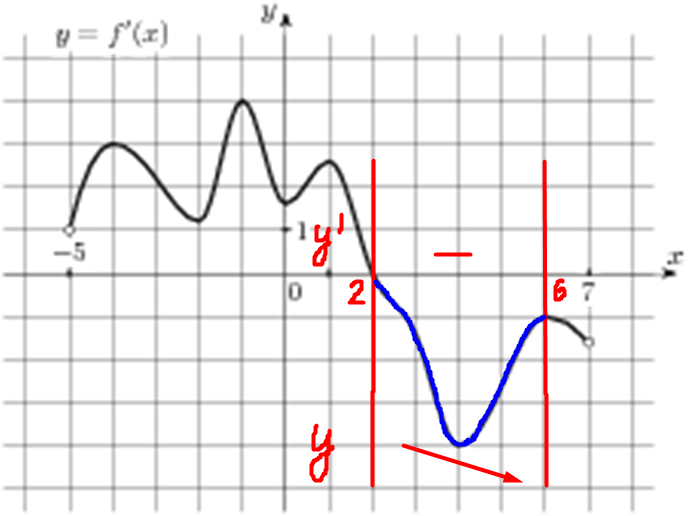
| Задача 5. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 5;7} right)). В какой точке отрезка (left[ {2;;6} right]) (fleft( x right)) принимает наименьшее значение?
Ответ
ОТВЕТ: 6. Решение
На отрезке (left[ {2;,6} right]) график производной расположен ниже оси Оx (см. рисунок), следовательно, производная принимает неположительные значения, поэтому функция на этом отрезке убывает и принимает наименьшее значение в правом конце отрезка, то есть в точке 6. Ответ: 6. |
 |
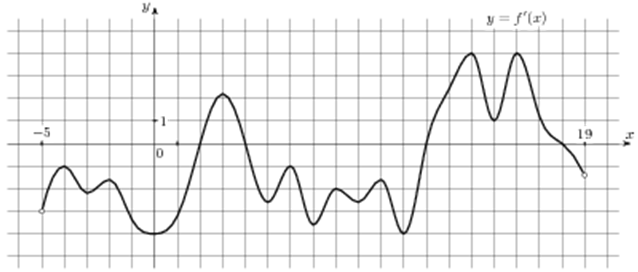
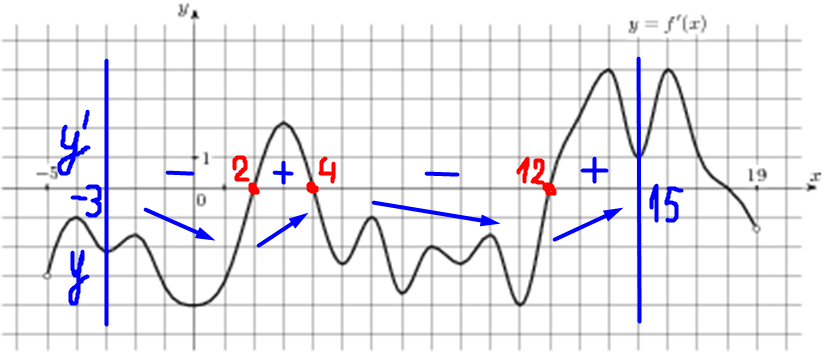
| Задача 6. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 5;19} right)). Найдите количество точек максимума функции (fleft( x right)), принадлежащих отрезку (left[ { — 3;;15} right]).
Ответ
ОТВЕТ: 1. Решение
Значение производной (f’left( x right)) в точках максимума и минимума функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек максимума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется с «+» на «-». В данном случае на отрезке (left[ { — 3;,15} right]) производная равна нулю в точках (x = 2,,,x = 4,,,x = 12) (выделены красным цветом см. рисунок). На промежутках (left[ { — 3;,2} right]) и (left[ {4;,12} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ {2;,4} right]) и (left[ {12;,15} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак с «+» на «-» только при переходе через точку (x = 4), поэтому функция имеет 1 точку максимума. Ответ: 1. |
 |
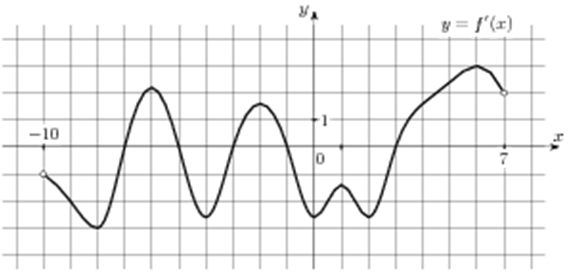
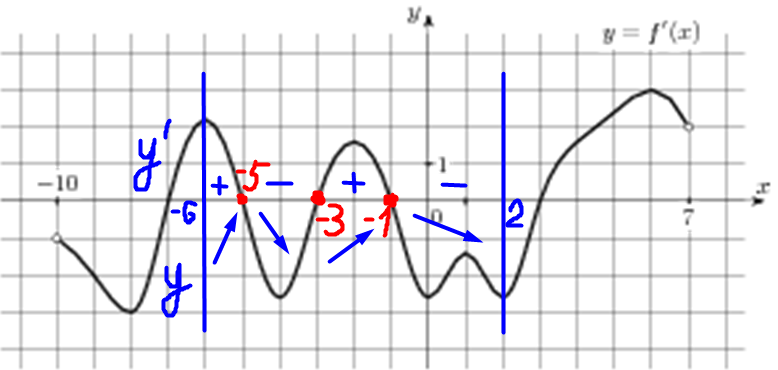
| Задача 7. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 10;7} right)). Найдите количество точек минимума функции (fleft( x right)), принадлежащих отрезку (left[ { — 6;;2} right]).
Ответ
ОТВЕТ: 1. Решение
Значение производной (f’left( x right)) в точках максимума и минимума функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек минимума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется с «-» на «+». В данном случае на отрезке (left[ { — 6;,2} right]) производная равна нулю в точках (x = — 5,,,x = — 3,,,x = — 1) (выделены красным цветом см. рисунок). На промежутках (left[ { — 5;, — 3} right]) и (left[ { — 1;,2} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ { — 6;, — 5} right]) и (left[ { — 3;, — 1} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак с «-» на «+» только при переходе через точку (x = — 3), поэтому функция имеет 1 точку минимума. Ответ: 1. |
 |
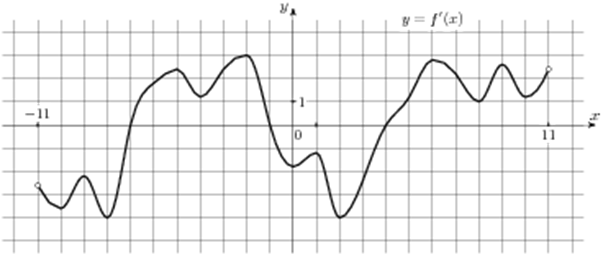
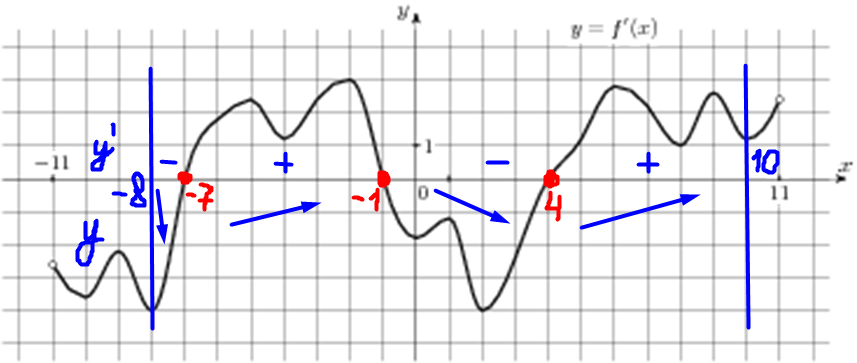
| Задача 8. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 11;11} right)). Найдите количество точек экстремума функции (fleft( x right)), принадлежащих отрезку (left[ { — 8;;10} right]).
Ответ
ОТВЕТ: 3. Решение
Значение производной (f’left( x right)) в точках экстремума (в точках максимума и минимума) функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения количества точек экстремума необходимо найти количество нулевых значений производной при переходе через которые знак производной меняется. В данном случае на отрезке (left[ { — 8;,10} right]) производная равна нулю в точках (x = — 7,,,x = — 1,,,x = 4) (выделены красным цветом см. рисунок). На промежутках (left[ { — 8;, — 7} right]) и (left[ { — 1;,4} right]) график производной расположен ниже оси Ox, следовательно, производная принимает неположительные значения, а на промежутках (left[ { — 7;, — 1} right]) и (left[ {4;,10} right]) график производной расположен выше оси Ox, следовательно, производная принимает неотрицательные значения. Таким образом, производная меняет знак при переходе через точки (x = — 7,,,x = — 1,,,x = 4), поэтому функция имеет 3 точки экстремума. Ответ: 3. |
 |
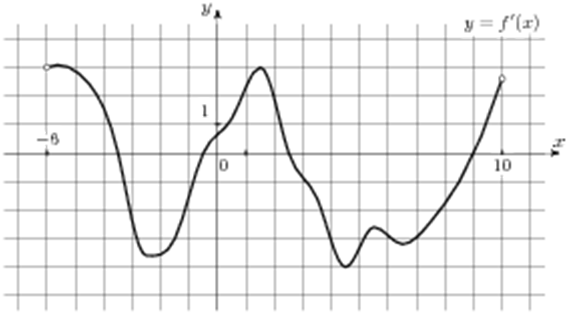
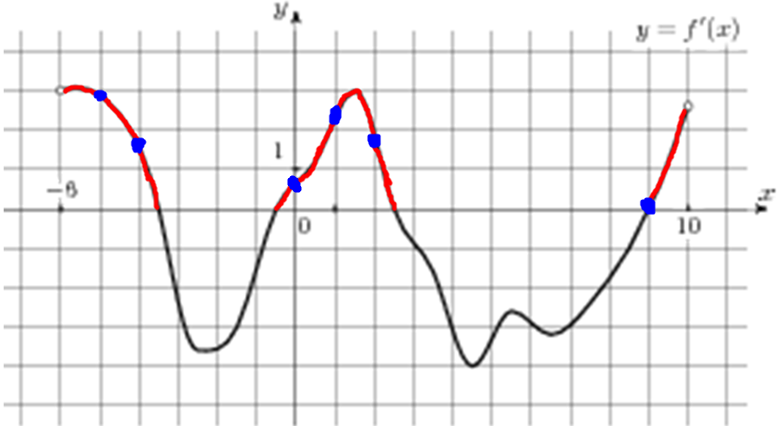
| Задача 9. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 6;10} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ
ОТВЕТ: 3. Решение
На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае производная принимает неотрицательные значения на промежутках (left( { — 6;, — 3,5} right],,,,left[ { — 0,5;,2,5} right]) и (left[ {9;,10} right)) (выделены красным цветом см. рисунок), которые и являются промежутками возрастания функции (fleft( x right)). Целые точки, входящие в эти промежутки по оси абсцисс: ( — 5,,,, — 4,,,,0,,,,1,,,,2,,,,9) (выделены синим цветом) и их сумма равна ( — 5 — 4 + 0 + 1 + 2 + 9 = 3.) Ответ: 3. |
 |
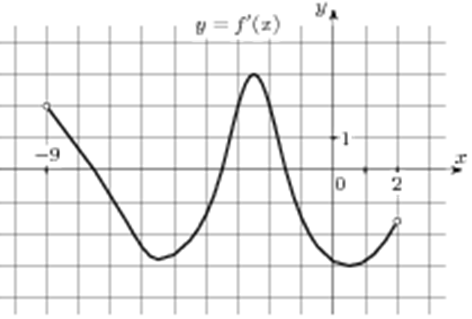
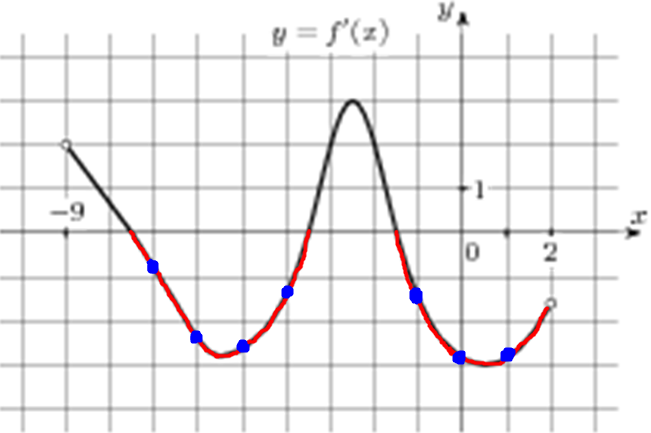
| Задача 10. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;2} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ
ОТВЕТ: — 22. Решение
На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае производная принимает неположительные значения на промежутках (,left[ { — 7,5;, — 3,5} right]) и (left[ { — 1,5;,2} right)) (выделены красным цветом см. рисунок), которые и являются промежутками убывания функции (fleft( x right)). Целые точки, входящие в эти промежутки по оси абсцисс: ( — 7,,,, — 6,,,, — 5,,,, — 4,,,, — 1,,,,0,,,,1) (выделены синим цветом) и их сумма равна ( — 7 — 6 — 5 — 4 — 1 + 0 + 1 = — 22.) Ответ: –22. |
 |
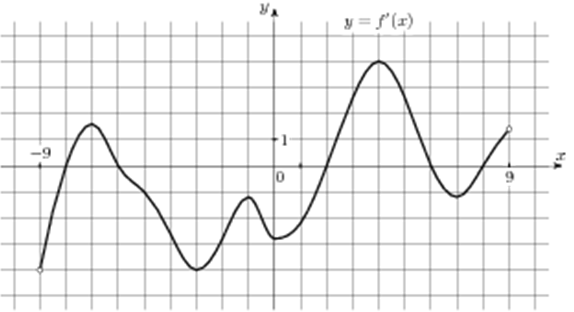
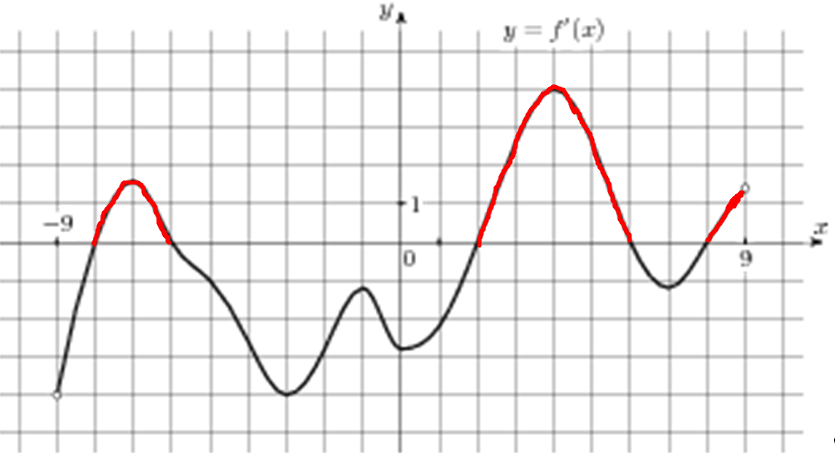
| Задача 11. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 9;9} right)). Найдите промежутки возрастания функции (fleft( x right)). В ответе укажите длину наибольшего из них.
Ответ
ОТВЕТ: 4. Решение
На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае производная принимает неотрицательные значения на промежутках (left[ { — 8;, — 6} right],,,,left[ {2;,6} right]) и (left[ {8;,9} right)) (выделены красным цветом см. рисунок), которые являются промежутками возрастания функции (fleft( x right)). Длина первого промежутка равна ( — 6 — left( { — 8} right) = 2,) длина второго (6 — 2 = 4,) а длина третьего (9 — 8 = 1.) Следовательно, длина наибольшего из них равна 4. Ответ: 4. |
 |
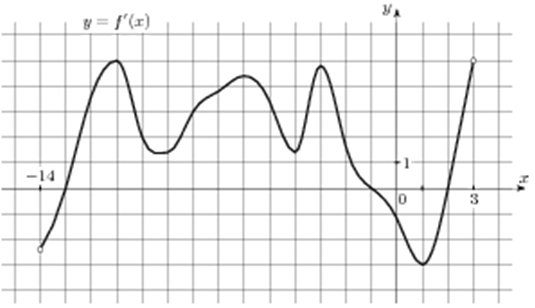
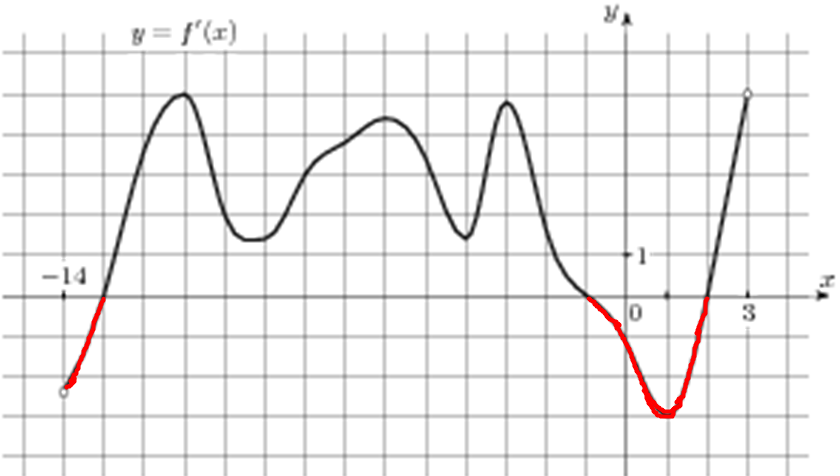
| Задача 12. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 14;3} right)). Найдите промежутки убывания функции (fleft( x right)). В ответе укажите длину наибольшего из них.
Ответ
ОТВЕТ: 3. Решение
На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае производная принимает неположительные значения на промежутках (left( { — 14;, — 13} right]) и (left[ { — 1;,2} right]) (выделены красным цветом см. рисунок), которые являются промежутками убывания функции (fleft( x right)). Длина первого промежутка равна ( — 13 — left( { — 14} right) = 1,) а длина второго (2 — left( { — 1} right) = 3.) Следовательно, длина наибольшего из них равна 3. Ответ: 3. |
 |
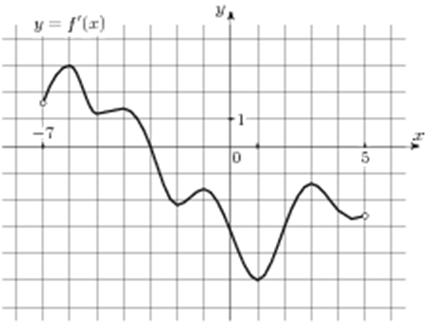
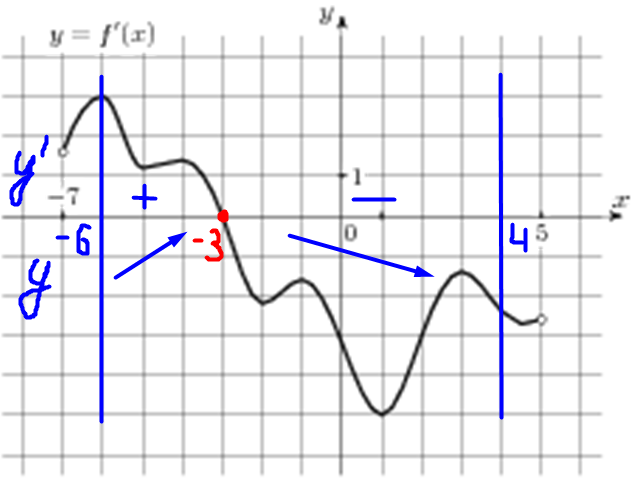
| Задача 13. На рисунке изображен график (y = f’left( x right)) — производной функции (fleft( x right)), определенной на интервале (left( { — 7;5} right)). Найдите точку экстремума функции (fleft( x right)), принадлежащую отрезку (left[ { — 6;,4} right]).
Ответ
ОТВЕТ: — 3. Решение
Значение производной (f’left( x right)) в точках экстремума (в точках максимума и минимума) функции (fleft( x right)) равно нулю. При этом в точках максимума производная меняет знак с «+» на «-», а в точках минимума с «-» на «+». Следовательно, для нахождения точки экстремума необходимо найти точку в которой производная равна нулю и при переходе через которую производная меняет знак. В данном случае на отрезке (left[ { — 6;,4} right]) производная равна нулю в точке (x = — 3) (выделена красным цветом см. рисунок), при переходе через которую производная меняет знак с «+» на «-». Следовательно, точка (x = — 3) является точкой экстремума. Ответ: –3. |
 |
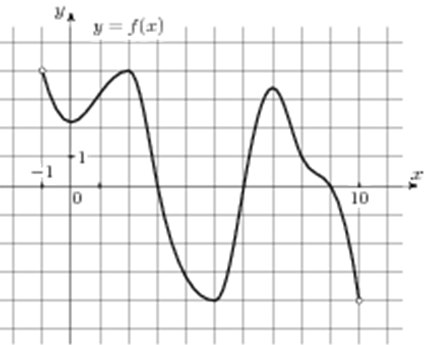
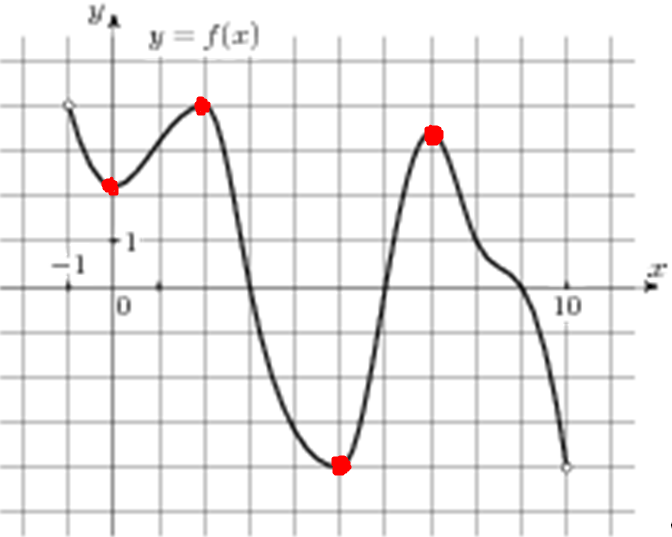
| Задача 14. На рисунке изображен график функции (y = fleft( x right)), определенной на интервале (left( { — 1;10} right)). Найдите количество точек, в которых производная функции (fleft( x right)) равна 0.
Ответ
ОТВЕТ: 4. Решение
Производная функции (fleft( x right)) равна нулю в точках экстремума (точки максимума и минимума). Выделим их на графике красным цветом (см. рисунок). Всего таких точек 4. Ответ: 4. |
 |
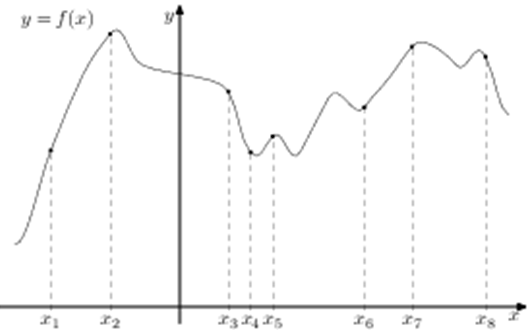
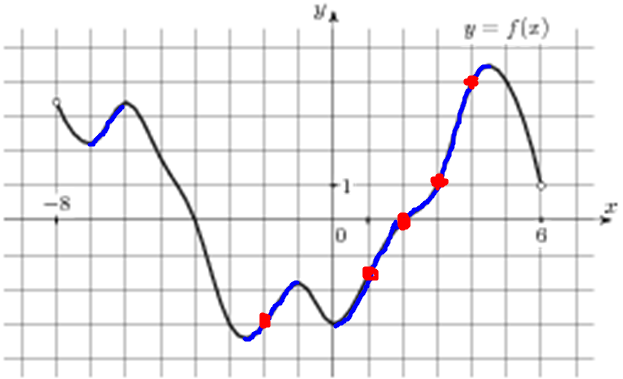
| Задача 15. На рисунке изображён график функции (y = fleft( x right)) и восемь точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек производная функции (fleft( x right)) положительна?
Ответ
ОТВЕТ: 5. Решение
Производная функции положительна в тех интервалах, на которых функция возрастает. В данном случае из 8 заданных точек функция возрастает в точках ({x_1},,,,{x_2},,,,{x_5},,,,{x_6},,,,{x_7},) то есть в 5 точках. Ответ: 5. |
 |
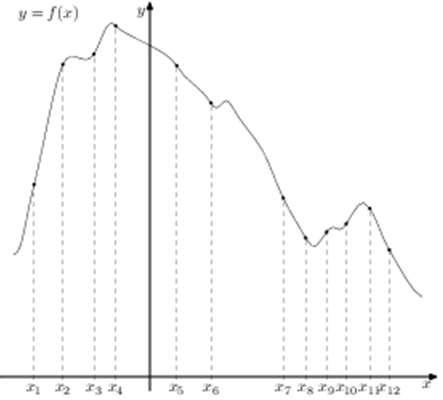
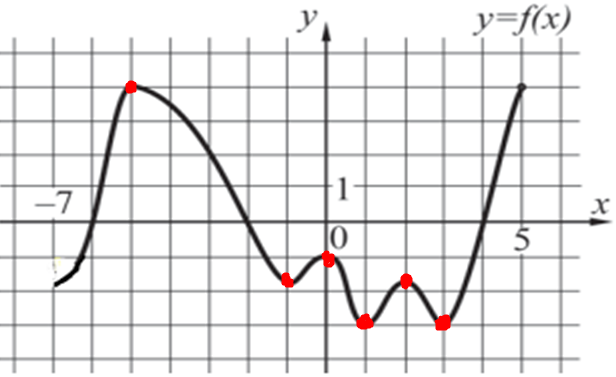
| Задача 16. На рисунке изображён график функции (y = fleft( x right)) и двенадцать точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_{12}}.) В скольких из этих точек производная функции (fleft( x right)) отрицательна?
Ответ
ОТВЕТ: 7. Решение
Производная функции отрицательна в тех интервалах, на которых функция убывает. В данном случае из 12 заданных точек функция убывает в точках ({x_4},,,,{x_5},,,,{x_6},,,,{x_7},,,,{x_8},,,,{x_{11}},,,,{x_{12}},) то есть в 7 точках. Ответ: 7. |
 |
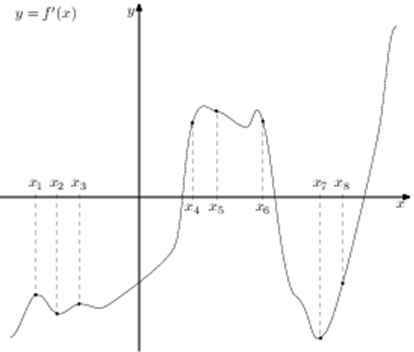
| Задача 17. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) возрастает?
Ответ
ОТВЕТ: 3. Решение
На промежутках возрастания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неотрицательные значения. В данном случае из 8 заданных точек производная неотрицательная в точках ({x_4},,,,{x_5},,,,{x_6},) то есть в 3 точках. Ответ: 3. |
 |
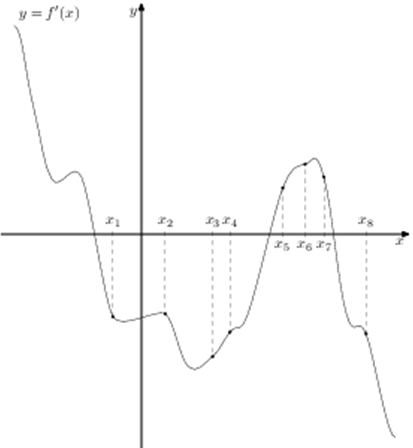
| Задача 18. На рисунке изображён график (y = f’left( x right)) производной функции (fleft( x right)) и восемь точек на оси абсцисс: ({x_1},,{x_2},;{x_3},,…,{x_8}). В скольких из этих точек функция (fleft( x right)) убывает?
Ответ
ОТВЕТ: 5. Решение
На промежутках убывания функции (fleft( x right)) её производная (f’left( x right)) должна принимать неположительные значения. В данном случае из 8 заданных точек производная неположительная в точках ({x_1},,,,{x_2},,,,{x_3},,,,{x_4},,,,{x_8},) то есть в 5 точках. Ответ: 5. |
 |
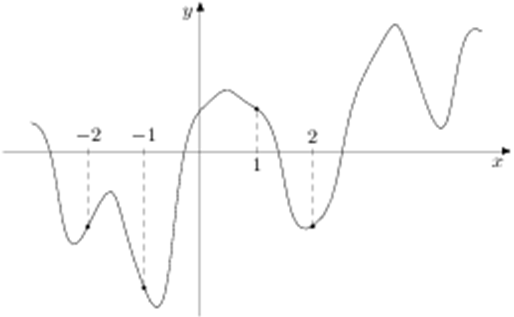
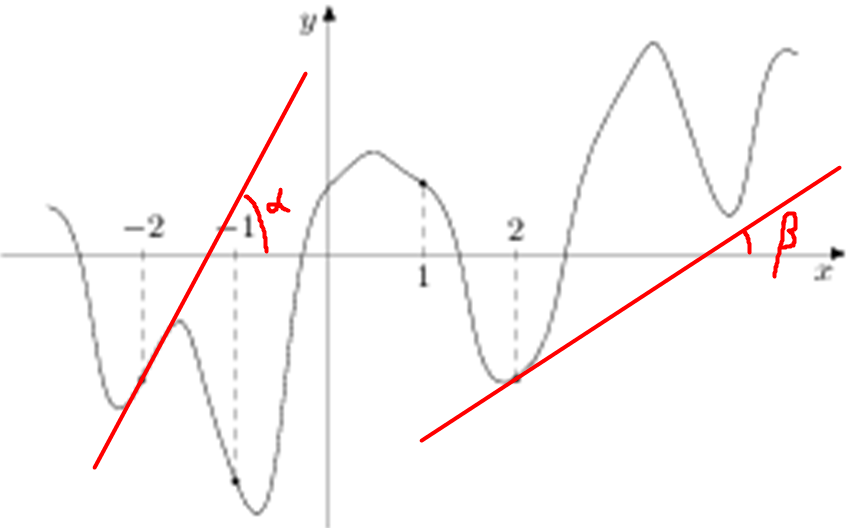
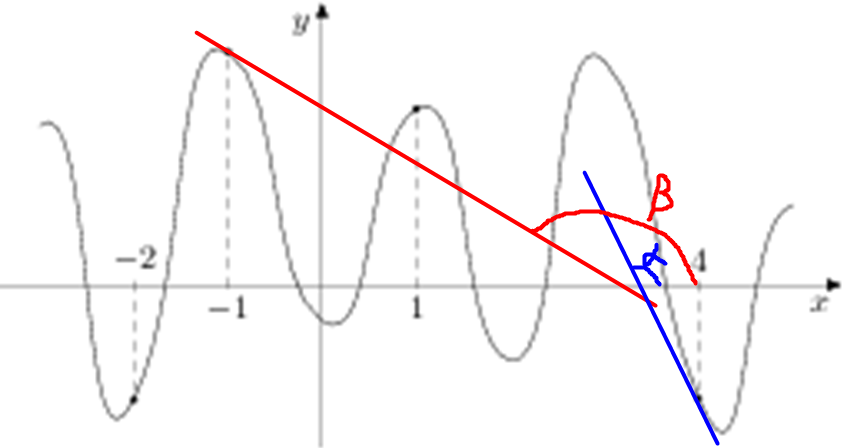
| Задача 19. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки ( — 2,; — 1,;1,;2). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ
ОТВЕТ: — 2. Решение
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках –1, 1 (так как в них функция убывает) и положительна в точках –2, 2 (так как в них функция возрастает). Следовательно, значение производной будет наибольшим либо в точке –2, либо в точке 2. В точке –2 касательная образует угол наклона равный ({rm{alpha }}), а в точке 2 угол ({rm{beta }}) (см. рисунок). Так как ({rm{alpha }} > {rm{beta }}) и ({rm{alpha }},,{rm{beta }} in left( {{0^ circ };,{{90}^ circ }} right)), то ({rm{tg}},{rm{alpha }} > {rm{tg}},{rm{beta }}), поэтому значение производной из 4 заданных точек в точке –2 будет наибольшим. Ответ: –2. |
 |
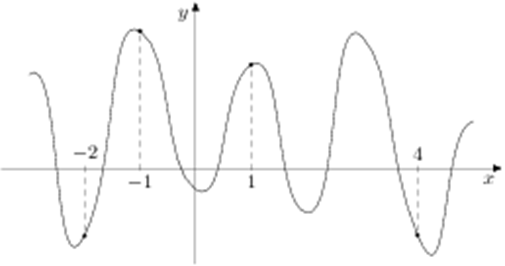
| Задача 20. На рисунке изображен график функции (y = fleft( x right)) и отмечены точки ( — 2,; — 1,;1,;4). В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ
ОТВЕТ: 4. Решение
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках –1, 4 (так как в них функция убывает) и положительна в точках –2, 1 (так как в них функция возрастает). Следовательно, значение производной будет наименьшим либо в точке –1, либо в точке 4. В точке 4 касательная образует угол наклона равный ({rm{alpha }}), а в точке –1 угол ({rm{beta }}) (см. рисунок). Так как ({rm{alpha }}, < ,{rm{beta }}) и ({rm{alpha }},,{rm{beta }} in left( {{{90}^ circ };,{{180}^ circ }} right)), то ({rm{tg}},{rm{alpha }}, < ,{rm{tg}},{rm{beta }}), поэтому значение производной из 4 заданных точек в точке 4 будет наименьшим. Ответ: 4. |
 |
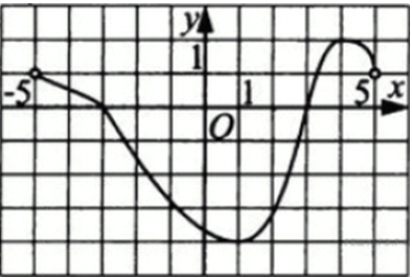
| Задача 21. Функция (y = fleft( x right)) определена и непрерывна на отрезке (left[ { — 5;,5} right]). На рисунке изображён график её производной. Найдите точку x0, в которой функция принимает наименьшее значение, если (fleft( { — 5} right) geqslant fleft( 5 right)).
Ответ
ОТВЕТ: 3. Решение
На промежутках (left[ { — 5;, — 3} right]) и (left[ {3;,5} right]) производная принимает неотрицательные значения, следовательно, они являются промежутками возрастания функции (fleft( x right)), а на промежутке (left[ { — 3;3} right]) производная принимает неположительные значения, следовательно, он является промежутком убывания функции (fleft( x right)) (см. рисунок). Поэтому функция будет принимать наименьшее значения либо в точке –5, либо в точке 3. Так как по условию (fleft( { — 5} right) ge fleft( 5 right)), а (fleft( 5 right) > fleft( 3 right)), то (fleft( 3 right) < fleft( { — 5} right).) Поэтому наименьшее значение функции (fleft( x right)) на отрезке (left[ { — 5;,5} right]) будет в точке 3. Ответ: 3. |
 |
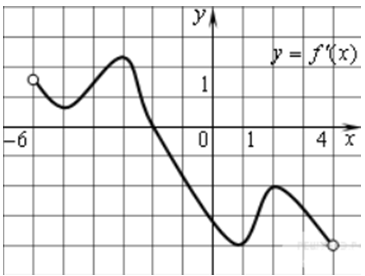
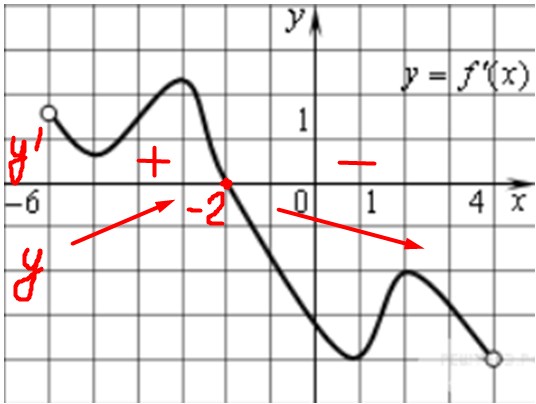
| Задача 22. Функция (y = fleft( x right)) определена на промежутке (left( { — 6;,4} right)). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция (y = fleft( x right)) принимает наибольшее значение.
Ответ
ОТВЕТ: — 2. Решение
На промежутке (left( { — 6;, — 2} right]) график производной расположен выше оси Оx, то есть значения производной неотрицательны, поэтому на этом промежутке функция (fleft( x right)) возрастает, а на промежутке (left[ { — 2;,4} right)) ниже оси Оx, то есть значения производной неположительны, поэтому на этом промежутке функция (fleft( x right)) убывает (см. рисунок). Следовательно, точка (x = — 2) является точкой максимума и в ней на интервале (left( { — 6;,4} right)) функция будет принимать наибольшее значение. Ответ: –2. |
 |
Задание 7 121215 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д2 № 121215
Прямая является касательной к графику функции Найдите B, учитывая, что абсцисса точки касания больше 0.
Условие касания графика функции и прямой задаётся системой требований:
В нашем случае имеем:
По условию, абсцисса точки касания положительна, поэтому X=1,5, B=−29.
Задания Д2 № 121215
—>
Задания Д2 121215.
Mathb-ege. sdamgia. ru
22.11.2019 7:10:17
2019-11-22 07:10:17
Источники:
Http://mathb-ege. sdamgia. ru/problem? id=121215
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 7 121215 егэ математика
Задание 7 121215 егэ математика
Задание 7 121215 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 6 № 121215
Прямая является касательной к графику функции Найдите B, учитывая, что абсцисса точки касания больше 0.
Условие касания графика функции и прямой задаётся системой требований:
В нашем случае имеем:
По условию, абсцисса точки касания положительна, поэтому X=1,5, B=−29.
—>
Задание 6 № 121215
В нашем случае имеем.
Ege. sdamgia. ru
29.08.2020 18:07:29
2020-08-29 18:07:29
Источники:
Http://ege. sdamgia. ru/test? pid=121215
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 7 121215 егэ математика
Задание 7 121215 егэ математика
Задание 7 121215 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 6 № 121215
Прямая является касательной к графику функции Найдите B, учитывая, что абсцисса точки касания больше 0.
Условие касания графика функции и прямой задаётся системой требований:
В нашем случае имеем:
По условию, абсцисса точки касания положительна, поэтому X=1,5, B=−29.
Задание 6 № 121215
—>
Задание 7 121215 егэ математика.
Math-ege. sdamgia. ru
26.06.2017 5:04:42
2017-06-26 05:04:42
Источники:
Http://math-ege. sdamgia. ru/test? pid=121215
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Первообразная функции»
Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1164
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна frac{4+3}{2}cdot 3=10,5.
Ответ
10,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1158
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1155
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.
Её площадь равна frac{5+3}{2}cdot 3=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1149
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.
Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1146
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).
Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.
Ответ
10
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №907
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №307
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
По формуле Ньютона-Лейбница S=F(-1)-F(-5).
F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.
F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.
F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.
Ответ
576
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №306
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.
Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №104
Тип задания: 7
Тема:
Первообразная функции
Условие
На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.
Показать решение
Решение
На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:
intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)
Подставим значение первообразной из условия и получим площадь фигуры:
F(-1)-F(-4)=
=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=
=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5
Ответ
4,5
Задание №103
Тип задания: 7
Тема:
Первообразная функции
Условие
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].
Показать решение
Решение
Формула первообразной имеет следующий вид:
f(x) = F'(x)
По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.
Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.
На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.
Ответ
3
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Регистрация Форум Текущее время: 10 мар 2023, 23:47 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Начать новую тему»> Ответить Тренировочный вариант №420
Тренировочный вариант №420
Страница 1 из 2 [ Сообщений: 12 ] На страницу 1, 2 След. Текущее время: 10 мар 2023, 23:47 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
Задание 1
Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
Скрыть
$$S=rp$$
$$p=frac{S}{r}$$
$$P=frac{2S}{r}=frac{2cdot208}{8}=52$$
Задание 2
В прямоугольном параллелепипеде $$АВСDА_1B_1C_1D_1$$ известны длины ребер: $$АВ = 11, AD = 20, AA_1 = 4.$$ Найдите расстояние от вершины $$С$$ до центра грани $$АА_1D_1D.$$
Ответ: 15
Скрыть
OC — искомое расстояние
$$A_1D=sqrt{416}=2sqrt{104}$$
$$BD=sqrt{104}$$
$$OC=sqrt{OD^2+DC^2}=sqrt{104+11^2}=15$$
Задание 3
Из лова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
Скрыть
Всего букв $$n= 8$$
Удовлетворяющих букв $$m= 5$$ — (а, к, с, и, у)
$$P(A) =frac{m}{n}=frac{5}{8} = 0,625$$
Задание 4
Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
Скрыть
Для того чтобы определить вероятность того, что извлеченный наугад кубик будет иметь окрашенную грань необходимо воспользоваться формулой классического определения вероятности:
$$P(A) = frac{m}{n},$$
Где P(A) – вероятность интересующего нас события A, то есть выбор кубика с окрашенной гранью, m – число исходов благоприятствующих событию, n – число всех равновозможных исходов испытания. Определим m и n:
$$n = 1000;$$
$$m = 100 + 100 + (100 – 20) + (100 – 20) + (100 – 20 – 16) + (100 – 20 – 16) = 488.$$
Тогда:
$$P(A) = frac{488}{1000} = 0,488.$$
Задание 5
Решите уравнение $$2cos^2frac{pi x}{18}+5sinfrac{pi x}{18}=-1.$$ В ответе запишите наибольший отрицательный корень уравнения.
Ответ: -3
Скрыть
$$2(1-sin^2frac{pi x}{18})+5sinfrac{pi x}{18}+1=0$$
$$-2sin^2frac{pi x}{18}+5sinfrac{pi x}{18}+3=0$$
$$2sin^2frac{pi x}{18}-5sinfrac{pi x}{18}-3=0$$
$$frac{5pmfrac{7}{125+24}}{4}$$
$$left[begin{matrix} sinfrac{pi x}{18}=3; н.р.\ sinfrac{pi x}{18}=-frac{1}{2} end{matrix}right.$$
$$frac{pi x}{18}=(-1)^{k+1}cdotfrac{frac{1}{pi}}{6}+pi k$$
$$x=(-1)^{k+1}cdotfrac{18}{6}+18k$$
$$x=(-1)^{k+1}cdot3+18k$$
при $$k=0$$ $$x=-3$$
Задание 6
Найдите значение выражения $$frac{6cos^234^{circ}-3}{cos 169^{circ}cdotcos 79^{circ}}.$$
Ответ: -6
Скрыть
$$frac{6cos^234^{circ}-3}{cos 169^{circ}cdotcos 79^{circ}}=frac{3(2cos^234^{circ}-1)cdot2}{-sin 79^{circ}cdotcos 79^{circ}cdot2}=-frac{(1+cos 68^{circ}-1)}{sin 158^{circ}}=-6$$
Задание 7
На рисунке изображен график $$y=f'(x)$$ – производной функции $$f(x),$$ определенной на интервале $$(–3;8).$$ В какой точке отрезка $$[–2;3]$$ функция $$f(x)$$ принимает наименьшее значение?
Ответ: 3
Скрыть
На отрезке $$[-2;3] f'(x)<0 Rightarrow$$ функция $$f(x)$$ монотонно убывает, достигая наименьшего значения при $$x=3.$$
Задание 8
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой $$m = 8$$ кг и радиуса $$R = 10$$ см, и двух боковых с массами $$M = 1$$ кг и с радиусами $$R+h.$$ При этом момент инерции катушки относительно оси вращения, выражаемый в $$кгcdot см^2,$$ задаётся формулой $$I=frac{(m+2M)R^2}{2}+M(2Rh+h^2).$$ При каком максимальном значении $$h$$ момент инерции катушки не превышает предельного значения $$625 кгcdot см^2?$$ Ответ выразите в сантиметрах.
Ответ: 5
Скрыть
$$frac{(8+2)cdot 10^2}{2}+1cdot (2cdot 10cdot h+h^2) le 625,$$
$$500+20h+h^2 le 625,$$
$$h^2+20h-125 le 0,$$
$$-25 le h le 5.$$
Значит, максимальное значение h, при котором момент инерции катушки не превышает предельного значения $$625 кг cdot см^2,$$ равно 5 см.
Задание 9
Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
Скрыть
Пусть масса сплавов равна М, обозначим процентное содержание никеля в первом сплаве через х.
Масса никеля в первом сплаве равна $$0,01cdot хcdot М,$$ во втором сплаве — $$0,01cdot х+0,25cdot М,$$ в третьем — $$0,01cdot х+0,29cdot М$$ (25+4=29% процентов). Четвертый сплав имеет массу $$3cdot М$$ и масса никеля в нем $$0,64cdot3cdot М.$$
Получаем уравнение:
$$0,01cdot хcdot М + (0,01cdot х+0,25)cdot М + (0,01cdot х+0,29)cdot М = 0,64cdot3cdot М$$ $$| :M$$
$$0,03cdot х + 0,25 + 0,29 = 1,92 (0,64*3=1,92)$$
$$0,03cdot х=1,38$$
$$х=0,46$$ или $$46$$ процентов.
Задание 10
На рисунке изображен график функции $$f(x)=acos x+b.$$ Найдите $$a.$$
Ответ: -2,5
Скрыть
Точка $$(0;-1,5)$$:
$$acos 0+b=-1,5$$
Точка $$(pi;frac{7}{2})$$:
$$acospi+b=frac{7}{2}$$
$$-left{begin{matrix} a+b=-frac{3}{2}\ -a+b=frac{7}{2} end{matrix}right.$$
$$2a=-5Rightarrow a=-2,5$$
Задание 11
Найдите наибольшее значение функции $$y=(4x-3)^2cdot(x+6)-9$$ на отрезке $$[-6;3].$$
Ответ: 720
Скрыть
$$y=(4x-3)^2cdot(x+6)-9$$
$$y’=2(4x-3)cdot4cdot(x+6)+(4x-3)^2$$
$$y’=(4x-3)cdot(8x+48+4x-3)$$
$$y’=(4x-3)cdot(12x+45)$$
$$y’=12(4x-3)(x+frac{15}{4})$$
$$x_{max}=-frac{15}{4}$$ и $$x_{min}=frac{3}{4}$$
$$y(-frac{15}{4})=(frac{4cdot(-15)}{4}-3)^2(-frac{15}{4}+6)-9=289cdotfrac{9}{4}-9=frac{289cdot9-4cdot9}{4}=frac{9cdot285}{4}$$
$$y(3)=81cdot9-9=720$$
Задание 12
A)Решите уравнение $$sin(3x-frac{3pi}{2})+sin(x+frac{7pi}{2})=sqrt{3}cos(x+frac{3pi}{2})$$
Б)Найдите все корни уравнения, принадлежащие отрезку $$[7pi ;8pi]$$
Ответ: А)$$pi n;-frac{pi}{6}+pi n;-frac{pi}{3}+pi n,nin Z$$ Б)$$7pi,frac{23pi}{3},frac{47pi}{6},8pi$$
Задание 13
В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4.
А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды.
Б) Найдите объем пирамиды CDKM.
Ответ: $$frac{9sqrt{11}}{7}$$
Задание 14
Решите неравенство: $$6(4x+3)(x^2-x+9)<9(4x+3)^2+(x^2-x+9)^2$$
Ответ: $$(-infty;)cup(0;13)cup(13;+infty)$$
Задание 15
В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
— каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.;
— к июлю 2029 года долг должен быть выплачен полностью.
Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
Задание 16
Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D.
А) Докажите, что прямые АС и BD параллельны.
Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
Ответ: 4
Задание 17
Найдите все значения параметра а, при каждом из которых система:
$$left{begin{matrix} x^2-2xy-3y^2=8,\ 2x^2+4xy+5y^2=a^4-4a^3+4a^2-12+sqrt{105} end{matrix}right.$$
имеет хотя бы одно решение.
Ответ: $$(-infty;-1]cup[3;+infty)$$
Задание 18
Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из-за чего количество книг с бирками «выгодно» уменьшилось.
а) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
в) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Ответ: да; да; 20
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задача 11 ЕГЭ математика профиль (ранее 12 задание) на исследование функции проверяет ваши знания по производным и первообразным. Обычно решается достаточно просто. Материал изучается чаще всего в 11 классе и требует знаний таблицы производных, первообразных и правил работы с ними.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 12 ЕГЭ математика профиль из 1 варианта сборника профильных заданий.
Найдите наибольшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наибольшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 12 ЕГЭ математика профиль из 2 варианта сборника профильных заданий.
Найдите наименьшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наименьшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 12 ЕГЭ математика профиль из 3 варианта сборника профильных заданий.
Найдите наибольшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наибольшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача 12 ЕГЭ математика профиль из 4 варианта сборника профильных заданий.
Найдите наибольшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наибольшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 5 варианта сборника профильных заданий.
Найдите точку максимума функции 
Нужно найти производную, приравнять к нулю и поставить получившиеся значения на отрезок. Далее выяснить знак производной и как себя ведет функция. Среди результатов выбрать точку, в которой функция слева возрастает, а справа убывает. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 6 варианта сборника профильных заданий.
Найдите наименьшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наименьшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 7 варианта сборника профильных заданий.
Найдите наименьшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наименьшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 8 варианта сборника профильных заданий.
Найдите наименьшее значение функции 
Нужно найти производную, приравнять к нулю и проверить получившиеся значения на попадание в отрезок. Далее подставить концы отрезка и найденные значения в функцию и посчитать результаты. Среди результатов выбрать наименьшее. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 9 варианта сборника профильных заданий.
Найдите точку максимума функции 
Нужно найти производную, приравнять к нулю и поставить получившиеся значения на отрезок. Далее выяснить знак производной и как себя ведет функция. Среди результатов выбрать точку, в которой функция слева возрастает, а справа убывает. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 10 варианта сборника профильных заданий.
Найдите наибольшее значение функции 
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 11 варианта сборника профильных заданий.
Найдите точку минимума функции 
Нужно найти производную, приравнять к нулю и поставить получившиеся значения на отрезок. Далее выяснить знак производной и как себя ведет функция. Среди результатов выбрать точку, в которой функция слева убывает, а справа возрастает. Не забывайте, что ответом не может быть бесконечная дробь.
Задача 12 ЕГЭ математика профиль (ЕГЭ-2019. Математика. Профильный уровень. 36 вариантов. И.В. Ященко)
Задача из 12 варианта сборника профильных заданий.
Найдите точку минимума функции 
Нужно найти производную, приравнять к нулю и поставить получившиеся значения на отрезок. Далее выяснить знак производной и как себя ведет функция. Среди результатов выбрать точку, в которой функция слева убывает, а справа возрастает. Не забывайте, что ответом не может быть бесконечная дробь.















.png)

.png)



 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 


















