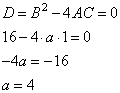Задание 7 9649 математика егэ - Помощь в подготовке к экзаменам и поступлению

Задания

Версия для печати и копирования в MS Word

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Спрятать решение

Решение.

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому

Ответ: 0,25.

Источник

Решу егэ математика 9649

Задание 6 № 9649

На рисунке изображён график функции Y=f(x) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции F(x) в точке X0.

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому

Задание 6 № 9649

Решу егэ математика 9649.

Ege. sdamgia. ru

14.08.2017 20:56:34

2017-08-14 20:56:34

Источники:

Https://ege. sdamgia. ru/problem? id=9649

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 9649

Решу егэ математика 9649

Задание 6 № 530551

На рисунке изображён график функции Y = F(X) и касательная к нему в точке с абсциссой X0. Найдите значение производной функции F(X) в точке X0.

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A(3; 3), B(3; −7), C(−5; −7). Угол наклона касательной к оси абсцисс будет равен:

Задание 6 № 530551

Построим треугольник с вершинами в точках A 3; 3 , B 3; 7 , C 5; 7.

Math-ege. sdamgia. ru

02.12.2020 22:22:19

2020-12-02 22:22:19

Источники:

Https://math-ege. sdamgia. ru/problem? id=530551

ЕГЭ–2022, информатика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика 9649

Решу егэ математика 9649

Задание 12 № 9649

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия.

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.

Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервётся.

Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

Сверху свободно

Снизу свободно

Слева свободно

Справа свободно

Выполняется, пока условие истинно.

Выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Сколько клеток лабиринта соответствуют требованию, что, начав движение в этой клетке и выполнив предложенную программу, Робот уцелеет и остановится в закрашенной клетке (клетка А6)?

При выполнении данной программе РОБОТ поступает следующим образом: сперва РОБОТ проверяет, свободна ли клетка слева или снизу от него. Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом цикле если у нижней стороны клетки, в которой находится РОБОТ, нет стены, он двигается вниз, в противном случае он перемещается влево. После этого возвращается к началу внешнего цикла. Проанализировав эту программу, приходим к выводу, что РОБОТ не может разбиться.

Проверив все клетки по выведенному нами правилу движения РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи, равно 25: A1-A6, B1, B3-B6, C1-C6, D1-D6, E1, E2.

Задание 12 № 9649

При выполнении данной программе РОБОТ поступает следующим образом сперва РОБОТ проверяет, свободна ли клетка слева или снизу от него.

Inf-ege. sdamgia. ru

22.10.2019 17:25:14

2019-10-22 17:25:14

Источники:

Https://inf-ege. sdamgia. ru/problem? id=9649

Источник


3649	На рисунке изображён график y = f ‘(x) — производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение? Решение График	На рисунке изображён график y = f ‘(x) — производной функции f(x), определённой на интервале (−5; 5) ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 7

3580	Прямая y=5x+11 является касательной к графику функции y=x^3+4x^2+9x+11. Найдите абсциссу точки касания Решение График	Прямая y=5x +11 является касательной к графику функции y= x3 +4×2 +9x +11 ! 36 вариантов ФИПИ Ященко 2023 Вариант 17 Задание 7

3508	Прямая y=5x-8 является касательной к графику функции y=6x^2+bx+16. Найдите b, учитывая, что абсцисса точки касания больше 0 Решение График	Прямая y=5x-8 является касательной к графику функции y=6×2 +bx +16 ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 7

3453	На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (–3;8). В какой точке отрезка [–2;3] функция f(x) принимает наименьшее значение? Решение	На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале ! Тренировочный вариант 397 от Ларина Задание 7

3280	Прямая y=6x+7 параллельна касательной к графику функции y=x^2-5x+6. Найдите абсциссу точки касания Решение График	Прямая y= 6x+7 параллельна касательной к графику функции y=x2 -5x +6 ! 36 вариантов ФИПИ Ященко 2022 Вариант 26 Задание 6

3257	На рисунке изображён график функции y=f(x). Функция F(x)=-10/27x^3-25/3x^2-60x-5/11. — одна из первообразных функций f(x). Найдите площадь закрашенной фигуры Решение График	Функция F(x)=-10/27×3 — 25/3×2 — 60x- 5/11 — одна из первообразных функций f(x) ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 18 Задание 6

3253	Материальная точка движется прямолинейно по закону x(t)=1/2t^3-2t^2+6t+25, где x — расстояние от точки отсчёта в метрах, t — время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=4 Решение	Материальная точка движется прямолинейно по закону x(t)= 1/2t3 -2t2 +6t +25 ! 36 вариантов ФИПИ Ященко 2022 Вариант 20 Задание 6

3249	На рисунке изображён график функции y=f(x). Функция F(x)=-1/4x^3-6x^2-189/4x-1. — одна из первообразных функций f(x). Найдите площадь закрашенной фигуры Решение График	На рисунке изображён график функции y=f(x). Функция F(x)=-1/4×3 — 6×2 -189/4x -1 — одна из первообразных функций f(x) ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 17 Задание 6

3231	На рисунке изображён график функции y=f(x). Функция F(x)=-4/9x^3-34/3x^2-280/3x-18/5. — одна из первообразных функций f(x). Найдите площадь закрашенной фигуры Решение График	Функция F(x) — одна из первообразных функций f(x). Найдите площадь закрашенной фигуры ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 16 Задание 6

3185	На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-9; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-8; 5] Решение	Найдите количество точек минимума функции f(x), принадлежащих отрезку [-8; 5] ! 36 вариантов ФИПИ Ященко 2022 Вариант 11 Задание 6

Показана страница 1 из 4

Clear

Hide

Источник

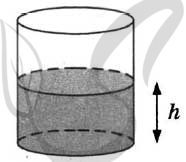
9689. В бак, имеющий форму цилиндра, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9689.

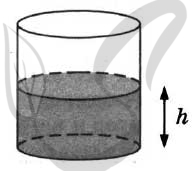
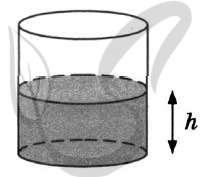
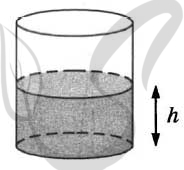
9669. Вода в сосуде цилиндрической формы находится на уровне h = 50 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в два с половиной раза больше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9669.

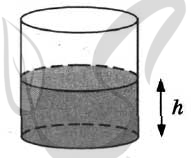
9649. Вода в сосуде цилиндрической формы находится на уровне h = 10 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания втрое меньше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9649.

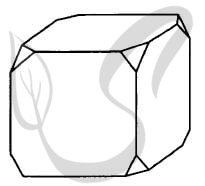
9629. От деревянного кубика отпилили все его вершины (см. рис.). Сколько рёбер у получившегося многогранника (невидимые рёбра на рисунке не изображены)?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9629.

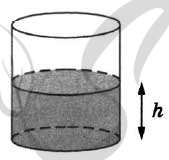
9609. Вода в сосуде цилиндрической формы находится на уровне h = 20 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в полтора раза меньше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9609.

9589. От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9589.

9569. Вода в сосуде цилиндрической формы находится на уровне h = 20 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в полтора раза меньше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9569.

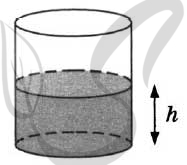
9549. Вода в сосуде цилиндрической формы находится на уровне h = 20 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9549.

9529. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в четыре раза больше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9529.

9509. Вода в сосуде цилиндрической формы находится на уровне h = 40 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в полтора раза меньше, чем у данного? Ответ дайте в сантиметрах.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 9509.

Для вас приятно генерировать тесты, создавайте их почаще

Источник

2022 год

база 6 (2022).pdf

Adobe Acrobat Document
188.2 KB

2022 год

база 8 (2022).pdf

Adobe Acrobat Document
523.5 KB

2022 год

база 10 (2022).pdf

Adobe Acrobat Document
406.8 KB

Прототипы задания 3 ЕГЭ по математике (базовый уровень)

база3.doc

Microsoft Word Document
39.0 KB

Прототипы задания 4 ЕГЭ по математике (базовый уровень)

база4.doc

Microsoft Word Document
157.5 KB

Прототипы задания 5 ЕГЭ по математике (базовый уровень)

база 5.doc

Microsoft Word Document
61.0 KB

Прототипы задания 6 ЕГЭ по математике (базовый уровень)

база 6.doc

Microsoft Word Document
38.0 KB

Прототипы задания 7 ЕГЭ по математике (базовый уровень)

база 7.doc

Microsoft Word Document
43.5 KB

прототипы задания 8 ЕГЭ по математике (базовый уровень)

база 8.doc

Microsoft Word Document
280.5 KB

Прототипы задания 9 ЕГЭ по математике (базовый уровень)

база 9.doc

Microsoft Word Document
114.0 KB

Прототипы задания 10 ЕГЭ по математике (базовый уровень)

база 10.doc

Microsoft Word Document
43.5 KB

Прототипы задания 12 ЕГЭ по математике (базовый уровень)

база 12.doc

Microsoft Word Document
199.0 KB

Прототипы задания 13 ЕГЭ по математике (базовый уровень)

база 13.doc

Microsoft Word Document
252.0 KB

Прототипы задания 14 ЕГЭ по математике (базовый уровень)

база 14.doc

Microsoft Word Document
482.5 KB

Прототипы задания 17 ЕГЭ по математике (базовый уровень)

база17.doc

Microsoft Word Document
379.5 KB

Прототипы задания 18 ЕГЭ по математике (базовый уровень)

база 18.doc

Microsoft Word Document
50.0 KB

Прототипы задания 19 ЕГЭ по математике (базовый уровень)

база 19.doc

Microsoft Word Document
33.5 KB

Прототипы задания 20 ЕГЭ по математике (базовый уровень)

база 20.doc

Microsoft Word Document
31.5 KB

Источник

: ЕГЭ по математике профиль

Прототипы задания №7 ЕГЭ по математике профильного уровня — задачи с прикладным содержанием. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №7 необходимо уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни.

Практика

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Максимальный балл за выполнение задания — 1

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 6

Связанные страницы:

Источник

Производная и первообразные функции

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

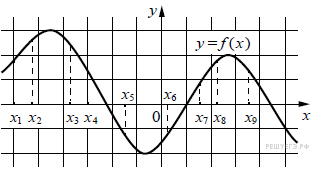
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

Алгоритм решения:

Рассматриваем график функции.
Ищем точки, в которых функция убывает.
Подсчитываем их количество.
Записываем ответ.

Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x₃, x₄, x₅, x₉. Таких точек 4.

Ответ: 4.

Второй вариант задания (из Ященко, №4)

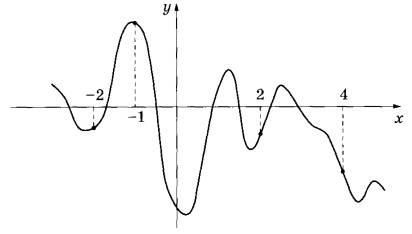
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Алгоритм решения:

Рассматриваем график функции.
Рассматриваем поведение функции в каждой из точек и знак производной в них.
Находим точки в наибольшим значением производной.
Записываем ответ.

Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

Третий вариант задания (из Ященко, №21)

Прямая является касательной к графику функции . Найдите а.

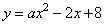
Алгоритм решения:

Приравняем уравнения касательной и функции.
Упрощаем полученное равенство.
Находим дискриминант.
Определяем параметр а, при котором решение единственное.
Записываем ответ.

Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:

Ответ: 4.

Источник