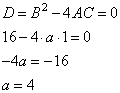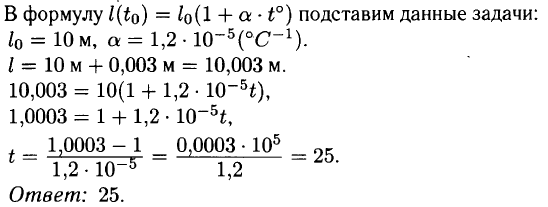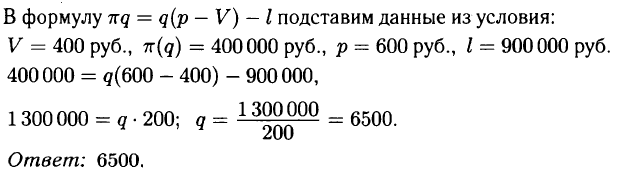Задание 7 егэ профильная математика объяснение всех видов заданий

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

.

Ответ: 3.

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает
		0		0

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

---

Производная и первообразные функции

---

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

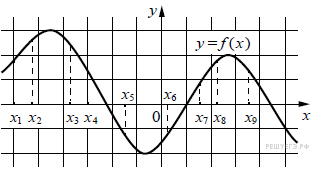
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

[/su_note]

Алгоритм решения:

1. Рассматриваем график функции.
2. Ищем точки, в которых функция убывает.
3. Подсчитываем их количество.
4. Записываем ответ.

Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x₃, x₄, x₅, x₉. Таких точек 4.

Ответ: 4.

---

Второй вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

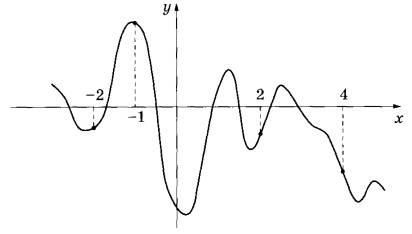
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

[/su_note]

Алгоритм решения:

1. Рассматриваем график функции.
2. Рассматриваем поведение функции в каждой из точек и знак производной в них.
3. Находим точки в наибольшим значением производной.
4. Записываем ответ.

Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

---

Третий вариант задания (из Ященко, №21)

[su_note note_color=”#defae6″]

Прямая  является касательной к графику функции . Найдите а.

[/su_note]

Алгоритм решения:

1. Приравняем уравнения касательной и функции.
2. Упрощаем полученное равенство.
3. Находим дискриминант.
4. Определяем параметр а, при котором решение единственное.
5. Записываем ответ.

Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:

Ответ: 4.

Даниил Романович | Просмотров: 11.9k

ЕГЭ по математике Профиль. Задание 7: Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 7

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 7 проверяет умение использовать приобретённые математические знания и навыки в практической деятельности и повседневной жизни. Задание представляет собой задачу из разных разделов физики, которая решается с помощью уравнения или неравенства. Ответом является целое число или конечная десятичная дробь.

План выполнения

1. Внимательно прочитайте условие задачи.
2. Подставьте в данную формулу известные величины. Определите критерии выполнения условия.
3. Составьте уравнение или неравенство. Решите его на черновике.
4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Для выполнения данного задания можно воспользоваться также теоретическим материалом к заданиям № 1 и № 4.

1) Задачи на Линейные, квадратные,
степенные уравнения и неравенства

В заданиях этого типа используют линейные, квадратные и степенные зависимости физических величин. При подготовке необходимо повторить основные методы решения линейных, квадратных и степенных уравнений и неравенств. Подробные формулы для вычисления физических величин даны в условии задачи. Все величины должны быть выражены в указанных единицах измерения.

Задача № 7 (1). Мотоциклист, движущийся со скоростью v₀ = 12 км/ч, разгоняется с постоянным ускорением а = 6км/ч . Расстояние до мотоциклиста от исходной точки определяется по формуле S = v₀t + (at²)/2. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне 15 км от исходной точки. Ответ укажите в минутах.

Решение: Мотоциклист будет находиться в зоне, если S ≤ 15 км. Подставим данные в формулу:
S = 24t + (6t²)/2 ≤ 15  ⇔  3t² + 12t – 15 ≤ 0   ⇔   t² + 4t – 5 ≤ 0   ⇔   –5 ≤ t ≤ 1.
Учитывая, что время — неотрицательная величина, получаем: 0 < t <1. Наибольшее время t = 1 ч = 60 мин.
Ответ: 60.
ПРИМЕЧАНИЕ: Ответ нужно указать в минутах.

Задача № 7 (2). Температура звёзд вычисляется по закону Стефана — Больцмана P = σST⁴, где Р — мощность излучения звезды (в ваттах), σ = 5,7 • 10^–8 Вт/(м²К⁴) – постоянная, S — площадь поверхности звезды (в квадратных метрах), Т — температура (в градусах Кельвина). Площадь поверхности звезды равна — 1/9 • 10²¹ м², мощность излучения 5,13 • 10²⁶ Вт. Найдите температуру звезды в градусах Кельвина.

Решение: Подставив значения, получаем: 5,7 • 10^–8 • 1/9 • 10²¹Т⁴ = 5,13 • 10²⁶;
Т⁴ = (5,13 • 10²⁶) / (5,7 – 10^–8 • 1/9 • 10²¹) = 8,1 • 10¹³;
Т = ⁴√[8,1 • 10¹³] = ⁴√[81 • 10¹²] = 3 • 10³ = 3000 (К).
Ответ: 3000.

2) Задачи на Рациональные и
иррациональные уравнения и неравенства

В заданиях этого типа используют рациональные и иррациональные зависимости физических величин. При подготовке необходимо повторить основные методы решения рациональных и иррациональных уравнений и неравенств.

Задача № 7 (3). Из–за эффекта Доплера частота звука зависит от скорости и меняется по закону f(v) = f₀ / (1 – v/c) (Гц), где с — скорость звука (с = 315 м/с). Первоначальная частота звука f₀ = 440 Гц. С какой минимальной скоростью приближался звук, если он отличался от первоначального не менее чем на 10 Гц? Ответ выразите в м/с.

Решение: Задача сводится к решению неравенства f(v) – f₀ ≥ 0 при f₀ = 440 Гц. Подставив значения, получим:
f₀ / (1 – v/c) – f₀ ≥ 10;  ⇒  440 / (1 – v/315) – 440 ≥ 10;   ⇒
1 – v/315 ≤ 44/45;   ⇒  v ≥ 315/45;  ⇒   v ≥ 7 м/с.
Минимальная скорость равна 7.
Ответ: 7.
ПРИМЕЧАНИЕ: В задаче нужно найти минимальную скорость.

Задача № 7 (4). Батискаф, равномерно погружающийся вертикально вниз, испускает ультразвуковые импульсы частотой 374 МГц. Скорость погружения батискафа вычисляется по формуле v = c • (f – f₀)/(f + f₀), где с = 1500 м/с — скорость звука в воде, f₀ — частота испускаемых импульсов, f — частота сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 4 м/с.

Решение: Задача сводится к решению уравнения при v = 4 (м/с). Подставив значения, получаем: 1500 • (f – 374)/(f + 374) = 4;
1500(f – 374) = 4(f + 374);   ⇒  f = 376 (МГц).
Ответ: 376.
ПРИМЕЧАНИЕ: Будьте внимательны: в задаче нужно найти частоту отражённого сигнала.

3) Задачи на Показательные и
логарифмические уравнения и неравенства

Задача № 7 (5). При адиабатическом процессе для идеального газа выполняется закон PV^k = 10⁵ Па•м⁵, где Р — давление в газе (в Па), V — объём газа (в м³), k = 2. Газ начинают сжимать. Какой наибольший объём V (в м³) будет занимать газ при давлении не ниже Р = 1,6 • 10 Па?

Решение: Из закона для идеального газа получаем: р = 10⁵/V^k = 10⁵/V². По условию задачи давление должно быть не ниже 1,6 • 10⁶ Па. Получим неравенство: 10⁵/V² ≥ 1,6 • 10°  <=>  V² ≤ 10⁵/(1,6 • 10⁶)  <=>  V² ≤ 1/16.
Учитывая, что V ≥ 0, приходим к решению V ≤ 1/4. Следовательно, наибольший объём будет равен V = 1/4 = 0,25.
Ответ: 0,25.

4) Задачи на Тригонометрические
уравнения и неравенства

Задача № 7 (6). Датчик преобразует электрический сигнал, изменяющийся со временем по закону U = U₀ sin(wt + φ), где t — время (в секундах), U₀ = 8 — напряжение (в вольтах), w = 160°/с — частота, φ = –10° — фаза. Датчик настроен так, что если напряжение в нём не ниже чем 4 В, загорается лампочка. Какую часть времени (в процентах) будет гореть лампочка на протяжении первой секунды после начала работы?

Решение: Подставив U = 4, получим 8 sin (160°t – 10°) = 4;
sin (160°t – 10°) = 1/2;   160°t – 10° = 30°;   t = 0,25. Это значит, что в течение 0,25 с напряжение было меньше 4 В и лампочка не горела. Тогда на протяжении первой секунды лампочка будет гореть 1 – 0,25 = 0,75 с, то есть 75 % времени.
Ответ: 75.
ПРИМЕЧАНИЕ: Периодичность синуса можно не учитывать.

---

Тренировочные задания с самопроверкой

№ 7.1. При температуре 0°С рельс имеет длину l₀ = 10 м. При возрастании температуры происходит тепловое расширение рельса и его длина, выраженная в метрах, меняется по закону l(t₀) = l₀(1 + a • t°), где a = 1,2 • 10^–5(°C)^–1 – коэффициент теплового расширения, t° –температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ дайте в градусах Цельсия.

№ 7.2. Некоторая компания продаёт свою продукцию по цене р = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют V = 400 руб., постоянные расходы предприятия составляют l = 900 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q) = q(p – V) – l. Определите месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 400 000 руб.

№ 7.3. Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1 + 8t – 5t², где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?

№ 7.4. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = Т₀ + bt + at², где t – время в минутах, Т₀ = 50 К, а = –0,25 К/мин2, b = 20 К/мин. Известно, что при температуре нагревательного элемента свыше 350 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

№ 7.5. . Груз массой 0,4 кг колеблется на пружине. Его скорость меняется по закону v = v₀ cos (2πt/T). где t – время с момента начала колебаний, Т = 2 с – период колебаний, v₀ = 0,3 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле Е = mv²/2, где m – масса груза в килограммах, v – скорость груза в м/с. Найдите кинетическую энергию груза через 4 секунды после начала колебаний. Ответ дайте в джоулях.

---

Вы смотрели: ЕГЭ по математике Профиль. Задание 7: Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Просмотров:
10 802