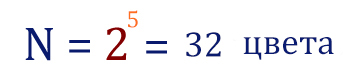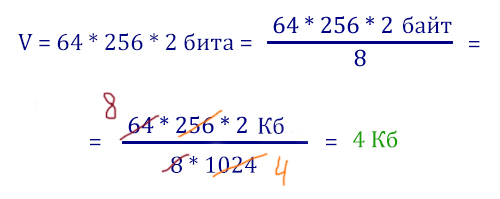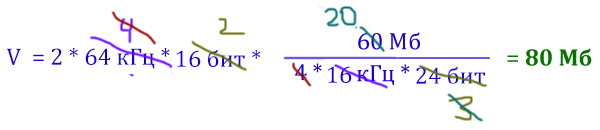Задание 7 информатика егэ музыкальный фрагмент - Помощь в подготовке к экзаменам и поступлению

Урок посвящен разбору задания 7 ЕГЭ по информатике

Содержание:

Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных

7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации

До ЕГЭ 2021 года — это было задание № 9 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию»

ФГБНУ «Федеральный институт педагогических измерений»

Кодирование текстовой информации

I = n * i

где:

n — количество символов

i — количество бит на 1 символ (кодировка)

Кодирование графической информации

Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.

Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
Разрешение – это количество пикселей на дюйм размера изображения.
Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
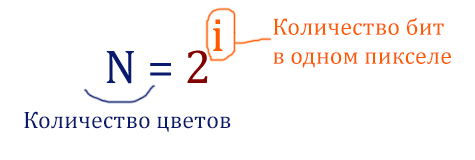
Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов.

Формула для нахождения количества цветов в используемой палитре:

i = log₂N

N — количество цветов
i — глубина цвета
В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 2⁸ вариантов на каждый из трех цветов.
R G B: 24 бита = 3 байта — режим True Color (истинный цвет)

Найдем формулу объема памяти для хранения растрового изображения:

I = M * N * i

где:

I — объем памяти, требуемый для хранения изображения
M — ширина изображения в пикселях
N — высота изображения в пикселях
i — глубина кодирования цвета или разрешение

Или можно формулу записать так:

I = N * i битов

где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)

* для указания объема выделенной памяти встречаются разные обозначения (V или I).

Следует также помнить формулы преобразования:

1 Мбайт = 2²⁰ байт = 2²³ бит,
1 Кбайт = 2¹⁰ байт = 2¹³ бит

Кодирование звуковой информации

Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.

Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.

Дискретизация, объяснение задания 7 ЕГЭ

T – интервал дискретизации (измеряется в с)
ƒ — частота дискретизации (измеряется в Гц, кГц)

* Изображение взято из презентации К. Полякова

Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.

Разрядность кодирования

* Изображение взято из презентации К. Полякова

Получим формулу объема звукового файла:

Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

S для моно = 1, для стерео = 2, для квадро = 4

Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:

✍ Решение:

I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 2³ * 1000 * 2⁴ * 2⁷ / 2³ = 2¹⁴ / 2³ =2¹¹ =
= 2048000 байт

Определение скорости передачи информации

Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)

Объем переданной информации I вычисляется по формуле:

I = V * t

I — объем информации
v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
t — время передачи

* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q

Скорость передачи данных определяется по формуле:

V = I/t

и измеряется в бит/с

Егифка ©:

Решение заданий 7 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Тема: Кодирование изображений

7_1:

Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Используем формулу нахождения объема:
Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
M x N:

160 * 160 = 20 * 2³ *  20 * 2³ = 400 * 2⁶ = 
= 25 * 2⁴ * 2⁶

Нахождение глубины кодирования i:

256 = 2⁸ 
т.е. 8 бит на пиксель  (из формулы кол-во цветов = 2ⁱ)

Находим объем:

I = 25 * 2⁴ * 2⁶ * 2³ = 25 * 2¹³ - всего бит на всё изображение

Переводим в Кбайты:

(25 * 2¹³) / 2¹³ = 25 Кбайт

Результат: 25

Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.2:

Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:
где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:

128 * 256 = 2⁷ * 2⁸ = 2¹⁵

В вышеуказанной формуле i — это глубина цвета, от которой зависит количество цветов в палитре:
Найдем i из той же формулы:

i = I / (M*N)

Учтем, что 24 Кбайт необходимо перевести в биты. Получим:

2³ * 3 * 2¹⁰ * 2³:
i = (2³ * 3 * 2¹⁰ * 2³) / 2¹⁵ = 
= 3 * 2¹⁶ / 2¹⁵ = 6 бит

Теперь найдем количество цветов в палитре:

2⁶ = 64 вариантов цветов в цветовой палитре

Результат: 64

Смотрите видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.3:

После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

i можно найти, зная количество цветов в палитре:

до преобразования: i = 8 (2⁸ = 256)
после преобразования: i = 2 (2² = 4)

Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей (разрешение):

I = x * 8
I - 18 = x * 2

Выразим x в первом уравнении:

x = I / 8

Подставим во второе уравнение и найдем I (объем файла):

I - 18 = I / 4
4I - I = 72
3I = 72
I = 24

Результат: 24

Подробный разбор 7 задания ЕГЭ смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.4:

Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:

42 = N * i
I = N / 4 * 4i

Выразим i в первом уравнении:

i = 42 / N

Подставим во второе уравнение и найдем I (объем файла):

[ I= frac {N}{4} * 4* frac {42}{N} ]

После сокращений получим:

I = 42

Результат: 42

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.5:

Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?

Типовые задания для тренировки

✍ Решение:

По формуле скорости передачи файла имеем:

где I — объем файла, а t — время

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
Изменим формулу получения объема файла для города Б:

[ I= frac {2*N * i}{3} ]

Для города А и Б заменим значения объема в формуле для получения скорости:

Город А:

[ V= frac {N*i}{72} ]

Город Б:

[ 3*V= frac{frac {4*N*i}{3}}{t} ]

или:

[ t*3*V= frac {4*N*i}{3} ]

Подставим значение скорости из формулы для города А в формулу для города Б:

[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]

Выразим t:

t = 4 * 72 / (3 * 3) = 32 секунды

Результат: 32

Другой способ решения смотрите в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.6:

Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для терировки

✍ Решение:

Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:

900 Кбайт = 2² * 225 * 2¹⁰ * 2³ = 225 * 2¹⁵

Посчитаем общее количество пикселей (из заданного размера):

1024 * 768 = 2¹⁰ * 3 * 2⁸

Определим объем памяти, необходимый для хранения не общего количества пикселей, а одного пикселя ([память для кадра]/[кол-во пикселей]):

[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]

9 бит на 1 пиксель

9 бит — это i — глубина кодирования цвета. Количество цветов = 2ⁱ:

2⁹ = 512

Результат: 512

Смотрите подробное решение на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

7_8: Демоверсия ЕГЭ 2018 информатика:

Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Посмотрим, что из формулы нам уже дано:

I = 320 Кбайт, 
N = 640 * 420 = 307200 = 75 * 2¹² всего пикселей, 
i - ?

Количество цветов в изображении зависит от параметра i, который неизвестен. Вспомним формулу:

количество цветов = 2ⁱ

Поскольку глубина цвета измеряется в битах, то необходимо объем перевести из Килобайт в биты:

320 Кбайт = 320 * 2¹⁰ * 2³ бит  = 320 * 2¹³ бит

Найдем i:

[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]

Найдем количество цветов:

2ⁱ = 2⁸ = 256

Результат: 256

Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

7_21: : ЕГЭ по информатике задание 7.21:

Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.

Определите количество цветов в палитре до оптимизации.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).

Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:

I = значение ppi² * N * i

Формула количества цветов:

количество цветов = 2ⁱ

Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:

Неэкономный вариант:
I = 5 Мбайт = 5 * 2²³ бит, 
N - ?, 
i - ?
300 ppi

Экономный вариант:
I = 512 Кбайт = 2⁹ * 2¹³ бит = 2²² бит, 
N - ?, 
i = 4 бит (2⁴ = 16)
150 ppi

Так как в экономном режиме нам известны все составляющие формулы, кроме разрешения (N), то найдем разрешение:

N = I / (i * 150*150 ppi)
N = 2²² / (4 * 22500)

Подставим все известные значения, включая найденное N, в формулу для неэкономного режима:

I = N * 300*300 ppi * i
5 * 2²³ = (2²² * 300 * 300 * i) / (22500 * 4);

Выразим i и вычислим его значение:

i = (5 * 2²³ * 22500 * 4) / (2²² * 300 * 300) = 9000 / 900 = 10 бит

По формуле нахождения количества цветов в палитре имеем:

2¹⁰ = 1024

Результат: 1024

Тема: Кодирование звука

7_7:

На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.

С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.

Типовые задания для тренировки

✍ Решение:

По формуле объема звукового файла получим:

I = β * t * ƒ * S

Из задания имеем:

I= 7500 Кбайт
β= 32 бита
t= 30 секунд
S= 4 канала

ƒ — частота дискретизации — неизвестна, выразим ее из формулы:

[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]

2⁴ = 16 КГц

Результат: 16

Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_9:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.

Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Для решения понадобится формула нахождения скорости передачи данных формулы:

V = I/t

Вспомним также формулу объема звукового файла:

I = β * ƒ * t * s

где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)

Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):

город Б: 
β - в 2 раза выше
ƒ - в 3 раза меньше
t - 15 секунд, 
пропускная способность (скорость V) - в 4 раза выше

Исходя из предыдущего пункта, для города А получаем обратные значения:

город А: 
β_Б / 2
ƒ_Б * 3
I_Б / 2
V_Б / 4
t_Б / 2, t_Б * 3, t_Б * 4  -  ?

Дадим объяснения полученным данным:
так как глубина кодирования (β) для города Б выше в 2 раза, то для города А она будет ниже в 2 раза, соответственно, и t уменьшится в 2 раза:

t = t/2

так как частота дискретизации (ƒ) для города Б меньше в 3 раза, то для города А она будет выше в 3 раза; I и t изменяются пропорционально, значит, при увеличении частоты дискретизации увеличится не только объем, но и время:

t = t * 3

скорость (V)(пропускная способность) для города Б выше в 4 раза, значит, для города А она будет ниже в 4 раза; раз скорость ниже, то время выше в 4 раза (t и V — обратно пропорциональная зависимость из формулы V = I/t):

t = t * 4

Таким образом, с учетом всех показателей, время для города А меняется так:

[ t_А = frac {15}{2} * 3 * 4 ]

90 секунд

Результат: 90

Подробное решение смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7.10:

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.

Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов

Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:

1 состояние:
S = 2 канала
I = 30 Мбайт

2 состояние:
S = 1 канал
β = в 2 раза выше
ƒ = в 1,5 раза ниже
I = ?

Так как изначально было 2 канала связи (S), а стал использоваться один канал связи, то файл уменьшился в 2 раза:

I = I / 2

Глубина кодирования (β) увеличилась в 2 раза, то и объем (I) увеличится в 2 раза (пропорциональная зависимость):

I = I * 2

Частота дискретизации (ƒ) уменьшилась в 1,5 раза, значит, объем (I) тоже уменьшится в 1,5 раза:

I = I / 1,5

Рассмотрим все изменения объема преобразованного файла:

I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт

Результат: 20

Смотрите видеоразбор данной задачи:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звуковых файлов:

ЕГЭ по информатике задание 7_11:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время

Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:

А:
t = 100 c.

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.

✎ 1 способ решения:

Скорость передачи данных (пропускная способность) зависит от времени передачи файла: чем больше время, тем ниже скорость. Т.е. во сколько раз увеличится время передачи, во столько раз уменьшится скорость и наоборот.
Из предыдущего пункта видим, что если мы вычислим, во сколько раз уменьшится или увеличится время передачи файла в город Б (по сравнению с городом А), то мы поймем, во сколько раз увеличится или уменьшится скорость передачи данных в город Б (обратная зависимость).
Соответственно, представим, что преобразованный файл передается в город А. Объем файла изменился в 3/4 раза (глубина кодирования (β) в 3 раза выше, частота дискретизации (ƒ) в 4 раза ниже). Объем и время изменяются пропорционально. Значит и время изменится в 3/4 раза:

 t_{A для преобразов.} = 100 секунд * 3 / 4 = 75 секунд

Т.е. преобразованный файл передавался бы в город А 75 секунд, а в город Б 15 секунд. Вычислим, во сколько раз снизилось время передачи:

75 / 15 = 5

Раз время передачи в город Б снизилось в 5 раз, соответственно, скорость увеличилась в 5 раз.

Ответ: 5

✎ 2 способ решения:

Выпишем отдельно все данные, касающиеся файла, переданного в город А:
```
А:
t_А = 100 c.
V_А = I / 100
```
Поскольку увеличение или уменьшение во сколько-то раз разрешения и частоты дискретизации приводит к соответствующему увеличению или уменьшению объема файла (пропорциональная зависимость), то запишем известные данные для преобразованного файла, переданного в город Б:

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.
I_Б = (3 / 4) * I
V_Б = ((3 / 4) * I) / 15

Теперь найдем соотношение V_Б к V_А:

[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]

(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5

Результат: 5

Подробный видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_12:

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

✍ Решение:

Вспомним формулу объема звукового файла:

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:

β = 32 бита
ƒ = 32кГц = 32000Гц
t = 2 мин = 120 с

Подставим данные в формулу; учтем, что результат необходимо получить в Мбайтах, соответственно, произведение будем делить на 2²³ (2³ (байт) * 2¹⁰ (Кбайт) * 2¹⁰(Мбайт)):

(32 * 32000 * 120) / 2²³ = 
=( 2⁵ * 2⁷ * 250 * 120) / 2²³ = 
= (250*120) / 2¹¹ = 
= 30000 / 2¹¹ = 
= (2⁴ * 1875) / 2¹¹ =
= 1875 / 128 ~ 14,6

Полученный результат значения объема умножим на 4 с учетом количества каналов связи:

 14,6 * 4 = 58,5

Ближайшее число, кратное 10 — это 60.

Результат: 60

Смотрите подробное решение:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):

Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.

Какая из приведённых ниже величин наиболее близка к размеру полученного файла?

1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения:

I = 48000 * 32 * 300 * 2

Поскольку значения большие, необходимо числа 48000 и 300 выразить в степенях двойки:

48000 | 2
24000 | 2
12000 | 2
 6000 | 2     = 375 * 2⁷
 3000 | 2
 1500 | 2
  750 | 2 
  375 | 2 - уже не делится
 187,5

300 | 2     = 75 * 2²
150 | 2
 75 | 2 - уже не делится 
37,5

Получим:

I = 375 * 75 * 2¹⁵

В предложенных вариантах ответа видим, что результат везде в Мбайт. Значит, необходимо разделить полученный нами результат на 2²³ (2³ * 2¹⁰ * 2¹⁰):

I = 375 * 75 * 2¹⁵ / 2²³ = 28125 / 2⁸

Найдем приближенное к числу 28125 значение в степени двойки:

Получаем:

2¹⁰ * 2⁵ = 2¹⁵ = 32768
2¹⁰ * 2⁴ = 2¹⁴ = 16384

Число 28125 лежит между этими значениями, значит берем их:

2¹⁵ / 2⁸ = 2⁷ = 128
2¹⁴ / 2⁸ = 2⁶ = 64

Выбираем ответ, значение в котором находится между двумя этими числами: вариант 4 (110 Мбайт)

Результат: 4

Подробное решение ГВЭ задания 7 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_20:

Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения. Для удобства будем использовать степени двойки:

ƒ = 4 кГЦ = 4 * 1000 Гц ~ 2² * 2¹⁰
B = 64 бит = 2⁶ / 2²³ Мбайт
t = 1 мин = 60 c = 15 * 2² c
S = 2

Подставим значения в формулу объема звукового файла:

I = 2⁶ * 2² * 2¹⁰ * 15 * 2² * 2¹ / 2²³ = 15/4 ~ 3,75

Ближайшее целое, кратное двум — это число 4

Результат: 4

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование видео

7_22:

Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.

Сколько Мбайт в среднем занимает 1 минута исходного видео?

Типовые задания для тренировки

✍ Решение:

Посмотрим, как изменялись параметры файла до преобразования и после:

ДО:
ƒ = 120, 
i = 24 бит

ПОСЛЕ:
ƒ = 20, 
i = 8 бит (2⁸ = 256)
t = 10 секунд
I = 512 Кбайт = 2⁹ Кбайт

Поскольку после преобразования количество кадров в секунду уменьшилось в 6 раз (120 / 20 = 6), а количество бит на пиксель уменьшилось в 3 раза (24 / 8 = 3), то и объем уменьшился в целом в 18 раз (6 * 3 = 18).
Вычислим объем файла, передаваемого за 10 секунд, до его преобразования:

за 10 секунд: I * 18 = 2⁹ * 18 Кбайт = (2⁹ * 18) . 2¹⁰ Мбайт = 9 Мбайт

Чтобы получить объем, переданный за 1 минуту, необходимо полученное значение умножить на 6:

за 1 мин: 9 * 6 = 54 Мбайт

Результат: 54

Тема: Скорость передачи данных

ЕГЭ по информатике задание 7_13:

Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.

Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Что нам известно из формулы (для удобства решения будем использовать степени двойки):

V = 128000 бит/с = 2¹⁰ * 125 бит/с
t = 1 мин = 60 с = 2² * 15 с
1 символ кодируется 16-ю битами
всего символов - ?

Если мы найдем, сколько бит необходимо для всего текста, тогда, зная что на 1 символ приходится 16 бит, мы сможем найти сколько всего символов в тексте. Таким образом, найдем объем:

Q = 2¹⁰ * 125 * 2² * 15 = 
= 2¹² * 1875 бит на все символы

Когда мы знаем, что на 1 символ необходимо 16 бит, а на все символы 2¹² * 1875 бит, то можем найти общее количество символов:

кол-во символов = 2¹² * 1875 / 16 = 2¹² * 1875 / 2⁴ = 
= 2⁸ * 1875 = 480000

Результат: 480000

Разбор 7 задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_14:

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁶ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.

Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Определим, что нам известно:

Вася: V = 2¹⁷ бит/с
Петя: V = 2¹⁶ бит/с
Общий объем Q = 8 Мбайт

Для начала переведем объем в биты:

Q = 8Мбайт = 8 * 2²³ бит = 2³ * 2²³ = 2²⁶ бит

Также известно, что сначала 1024 Кбайта будут передаваться по скоростному каналу Васи со скоростью 2¹⁷ бит/с (примем за t1), а затем все 8 Мбайт будут передаваться по низкоскоростному каналу (примем за t2). Найдем время по двум промежуткам:

t1 = 1024 Кбайт / 2¹⁷ = 2¹⁰ * 2¹³ бит / 2¹⁷ = 
= 2¹⁰ / 2⁴ = 64 с

t2 = 2²⁶ / 2¹⁶ = 2¹⁰ = 1024 c

Найдем общее время:

t = t1 + t2 = 64 + 1024 = 1088

Результат: 1088

Подробный разбор смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_15:

Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Отсюда получаем формулу для времени:
Для нахождения времени вычислим объем сообщения по формуле:

N — общее количество пикселей или разрешение, 
i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Q = 4 * 480000

Теперь найдем время:

t = 4 * 480000 / 32000 = 60 секунд

Результат: 60

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_16:

Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?

✍ Решение:

Формула скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

При 1/3 t скорость (V) равна 60 Мбит/c
При 2/3 t скорость(V) равна 90 Мбит/c
Объем переданных данных выразим в Мбитах:

1 Мбайт = 8 Мбит

 Q = 9000 Мбайт * 8 = 72000 Мбит

Из формулы выразим объем:
Так как общий объем данных у нас известен, получим уравнение:

(60 * 1/3t)  + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин

Результат: 15

Решение задания можно посмотреть и на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7.17:

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,
объем сжатого архиватором документа равен 20% от исходного,
время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

Типовые задания для тренировки

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 2²³ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Получим t с учетом времени на сжатие и распаковку:

t = Q / V + 7 + 1 = 8 + 2²³ / 2¹⁸ = 8 + 2⁵ = 40 c

Рассмотрим способ Б:

Для этого способа можно сразу найти время (по формуле):

t = Q / V = 5 * 2²³ / 2¹⁸ = 5 * 2⁵ = 5 * 32 = 160 c

Получаем, что способ А быстрее; вычислим насколько быстрее:

160 с - 40 с = 120 с

Результат: А120

Решение также можно посмотреть в видеоуроке:

📹 YouTube здесьздесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_18:

Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2²⁰ бит в секунду,
объём документа, сжатого архиватором-1, равен 20% от исходного,
на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
объём документа, сжатого архиватором-2, равен 10% от исходного,
на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 20 Мбайт * 0.2  = 4 Мбайт = 2² * 2²³ бит  = 2²⁵ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Найдем время для способа А с учетом времени на сжатие и распаковку:

t_A = 2²⁵ / 2²⁰ + 17 с = 2⁵ + 17 = 49 с

Рассмотрим способ Б:

Сначала найдем объем документа, зная, что он составляет 10% от исходного:

Q (объем) = 20 Мбайт * 0.1  = 2 Мбайт = 2¹ * 2²³ бит  = 2²⁴ бит

Найдем общее время с учетом потраченного времени на сжатие и распаковку:

t_Б = 2²⁴ / 2²⁰ + 24 с = 2⁴ + 24 = 40 с

Получили, что второй способ (Б) быстрее. Выясним насколько быстрее:

49 - 40 = 9 с

Результат: Б9

Тема: Скорость передачи информации:

Решение 7 ЕГЭ по информатике, задание 7_19:

Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.

Чему равен размер упакованного документа (в Мбайт)?

✍ Решение:

Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:

неупакованный:

I₁ = 45 Мбайт
t₁ = 100 секунд (60 секунд + 40 секунд = 100)

упакованный:

I₂ = x Мбайт
t₂ = 20 секунд (30 секунд - 10 секунд = 20)

Получим систему уравнений:

45 = 100
х = 20

Выразим x, т.е. объем упакованного документа:

х = (45 * 20) / 100 = 9 Мбайт

Результат: 9

Источник

Седьмое задание из ЕГЭ по информатике 2022. Отличное задание, которое нужно решать!

Данное задание проверяет умение определять объём памяти, необходимый для хранения графической и звуковой информации.

Приступим к примерным вариантам из ЕГЭ по информатике.

Задача (классика, количество цветов изображения)

Какое максимальное количество цветов может быть в палитре неупакованного растрового изображения, имеющего размер 1024 * 256 пикселей и занимающего на диске не более 165 кб.

Решение:

1. Найдём сколько будет весить один пиксель! У нас всего 1024 * 256 пикселей. Берём максимально возможный объём картинки (165 Кб) и разделим его на количество пикселей.

Важно: Мы не пытаемся сразу вычислить, например, количество пикселей во всём изображении. А записываем сначала в виде действия 1024 * 256. Когда уже получается дробь, пытаемся сократить эту дробь по максимуму. Это позволяет экономить силы при решении седьмого задания из ЕГЭ по информатике 2022.

Нам нужно найти: сколько именно целых бит занимает один пиксель. Округляем количество бит в меньшую сторону, потому что мы не можем «перевалить» за максимальную отметку 165 Кб для всего изображения.

Применим формулу, которую нужно твёрдо знать для решения 7 задания из ЕГЭ по информатике.

Ответ: 32

Задача (Резервирование памяти)

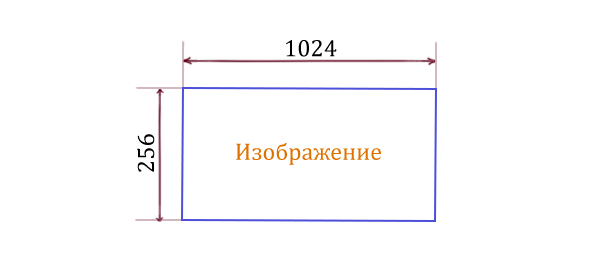
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 * 256 пикселей при условии, что в изображении могут использоваться 4 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

Задача обратная предыдущей. Первый вопрос на который нужно ответить: сколько весит 1 пиксель? Снова используется формула N = 2 ⁱ.

Видно, что 1 пиксель имеет объём i = 2 бита. Количество пикселей в изображении равно 64 * 256. Важно опять умножать эти два числа не сразу. Тогда объём картинки будет равен: количество пикселей (64 * 256) умножить на объём одного пикселя (2 бита).

В подобных задачах из ЕГЭ по информатике фишка в том, чтобы составить дробь и потом сократить её, тем самым вычисление делается без калькулятора и без лишних усилий.

Ответ: 4

Задача (работа со звуком)

Производится звукозапись музыкального фрагмента в формате квадро (четырёхканальная запись) с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла 60 Мбайт. Затем производится повторная запись этого же фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 64 кГц и 16-битным разрешением. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

Общая формула для решения 7-ого задания на тему звуковых файлов из ЕГЭ по информатике.

Её легко запомнить. Объём записанного файла равен произведению всех остальных параметров. Важно соблюдать единицы измерения.

Распишем формулу дискретизации для первой звукозаписи и для второй. В первом случае у нас режим квадро, значит, нужно к произведению добавить ещё 4. Во втором случае режим стерео, значит, должны поставить коэффициент 2. Т.к. производилась запись этого же фрагмента, то время в обоях случаях одинаковое.

Выражаем время из первого уравнения и подставляем во второе.

Опять удобно решать с помощью сокращение дробей.

Ответ: 80

Закрепим результат, решив ещё одну тренировочную задачу из ЕГЭ по информатике 2021.

Задача (ЕГЭ по информатике 2020, Досрочная волна)

Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объём не учитывает размера заголовка файла.

Решение:

Вначале выписываем формулу для первого файла и для второго файла. Подставляем всё, что нам известно.

Для второго звукового файла коэффициенты все переносим в одну сторону.

Выражаем из первого уравнения произведение M * i * t и подставляем его во второе уравнение.

После небольших сокращений получаем 4 Мб для второго звукового файла.

Время было для обоих файлов одинаковым, потому что было сказано, что тот же музыкальный файл перезаписали второй раз с другими параметрами.

Ответ: 4

Удачи при решении 7 задания из ЕГЭ по информатике 2022!

Источник

25 декабря 2022

В закладки

Обсудить

Жалоба

Разнотипные задания и методы их решения.

Ссылки на разбор в конце документа.

52 задачи: z7inf.pdf

Задание 7.1

Для хранения произвольного растрового изображения размером 1024×512 пикселей отведено 64 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

Задание 7.2

Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 223 бит в секунду. От начала передачи данных из пункта А до их полного получения в пункте В прошло 10 минут. Сколько времени в секундах составила задержка в пункте Б, т.е. время между окончанием приема данных из пункта А и началом передачи данных в пункт В?

Задание 7.3

Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Задание 7.4

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 219 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 215 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 10 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Задание 7.5

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 2 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 12 секунд; пропускная способность канала связи с городом Б в 5 раз выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Задание 7.6

Стереоаудиофайл передается со скоростью 32000 бит/с. Файл был записан с такими параметрами: глубина кодирования – 16 бит на отсчет, частота дискретизации – 48000 отсчетов в секунду, время записи – 90 с. Сколько минут будет передаваться файл?

Задание 7.7

Задание 7.8

Камера снимает видео без звука с частотой 60 кадров в секунду, при этом изображения используют палитру, содержащую 216 = 65536 цветов. 1 минута видео в среднем занимает 12 Мегабайт. При записи файла на сервер полученное видео преобразуют так, что его частота кадров уменьшается до 20 кадров в секунду, а изображения преобразуют в формат, содержащий палитру из 256 цветов.
Другие преобразования и иные методы сжатия не используются. Сколько Мбайт в среднем занимает 5 минут преобразованной видеозаписи?

Задание 7.9

Один известный человек записывает новогоднее обращение для жителей одной не менее известной страны. Известно, что видео и звук записываются отдельно. При этом видео записывается покадрово с разрешением 1152*1536, частотой кадров 16 кадров в секунду и глубиной цвета 8 бит. 1 минута звуковой дорожки занимает 512 КБайт. Рассказ о том, как хорошо будут жить граждане, вышел длиной 6 минут. Укажите в МБайтах объем полученного файла.

Задание 7.10

Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт. Определите количество цветов в палитре до оптимизации.

Ответы

7.1) 2
7.2) 60
7.3) 42
7.4) 2576
7.5) 40
7.6) 72
7.7) 90
7.8) 10
7.9) 9723
7.10 1024

Источник: vk.com/inform_web

Источник

ЕГЭ информатика 7 задание разбор, теория, как решать.

Кодирование графической-звуковой информации. Передача информации, (Б) — 1 балл

Е7.40 с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше

Е7.39 Суммарно (сведения и фотография) информация об объекте занимает 7 Мбайт.

В информационной системе хранятся сведения о некотором объекте и его чёрно-белая фотография, содержащая 256 оттенков цвета. Суммарно (сведения и фотография) информация об объекте занимает 7 Мбайт. Фотографию объекта заменили на цветную, сделанную в режиме TrueColor (224 цветов), при этом разрешение и коэффициент сжатия изображения не изменились. После замены информация об объекте стала занимать 11 Мбайт. …

Е7.38 размером 1024х1536 пикселей отведено не более 2 Мбайт памяти

Для хранения произвольного растрового изображения размером 1024х1536 пикселей отведено не более 2 Мбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении? Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – …

Е7.37 Во время эксперимента автоматическая фотокамера каждые n секунд

Во время эксперимента автоматическая фотокамера каждые n секунд (n – целое число) делает чёрно-белые снимки с разрешением 320×240 пикселей и использованием 256 оттенков цвета. Известно, что для хранения полученных в течение часа фотографий (без учёта сжатия данных и заголовков файлов) достаточно 27 Мбайт. Определите минимально возможное значение n. Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание …

Е7.36 Какой способ быстрее и на сколько?

Стоит задача передать файл размером 500 Мбайт между компьютерами в одной локальной сети. При этом есть два способа: А) записать файл на USB-накопитель, перенести физически накопитель до приемника, выгрузить файл, Б) передать по локальной сети со скоростью 10 Мбит/сек. Известно, что скорость записи и чтения файла через У$В составляет 100 Мбит/сек. На перемещение USB-накопителя понадобится …

Е7.35 Рисунок размером 5×6 дюймов отсканировали с разрешением 128 dpi

Рисунок размером 5×6 дюймов отсканировали с разрешением 128 dpi и использованием 8192 цветов. Определите размер полученного файла без учёта служебных данных и возможного сжатия. В ответе запишите целое число – размер файла в Кбайтах. Ответ:

Е7.34 с разрешением в 3 раза выше и частотой дискретизации в 1,5 раза меньше

с разрешением в 3 раза выше и частотой дискретизации в 1,5 раза меньше Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 50 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой …

Е7.33 с разрешением в 4 раза выше и частотой дискретизации в 8 раз меньше

с разрешением в 4 раза выше и частотой дискретизации в 8 раз меньше Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза выше и частотой дискретизации в 8 …

Е7.32 с разрешением в 6 раз ниже и частотой дискретизации в 1,5 раза больше

с разрешением в 6 раз ниже и частотой дискретизации в 1,5 раза больше. Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 18 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 6 …

Е7.31 Во сколько раз размер повторной записи будет больше изначальной?

Во сколько раз размер повторной записи будет больше изначальной? Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла с использованием сжатия данных. При этом производилось сжатие данных, объем сжатого фрагмента стал равен 40% от первоначальной записи. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован …

Источник

КОДИРОВАНИЕ ИНФОРМАЦИИ ( 10 -11классы) Тест 2

Учебная презентация

Автор: Звездина Вера Алексеевна ,

учитель информатики

МБОУ го. Ивантеевка Московской области

«Средняя общеобразовательная школа №7»

Кодирование информации, тест 2, задача 1

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 16-битным разрешением. В результате был получен файл размером 48 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число .

______________________________________________________

Решение :

Время записи t = (48* 2 23 ) / (64 000 * 16 * 2 * 60) =

= (3 * 2 4 * 2 23 ) / (2 6 * 2 3 * 125 * 2 4 * 2* 60) ≈ 3 минуты

Кодирование информации, тест 2, задача 2

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 48 кГц и 24-битным разрешением. В результате был получен файл размером 5625 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5. ______________________________________________________

Решение :

Время записи t = (5625 * 2 23 ) / (48 000 * 24 * 2 * 60) ≈ 5 минут.

Кодирование информации, тест 2, задача 3

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 24 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 4 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

______________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 3

Решение:

Объём музыкального файла вычисляется по формуле

I = f * r * k * t , где f – частота дискретизации, r — разрешение (глубина кодирования), k — количество каналов, t – время звучания. При этом:

при переводе формата записи из моно в стерео объем увеличивается в 2 раза
при повышении разрешения (количества битов на хранения одного отсчёта) в 4 раза объём файла (при прочих равных условиях) увеличивается в 4 раза, поэтому время тоже увеличится в 4 раза

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 3

Решение (окончание):

при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 1,5 раза объём файла (при прочих равных условиях) уменьшается в 1,5 раза, поэтому время тоже уменьшится в 1,5 раза

Поэтому исходный объем файла нужно:

— умножить на 2,

— умножить на 4,

— разделить на 1,5.

Получаем 24 * 2 * 4 / 1,5 = 128 Мбайт

Кодирование информации, тест 2, задача 4

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

______________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 4

Решение:

Объём музыкального файла вычисляется по формуле

при переводе формата записи из стерео в моно объем уменьшается в 2 раза
при повышении разрешения (количества битов на хранения одного отсчёта) в 2 раза объём файла (при прочих равных условиях) увеличивается в 2 раза, поэтому время тоже увеличится в 2 раза

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 4

Решение (окончание):

при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 1,5 раза объём файла (при прочих равных условиях) уменьшается в 1,5 раза, поэтому время тоже уменьшится в 1,5 раза

Поэтому исходный объем файла нужно:

— разделить на 2,

— умножить на 2,

— разделить на 1,5.

Получаем 30 / 2 * 2 / 1.5 = 20 Мбайт

Кодирование информации, тест 2, задача 5

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А? ______________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 5

Решение:

Объём музыкального файла вычисляется по формуле

I = f * r * k * t , где f – частота дискретизации, r — разрешение (глубина кодирования), k — количество каналов, t – время звучания. Пропускная способность канала (скорость передачи файла) V вычисляется как V = I / t . При этом:

при повышении разрешения (количества битов на хранения одного отсчёта) в 3 раза объём файла (при прочих равных условиях) увеличивается в 3 раза, поэтому время тоже увеличится в 3 раза

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 5

Решение (окончание):

при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 4 раза объём файла (при прочих равных условиях) уменьшается в 4 раза, поэтому время тоже уменьшится в 4 раза
при увеличении пропускной способности канала связи (здесь это то же самое, что и скорость передачи данных) в N раз время передачи (при прочих равных условиях) увеличится в N раз.

Время передачи файла в город Б больше времени передачи в город А больше в t 2 = 100 / 15 = 20 / 3 раза.

С учетом коэффициентов изменения объема файла получаем время передачи в город Б больше времени передачи в город А больше в

t 2 = (20 * 3) / (3 * 4) = 5 раз

Кодирование информации, тест 2, задача 6

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 88 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза выше и частотой дискретизации в 3 раза выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 264 секунды. Во сколько раз скорость пропускная способность канала в город Б больше пропускной способности канала в город А? ______________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 6

Решение:

Объём музыкального файла вычисляется по формуле

при повышении разрешения (количества битов на хранения одного отсчёта) в 4 раза объём файла (при прочих равных условиях) увеличивается в 3 раза, поэтому время тоже увеличится в 4 раза

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 6

Решение (окончание):

при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 3 раза объём файла (при прочих равных условиях) уменьшается в 3 раза, поэтому время тоже уменьшится в 3 раза
при увеличении пропускной способности канала связи (здесь это то же самое, что и скорость передачи данных) в N раз время передачи (при прочих равных условиях) увеличится в N раз.

Время передачи файла в город Б больше времени передачи в город А больше в t 2 = 264 / 88 = 3 раза.

t 2 = 3 * 4 / 3 = 4 раза

Кодирование информации, тест 2, задача 7

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла — 45 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 5 раз выше и частотой дискретизации в 4,5 раз меньше, чем в первый раз. При этом производилось сжатие данных, объем повторной записи сократился на 40%. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. ______________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 7

Решение:

Объём музыкального файла вычисляется по формуле

при переводе формата записи из стерео в моно объем уменьшается в 2 раза
при повышении разрешения (количества битов на хранения одного отсчёта) в 5 раз объём файла (при прочих равных условиях) увеличивается в 5 раз, поэтому время тоже увеличится в 5 раз

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 7

Решение (окончание):

при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 4,5 раза объём файла (при прочих равных условиях) уменьшается в 4,5 раза, поэтому время тоже уменьшится в 4,5 раза
изменение полученного объема от исходного составило 100% — 40% = 60%

Поэтому исходный объем файла нужно:

1) разделить на 2; 2) умножить на 5;

3) разделить на 4,5; 4) умножить на 0,6 (60%)

С учетом изменения объема получаем 45 / 2 * 5 / 4.5 = 25 , что с учетом сжатия составит 25 * 0,6 = 15 Мбайт.

Кодирование информации, тест 2, задача 8

Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 3 раза меньше и частотой дискретизации в 2,5 раза больше, чем в первый раз. При этом производилось сжатие данных, объем повторной записи сократился на 60%. Размер полученного файла — 6 Мбайт. Укажите размер файла в Мбайт, полученного при начальной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

___________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 8

Решение:

Объём музыкального файла вычисляется по формуле

при переводе формата записи из квадро в моно объем уменьшается в 4 раза
при уменьшении разрешения (количества битов на хранения одного отсчёта) в 3 раза объём файла (при прочих равных условиях) увеличивается в 3 раза, поэтому время тоже уменьшится в 3 раза

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 8

Решение (окончание):

при увеличении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 2,5 раза объём файла (при прочих равных условиях) уменьшается в 2,5 раза, поэтому время тоже увеличится в 2,5 раза
изменение полученного объема от исходного составило 100% — 60% = 40%

Так как в этой задаче задан размер полученного файла, а нужно найти исходный, то все действия заменяем на противоположные.

Поэтому полученный объем файла нужно:

1) разделить на 4; 2) умножить на 3;

3) разделить на 2,5; 4) умножить на 0,4 (40%)

С учетом изменения объема получаем 6 * 3 / 4 / 2.5 * 0.4 = 72 Мбайт

Кодирование информации, тест 2, задача 9

Стерео аудиофайл передается со скоростью 32000 бит/с. Файл был записан с такими параметрами: глубина кодирования – 16 бит на отсчет, частота дискретизации – 48000 отсчетов в секунду, время записи – 90 с. Сколько минут будет передаваться файл?

_______________________________________________________

Решение :

Время передачи файла равно объему, деленному на скорость

передачи, тогда получаем

t = 4800 * 16 * 90 * 2 / 32000 / 60 =

= 4320 сек = 72 минуты

Кодирование информации, тест 1, задача 10

В течение 4 минут производится двухканальная (стерео) звукозапись. Результаты записи записываются в полученного файла — 40 Мбайт (c точностью до 10 Мбайт); сжатие данных не производилось. Среди перечисленных ниже режимов укажите тот, в котором проводилась звукозапись файл, размер.

1) Частота дискретизации 16 кГц и 24-битное разрешение 2) Частота дискретизации 16 кГц и 16-битное разрешение 3) Частота дискретизации 32 кГц и 24-битное разрешение 4) Частота дискретизации 32 кГц и 16-битное разрешение

___________________________________________________________________

(решение на следующем слайде)

Кодирование информации, тест 2, задача 10

Решение:

Решаем по формуле : V = F * n * i * t, где F — частота дискретизации (в герцах), n — количество каналов (в задаче двухканальная звукозапись), i — глубина звука (вес одного уровня) в битах, t — Время звучания (в секундах)

1. Частота дискретизации 16 кГц и 24 -битное разрешение :

V = 16000 * 24 * 2 * 240 = 184320000 бит = 23040000 байт = 22500 Кбайт = 21,97 Мбайт ( данный ответ не подходит)

(окончание решения — на следующем слайде)

Кодирование информации, тест 2, задача 10

Решение (окончание):

2 . Частота дискретизации 16 кГц и 16 -битное разрешение :

V=16000*16*2*240=122880000 бит=15360000 байт=15000 Кбайт =14,64 Мбайт (данный ответ не подходит)

3. Частота дискретизации 32 кГц и 24 -битное разрешение :

V = 32000 * 24 * 2 * 240 = 368640000 бит = 46080000 байт = 43,94 Мбайт (так как в условии сказано, что объем вычисляется с точностью до 10, т.е. подходит )

4. Частота дискретизации 32 кГц и 16 -битное разрешение :

V = 32000 * 16 * 2 * 240 = 245760000 бит = 30720000 байт = 30000 Кбайт = 29,29 Мбайт ( данный ответ не подходит)

Источник

В решение заданий демо-версии используется язык программирования Python.

Задание 1. Анализ информационных моделей

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число.

На графе расставим веса вершин.
Мы видим, что вершина В уникальна, имеет вес 2 и связана с двумя «тройками по весу».
Из таблицы видим, В это 4, далее видим, что «тройки по весу» это вершины 2 и 7.
7 вершина связана кроме В, еще с двумя «тройками по весу», значит D это 7, а F это 2.

Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6.
Рассуждая дальше видим, что С это 1, G это 2.

Сумма дорог BD + AF = 53 + 5 = 58

Ответ: 58

Задание 2. Построение таблиц истинности логических выражений

Миша заполнял таблицу истинности логической функции F

F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx.

¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.

y	x	z	w
0	0	1	0
0	1	1	0
1	1	1	0

Решение на Python

Ответ: YXZW

Задание выполняется с использованием прилагаемых файлов

Задание 3. Базы данных. Файловая система

В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня.

На рисунке приведена схема указанной базы данных.

Используя информацию из приведённой базы данных, определите общий вес
(в кг) крахмала картофельного, поступившего в магазины Заречного района
за период с 1 по 8 июня включительно. В ответе запишите только число.

На третьем листе книги применим фильтр по району и получим ID четырех магазинов.

На втором листе применим фильтр по товару и получим ID товара.

На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим:

Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг.

Ответ: 355

Задание 4. Кодирование и декодирование информации

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений.

Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Ответ: 14

Задание 5. Анализ и построение алгоритмов для исполнителей

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.

1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число
10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе запишите это число в десятичной системе счисления.

Минимальное R, большее 40, это 41.
В результате выполнения алгоритма число R должно либо начинаться на 10 и оканчиваться 0, либо начинаться на 11 и оканчиваться 1.
Из чисел, больших 41, это 42, 44, 46, 49, и т.д.
Мы должны найти минимальное N, из которого данное число получено.
Поскольку первые цифры заменялись, то мы видим, что данные числа могли быть получены из чисел 29, 30, 23, 16.
Из которых 16 минимальное, и меньше уже быть не может.

ИЛИ программное решение

Ответ: 16

Задание 6. Определение результатов работы простейших алгоритмов

Исполнитель Черепаха действует на плоскости с декартовой системой координат.
В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n–целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

ИЛИ

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90]
Поднять хвост
Вперёд 3 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]

Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Сначала нужно построить фигуру.
Это можно сделать к примеру, на тетрадном листе, при помощи библиотеки Turtle или в Excel.

Далее мы находим уравнения прямых, которыми ограничена фигура и решаем
систему уравнений программно.

ИЛИ
Фигуру можно построить программно или к примеру, в Excel.
Далее анализируем и считаем точки.

Ответ: 1 задание — 38, 2 задание — 128

Задание 7. Кодирование и декодирование информации. Передача информации

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц),

i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро)

I₁ = ν ⋅ i ⋅ t
I₂ = ν/2 ⋅ 3,5 ⋅ i ⋅ t ⋅ 2 = 3,5 ⋅ I₁

I₂ = 3,5 · 28 = 98

Ответ: 98

Задание 8. Перебор слов и системы счисления

Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6.

* * * * * — пятизначное число.
В восьмеричной системе счисления в алфавите 8 цифр: 0..7.
Первая цифра 0 быть не может.
Цифра 6 — одна, при этом стоит рядом только с четными цифрами — 0, 2 или 4.
Получим:

6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029
* 6 * * * — вариантов 2 ⋅ 3 ⋅ 7 ⋅ 7 = 294
* * 6 * * — вариантов 6 ⋅ 3 ⋅ 3 ⋅ 7 = 378
* * * 6 * — вариантов 6 ⋅ 7 ⋅ 3 ⋅ 3 = 378
* * * * 6 — вариантов 6 ⋅ 7 ⋅ 7 ⋅ 3 = 882

Ответ: 2961

Задание выполняется с использованием прилагаемых файлов

Задание 9. Работа с таблицами

Файл с данными

Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
– в строке только одно число повторяется дважды;
– среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.

Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке.

Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6.

Далее мы найдем среднее арифметическое неповторяющихся значений.

Затем найдем сумму повторяющихся значений.

Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия.

Ответ: 2241

Задание выполняется с использованием прилагаемых файлов

Задание 10. Поиск символов в текстовом редакторе

Файл с данными

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.

В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз.

Ответ: 45

Задание 11. Вычисление количества информации

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.

I = K · i, N = 2 ⁱ

ID : ****….**** – всего 250 различных символов в наборе

N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 2¹¹, значит для кодирования одного символа нужно 11 бит.

I_ID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт

I₆₅₅₃₆ = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего

Ответ: 22016

Задание 12. Выполнение алгоритмов для исполнителей

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
    ПОКА условие
        последовательность команд
    КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

    ЕСЛИ условие
        ТО команда 1
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно).

В конструкции

    ЕСЛИ условие
        ТО команда 1
        ИНАЧЕ команда 2
    КОНЕЦ ЕСЛИ

выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно).

Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке. Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

def pr(n): #функция определяет простое ли число
for i in range(2,int(n**0.5)+1):
if (n%i) == 0:
return False
return True

for n in range(100): #перебираем n
s=’>’ + 39*’0′ + n*’1′ + 39*’2′
while ‘>1’ in s or ‘>2’ in s or ‘>0’ in s:
if ‘>1’ in s:
s=s.replace(‘>1′,’22>’,1)

if ‘>2’ in s:
s=s.replace(‘>2′,’2>’,1)

if ‘>0’ in s:
s=s.replace(‘>0′,’1>’,1)

sum_s = 0
for i in s[:-1]: #считаем сумму цифр в строке
sum_s += int(i)
if pr(sum_s): #проверяем на простоту
print(n)
break

Ответ: 5

Задание 13. Поиск путей в графе

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.

Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л.

Ответ: 21

Задание 14. Кодирование чисел. Системы счисления

Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

for x in range(15):
s1=’123’+ str(x) +’5′
s2=’1’+ str(x) +’233′
n= int(s1,15)+ int(s2,15)

if n%14 == 0:
print(n//14)
break

Ответ: 8767

Задание 15. Преобразование логических выражений

На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) & ¬(x ∈ A)) → ¬(x ∈ D)) истинно (т.е. принимает значение 1) при любом значении переменной х.

def deli(n,m):
if n%m == 0:
return True

for A in range(1,1000):
Ok = True
for x in range(1,10000):
Ok*=( (not(deli(x,2)) or (not(deli(x,3)))) or ((x+A)>=100) )

if Ok:
print(A)
break

Ответ: 94

Задание 16. Рекурсивные алгоритмы

Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n — 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

F(2023) = 2023! = 2023 ⋅ 2022!

F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 =

= 8266912626

Ответ: 8266912626

Задание выполняется с использованием прилагаемых файлов

Задание 17. Проверка на делимость

Файл с данными

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых
только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

f= open(’17.txt’)
p=[int(i) for i in f]
f.close()

k = 0
PP = 0
M3 = 0

for i in p:
if (abs(i))%10 == 3:
M3 = max(i, M3)

for i in range(1,len(p)): #Осторожно, скобки!
if ( ((abs(p[i-1])%10 == 3) + ((abs(p[i])% 10 == 3)) ==1 ) and ((p[i-1]**2 + p[i]**2) >= M3**2) ):
k+=1
PP = max(PP, p[i-1]**2 + p[i]**2)

print(k,PP)

Ответ: 180 190360573

Задание выполняется с использованием прилагаемых файлов

Задание 18. Робот-сборщик монет

Файл с данными

Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:

1	8	8	4
10	1	1	3
1	3	12	2
2	3	5	6

Для указанных входных данных ответом должна быть пара чисел 41 и 22.

Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен.

Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1.

Далее делаем замену всех формул МАКС на МИН.

Ответ: 1099 1026

Задание 19. Выигрышная стратегия. Задание 1

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом.

Ответ: 64

Задание 20. Выигрышная стратегия. Задание 2

Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в порядке возрастания.

Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом.

Ответ: 32 63

Задание 21. Выигрышная стратегия. Задание 3

Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:

у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них.

Ответ: 62

Задание 22. Многопроцессорные системы

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

В независимых процессах время считается от 0,
в зависимых прибавляется к времени процесса, от которого зависит.

Ответ: 17

Задание 23. Анализ программы с циклами и условными операторами

Исполнитель преобразует число на экране.
У исполнителя есть две команды, которые обозначены латинскими буквами:
A. Прибавить 1
B. Умножить на 2
Программа для исполнителя – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов
выполнения всех команд программы. Например, для программы ABA при
исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

def f(x, y):
if x == y:
return 1
if x > y or x == 17:
return 0
else:
return f(x + 1, y) + f (2 * x, y)

print (f(1,10) * f(10, 35))

Ответ: 98

Задание выполняется с использованием прилагаемых файлов

Задание 24. Анализ программы с циклами и условными операторами

Файл с данными

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная
в прилагаемом файле. Для выполнения этого задания следует написать программу.

f=open(’24.txt’)
p= f.readline()
f.close()

PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’]
M=k=0

for i in range(1, len(p), 2):
x = p[i-1] + p[i]
if x in PP:
k += 1
else:
k = 0
M=max(M,k)
print(M)

Ответ: 95

Задание 25. Анализ программы с циклами и условными операторами

Назовём маской числа последовательность цифр, в которой также могут
встречаться следующие символы:
– символ «?» означает ровно одну произвольную цифру;
– символ «*» означает любую последовательность цифр произвольной длины;
в том числе «*» может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.

Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2023. Количество строк в таблице для ответа избыточно.

Самый простой способ использовать библиотеку fnmatch.
Функция fnmatch() проверяет, соответствует ли строка шаблонной строке, возвращая True или False

или так полным перебором:

y = {»,’0′,’00’,’000′}
for x in y:
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + x + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023)

for x in range (1000):
for j in range(10):
s = ‘1’ + str(j) + ‘2139’ + str(x) + ‘4’
if int(s) % 2023 == 0:
print (s, int(s)//2023

Ответ: 162139404 80148
1321399324 653188
1421396214 702618
1521393104 752048

Задание выполняется с использованием прилагаемых файлов

Задание 26. Анализ программы с циклами и условными операторами

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.

Задание выполняется с использованием прилагаемых файлов

Задание 27. Анализ программы с циклами и условными операторами

У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные

Файл А
Файл В

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 ∙ 2 + 3 ∙ 1 + 5 ∙ 1 + 6 ∙ 1 + 8 ∙ 2.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Ответ: 51063 5634689219329

Источник

19200. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 32 пикселей при условии, что в изображении могут использоваться 16 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19200.

19173. Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 64-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла — 80 Мбайт. Определите приблизительно время записи (в минутах). В качестве ответа укажите ближайшее к времени записи целое число.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19173.

19146. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 24 секунды. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза ниже, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19146.

19119. Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 64-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла — 80 Мбайт. Определите приблизительно время записи (в минутах). В качестве ответа укажите ближайшее к времени записи целое число.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19119.

19092. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в студию А по каналу связи за 96 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 6 раз выше и частотой дискретизации в 3 раза ниже, чем в первый раз. Сжатие данных не производилось.

Полученный файл был передан в студию Б за 16 секунд. Во сколько раз скорость пропускная способность канала в студии Б больше пропускной способности канала в студию А?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19092.

19065. Для хранения произвольного растрового изображения размером 512×640 пикселей отведено 80 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19065.

19038. Автоматическая фотокамера каждые 15 секунд создаёт растровое изображение, содержащее 256 цветов. Размер изображения – 240 x 320 пикселей. Все полученные изображения и коды пикселей внутри одного изображения записываются подряд, никакая дополнительная информация не сохраняется, данные не сжимаются. Сколько Кбайт нужно выделить для хранения всех изображений, полученных за 1 минуту? В ответе укажите только целое число – количество Кбайт, единицу измерения указывать не надо.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19038.

19011. Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16777216 цветов. Средний размер фотографии составляет 12 Мбайт. Для хранения в базе данных фотографии преобразуют в формат с палитрой, содержащей 2¹⁶ = 65536 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 19011.

18984. Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором, передать архив по каналу связи, распаковать;
Б) передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

     - средняя скорость передачи данных по каналу связи составляет 2²³ бит в секунду
     - объём сжатого архиватором документа равен 20% от исходного
     - время, требуемое на сжатие документа, 18 секунд, на распаковку – 2 секунд?

В ответе напишите букву А, если способ А быстрее, или Б, если быстрее способ Б. Сразу после буквы напишите на сколько секунд один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18984.

18957. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 88 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 4 раза выше и частотой дискретизации в 3 раз выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 264 секунды. Во сколько раз пропускная способность канала в город Б больше пропускной способности канала в город А?

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 18957.

Для вас приятно генерировать тесты, создавайте их почаще

Источник