Задание 8 профильного егэ по математике цилиндр конус шар - Помощь в подготовке к экзаменам и поступлению

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №8. Цилиндр, конус, шар

ЕГЭ Профиль №8. Цилиндр, конус, шарadmin2020-01-19T19:46:05+03:00

Используйте LaTeX для набора формулы

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 138.

Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 42. Найдите объём цилиндра.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 36. Найдите объём цилиндра.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 63. Найдите объём цилиндра.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.

Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 3

Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.

Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Инфоурок

›

Геометрия

›Другие методич. материалы›Набор задач по теме «Цилиндр, конус, шар, комбинированные тела» из текстов ЕГЭ

Набор задач по теме «Цилиндр, конус, шар, комбинированные тела» из текстов ЕГЭ

Скачать материал

Сейчас обучается 138 человек из 41 региона

Сейчас обучается 38 человек из 28 регионов

Сейчас обучается 82 человека из 34 регионов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 157 295 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»

Скачать материал
- 08.10.2021
  
  4399
- PDF
  858.1 кбайт
- 682
  скачивания
- Рейтинг:
  4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Михалева Татьяна Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 8 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 67250
- Всего материалов:
  
  29

Источник

Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.

Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.

Как решать задания по стереометрии из первой части Профильного ЕГЭ?

Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)

Проверим себя – умеем ли мы рисовать чертежи?

Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.

Запоминаем один из главных лайфхаков решения задач по стереометрии:

Отношение объемов подобных тел равно кубу коэффициента подобия.

Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в k^2 раз, а объем в k^3 раз.

И решаем задачи. У нас все получится!

1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?

Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.

2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.

3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.

Меньшая пирамида подобна большой, коэффициент подобия $k=frac{1}{2}.$ Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен $frac{10}{8}=1,25.$

4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.

Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен $frac{116}{4}=29.$

5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна Найти объем пирамиды SABCD .

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что Соответственно, сторона основания пирамиды равна Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора, для треугольника SHE – она равна 2.

Применяя формулу для объема пирамиды $V=frac{1}{3}S_{ABCD}cdot h$ , получаем ответ: 16.

Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.

Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.

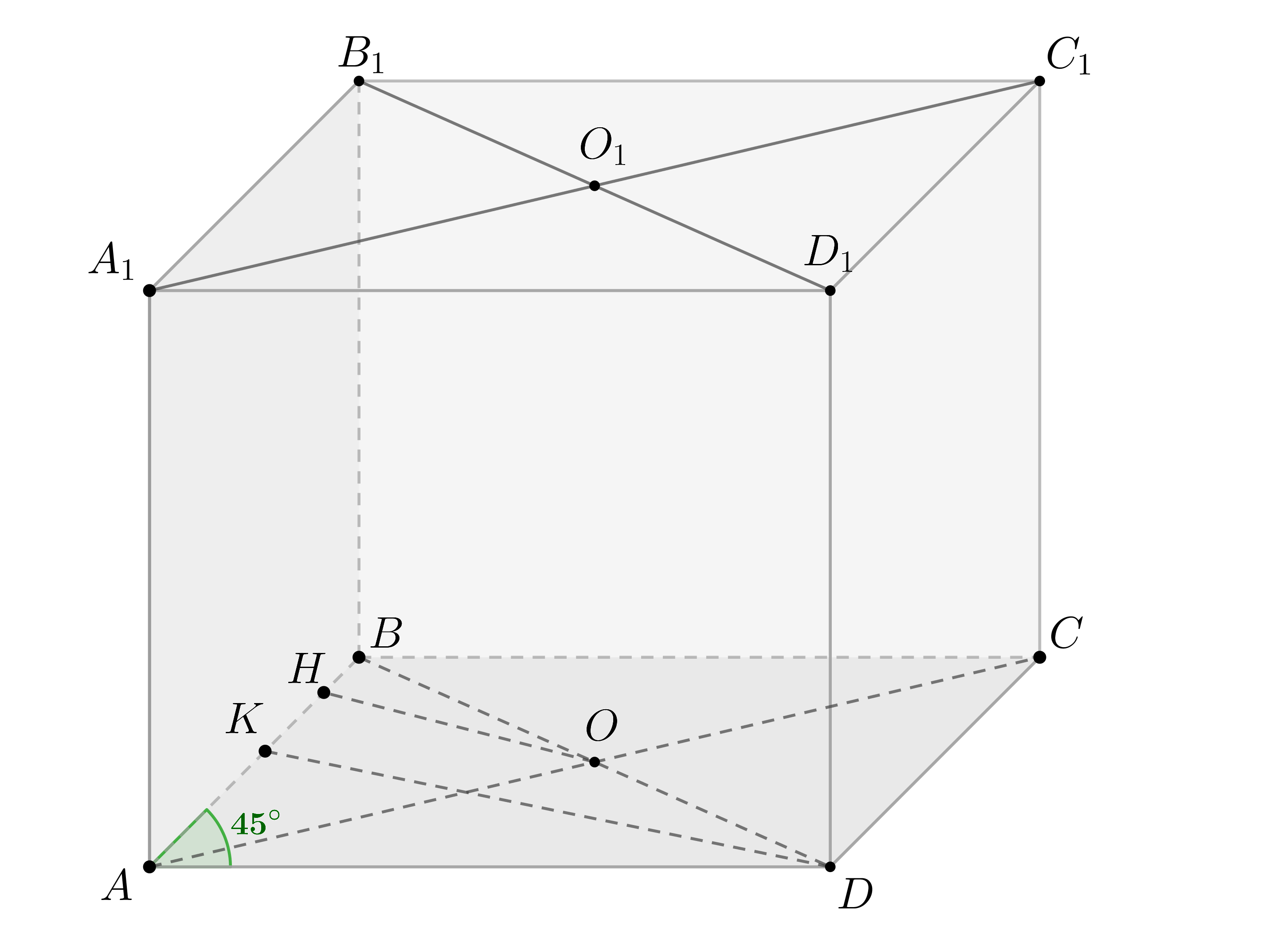
6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.

Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.

Радиус описанной окружности найдем по формуле

$R=frac{abc}{4S}.$

Площадь найдем по формуле Герона:

$S_{triangle ABC}=sqrt{p(p-a)(p-b)(p-c)}$ , где $p=frac{15+16+17}{2}=24$ – полупериметр.

$S_{triangle ABC}= sqrt{24cdot 9cdot 8cdot 7}=sqrt{3cdot 8cdot 3cdot 3cdot 8cdot 7}=24sqrt{21};$

$R=frac{15cdot 16cdot 17}{4cdot 24sqrt{21}}=frac{5cdot 17}{2sqrt{21}};$

$V=frac{1}{3}S_{triangle ABC}cdot OS=frac{1}{3}cdot 24sqrt{21}cdot frac{5cdot 17}{2cdot sqrt{21}}=4cdot5cdot17=340.$

Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.

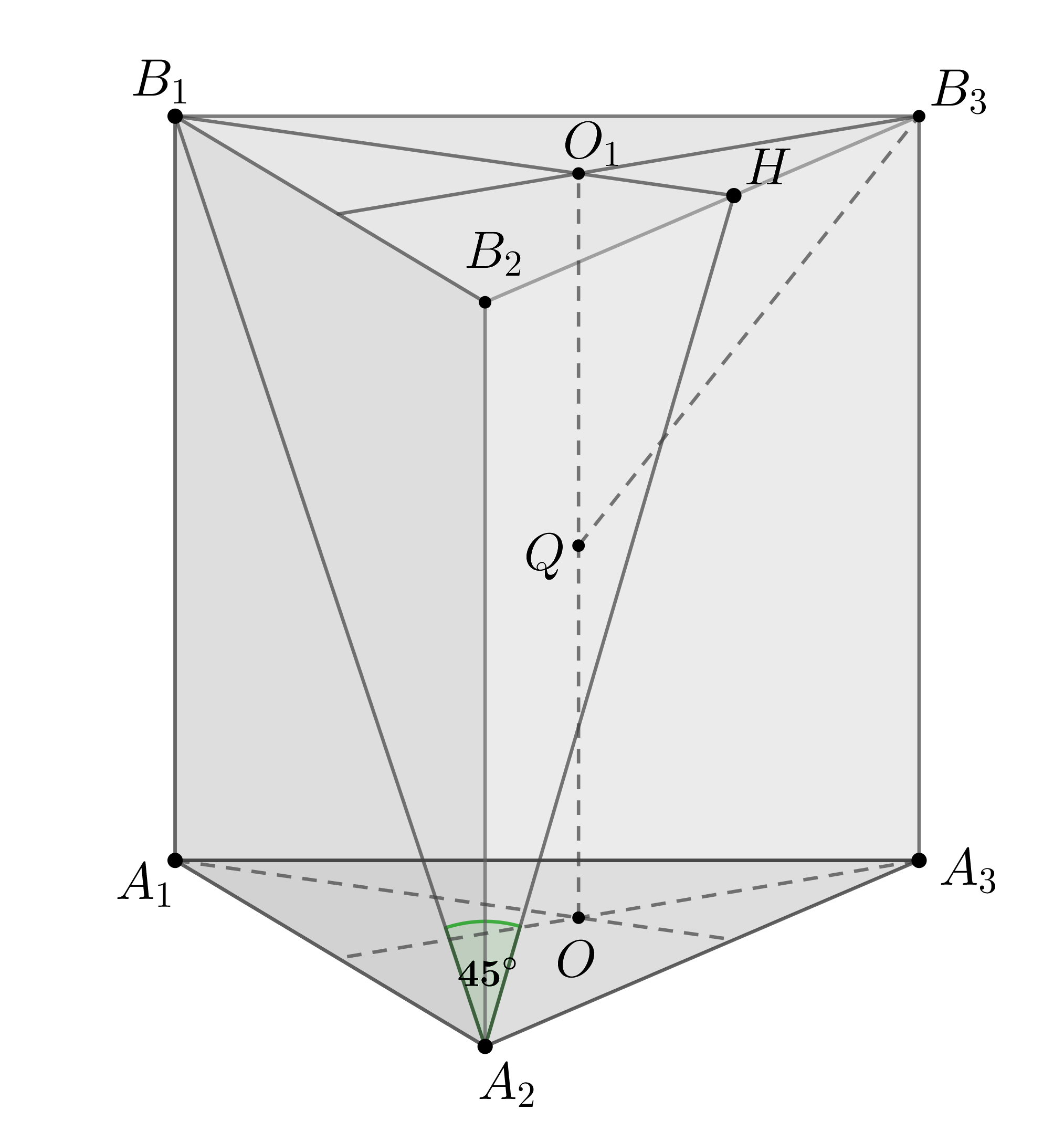
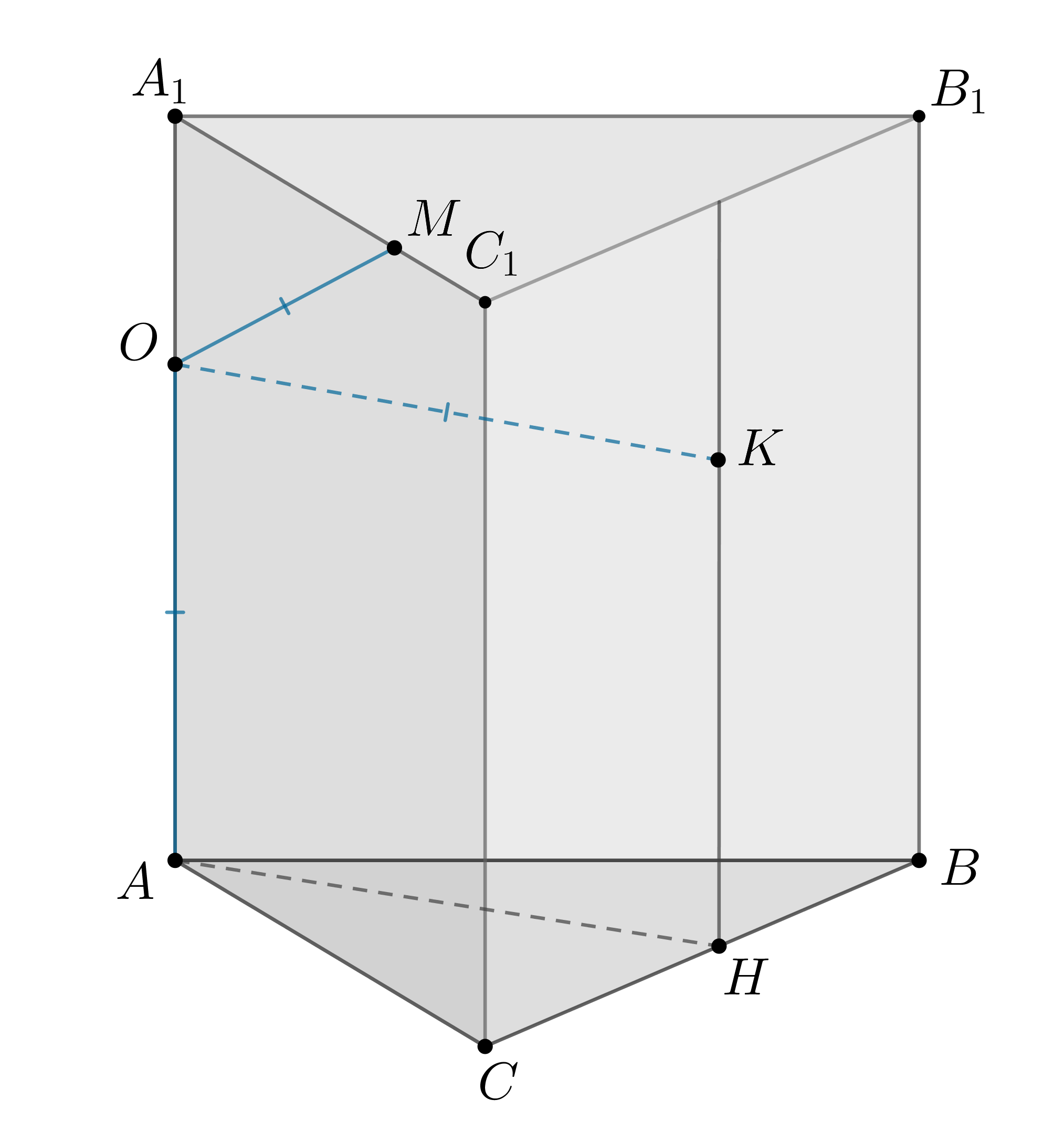
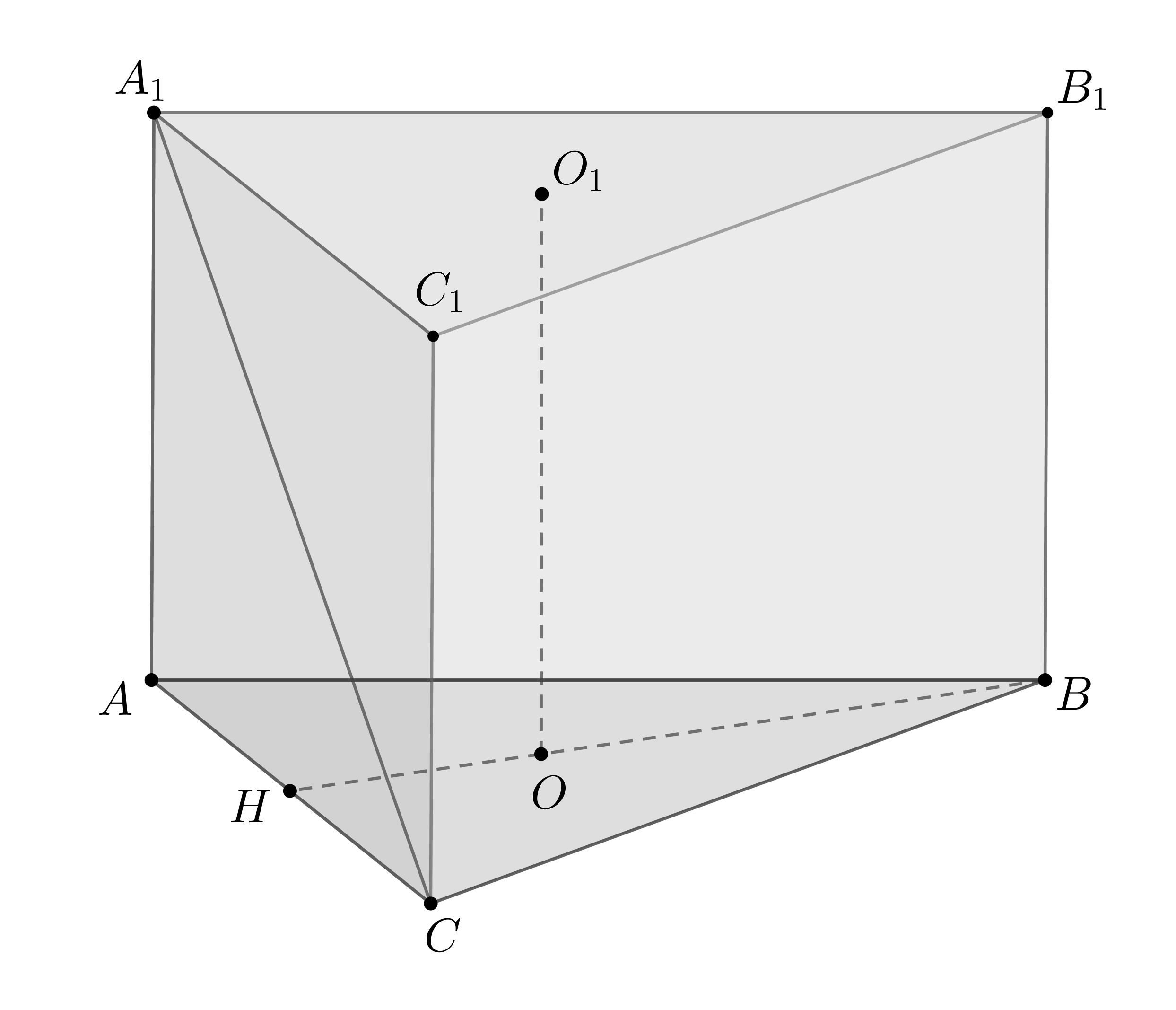
7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и . Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку CC_1 и AA_1 параллельны, найдем угол между CC_1 и BC_1 . Он равен 45 градусов, так как грань – квадрат.

Ответ: 45.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Тема 13.

Задачи по стереометрии

Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи по стереометрии

13.01Задачи из ЕГЭ прошлых лет

13.02Задачи из сборника И.В. Ященко ЕГЭ 2023

13.03Задачи формата ЕГЭ на многогранники. Пирамида, призма

13.04Задачи формата ЕГЭ на тела вращения. Шар, цилиндр, конус

13.05Аксиомы. Доказательство базовых фактов

13.06Параллельность. Доказательство базовых фактов

13.07Перпендикулярность. Доказательство базовых фактов

13.08Тела вращения. Доказательство базовых фактов

13.09Задачи на построение

13.10Упрощенные задачи

13.11Построение сечений

13.12Нахождение площади сечения

13.13Расстояние от точки до прямой

13.14Расстояние от точки до плоскости

13.15Угол между прямой и плоскостью

13.16Угол между плоскостями

13.17Нахождение объема или площади поверхности

13.18Угол между скрещивающимися прямыми

13.19Расстояние между скрещивающимися прямыми

13.20Метод объемов

Решаем задачи

Показать ответ и решение

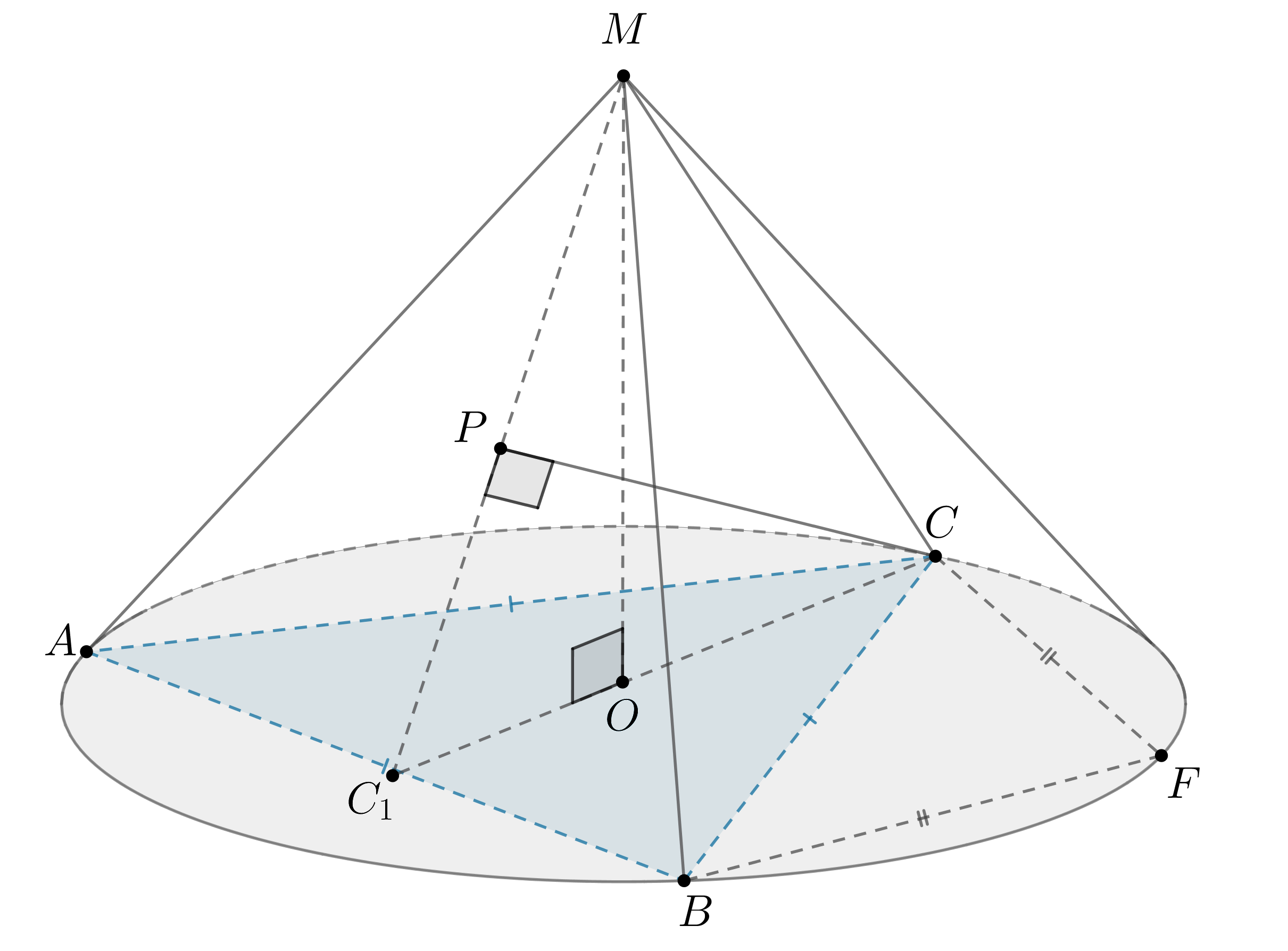
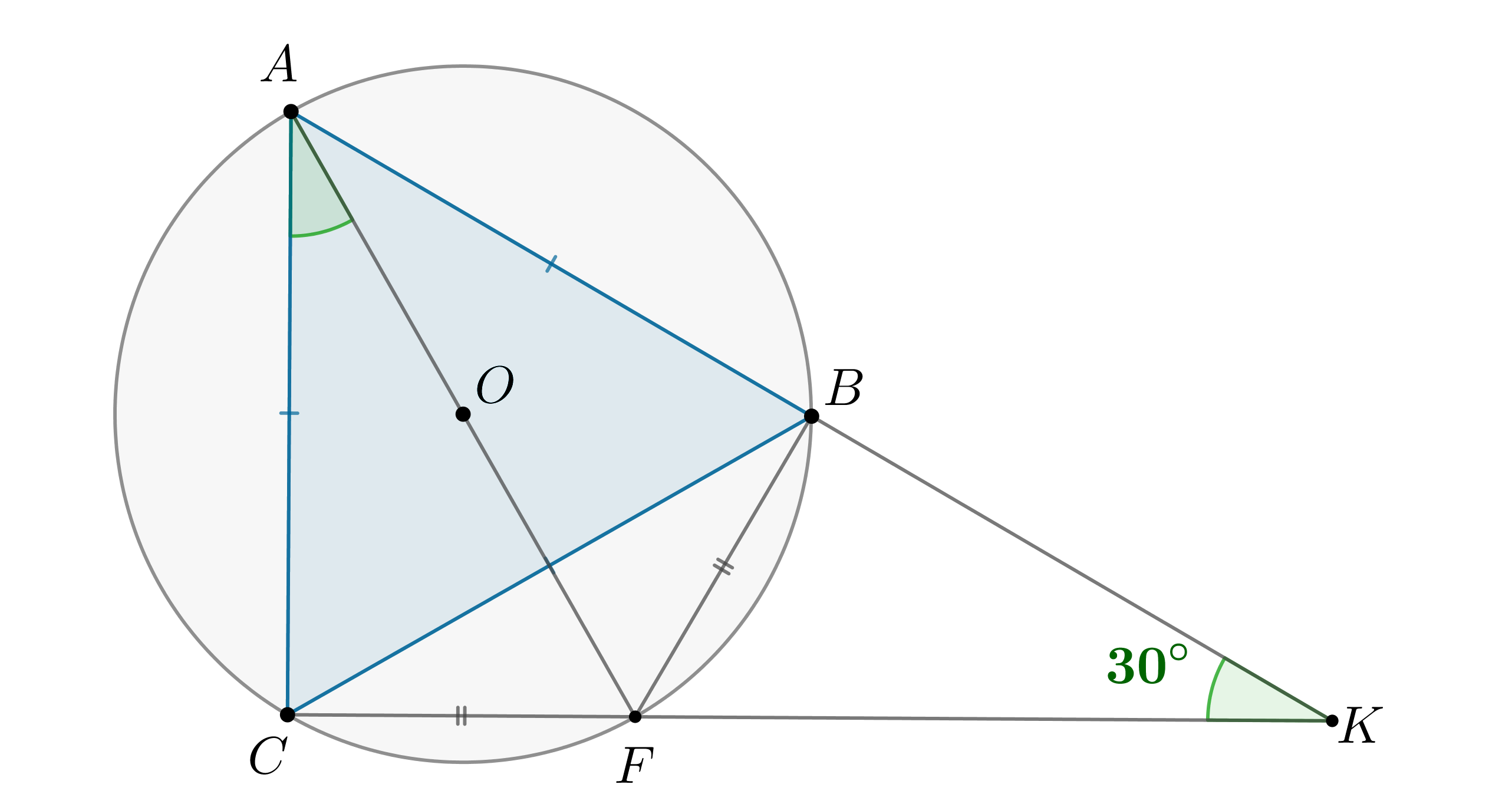
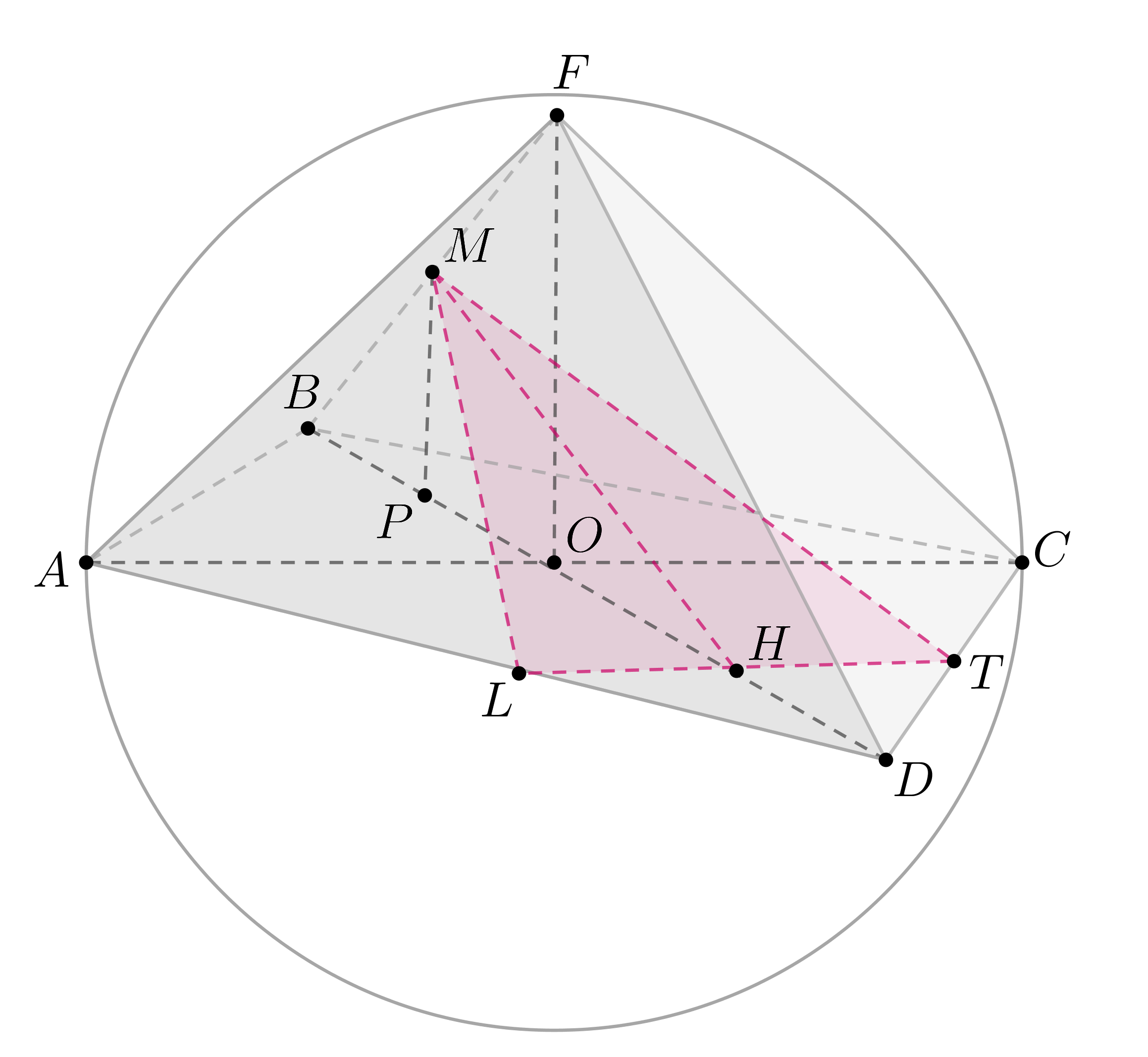
а) Пусть — центр основания конуса. Так как точки и делят окружность
основания на две дуги, которые относятся как 1:5, то можно меньшую дугу
принять за а большую за 5x. Тогда вся окружность равна 6x, следовательно,
меньшая дуга составляет 1
6 от всей окружности, то есть в градусах равна
1 ⋅360∘ = 60∘.
6

Таким образом, ∘
∠AOB = 60 как центральный угол. Так как AO = BO —
радиусы, то △AOB равнобедренный. Поскольку один из его углов равен 60∘ , то
△AOB равносторонний и

Проведем также является и медианой. Тогда для
прямоугольного треугольника SAH и треугольника SAB имеем:

3 AH 1) AH = 3a
√---= cos∠SAB = AS- ⇒ 2) AB = 2AH = 6a ⇒
58 3) AS = √58a
∘ ----------
⇒ SH = AS2 − AH2 = 7a = 7AB ⇒
1 1 7 6 7 2
⇒ S △SAB = 2SH ⋅AB = 2 ⋅ 6AB ⋅AB = 12AB

б) Из формулы площади треугольника SAB находим радиус основания
конуса:

Тогда по теореме Пифагора в треугольнике SOA :

Тогда объем конуса равен

1 2 √--
Vконус = 3 ⋅SO ⋅π⋅AB = 48π 11

Ответ:

б)

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

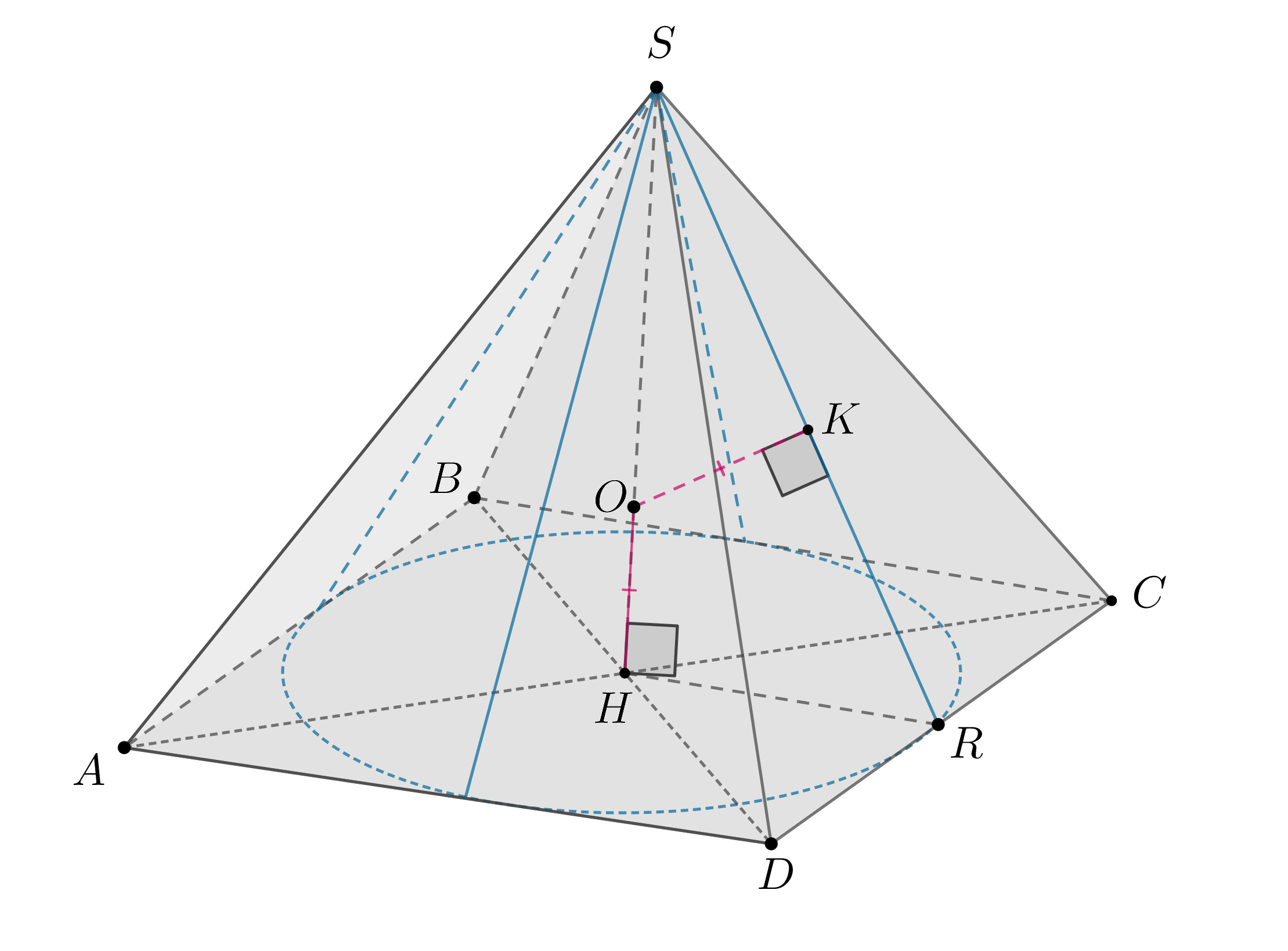
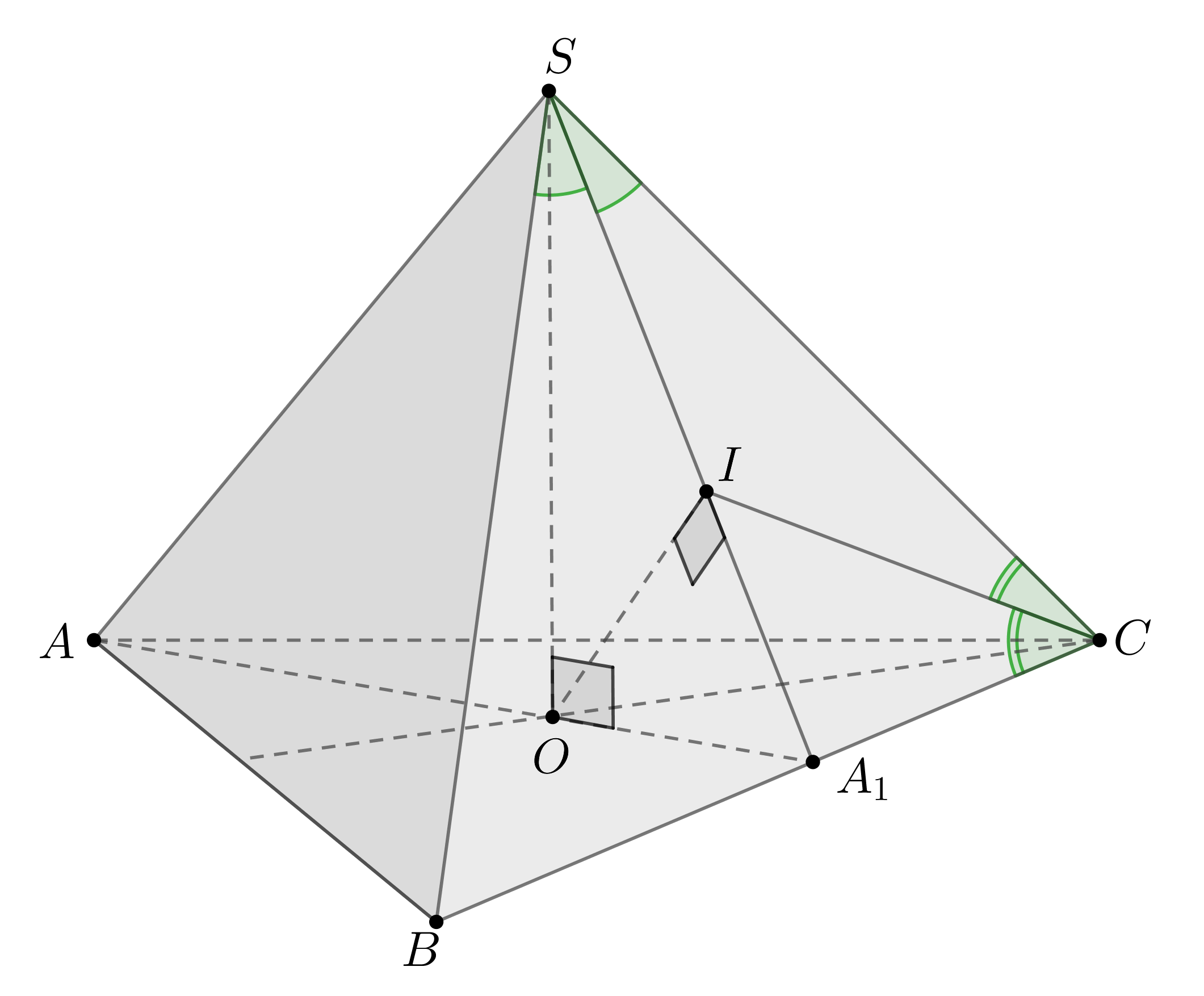
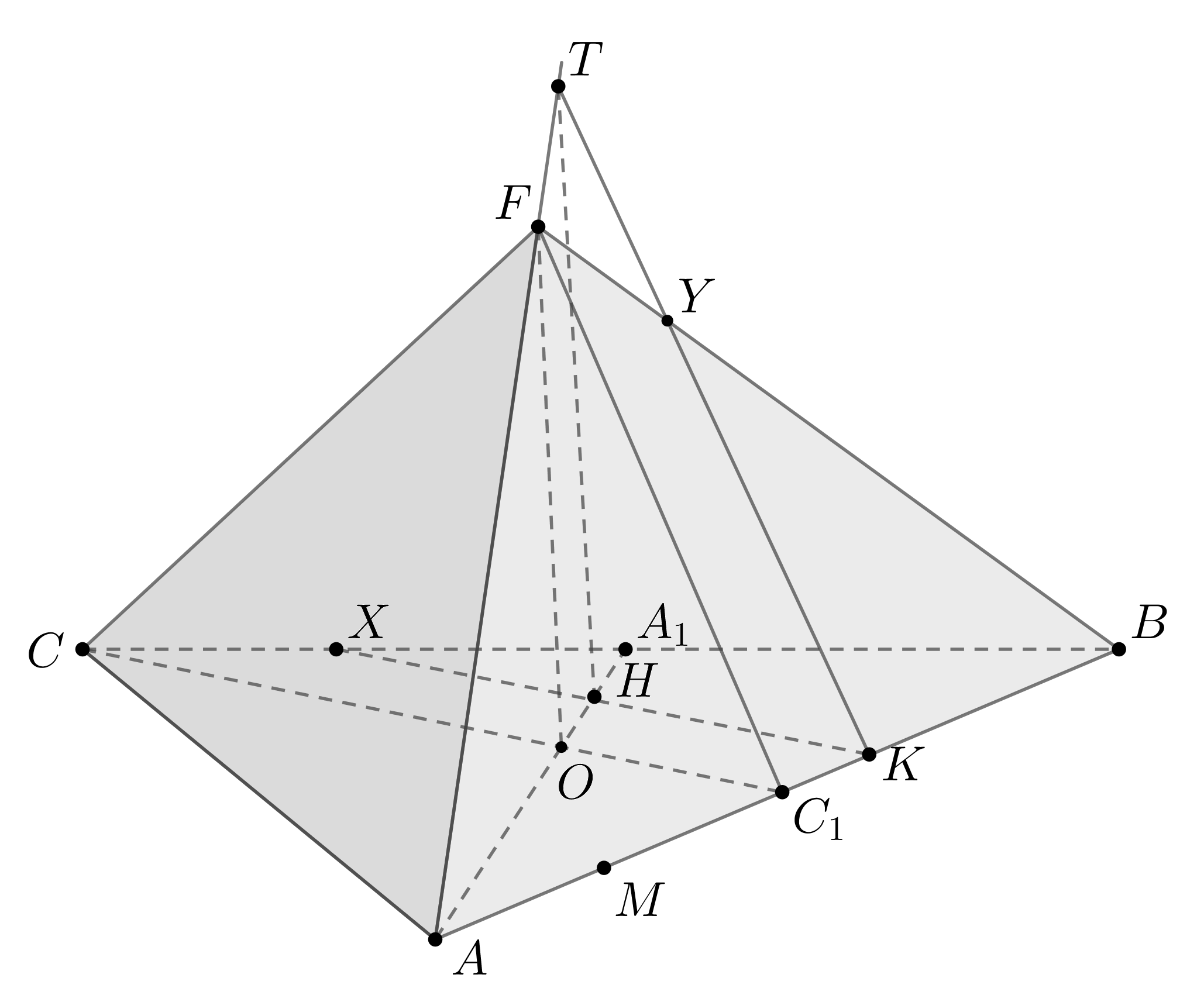
Конус вписан в правильную четырехугольную пирамиду. Общая высота
пирамиды и конуса равна 9
4 , а радиус вписанной в конус сферы равен
1.

а) Докажите, что данная сфера касается боковых граней пирамиды, причем
точки касания лежат на апофемах.

б) Найдите разность объемов пирамиды и конуса.

Показать ответ и решение

а) Пусть дана пирамида SABCD , — точка пересечения диагоналей
основания ABCD . По свойству правильной пирамиды — ее высота,
следовательно, и высота конуса. Пусть — центр сферы, вписанной
в конус, следовательно, лежащий на . Тогда — радиус этой
сферы.

Окружность основания конуса касается стороны в ее середине. Назовем
эту точку касания . Тогда , — радиус основания конуса.
Рассмотрим △SHR . Проведем . Так как — проекция на
плоскость ABC и , то по ТТП и . Следовательно,
перпендикулярна двум прямым и из плоскости SCD , следовательно,
. Значит, — точка касания сферы с гранью SCD , лежащая на
. А так как — середина , то по определению — апофема грани
SCD . Для других граней пирамиды доказательство аналогично, так как
пирамида правильная.

Чтд.

Заметим, что — образующая конуса и — одна из точек касания
сферы с боковой поверхностью конуса.

б) Пусть сторона основания ABCD равна . 1
HR = 2AB = a (так как
— средняя линия в △ACD ).

Прямоугольные по острому углу ( ∠HSR — общий),
следовательно,

OK-- SO- 1 ----94 −-1--
HR = SR ⇒ a = ∘ (a)2 +(9)2 ⇔
4
∘ -------
5 a= a2+ 81 ⇔ a= 3 ⇒ AB = 2a = 6.
4 16

Следовательно,

1 2 1 9 2
1) VSABCD = 3SH ⋅AB = 3 ⋅4 ⋅6
⇒ VSABCD −Vконус = 1⋅9⋅32(4−π) = 27(4− π).
2) Vконус = 1SH ⋅π ⋅HR2 = 1⋅ 9⋅π⋅32 3 4 4
3 3 4

Ответ:

б) 27(4 − π)
4

Показать ответ и решение

а) По формуле площади произвольного четырехугольника имеем:

Следовательно, если — диаметры сферы и
то есть Следовательно, OVAL — квадрат.

Расстояние от точки до плоскости (OV A) наибольшее, если
и — радиус сферы. Тогда объем пирамиды равен

Что и требовалось доказать.

б) Проведем где Тогда и

Так как то следовательно, по теореме о трех
перпендикулярах где

Далее имеем:

1 1 1 1
HL = QH = 4 VL, PH = 2V L =R, SP = 2 KQ = 2R

Тогда по теореме Пифагора в треугольнике SP H :

∘-------- √ -
SH = R2 + 1R2 = R--5
4 2

Так как NU = 1OA = R
2 , то площадь треугольника SUN равна

√ -
64√5-= 1R ⋅--5R ⇔ R2 = 64⋅4 ⇔ R = 16
2 2

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

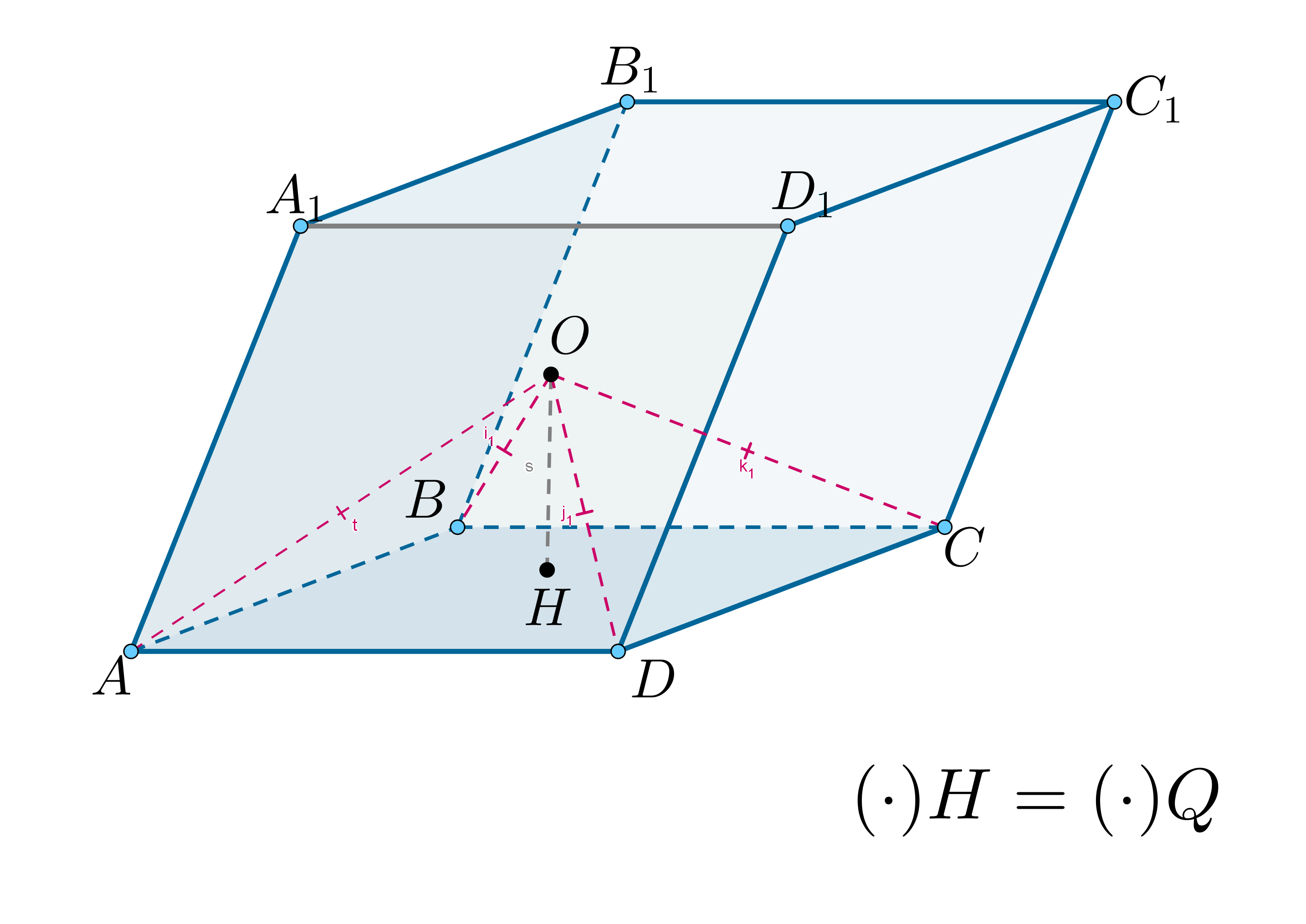
Дан параллелепипед .

а) Докажите, что около параллелепипеда можно описать сферу тогда и только
тогда, когда он прямоугольный.

б) Найдите площадь поверхности данного параллелепипеда, если его
объем равен 8, а радиус сферы, описанной около параллелепипеда, равен
√3- .

Показать ответ и решение

а) Если сфера описана около параллелепипеда, то ее центр находится на
одинаковом расстоянии от всех вершин параллелепипеда.

Будем сокращенно записывать как A ...D1 .

A ...D
1 — вписанный — прямоугольный

Пусть — центр сферы. Расстояния от точки до вершин A...D
1
одинаковы и равны .

Проведем . Рассмотрим △AOH , △BOH , △COH ,
△DOH . Они равны как прямоугольные по общему катету и гипотенузе.
Следовательно, равноудалена от вершин ABCD , то есть — центр
описанной около ABCD окружности. Если около параллелограмма можно
описать окружность, то он — прямоугольник.

Аналогично поступаем с каждой гранью A...D1 и получаем, что все
его грани — прямоугольники. Это по определению и есть прямоугольный
параллелепипед.

A ...D1 — прямоугольный A...D1 — вписанный

Все грани A ...D1 — прямоугольники. Рассмотрим прямую QQ1 , где и
— центры нижнего и верхнего оснований соответственно (точки пересечения
диагоналей). QQ1 параллельна боковым ребрам A ...D1 и перпендикулярна
основаниям. Пусть — середина QQ1 . Так как расстояния от точки
до вершин ABCD равны, расстояния от до вершин
равны, а также все эти расстояния равны между собой, имеем: треугольники

как прямоугольные по двум катетам. Следовательно, гипотенузы равны, то есть

расстояния от точки до всех вершин A...D1 одинаковы. Значит, около него
можно описать окружность.

Зааметим, что диагонали параллелепипеда пересекают QQ1 в точке ,
следовательно, центр сферы, описанной около параллелепипеда есть точка
пересечения его диагоналей, причем диагонали являются диаметрами
сферы.

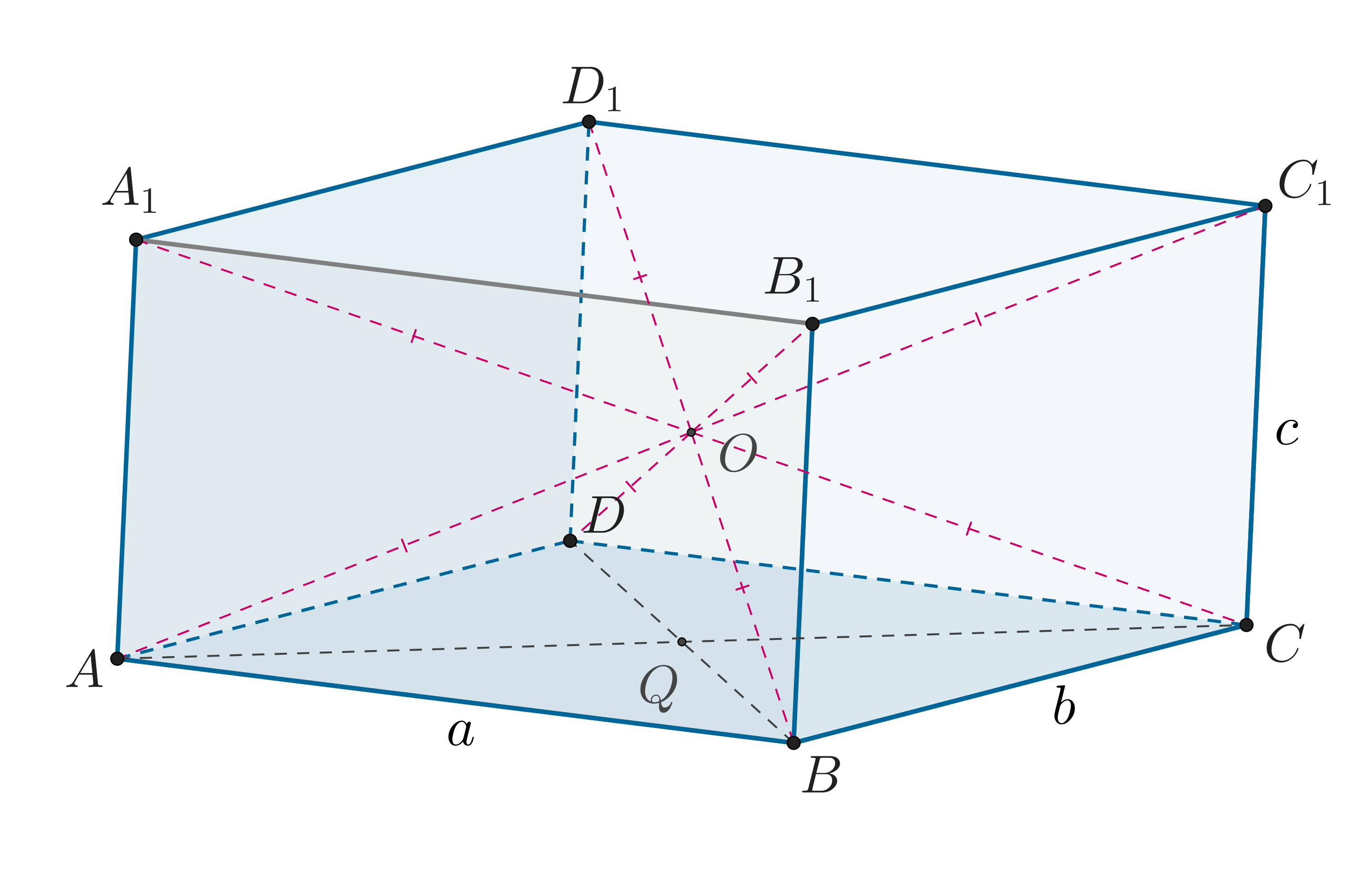
б) Обозначим ребра A...D1 как , , , как показано на рисунке.

В пункте а) мы доказали, что точка пересечения диагоналей A ...D1 есть
центр описанной сферы. Следовательно, половина диагонали параллелепипеда есть
радиус этой сферы. То есть .

Нам требуется найти площадь полной поверхности A...D1 , то есть выражение
.

Известно, что , √- √ -2--2---2-
A1C = 2R = 2 3= a + b +c .

По неравенству о среднем

∘ ---------- ∘ -√----
a2+-b2-+c2-≥ 3√abc ⇔ (2--3)2-≥ 3√8 ⇔ 2 ≥ 2
3 3

Равенство достигается тогда и только тогда, когда .

Следовательно,

Ответ:

б)

Показать ответ и решение

Сечение шара многоугольником — окружность с центром в точке ,
и все вершины этого многоугольника лежат на этой окружности, следовательно,
он вписанный. Аналогично вписан в окружность с центром
.

Пусть — центр шара. Проведем и
Следовательно, Q, O,O1 лежат на одной прямой, перпендикулярной основаниям
(так как основания параллельны). Рассмотрим A OO B
1 1 1 — прямоугольник,
так как ∘
∠A1OO1 = 90 , , . Следовательно,
, то есть A1B1 перпеникулярна основаниям призмы. Значит, призма
прямая.

б) , O
1 — центры оснований. Проведем B H ⊥ B B
1 2 3 . Тогда
следовательно, A2H — проекция A2B1 на плоскость
. Значит, . Получили прямоугольный равнобедренный
, значит, . Пусть , Тогда

2 2
h2+ a-= A2H2 = 3a- ⇔ h = √a-
4 4 2

— середина OO1 , следовательно, из

2 2 (1 )2 ( 1 )2 11 2
R = QB 3 = 2h + √3-a = 24a

Объем призмы равен

√ - √ -
9= V = h ⋅ a2-3= a3√-3 ⇔ a= √6-
2 4 4 2

Следовательно, площадь поверхности шара равна

2 11
S = 4πR = 4⋅24 ⋅6π = 11π

Ответ:

б) 11π

Показать ответ и решение

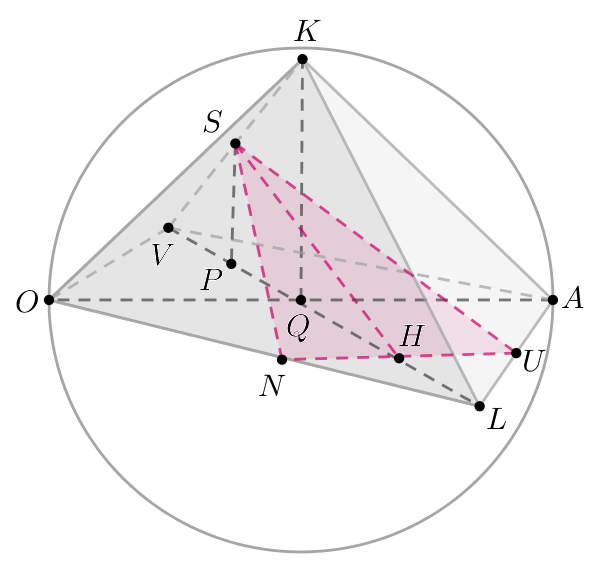
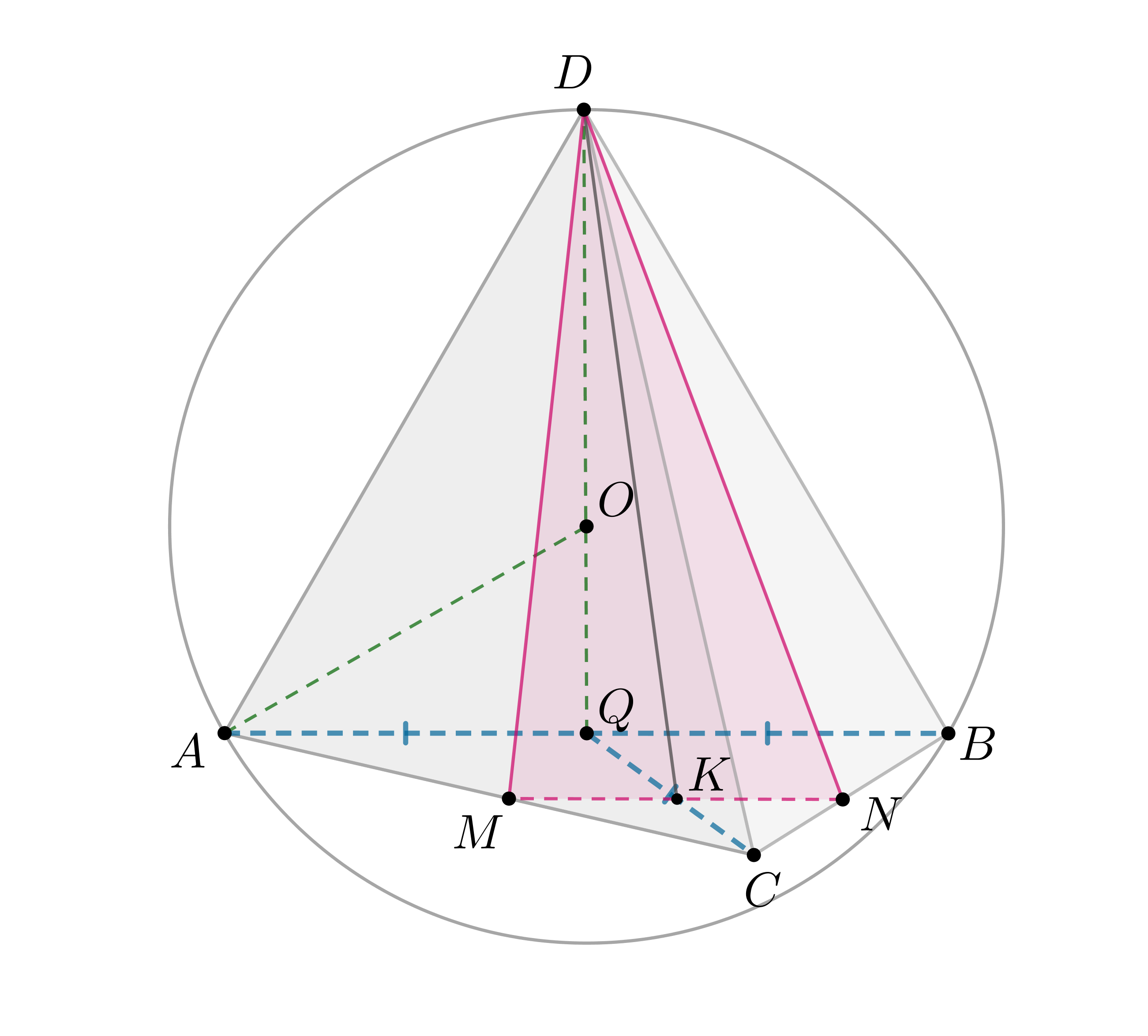
а) Боковые ребра пирамиды MABC равны, так как это образующие конуса.
Так как плоские углы при вершине равны, то пирамида правильная,
следовательно, △ABC равносторонний. Рассмотрим основание. Наибольший
объем пирамида MABF C имеет тогда, когда наибольшую площадь имеет
△BF C . Так как основание этого треугольника фиксировано, то наибольшую
площадь он имеет, когда высота к наибольшая. Следовательно, точка —
середина дуги . Тогда , следовательно,
следовательно, — диаметр.

Если — радиус окружности, описанной около правильного треугольникав, то
сторона треугольника равна √-
a= r 3 . Следовательно,

√- √ -
SABFC =2SABF = r 3 ⋅r = r2 3

Найдем — высоту. Пусть . Тогда .

√ -
ctg α-= MC1 ⇒ MC1 = AC1ctg α-= r-3ctg α-
2 AC1 2 2 2

OC1 = r
2 , следовательно, из △MOC1 :

Следовательно, объем

∘ ---------- ∘----------
VMABFC = 1 ⋅ r 3ctg2 α− 1⋅r2√3 = r3 3 ctg2 α-− 1
3 2 2 6 2

Чтд.

б) — перпендикуляр на (AMB ) . Пусть . Тогда если
, то по подобию .

следовательно, , следовательно,
1
BF = 2KF, то есть

Таким образом,

FH FK 2 2
CP- = CK- = 3 ⇔ FH = 3CP

Пусть . Тогда для △MCC1 :

1 1 2 2 2 2
2MO ⋅CC1 = SMCC1 = 2CP ⋅MC1 ⇔ MO ⋅CC 1 = CP ⋅MC 1

Следовательно,

2( 2 α )
CP 2 = 3r-3ctg-2 −-1
4ctg2 α2

Тогда

∘ ----2 α---
FH = √r-⋅ 3ctg-2α− 1
3 ctg22

Так как ∘--
sin α = 5
2 7 , то ∘ --
ctg α = 2,
2 5 следовательно,

∘ -------
6√6- 3⋅ 25 − 1
FH = -√3-⋅ ---2---= 6.
5

Ответ:

б)

Показать ответ и решение

б) — перпендикуляр на (AMB ) . Пусть . Тогда ессли
, то по подобию .

следовательно, , следовательно,
1
BF = 2KF, то есть

Таким образом,

FH--= FK-= 2 ⇔ FH = 2 CM
CM CK 3 3

У правильного треугольника со стороной радиус описанной окружности
равен 2
3 от высоты треугольника, то есть a-
√3. Следовательно, √ -
a= r 3 . Из
прямоугольного равнобедренного треугольника AMC :

√- ∘ 3-
CM = AC : 2 = 2 r

Тогда

√ -
F H = 2CM =2 6.
3

Ответ:

б) 2√6

Дана правильная треугольная пирамида SABC со стороной основания, равной
√ -
2 7 . Центр основания пирамиды является вершиной конуса, окружность
основания которого вписана в боковую грань пирамиды.

а) Пусть AA1 — высота основания. Докажите, что ∘ ----
SOOA1 = CSAC1 .

б) Найдите радиус основания конуса.

Показать ответ и решение

а) Пусть SC = x , — центр вписанной в SBC окружности. Тогда
√-
SI :IA1 = x : 7 , следовательно, SI = xk , √-
IA1 = k 7.

Рассмотрим △SOA1 :

SO xk OI ∘ -√--
OA1- = OI-= k√7- ⇔ OI = x 7k

Тогда

∘ --- ∘ ----
SO--= -O√I-= √x-= SC--
OA1 k 7 7 CA1

Чтд.

б) Так как OA1 = √21,
3 то SO = √21⋅∘ x√--
3 7 , тогда из

2 4 21 x 2 √ -
x = 9 ⋅21+-9 ⋅√7- ⇔ 9x − 3 7x− 4⋅21= 0

Решая это уравнение, получаем √-
x = 43 7.

Тогда --------
∘ 16 7
SA1 = 9 ⋅7− 7 = 3, следовательно,

2S 7 ⋅2√7-
r =-PSSBBCC-= -83√----√- = 1.
3 7+ 2 7

Ответ:

б)

Показать ответ и решение

а) По условию центр описанной сферы лежит на . Следовательно, так как он
равноудален от точек и , то центр — середина . Также имеем
. Если медиана треугольника равна половине стороны, к
которой она проведена, то она проведена из прямого угла треугольника,
следовательно, Чтд.

б) Отметим — середину . Тогда .
Если провести перпендикуляр из точки на плоскость AF C , то его основание
будет лежать на (так как плоскости (AF B) и (ABC ) перпендикулярны).
Следовательно, — проекция на (AFB ) . Тогда из
следует, что

Проведем и восстановим из точки перпендикуляр к ,
который пересечет в точке . Тогда точка лежит в плоскости,
перпендикулярной и проходящей через его середину, следовательно,
любая точка этой плоскости равноудалена от и , следовательно,

По теореме Пифагора ;
Тогда √ --
AP = 13x 26.

, следовательно,

15⋅13√26
TP = ---11---x

Следовательно,

√--
1 1 1 15⋅13-26- 1
VACMT = 3TP ⋅2AC ⋅CM = 3 ⋅ 11 x⋅ 2 ⋅75x⋅11x

Площадь сферы равна 2
36π = 4πR , следовательно, R = 3. Тогда
√--
2R = AB = 15x 26 , откуда Подставляя это значение в выражение
объема ACMT, получаем

V =6.

Ответ:

б)

Показать ответ и решение

а) Так как , то , . Проведем через
точку — середину отрезка , прямую , .
Проведем , тогда . Следовательно, ,
следовательно, (LHK ) — плоскость, проведенная через середину отрезка
перпендикулярно ему. Значит, любая точка этой плоскости равноудалена от
концов этого отрезка. Следовательно, равноудалена от точек и
.

Если , то , следовательно, ∠BCA — угол между
прямой и плоскостью AF C . Тогда , тогда AB = 3x ,
BC =x . Тогда , . , следовательно,
. Чтд.

б) , следовательно, если AH = 7y , то

Из △ABC по теореме Пифагора получаем
y = √x-
10 . Следовательно,

√--
48 = 1⋅LH ⋅ 1AB ⋅MC ⇒ 48= 1⋅16⋅√x--⋅-9x2 ⇔ x = 10
3 2 3 10 10

Так как центр описанной сферы лежит в основании ABCD , то центр сферы —
точка пересечения диагоналей и . Следовательно,

x
R = 5y = 5√10-= 5.

Ответ:

б)

Показать ответ и решение

а) Так как пирамида правильная, то центр сферы, описанной около пирамиды,
лежит на перпендикуляре, проведенном через центр основания. В нашем случае
центр основания и есть центр этой сферы. Следовательно, OA = OF и
. Следовательно, △AOF прямоугольный и равнобедренный„ то есть
. Это и есть угол между ребром F A и плоскостью основания.
Аналогично доказывается для других боковых ребер пирамиды.

б) Пусть — середина . Проведем , .
Следовательно, так как , то . Таким образом, в
плоскости (XKY ) любая точка равноудалена от точек и , так как лежит
на серединном перпендикуляре к этому отрезку. Продлим до пересечения с
AF : получим точку . и .

Рассомтрим основание ABC . Пусть AB = a , 3
MB = 4a , 3
BK = 8a ,
. Следовательно, по теореме Фалеса .
Следовательно, по теореме Фалеса , откуда (
— радиус сферы).

Следовательно, получаем

5 1 5 9√3 2 1
64-= 3 ⋅4R ⋅16-R ⇔ R = √3

Ответ:

б) 1√--
3

Показать ответ и решение

а) Имеем

Следовательно, , если — диаметры сферы,
, то есть . Следовательно, ABCD — квадрат.
Расстояние от до (ABC ) наибольшее, если , — радиус
сферы. Тогда

Чтд.

б) Проведем , . Тогда
. Так как , то , следовательно, по ТТП
(). HD = OH = 1BD
4 , следовательно, PH = 1BD
2 ,
1
MP = 2FO , следовательно, по теореме Пифагора

∘ ----1--- R √5
MH = R2+ 4R2 = --2-

Так как , то

√ - √ -
64 5= 1R ⋅--5R ⇔ R2 = 64⋅4 ⇔ R = 16.
2 2

Ответ:

б)

Показать ответ и решение

а) Пусть — перпендикуляр к плоскости (ABC ) , следовательно, — центр
окружности, описанной около △ABC . Наибольшее расстоние от точки
, лежащей на сфере, до (ABC ) достигается, если один из концом
диаметра сферы, проходящего через , причем DQ > EQ . S△ABC
наибольшая, если △ABC — равнобедренный прямоугольный, то есть
. Тогда имеем: , следовательно, ,
чтд.

б) Пусть . По ТТП (так как ) имеем
.

По теореме Пифагора из

Следовательно, по теореме Пифагора из △DOK :

∘-------√--- √-
DK = 162+ (4 2)2 = 12 2

Так как 1 √-
MN = 2AB = 8 2 , то

1 √ - √ -
S△DMN = 2 ⋅8 2⋅12 2= 96.

Ответ:

б)

Показать ответ и решение

а) Рассмотрим плоскость (PMN ) . Треугольник PMN прямоугольный,
∘
∠M = 90 , так как опирается на диаметр. Его площадь наибольшая в том случае,
если он равнобедренный, то есть . Расстояние от точки до
(PMN ) наибольшее, если , то есть △P LN — прямоугольный
равнобедренный. Тогда , , следовательно, по ТТП
. Чтд.

б) Проведем , , . Тогда если — радиус
сферы, то ,

∘ ---------- ∘ -------- √ -
NH = NO2 + OH2 = R2+ 1R2 = a--5
4 2

Тогда

∘ 5-2---1-2- ∘ 3-
TN = 4R + 4R = 2R

Следовательно,

TH- 1--
∠(TN, (P MN ))= ∠TNH = arcsin TN = √6

Ответ:

б) 1√--
6

Показать ответ и решение

а) Так как , то — точка касания сферы с (ABC ) . Проведем
. Следовательно, , ,
— точка касания сферы и (BCC1 ) . Заметим, что AOKH — квадрат, так как
это прямоугольник с равными смежными сторонами, и его стороны равны радиусу
сферы. Следовательно, если AB = a , то √-
R = a23 .

Рассмотрим ACC1A1 . MA1 = 3a
4 , следовательно,

∘ ---------- √-
∘ ---2------2- 3 2 -9 2 a-3-
OA1 = OM − A1M = 4a − 16a = 4

Следовательно, , чтд.

б) Так как AB = 12 , то √ -
AA1 =9 3 . Следовательно,

Ответ:

б)

Показать ответ и решение

а) Рассмотрим диаметральное сечение сферы плоскостью, проходящей через
диаметр . Прямая касается этой окружности в точке .
пересекает окружность в точке . — касательная к окружности,
. По свойству касательной, проведенной из одной точки к окружности,
AK = KM .

Пусть , .
Тогда ∘ ∘
∠KMC = 180 − 90 − α = β .

Заметим, что , то . Следовательно,
. Следовательно, радиус основания конуса .

б) Проведем b⊥ a , . Рассмотрим △KSC : .
tgα = tg∠ABC =AC :AB = 1
4 , следовательно,

-2tgα-- -8
tg2α= 1− tg2α = 15

Следовательно, , следовательно,

4
SC = KC ⋅tg2α = 15

Ответ:

б) 4-
15

В прямую призму, в основании которой лежит ромб с углом 45∘ , вписан цилиндр.
Расстояние между осью цилиндра и диагональю боковой грани призмы равно
√ -
5 2 .

а) Докажите, что отношение объема призмы к объему цилиндра равно
√ -
2:π .

б) Найдите площадь полной поверхности цилиндра, если объем призмы равен
120.

Показать ответ и решение

а) Пусть дана призма , , O,O1 — центры нижнего и
верхнего оснований соответственно (точки пересечения диагоналей, центры
вписанных окружностей). Следовательно, OO1 — ось цилиндра.

Пусть . Тогда , следовательно, перпендикулярна
диагонали боковой грани, следовательно, √-
OH = 5 2 и OH = r — радиус
основания цилиндра.

Проведем . Получаем прямоугольный равнобедренный треугольник
ADK , откуда √ - √-
AD = DK 2= 2r 2 .

Если AA1 = h — боковое ребро призмы, то

√ -
Vпризмы--= AB-⋅DK-⋅AA1-= --2
Vцилиндра πr2⋅AA1 π

Чтд.

б)

√ - 3
Vпризмы = 120= 4 2r2h ⇔ h = -√--
5 2

Следовательно,

2 ( √- --3- )
S = 2πrh+ 2πr = 2π 5 2⋅5√2-+ 50 =106π.

Ответ:

б) 106π

Около треугольной призмы, объем которой равен 288, описан цилиндр.
Расстояние между осью цилиндра и диагональю боковой грани призмы равно
√ -
4 3 .

а) Докажите, что отрезок, соединяющий центры окружностей, описанных около
оснований данной треугольной призмы, параллелен и равен боковому ребру
призмы, а также перпендикулярен основаниям призмы.

б) Пусть призма правильная. Найдите площадь полной поверхности
цилиндра.

Показать ответ и решение

а) Пусть дана призма . Если около нее описан цилиндр, то
основания цилиндра описаны около оснований призмы. Пусть O,O1 — центры
описанных около оснований призмы окружностей. Тогда OO1 — ось цилиндра.
Следовательно, . Тогда боковые ребра призмы —
образующие цилиндра, следовательно, они параллельны OO1 и равны
OO1 .

б) — точка пересечения высот основания ABC , , .
, следовательно, , следовательно, , то
есть √ -
OH =4 4 .

, AC = 2√-BH
3 , следовательно,

Так как , то

Ответ:

б) 416π

Около четырехугольной призмы описан цилиндр.

а) Докажите, что призма является прямоугольным параллелепипедом.

б) Диагональ и меньшая сторона основания призмы образуют угол ∘
60 .
Площадь боковой поверхности призмы равна √ -
120 3 , а расстояние между боковым
ребром и скрещивающейся с ним диагональю основания равно √-
1+ 3 . Найдите
объем цилиндра.

Показать ответ и решение

а) Призма прямая, так как ее боковые ребра параллельны оси цилиндра.
Основание призмы вписано в окружность (условие цилиндра), следовательно,
является прямоугольном. Таким образом, призма — прямоугольный
параллелепипед.

б) Пусть AB < BC . Расстояние между DD1 и скрещивающейс с ней
диагональю основания — это . Пусть √ -
DH = x= 1 + 3 , тогда
∘
AD =DH :sin30 =2x , ∘ 2x
AB = DH :sin 60 = √3 , 4x
AC = √3.

Пусть AA1 = h . Площадь боковой поверхности призмы равна

√ - ( 2x ) 1 + √3 120⋅3
120 3= 2h(AB +AD )= 2h √3-+ 2x = 4hx⋅--√3-- ⇒ h = 4(1+-√3)2

Тогда √ -
V = h⋅π (1AC)2 = -120⋅√3---⋅ 4(1-+-3)2π = 120π.
2 4(1+ 3)2 3

Ответ:

б) 120π

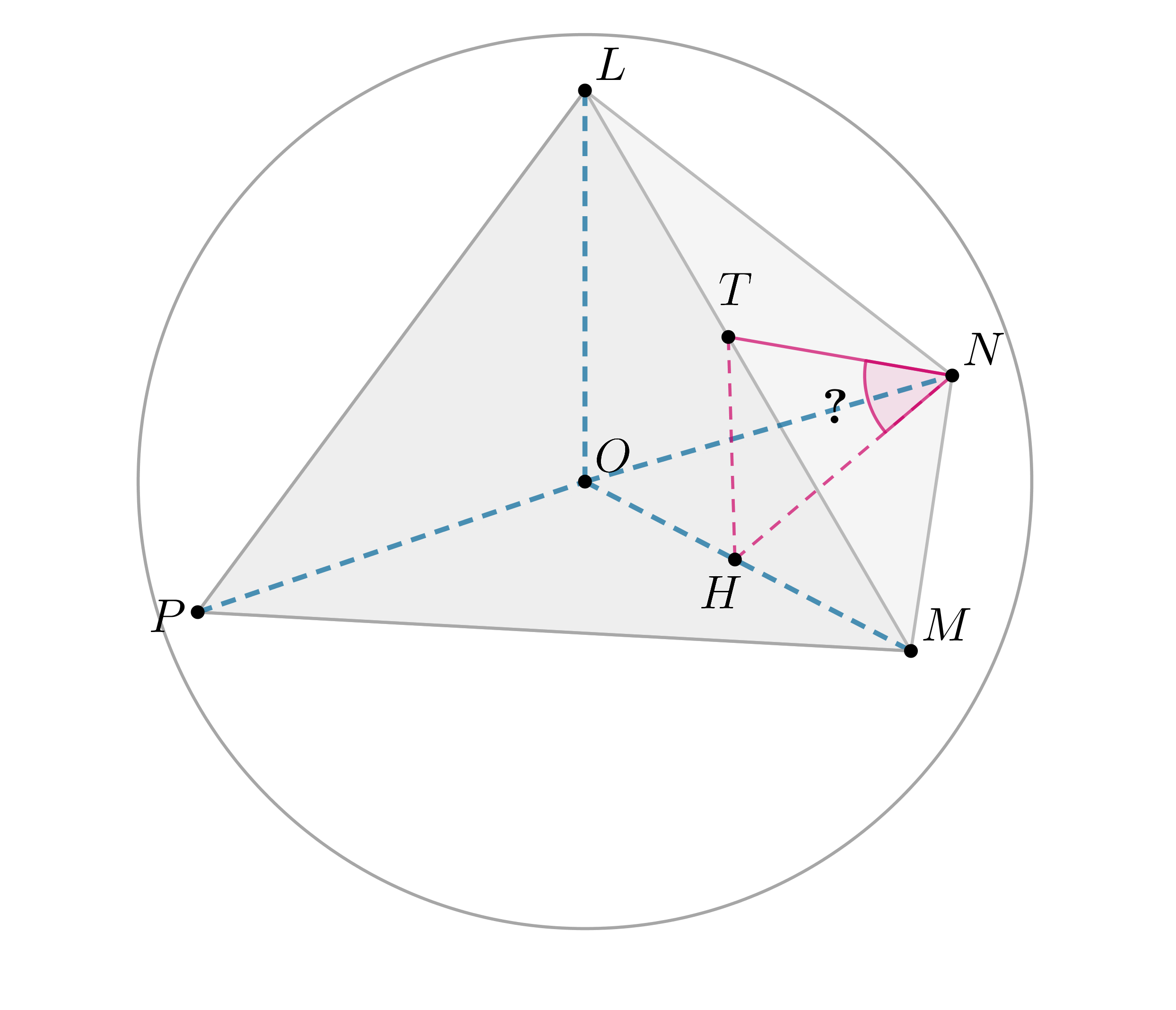
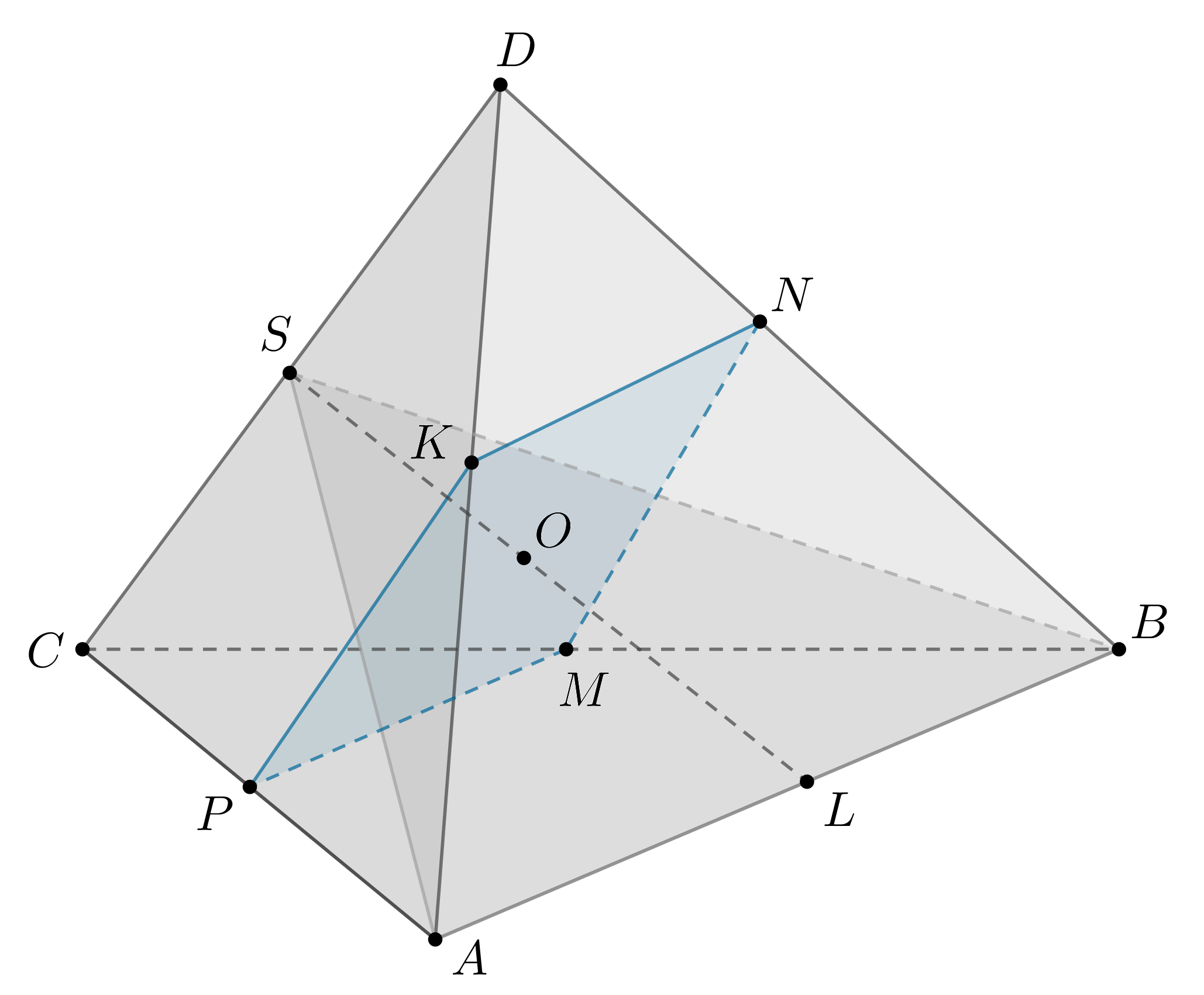
Внутри правильного тетраэдра ABCD расположен конус, вершина которого
является серединой ребра . Основание конуса вписано в сечение тетраэдра,
проходящее через середину ребра параллельно прямым и .

а) Докажите, что сечением является квадрат.

б) Найдите объем конуса, если ребро тетраэдра равно 12.

Показать ответ и решение

а) Пусть — середина . Тогда △ASB равнобедренный, так как и
— медианы (высоты) в равных правильных треугольниках. Следовательно,

Назовем сечением MNKP . , . Так как ,
то , . Следовательно, MNKP — параллелограмм.
Так как , то , то есть MNKP — ромб. Так как
MN = 1CD
2 , MP = 1AB
2 , CD = AB , то MNKP — квадрат со стороной
1
2AB =6 .

б) Проведем , . Тогда , следовательно,
, следовательно, — высота конуса.

. . Следовательно,

1 1 ( 1 )2 √-
Vконус = 3 ⋅2SL ⋅π 2MN = 9π 2.

Ответ:

б)

Источник

1. Нахождение объемов и площадей поверхности по готовым рисункам

1.1	Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).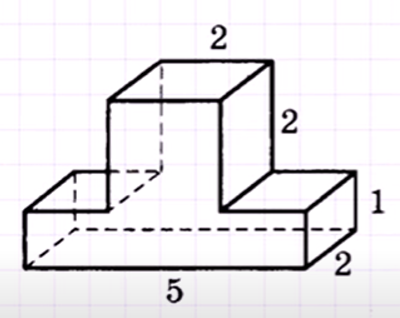	Смотреть видеоразбор
1.2	Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).	Смотреть видеоразбор
1.3	Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).	Смотреть видеоразбор
1.4	Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).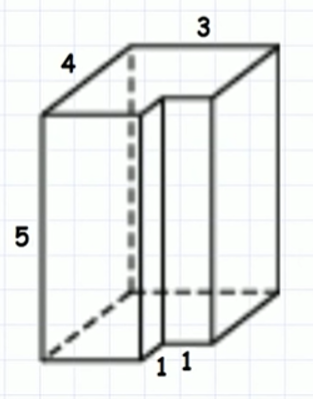	Смотреть видеоразбор
1.5	Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).	Смотреть видеоразбор
1.6	Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).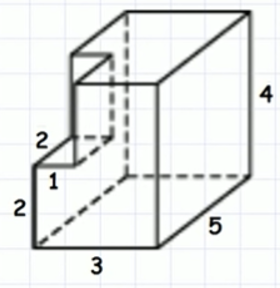	Смотреть видеоразбор

2. Призма, пирамида

2.1	В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите её объём	Смотреть видеоразбор
2.2	В правильной шестиугольной пирамиде боковое ребро равно 17, а сторона основания равна 8. Найдите высоту пирамиды.	Смотреть видеоразбор
2.3	Объем куба равен 126. Найдите объем четырехугольной пирамиды, основанием которой является грань, а вершиной — центр куба.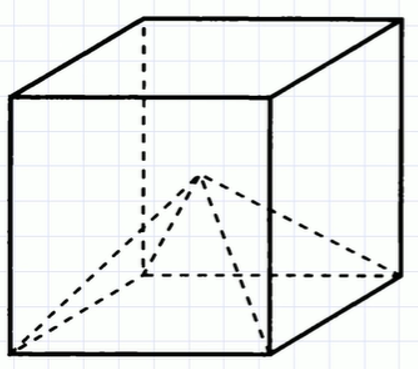	Смотреть видеоразбор
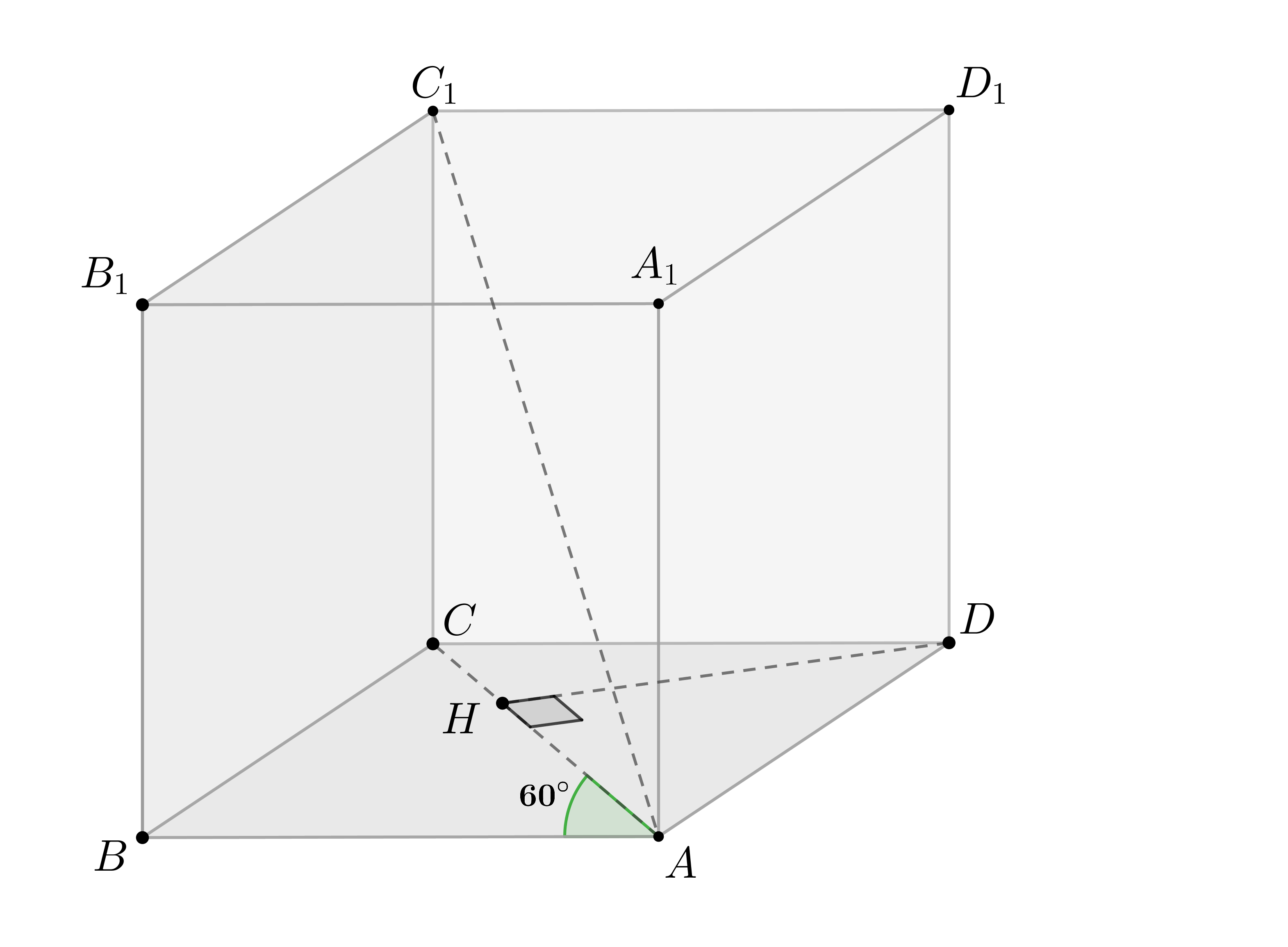
2.4	Найдите объем куба, если объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины, равен 21. Другая формулировка условия: В кубе ABCDA_1B_1C_1D_1 точки E, F, E_1 и F_1 являются серединами ребер BC, DC, B_1C_1 и D_1C_1 соответственно. Объем призмы, отсекаемой от куба плоскостью EFF_1, равен 21. Найдите объем куба.	Смотреть видеоразбор

3. Цилиндр и конус

3.1	Найдите площадь осевого сечения конуса, радиус основания которого равен 3, а образующая равна 5.	Смотреть видеоразбор
3.2	В цилиндрический сосуд налили 600 кубических сантиметров воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,6 раза. Найдите объем детали. Ответ выразите в кубических сантиметрах.	Смотреть видеоразбор
3.3	Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.	Смотреть видеоразбор
3.4	Площадь боковой поверхности конуса равна 36pi, а площадь его осевого сечения рана 15sqrt{9}. Найдите косинус угла между образующей конуса и плоскостью его основания.	Смотреть видеоразбор
3.5	Шар, объем которого равен pi, вписан в куб. Найдите объем куба	Смотреть видеоразбор
3.6	Шар вписан в цилиндр объемом 42. Найдите объем шара.	Смотреть видеоразбор
3.7	В сосуд в виде конуса налита жидкость до frac{1}{3} высоты. Объём налитой жидкости 16 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?	Смотреть видеоразбор
3.8	Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна 80. Найдите площадь боковой поверхности цилиндра.	Смотреть видеоразбор

Источник

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V=πR^2·h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Пример:

Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.

Решение:

Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.

$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$

Распишем формулы объема цилиндра и шара.

$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$

$V_{шара}={4π·R_{шар}^3}/{3}$

Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.

${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.

$V_{шара}=30:1.5=20$

Ответ: $20$

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

$l=SA$

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

$SО$ — высота и ось конуса.

Свойства конуса:

Все образующие конуса равны.
Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

$S_{бок.пов.}=πR·l$

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$

Объем конуса равен трети произведения площади основания на высоту.

$V={πR^2·h}/{3}$

Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Признаки подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Источник