Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
2
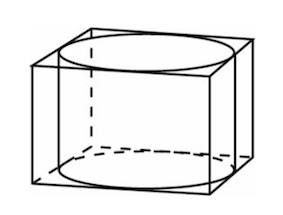
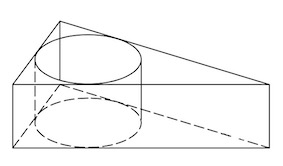
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
3
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
4
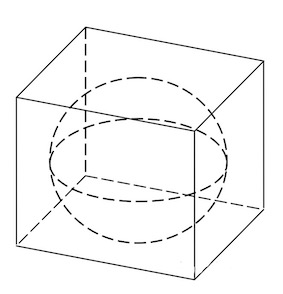
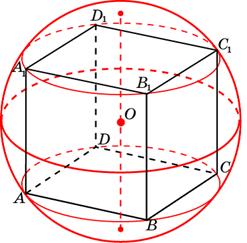
В куб вписан шар радиуса 1. Найдите объем куба.
5
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Пройти тестирование по этим заданиям
ЕГЭ Профиль №8. Комбинация тел
Данная тема посвящена задачам на комбинацию пространственных фигур, нахождению элементов вписанных и описанных цилиндров, конусов и сфер.
Рассмотрим объемные тела:
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а, b$ и $с$ — длина, ширина и высота соответственно;
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac)$.
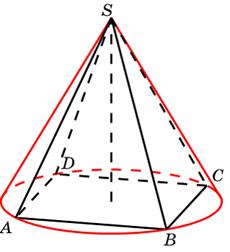
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые)- треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
$SO$ — высота
Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее высота приходит в центр основания (в центр описанной окружности). Все боковые ребра правильной пирамиды равны, следовательно, все боковые грани являются равнобедренными треугольниками.
Формулы вычисления объема и площади поверхности правильной пирамиды.
$h_a$ — высота боковой грани (апофема)
$S_{бок}={P_{осн}·h_a}/{2}$
$S_{п.п}=S_{бок}+S_{осн}$
$V={1}/{3}S_{осн}·h$
В основании лежат правильные многоугольники, рассмотрим их площади:
- Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.
- Квадрат $S=a^2$, где $а$ — сторона квадрата.
- Правильный шестиугольник.
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
$S_{бок}=P_{осн}·h$
$S_{п.п}=S_{бок}+2S_{осн}$
$V=S_{осн}·h$
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
Объем куба: $V=a^3={d^3}/{3√3}$.
Площадь полной поверхности: $S_{п.п}=6а^2=2d^2$
Радиус сферы, описанной около куба: $R={a√3}/{2}$
Радиус сферы, вписанной в куб: $r={a}/{2}$
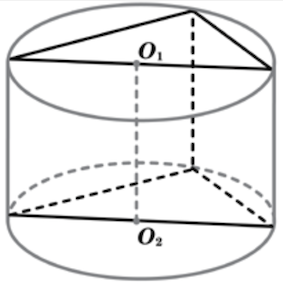
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующим).
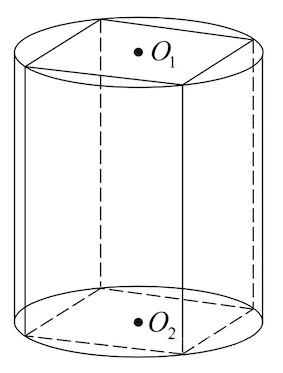
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
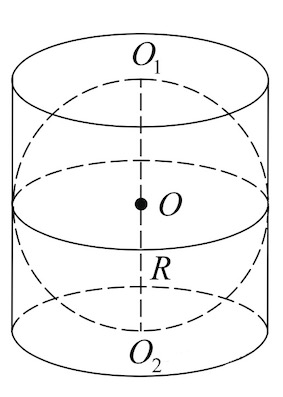
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоте цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей основания и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей
$АВ=a_n$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2·R·sin{180°}/{n}$;
$r=R·cos{180°}/{n}$;
$a_n=2·r·tg{180°}/{n}$.
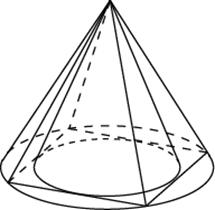
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются ($l$).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
1. Все образующие конуса равны.
2. Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
3. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник и угол при вершине осевого сечения равен 60° и радиус основания равен высоте конуса.
$R_{осн}=h$
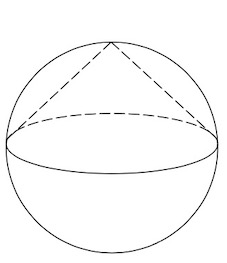
4. Если конус вписан в сферу, то сфера содержит окружность конуса и его вершину, радиус сферы равен радиусу конуса и равен высоте конуса.
$R_{сферы}=R_{конуса}=h_{конуса}$
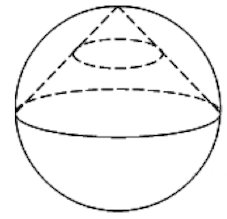
5. Если в конус, осевое сечение которого – равносторонний треугольник, вписан шар, то радиус основания конуса в $√3$ раз больше радиуса шара, а высота конуса в $3$ раза больше радиуса шара.
$r=R√3; SO_1=3R$
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
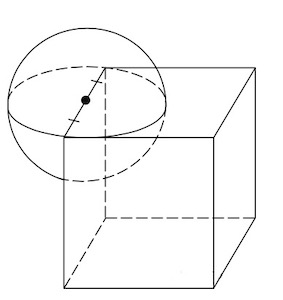
Задача 1. Объем прямоугольного параллелепипеда, описанного около сферы, равен Найдите радиус сферы.
Решение: + показать
Задача 2. В куб вписан шар радиуса Найдите объем куба.
Решение: + показать
Задача 3. Шар, объём которого равен вписан в куб. Найдите объём куба.
Решение: + показать
Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен Объем параллелепипеда равен
Найдите высоту цилиндра.
Решение: + показать
Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объем параллелепипеда.
Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны Найдите площадь боковой поверхности призмы.
Решение: + показать
Задача 7. В основании прямой призмы лежит квадрат со стороной . Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 8. Около шара описан цилиндр, площадь поверхности которого равна Найдите площадь поверхности шара.
Решение: + показать
Задача 9. Цилиндр описан около шара. Объем цилиндра равен Найдите объем шара.
Решение: + показать
Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен Найдите объем шара.
Решение: + показать
Задача 12. Середина ребра куба со стороной является центром шара радиуса
Найдите площадь
части поверхности шара, лежащей внутри куба. В ответе запишите
Решение: + показать
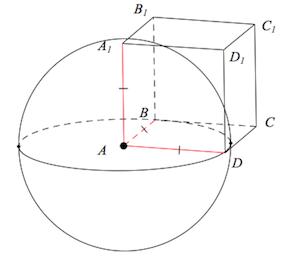
Задача 13. Вершина куба
со стороной
является центром сферы, проходящей через точку
. Найдите площадь
части сферы, содержащейся внутри куба. В ответе запишите величину
.
Решение: + показать
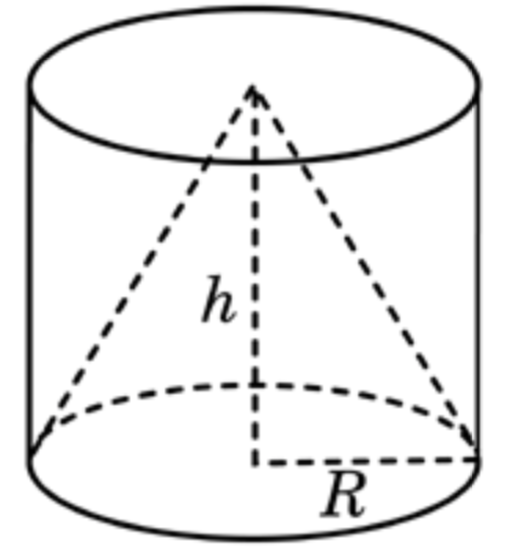
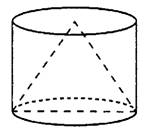
Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен
Решение: + показать
Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
Решение: + показать
Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания и высотой
Найдите его объем, деленный на
.
Решение: + показать
Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Решение: + показать
Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен Найдите объем конуса.
Решение: + показать
Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Найдите образующую конуса.
Решение: + показать
Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами и
Боковые ребра равны
. Найдите объем цилиндра, описанного около этой призмы.
Решение: + показать
Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен а высота равна
Решение: + показать
Задача 22. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен а высота равна
Решение: + показать
Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен
Решение: + показать
Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна
Решение: + показать
Задача 26. Около куба с ребром описан шар. Найдите объем этого шара, деленный на
Решение: + показать
Задача 27. Куб вписан в шар радиуса Найдите объем куба.
Решение: + показать


Задача 1. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 1). Вычислите объём цилиндра, если объём конуса равен 16.
Рис. 1.
Решение.
Объём конуса равен , а объём цилиндра —
, где
— площадь их общего основания,
— общая высота. Видно, что объём цилиндра в 3 раза больше объёма конуса и равен
.
Ответ: 48.
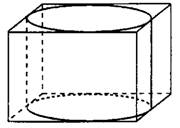
Задача 2. Прямоугольный параллелепипед описан около цилиндра (см. рис. 2), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.
Решение.
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть . Площадь основания параллелепипеда равна
.
Рис. 2.
Высоту параллелепипеда находим из формулы объёма параллелепипеда:
. Найденная высота параллелепипеда одновременно является и высотой цилиндра.
Ответ: 6.
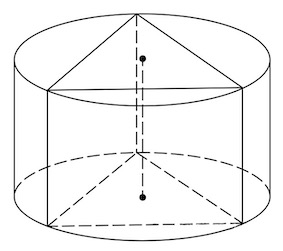
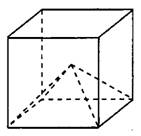
Задача 3. Объём куба равен 30 (см. рис. 3). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Рис. 3.
Решение.
Рассмотрим куб как четырёхугольную призму. Его объём равен . Основание пирамиды совпадает с основанием призмы, а высота вдвое меньше высоты призмы. Поэтому
Ответ: 5.
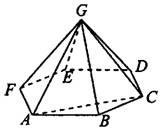
Задача 4. Объём правильной шестиугольной пирамиды равен 60 (см. рис. 4). Найдите объём треугольной пирамиды
.
Рис. 4.
Решение.
Обозначим сторону шестиугольника в основании пирамиды через . Правильный шестиугольник можно разбить на 6 правильных треугольников, поэтому площадь шестиугольника равна
Найдём площадь треугольника
.
Таким образом, площадь основания пирамиды в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
Ответ: 10.
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Комбинации геометрических фигур»
Открытый банк заданий по теме комбинации геометрических фигур. Задания B8 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №1074
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Цилиндр, объём которого равен 66, описан около шара. Найдите объём шара.
Показать решение
Решение
Из рисунка видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим объём цилиндра: Vцил. = Sосн. · H =pi R^2 cdot 2R = 2pi R^3. По условию 66 = 2pi R^3. Отсюда pi R^3 = 33. Так как Vшара = R^3, то искомый объём равен frac43cdot33=44.
Ответ
44
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1073
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 24. Найдите площадь поверхности шара.
Показать решение
Решение
Из рисунка, указанного в условии, видно, что, с одной стороны, диаметр шара является диаметром окружности основания цилиндра, а с другой стороны, является высотой цилиндра. Пусть радиус шара равен R, тогда его диаметр равен 2R, значит, высота цилиндра H равна 2R. Находим площадь полной поверхности цилиндра: S полн. пов. цил. = 2S осн. цил. + S бок. пов. цил. = 2pi R^2 + 2pi RH.
2pi R^2 + 2pi RH = 2pi R^2 + 2pi Rcdot 2R = 6pi R^2. По условию 24 = 6pi R^2. Отсюда pi R^2 = 4. Так как S пов. шара = 4pi R^2, то искомая площадь равна 4cdot 4 = 16.
Ответ
16
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1072
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Шар, объём которого равен 36pi, вписан в куб. Найдите объём куба.
Показать решение
Решение
Пусть радиус шара равен R, тогда объём шара находится по формуле V = frac43pi R^3.
По условию 36pi = frac43pi R^3. 108 = 4R^3, R^3 = 27, R = 3. Так как шар вписан в куб, то длина ребра куба равна длине диаметра шара, но диаметр шара в два раза больше радиуса и равен 3cdot 2 = 6. Объём куба V находится по формуле V = a^3, где a — ребро куба. Поэтому V = a^3 = 6^3 = 216.
Ответ
216
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1071
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого и высота равны 5. Найдите объём параллелепипеда.
Показать решение
Решение
Основанием параллелепипеда является прямоугольник, описанный около окружности радиусом 5. Значит, этот прямоугольник является квадратом, сторона которого равна диаметру окружности основания цилиндра. Так как радиус r этой окружности равен 5, то диаметр равен двум радиусам, то есть 10. Объём параллелепипеда V находим по формуле V = Sосн · h = (2cdot r)^2cdot r, где h — высота параллелепипеда, которая равна высоте цилиндра, то есть равна 5. Значит, объем параллелепипеда V=10^2cdot5=500.
Ответ
500
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №917
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 5sqrt2 Найдите радиус сферы.
Показать решение
Решение
Обозначим вершину конуса через A, а центр основания через O. Проведём через AO плоскость. В этой плоскости будет находиться диаметр сферы CB, AB — образующая конуса.
Тогда треугольник AOB — прямоугольный с прямым углом AOB. При этом AO=OB=R, где R — радиус сферы. По теореме Пифагора (AO)^2+(OB)^2=(AB)^2, R^2+R^2=(5sqrt2)^2, 2R^2=25cdot2, R^2=25, R=5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №910
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Куб описан около сферы радиусом 2. Найдите объём куба.
Показать решение
Решение
Так как куб описан около сферы, то длина диаметра этой сферы равна длине ребра куба. По условию радиус сферы равен 2, поэтому диаметр сферы в два раза больше и равен 4. Объём куба V находится по формуле V=a^3, где a — ребро куба. Поэтому V=a^3=4^3=64.
Ответ
64
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №909
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
В основании прямой призмы лежит квадрат со стороной 4. Боковое ребро призмы равно frac{4}{pi}. Найдите объём цилиндра, описанного около этой призмы.
Показать решение
Решение
Рассмотрим рисунок, приведённый в условии. Диаметр основания цилиндра является диагональю AC квадрата ABCD, а радиус R основания цилиндра равен половине AC. Согласно теореме Пифагора AC= sqrt{AB^2+BC^2}= sqrt{4^2+4^2}= sqrt{32}= 4cdotsqrt2. R=2cdotsqrt2. Заметим, что высота цилиндра совпадает с высотой призмы h. Отсюда следует, что V = Sосн. · h = picdot R^2cdot h= picdot(2sqrt2)^2cdotfrac{4}{pi}= 8cdot4= 32.
Ответ
32
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №316
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Тетраэдр содержит в себе многогранник, вершинами которого являются середины ребер данного тетраэдра. Найдите площадь поверхности образованного многогранника, если площадь поверхности тетраэдра равна 46.
Показать решение
Решение
Площадь поверхности тетраэдра равна сумме площадей 4 одинаковых граней. Площадь грани равна frac{46}{4}. Площадь поверхности многогранника равна сумме площадей 8 его граней, при этом каждая его грань — треугольник, образованный средними линиями грани тетраэдра, поэтому площадь этой грани равна frac14 площади грани тетраэдра.
Искомая площадь равна frac14cdotfrac{46}{4}cdot8=23.
Ответ
23
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №314
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Основанием прямой призмы является квадрат, сторона которого равна 4. Длина бокового ребра призмы равна frac{8}{pi}. Найдите объем цилиндра, описанного около этой призмы.
Показать решение
Решение
Радиус окружности, описанной вокруг квадрата со стороной 4, равен r=frac{4}{sqrt2}=2sqrt2.
Объем цилиндра равен V= pi r^2h= picdot(2sqrt2)^2cdotfrac{8}{pi}= picdot8cdotfrac{8}{pi}= 64.
Ответ
64
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №113
Тип задания: 8
Тема:
Комбинации геометрических фигур
Условие
Около конуса с образующей равной 7sqrt{2} описана сфера. Сфера содержит вершину конуса и его основание. Центр основания конуса и центр сферы совпадают. Найдите радиус сферы.
Показать решение
Решение
Так как центры сферы и основания конуса совпадают, то образующие конуса пересекаются под прямым углом. Найдем гипотенузу прямоугольного треугольника, катетами которого являются образующие конуса, а гипотенузой – диаметр сферы. Воспользуемся теоремой Пифагора:
d^2=2cdot (7sqrt{2})^2=2cdot 2cdot 7^2=2^2cdot 7^2
d = 2cdot 7 = 14
Отсюда радиус равен frac{d}{2}=7
Ответ
7
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
1.
#2654
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
1
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
2.
#1417
Номер в банке заданий «Хижина математика»
Сложность «Легко»
2
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 12. Найдите объём цилиндра.
3.
#1477
Номер в банке заданий «Хижина математика»
Сложность «Средне»

Официальное задание из открытого банка ЕГЭ
3
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна $$12sqrt{2}$$. Найдите площадь боковой поверхности конуса.
4.
#1631
Номер в банке заданий «Хижина математика»
Сложность «Средне»

Официальное задание из открытого банка ЕГЭ
4
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
5.
#1818
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
5
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 0,5. Найдите объём параллелепипеда.
6.
#1819
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
6
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 1,5. Найдите объём параллелепипеда.
7.
#1820
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
7
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 5,5. Найдите объём параллелепипеда.
8.
#1821
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
8
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объём параллелепипеда.
9.
#19281
Номер в банке заданий «Хижина математика»
Сложность «Средне»

Официальное задание из открытого банка ЕГЭ
9
Цилиндр, объём которого равен 60, описан около шара. Найдите объём шара
10.
#2956
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Официальное задание из открытого банка ЕГЭ
10
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна $$28sqrt{2}$$. Найдите радиус сферы.
11.
#8000
Номер в банке заданий «Хижина математика»
Сложность «Средне»
Официальное задание из банка ФИПИ
11
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 5. Объем параллелепипеда равен 700. Найдите высоту цилиндра.
12.
#8001
Номер в банке заданий «Хижина математика»
Сложность «Средне»
Официальное задание из банка ФИПИ
12
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 5,5. Объем параллелепипеда равен 242. Найдите высоту цилиндра.
13.
#314
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Задание взято из реального ЕГЭ прошлых лет
13
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 21. Найдите объём конуса.
14.
#86
Номер в банке заданий «Хижина математика»
Сложность «Легко»

Задание взято из реального ЕГЭ прошлых лет
14
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 30. Найдите объём цилиндра.





.png)










