ЕГЭ Профиль №9. Прямая
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Прямая
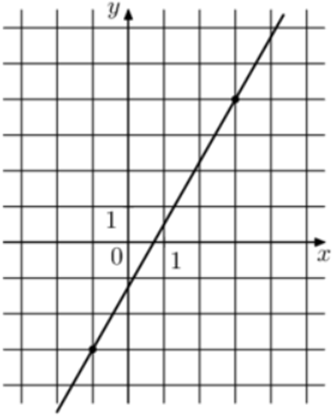
| Задача 1. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: — 10. |
 |
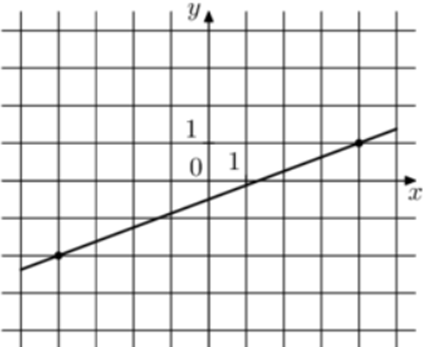
| Задача 2. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( {12} right).)
Ответ
ОТВЕТ: 4. |
 |
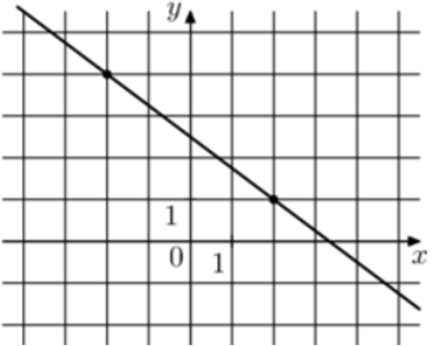
| Задача 3. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 14,5. |
 |
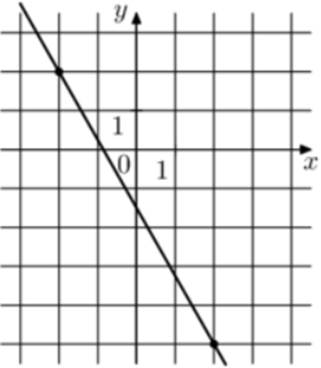
| Задача 4. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 26,5. |
 |
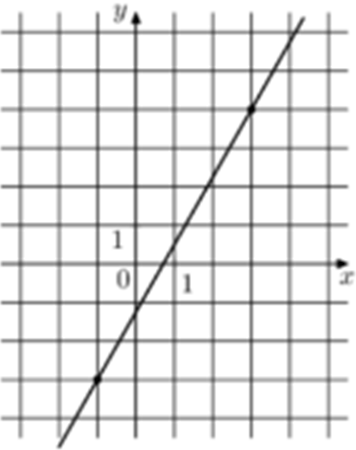
| Задача 5. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 13,5.)
Ответ
ОТВЕТ: — 7. |
 |
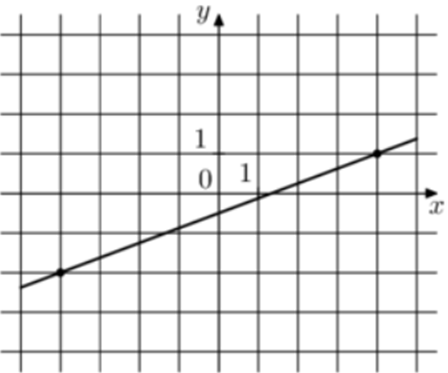
| Задача 6. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 4,75.)
Ответ
ОТВЕТ: 14. |
 |
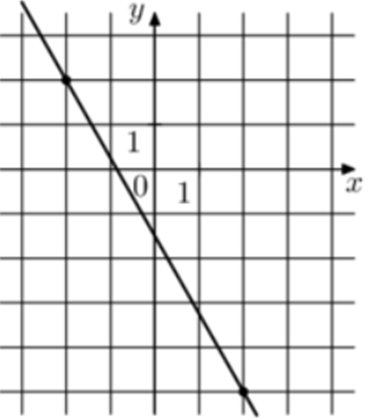
| Задача 7. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 16.)
Ответ
ОТВЕТ: — 10. |
 |
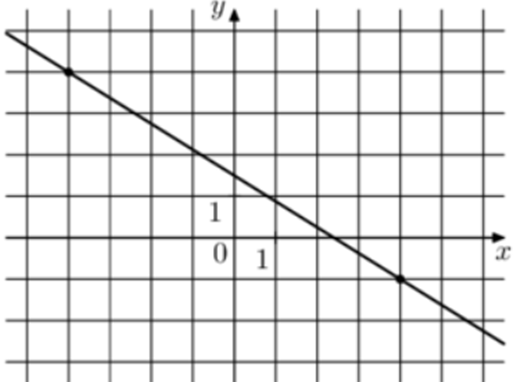
| Задача 8. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 7,25.)
Ответ
ОТВЕТ: 14. |
 |
| Задача 9. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 5. |
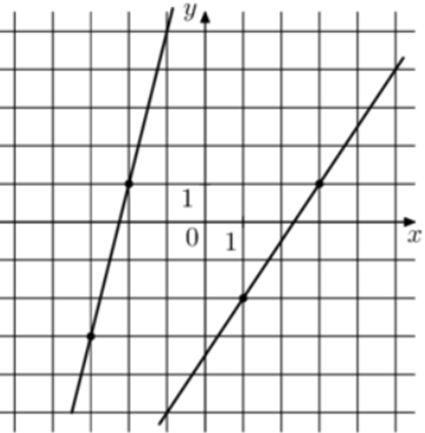 |
| Задача 10. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите абсциссу точки А.
Ответ
ОТВЕТ: 13. |
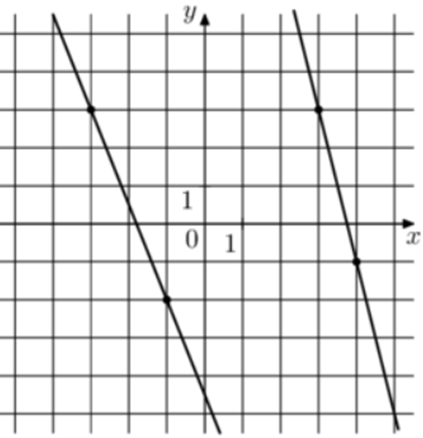 |
| Задача 11. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 11. |
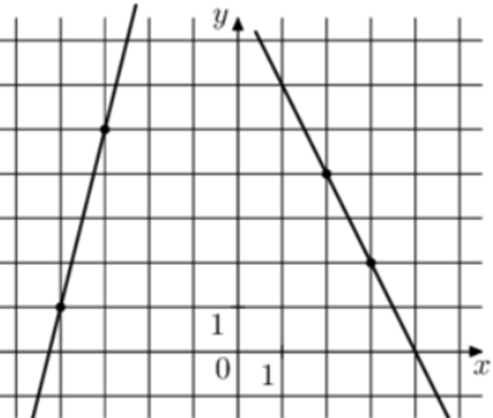 |
| Задача 12. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите ординату точки А.
Ответ
ОТВЕТ: — 11. |
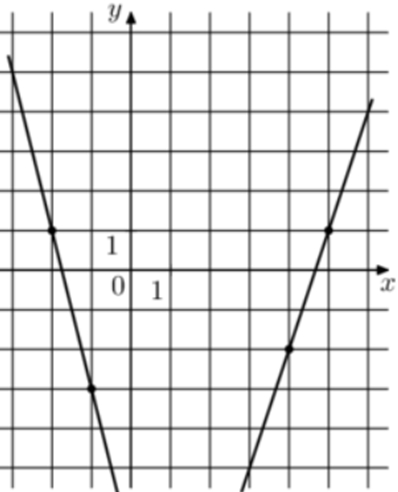 |
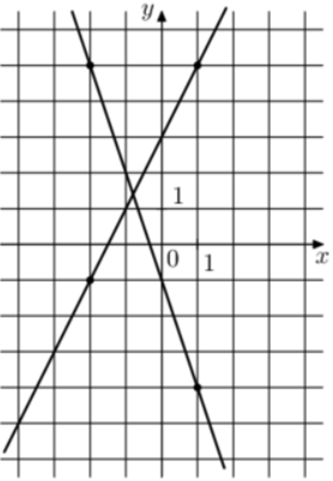
| Задача 13. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 0,8. |
 |
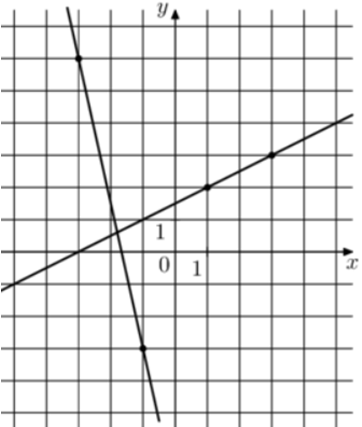
| Задача 14. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 1,8. |
 |
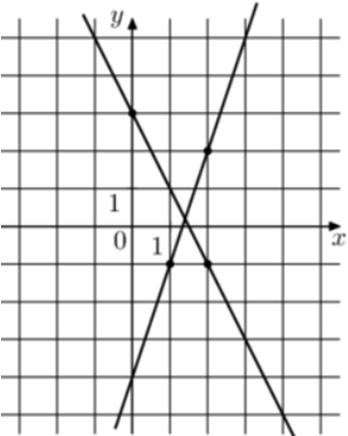
| Задача 15. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 0,2. |
 |
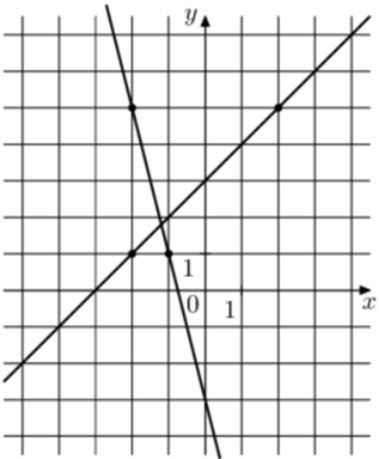
| Задача 16. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 1,8. |
 |
Задание 9 профильного егэ по математике math100 ru
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
A) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Укажите корни, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Укажите корни уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащее отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение:
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
На рисунке изображён график функции mbox<$fleft(xright)=dfrac $>. Найдите~$k$.
—>
Решения заданий с развернутым ответом не проверяются автоматически.
Ege. sdamgia. ru
20.06.2017 9:58:52
2017-06-20 09:58:52
Источники:
Https://ege. sdamgia. ru/test? id=13220838
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
| 3633 | На рисунке изображён график функции f(x)=k/(x+a). Найдите f(-7)
|
На рисунке изображён график функции f(x)=k / x+a Найдите f(-7) ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 10 | |
| 3610 | На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков
|
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков ! 36 вариантов ФИПИ Ященко 2023 Вариант 22 Задание 10 | |
| 3563 | На рисунке изображены графики функций f(x)=3x+3 и g(x)=ax^2+bx+c., которые пересекаются в точках A(-1; 0) и B (x0; y0). Найдите y0
|
На рисунке изображены графики функций f(x)=3x+3 и g(x)= ax2 + bx+c ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 10 | |
| 3507 | На рисунке изображён график функции f(x)=a^(x+2). Найдите f(6)
|
На рисунке изображён график функции f(x)=a^(x+2). Найдите f(6) ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 10 | |
| 3482 | На рисунке изображены части графиков функций иf(x)=k/x и g(x)=c/x+d. Найдите ординату точки пересечения графиков этих функций |
На рисунке изображены части графиков функций. Найдите ординату точки пересечения графиков этих функций ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 10 | |
| 3456 | На рисунке изображен график функции f(x)=acosx+b. Найдите a |
На рисунке изображен график функции f(x)=acosx+b ! Тренировочный вариант 397 от Ларина Задание 10 | |
| 3307 | На рисунке изображён график функций f(x)=(kx+a)/(x+b). Найдите k
|
На рисунке изображён график функций f(x)= kx+a / (x+b). Найдите k ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 9 | |
| 3306 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точках A(x0; y0) и B(4; 5). Найдите y0
|
На рисунке изображены графики функций, которые пересекаются в точках A(x0; y0) и B(4; 5) ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 9 | |
| 3304 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точке A. Найдите абсциссу точки A
|
На рисунке изображены графики функций. Найдите абсциссу точки A ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 9 | |
| 3301 | На рисунке изображён график функции f(x)=a^(x+b). Найдите f(-1)
|
На рисунке изображён график функции f(x)=a x+b ! 36 вариантов ФИПИ Ященко 2022 Вариант 29 Задание 9 | |
За это задание ты можешь получить 1 балл. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 72.7%
Ответом к заданию 9 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Свежие подосиновики содержат $78%$ воды, а сушёные — $12%$. Сколько килограммов свежих подосиновиков требуется для получения $3$ кг сушёных грибов?
Решение
Предположим, что подосиновики состоят из воды и «сухого остатка». В сушёных грибах содержится 100% — 12% = 88% «сухого остатка», в свежих — 100% — 78% = 22% «сухого остатка». В 3 кг сушёных грибов содержится 3 · 0.88 = 2,64 кг «сухого остатка», в свежих грибах, из которых приготовили сушёные, этого остатка было столько же, но в процентах это составляет уже 22%.
Если 2.64 кг — это 22%, то 100% это 2.64 : 0,22 = 12 кг. Требуется 12 килограммов свежих подосиновиков.
Ответ: 12
Задача 2
Смешали некоторое количество $12 $-процентного раствора уксуса с вчетверо большим количеством $9 $-процентного раствора уксуса. Сколько процентов составляет концентрация уксуса в получившемся растворе?
Решение
Чтобы найти концентрацию уксуса в растворе, надо найти отношение массы уксуса к массе раствора и умножить это отношение на $100%$. Найдем, сколько уксуса содержится в каждом растворе, обозначим количество 12-процентного раствора уксуса через $x$. При этом 9-процентного раствора уксуса вчетверо больше, то есть $4x$.Тогда в первом растворе $x · {12}/{100}$ кг уксуса, а во втором $4x · {9}/{100} = 0.36x$ кг уксуса. Масса получившегося раствора $5x$ кг, и в нём $0.12x + 0.36x = 0.48x$ кг уксуса.
Концентрация уксуса в получившемся растворе равна ${0.48x}/{5x} · 100% = 9.6%.$
Ответ: 9.6
Задача 3
Смешали некоторое количество $12 $-процентного раствора уксуса с таким же количеством $6 $-процентного раствора уксуса. Сколько процентов составляет концентрация уксуса в получившемся растворе?
Решение
Чтобы найти концентрацию уксуса в растворе, надо найти отношение массы уксуса к массе раствора и умножить это отношение на $100%$. Найдем, сколько уксуса содержится в каждом растворе ($a_1$ кг — в первом растворе и $a_2$ кг — во втором растворе), обозначим количество каждого раствора через $x$ кг. $a_1 = x · {12}/{100}, a_2 = x · {6}/{100}$. Количество получившегося раствора $2x$ кг, и в нём $a_1 + a_2 = 0.12x + 0.06x = 0.18x$.
Концентрация уксуса в получившемся растворе равна ${0.18x}/{2x} · 100% = 9%.$
Ответ: 9
Задача 4
Теплоход в 6:00 вышел из пункта $A$ в пункт $B$, расположенный в $204$ км по реке от пункта $A$. Пробыв в пункте $B$ 2 часа 20 минут, теплоход отправился назад и вернулся в пункт отправления в 20:00 того же дня. Найдите скорость течения, если собственная скорость теплохода равна $35$ км/ч. Ответ дайте в км/ч.
Решение
Обозначим скорость течения реки через $x$ км/ч. Тогда скорость теплохода по течению реки — $(35 + x)$ км/ч, а скорость теплохода против течения реки $(35 — x)$ км/ч.
По условию на весь путь теплоход затратил $20-6-2{1}/{3} = 11{2}/{3} = {35}/{3}$ (ч).
Составим и решим уравнение:
${204}/{35 + x} + {204}/{35 — x} = {35}/{3}$,
$204·3(35-x+35+x) = 35(35-x)(35+x)$,
$204·3·70= 35(35-x)(35+x) $ | $:35$,
$1224 = 1225-x^2$,
$x^2 = 1$,
$x_1 = 1, x_2 = -1$.
Скорость течения положительна, она равна $1$ км/ч.
Ответ: 1
Задача 5
От продовольственного склада до супермаркета, расстояние между которыми $240$ км, с постоянной скоростью выехала фура. На следующий день она отправилась обратно со скоростью на $20$ км/ч больше прежней. По дороге фура сделала остановку на 2 часа. В результате она затратила на обратный путь столько же времени, сколько на путь до супермаркета. Найдите скорость фуры по пути от продовольственного склада до супермаркета. Ответ дайте в км/ч.
Решение
Обозначим скорость фуры по пути от продовольственного склада до супермаркета через $x$ км/ч, тогда путь $240$ км она проедет за ${240}/{x}$ ч. Скорость фуры на обратном пути равна $(x + 20)$ км/ч, таким образом, время, затраченное на обратный путь, равно ${240}/{x + 20}$ ч. Составим и решим уравнение: ${240}/{x} — {240}/{x+20} = 2, 240 · 20 = 2x(x + 20), x^2 + 20x — 2400 = 0, x_1 = 40, x_2 = -60$.
Скорость $-60$ км/ч не удовлетворяет условию, поэтому скорость фуры по пути от продовольственного склада до супермаркета равна $40$ км/ч.
Ответ: 40
Задача 6
От замка А к замку В, расстояние между которыми $20$ км, одновременно вылетели два почтовых голубя. Известно, что за час первый голубь пролетает на $20$ км меньше, чем второй. Найдите скорость второго голубя, если он прилетел в замок В на $ 5$ минут раньше первого голубя. Ответ дайте в км/ч.
Решение
Обозначим скорость второго голубя через $x$ км/ч, тогда по условию скорость первого голубя $(x — 20)$ км/ч. Время, затраченное на полёт первым голубем, равно ${20}/{x — 20}$ ч. Время, затраченное на полёт вторым голубем, равно ${20}/{x}$ ч.
Составим и решим уравнение: ${20}/{x — 20} — {20}/{x} = {5}/{60}, {4}/{x — 20} — {4}/{x} = {1}/{60}, 4x — 4(x — 20) = {x(x — 20)}/{60}, x^2 — 20x — 4800 = 0, x_1 = 80, x_2 = -60$.
Отрицательная скорость не удовлетворяет условию. Скорость второго голубя $80$ км/ч.
Ответ: 80
Задача 7
Семья состоит из мужа, жены и их сына-студента. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы вдвое, а если бы зарплата жены сократилась впятеро, то общий доход семьи сократился бы на $ 32%$. Сколько процентов от общего дохода семьи составляет стипендия их сына-студента?
Решение
Если бы зарплата мужа увеличилась втрое, то есть прибавилось бы ещё две зарплаты, то общий доход семьи вырос бы вдвое, то есть увеличился на $100%$. Из этого можно сделать вывод, что одна зарплата мужа составляет ${100%}/{2} = 50%$ общего дохода семьи. Если бы зарплата жены сократилась бы впятеро, то есть стала равной ${1}/{5}$ имеющейся её зарплаты, то общий доход семьи сократился бы на ${4}/{5}$ имеющейся зарплаты, что по условию составляет $32%$ общего дохода семьи. Значит вся зарплата жены составляет ${32%}/{4/5} = 40%$ общего дохода семьи. На долю стипендии сына остаётся $100% — 50% — 40% = 10%$.
Ответ: 10
Задача 8
Цена мультиварки в магазине ежемесячно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый месяц уменьшалась цена мультиварки, если выставленная на продажу за $6800$ рублей через два месяца она была продана за $5508$ рублей?
Решение
Стоимость мультиварки первоначально была $6800$ рублей. Через месяц она стала $6800-6800·0.01x = 6800(1-0.01x)$ рублей, где $x$ — количе ство процентов, на которые уменьшается ежемесячно цена мультиварки. Тогда через два месяца её стоимость стала $6800(1 — 0.01x)(1 — 0.01x) = 6800(1 — 0.01x)^2$.
Составим и решим уравнение: $6800(1 — 0.01x)^2 = 5508, 1 — 0.01x = 0.9, x = 10$. Цена мультиварки уменьшалась на $10$ процентов.
Ответ: 10
Задача 9
В сентябре в магазине продали товаров на $585000$ рублей. В октябре сумма продаж возросла на $8%$, а в ноябре — на $10%$ по сравнению с октябрём. На сколько рублей продал магазин товаров в ноябре?
Решение
В октябре сумма продаж возросла на $8%$, то есть стала $108%=1{,}08$, что равно $585000⋅ 1{,} 08 $ (рублей). В ноябре сумма продаж возросла на $10%$ (стала $110%=1{,}1$) по сравнению с октябрём, то есть сумма продаж стала равна $585000⋅ 1{,}08⋅1{,}1=694 980$ (рублей).
Ответ: 694980
Задача 10
Три трубы наполняют бак за $2$ минуты, первая труба — за $9$ минут, а вторая — за $18$ минут. За сколько минут наполнит бак третья труба?
Решение
Объём бака примем за 1, тогда за 1 минуту три трубы заполнят ${1}/{2}$ часть бака, первая труба за 1 минуту заполнит ${1}/{9}$ часть бака, вторая труба — ${1}/{18}$ часть бака. Тогда третья труба за 1 минуту заполнит ${1}/{2} — {1}/{9} — {1}/{18} = {1}/{3}$ часть бака. Весь бак третья труба заполнит за $1 : {1}/{3} = 3$ минуты.
Ответ: 3
Задача 11
Роберт покрасит стену дома за $10$ часов, а Давид — за $15$ часов. За сколько часов покрасят эту стену Роберт и Давид, работая вместе?
Решение
Весь объём работы примем за $1$, тогда ${1}/{10}$ — часть стены, которую красит Роберт за $1$ час, ${1}/{15}$ — часть стены, которую красит Давид за $1$ час. Тогда оба мальчика за $1$ час покрасят ${1}/{10} + {1}/{15} = {1}/{6}$. Всю стену мальчики покрасят за $1 : {1}/{6} = 6$ часов.
Ответ: 6
Задача 12
Гаянэ и Милена выполняют одинаковый тест. Гаянэ отвечает за час на $16$ вопросов теста, а Милена — на $18$. Они одновременно начали отвечать на вопросы теста, и Гаянэ закончила свой тест позже Милены на $20$ минут. Сколько вопросов содержит тест?
Решение
Пусть в тесте $x$ вопросов. В среднем, Гаянэ отвечает на ${16}/{60}$ вопроса в минуту, а Милена на ${18}/{60}$ вопроса в минуту. На все вопросы теста Гаянэ ответит за $x : {16}/{60} = {60x}/{16}$ минут, а Милена за $x : {18}/{60} = {60x}/{18}$ минуты. По условию Гаянэ закончила свой тест позже Милены на $20$ минут, можно составить уравнение ${60x}/{16} — {60x}/{18} = 20$. Получаем $x = 48$.
Ответ: 48
Задача 13
Поезд, двигаясь равномерно со скоростью $84$ км/ч, проезжает мимо здания вокзала, длина которого равна $250$ метров, за $2$ минуты. Найдите длину поезда в метрах.
Решение
Обозначим длину поезда $x$ км. Длина здания равна $250$ метров, то есть $0.25$ км. Путь, который поезд проехал мимо здания вокзала, равен $(x + 0.25)$ км. Время, за которое поезд проезжает мимо здания вокзала, равно ${x + 0.25}/{84}$ ч. По условию это $2$ минуты ($2$ мин = ${2}/{60}$ часа).
Составим и решим уравнение: ${x + 0.25}/{84} = {2}/{60}; x = 2.55$ (км).
Длина поезда равна $2550$ м.
Ответ: 2550
Задача 14
Электричка, двигаясь равномерно со скоростью $50$ км/ч, проезжает мимо семафора за $45$ секунд. Найдите длину поезда в метрах.
Решение
Обозначим длину электрички $x$ км. Тогда время, за которое электричка проезжает мимо семафора, равно ${x} / {50}$ ч. По условию это $45$ секунд, то есть ${45} / {3600}$ ч. ${x} / {50}={45} / {3600}$, $x= {50⋅ 45} / {3600}, x=0{,} 625$ (км). Длина электрички равна $625$ м.
Ответ: 625
Задача 15
Первые два часа снегоход ехал со скоростью $15$ км/ч, следующие три часа — со скоростью $20$ км/ч, а затем один час — со скоростью $18$ км/ч. Найдите среднюю скорость снегохода на протяжении всего пути. Ответ дайте в км/ч.
Решение
Снегоход был в пути $2 + 3 + 1 = 6$ часов, за это время он проехал $15·2 + 20·3 + 18 = 108$ км. Т.к. средняя скорость снегохода равна $v_{ср} ={S}/{t}$, где $S$ — пройденный путь, $t$ — время, затраченное на весь путь, то $v_{ср} = {108}/{6} = 18$ (км/ч).
Ответ: 18
Задача 16
Из городов $A$ и $B$, расстояние между которыми равно $160$ км, навстречу друг другу одновременно выехали велосипед и мопед и встретились через $4$ часа на расстоянии $64$ км от города $B$. Найдите скорость мопеда, выехавшего из города $A$. Ответ дайте в км/ч.
Решение
Мопед и велосипед встретились через 4 часа на расстоянии 160 — 64 = 96 км от города A. Тогда скорость мопеда, выехавшего из города A, равна 96 : 4 = 24 км/ч.
Ответ: 24
Задача 17
Из двух городов, расстояние между которыми равно $720$ км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны $56$ км/ч и $64$ км/ч?
Решение
Скорость сближения автомобилей равна сумме скоростей 56 + 64 = 120 (км/ч). Автомобили встретятся через 720 : 120 = 6 (ч).
Ответ: 6

