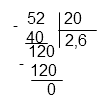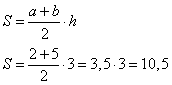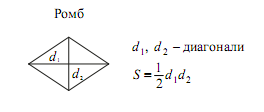Задание егэ с нахождением площади

16. Задачи по планиметрии


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи, решаемые методом площадей

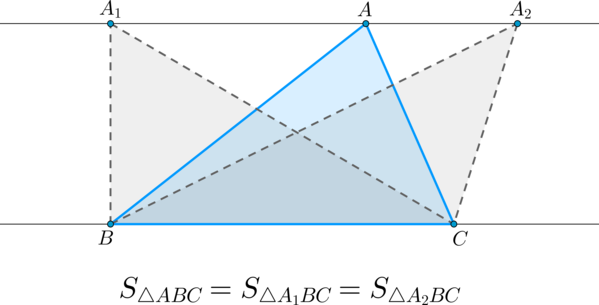
(blacktriangleright) Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.

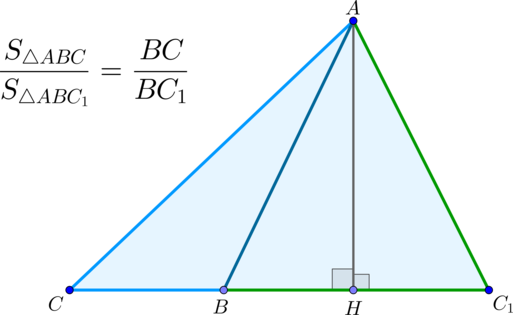
(blacktriangleright) Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.

(blacktriangleright) Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.

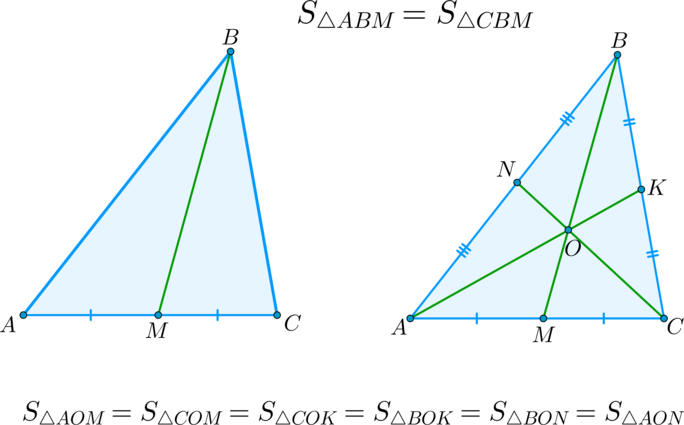
(blacktriangleright) Следствие: медиана треугольника делит его на два треугольника, равных по площади.

(blacktriangleright) Следствие: все три медианы треугольника делят его на шесть треугольников, равных по площади.

(blacktriangleright) Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.

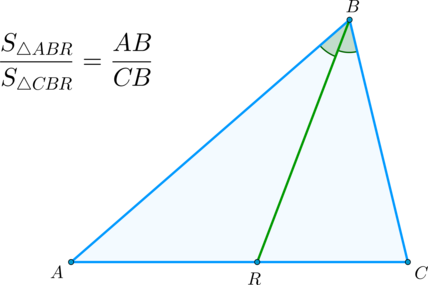
(blacktriangleright) Следствие: биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.

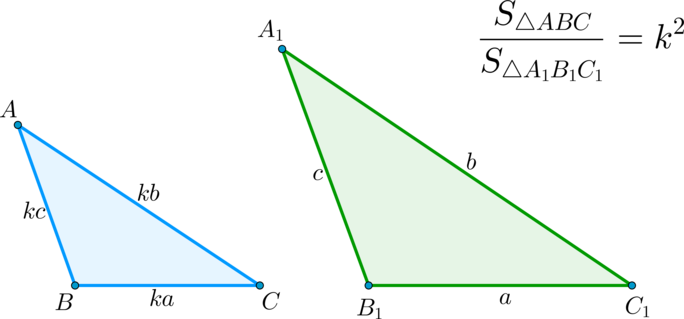
(blacktriangleright) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

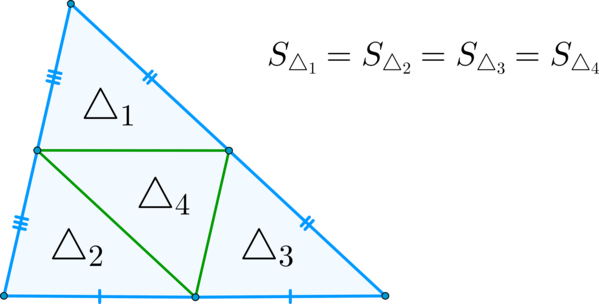
(blacktriangleright) Следствие: все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.


Задание
1

#2436

Уровень задания: Легче ЕГЭ

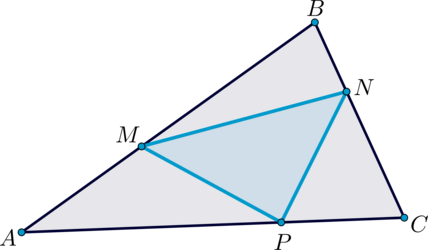
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).

(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).

Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то

[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]

Аналогично рассуждая, получаем, что

[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]

Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]

Ответ: 45


Задание
2

#2444

Уровень задания: Легче ЕГЭ

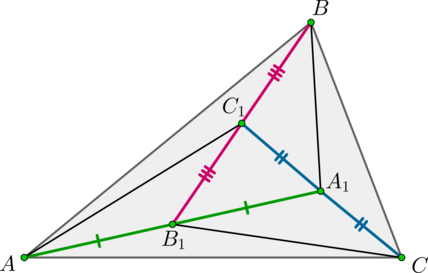
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).

Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).

Т.к. медиана делит треугольник на два равновеликих треугольника, то

[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]

Аналогично,

[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]

Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,

[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]

Ответ:

(1:7)


Задание
3

#1760

Уровень задания: Равен ЕГЭ

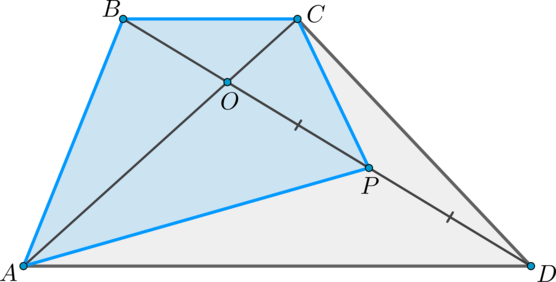
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).

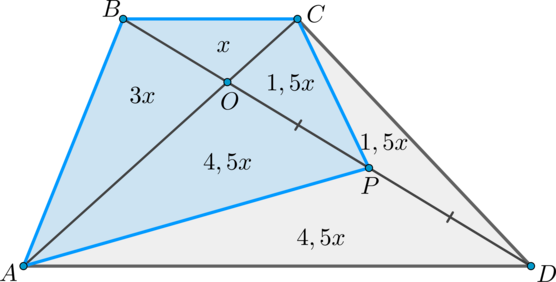
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.

Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]

(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).
 

(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).
 

Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).

Ответ: 30


Задание
4

#2441

Уровень задания: Равен ЕГЭ

Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.

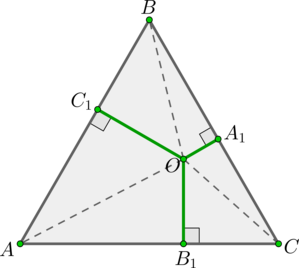
Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.

Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:

[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]

Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.

Ответ:

(dfrac{sqrt3}2m)


Задание
5

#1287

Уровень задания: Равен ЕГЭ

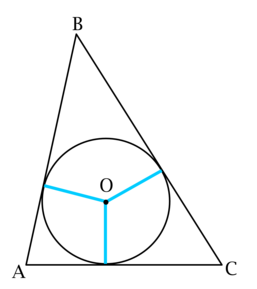
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.

а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.

б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.

а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.

Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).

В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.

б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).

Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).

Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.

При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).

Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).

Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.

Ответ:

б) (21).


Задание
6

#1288

Уровень задания: Равен ЕГЭ

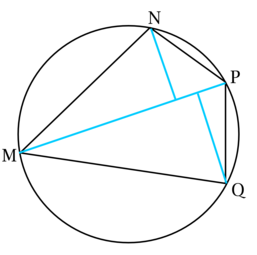
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).

а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).

а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).

Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).

В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]

С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).

Ответ:

б) (2).


Задание
7

#1289

Уровень задания: Равен ЕГЭ

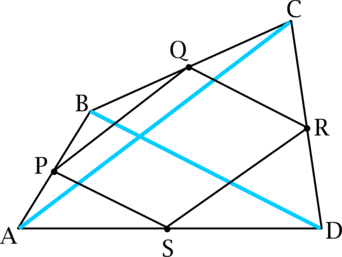
(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).

а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.

б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).

а) Проведём диагонали (AC) и (BD).

Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).

Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).

Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]

Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]

Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).

В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]

Ответ:

б) (1).

Практика показывает, что задачи на нахождение площади треугольника встречаются в ЕГЭ из года в год. Именно поэтому, если учащиеся хотят получить достойные баллы по итогам прохождения аттестационного испытания, им непременно стоит повторить эту тему и снова разобраться в материале.

Как подготовиться к экзамену?

Научиться решать задачи на нахождение площади треугольника, подобные тем, которые встречаются в ЕГЭ, вам поможет образовательный проект «Школково». Здесь вы найдете весь необходимый материал для подготовки к прохождению аттестационного испытания.

Для того чтобы упражнения по теме «Площадь треугольника в задачах ЕГЭ» не вызывали у выпускников затруднений, рекомендуем прежде всего освежить в памяти базовые тригонометрические понятия и правила. Для этого достаточно перейти в раздел «Теоретическая справка». Там представлены основные определения и формулы, которые помогут при нахождении правильного ответа.

Чтобы закрепить усвоенный материал и попрактиковаться в решении задач, предлагаем выполнить упражнения, которые подобрали специалисты образовательного проекта «Школково». Каждое задание на сайте имеет правильный ответ и подробное описание способа решения. Учащиеся могут практиковаться как с простыми, так и с более сложными задачами.

«Прокачать» свои навыки в выполнении подобных упражнений школьники могут в режиме онлайн как в Москве, так и в любом другом городе России. В случае необходимости выполненное задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить ход решения с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

11 августа 2022

В закладки

Обсудить

Жалоба

Разбор основных прототипов задач на нахождение площадей фигур: треугольник, параллелограмм, трапеция, ромб.

planimetria_ploschad_figur.pdf

Автор: Марсель Нуртдинов.

Источник: vk.com/marsel_tutor

Источник
Skip to content

ЕГЭ Профиль №2. Площадь поверхности и объем составного многогранника

ЕГЭ Профиль №2. Площадь поверхности и объем составного многогранникаadmin2022-08-28T09:31:58+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №2. Площадь поверхности и объем составного многогранника

Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 18.
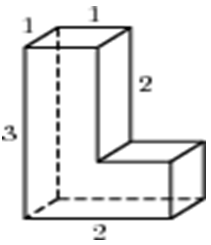Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 76.
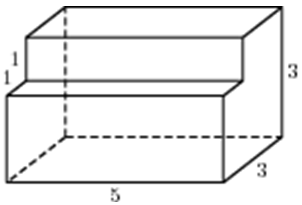Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 92.
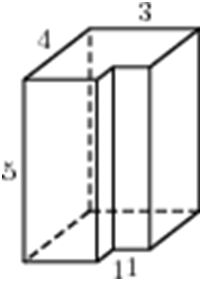Задача 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 110.
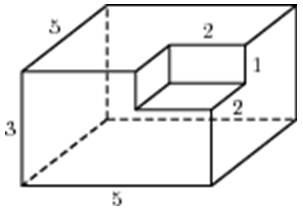Задача 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 94.
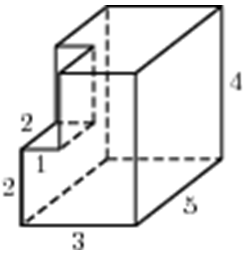Задача 6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 132.
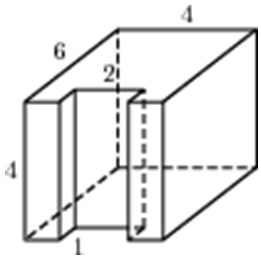Задача 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 114.
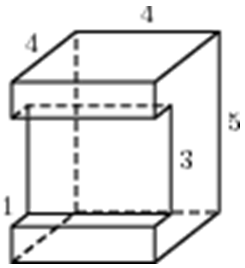Задача 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 48.
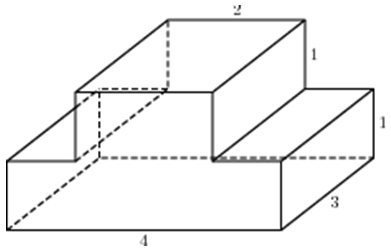Задача 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 84.
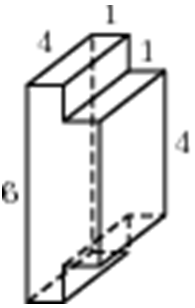Задача 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 96.
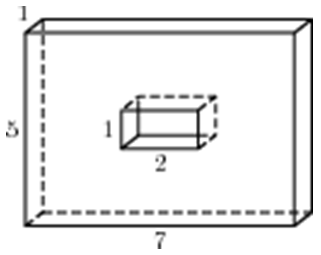Задача 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 124.
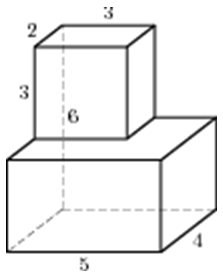Задача 12. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Ответ

ОТВЕТ: 14.
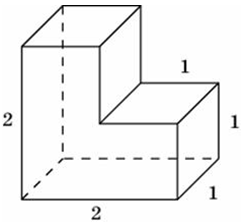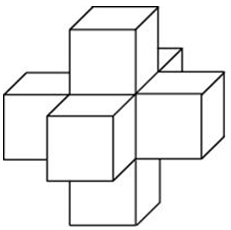
Задача 13. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Ответ

ОТВЕТ: 30.
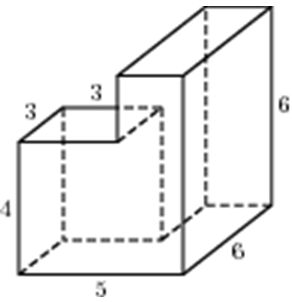
Задача 14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 162.
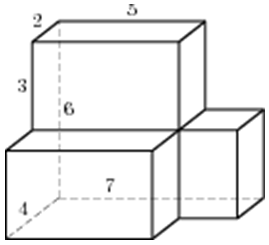
Задача 15. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 156.
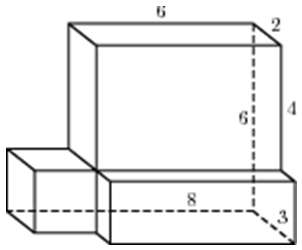
Задача 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 152.
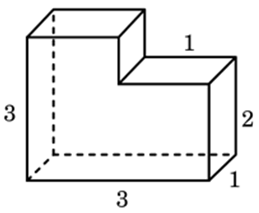
Задача 17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Ответ

ОТВЕТ: 8.
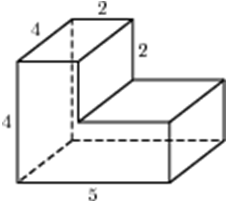
Задача 18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 56.
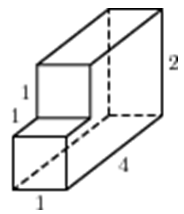
Задача 19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 7.
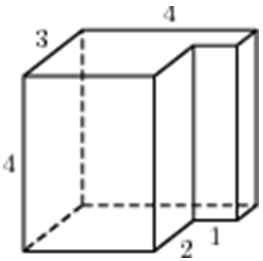
Задача 20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 40.
Задача 21. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 34.
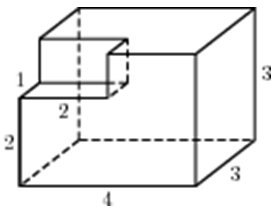Задача 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 36.
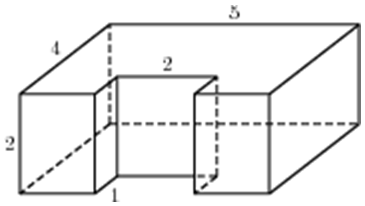Задача 23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 90.
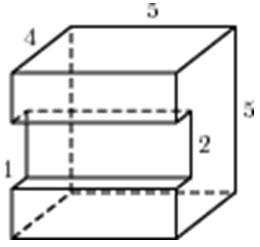Задача 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 18.
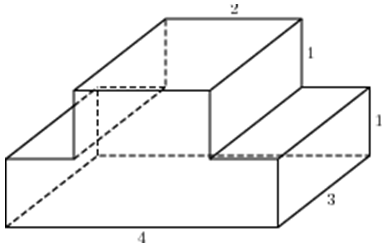Задача 25. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 24.
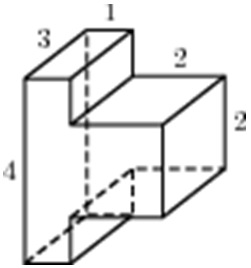Задача 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 45.
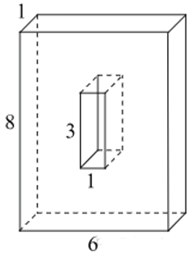Задача 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 78.
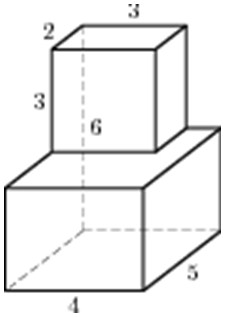Задача 28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 104.
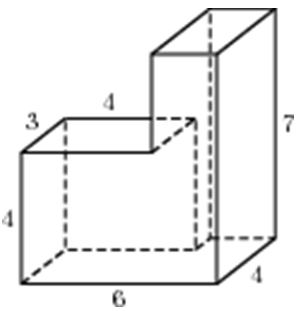Задача 29. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 87.
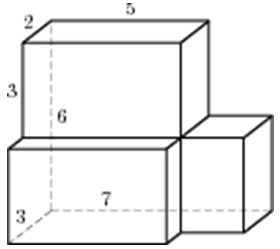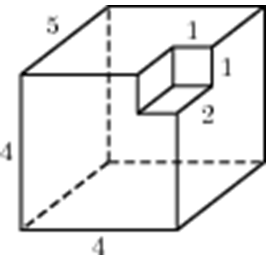
Задача 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 114.
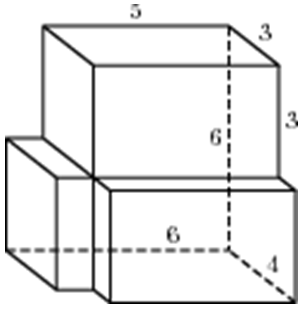Задача 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ

ОТВЕТ: 78.

Источник

Прикладная геометрия

В задании №8 ЕГЭ по математике нас ждут задания из области прикладной геометрии. Задачи простые на знания основных понятий, адаптированные под реальные жизненные ситуации. Перейдем к разбору и решению типовых заданий №8.

Разбор типовых вариантов заданий №8 ЕГЭ по математике базового уровня

Вариант 8МБ1

[su_note note_color=”#defae6″]

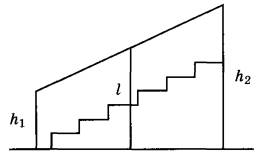
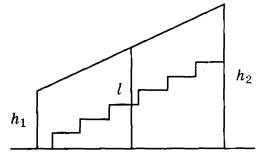
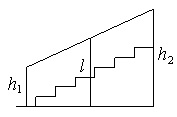
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах.

image001

[/su_note]

Алгоритм выполнения
  1. Определить, что за фигура на рисунке.
  2. Вспомнить определение средней линии трапеции.
  3. Записать формулу для нахождения средней линии трапеции.
  4. Подставить данные.
  5. Вычислить среднюю линию трапеции.
Решение:

Определим, что за фигура на рисунке. Для этого вспомним определение трапеции.

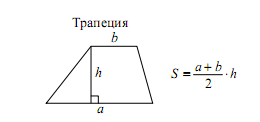
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.

Стороны h1 и h2 параллельны, остальные две стороны не параллельны. Значит перед нами трапеция. Стороны h1 и h2 называются основаниями трапеции.

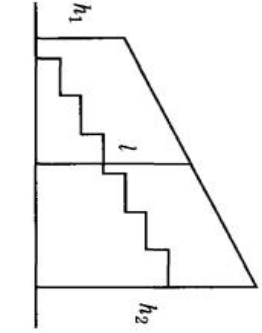
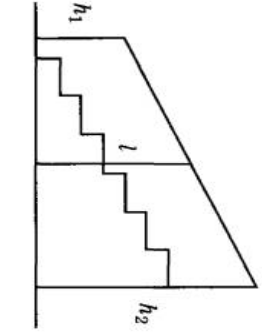
Если перевернуть рисунок, то получим трапецию в более привычном виде.

Вспомним определение средней линии трапеции.

Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям.

По условию столб l закреплен посередине, следовательно, l – средняя линия трапеции.

Запишем формулу для нахождения средней линии трапеции.

Формулу нахождения средней линии трапеции можно найти в справочных материалах (полусумма оснований).

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

То есть l = ( h1 + h2 )/2

Подставим данные и вычислим.

l = (1,25 м + 2,25 м)/2 = (3,5 м)/2 = 1,75 м

image003

Примечание: Десятичные дроби складывают столбиком, записав запятую под запятой.

Ответ: 1,75.

Решение в общем виде:

Столб длиной l представляет собой среднюю линию трапеции с основаниями h1 и h2, поэтому длину этого столба можно вычислить по формуле средней линии трапеции как

image002

Выполняем деление 3,5 на 2, имеем:

image003

Ответ: 1,75.

Вариант 8МБ2

[su_note note_color=”#defae6″]

Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 2,1 м, а наибольшая высота h2 равна 3,1 м. Ответ дайте в метрах.

image001

[/su_note]

Алгоритм выполнения
  1. Определить, что за фигура на рисунке.
  2. Вспомнить определение средней линии трапеции.
  3. Записать формулу для нахождения средней линии трапеции.
  4. Подставить данные.
  5. Вычислить среднюю линию трапеции.
Решение:

Определим, что за фигура на рисунке. Для этого вспомним определение трапеции.

Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.

Стороны h1 и h2 параллельны, остальные две стороны не параллельны. Значит перед нами трапеция. Стороны h1 и h2 называются основаниями трапеции.

Если перевернуть рисунок, то получим трапецию в более привычном виде.

Вспомним определение средней линии трапеции.

Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям.

По условию столб l закреплен посередине, следовательно, l – средняя линия трапеции.

Запишем формулу для нахождения средней линии трапеции.

Формулу нахождения средней линии трапеции можно найти в справочных материалах.

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

То есть l = ( h1 + h2 )/2

Подставим данные и вычислим.

l = (2,1 м + 3,1 м)/2 = (5,2 м)/2 = 2,6 м

Примечание: Десятичные дроби складывают столбиком, записав запятую под запятой. В данном случае удобно устно сложить целые части и дробные.

Ответ: 2,6.

Решение в общем виде:

Столб представляет собой среднюю линию трапеции с основаниями h1 и h2, поэтому длину столба l можно найти по формуле средней линии трапеции:

image002

Ответ: 2,6.

Вариант 8МБ3

[su_note note_color=”#defae6″]

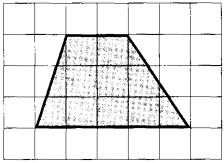
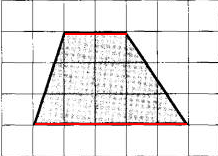
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.

image001

[/su_note]

Алгоритм выполнения
  1. Определить что за фигура на рисунке.
  2. Записать формулу нахождения площади данной фигуры.
  3. Определить по чертежу все необходимые данные.
  4. Вычислить площадь участка.
Решение:

Определим, что за фигура на рисунке.

Видно, что у данного четырехугольника две противоположные стороны параллельны.

Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.

Следовательно, перед нами трапеция.

Записываем формулу нахождения площади данной фигуры.

Площадь трапеции равна произведению полусуммы оснований на высоту.

Определяем по чертежу все необходимые данные.

Основания трапеции – параллельные стороны.

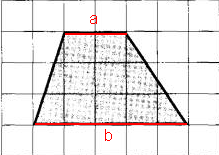
На рисунке красным выделены основания. Обозначим их a и b.

a = 2 м( длина 2 клеточек, каждая из которых по условию 1 м х 1 м)

b = 5 м(длина 5 клеточек, каждая из которых по условию 1 м х 1 м)

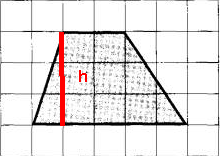
Высота трапеции -отрезок, соединяющий основания и при этом перпендикулярный им. Обозначим высоту трапеции h.

h = 3 м (длина 3 клеточек, каждая из которых по условию 1 м х 1 м)

Вычислим площадь участка.

Найдем площадь трапеции с основаниями a = 2, b = 5 и высотой h = 3:

image002

Ответ: 10,5.

Вариант 8МБ4

[su_note note_color=”#defae6″]

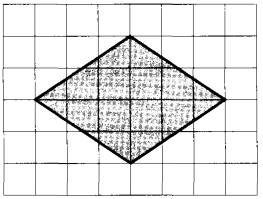
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.

image001

[/su_note]

Алгоритм выполнения
  1. Определить что за фигура на рисунке.
  2. Записать формулу нахождения площади данной фигуры.
  3. Определить по чертежу все необходимые данные.
  4. Вычислить площадь участка.
Решение:

Определим, что за фигура на рисунке.

Видно, что у данного четырехугольника все стороны равны, проверяем это с помощью линейки.

Ромб — это параллелограмм, у которого все стороны равны.

Следовательно, перед нами ромб.

Запишем формулу нахождения площади данной фигуры.

Площадь ромба равна половине произведения диагоналей.

Определим по чертежу все необходимые данные.

Диагонали ромба – это прямые, соединяющие противоположные вершины.

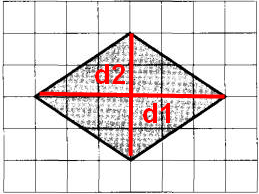
На рисунке красным выделены диагонали. Обозначим их d1 и d2.

d1 = 4 м(длина 4 клеточек, каждая из которых по условию 1 м х 1 м)

d2 = 6 м(длина 5 клеточек, каждая из которых по условию 1 м х 1 м)

Вычислим площадь участка.

Нужно найти площадь ромба с диагоналями 6 и 4, получим:

image002

Ответ: 12.

Вариант восьмого задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

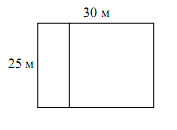
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.

 

 

 

 

[/su_note]

Алгоритм выполнения
  1. Вычислить периметр прямоугольника.
  2. Прибавить длину разделяющей части.
Решение:

Вычислим периметр прямоугольника.

Периметр – сумма длин всех сторон.

В прямоугольнике противоположные стороны равны.

P = 30 м + 30 м + 25 м + 25 м = 110 м.

110 м – длина забора без перегородки.

Прибавим длину разделяющей части.

По рисунку видно, что длина разделяющей части 25 м.

110 м + 25 м = 135 м.

Ответ: 135.

Вариант 8МБ5

[su_note note_color=”#defae6″]

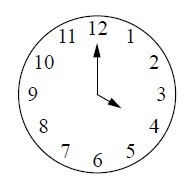
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?

Задание №8 ЕГЭ по математике базовый уровень

[/su_note]

Алгоритм выполнения
  1. Сначала мы найдем, сколько в градусах занимает один час.
  2. Затем найдем угол, который образуют стрелки в 16:00
Решение:

Так как вся окружность – 360°, а часов 12, то один час:

360° : 12 = 30°

Значит в четыре часа угол будет равен:

30° • 4 = 120°

Ответ: 120°

Вариант 8МБ6

[su_note note_color=”#defae6″]

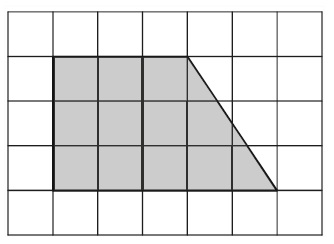
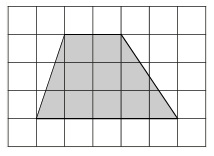
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.

Задание №8 ЕГЭ по математике базовый уровень

[/su_note]

Алгоритм выполнения
  1. Так как перед нами изображена трапеция, то вспомним площадь трапеции: полусумма оснований умноженная на высоту.
  2. В нашем примере большее основание равно пяти, меньшее – трем, высота равна трем, следовательно площадь участка:

Решение:

(5 + 3) : 2 • 3 = 12

Ответ: 12

Вариант 8МБ7

[su_note note_color=”#defae6″]

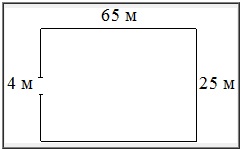
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.

C:UsersКсеньяDesktopматме1.jpg

Алгоритм выполнения
  1. Находим периметр данного прямоугольного участка по ф-ле Р=2(a+b), где a – его длина, b – ширина.
  2. Вычитаем из полученного числа 4 (в метрах), т.е. ширину, выделенную для проезда.
Решение:

2 · (25 + 65) = 2 · 90 = 180 (м) – периметр прямоугольного участка

180 – 4 = 176 (м) – длина забора

Ответ: 176

Вариант 8МБ8

[su_note note_color=”#defae6″]

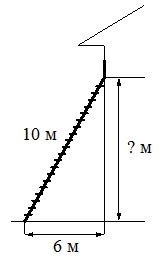
Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.

C:UsersКсеньяDesktopматме2.jpg

[/su_note]

Алгоритм выполнения

Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора.

Решение:

По теореме Пифагора с2=a2+b2, где с – гипотенуза, a и b – катеты. Примем, что а – расстояние между нижним концом лестницы и основанием дома. Тогда b – расстояние от основания дома до верхнего конца лестницы.

В данном случае с=10, а=6. Отсюда получаем: 100-36=64, квадратный корень из 64 – 8.

Ответ: 8

Вариант 8МБ9

[su_note note_color=”#defae6″]

Какой наименьший угол (в градусах) образуем минутная и часовая стрелки часов в 11:00?

C:UsersКсеньяDesktopматме3.jpg

[/su_note]

Алгоритм выполнения

В момент времени 11:00 минутная стрелка стоит на 12, а часовая – на 11, т.е. они находятся на соседних числах циферблата. Определяем, какую часть (долю) от полного круга составляет угол между парой соседних чисел на циферблате, а затем находим, сколько эта доля составляет в градусах.

Решение:

На циферблате 12 чисел-делений. Соответственно, угол между соседними числами составляет 1/12 долю от полного круга. Поскольку полный круг равен 3600, то 1/12 его часть равна:

3600:12=300.

Ответ: 30

Вариант 8МБ10

[su_note note_color=”#defae6″]

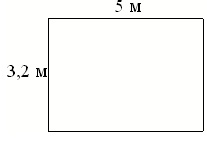
На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.

На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?

C:UsersКсеньяDesktopматме4.jpg

[/su_note]

Алгоритм выполнения
  1. Находим площадь комнаты, используя параметры, полученные в результате точных измерений. Используем для этого формулу для вычисления площади прямоугольника S=ab, где a – его длина, b – ширина.
  2. Находим разницу между полученным числом и величиной площади, указанной на плане (от большего числа отняв меньшее).
Решение:

3,2 · 5 = 16 (кв.м) – площадь комнаты, определенная на основании точных измерений

16 – 15,7 = 0,3 (кв.м) – отличие найденного значения площади от того, которое указано на плане

Ответ: 0,3

Вариант 8МБ11

[su_note note_color=”#defae6″]

План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.

C:UsersКсеньяDesktopматме5.jpg

[/su_note]

Алгоритм выполнения
  1. Условно разбиваем план на 3 части: 1) прямоугольник из полностью окрашенных квадратов площадью 2×3 (посередине); 2) прямоугольник из частично окрашенных квадратов площадью 1×3 (слева); 3) прямоугольник из частично окрашенных квадратов площадью 2×3 (справа).
  2. Площади участков вычисляем по ф-ле для прямоугольника. При этом учитываем, что участки слева и справы окрашены ровно наполовину. Это можно утверждать на основании того, что границы окрашивания являются диагоналями рассматриваемых прямоугольных участков.
  3. Находим суммарную площадь.
Решение:

Площадь участка посередине (полностью окрашенного, размером 2×3 клетки) равна: 2 ·3 = 6 (кв.м).

Площадь участка слева (частично окрашенного, размером 1×3 клетки) составляет: (1 · 3) / 2 = 1,5 (кв.м).

Площадь участка справа (частично окрашенного, размером 2×3 клетки) равна: (2 · 3) / 2 = 3 (кв.м).

Общая площадь местности: 6 + 1,5 + 3 = 7,5 (кв.м).

Ответ: 7,5

Вариант 8МБ12

[su_note note_color=”#defae6″]

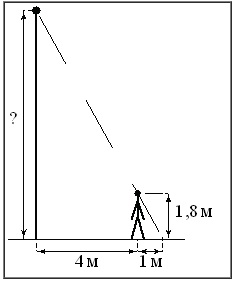
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).

C:UsersКсеньяDesktopматме6.jpg

[/su_note]

Алгоритм выполнения
  1. Рассматриваем 2 подобных треугольника: 1) образуемый человеком и длиной его тени; 2) формируемый линией фонаря, а также расстоянием между его основанием и человеком + линией отбрасываемой им тени.
  2. Поскольку у подобных треугольников длины соответствующих сторон пропорциональны, то формируем пропорцию, включающую искомую величину.
  3. Вычисляем высоту фонаря.
Решение:

Обозначим через х искомую высоту фонаря.

Имеем 2 подобных прямоуг.треугольника. Первый (больший) имеет катеты 4+1=5 м и х. Второй (меньший) – 1,8 м (рост человека) и 1 м. Поскольку треугольники подобны, то можем записать: х : 5 = 1,8 : 1.

Решим полученную пропорцию: х · 1 = 5 · 1,8 → х = 9 (м) – высота фонаря.

Ответ: 9

Вариант 8МБ13

[su_note note_color=”#defae6″]

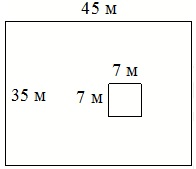
Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.

C:UsersКсеньяDesktopматме7.jpg

[/su_note]

Алгоритм выполнения
  1. Находим площадь прямоугольного участка.
  2. Находим площадь квадратного дома.
  3. Находим разность этих площадей, отняв от большего числа меньшее.
Решение:

35 · 45 = 1575 (кв.м) – площадь всего участка

7 · 7 = 49 (кв.м) – площадь дома

1575 – 49 = 1526 (кв.м) – площадь оставшейся части участка

Ответ: 1526

Вариант 8МБ14

[su_note note_color=”#defae6″]

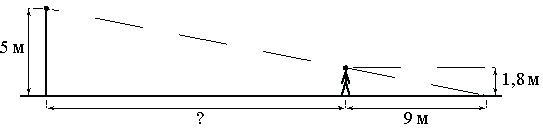
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?

C:UsersКсеньяDesktopматме8.jpg

[/su_note]

Алгоритм выполнения
  1. Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени.
  2. Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию.
  3. Из полученной пропорции выражаем искомую величину. Вычисляем ее.
Решение:

Обозначим искомое расстояние через х.

Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и (х+9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников:

5 : 1,8 = (х + 9) : 9.

Из пропорции получим:

5 · 9 = 1,8 · (х + 9)

1,8х + 16,2 = 45

1,8х = 28,8

х = 16 (м)

Ответ: 16

Вариант 8МБ15

[su_note note_color=”#defae6″]

Перила лестницы дачного дома для надежности укреплены посередине вертикальным способом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 0,7 м, а наибольшая h2 равна 1,5 м. Ответ дайте в метрах.

C:UsersКсеньяDesktopматме9.jpg

[/su_note]

Алгоритм выполнения
  1. Из рисунка можно (и нужно) заметить, что фигура, построенная на горизонтальном основании, на сторонах h1 и h2 и на линии перил, представляет собой лежащую на боковой стороне прямоугольную трапецию. Тогда h1 и h2 – основания этой трапеции.
  2. Поскольку линия l тоже направлена вертикально, то это значит, что она параллельна h1 и h2. А т.к. она равноудалена от h1 и h2, то означает, что l является средней линией трапеции. Ср.линию трапеции найдем как ср.арифметическое ее оснований.
Решение:

L = (h1 + h2) / 2

L = (0,7+1,5) / 2 = 2,2 / 2 = 1,1 (м)

Ответ: 1,1

Вариант 8МБ16

[su_note note_color=”#defae6″]

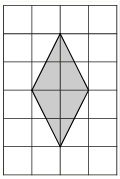
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.

C:UsersКсеньяDesktopматме10.jpg

[/su_note]

Алгоритм выполнения
  1. На плане изображен ромб. Условно разбиваем его на 4 части диагоналями, т.е. парой отрезков, соединяющих вертикальные вершины ромба и горизонтальные. Эти части равны в соответствии со свойствами ромба. Тогда общую площадь на плане будем вычислять как сумму 4 одинаковых частей плана, охватываемых прямоугольниками 1×3 клетки.
  2. Каждая из 4 частей представляет собой половину площади прямоугольника 1×3 клетки. Это именно так, поскольку ее граница на плане (сторона ромба) является диагональю прямоугольника, в котором она размещается.
Решение:

Обозначим общую площадь на плане через S, каждую из 4-х одинаковых частей, на которые эта площадь разделена, – через S1. Тогда S = 4S1.

Т.к. каждая часть охватывает половину участка 1×3 клетки, то S1 = (1 · 3) / 2 =1,5 (кв.м). поэтому S = 4 · 1,5 = 6 (кв.м).

Ответ: 6

Даниил Романович | Просмотров: 11.1k

Источник

Понравилась статья? Поделить с друзьями:
  • Задание егэ правописание местоимений
  • Задание егэ по теме субъекты гражданского права
  • Задание егэ по теме общество как система
  • Задание егэ по теме законотворческий процесс в рф ответы
  • Задание егэ по теме демократические выборы 11 класс