Диаграммы, графики, таблицы
В задании №11 базового уровня ЕГЭ по математике нас ждут задачи с диаграммами, графиками и таблицами данных из окружающего мира. Задания совсем несложные, поэтому сразу перейдем к рассмотрению примеров.
Разбор типовых вариантов заданий №11 ЕГЭ по математике базового уровня
Вариант 11МБ1
[su_note note_color=”#defae6″]
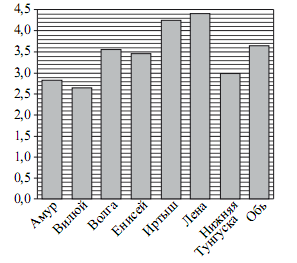
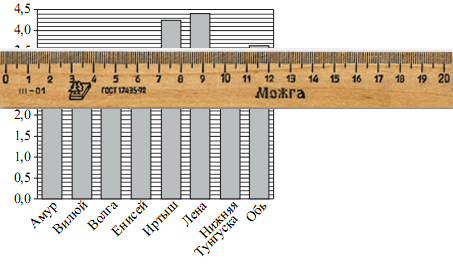
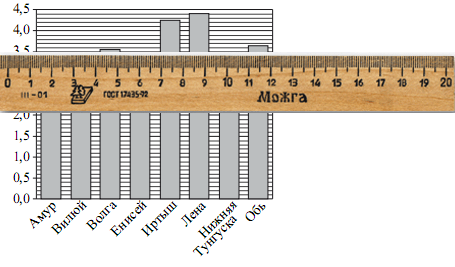
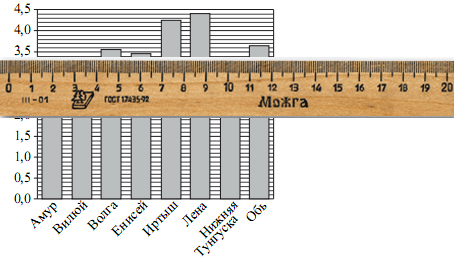
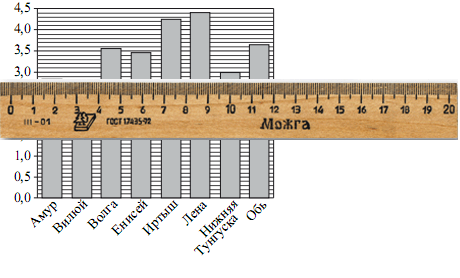
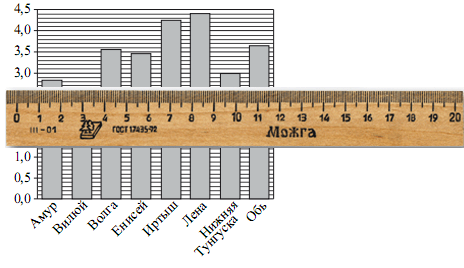
На диаграмме приведены данные о длине крупнейших рек России(в тысячах километров). Первое место по длине занимает река Лена.
На каком месте по длине находится река Амур?
[/su_note]
Алгоритм выполнения:
- Приложить линейку или лист бумаги, или любой прямой предмет к столбцу, символизирующему реку Лену.
- Медленно опускайте линейку перпендикулярно вертикальной оси.
- Считайте, сколько столбцов повстречалось.
- Каким по счету окажется Амур и будет его место по длине.
Решение:
Приложим линейку или лист бумаги, или любой прямой предмет к столбцу, символизирующему реку Лену.
Медленно опускаем линейку перпендикулярно вертикальной оси.
Считаем, сколько столбцов повстречалось.
Вторая по длине река Иртыш.
Третья по длине река Обь.
Четвертая по длине река Волга.
Пятая по длине река Енисей.
Шестая по длине Нижняя Тунгуска.
А вот и Амур. Он седьмой по длине.
Ответ: 7.
Вариант 11МБ2
[su_note note_color=”#defae6″]
В таблице представлены данные о ценах некоторой модели смартфона в различных магазинах.
| Магазин | Цена смартфона (руб.) |
| ОК-Техника | 9084 |
| Скоростной | 9059 |
| Клик | 9099 |
| И-фон | 9105 |
| Смартфон и Ко | 9045 |
| Прогресс-К | 9233 |
| Адажио | 9079 |
| Макропоиск | 9150 |
| Вселенная телефонов | 9054 |
Найдите наименьшую цену смартфона из представленных предложений. Ответ дайте в рублях.
[/su_note]
Алгоритм выполнения:
- Сравнить разряд единиц в классе тысяч.
- Сравнить разряд сотен в классе единиц. Выбрать наименьшие.
- Сравнить разряд десятков в классе единиц в оставшихся числах.
- Сравнить разряд единиц в классе единиц.
- Выбрать наименьшее число.
Для справки:
Если проще, сравнить все числа по цифрам слева на право.
Решение:
- Сравним разряд единиц в классе тысяч. У всех чисел в разряде единиц в классе тысяч 9. Никакого вывода сделать не получится.
- Сравним разряд сотен в классе единиц. У шести чисел в разряде сотен в классе единиц 0. Однозначный вывод не ясен. Остается сравнить числа 9054, 9079,9045, 9099, 9059, 9084.
- Сравним разряд десятков в классе единиц в оставшихся числах. Наименьшее 4. Следовательно, наименьшее число – 9045.
- Сравнивать разряд единиц в классе единиц нет необходимости.
Решение в общем виде:
В задании нужно выбрать наименьшее число в правой колонке таблицы. Из таблицы видно, что это число 9045, соответствующая магазину «Смартфон и Ко».
Ответ: 9045.
Вариант 11МБ3
[su_note note_color=”#defae6″]
В таблице представлены данные о ценах некоторой модели смартфона в различных магазинах.
| Магазин | Цена смартфона (руб.) |
| ОК-Техника | 13 200 |
| Скоростной | 12 300 |
| Клик | 12 372 |
| И-фон | 13 190 |
| Смартфон и Ко | 13 099 |
| Прогресс-К | 12 105 |
| Адажио | 12 230 |
| Макропоиск | 13 130 |
| Вселенная телефонов | 12 290 |
Найдите наименьшую цену смартфона из представленных предложений. Ответ дайте в рублях.
[/su_note]
Алгоритм выполнения:
- Сравнить разряд десятков в классе тысяч.
- Сравнить разряд единиц в классе тысяч.
- Сравнить разряд сотен в классе единиц. Выбрать наименьшие.
- Сравнить разряд десятков в классе единиц в оставшихся числах.
- Сравнить разряд единиц в классе единиц.
- Выбрать наименьшее число.
Для справки:
Если проще, сравнить все числа по цифрам слева на право.
Решение:
- Сравним разряд десятков в классе тысяч. У всех чисел в разряде десятков в классе тысяч 1. Никакого вывода сделать не получится.
- Сравним разряд единиц в классе тысяч. У пяти чисел в разряде сотен в классе единиц 2. Однозначный вывод не ясен. Остается сравнить числа 12300, 12372, 12105, 12230, 12290.
- Сравним разряд сотен в классе единиц в оставшихся числах. Наименьшее 1. Следовательно, наименьшее число – 12105.
- Сравнивать разряд единиц в классе единиц нет необходимости.
Решение в общем виде:
В данной задаче необходимо выбрать наименьшее число в правой колонке таблицы. Из всех представленных чисел, наименьшим является число 12105 для магазина «Прогресс-К».
Ответ: 12105.
Вариант 11МБ4
[su_note note_color=”#defae6″]
В таблице показано расписание пригородных электропоездов по направлению Москва Белорусская — Бородино.
| Номер электрички | Москва Белорусская | Бородино | Время в пути |
| 1 | 06:18 | 08:20 | 2:02 |
| 2 | 07:51 | 10:09 | 2:18 |
| 3 | 09:52 | 12:19 | 2:27 |
| 4 | 15:24 | 17:24 | 2:00 |
| 5 | 17:26 | 19:40 | 2:14 |
Укажите номер электрички, которая в пути меньше всего времени.
[/su_note]
Алгоритм выполнения:
- Сравнить количество часов в пути.
- Сравнить количество минут в пути.
Решение:
Сравним количество часов в пути. Все электрички были в пути 2 часа.
Сравним количество минут в пути. Наименьшее количество минут в пути 00. Это соответствует времени 2:00 (2 часа), стоящем под номером 4.
Ответ: 4.
Вариант 11МБ5
[su_note note_color=”#defae6″]
В таблице показано расписание пригородных электропоездов по направлению Москва Савёловская — Дубна.
| Номер электрички | Москва Савёловская | Дубна | Время в пути |
| 1 | 17:30 | 19:33 | 2:03 |
| 2 | 18:18 | 20:52 | 2:34 |
| 3 | 19:39 | 22:05 | 2:26 |
| 4 | 20:44 | 23:21 | 2:37 |
| 5 | 22:00 | 00:01 | 2:01 |
Укажите номер электрички, которая в пути меньше всего времени.
[/su_note]
Алгоритм выполнения:
- Сравнить количество часов в пути.
- Сравнить количество минут в пути.
Решение:
Сравним количество часов в пути. Все электрички были в пути 2 часа.
Сравним количество минут в пути. Наименьшее количество минут в пути 01.Это соответствует времени 2:01 (2 часа и 1 минута), стоящем под номером 5.
Ответ: 5.
Вариант 11МБ6
[su_note note_color=”#defae6″]
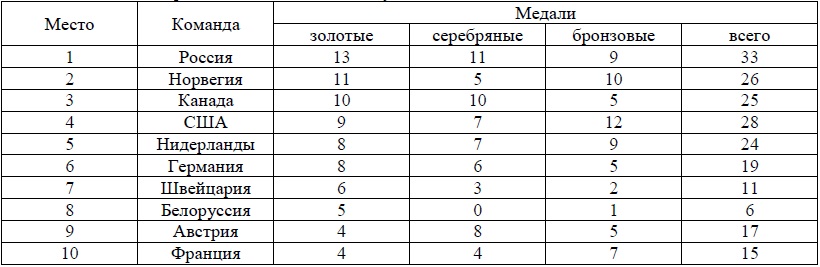
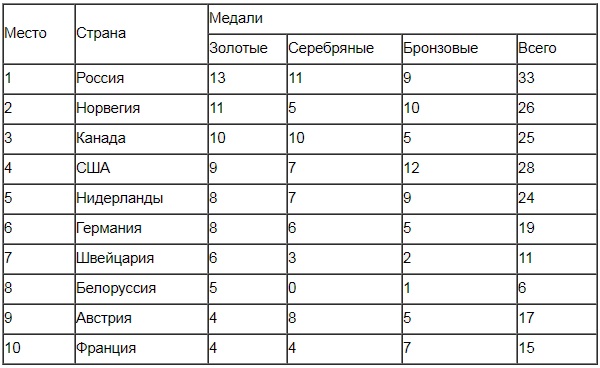
В таблице показано распределение медалей на XXII Зимних Олимпийских играх в Сочи среди команд, занявших первые 10 мест по количеству золотых медалей.
Определите с помощью таблицы, сколько серебряных медалей у команды, занявшей второе место по количеству золотых медалей.
[/su_note]
Чем дальше – тем проще примеры. Список уже ранжирован по числу золотых медалей – нам об этом сказано в условии. Тогда просто находим второе место – Норвегия – и видим, что у этой команды 5 серебряных медалей.
Ответ: 5
Вариант 11МБ7
[su_note note_color=”#defae6″]
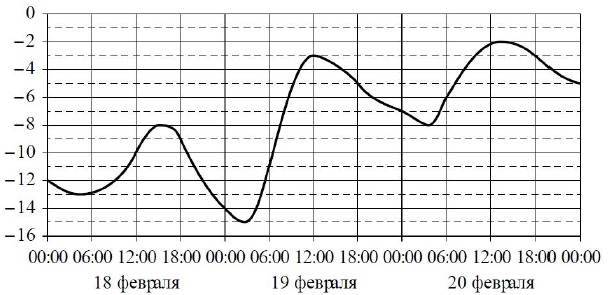
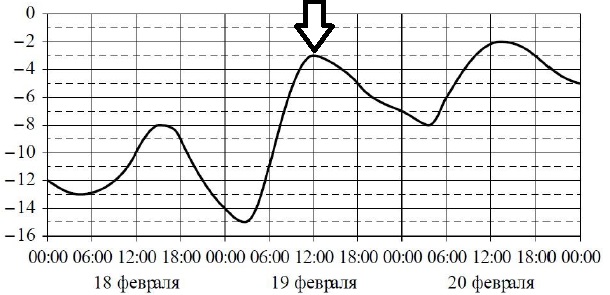
На графике показано изменение температуры воздуха на протяжении трех суток. На горизонтальной оси отмечается число, месяц, время суток в часах; на вертикальной оси – значение температуры в градусах Цельсия.
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
[/su_note]
Находим “гору” в полосе между ночами с 18-го на 19-ое и с 19-го на 20-е февраля. Вершине этой горы и будет соответствовать искомая наибольшая температура. Пунктирная линия между –4 и –2 соответствует значению –3 градуса Цельсия.
Ответ: -3
Вариант 11МБ8
[su_note note_color=”#defae6″]
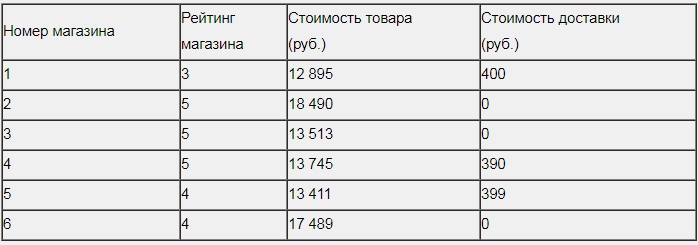
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определенной модели. В таблице показано 6 предложений от разных интернет-магазинов. Сергей Петрович считает, что покупку нужно делать в магазине, рейтинг которого не ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой низкой стоимостью покупки с учетом доставки.
В ответе запишите номер выбранного магазина.
[/su_note]
Алгоритм выполнения
- Отбрасываем магазины с рейтингом 3 (т.е. ниже 4).
- Поскольку требуется найти стоимость покупки с учетом доставки, то для оставшихся позиций суммируем соответствующие значения в 3-й и 4-й ячейках.
- Определяем минимальную сумму. Фиксируем соответствующий ей номер в 1-м столбце.
Решение:
Отбрасываем 1 строку таблицы, магазин, имеющий рейтинг 3.
Получаем 5 позиций – для магазинов №№ 2-6.
Магазины 2 и 6 можно сразу отбросить – слишком высокая стоимость даже на глаз. Остаются три магазина -3,4,5.
Находим стоимость покупки:
- для магазина №3: 13513+0=13513 (руб.)
- для магазина №4: 13745+390=14135 (руб.)
- для магазина №5: 13411+399=13810 (руб.)
Отсюда получаем, что минимальная стоимость покупки предложена в магазине под номером 3.
Вариант 11МБ9
[su_note note_color=”#defae6″]
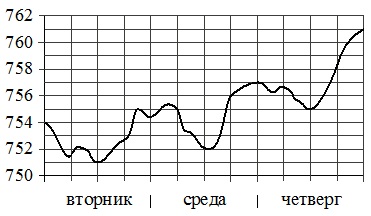
На рисунке изображен график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления за данные три дня (в миллиметрах ртутного столба).
[/su_note]
Алгоритм выполнения
- Определяем цену деления для вертикальной шкалы значений.
- Находим самую низкую (по вертикали) точку на линии графике.
- Вычисляем значение найденной наименьшей точки.
Решение:
Фиксируем пару соседних числовых значений на вертикальной оси графика. Возьмем, например, значения 754 и 756. Между ними 2 черты деления. Следовательно, получаем цену деления: (756 – 754) / 2 = 1 мм рт.ст.
Наименьшая точка на графике соответствует вторнику и фиксирует точку на черте деления между значениями 750 и 752. Поэтому значение этой точки равно: 750 + 1 = 751 (мм рт.ст.).
Вариант 11МБ10
[su_note note_color=”#defae6″]
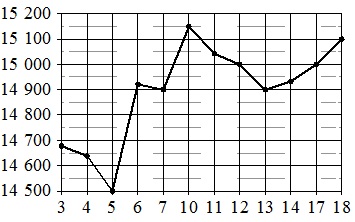
На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов вовсе рабочие дни с 3 по 18 сентября 207 года. По горизонтали указываются числа месяца, по вертикали – цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линиями.
Определите по рисунку, какого числа цена олова на момент закрытия торгов впервые за данный период стала равна 14900 долларов США за тонну.
[/su_note]
Алгоритм выполнения
- Находим на вертикальной оси искомое значение, равное 14900 долларов.
- Фиксируем точки на графике, соответствующие этому значению.
- Находим проекции этих точек на горизонтальную ось. Определяем числа (дни), которым они соответствуют.
- Определяем наименьшее среди найденных чисел.
Решение:
Число 14900 по вертикали находится на линии, соединяющей 4-ю и 5-ю клетки (отсчитывая снизу вверх). Проведя горизонтальную линию на этой высоте, получим, что это значение имеют три точки. Они соответствуют 6-му числу сентября, 7-му и 13-му. Наименьшее среди них – 6-е. То есть ответ – 6.
Вариант 11МБ11
[su_note note_color=”#defae6″]
В таблице показано распределение медалей на зимних Олимпийских играх в Сочи среди стран, занявших первые 10 мест по количеству золотых медалей.
Определите с помощью таблицы, сколько серебряных медалей у страны, занявшей второе место по числу золотых медалей.
[/su_note]
Алгоритм выполнения
- Анализируем 3-й столбец таблицы («Медали Золотые»). Находим 2-е по величине числовое значение.
- В той же строке перемещаемся в 4-ю ячейку (столбец «Медали Серебряные»). Отображенное в ней число является ответом на вопрос задачи.
Решение:
Второе по величине кол-во золотых медалей имеет Норвегия. В строке, отображающей данные результатов для этой страны, для числа серебряных медалей зафиксировано значение 5.
Вариант 11МБ12
[su_note note_color=”#defae6″]
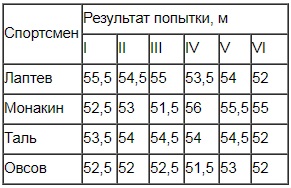
В соревнованиях по метанию молота участники показали следующие результаты. Места распределяются по результатам лучшей попытки каждого спортсмена: чем дальше метнул молот, чем лучше.
Какое место занял спортсмен Лаптев?
[/su_note]
Алгоритм выполнения
- Находим результат лучшей попытки метания для каждого спортсмена.
- Распределяем полученные числовые значения в порядке убывания.
- Определяем позицию Лаптева в сформированном ряду.
Решение:
Находим лучшие результаты метания для каждого спортсмена:
- у Лаптева – 55,5 м
- у Монакина – 56 м
- у Таля – 54,5 м
- у Овсова – 53 м
Распределяем места рейтинга:
- Монакин (56 м)
- Лаптев (55,5 м)
- Таль (54,5 м)
- Овсов (53 м)
Следовательно, Лаптев занял 2-е место.
Вариант 11МБ13
[su_note note_color=”#defae6″]
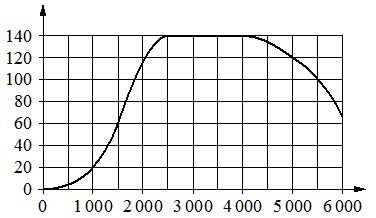
На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси – крутящий момент в Н·м. Чтобы автомобиль начал движение. Крутящий момент должен быть не менее 20 Н·м.
Определите по графику, какого наименьшего числа оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение.
[/su_note]
Алгоритм выполнения
- Находим на графике точку, соответствующую значению 20 на вертикальной оси.
- Находим проекцию этой точки на горизонтальную ось. Фиксируем числовое значение на этой оси.
Решение:
Условие «должен быть не менее 20» означает, что это числовое значение является минимально допустимым для начала движения. Поэтому необходимо найти на графике точку, соответствующую именно 20 (Н·м) на вертикальной оси.
Опускаем из найденной точки перпендикуляр на горизонтальную ось. Получаем проекцию. Ее значение равно 1000 об./мин. Итак, ответ: 1000.
Вариант 11МБ14
[su_note note_color=”#defae6″]
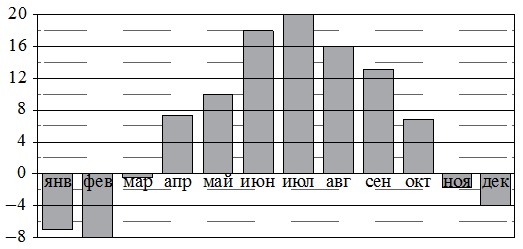
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия.
Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
[/su_note]
Алгоритм выполнения
- Отбрасываем положительные значения температур, будем рассматривать только отрицательные.
- Среди них определяем числовое значение наиболее длинного элемента-столбца диаграммы.
Решение:
Поскольку требуется найти минимальное значение, то элементы диаграммы, имеющие положительные величины, следует отбросить, т.к. вне зависимости от модуля числа отрицательное всегда меньше положительного.
Одно из свойств отрицат.чисел заключается в том, что из произвольных 2-х таких чисел меньше то, которое больше по модулю. Отсюда делаем вывод, что минимальная среднемес.температура соответствовала февралю. Ее значение составило –80С.
Вариант 11МБ15
[su_note note_color=”#defae6″]
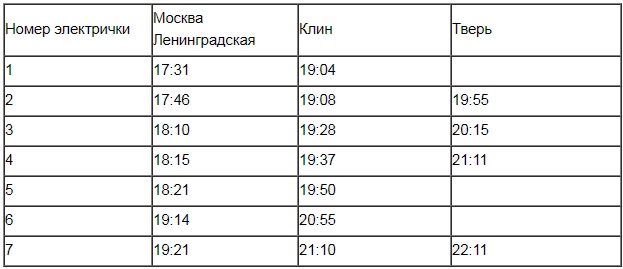
В таблице показано расписание пригородных электропоездов по направлению Москва ленинградская – Клин – Тверь.
Владислав пришел на станцию Москва Ленинградская в 18:20 и хочет уехать в Тверь на ближайшей электричке. В ответе укажите номер этой электрички.
[/su_note]
Алгоритм выполнения
- Отбрасываем все строки таблицы, для которых указано время отбытия из С-Петербурга более раннее, чем 18:20.
- Среди оставшихся строк отбрасываем те, которые не направляются в Тверь, а имеют конечным пунктом Клин.
- Из остальных подходящих выбираем электричку с наиболее ранним временем прибытия в Тверь.
Решение:
Отбрасываем электрички под номерами 1–4. На них Владислав уже опоздал, поскольку они отправились раньше, чем в 18:20.
Среди электричек №№5–7 отбрасываем номера 5 и 6, т.к. они не идут в Тверь, а имеют конечным пунктом Клин. Подходящим остался единственный вариант – электричка №7.
Вариант 11МБ16
[su_note note_color=”#defae6″]
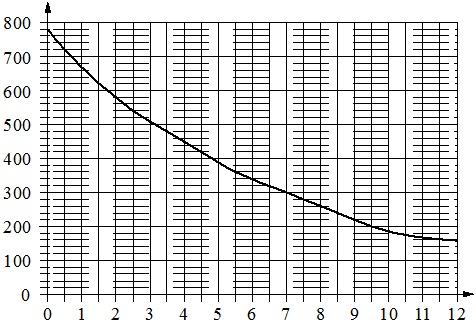
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря, на вертикальной – давление в миллиметрах ртутного столба.
Определите по графику, чему равно атмосферное давление на высоте 6,5 км. Овеет дайте в миллиметрах ртутного столба.
[/su_note]
Алгоритм выполнения
- Вычисляем цену деления для шкал по горизонтальной и вертикальной осям.
- Находим точку на графике, соответствующую 6,5 м над уровнем моря.
- Находим проекцию этой на вертикальную ось, определяем соответствующее числовое значение на вертикальной оси.
Решение:
Цена деления на горизонтальной оси составляет: (1 – 0) / 2 = 0,5 км.
Цена деления на вертикальной оси равна: (100 – 0) / 5 = 20 мм рт.ст.
Из значения 6,5 (посередине между 6 и 7) на горизонт.оси проводим перпендикуляр на график, фиксируем соответствующую точку на его линии. Из этой точки проводим перпендикуляр на вертик.ось, отмечаем полученное числовое значение. Оно равно 300 + 20 = 320 (мм рт.ст.).
Вариант 11МБ17
[su_note note_color=”#defae6″]
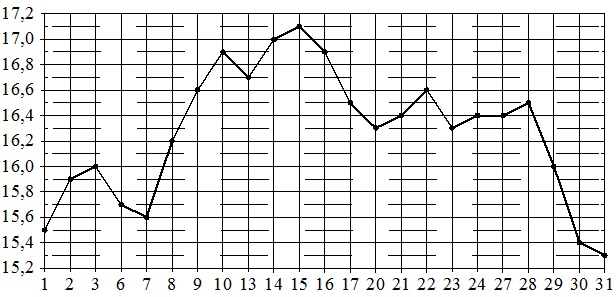
На рисунке жирными точками указана цена серебра, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали – цена серебра в рублях за грамм. Для наглядности жирные точки точки на рисунке соединены линией.
Определите по рисунку наибольшую цену серебра в период с 20 по 30 октября. Ответ дайте в рубля за грамм.
[/su_note]
Алгоритм выполнения
- Отбрасываем часть графика, не соответствующую указанному в условии периоду 20–30 октября.
- На выбранной части находим точку с максимальным значением по вертикали.
Решение:
Проводим перпендикуляры на график с горизонт.оси из точек, соответствующих числам 20 и 30. Выделяем часть линии графика между этим точками, учитывая и их.
На выделенном фрагменте графика находим самую высокую точку. Ее проекция на вертик.ось дает числовое значение для ответа. Оно составляет 16,6 (руб./г).
Даниил Романович | Просмотров: 5.1k
ЕГЭ База по математике . Задание №11
Практика по заданию №11 ЕГЭ по математике базового уровня — теория вероятностей.
Для выполнения задания №11 необходимо уметь строить и исследовать простейшие математические модели.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 6.3.1
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 10
Примеры заданий:
1. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из России и 6 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что пятым будет выступать прыгун из Китая.
2. В сборнике билетов по философии всего 50 билетов, в 6 из них встречается вопрос по теме «Кант». Найдите вероятность того, что в случайно выбранном на экзамене билете студенту достанется вопрос по теме «Кант».
3. Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
4. На семинар приехали 3 учёных из Норвегии, 3 из России и 4 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.
5. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 – из Норвегии. Порядок, в котором вы-ступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Швеции.
Связанные страницы:

За это задание ты можешь получить 1 балл.
Разбор сложных заданий в тг-канале
Посмотреть
Задачи для практики
Показать еще
Рекомендуемые курсы подготовки
математика база
егэ по математике
математика с нуля
математика 10 класс
математика 11 класс
математика акции
егэ и огэ математика
Показать еще…
Популярные материалы
-
Задание 10. Прикладная геометрия
-
Задание 12. Планиметрия
Готовим к ЕГЭ на 85+ баллов и побеждаем лень
Каждый месяц 12 онлайн-занятий в дружелюбной атмосфере + 16 домашних работ с жесткими сроками.
Не готовишься — вылетаешь.
Подробнее о курсе
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая втрое уже первой. Во сколько раз объём первой коробки больше объёма второй?
Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в двое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй коробки больше объёма первой?
В бак цилиндрической формы, площадь основания которого равна 80 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
Вода в сосуде цилиндрической формы находится на уровне h = 20 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в полтора раза меньше, чем у данного? Ответ дайте в сантиметрах.
Часть лестницы покрасили в темный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступени равна 30 см, высота – 15 см, а ширина – 95 см. Ответ дайте в квадратных сантиметрах.
Часть лестницы покрасили в темный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступени равна 40 см, высота – 15 см, а ширина – 90 см. Ответ дайте в квадратных сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 2,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
В сосуде, имеющем форму конуса, уровень жидкости достигает (displaystyle frac{4}{5}) высоты. Объём сосуда равен (2000) мл. Найдите объём налитой жидкости. Ответ дайте в миллилитрах.
Аквариум имеет форму прямоугольного параллелепипеда с размерами 70 см х 20 см х 60 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см х 30 см х 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
1. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
2. У бабушки 10 чашек: 3 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку.Найдите вероятность того,что это будет чашка с синими цветами.
3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
4. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что оба раза выпадет решка.
5. 11 апреля на запись в первый класс независимо друг от друга пришли два будущих первоклассника. Считая, что приходы мальчика и девочки равновероятны, найдите вероятность того, что пришли мальчик и девочка.
6. В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,3 независимо от другого автомата. Найдите вероятность того, что оба автомата неисправны.
7. В чемпионате по гимнастике участвуют 75 спортсменок: 15 из Чехии, 30 из Словакии, остальные — из Австрии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Австрии.
8. На экзамене 20 билетов, Оскар не выучил 7 из них. Найдите вероятность того, что ему попадется выученный билет.
9. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с картошкой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
10. В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 4 раза больше, чем пакетиков в зеленым. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зеленым чаем.
11. В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 9 раз больше, чем пакетиков в зеленым. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зеленым чаем.
12. В ящике находятся черные и белые шары, причем черных в 3 раза больше, чем белых. Из ящика случайным образом достали один шар. Найдите вероятность того, что он будет белым.
13. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет хотя бы один раз.
14. Какова вероятность того, что последние две цифры телефонного номера случайного абонента в сумме дают 7?
15. Два автомобилиста независимо друг от друга выезжают из пункта А в пункт В. Навигатор предлагает каждому из них 4 равноценных маршрута, и автомобилисты выбирают маршрут случайным образом. Найдите вероятность того, что автомобилисты выберут различные маршруты.
16. Какова вероятность того, что последние две цифры телефонного номера случайного абонента в сумме дают 9?
17. Два автомобилиста независимо друг от друга выезжают из пункта А в пункт В. Навигатор предлагает каждому из них 10 равноценных маршрута, и автомобилисты выбирают маршрут случайным образом. Найдите вероятность того, что автомобилисты выберут один и тот же маршрут
18. Вероятность того, что новая батарейка окажется бракованной, равна 0.3 независимо от других батареек. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся неисправными.
19. Датчик измеряет уровень воды в водохранилище по отношению к ординару (нормальному уровню). Расположите события в порядке убывания их вероятностей:
1. «уровень выше отметки 0.6 м выше ординара»;
2. «уровень выше отметки 1.4 м выше ординара»;
3. «уровень воды между отметками 1.7 и 2.1 м выше ординара;
4. «уровень воды не ниже ординара»
В ответе запишите последовательность цифр без пробелов и других посторонних знаков.
20. В ящике находятся черные и белые шары, причем черных в 3 раза больше, чем белых.Вероятность того, что новая батарейка окажется бракованной, равна 0.05 независимо от других батареек. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся неисправными. Из ящика случайным образом достали один шар. Найдите вероятность того, что он будет белым.
21. При изготовлении труб диаметром 30 мм вероятность того, что диаметр будет отличаться от заданного более чем на 0.02 мм, равна 0.063. Найдите вероятность того, что диаметр случайно выбранной для контроля трубы будет в пределах от 29.98 мм до 30.02 мм.
22. В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0.06 независимо от другого автомата. Найдите вероятность того, что оба автомата неисправны.
23. При изготовлении водопроводных труб диаметром 2 дюйма, то есть 5.08 см, вероятность отклонения диаметра в ту или иную сторону от заданного значения более чем на 0.1 мм равна 0.13. Найдите вероятность того, что диаметр случайно выбранной для контроля трубы будет в пределах от 50.07 мм до 50.09 мм
24. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый.
25. На олимпиаде по математике 400 участников разместили в трех аудиториях. В первых двух удалось разместить по 100 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в другой аудитории
26. 11 апреля на запись в первый класс независимо друг от друга пришли два будущих первоклассника. Считая, что приходы мальчика и девочки равновероятны, найдите вероятность того, что обе пришедшие оказались девочками.
27. В чемпионате мира учувствуют 8 команд. С помощью жребия их нужно разделить на четыре группы по две команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 2, 2, 3, 3, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
28. Механические часы с двенадцатичасовым циферблатом в какой- то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.

Диаграммы, графики, таблицы
В задании №11 базового уровня ЕГЭ по математике нас ждут задачи с диаграммами, графиками и таблицами данных из окружающего мира. Задания совсем несложные, поэтому сразу перейдем к рассмотрению примеров.
Разбор типовых вариантов заданий №11 ЕГЭ по математике базового уровня
Вариант 11МБ1
На диаграмме приведены данные о длине крупнейших рек России(в тысячах километров). Первое место по длине занимает река Лена.
На каком месте по длине находится река Амур?
Алгоритм выполнения:
- Приложить линейку или лист бумаги, или любой прямой предмет к столбцу, символизирующему реку Лену.
- Медленно опускайте линейку перпендикулярно вертикальной оси.
- Считайте, сколько столбцов повстречалось.
- Каким по счету окажется Амур и будет его место по длине.
Решение:
Приложим линейку или лист бумаги, или любой прямой предмет к столбцу, символизирующему реку Лену.
Медленно опускаем линейку перпендикулярно вертикальной оси.
Считаем, сколько столбцов повстречалось.
Вторая по длине река Иртыш.
Третья по длине река Обь.
Четвертая по длине река Волга.
Пятая по длине река Енисей.
Шестая по длине Нижняя Тунгуска.
А вот и Амур. Он седьмой по длине.
Ответ: 7.
Вариант 11МБ2
В таблице представлены данные о ценах некоторой модели смартфона в различных магазинах.
| Магазин | Цена смартфона (руб.) |
| ОК-Техника | 9084 |
| Скоростной | 9059 |
| Клик | 9099 |
| И-фон | 9105 |
| Смартфон и Ко | 9045 |
| Прогресс-К | 9233 |
| Адажио | 9079 |
| Макропоиск | 9150 |
| Вселенная телефонов | 9054 |
Найдите наименьшую цену смартфона из представленных предложений. Ответ дайте в рублях.
Алгоритм выполнения:
- Сравнить разряд единиц в классе тысяч.
- Сравнить разряд сотен в классе единиц. Выбрать наименьшие.
- Сравнить разряд десятков в классе единиц в оставшихся числах.
- Сравнить разряд единиц в классе единиц.
- Выбрать наименьшее число.
Для справки:
Если проще, сравнить все числа по цифрам слева на право.
Решение:
- Сравним разряд единиц в классе тысяч. У всех чисел в разряде единиц в классе тысяч 9. Никакого вывода сделать не получится.
- Сравним разряд сотен в классе единиц. У шести чисел в разряде сотен в классе единиц 0. Однозначный вывод не ясен. Остается сравнить числа 9054, 9079,9045, 9099, 9059, 9084.
- Сравним разряд десятков в классе единиц в оставшихся числах. Наименьшее 4. Следовательно, наименьшее число – 9045.
- Сравнивать разряд единиц в классе единиц нет необходимости.
Решение в общем виде:
В задании нужно выбрать наименьшее число в правой колонке таблицы. Из таблицы видно, что это число 9045, соответствующая магазину «Смартфон и Ко».
Ответ: 9045.
Вариант 11МБ3
В таблице представлены данные о ценах некоторой модели смартфона в различных магазинах.
| Магазин | Цена смартфона (руб.) |
| ОК-Техника | 13 200 |
| Скоростной | 12 300 |
| Клик | 12 372 |
| И-фон | 13 190 |
| Смартфон и Ко | 13 099 |
| Прогресс-К | 12 105 |
| Адажио | 12 230 |
| Макропоиск | 13 130 |
| Вселенная телефонов | 12 290 |
Найдите наименьшую цену смартфона из представленных предложений. Ответ дайте в рублях.
Алгоритм выполнения:
- Сравнить разряд десятков в классе тысяч.
- Сравнить разряд единиц в классе тысяч.
- Сравнить разряд сотен в классе единиц. Выбрать наименьшие.
- Сравнить разряд десятков в классе единиц в оставшихся числах.
- Сравнить разряд единиц в классе единиц.
- Выбрать наименьшее число.
Для справки:
Если проще, сравнить все числа по цифрам слева на право.
Решение:
- Сравним разряд десятков в классе тысяч. У всех чисел в разряде десятков в классе тысяч 1. Никакого вывода сделать не получится.
- Сравним разряд единиц в классе тысяч. У пяти чисел в разряде сотен в классе единиц 2. Однозначный вывод не ясен. Остается сравнить числа 12300, 12372, 12105, 12230, 12290.
- Сравним разряд сотен в классе единиц в оставшихся числах. Наименьшее 1. Следовательно, наименьшее число – 12105.
- Сравнивать разряд единиц в классе единиц нет необходимости.
Решение в общем виде:
В данной задаче необходимо выбрать наименьшее число в правой колонке таблицы. Из всех представленных чисел, наименьшим является число 12105 для магазина «Прогресс-К».
Ответ: 12105.
Вариант 11МБ4
В таблице показано расписание пригородных электропоездов по направлению Москва Белорусская — Бородино.
| Номер электрички | Москва Белорусская | Бородино | Время в пути |
| 1 | 06:18 | 08:20 | 2:02 |
| 2 | 07:51 | 10:09 | 2:18 |
| 3 | 09:52 | 12:19 | 2:27 |
| 4 | 15:24 | 17:24 | 2:00 |
| 5 | 17:26 | 19:40 | 2:14 |
Укажите номер электрички, которая в пути меньше всего времени.
Алгоритм выполнения:
- Сравнить количество часов в пути.
- Сравнить количество минут в пути.
Решение:
Сравним количество часов в пути. Все электрички были в пути 2 часа.
Сравним количество минут в пути. Наименьшее количество минут в пути 00. Это соответствует времени 2:00 (2 часа), стоящем под номером 4.
Ответ: 4.
Вариант 11МБ5
В таблице показано расписание пригородных электропоездов по направлению Москва Савёловская — Дубна.
| Номер электрички | Москва Савёловская | Дубна | Время в пути |
| 1 | 17:30 | 19:33 | 2:03 |
| 2 | 18:18 | 20:52 | 2:34 |
| 3 | 19:39 | 22:05 | 2:26 |
| 4 | 20:44 | 23:21 | 2:37 |
| 5 | 22:00 | 00:01 | 2:01 |
Укажите номер электрички, которая в пути меньше всего времени.
Алгоритм выполнения:
- Сравнить количество часов в пути.
- Сравнить количество минут в пути.
Решение:
Сравним количество часов в пути. Все электрички были в пути 2 часа.
Сравним количество минут в пути. Наименьшее количество минут в пути 01.Это соответствует времени 2:01 (2 часа и 1 минута), стоящем под номером 5.
Ответ: 5.
Вариант 11МБ6
В таблице показано распределение медалей на XXII Зимних Олимпийских играх в Сочи среди команд, занявших первые 10 мест по количеству золотых медалей.
Определите с помощью таблицы, сколько серебряных медалей у команды, занявшей второе место по количеству золотых медалей.
Чем дальше — тем проще примеры. Список уже ранжирован по числу золотых медалей — нам об этом сказано в условии. Тогда просто находим второе место – Норвегия – и видим, что у этой команды 5 серебряных медалей.
Ответ: 5
Вариант 11МБ7
На графике показано изменение температуры воздуха на протяжении трех суток. На горизонтальной оси отмечается число, месяц, время суток в часах; на вертикальной оси – значение температуры в градусах Цельсия.
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Находим «гору» в полосе между ночами с 18-го на 19-ое и с 19-го на 20-е февраля. Вершине этой горы и будет соответствовать искомая наибольшая температура. Пунктирная линия между –4 и –2 соответствует значению –3 градуса Цельсия.
Ответ: -3
Вариант 11МБ8
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определенной модели. В таблице показано 6 предложений от разных интернет-магазинов. Сергей Петрович считает, что покупку нужно делать в магазине, рейтинг которого не ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой низкой стоимостью покупки с учетом доставки.
В ответе запишите номер выбранного магазина.
Алгоритм выполнения
- Отбрасываем магазины с рейтингом 3 (т.е. ниже 4).
- Поскольку требуется найти стоимость покупки с учетом доставки, то для оставшихся позиций суммируем соответствующие значения в 3-й и 4-й ячейках.
- Определяем минимальную сумму. Фиксируем соответствующий ей номер в 1-м столбце.
Решение:
Отбрасываем 1 строку таблицы, магазин, имеющий рейтинг 3.
Получаем 5 позиций – для магазинов №№ 2-6.
Магазины 2 и 6 можно сразу отбросить — слишком высокая стоимость даже на глаз. Остаются три магазина -3,4,5.
Находим стоимость покупки:
- для магазина №3: 13513+0=13513 (руб.)
- для магазина №4: 13745+390=14135 (руб.)
- для магазина №5: 13411+399=13810 (руб.)
Отсюда получаем, что минимальная стоимость покупки предложена в магазине под номером 3.
Вариант 11МБ9
На рисунке изображен график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали – значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления за данные три дня (в миллиметрах ртутного столба).
Алгоритм выполнения
- Определяем цену деления для вертикальной шкалы значений.
- Находим самую низкую (по вертикали) точку на линии графике.
- Вычисляем значение найденной наименьшей точки.
Решение:
Фиксируем пару соседних числовых значений на вертикальной оси графика. Возьмем, например, значения 754 и 756. Между ними 2 черты деления. Следовательно, получаем цену деления: (756 – 754) / 2 = 1 мм рт.ст.
Наименьшая точка на графике соответствует вторнику и фиксирует точку на черте деления между значениями 750 и 752. Поэтому значение этой точки равно: 750 + 1 = 751 (мм рт.ст.).
Вариант 11МБ10
На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов вовсе рабочие дни с 3 по 18 сентября 207 года. По горизонтали указываются числа месяца, по вертикали – цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линиями.
Определите по рисунку, какого числа цена олова на момент закрытия торгов впервые за данный период стала равна 14900 долларов США за тонну.
Алгоритм выполнения
- Находим на вертикальной оси искомое значение, равное 14900 долларов.
- Фиксируем точки на графике, соответствующие этому значению.
- Находим проекции этих точек на горизонтальную ось. Определяем числа (дни), которым они соответствуют.
- Определяем наименьшее среди найденных чисел.
Решение:
Число 14900 по вертикали находится на линии, соединяющей 4-ю и 5-ю клетки (отсчитывая снизу вверх). Проведя горизонтальную линию на этой высоте, получим, что это значение имеют три точки. Они соответствуют 6-му числу сентября, 7-му и 13-му. Наименьшее среди них – 6-е. То есть ответ – 6.
Вариант 11МБ11
В таблице показано распределение медалей на зимних Олимпийских играх в Сочи среди стран, занявших первые 10 мест по количеству золотых медалей.
Определите с помощью таблицы, сколько серебряных медалей у страны, занявшей второе место по числу золотых медалей.
Алгоритм выполнения
- Анализируем 3-й столбец таблицы («Медали Золотые»). Находим 2-е по величине числовое значение.
- В той же строке перемещаемся в 4-ю ячейку (столбец «Медали Серебряные»). Отображенное в ней число является ответом на вопрос задачи.
Решение:
Второе по величине кол-во золотых медалей имеет Норвегия. В строке, отображающей данные результатов для этой страны, для числа серебряных медалей зафиксировано значение 5.
Вариант 11МБ12
В соревнованиях по метанию молота участники показали следующие результаты. Места распределяются по результатам лучшей попытки каждого спортсмена: чем дальше метнул молот, чем лучше.
Какое место занял спортсмен Лаптев?
Алгоритм выполнения
- Находим результат лучшей попытки метания для каждого спортсмена.
- Распределяем полученные числовые значения в порядке убывания.
- Определяем позицию Лаптева в сформированном ряду.
Решение:
Находим лучшие результаты метания для каждого спортсмена:
- у Лаптева – 55,5 м
- у Монакина – 56 м
- у Таля – 54,5 м
- у Овсова – 53 м
Распределяем места рейтинга:
- Монакин (56 м)
- Лаптев (55,5 м)
- Таль (54,5 м)
- Овсов (53 м)
Следовательно, Лаптев занял 2-е место.
Вариант 11МБ13
На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси – крутящий момент в Н·м. Чтобы автомобиль начал движение. Крутящий момент должен быть не менее 20 Н·м.
Определите по графику, какого наименьшего числа оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение.
Алгоритм выполнения
- Находим на графике точку, соответствующую значению 20 на вертикальной оси.
- Находим проекцию этой точки на горизонтальную ось. Фиксируем числовое значение на этой оси.
Решение:
Условие «должен быть не менее 20» означает, что это числовое значение является минимально допустимым для начала движения. Поэтому необходимо найти на графике точку, соответствующую именно 20 (Н·м) на вертикальной оси.
Опускаем из найденной точки перпендикуляр на горизонтальную ось. Получаем проекцию. Ее значение равно 1000 об./мин. Итак, ответ: 1000.
Вариант 11МБ14
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия.
Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
Алгоритм выполнения
- Отбрасываем положительные значения температур, будем рассматривать только отрицательные.
- Среди них определяем числовое значение наиболее длинного элемента-столбца диаграммы.
Решение:
Поскольку требуется найти минимальное значение, то элементы диаграммы, имеющие положительные величины, следует отбросить, т.к. вне зависимости от модуля числа отрицательное всегда меньше положительного.
Одно из свойств отрицат.чисел заключается в том, что из произвольных 2-х таких чисел меньше то, которое больше по модулю. Отсюда делаем вывод, что минимальная среднемес.температура соответствовала февралю. Ее значение составило –80С.
Вариант 11МБ15
В таблице показано расписание пригородных электропоездов по направлению Москва ленинградская – Клин – Тверь.
Владислав пришел на станцию Москва Ленинградская в 18:20 и хочет уехать в Тверь на ближайшей электричке. В ответе укажите номер этой электрички.
Алгоритм выполнения
- Отбрасываем все строки таблицы, для которых указано время отбытия из С-Петербурга более раннее, чем 18:20.
- Среди оставшихся строк отбрасываем те, которые не направляются в Тверь, а имеют конечным пунктом Клин.
- Из остальных подходящих выбираем электричку с наиболее ранним временем прибытия в Тверь.
Решение:
Отбрасываем электрички под номерами 1–4. На них Владислав уже опоздал, поскольку они отправились раньше, чем в 18:20.
Среди электричек №№5–7 отбрасываем номера 5 и 6, т.к. они не идут в Тверь, а имеют конечным пунктом Клин. Подходящим остался единственный вариант – электричка №7.
Вариант 11МБ16
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря, на вертикальной – давление в миллиметрах ртутного столба.
Определите по графику, чему равно атмосферное давление на высоте 6,5 км. Овеет дайте в миллиметрах ртутного столба.
Алгоритм выполнения
- Вычисляем цену деления для шкал по горизонтальной и вертикальной осям.
- Находим точку на графике, соответствующую 6,5 м над уровнем моря.
- Находим проекцию этой на вертикальную ось, определяем соответствующее числовое значение на вертикальной оси.
Решение:
Цена деления на горизонтальной оси составляет: (1 – 0) / 2 = 0,5 км.
Цена деления на вертикальной оси равна: (100 – 0) / 5 = 20 мм рт.ст.
Из значения 6,5 (посередине между 6 и 7) на горизонт.оси проводим перпендикуляр на график, фиксируем соответствующую точку на его линии. Из этой точки проводим перпендикуляр на вертик.ось, отмечаем полученное числовое значение. Оно равно 300 + 20 = 320 (мм рт.ст.).
Вариант 11МБ17
На рисунке жирными точками указана цена серебра, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали – цена серебра в рублях за грамм. Для наглядности жирные точки точки на рисунке соединены линией.
Определите по рисунку наибольшую цену серебра в период с 20 по 30 октября. Ответ дайте в рубля за грамм.
Алгоритм выполнения
- Отбрасываем часть графика, не соответствующую указанному в условии периоду 20–30 октября.
- На выбранной части находим точку с максимальным значением по вертикали.
Решение:
Проводим перпендикуляры на график с горизонт.оси из точек, соответствующих числам 20 и 30. Выделяем часть линии графика между этим точками, учитывая и их.
На выделенном фрагменте графика находим самую высокую точку. Ее проекция на вертик.ось дает числовое значение для ответа. Оно составляет 16,6 (руб./г).