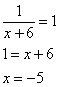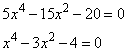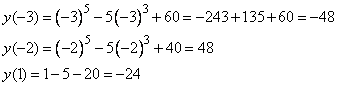СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование произведений
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 26691
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 26691: 3383 69993 3385 3387 3389 3391 3393 3395 3397 3399 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции во внутренней точке отрезка
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 11 № 26710
Найдите точку минимума функции
Аналоги к заданию № 26710: 3773 3781 70837 548382 3775 3777 3779 3783 3785 3787 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 11 № 26711
Найдите точку максимума функции
Аналоги к заданию № 26711: 3791 70887 509578 3793 3795 3797 3799 3801 3803 3805 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
4
Тип 11 № 26712
Найдите точку минимума функции
Аналоги к заданию № 26712: 3811 70937 3813 3815 3817 3819 3821 3823 3825 3827 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
5
Тип 11 № 26713
Найдите точку максимума функции
Аналоги к заданию № 26713: 3829 70987 3831 3833 3835 3837 3839 3841 3843 3845 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.2.1 Применение производной к исследованию функций и построению графиков, Наименьшее (наибольшее) значение функции на бесконечном промежутке
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Задачи из сборников Ященко, 2021 год
Квадратные уравнения
Показательные уравнения
Логарифмические уравнения
Модуль числа
Уравнения с модулем
Тригонометрический круг
Формулы тригонометрии
Формулы приведения
Простейшие тригонометрические уравнения 1
Простейшие тригонометрические уравнения 2
Тригонометрические уравнения
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
. От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
Давайте потренируемся.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Ответ:
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где
— целое, а найти надо корни на отрезке
На указанном промежутке лежит точка
От нее и отсчитываем.
Получим:
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
а)
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и
из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а)
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Сначала серия
Теперь серия
Ответ: .
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке
Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие
появляется, поскольку в уравнении есть
ОДЗ:
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси
.
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
и
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или
. Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие
. Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
На отрезке нам подходит корень
.
На отрезке нам подходят корни
.
На отрезке — корни
Ответ в пункте б):
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
- ЕГЭ по математике профиль
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
Связанные страницы:
Всё варианты 12 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 12 ЕГЭ по математике профильного уровня 2022 год (уравнения)
1) (28.03.2022 досрочная волна) а) Решите уравнение ({4^{sin x}} + {4^{sin left( {pi + x} right)}} = frac{5}{2}.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};;4pi } right]).
ОТВЕТ: а) ( pm frac{pi }{6} + pi k;;;k in Z;) б) (frac{{17pi }}{6};,,,,,frac{{19pi }}{6};,,,,,frac{{{text{23}}pi }}{6}.)
2) (28.03.2022 досрочная волна) а) Решите уравнение ({81^{cos x}} — 12 cdot {9^{cos x}} + 27 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,4pi ;,,, — frac{{{text{5}}pi }}{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;;;2pi k;;;k in Z;) б) ( — frac{{11pi }}{3};,,,, — 4pi .)
3) (28.03.2022 досрочная волна) а) Решите уравнение ({16^{sin x}} — 1,5 cdot {4^{sin x + 1}} + 8 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,5pi ;,,, — frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) ( — frac{{{text{23}}pi }}{6};,,,, — frac{{7pi }}{2}.)
4) (02.06.2022 основная волна) а) Решите уравнение (2{sin ^2}x — cos left( { — x} right) — 1 = 0.)
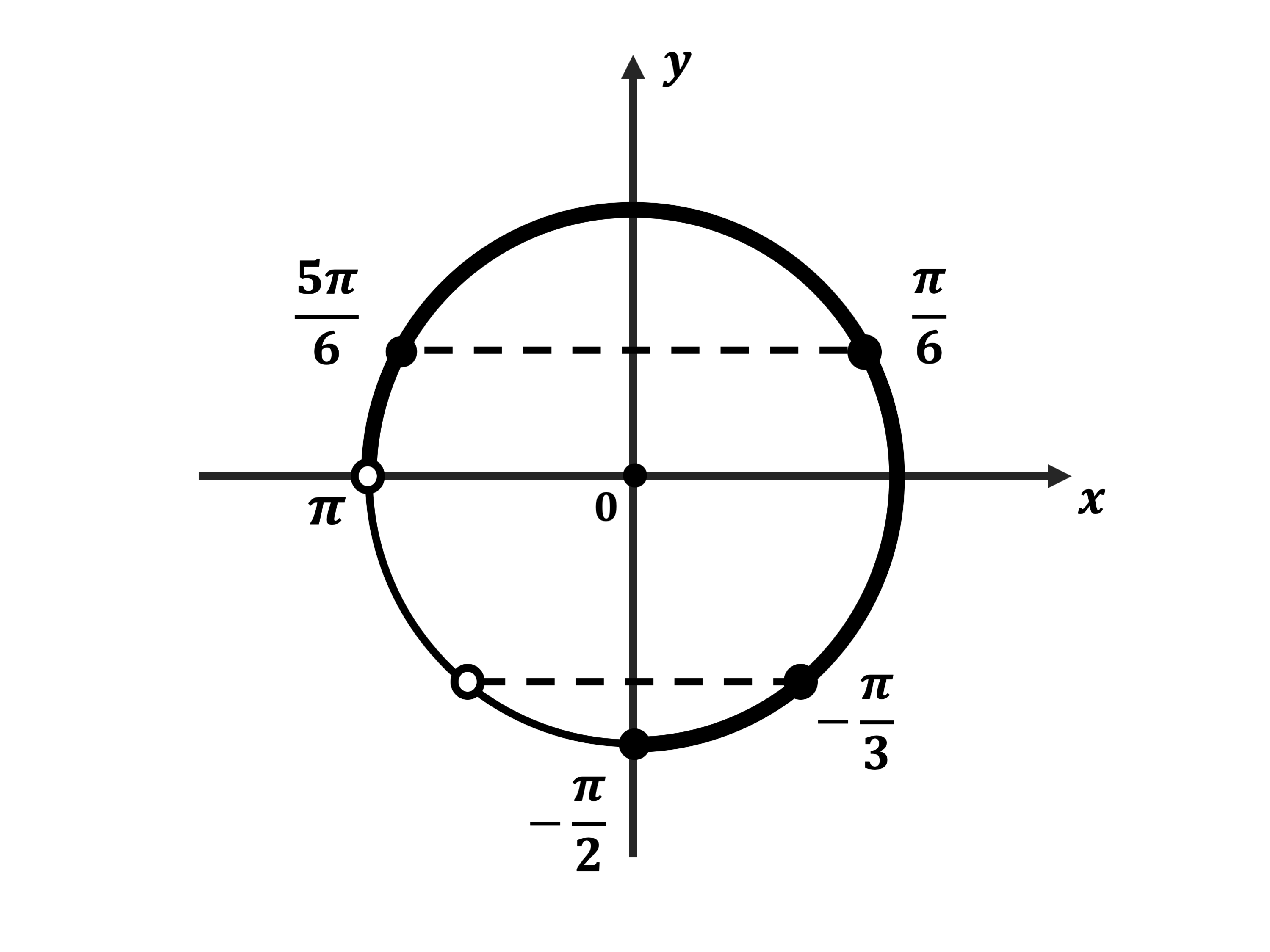
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — ,pi ;,,,frac{pi }{2}} right]).
ОТВЕТ: а) ( pm frac{pi }{3} + 2pi k;,,;pi + 2pi k;;;k in Z;) б) ( — pi ;,,, — frac{pi }{3};,,,,frac{pi }{3}.)
5) (06.2022 основная волна) а) Решите уравнение (2{cos ^2}x — 3sinleft( { — x} right) — 3 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{5}}pi }}{2};,,4pi } right]).
ОТВЕТ: а) (frac{pi }{6} + 2pi k;,,;frac{{{text{5}}pi }}{6} + 2pi k;;;frac{pi }{2} + 2pi k;;;k in Z;) б) (frac{{{text{17}}pi }}{6};,,,,frac{{{text{5}}pi }}{2}.)
6) (06.2022 основная волна) а) Решите уравнение (cos 2x + sinleft( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{pi }{2};,,2pi } right]).
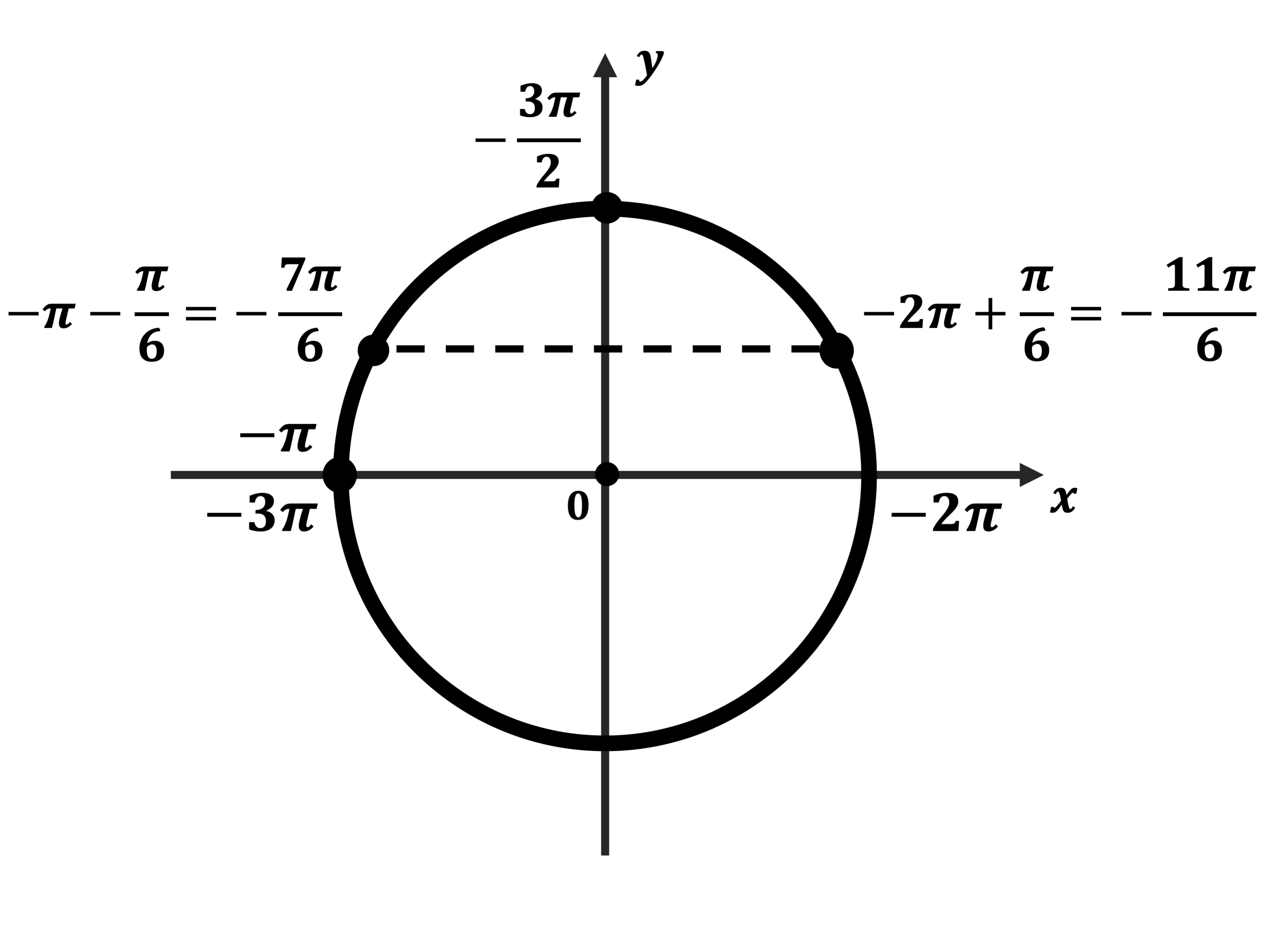
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;pi k;;;k in Z;) б) (pi ;,,,,frac{{{text{7}}pi }}{6};,,,,frac{{{text{11}}pi }}{6};,,,2pi .)
7) (06.2022 основная волна) а) Решите уравнение (cos 2x + 3sinleft( { — x} right) — 2 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;; — frac{pi }{{text{2}}}{text{ + 2}}pi k;;;k in Z;) б) (frac{{{text{3}}pi }}{2};,,,,frac{{{text{11}}pi }}{6}.)

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{3}}pi ;,,frac{{{text{9}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{2} + 2pi k;,,;2pi k;;;;k in Z;) б) (frac{{{text{7}}pi }}{2};,,,4pi .)
9) (06.2022 основная волна) а) Решите уравнение (sin 2x + 2sin left( { — x} right) + cos left( { — x} right) — 1 = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {{text{2}}pi ;,,frac{{{text{7}}pi }}{2}} right]).
ОТВЕТ: а) ( — frac{pi }{6} + 2pi k;,,; — frac{{{text{5}}pi }}{6} + 2pi k;;;2pi k;;;k in Z;) б) (frac{{{text{19}}pi }}{6};,,,2pi .)
10) (27.06.2022 резервная волна) а) Решите уравнение ({log _{11}}left( {2{{sin }^2}x + 7sqrt 3 sin x — 11} right) = 0.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ {frac{{{text{3}}pi }}{2};,,3pi } right]).
ОТВЕТ: а) (frac{pi }{3} + 2pi k;,,;frac{{{text{2}}pi }}{3} + 2pi k;;;k in Z;) б) (frac{{{text{7}}pi }}{3};,,,frac{{{text{8}}pi }}{3}.)
11) (27.06.2022 резервная волна) а) Решите уравнение ({log _9}left( {sqrt 2 sin x + sin 2x + 9} right) = 1.)
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[ { — frac{{{text{7}}pi }}{2};,, — 2pi } right]).
ОТВЕТ: а) ( pm frac{{{text{3}}pi }}{4} + 2pi k;,,;;pi k;;;k in Z;) б) ( — frac{{{text{13}}pi }}{4};,, — 3pi ;,,, — frac{{{text{11}}pi }}{4};,, — 2pi .)
Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
Материал для подготовки к заданию номер 12 из ЕГЭ по профильной математике
Все уравнения можно разделить на несколько групп:
— Целые рациональные уравнения
Каждая группа уравнений имеет свои особенности. На первый взгляд может показаться, что это очень большой материал и на его изучение понадобится много времени, однако на самом деле для подготовки в экзамену и выполнению задания номер 12 можно подготовиться достаточно быстро, используя верно подобранные материалы и разбирая примеры заданий
Комбинируя все представленные в данных материалах способы и обладая базовыми знаниями математики, можно успешно решить большинство уравнений, которые могут встретиться учащимся во время обучения в средней и старшей школе а так же успешно решить задания на данную тему в контрольно-измерительных материалах
СОВЕТ: после прохождения какой-либо темы в моём пособии, необходимо прорешать похожие уравнения (этой же группы) на одном из подобранных мной сайтов (смотрите ниже)
Часть I. Способы решения уравнений. Метод “Замена переменной”
Уравнение вида af²(x)+bf (x)+c=0 Такие уравнения (их иногда называют трехчленными) являются одними из наиболее распространенных. Скорее всего, самый известный и яркий пример этого типа уравнений — биквадратное уравнение ax⁴ + bx2 + c = 0 (здесь f (x) = x 2 ). Заменой переменной t = f (x) трехчленное уравнение сводится к квадратному относительно переменной t уравнению at² + bt + c = 0
Решить уравнение (2x² – 3x + 1) = 22x² – 33x + 1.
Задание 12. Тригонометрическое уравнение
Типичная задача №12 из ЕГЭ по математике 2022 содержит два пункта:
- Решить несложное тригонометрическое уравнение (хотя иногда попадаются довольно сложные).
- Среди полученных корней отобрать те, которые принадлежат заданному отрезку. Вот здесь большинство учеников «пасует».
Все видеоуроки по задачам 12, опубликованные на моем сайте, содержат оба пункта: и решение уравнения (со всеми тонкостями), и различные подходы к отбору корней.
Глава 1. Тригонометрические уравнения § 1. Задача C1: тригонометрические уравнения с ограничением 












источники:
http://vc.ru/u/1019775-egor-borodin/330865-material-dlya-podgotovki-k-zadaniyu-nomer-12-iz-ege-po-profilnoy-matematike
http://www.berdov.com/ege/equation-root/
Значения функции: наибольшее и наименьшее
В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.
Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
Найти точку максимума функции y = ln(x+4)2+2x+7.
[/su_note]
Алгоритм решения:
- Определяем область определения функции.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие области определения.
- Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
- Записываем ответ.
Решение:
1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:
(x+4)2 > 0
Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.
2. Находим производную:
у’=(ln(x+4)2 + 2x + 7)’
По свойству логарифма получаем:
у’=(ln(x+4)2 )’+(2x)’+(7)’.
По формуле производной сложной функции:
(lnf)’=(1/f)∙f’. У нас f=(x+4)2
у, = (ln(x+4)2 )’+ 2 + 0 = (1/(x+4)2 )∙((x+4)2)’ + 2=(1/(x+4)2 2)∙(х2 + 8х + 16)’ +2=2(х + 4) /((х + 4)2) + 2
у’= 2/(х + 4) + 2
3. Приравниваем производную к нулю:
у, = 0 → (2+2∙(х + 4))/(х + 4)=0,
2 +2х +8 =0, 2х + 10 = 0,
2х = -10,
х = -5
Ответ: -5.
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
Найдите точку минимума функции y = x – ln(x+6) + 3.
[/su_note]
Алгоритм решения:
- Определяем область определения функции.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие области определения.
- Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
- Записываем ответ.
Решение:
1. ОДЗ: .
2. Найдем производную функции:
3. Приравниваем полученное выражение к нулю:
4. Получили одну точку x=-5, принадлежащую области определения функции.
5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4
При х=-5,5 производная функции отрицательна, так как
Значит, точка х=-5 является точкой минимума.
Ответ: -5.
Третий вариант задания (из Ященко, №12)
[su_note note_color=”#defae6″]
Найдите наибольшее значение функции на отрезке [-3; 1].
[/su_note]
Алгоритм решения:.
- Находим производную.
- Определяем, в каких точках производная равна 0.
- Исключаем точки, не принадлежащие заданному отрезку.
- Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
- Находим значения функции на концах отрезка.
- Ищем среди полученных значений наибольшее.
- Записываем ответ.
Решение:
1. Вычисляем производную от функции, получим
2. Приравниваем производную к нулю:
Решение уравнения дает два корня
– не принадлежит множеству действительных чисел
.
3. Значение и остается одна точка
.
4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:
Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.
Ответ: 48.
Даниил Романович | Просмотров: 11.8k
За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.
Решение
а) $11cos 2x=7sin (x-{π} / {2})-9$,
$11(2cos^2 x-1)=-7cos x-9$,
$22cos^2 x -11+7cos x +9=0$,
$22cos^2 x+7cos x -2=0$.
Обозначим $cos x=t$, $|t|⩽1$.
Тогда уравнение примет вид: $22t^2+7t-2=0$.
Решим его. $22t^2+7t-2=0$,
$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,
$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.
$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;
$x=± {2π} / {3}+2π n$, $n∈ Z$.
$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.
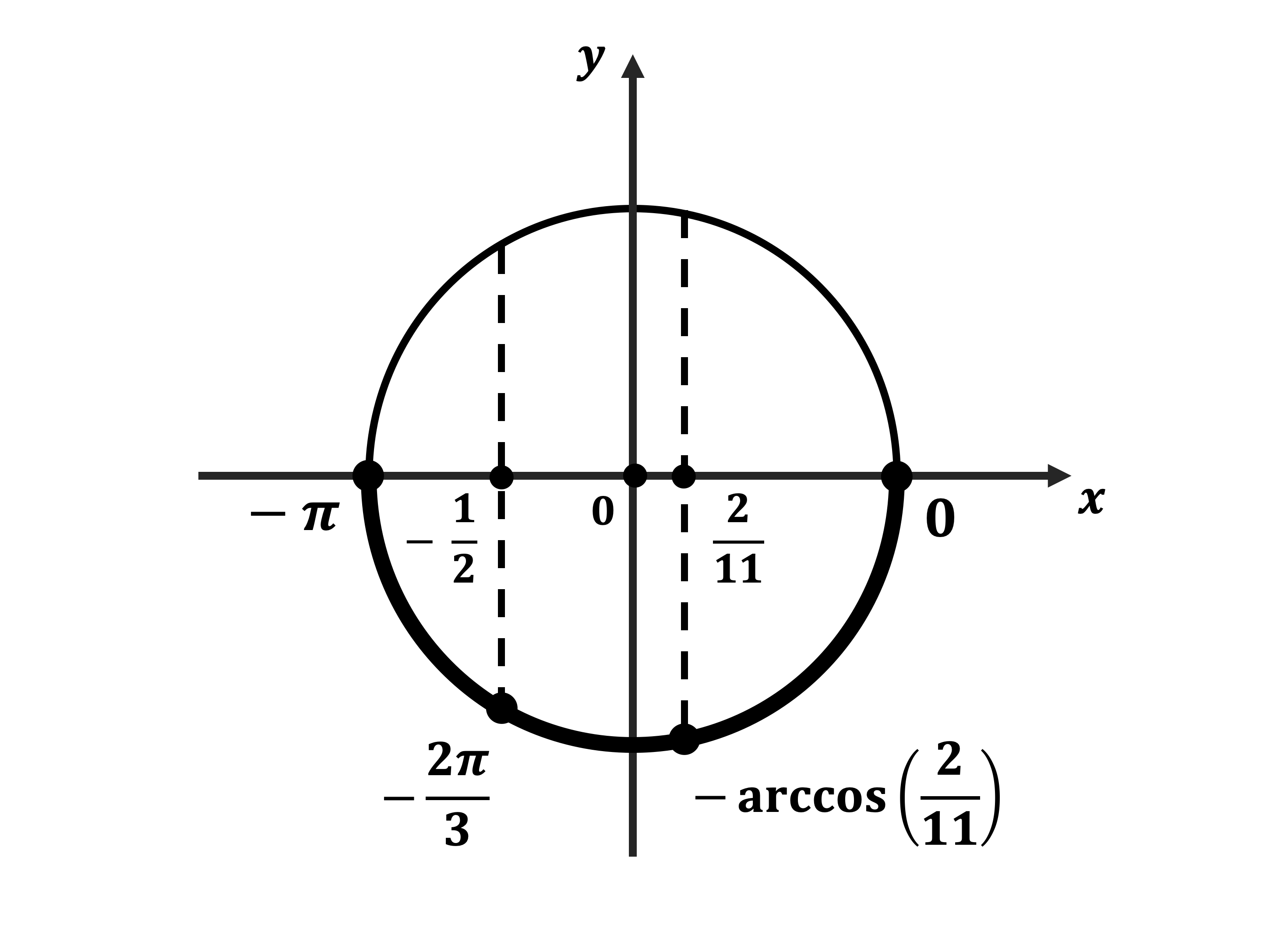
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.
$x_1=-π+{π} / {3}=-{2π} / {3}$
$x_2=-arccos {2} / {11}$.
Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$
Задача 2
а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$cos(x+{π}/{2})=-sinx,$
$2sin^2x + 7sinx -4 = 0$
Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим
$2t^2 + 7t -4 = 0.$
$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $
$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.
Вернёмся к исходной переменной:
$sinx ={1}/{2}$,
$x = {π}/{6} + 2πn, n ∈ Z$
$x = {5π}/{6} + 2πk, k ∈ Z$
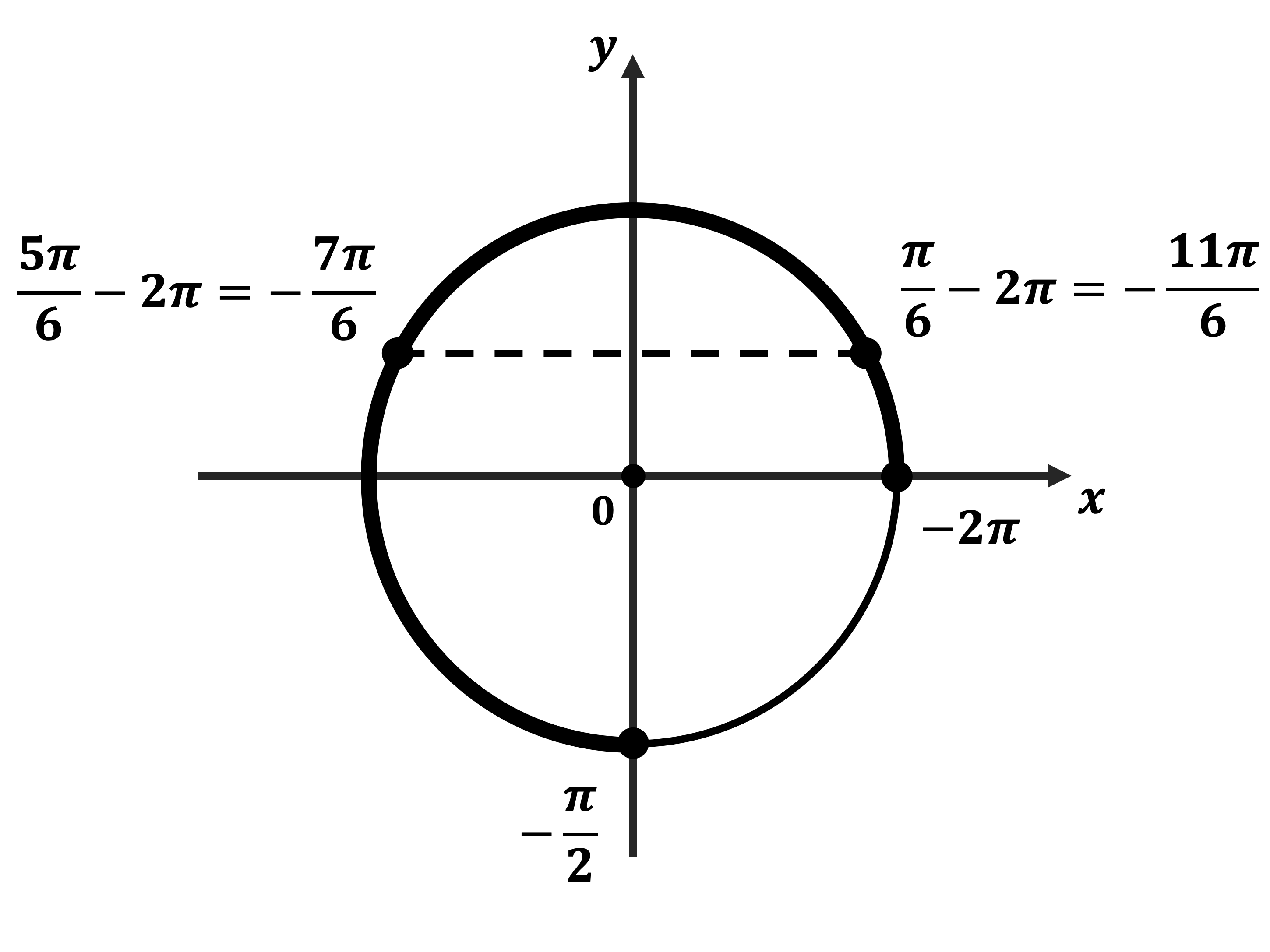
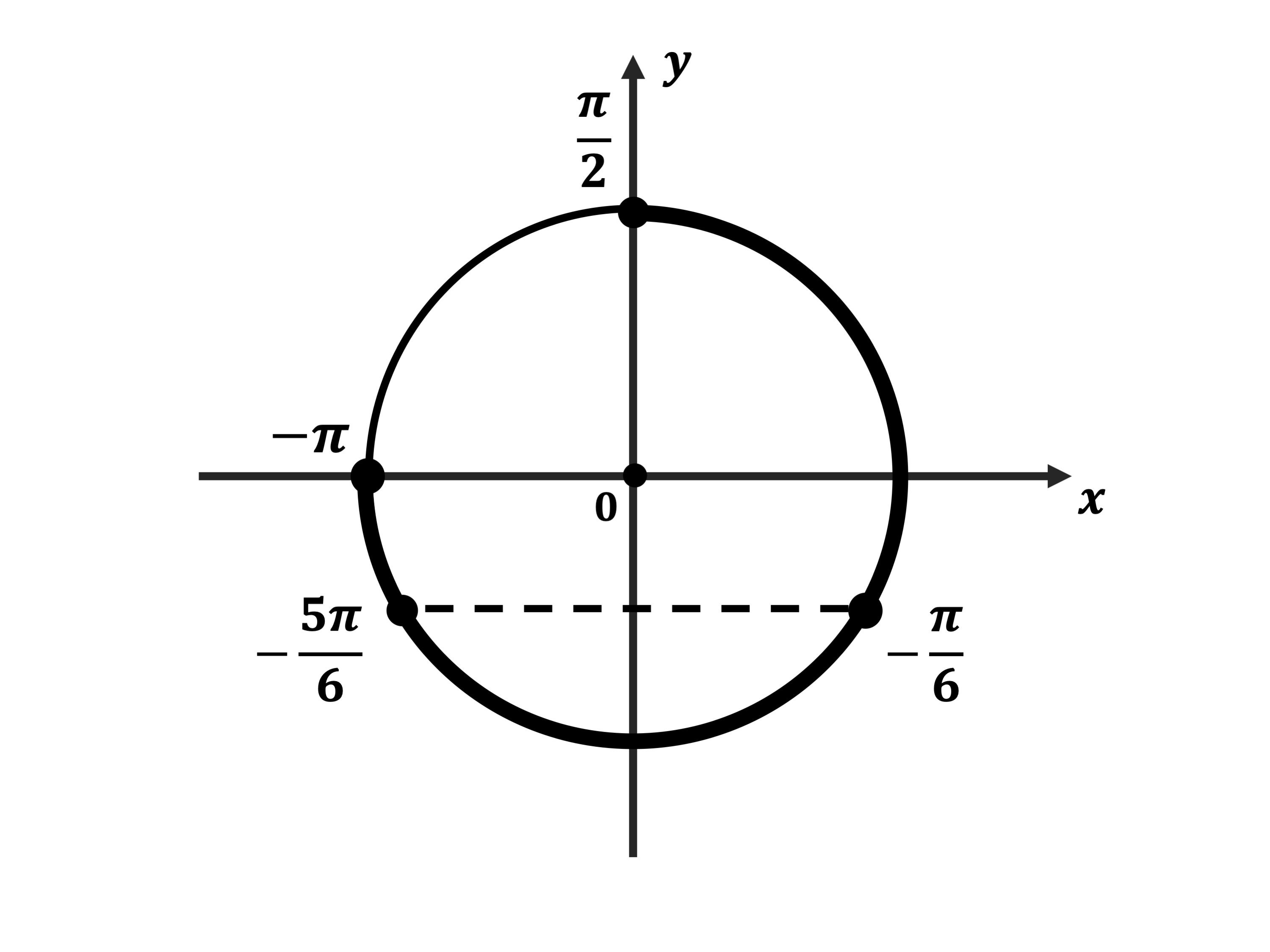
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.
Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$
Задача 3
а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.
Решение
а) Преобразуем уравнение, согласно формуле приведения:
$sin(x+{3π}/{2})=-cosx,$
$2cos^2x + 5 cos x + 2 = 0$
Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.
Вернёмся к исходной переменной: $cos x = − {1}/{2}$,
$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$
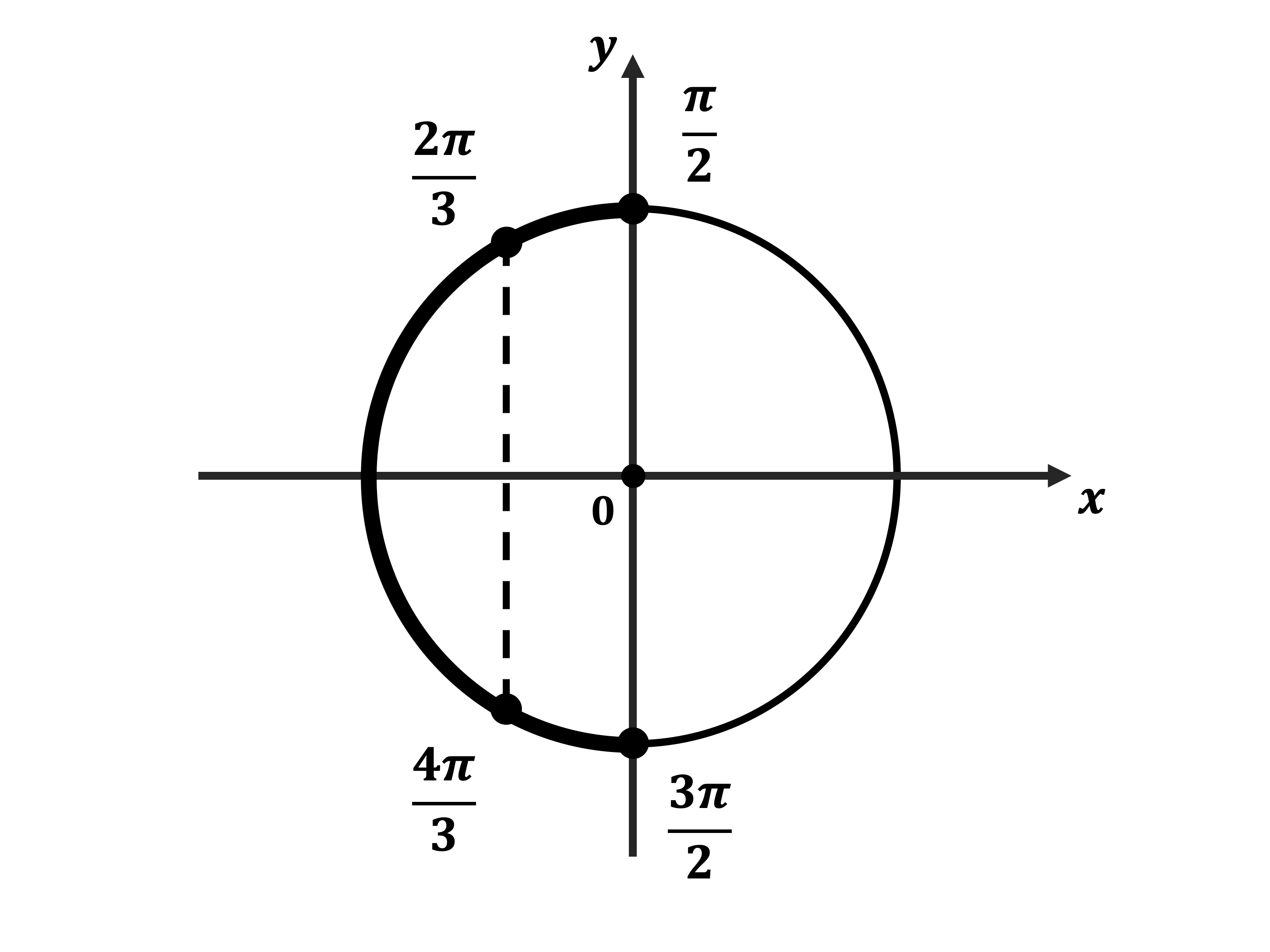
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.
Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$
Задача 4
а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.
Решение
а) Преобразуем уравнение:
$−sin x = sin 2x,$
$sinx + 2 sin x cos x = 0,$
$sinx(1 + 2 cos x) = 0,$
$sin x = 0;x = πn, n ∈ Z,$
$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$
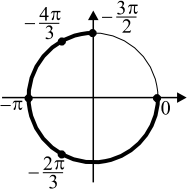
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.
Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.
Задача 5
а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.
Решение
а) Преобразуем уравнение:
$cos x = − sin 2x,$
$cos x + 2 sin x cos x = 0,$
$cos x(1 + 2 sin x) = 0,$
$cos x = 0;$
$x = {π}/{2} + πn, n ∈ Z$
$sin x = −{1}/{2},$
$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$
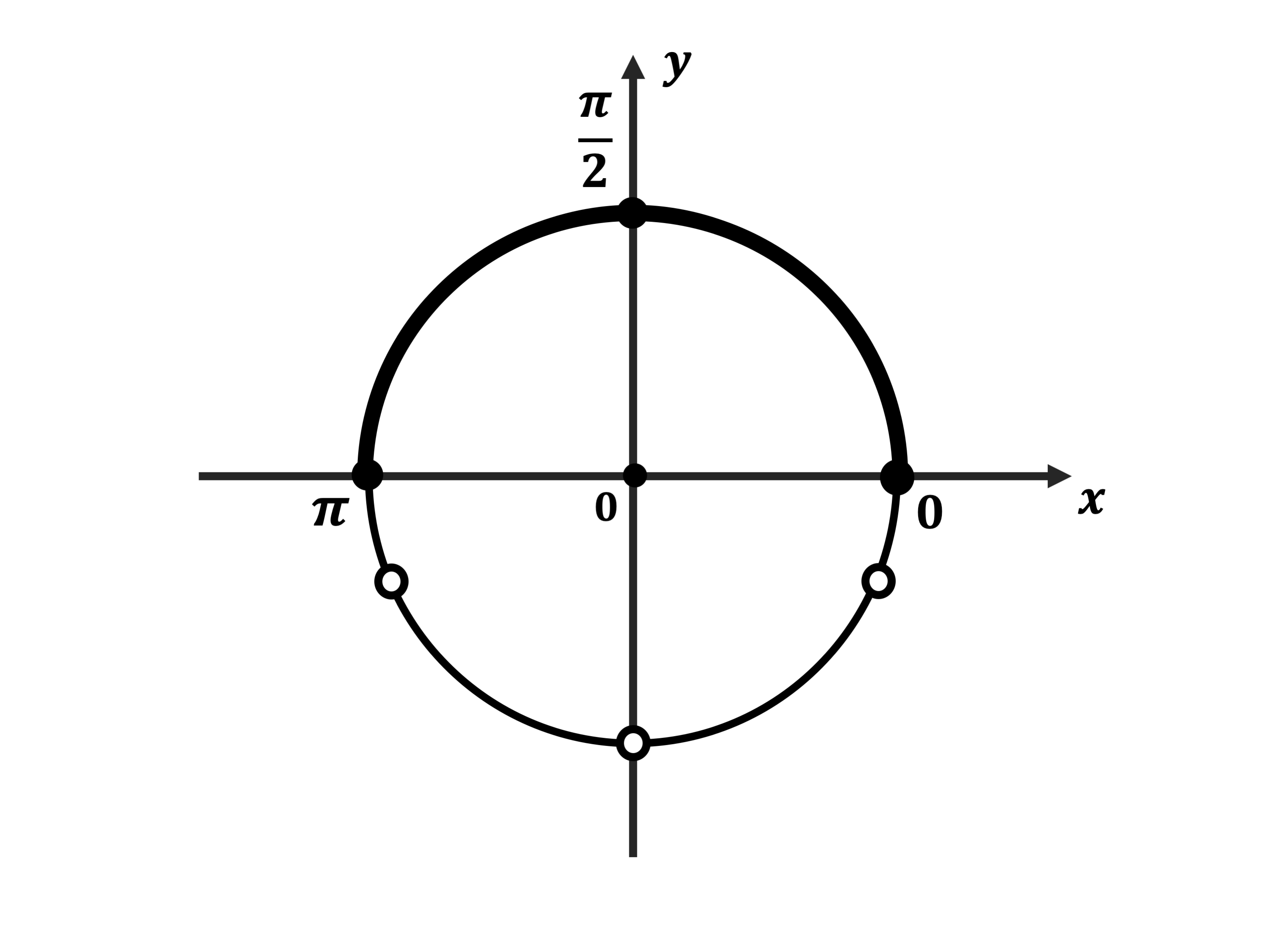
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число ${π}/{2}$.
Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$
Задача 6
а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.
Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.
Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$
б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$
Задача 7
а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.
б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.
Решение
a) $4cos^{2}x = 3cos2x+1$,
$4cos^{2}x = 3(2cos^{2}x-1)+1$,
$4cos^{2}x=6cos^{2}x-3+1$,
$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$
б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$
$x_1=-4π, x_2=-3π, x_3=-2π$.
Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$
Задача 8
а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.
Решение
a) $cos(2x) + 3sinx-2=0$,
$1 — 2sin^{2}x + 3 sin x -2 = 0$,
$2 sin^{2}x — 3sin x +1 = 0$,
Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид
$2y^2 — 3y + 1 = 0$,
$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$
$ y_1=1, y_2={1}/{2}$.
$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.
б) Найдём корни уравнения на отрезке $[-3π;-π]$.
С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.
Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$
Задача 9
а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.
б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.
Решение
a) $2 cos^{2}x + 19sinx+8=0$,
$2(1 — sin^{2}x) + 19 sin x +8 = 0$,
$-2 sin^{2}x + 19 sin x +10 = 0$,
$2 sin^{2}x — 19 sin x -10 = 0$.
Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.
$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.
б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.
Это числа $-{5π}/{6}$ и $-{π}/{6}$.
Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$
Задача 10
а) Решите уравнение $8sin x + 4 cos^2 x = 7$.
б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.
Решение
a) $8 sin x + 4 cos^{2} x = 7$,
$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,
$-4 sin^{2}x + 8 sin x — 3 = 0$,
$4 sin^{2}x — 8 sin x + 3 = 0$.
Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.
$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.
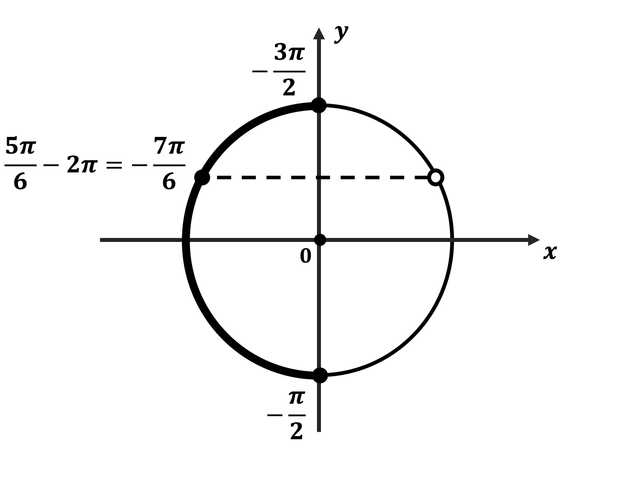
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.
Это число ${5π}/{6} — 2π = -{7π}/{6}$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$
Задача 11
а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.
Решение
а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.
Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.
$−2sinx = 1, sinx =−{1}/{2}$.
$x=−{π}/{6}+2πn, n ∈ Z;$
$x=-{5π}/{6}+ 2πk, k ∈ Z$.
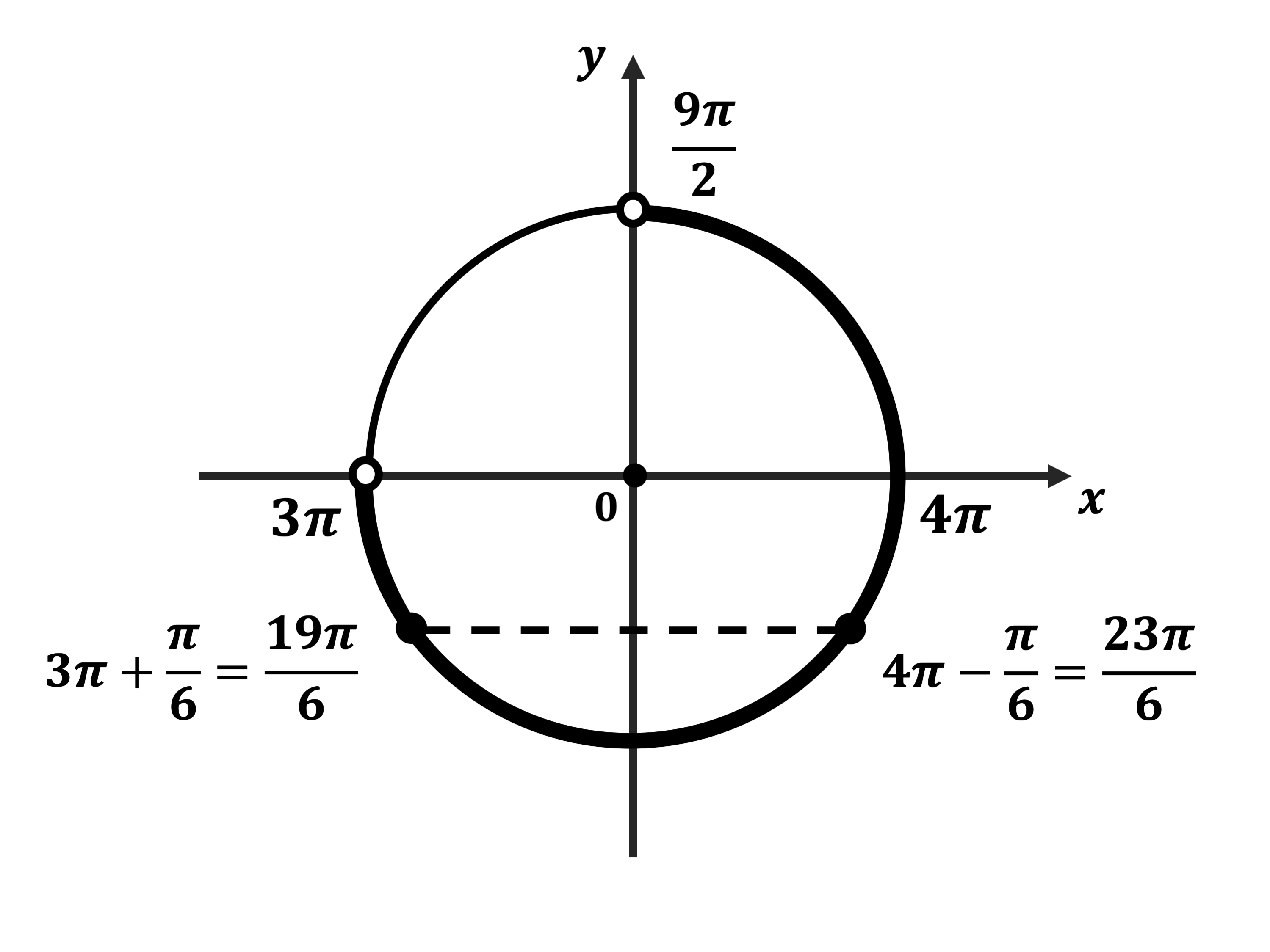
б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.
$x_1=3π+{π}/{6}={19π}/{6}$,
$x_2=4π−{π}/{6}={23π}/{6}$.
Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$
Задача 12
а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.
Решение
а)${sin2x}/{sin(π — x)}=√2$.
а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.
Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.
Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:
$2cosx=√2$,
$cosx = {√2}/{2}$,
$x = ±{π}/{4} + 2πk, k∈Z$;
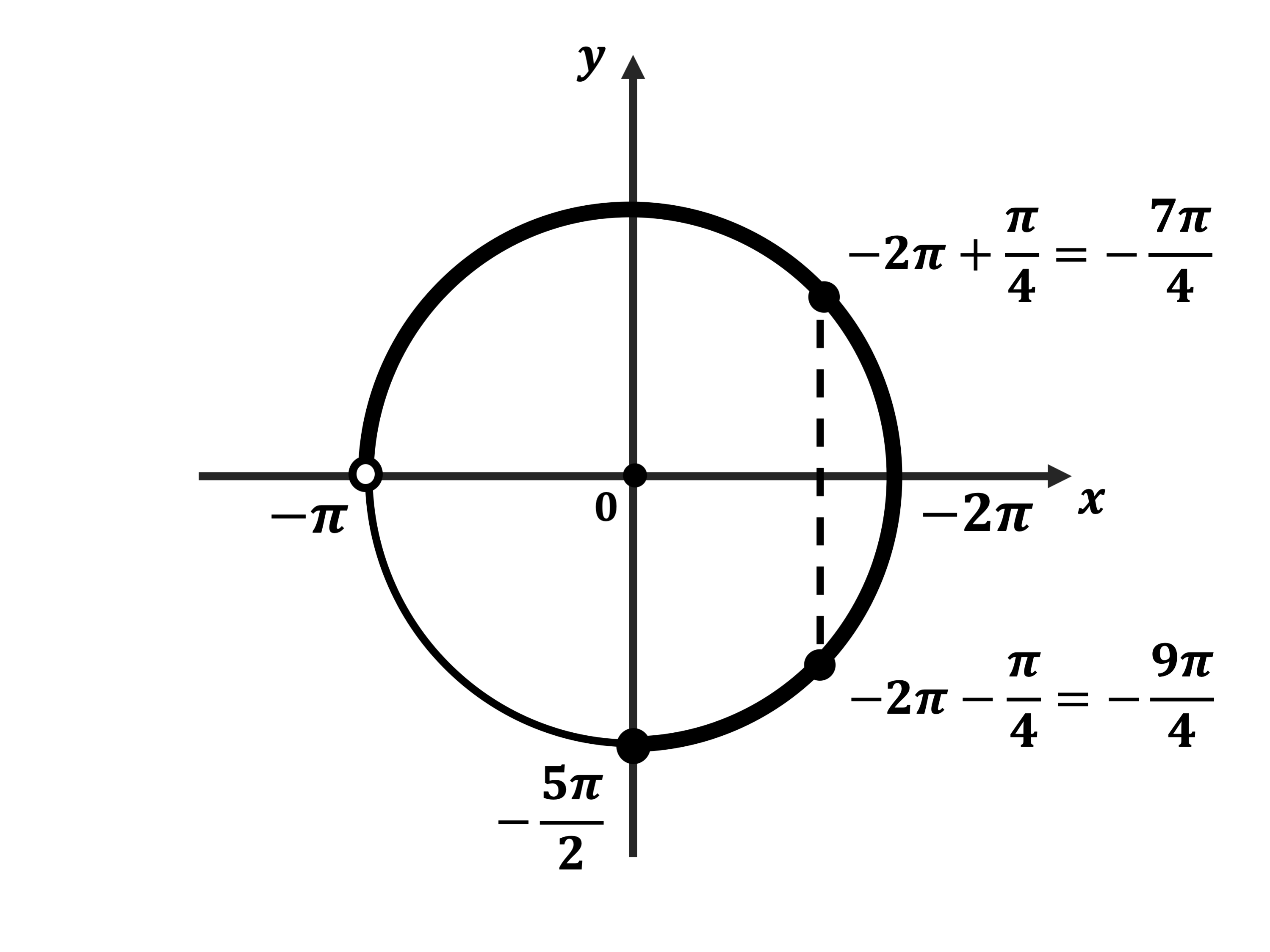
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.
$x_1=-2π+{π}/{4}=-{7π}/{4}$
$x_2=-2π-{π}/{4}=-{9π}/{4}$
Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$
Задача 13
а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.
б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
Решение
а)${sin2x}/{cos(π + x)}=-√2$.
Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.
Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:
$2sinx=√2$,
$sinx = {√2}/{2}$,
$x = {π}/{4} + 2πn, n∈Z$;
$x = {3π}/{4} + 2πk, k∈Z$.
б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.
1. $x = {π}/{4} + 2πn, n∈Z$.
$-2π < {π}/{4} + 2πn < -{π}/{2},$
$-2 < {1}/{4} + 2n < -{1}/{2},$
$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$
$-{9}/{4} < 2n < -{3}/{4},$
$-{9}/{8} < n < -{3}/{8},$
$n = -1$.
При $n =-1$
$x = {π}/{4}-2π=-{7π}/{4}$.
2. $x = {3π}/{4} + 2πk, k∈Z$.
$-2π < {3π}/{4} + 2πk < -{π}/{2}$,
$-2 < {3}/{4} + 2k < -{1}/{2}$,
$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,
$-{11}/{4} < 2k < -{5}/{4}$,
$-{11}/{8} < k < -{5}/{8}$,
$k = -1$.
При $k = -1$
$x = {3π}/{4}-2π = -{5π}/{4}$.
Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$
Задача 14
а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.
Решение
а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим
$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.
Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.
Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.
При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.
При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.
При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.
Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$
Задача 15
а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.
Решение
а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:
$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.
б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.
Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.
При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.
Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$
Задача 16
а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.
Решение
а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.
$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.
$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$
$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$
б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:
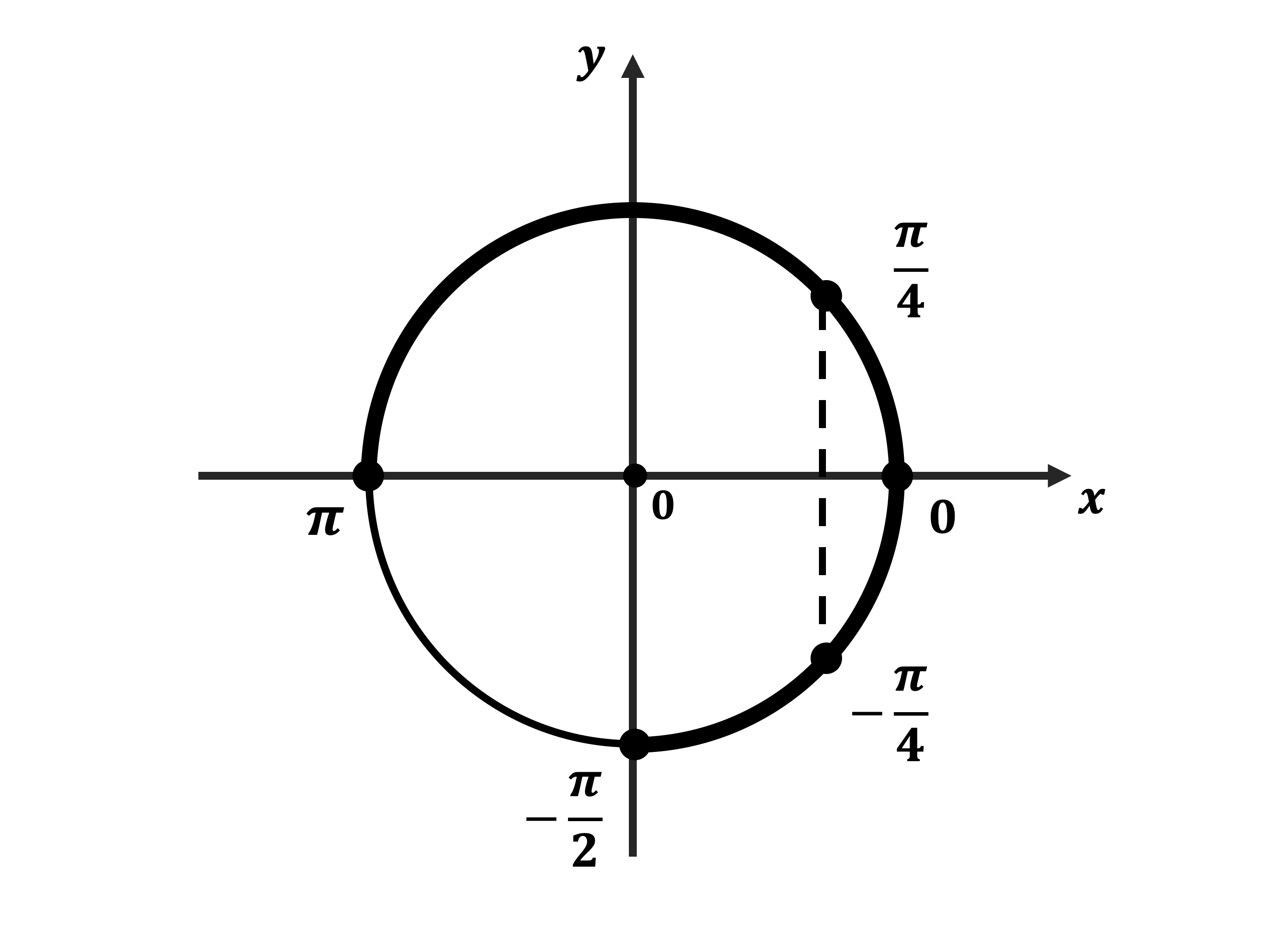
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$
Задача 17
а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.
Решение
а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$
$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$
$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$
б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:
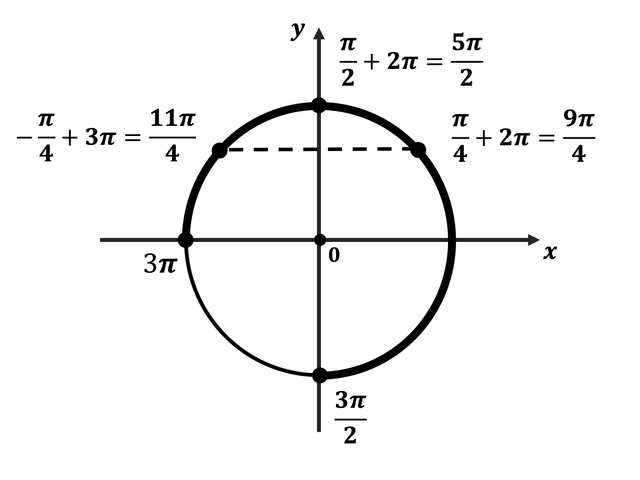
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.
Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$
Задача 18
а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.
б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,
$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,
$(3^{2x} — 81)(3^x — 5) = 0$.
Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.
Ответ: а)$2;log_{3}5$; б)$2$
Задача 19
а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.
Решение
а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.
Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.
Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.
Уравнение $(cosx)_2 = √2$ корней не имеет.
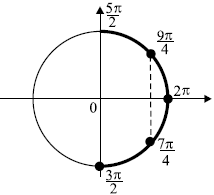
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.
Получим числа
$2π -{π}/{4} ={7π}/{4}$;
$2π + {π}/{4} = {9π}/{4}$.
Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$
Задача 20
а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.
Решение
а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.
Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.
Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.
Уравнение $(sin x)_2 = √3$ корней не имеет.
б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$
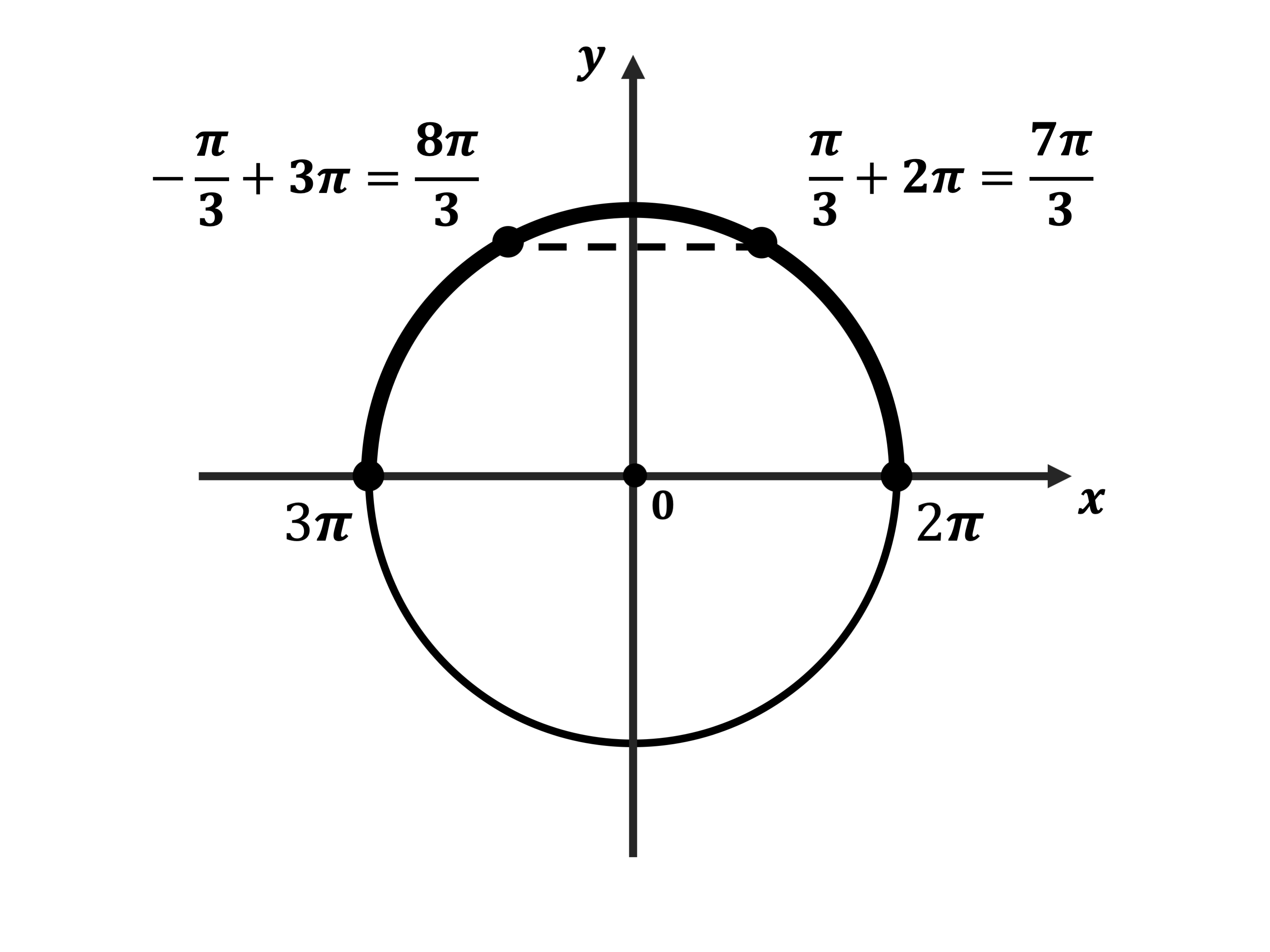
Получим числа:
$2π +{π}/{3}={7π}/{3}$;
$3π -{π}/{3}={8π}/{3}$.
Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$