Задание по егэ по математике 2016 профильный уровень - Помощь в подготовке к экзаменам и поступлению

10 апреля 2016

В закладки

Обсудить

Жалоба

Задания с экзамена + решения + критерии оценки.

Источник: alexlarin.net.

Подробные решения контрольных измерительных материалов Единого государственного экзамена по МАТЕМАТИКЕ от 06.06.2016. Профильный уровень. Основная волна

Условия КИМов реального ЕГЭ 2016 по математике (тип 1)
Часть 1

1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 сентября составляли 103 куб, м воды, а 1 октября — 114 куб. м. Сколько нужно заплатить за холодную воду за сентябрь, если стоимость 1 куб, м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
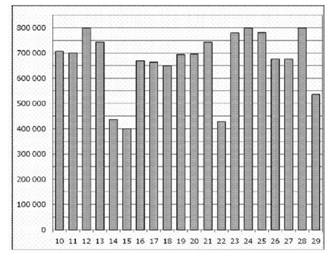
2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.

3. Найдите площадь треугольника, изображенного на рисунке.

4. В соревнованиях по толканию ядра участвуют 8 спортсменов из Великобритании, 6 спортсменов из Франции, 5 спортсменов из Германии и 5 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
5. Наидите корень уравнения: $displaystyle 2^{4x-14}=frac{1}{64}$ .
6. В четырехугольник ABCD , периметр которого равен 48 вписана окружность, AB=15 . Найдите .

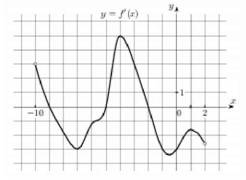
7. На рисунке изображён график displaystyle y=f'(x) производной функции displaystyle f(x) , определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой displaystyle y=-2x-11 или совпадает с ней.

8. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Часть 2

9. Найдите значение выражений $displaystyle frac{log_{8}20}{log_{8}5}+log_{5}0,05$ .
10. Груз массой 0,8 кг колеблется на пружине. Его скорость displaystyle v меняется по закону $displaystyle v=v_{0}sin frac{2pi t}{T}$ . где displaystyle t — время с момента начала колебаний, displaystyle T=16 — период колебаний, $displaystyle v_{0}=0,5$ м/с. Кинетическая энергия (в джоулях) груза вычисляется по формуле $displaystyle E=frac{mv^{2}}{2}$ , где — масса груза в килограммах, — скорость груза в м/с.
Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях
11. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
12. Найдите точку минимума функции $displaystyle y=2x-ln(x+8)^{2}.$

Тип 1

13. а) Решите уравнение $displaystyle 2log_{2}^{2}(2sin x)-7log_{2}(2sin x)+3=0.$
б) Укажите корни этого уравнения, принадлежащие отрезку $displaystyle left [ frac{pi }{2};2pi right ]$ .
14. В правильной треугольной призме $displaystyle ABCA_{1}B_{1}C_{1}$ сторона основания равна 6, а боковое ребро $displaystyle AA_{1}$ равно 3 . На ребре $displaystyle B_{1}C_{1}$ отмечена точка так, что $displaystyle B_{1}L=1$ . Точки и — середины ребер и $displaystyle A_{1}C_{1}$ соответственно. Плоскость displaystyle gamma параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости ;
б) Найдите объем пирамиды, вершина которой — точка , а основание — сечение данной призмы плоскостью displaystyle gamma .
15. Решите неравенство: $displaystyle frac{49^{x}-6cdot 7^{x}+3}{7^{x}-5}+frac{6cdot 7^{x}-39}{7^{x}-7}leq 7^{x}+5.$
16. В трапеции ABCD боковая сторона перпендикулярна основаниям. Из точки на сторону опустили перпендикуляр . На стороне отмечена точка так, что прямые и перпендикулярны.
а) Докажите, что прямые и параллельны.
б) Найдите отношение BH:ED , если угол $displaystyle BCD=135^{circ}$ .
17. 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение , при котором общая сумма выплат будет составлять более 1,25 млн рублей.
18. Найдите все значения параметра , при каждом из которых уравнение
$displaystyle sqrt{15x^{2}+6ax+9}=x^{2}+ax+3$
имеет ровно три различных решения
19. На доске написаны числа 1, 2, 3, …,30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов, б (Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?

Подробные решения КИМов ЕГЭ №№1-12 и №№13-19(тип 1)

Условия КИМов основного ЕГЭ 2016 по математике (тип 2)

13. а) Решите уравнение $displaystyle 2cos ^{2}x+1=2sqrt{2}cos left ( frac{3pi }{2}-x right ).$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ frac{3pi }{2};7pi right ].$
14. В правильной четырехугольной пирамиде SABCD сторона основания равна 16, а высота равна 4. На ребрах AB, CD и отмечены точки M, N и соответственно, причем AM=DN=4 и AK=3 .
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки до плоскости SBC .
15. Решите неравенство $displaystyle frac{4^{x}-2^{x+3}+7}{4^{x}-5cdot 2^{x}+4}leq frac{2^{x}-9}{2^{x}-4}+frac{1}{2^{x}-6}.$
16. В трапеции ABCD точка — середина основания , точка — середина боковой стороны . Отрезки и пересекаются в точке .
а) Докажите, что площади четырехугольника AMOE и треугольника COD равны
б) Найдите, какую часть от площади трапеции составляет площадь четырехугольника AMOE , если BC=3, AD=4.
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наибольшее значение , чтобы общая сумма выплат была меньше 50 млн рублей?
18. Найдите все значения , при каждом из которых уравнение $displaystyle frac{x-2a}{x+2}+frac{x-1}{x-a}=1$
имеет единственный корень.
19. На доске написаны числа 2 и 3. За один ход разрешено заменить написанные на доске числа и числами 2a-1 и a+b (например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Может ли после нескольких ходов на доска появиться число 19?
б) может ли через 100 ходов на доске быть написано число 200?
в) укажите наименьшую разность чисел через 1007 ходов.

Условия КИМов основного ЕГЭ 2016 по математике (тип 3)

13. а) Решите уравнение $displaystyle 2log_{3}^{2}(2cos x)-5log_{3}(2cos x)+2=0.$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ pi ;frac{5pi }{2} right ].$
14. В правильной треугольной призме $displaystyle ABCA_{1}B_{1}C_{1}$ сторона основания равна 6, а боковое ребро $displaystyle AA_{1}$ равно 3. На ребре отмечена точка так, что AK=1 . Точки и — середины ребер $displaystyle A_{1}C_{1}$ и $displaystyle B_{1}C_{1}$ соответственно. Плоскость у параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости displaystyle gamma .
б) Найдите расстояние от точки до плоскости .
15. Решите неравенство $displaystyle frac{25^{x}-5^{x+2}+26}{5^{x}-1}+frac{25^{x}+7cdot 5^{x}+1}{5^{x}-7}leq 2cdot 5^{x}-24.$
16. В треугольнике ABC проведены высоты и . На них из точек и опущены перпендикуляры и соответственно
а) Докажите, что прямые и параллельны.
б) Найдите отношение EH:AC , если угол ABC равен $displaystyle 30^{circ}$ .
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей

Найдите наибольшее значение , при котором общая сумма выплат будет составлять менее 1,2 млн. рублей.
18. Найдите все значения , при каждом из которых уравнение
$displaystyle sqrt{x^{4}-x^{2}+a^{2}}=x^{2}+x-a$
имеет ровно три различных решения.

Подробные решения КИМов ЕГЭ №№13-19(тип 2 и 3)

Условия КИМов основного ЕГЭ 2016 по математике (тип 4)

13. а) Решите уравнение $displaystyle 2cos 2x=4sin left ( frac{pi }{2}+x right )+1.$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ -frac{5pi }{2};-pi right ].$
14. В правильной треугольной пирамиде SABC сторона основания равна 12, а высота равна 1. На ребрах AB,AC и отмечены точки M,N и соответственно, причем AM=AN=3 и $displaystyle AK=frac{7}{4}.$
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки до плоскости SBC .
15. Решите неравенство $displaystyle frac{9^{x+frac{1}{2}}-4cdot 3^{x}+5}{9^{x+frac{1}{2}}-4cdot 3^{x}+1}+frac{5cdot 3^{x}-19}{3^{x}-4}leq frac{2cdot 3^{x+2}-12}{3^{x+1}-1}$ .
16. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17
а) Докажите, что данный четырехугольник — трапеция
б) Найдите отношение оснований этой трапеции
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наименьшее значение , чтобы общая сумма выплат была больше 10 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
$displaystyle frac{x^{3}+x^{2}-9a^{2}x-2x+a}{x^{3}-9a^{2}x}=1$
имеет единственный корень.

Подробные решения КИМов ЕГЭ №№13-19(тип 4)

Источник

Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

Ответ:

На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.

Ответ:

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:

В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Ответ:

Найдите корень уравнения 3^{x − 5} = 81.

Ответ:

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.

Ответ:

На рисунке изображён график дифференцируемой функции y  =  f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y  =  f(x) отрицательна. В ответе укажите количество найденных точек.

Ответ:

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.

Ответ:

Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Ответ:

Найдите точку максимума функции

Ответ:

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 6. Точки M и N— середины рёбер AA₁ и A₁C₁ соответственно.

а)  Докажите, что прямые BM и MN перпендикулярны.

б)  Найдите угол между плоскостями BMN и ABB₁.

Решите неравенство

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй  — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а)  Докажите, что прямые AD и BC параллельны.

б)  Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Найдите все положительные значения a , при каждом из которых система

имеет единственное решение.

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.

а)  Сколько чисел написано на доске?

б)  Каких чисел написано больше: положительных или отрицательных?

в)  Какое наибольшее количество положительных чисел может быть среди них?

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

2015-08-25
2018-08-30

2016

ЕГЭ 2016

Демоверсия ЕГЭ 2016

Демоверсия базового ЕГЭ по математике 2016

Демоверсия профильного ЕГЭ по математике 2016

Тренировочная работа по математике от 3 марта 2016

Профиль. варианты 1–4

Досрочный ЕГЭ от 28 марта 2016 г.

Вариант 1 (разбор заданий здесь)

Тренировочная работа по математике от 27 апреля 2016 г.

Профиль Восток, Запад (разбор заданий здесь на сайте)

База Восток, Запад

Реальный ЕГЭ по математике от 6 июня 2016

Основная волна (вариант 1)

Основная волна (вариант 2)

Разбор отдельных заданий на сайте Критерии

ЕГЭ по математике от 28 июня 2016 г. (резервный день)

Часть С

ОГЭ 2016

Демонстрационный вариант ОГЭ 2016

Демоверсия ОГЭ 2016

ОГЭ от 31 мая 2016

реальный экзамен

Источник

ЗАДАНИЕ № 17. ( С 5 )

Содержание критерия	Баллы.
Обоснованно получен верный ответ.	3
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано.	2
Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение не завершено.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0

Задачи на сложные проценты:

I тип задач: на какой минимальный срок взят кредит.

II тип задач: под какой процент был взят кредит.

III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.

I тип задач: на какой минимальный срок взят кредит.

Максим хочет взять кредит 1,5 млн. рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть последней), после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были бы не более 350 тыс. рублей?

Решение:

1) — остаток после первого погашения.

2) — остаток после второго погашения.

3) — остаток после третьего погашения.

4) — остаток после четвёртого погашения.

5) — остаток после пятого погашения.

6) — шестое погашение.

Ответ: 6 лет.

1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплат кредита следующая: 1 числа каждого следующего месяца банк начисляет 3% на оставшуюся сумму долга (то есть увеличивает долг на 3 %), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?

Решение:

1) остаток после первого погашения.

2) — остаток после второго погашения.

3) — остаток после третьего погашения.

4) — остаток после четвёртого погашения.

5) — остаток после пятого погашения.

6) шестое погашение кредита.

Ответ: 6 месяцев.

Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами ( кроме, может быть последней ) после начисления процентов. Ставка процентов 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?

Решение:

Год	Долг банку	Остаток долга после выплат
0	1 200 000	—
1	1 200 000	1 320 000 — 320 000 = 1 000 000
2	1 000 000	1 000 000 — 320 000 = 780 000
3	780 000	858 000 — 320 000 = 538 000
4	538 000	591 800 — 320 000 = 271 800
5	271 800	0

Ответ: 5 лет

июнь 2015

4. В июле планируется взять кредит в банке на сумму 6 млн. рублей на некоторый срок. Условия его возврата таковы:

— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1,8 млн. рублей?

Решение:

Пусть n срок, на который планируем взять кредит, тогда ежегодная сумма погашения составляет

( без начисления процентов). После первого погашения (т. е. в январе следующего года ) остаток по кредиту составит , после второго года и т. д.

После начисления процентов на момент оформления кредита, долг банку составит , тогда по окончании первого года кредитования остаток увеличивается на 20% т. е. .

Ежегодные выплаты банку находятся как разность между долгом банку и остатком по кредиту на данный момент. Составим таблицу по данным задачи:

Срок	Кредит	Долг	Выплаты
1	6
2
3
4
…	…	…	…

По условию задачи, выплаты составляют арифметическую прогрессию, где и т.д. Наибольший годовой платёж по кредиту не превышает 1,8 млн. рублей или

Ответ: 10.

июнь 2015

5. В июле планируется взять кредит на сумму 20 млн. рублей на некоторый срок ( целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 30 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн. рублей?

Решение:

I способ:

Срок	Кредит	Долг	Выплаты
1	20
2
3
4
….	…	…
Итого:			47

Выплаты составляют арифметическую прогрессию, где

Ответ: 8 лет.

II способ:

Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на r% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами

Ответ: 8 лет.

6. Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?

Решение:

Через n лет 1 сентября на первом счёте будет сумма

т.к. — сумма n — первых членов геометрической прогрессии, где .

В это же время на втором счёте будет сумма

По условию задачи, суммы вкладов сравняются, тогда составляем уравнение:

Таким образом, суммы на счетах сравняются через 11 лет после открытия первого вклада то есть в 2019 году.

Ответ: 2019 году

7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере

5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на . Определите срок хранения вклада.

Решение:

Пусть х рублей был первоначальный вклад (100 %), по истечении срока хранения первоначальная сумма вклада увеличилась на , то есть стала от х или .

По условию задачи,за время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Обозначим целое число месяцев, соответствующей процентной ставки.

Из первого уравнения системы получаем, что . Из последнего уравнения системы получаем , тогда

Ответ: 7 месяцев.

II тип задач: под какой процент был взят кредит.

8. 31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на определенное количество процентов), затем Борис переводит очередной транш. Борис выплатил кредит за два транша, переведя в первый раз 560 тыс. рублей, а во второй 644, 1 тыс. рублей. Под какой процент банк выдал кредит Борису?

Решение:

Пусть банк выдал кредит Борису под х% = 0,01х, тогда после начисления процентов Борис будет должен банку . После перевода первого транша сумма его долга станет После перевода второго транша сумма долга будет равна нулю, тогда составляем уравнение:

— не удовлетворяет условию задачи.

Ответ: 13 %

июнь 2015

9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:

— каждый январь долг возрастает на a% по сравнения с концом предыдущего года; — февраля по июнь каждого года необходимо выплатить часть долга. Найдите число a, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 55 000 рублей, а во второй год 69 000 рублей?

Решение:

Пусть банк выдал кредит под a% = 0,01a, тогда после начисления процентов долг банку будет. После перевода первого транша сумма его долга станет После перевода второго транша сумма долга будет равна нулю, тогда составляем уравнение:

— не удовлетворяет условию задачи.

Ответ: 15 %

июнь 2015

10. В июле планируется взять кредит в банке на сумму 6 млн. рублей на срок 15 лет. Условия его возврата таковы:

— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга за июль предыдущего года. Найти х, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший — не менее 0,5 млн. рублей?

Решение:

Срок	Кредит	Долг	Выплаты
1	6
2
3
…			…
15

По условию задачи: наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший — не менее 0,5 млн. рублей.

Ответ: 25 %

июнь 2015

11. 15 — го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы: — 1 — го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число месяца необходимо выплатить часть долга; — 15 — го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 — е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.

Решение:

Iспособ:

Пусть первоначальная сумма кредита S.

Срок	Кредит	Долг	Выплаты
1	S
2
3
4
….	…	…	….
38
39
40	0	0	0

Сумма всех выплат составит:

Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда

или ( по формулам арифметической прогрессии )

тогда найдем разность прогрессии

Найдём сумму выплат по формуле суммы n — первых членов арифметической прогрессии

Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда

Ответ: 1%

II способ: Пусть — сумма долга в конце n — го месяца, — первоначальная сумма долга.

, где

По условию задачи: сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц, тогда составляет арифметическую прогрессию, где

-формула n— го члена прогрессии.

Суммы выплат составляют арифметическую прогрессию.

Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда

Ответ: 1%

III способ:Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на r% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами

По условию задачи

Ответ: 1 %

аналогичные задания:

— 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

Ответ: 3 %

— Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

Ответ: 2 %.

— Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27 % больше, чем сумма, взятая им в кредит. Найдите r.

Ответ: 3 %.

12. 15 — го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг ( в % от кредита)	100 %	90 %	80 %	70 %	60 %	50 %	40 %

В конце каждого месяца, начиная с января, текущий долг увеличивается на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

Решение:

Пусть 15 — го числа текущего месяца долг равен х рублей, а 15 го числа предыдущего месяца у рублей. Тогда в конце предыдущего месяца долг равен и выплата в первой половине текущего месяца равна. В процентах отсуммы кредита выплаты в феврале составили ; в марте в июне

Общая сумма выплат составила 15 + 14,5 + 14 + 13,5 + 13 + 52,5 = 122,5 %.

Ответ: 22,5 %

III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.

июнь 2015

13. В июле планируется взять кредит в банке на сумму 10 млн. рублей на 5 лет. Условия его возврата таковы:

— каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Сколько млн. рублей составила общая сумма выплат после погашения кредита?

Решение:

год	кредит	долг	Выплаты
1	10
2	8
3	6
4	4
5	2

Найдем сумму всех выплат:.

Ответ: 13 млн. рублей.

июнь 2015

14. В июле планируется взять кредит на некоторую сумму. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за 3 года)?

Решение:

Пусть х рублей планируется взять в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 2, 16 млн. рублей после начисления 20 % на оставшуюся сумму долга.

Ответ: 4,55 млн. рублей

15. 31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12 % годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12 %), затем Сергей переводит в банк 3 512 320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами ( то есть за три года)?

Решение:

Пусть х рублей взял Сергей в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 3 512 320 рублей после начисления 12% на оставшуюся сумму долга.

Ответ: 8 436 000.

16. Жанна взяла в банке кредит 1,8 млн. рублей на срок 24 месяца. По договору Жанна должна возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

Решение:

I способ:

Срок	Кредит	Долг	Выплаты
1	1,8
2
3
4
….	…	…

Выплаты составляют арифметическую прогрессию, где

Ответ: 1,0665 млн. рублей.

IIспособ : Пусть — сумма долга в конце n — го месяца, — первоначальная сумма долга.

, где По условию задачи, надо найти сумму выплат Жанны за первый год кредитования, то есть .

— формула n— го члена прогрессии.

Суммы выплат составляют арифметическую прогрессию.

Ответ: 1 066 500.

июнь 2015

17. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого следующего года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами ( то есть за 4 года)?

Решение:

Пусть х рублей выплата по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по хруб. после начисления 20 % на оставшийся долг.

Ответ: 3 110 400

18. 31 декабря 2014 года Алексей взял в банке 9 282 000 рублей под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( за четыре года)?

Решение:

Пусть Х рублей выплата Алексея по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по х руб. после начисления 10 % на оставшийся долг.

Ответ: 2 928 200.

19. Фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых. Схема погашения кредита: раз в год клиент выплачивает банку одну и ту же сумму, которая состоит из двух частей. Первая часть составляет 20 % от оставшейся суммы долга, а вторая часть направлена на погашение оставшейся суммы долга. Каждый следующий год проценты начисляются только на оставшуюся часть долга. Какой должна быть ежегодная сумма выплат ( в рублях ), чтобы фермер полностью погасил кредит тремя равными платежами?

Решение:

Пусть х рублей должна быть ежегодная сумма выплат. Составим уравнение по условию задачи:фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых и погасил кредит тремя равными платежами.

Ответ: 1 728 000.

июнь 2015

20. В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом прошлого года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года ) по сравнению со случаем, если он будет полностью погашен двумя равными платежами ( то есть за 2 года )?

Решение:

I случай. Пусть по х рублей выплачивают , чтобы погасить кредит четырьмя равными платежами. Составим первое уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили четырьмя равными платежами.

II случай. Пусть по yрублей выплачивают, что бы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили двумя равными платежами.

Вопрос задачи: на сколько рублей больше отдали бы банку, если бы выплатили долг за четыре равных платежа или найти разность

Ответ: 950 400.

21. 31 декабря 2014 года Фёдор взял в банке 6 951 000 рублей в кредит под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляют проценты на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Фёдор переводит в банк платёж. Весь долг Фёдор выплатил за три равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа?

Решение:

I случай. Пусть по х рублей выплачивал Фёдор, что бы погасить кредит тремя платежами. Составим первое уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил тремя равными платежами.

II случай. Пусть по yрублей выплачивал Фёдор, чтобы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил двумя равными платежами.

Вопрос задачи: на сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа или найти разность

Ответ: 375 100.

Задачи на нахождение наибольшего или наименьшего значения.

досрочный 2015

1. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 2t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы ( на каждом из заводов ) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?

Решение:

Пусть количество единиц товара, произведённого на первом заводе 2х, а на втором заводе 5у. (Тогда за неделю нужно произвести 580 единиц товара или За каждый час работы Владимир платит рабочему 500 рублей, тогда составим функцию и исследуем её на наименьшее значение.

Выразим из первого уравнения у через х:

— точка минимума.

Ответ: 5 800 000.

досрочный 2015

2. Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, платит 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение:

Пусть количество единиц товара, произведённого на первом заводе х и суммарные затраты времени будут .Тогда количество единиц товара, произведённого на втором заводе y и суммарные затраты времени будут . Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, платит 200 рублей и готов выделять 900 000 рублей в неделю на оплату труда рабочих, тогда получаем уравнение.

Составим функцию количества единиц товара за неделю на двух заводах: .

Выразим из первого уравнения у через х: (

— точка максимума.

Ответ: 90.

досрочный 2015

3. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 3t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы ( на каждом из заводов ) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение:

Пусть количество единиц товара, произведённого на первом заводе 3х и суммарные затраты времени будут . Тогда количество единиц товара, произведённого на втором заводе 4y и суммарные затраты времени будут . Григорий платит рабочему 500 рублей и готов выделять 5 000 000 рублей в неделю на оплату труда рабочих, тогда получаем уравнение . или

Составим функцию количества единиц товара за неделю на двух заводах: .

Выразим из первого уравнения у через х: (

— точка максимума.

Ответ: 400.

4. Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме гб. входящей в него информации выходит 20t , с сервера № 2 при объёме гб. входящей в него информации выходит 21tгб обработанной информации; Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 гб?

Решение:

Пусть на севере № 1 обрабатывается , а на сервере № 2 обрабатывается гб. из всей первичной информации. Тогда общий объём входящей информации 3364 гб., тогда . Всего обработано будет гб. информации. Исследуем эту функцию на наибольшее значение.

— точка максимума.

Ответ: 1 682.

июнь 2015

5. Зависимость объёма Q ( в шт.) купленного у фирмы товара по цене Р ( в рублях за штуку) выражается формулой Доход от продажи товара составляет рублей. Затраты на производство Qединиц товара составляют рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену на продукцию на 20 %, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Решение:

Цена товара.	P
Объём товара.	Q
Доход от продажи
Затраты на производство.
Прибыль.

Рассмотрим функцию: прибыль в зависимости от цены товара.

— это квадратичная функция, графиком, которой является парабола, принимающая наибольшее значение в вершине. Ось симметрии параболы: прямая, параллельная оси ординат и проходящая через вершину параболы. Вершина параболы соответствует 90% цены, так как прибыль не изменилась, когда цену уменьшили на 20 %, тогда составляем пропорцию:

Ответ: 12,5 %

6. В первые классы поступают 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом — 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

Решение:

Пусть в меньший класс ( 21 человек) распределено х мальчиков ( . Тогда в больший класс попало ( 23 — х ) мальчиков.

Суммарная доля мальчиков в двух классах

— линейная функция с положительным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на правом конце промежутка [ 1; 21 ] , то есть при х = 21. Таким образом, меньший класс полностью должен состоять из мальчиков, а в большем классе должно быть 20 девочек и 2 мальчика.

Ответ: В одном классе — 21 мальчик, в другом — 20 девочек и 2 мальчика.

7. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера » люкс » площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер » люкс » — 4 000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Решение:

Номера

Площадь

номера

Количество номеров

Общая площадь

Стоимость

в сутки

Доход номера

Обычный

27x

2 000

2000x

Люкс

45y

4 000

4000y

Составим уравнения по условию задачи: Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр.

Найдём общую прибыль номеров в сутки: Выразим из первого уравнения y: ( 1

линейная функция с отрицательным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на левом конце промежутка ( при минимальном количестве обычных номеров ), то есть при х = 3, тогда y = 20. (

Ответ: 86 000 рублей.

аналогичная задача:

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера » люкс » площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 855 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер » люкс » — 3 000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Ответ: 63 000 рублей.

8. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Сколько сплава при таких условиях сможет произвести завод?

Решение:

Пусть за х часов на I шахте добывают алюминий, а за у часов на II шахте добывают алюминий.

	Количество рабочих	Суммарное время работы	Добыча алюминия	Добыча никеля
I шахта	100	500	х
II шахта	300	1500
Итого:				=

Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. Тогда составляем уравнение:

При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Рассмотрим функцию сплава:

Функция является убывающей, тогда наибольшее значение она достигает при наименьшем значении х,

при х = 0 S = 5 400.

Ответ: 5 400.

9. На каждом из двух комбинатов изготавливают детали А и В. На первом комбинате работает 40 человек, и один рабочий изготавливает за смену 5 деталей А или 15 деталей В. На втором комбинате работает 100 человек, и один рабочий изготавливает за смену 15 деталей А или 5 деталей В. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 2 детали А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать деталь так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?

Решение:

	Количество рабочих	Деталь	Количество деталей за смену ( 1 рабочий )	Количество рабочих	Количество всех деталей за смену
I комбинат	40	А	5	х	5х
В	15	40 — х	15(40 — х)
II комбинат	100	А	15	у	15у
В	5	100 — у	5( 100 — у)
Итого:		А			5х + 15у
В			15(40 — х ) + 5(100 — у ) = 1 100 — 15х — 5у

Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 2 детали А и 1 деталь В.

Рассмотрим функцию количества изделий из этих деталей:

Линейная функция с отрицательным угловым коэффициентом, будет достигать наибольшего значения при минимальном х .

Ответ: 1980

10. У фермера есть два поля, каждое площадью по 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц /га, а на втором 200 ц / га. Урожайность свёклы на первом поле составляет 200 ц / га, на втором 300 ц / га. Ферме может продавать картофель по цене 4 000 рублей за центнер, а свёклу по цене 5 000 рублей за центнер. Какой наибольший доход может получить фермер?

Решение:

		Урожайность	Площадь	Цена
I поле	картофель	300	x	4 000
свёкла	200	10- x	5 000
II поле	картофель	200	y	4 000
свёкла	300	10 — y	5 000

Составим функцию по условию задачи:

Наибольшего значение будет достигаться при у = 0, х = 10.

S =

Ответ: 27 000 000 рублей.

1 1. Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. Втечение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение:

Первоначальная стоимость ценной бумаги 7 тыс. рублей, цена бумаги возрастает каждый год на 2 тыс. рублей. Тогда рассматриваем арифметическую прогрессию, где

Нам надо найти номер максимального члена последовательности , где n — целое число,

;

Ответ: в течение восьмого года.

аналогичная задача:

Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8 %. Втечение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Ответ: в течение шестого года.

июнь 2015

1 2. Строительство нового завода стоит 78 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы ( в млн. рублей) за один год составит . Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более , чем за 3 года ?

Решение:

По условию задачи строительство завода должно окупиться не более, чем за три года. Так как годовая прибыль вычисляется по формуле тогда ;

Выразим p через х: . Исследуем эту функцию на наименьшее значение.

— точка минимума

Ответ: 10.

13. Производство х тыс. единиц продукции обходится в млн. рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции ( в млн. рублей ) составляет При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн. рублей?

Решение:

По условию задачи через три года суммарная прибыль должна быть не менее 75 млн. рублей. Так как годовая прибыль вычисляется по формуле тогда ;

Выразим p через х: . Исследуем эту функцию на наименьшее значение.

— точка минимума

Ответ: 9.

аналогичная задача:

— Производство х тыс. единиц продукции обходится в млн. рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции ( в млн. рублей ) составляет При каком наименьшем значении p через четыре года суммарная прибыль составит не менее 52 млн. рублей?

Ответ: 6

Раздаточный материал:

ЗАДАНИЕ № 17.

Содержание критерия	Баллы.
Обоснованно получен верный ответ.	3
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано.	2
Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение не завершено.	1
Решение не соответствует ни одному из критериев, перечисленных выше.	0

I тип задач: на какой минимальный срок взят кредит.

1. Максим хочет взять кредит 1,5 млн. рублей. Погашение кредита происходит раз в год равными суммами ( кроме, может быть последней), после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были бы не более 350 тыс. рублей?

2. 1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплат кредита следующая: 1 числа каждого следующего месяца банк начисляет 3% на оставшуюся сумму долга ( то есть увеличивает долг на 3 %), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит.чтобы ежемесячные выплаты были не более 220 тыс. рублей?

3. Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами ( кроме , может быть последней ) после начисления процентов. Ставка процентов 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?

4. В июле планируется взять кредит в банке на сумму 6 млн. рублей на некоторый срок. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1,8 млн. рублей?

5. В июле планируется взять кредит на сумму 20 млн. рублей на некоторый срок ( целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 30 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн. рублей?

7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на . Определите срок хранения вклада.

II тип задач: под какой процент был взят кредит.

9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата такова:

— каждый январь долг возрастает на a% по сравнения с концом предыдущего года;

— февраля по июнь каждого года необходимо выплатить часть долга. Найдите число a, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 55 000 рублей, а во второй год 69 000 рублей?

10. В июле планируется взять кредит в банке на сумму 6 млн. рублей на срок 15 лет. Условия его возврата таковы: — каждый январь долг возрастает на x% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга за июль предыдущего года. Найти х, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей.а наименьший — не менее 0,5 млн. рублей?

11. 15 — го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:

— 1 — го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число месяца необходимо выплатить часть долга;

— 15 — го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 — е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг ( в % от кредита)	100 %	90 %	80 %	70 %	60 %	50 %	40 %

III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.

13. В июле планируется взять кредит в банке на сумму 10 млн. рублей на 5 лет. Условия его возврата таковы: — каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Сколько млн. рублей составила общая сумма выплат после погашения кредита?

14. В июле планируется взять кредит на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за 3 года)?

17. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого следующего года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами ( то есть за 4 года)?

20. В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 20 % по сравнению с концом прошлого года;

— с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами ( то есть за 4 года ) по сравнению со случаем, если он будет полностью погашен двумя равными платежами ( то есть за 2 года )?

Задачи на нахождение наибольшего или наименьшего значения.

4. Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме гб. входящей в него информации выходит 20t , с сервера № 2 при объёме гб. входящей в него информации выходит 21tгб. обработанной информации; Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 гб.?

5. Зависимость объёма Q ( в шт.) купленного у фирмы товара по цене Р ( в рублях за штуку) выражается формулой Доход от продажи товара составляет рублей. Затраты на производство Q единиц товара составляют рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство.стремясь привлечь внимание покупателей, фирма уменьшила цену на продукцию на 20 %, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

8. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. В второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Сколько сплава при таких условиях сможет произвести завод?

11. Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

12. Строительство нового завода стоит 78 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы ( в млн. рублей) за один год составит . Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более , чем за 3 года ?

июнь 2015

Решение:

I способ:

Пусть первоначальная сумма кредита S.

Срок	Кредит	Долг	Выплаты
1	S
2
3
4
….	…	…	….
38
39
40	0	0	0

Сумма всех выплат составит:

Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда

Ответ: 1%

Источник

Попробуйте свои силы в решении типовых заданий прошлых лет.

Примеры решения заданий 2013 года >>
Примеры решения заданий 2014 года >>
Примеры решения заданий 2015 года >>

Ознакомившись с решением заданий, попробуйте свои силы в тесте ЕГЭ онлайн или скачайте демонстрационные варианты ЕГЭ.

Навигация:

Математика

Задание 2.

Задание:

Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?

Решение:

100% это 20 000 рублей.

Считаем, сколько рублей составляет один процент:
20 000 : 100 = 200

Вычисляем сумму налога:

200 * 13 = 2600

Вычитаем налог из зарплаты:

20 000 – 2600 = 17 400 (рублей)

Ответ: 17 400.

Источник: Демонстрационный вариант ЕГЭ по математике 2016, базовый уровень.

Задание 4

Задание:

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

Решение:

Из 25 билетов 23 не содержат вопроса о грибах, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о грибах, равна

2 / 25 = 2*4 / 25*4 = 8 / 100 = 0,08

Ответ: 0,08.

Источник: Демонстрационный вариант ЕГЭ по математике 2016, профильный уровень.
Русский язык

Задание 9

Задание:

Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите эти слова, вставив пропущенную букву.

бе..цельный, ра..кол

не..глядный, з..ходил

пр..обрёл, пр..белый

раз..скать, на..скось

пре..стать, о..бойный

Решение:

Приведём верное написание:

бесцельный, раскол

неоглядный, заходил

приобрёл, пребелый

разыскать, наискось

предстать, отбойный.

Ответ: бесцельный, раскол.

Источник: Демонстрационный вариант ЕГЭ по русскому языку 2016.

Задание 12

Задание:

Определите предложение, в котором НЕ со словом пишется СЛИТНО. Раскройте скобки и выпишите это слово.

Живопись И.К. Айвазовского получила признание зрителей (НЕ)ОБЫКНОВЕННО рано: уже в юности за этюд «Воздух над морем» художнику была присуждена серебряная медаль.

Автор проекта понимал: реконструируя старую часть города, ему придётся принять отнюдь (НЕ)ПРОСТОЕ решение.

Поэзия А.А. Ахматовой возвращает вещам первозданный смысл и останавливает внимание на том, что мы в обычном состоянии (НЕ)ОЦЕНИВАЕМ.

(НЕ)ПРЕКРАЩАВШИЙСЯ всю ночь сильный восточный ветер поднял большие волны.

С тёмного неба, из лохматых туч, в смятении давящих друг друга, (НЕ)ПЕРЕСТАВАЯ, раздаются раскаты грома.

Решение:

Приведём верное написание.

Живопись И. К. Айвазовского получила признание зрителей НЕОБЫКНОВЕННО (можно заменить синонимом «очень») рано: уже в юности за этюд «Воздух над морем» художнику была присуждена серебряная медаль.

Автор проекта понимал: реконструируя старую часть города, ему придётся принять отнюдь НЕ ПРОСТОЕ (есть зависимое слово ОТНЮДЬ) решение.

Поэзия А. А. Ахматовой возвращает вещам первозданный смысл и останавливает внимание на том, что мы в обычном состоянии НЕ ОЦЕНИВАЕМ (НЕ с глаголом).

НЕ ПРЕКРАЩАВШИЙСЯ (в составе причастного оборота, поэтому раздельно) всю ночь сильный восточный ветер поднял большие волны.

С тёмного неба, из лохматых туч, в смятении давящих друг друга, НЕ ПЕРЕСТАВАЯ (НЕ с деепричастием), раздаются раскаты грома.

Ответ: необыкновенно.

Источник: Демонстрационный вариант ЕГЭ по русскому языку 2016.
История

Задание 3

Задание:

Ниже приведён список терминов. Все они, за исключением одного, относятся к событиям (явлениям) XIX в.

1) вольные хлебопашцы;

2) министерства;

3) декабристы;

4) третьеиюньский переворот;

5) мировые судьи;

6) военные поселения.

Найдите и запишите порядковый номер термина, относящегося к другому историческому периоду.

Решение:

Третьеиюньский переворот относится к XX веку.

Ответ: 4.

Источник: Демонстрационный вариант ЕГЭ по истории 2016.

Задание 14

Задание:

Напишите название города, обозначенного на схеме цифрой «1».

Решение:

Цифрой «1» на карте обозначена столица Владимиро-Суздальского княжества г. Владимир.

Ответ: Владимир.

Источник: Демонстрационный вариант ЕГЭ по истории 2016.
Биология

Задание 8

Задание:

Сохранение признаков у гетерозисных гибридов растений возможно только при:

1) половом размножении;

2) вегетативном размножении;

3) отдалённой гибридизации;

4) использовании метода полиплоидии.

Решение:

Сохранение признаков у гетерозисных гибридов растений возможно только при вегетативном размножении.

Ответ: 2.

Источник: Демонстрационный вариант ЕГЭ по биологии 2016.

Задание 19

Задание:

Результатом внутривидовой борьбы в природе как движущей силы эволюции является:

1) ослабление конкуренции между видами;

2) появление мутаций у особей;

3) естественный отбор;

4) приспособленность организмов.

Решение:

Естественный отбор – основной движущий фактор эволюции, приводящий к выживанию и преимущественному размножению более приспособленных к данным условиям среды особей, обладающих полезными наследственными признаками.

Ответ: 3.

Источник: Демонстрационный вариант ЕГЭ по биологии 2016.
Информатика

Задание 6

Задание:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 125. В ответе это число запишите в десятичной системе счисления.

Решение:

Проверяем первое число, которое больше 125, – 126.

Переводим это число в двоичную систему счисления 126=1111110.

Убираем два последних разряда (10), которые получились в результате выполнения алгоритма.

Получаем 11111.

Теперь проверяем работу алгоритма:

Остаток от деления на 2 суммы 1+1+1+1+1=5 равен 1,

Остаток от деления на 2 суммы 1+1+1+1+1+1=6 равен 0.

Алгоритм выполняется, переводим число обратно в десятичную систему счисления:

N=11111=31

Ответ: 31.

Источник: Демонстрационный вариант ЕГЭ по информатике 2016.

Задание 13

Задание:

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, K, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт; это число одно и то же для всех пользователей.

Для хранения сведений о 20 пользователях потребовалось 400 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число – количество байт.

Решение:

Для хранения одного 12-символьного набора понадобится 4 бита, 2⁴ = 16, а если взять 2³ = 8, то будет мало.

Пароль состоит из 15 символов, следовательно, для хранения всего пароля понадобится 4*15 = 60 бит.

Из «В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит.» следует:

60 : 8 = 7,5 байт, но поскольку байт не может быть дробным, для хранения всей информации без потерь придется взять 8 байт.

Соответственно, для хранения 20 паролей потребуется 20*8 = 160 байт

Количество байт для хранения дополнительной информации на всех 20 пользователей компьютерной системы понадобится 400 – 160 = 240 байт. Откуда находим количество байт, приходящиеся на одного пользователя: 240 : 20 =12

Ответ: 12.

Источник: Демонстрационный вариант ЕГЭ по информатике 2016.

Источник