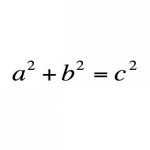Задания Д4 № 27544
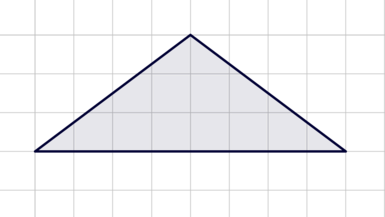
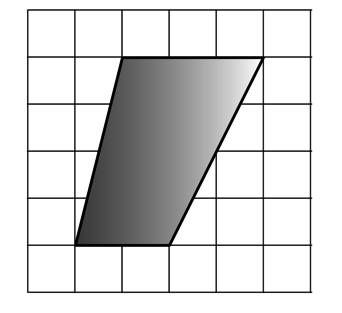
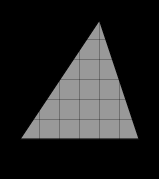
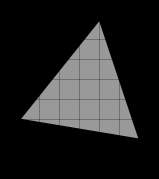
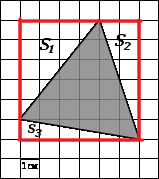
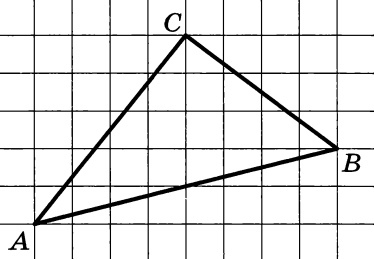
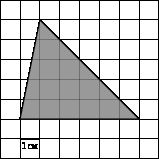
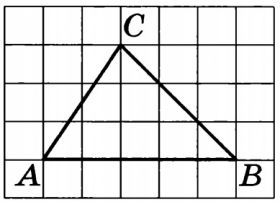
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 27544: 5093 5095 5165 509986 526205 5097 5099 5101 5103 5105 … Все
Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на клетчатой бумаге
(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.
(blacktriangleright) В равных прямоугольниках равны диагонали.
(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
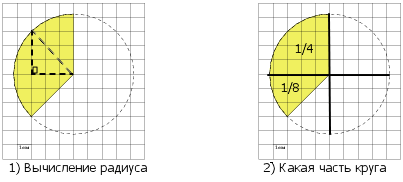
(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).
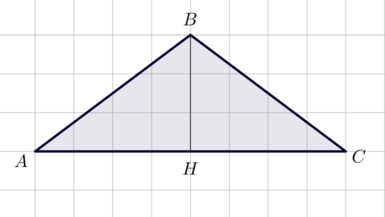
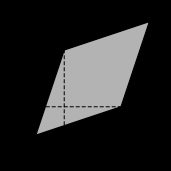
(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).
Задание
1
#3089
Уровень задания: Равен ЕГЭ
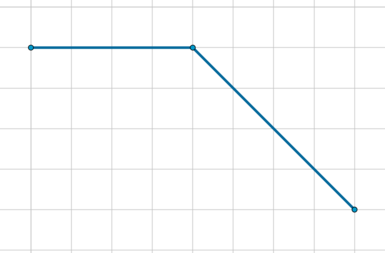
На клетчатой бумаге изображен угол. Найдите его градусную величину.
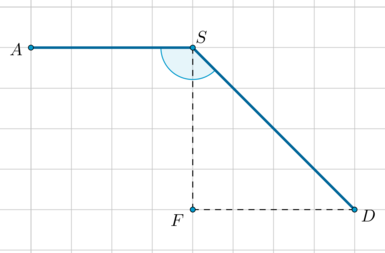
Обозначим этот угол (ASD). Отметим точку (F) так, чтобы получился прямоугольный (triangle SDF):
Тогда (angle ASD=angle ASF+angle FSD). Заметим, что (angle
ASF=90^circ). Заметим также, что (FS=FD), следовательно, (triangle
SDF) прямоугольный и равнобедренный, значит, его острые углы равны по (45^circ).
Следовательно, [angle ASD=90^circ+45^circ=135^circ.]
Ответ: 135
Задание
2
#3088
Уровень задания: Равен ЕГЭ
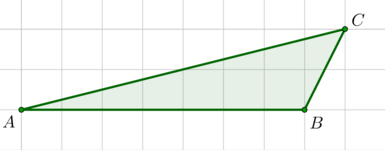
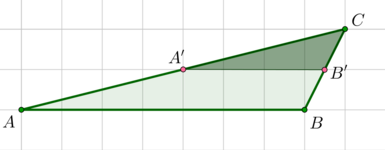
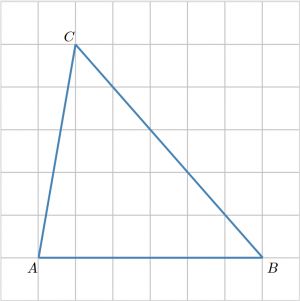
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите площадь треугольника (A’B’C), где (A’B’) – средняя линия, параллельная стороне (AB).
Пусть (A’in AC, B’in BC).
По свойству средней линии (triangle ABCsim triangle A’B’C) с коэффициентом подобия, равным (2). Следовательно, их площади относятся как коэффициент подобия в квадрате, то есть [dfrac{S_{ABC}}{S_{A’B’C}}=4] Высота (triangle ABC), опущенная из (C), равна (2), (AB=7). Следовательно, (S_{ABC}=frac12cdot 2cdot 7=7). Тогда [S_{A’B’C}=dfrac74=1,75.]
Ответ: 1,75
Задание
3
#3087
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите длину средней линии, параллельной стороне (AB).
Длина средней линии треугольника, параллельной стороне (AB), равна (frac12AB). Так как (AB=7), то средняя линия равна (3,5).
Ответ: 3,5
Задание
4
#3086
Уровень задания: Равен ЕГЭ
На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна (3).
Будем искать радиус вписанной окружности по формуле (S=pcdot r), где (S) – площадь, (p) – полупериметр.
Заметим, что треугольник равнобедренный: (AB=BC.)
Так как длина стороны клетки равна (3), то (AH=12, BH=9), следовательно, (AB=sqrt{AH^2+BH^2}=15.) Тогда [dfrac12cdot BHcdot AC=dfrac{AB+BC+AC}2cdot r quadRightarrowquad
r=4.]
Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна (1), а затем умножать полученный ответ на (3). Если бы длина одной клетки была равна (1), то (AH=4, BH=3), (AB=5) и (r=frac43). Тогда после умножения на (3) также получили бы (r=4). При решении задачи таким способом вычисления будут легче.
Ответ: 4
Задание
5
#297
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных миллиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть (0,5cdot (3 text{мм} + 4 text{мм})cdot 3 text{мм} = 10,5)мм(^2).
Ответ: 10,5
Задание
6
#298
Уровень задания: Равен ЕГЭ
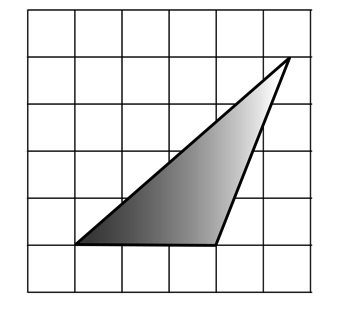
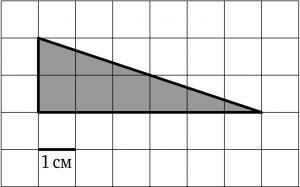
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован треугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, тогда площадь нарисованного треугольника есть (0,5cdot 3)мм (cdot 4)мм (= 6)мм(^2).
Ответ: 6
Задание
7
#299
Уровень задания: Равен ЕГЭ
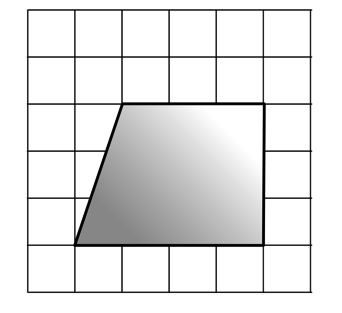
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.
У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна (0,5(2 text{мм} + 3 text{мм})cdot 4 text{мм} = 10) мм(^2).
Ответ: 10
Если выпускник готовится к сдаче ЕГЭ по математике и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит освоить принцип решения задач на клетчатой бумаге. Подобные планиметрические задания каждый год включаются в программу аттестационного испытания. Таким образом, справляться с задачами ЕГЭ на клетчатой бумаге должны все учащиеся, независимо от уровня их подготовки.
Полезная информация
Задания ЕГЭ на клетчатой бумаге часто решаются гораздо проще, чем задачи, для выполнения которых требуется применение аналитических методов. Чаще всего в подобных упражнениях необходимо найти площадь фигуры. Решить такие задачи можно, вспомнив основные теоремы и свойства трапеции, треугольника, шестиугольника и т. д.
Как подготовиться к экзамену?
Если задания ЕГЭ на клетчатой бумаге вызывают у вас трудности, обратитесь к образовательному порталу «Школково». С нами вы сможете повторить материал по темам, которые являются для вас сложными, например, векторы на координатной плоскости и таким образом восполнить пробелы в знаниях. В разделе «Теоретическая справка» представлена вся базовая информация. Ее наши специалисты подготовили и изложили в максимально доступной форме на основе богатого практического опыта.
Освоить принцип решения задач на клетчатой бумаге помогут упражнения, представленные в разделе «Каталог». Мы подготовили простые и более сложные задания. Тренироваться в их выполнении учащиеся из Москвы и других российских городов могут в онлайн-режиме.
Справившись с заданием, выпускники имеют возможность сохранить его в разделе «Избранное». Это позволит в дальнейшем вернуться к нему и, к примеру, обсудить алгоритм его решения со школьным преподавателем. База заданий на сайте «Школково» регулярно обновляется.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
№
1
На клетчатой бумаге с размером клетки 1×1
изображён угол. Найдите синус этого угла.
Ответ
5E362
2
На клетчатой бумаге с размером клетки 1×1
изображён угол. Найдите синус этого угла.
Ответ
576866
3
На клетчатой бумаге с размером клетки 1×1
изображён угол. Найдите косинус этого угла.
Ответ
582E12
4
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
Ответ
C1774A
5
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Ответ
6BB94E
6
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Ответ
C02FFF
7
Найдите площадь треугольника, изображённого
на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в
квадратных сантиметрах.
Ответ
85ECE4
8
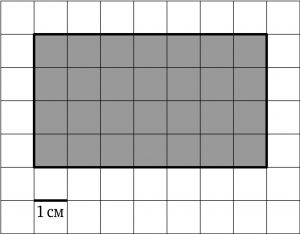
Найдите площадь квадрата, изображённого на клетчатой
бумаге с размером клетки 1 см × 1 см (см. рис.).
Ответ дайте в квадратных сантиметрах.
Ответ
556969
9
Найдите площадь треугольника, изображённого на
клетчатой бумаге с размером клетки 1 см × 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ
B67064
10
На клетчатой бумаге с размером клетки 1×1 изображён
угол. Найдите его градусную величину.
Ответ
e881D0
11
На клетчатой бумаге с размером клетки 1×1 изображена
трапеция. Найдите её площадь.
Ответ
e886DB
12
На клетчатой бумаге с размером клетки 1×1 изображена
трапеция. Найдите её площадь.
Ответ
e77491
13
На клетчатой бумаге с размером
клетки 1×1 изображён ромб. Найдите его площадь.
Ответ
0A79ec
14
Найдите площадь трапеции, изображённой
на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в
квадратных сантиметрах.
Ответ
43074B
15
Найдите площадь трапеции,
изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.).
Ответ дайте в квадратных сантиметрах.
Ответ
D41C6A
16
Найдите площадь квадрата,
изображённого на клетчатой бумаге с размером клетки
1 см × 1 см (см. рис.). Ответ дайте в квадратных
сантиметрах.
Ответ
888531
17
На клетчатой бумаге с размером
клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB.
Ответ
eD86cB
18
На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC. Найдите длину его средней линии, параллельной
стороне AB.

Ответ
34F604
19
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AB.
Ответ
c177cB
20
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на
сторону AB.
Ответ
347c22
21
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AB.
Ответ
2A58B6
22
На клетчатой бумаге с размером
клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите радиус
описанной около него окружности.
Ответ
4B38Be
23
На клетчатой бумаге с размером
клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите радиус
описанной около него окружности.
Ответ
4ec57F
24
На клетчатой бумаге с размером
клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину
его биссектрисы, выходящей из вершины прямого угла.
Ответ
c02c14
25
На клетчатой бумаге с размером
клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину
его медианы, проведённой к гипотенузе.
Ответ
04ccA9
26
На клетчатой бумаге с размером
клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
Ответ
5D95e4
27
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на
сторону AB.
Ответ
4BFD6D
28
На клетчатой бумаге с размером
клетки 1×1 изображён равносторонний треугольник. Найдите радиус описанной
около него окружности.
Ответ
cA4670
29
На клетчатой бумаге нарисован
круг площадью 1,2. Найдите площадь закрашенного сектора.
Ответ
6C9A76
30
На клетчатой бумаге нарисованы
два круга. Площадь внутреннего круга равна 37. Найдите площадь закрашенной
фигуры.
Ответ
308612
31
На клетчатой бумаге нарисован
круг площадью 2. Найдите площадь закрашенного сектора.
Ответ
C1E658
32
На клетчатой бумаге нарисованы
два круга. Площадь внутреннего круга равна 34. Найдите площадь закрашенной
фигуры.
Ответ
3AFAE3
33
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник. Найдите радиус описанной около него
окружности.
Ответ
005624
Площадь круга, изображённого
на клетчатой бумаге, равна 16. Найдите площадь заштрихованного кругового
сектора.
Ответ
4EF275
На клетчатой бумаге с размером
клетки 1×1 изображён квадрат. Найдите радиус вписанной в него окружности.
Ответ
67C410
Егэ математика площадь по клеточкам
Егэ математика площадь по клеточкам
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 5 № 522802
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
Обозначим квадраты буквами так, как показано на рисунке. Перенесём мысленно часть озера, находящуюся в квадрате D, в квадрат А. Сумма этих площадей меньше половины площади квадрата. Площадь части озера в квадрате С примерно половина площади квадрата, другая половина пустая — перенесем в неё части озера из А и D вместе взятые. Этим квадрат С будет заполнен. Теперь перенесём часть озера, лежащую ниже диагонали квадрата Е, на незанятую часть в квадрате F. Теперь квадрат F заполнен почти полностью, а квадрат Е заполнен наполовину. Итак, озеро покрывает приблизительно два полных квадрата С и F, почти полный квадрат В и половину квадрата Е. Значит, площадь озера больше 3 кв. км, но меньше 3,5 кв. км. Округляя, получаем 3 кв. км.
Примечание редакции Решу ЕГЭ.
Понимая необходимость умений проводить подобные оценки и прикидки в прикладных науках, все же отметим, что приведённые выше рассуждения не имеют никакого отношения к математике. Почему? Потому, что нет доказательств. Например, того, часть из Е действительно поместится в F. Доказательство можно было бы провести так: наложить карту на миллиметровку, найти количество квадратиков, в которые попала фигура, и точно установить границы, в которых лежит площадь: отбросив частично заполненные квадратики, получим площадь с недостатком, учитывая все частично заполненные квадратики, найдем площадь с избытком. Но это путь не для экзамена.
Примечание Д. Д. Гущина о применении палетки для определения площади.
Читательница Ольга Кулешова рассказала нам, что в начальных классах изучают способ нахождения площади фигуры с помощью палетки (квадратной сетки). Площадь фигуры считается равной количеству полностью заполненных клеток сетки плюс половина количества не полностью заполненных клеток. Решая данную задачу таким способом, найдем, что количество полностью заполненных клеток равно 0, количество частично заполненных клеток равно 6, следовательно, площадь фигуры равна 0 + 6 : 2 = 3.
Об этом необходимо сказать следующее.
Для фигур случайной формы, покрытых большим количеством клеток, указанное приближение площади нередко дает удовлетворительную точность. Однако в ряде случаев погрешность становится неприемлемой.
Найдем, к примеру, указанным методом площадь изображенных на рисунке круга и пятиугольника. Для круга сложим 5 целых клеток и половину от 16 частично заполненных, вместе 13 клеток. Как нетрудно проверить, используя формулу для площади круга найденная по клеточкам площадь круга мало отличается от расчетной. Но найдем теперь площадь пятиугольника: к 6 целым клеткам прибавим половину от 9, получим 10,5 или, округленно, 11 клеток. Однако в действительности площадь пятиугольника не 11 и даже не 10, а меньше 9 клеток. Ошибка превосходит 17%, а после округления — даже 22%.
По всей вероятности, точной формулы для оценки погрешности использования квадратной палетки при оценке площади не существует. Но ясно, что погрешность может быть достаточно велика, если все частично заполненные клетки заполнены более (либо менее), чем наполовину, или если покрывающих фигуру клеток слишком мало.
В приведенном выше задании ЕГЭ площадь покрыта всего шестью клетками. В таких случаях найденный ответ может получиться верным, но может оказаться и ошибочным. Поэтому на экзамене пользоваться указанным методом нельзя.
Подробнее прочитать о приближенном определении площадей можно, например, в учебном пособии для высших учебных заведений Инженерная геодезия. pdf.
—>
Задание 5 № 522802
Об этом необходимо сказать следующее.
Mathb-ege. sdamgia. ru
11.05.2018 23:58:03
2018-05-11 23:58:03
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=522802
Площадь сектора по клеточкам » /> » /> .keyword { color: red; } Егэ математика площадь по клеточкам
Площадь сектора по клеточкам
Площадь сектора по клеточкам
В этой статье мы разберем, как находить площадь сектора, нарисованного на бумаге в клеточку. Это задание В5 для подготовки к ЕГЭ по математике.
1. Найдите (в см 2 ) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите » />.
Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 4.
Тогда площадь круга равна r^2=4^2=16″ />


Ответ: 8
2. Найдите (в см 2 ) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите » />.
Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 3.
Тогда площадь круга равна r^2=3^2=9″ />
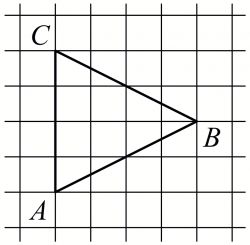
Найдем, какую часть заштрихованная фигура составляет от круга.
Мы видим, что заштрихованная фигура — это половина круга и еще одна четверть от половины, то есть одна восьмая.
Таким образом, площадь заштрихованной фигуры составляет от площади круга.
*9=5,625″ />

Ответ: 5,625
3. Найдите (в см 2 ) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите » />.
Сначала найдем радиус круга. Считаем клеточки, и получаем, что радиус равен 4.
Тогда площадь круга равна r^2=4^2=16″ />
Найдем, какую часть круга составляет незакрашенный сектор. Если мы незакрашенный центральный угол повернем на угол, то увидим, что его величина равна » />:
Сектор » /> — это часть круга. Следовательно, закрашенный сектор — это круга. И его площадь равна *16=12″ />

Тогда площадь круга равна r^2=3^2=9″ />
Тогда площадь круга равна r^2=4^2=16″ />
И его площадь равна 16 12.
Ege-ok. ru
14.10.2018 16:55:24
2018-10-14 16:55:24
Источники:
Https://ege-ok. ru/2013/11/30/ploshhad-sektora-po-kletochkam
Площадь фигуры по клеточкам | Подготовка к ЕГЭ по математике » /> » /> .keyword { color: red; } Егэ математика площадь по клеточкам
Площади фигур, нарисованных на клетчатой бумаге
Площади фигур, нарисованных на клетчатой бумаге
Рассмотрим несколько задач на вычисление площади фигуры, если фигура нарисована на бумаге в клетку.
Клетку считаем размером 1×1 ед.
Попробуйте решить сами предложенные задачи!
Могу сказать следующее – ответ будет выражаться целым числом 🙂 .
Надо сказать, что кто знаком с такого рода задачками, обычно выдает ответ в считанные секунды… Другие же озадачиваются зачастую тем, а что же делать с площадью круга. Куда ж спрятать …
Итак, ищем площадь «ракеты».
Задача 1.
Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.
Я буду кратка… Никаких слов.
Смотрите и все увидите сами:
Следующая задача предлагалась А. Лариным в одном из Тренировочных вариантов.
Задача 2.
Найдите площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток равными 1.
Ну уж если вы справились с «кувшином», то и с «плачущим сердцем» разберетесь также легко, уверена!
Задача 3.
Найдите суммарную площадь фигур, изображенных на рисунке, считая стороны квадратных клеток равными 1.
Ну а вам я, желаю, конечно, чтоб ваше сердце только б пело, радостно пело!
Чтобы не потерять страничку, вы можете сохранить ее у себя:
- С4 (№18) из тренировочной работы №53 А. Ларина Задание №18 (С4) из Тренировочного варианта №88 А. Ларина 03. Вычисление площадей 03. Круг Видеоразбор С4 (№18) ЕГЭ по математике Задача С4 (№18) диагностической работы от 12 декабря 2013 (11 класс)
Для чего нужны такие задачки? что-то подобное может быть на ЕГЭ? или они даны просто для проверки сообразительности? 🙂
Рассмотрим несколько задач на вычисление площади фигуры, если фигура нарисована на бумаге в клетку.
Площади фигур, нарисованных на клетчатой бумаге.
Egemaximum. ru
18.10.2017 0:21:16
2017-10-18 00:21:16
Источники:
Https://egemaximum. ru/ploshhadi-figur-narisovannyx-na-kletchatoj-bumage/
Методическое пособие для подготовки к ЕГЭ по математике
задания В3
Выполнила
Учитель математики
МБОУ СОШ №7
Тютюнникова Ирина Николаевна
ВЗ.Геометрические задачи с числовым ответом
Немного полезной информации
Мы рассмотрим простые виды задач по геометрии,
а именно задачи, в которых нужно найти площади плоских фигур,
нарисованных на клетчатой бумаге или расположенных на координатной плоскости.
Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.
Давайте вспомним эти формулы и разберём примеры их приме-
нения.
Теорема Пифагора: В прямоугольном треугольнике квад-
рат гипотенузы (с) равен сумме квадратов катетов (а и b).
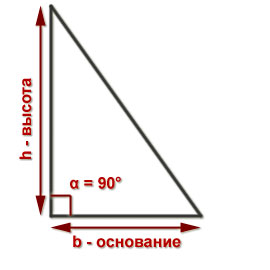
Площадь прямоугольного треугольника равнаи половине произведения его катетов: .
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная
называется гипотенузой, две прилежащие к прямому углу стороны
называют катетами.
Все задачи имеют один вопрос: Найти площадь какой-нибудь фигуры…
Отличие в другом – фигуры заданы по-разному:
либо на клетчатой бумаге:
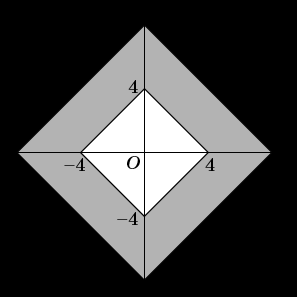
либо в координатной плоскости:
Чтобы решить её, надо знать ФУНДАМЕНТ – площади основных фигур:
На самом деле, для В3 достаточно знать S прямоугольника и S треугольника (чаще прямоугольного). Остальные S очень редко используются. Этот Жёлтый фундамент нужно один раз заложить себе в голову и пользоваться им ещё и в других задачах!
Есть несколько способов найти S. Примерь быстро каждый способ к фигуре и выбери лучший
Способ_1 (самый лучший и часто используемый)
1) достроить фигуру до прямоугольника или прямоугольного треугольника
2) Найти S1 полученной фигуры (прямоугольника или треугольника)
3) Найти S2 добавленных частей
4) Вычесть S1 – S2 = получим S нужной фигуры.
Пример: Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
Решение:
-
Достроим до квадрата:
2-3-4) Теперь
Ответ: 17.
Способ_1 замечательно подходит для фигур на клетчатой бумаге. Его можно использовать и для фигур на координатной плоскости.
Но тут быстрее вычислить S самой фигуры.
Способ_2
1) ПО формуле – самый простой способ
Способ_2 используется тогда, когда чётко видно, что за фигура и легко найти величины для вычисления S.
Например, для ромба найти длины диагоналей и использовать формулу из Жёлтого фундамента.
Для круга найти радиус.
Для трапеции основания и высоту.
Для треугольника сторону и высоту к этой стороне и т.д.
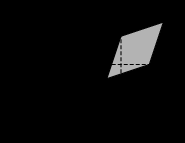
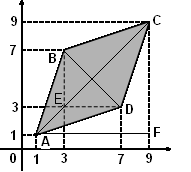
Пример: Найдите площадь ромба, изображенного на рисунке.
Решение:
Площадь ромба равна половине произведения его диагоналей:
Диагонали BD и АС найдем по теореме Пифагора из треугольников BED и AFC соответственно:
BD2 = BE2 + ED2 = 42 + 42 = 16 + 16 = 16·2; BD=
AC2 = AF2 + FC2 = 82 + 82 = 64 + 64 = 64·2; AC =
Ответ: 32
Ещё задача: Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.).
Решение: 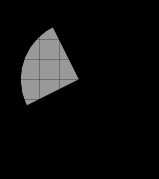
1) Найдем радиус окружности и посчитаем площадь всего круга по формуле
В этой задаче сразу видно, что R = 3 .
2)Теперь определим, какую часть круга составляет выделенный сегмент. Из рисунка видно, что четверть. Значит, его площадь равна
Ответ: 2,25
И последний пример: Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.).
Решение:
1) Радиус вычислим по теореме Пифагора, как показано на рисунке.
(Выбрали точку на окружности, лежащую строго на границе клеток, и мысленно достроили прямоугольный треугольник.)
R2 = 32 + 32 = 9 + 9 = 9·2
2) Выделенный сегмент можно разбить на две части. Одна часть составляет четверть круга, другая — половину четверти, то есть 1/8 круга.
Весь сегмент составит круга.
Ответ: 6,75
Задачи для самостоятельного решения
1.На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах
2.На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
3. Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
4.Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
5. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
6.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах
7.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Задачи на клетчатой бумаге. Формула Пика.
Задачи на бумаге в клетку помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.
При решении задач на клетчатой бумаге ученикам не понадобится знание основ планиметрии, а будет нужна именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.
Формула Пика
Наш сюжет будет разворачиваться на обычном листке клетчатой бумаги.[1]
Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.
Но тут нас ждёт много хлопот (попробуйте!). Давайте «схитрим»:
вычислим площадь заштрихованной фигуры, которая «дополняет» наш
Рис. 1
многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.
Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади нам пришлось потрудиться. А если бы многоугольник выглядел более причудливо?
Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 2).
Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую
Рис. 2
клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
S = В + 


Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + 
Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки!
Это и есть формула Пика.
Задача 1. Проверить формулу Пика для многоугольника на рисунке 1.
Решение.
В = 14, Г = 8. По формуле Пика: S = В + 
S = 14 + 8/2 – 1 = 17
Ответ: 17 кв. ед.
Можно убедиться в том, что формула Пика верна для всех рассмотренных примеров.
Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
Попробуйте вычислить площади многоугольников с рисунка 3, используя формулу Пика. Правда ведь, легко получается!
Рис. 3
Рассмотрим ещё некоторые задачи на клетчатой бумаге с клетками размером 1 см 
Задача 2.[3]
Найдите площадь прямоугольника АВСD (рис.4).
Решение. По формуле Пика: S = В + 
В = 8, Г = 6
S = 8 + 6/2 – 1 = 10 (см²)
Рис. 4 Ответ: 10 см².
Задача 3. Найдите площадь параллелограмма АВСD (рис.5)
Решение. По формуле Пика: S = В + 
В = 6, Г = 6
S = 6 + 6/2 – 1 = 8 (см²)
Ответ: 8 см².
Рис. 5
Задача 4. Найдите площадь треугольника АВС (рис.6)
Решение. По формуле Пика: S = В + 
В = 6, Г = 5
S = 6 + 5/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².
Рис. 6
Задача 5. Найдите площадь четырёхугольника АВСD (рис. 7)
Решение. По формуле Пика: S = В + 
В = 5, Г = 7
S = 5 + 7/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².
Рис. 7
Согласитесь, рассмотренные задания аналогичны заданию В
Например:
Задача 6.[2] В

Решение. По формуле Пика: S = В + 
В = 12, Г = 6
S = 12 + 6/2 – 1 = 14 (см²)
Ответ: 14
Рис. 8
Задача 7. В

Решение. Воспользуемся формулой Пика:
В = 12, Г = 17
S = 12 + 17/2 – 1 = 19,5 (см²)
Ответ: 19,5
Рис. 9
Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.
Задача 8.[4] Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 10)
Решение. Найдём S

В = 8, Г = 7. S
1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)
Ответ: м²
Рис. 10
Задача 9. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 11)
Решение. Найдём S

В = 7, Г = 4. S
1 см² — 200² м²; S = 40000 · 8 = 320 000 (м²)
Ответ: м²
Рис. 11
Получить полный текс
Задачи ЕГЭ база
-
1. Простейшие текстовые задачи
-
2. Величины и значения
-
3. Графики, диаграммы, таблицы
-
3.1. Графики
-
3.2. Диаграммы
-
3.3. Таблицы
-
-
4. Вычисления по формуле
-
5. Теория вероятностей
-
6. Выбор подходящих вариантов
-
7. Функции и производные
-
8. Выбор утверждений
-
9. Фигуры на квадратной решетке. Координатная плоскость
-
9.1. Элементы многоугольников
-
9.2. Площади многоугольников
-
9.3. Координатная плоскость
-
9.4. Элементы круга и окружности
-
9.5. Углы
-
-
10. Прикладные задачи по геометрии
-
11. Стереометрия. Тела вращения
-
12. Планиметрия
-
13. Стереометрия. Многогранники
-
14. Вычисления с дробями
-
14.1. Обыкновенные дроби
-
14.2. Десятичные дроби
-
14.3. Смешанные выражения
-
-
15. Проценты и пропорции
-
15.1. Проценты
-
15.2. Пропорции
-
-
16. Значения выражений
-
16.1. Рациональные выражения
-
16.2. Иррациональные выражения
-
16.3. Логарифмические выражения
-
16.4. Тригонометрические выражения
-
16.5. Вычисления со степенями
-
16.6. Свойства степеней
-
-
17. Уравнения
-
17.1. Рациональные уравнения
-
17.2. Иррациональные уравнения
-
17.3. Показательные уравнения
-
17.4. Логарифмические уравнения
-
-
18. Неравенства и числовая прямая
-
19. Свойства чисел
-
20. Текстовые задачи
-
21. Нестандартные задачи
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины B.
На клетчатой бумаге с размером клетки 1×1 изображён четырехугольник. Найдите радиус окружности, которую можно вписать в данный четырёхугольник.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки (1смtimes 1см). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки 1×1 изображен квадрат. Найдите радиус вписанной в него окружности.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1 см× 1 см) (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1смtimes 1см). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
На клетчатой бумаге с размером клетки 1 см ×1 см изображён треугольник. Найдите его площадь. Ответ дайте в (см^2).
На клетчатой бумаге с размером клетки (1times 1 ) изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.