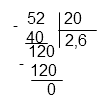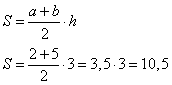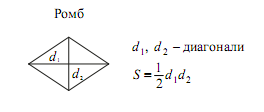Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, а высота фонаря равна 9 м?
2
Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
3
Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
4
Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
5
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рис.). Найдите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Пройти тестирование по этим заданиям
На какое наименьшее количество ступенек
Дата: 2015-01-20
4933
Категория: Физические задачи
Метка: ЕГЭ-№8
27986. Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
Нам необходимо вычислить высоту, на которую человек должен подняться. Для этого необходимо определить высоту, с которой он видит горизонт на расстоянии 4,8 км высоту, и высоту, с которой он увидит горизонт на расстоянии не менее 6,4 км.
Вычислим высоту, с которой человек видит 4,8 км:
Вычислим высоту, с которой человек видит 6,4 км:
То есть человеку нужно подняться как минимум на 3,2–1,8 = 1,4 метра.
Так как каждая ступенька высотой 20 см, то человеку при поставленных условиях необходимо подняться минимум на 7 ступенек.
*Примечание! 1,4 метра это 140 см. 140:20 = 7.
Ответ: 7
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Ступени лестницы покрасили в темный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступени равна 30 см, высота – 15 см, а ширина – 90 см. Ответ дайте в квадратных сантиметрах.
Решение
Найдем площадь вертикальных составляющих ступеней:
Sв = 5 · (15 · 90) = 6750 квадратных сантиметров.
Найдем площадь горизонтальных составляющих ступеней:
Sг = 4 · (30 · 90) = 10800 квадратных сантиметров.
Осталось найти площадь всей окрашенной поверхности ступеней лестницы:
S = Sв + Sг = 6750 + 10800 = 17550 квадратных сантиметров площадь всей окрашенной поверхности лестницы.
S в 5 15 90 6750 квадратных сантиметров.
Smartrepetitor. ru
14.04.2019 16:53:54
2019-04-14 16:53:54
Источники:
Https://smartrepetitor. ru/base-uroven/basic-zadanie-13/zadacha-13-9590.html
Решение 2848. Пять ступеней лестницы покрасили в тёмный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступеньки равна 40 см, высота — 15 см, а ширина — 90 см. » /> » /> .keyword { color: red; } Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Задание 13. Пять ступеней лестницы покрасили в тёмный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступеньки равна 40 см, высота — 15 см, а ширина — 90 см. Ответ дайте в квадратных сантиметрах.
Изобразим указанные размеры на рисунке:
Теперь, смотрите, у нас 5 ступенек высотой 15 см и 4 ступеньки глубиной 40 см. Если их вытянуть в линию, то получится общая длина:
Часть лестницы покрасили в темный цвет как показано на рисунке егэ.
Self-edu. ru
10.07.2017 13:22:34
2017-07-10 13:22:34
Источники:
Https://self-edu. ru/ege2021_base_30.php? id=5_13
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Часть лестницы покрасили в темный цвет как показано на рисунке егэ
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 13 № 518431
Пять ступеней лестницы покрасили в тёмный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступеньки равна 30 см, высота — 15 см, а ширина — 90 см. Ответ дайте в квадратных сантиметрах.
Площадь одной ступеньки равна 30 · 90 = 2700, а площадь подъема равна 15 · 90 = 1350. Найдем площадь закрашенной фигуры зная то, что всего 4 ступеньки и 5 подъемов: 4 · 2700 + 5 · 1350 = 17 550.
Аналоги к заданию № 518403: 518431 518451 518475 Все
Задание 13 № 518451
Пять ступеней лестницы покрасили в тёмный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступеньки равна 25 см, высота — 15 см, а ширина — 80 см. Ответ дайте в квадратных сантиметрах.
Площадь одной ступеньки равна 25 · 80 = 2000, а площадь подъема равна 15 · 80 = 1200. Найдем площадь закрашенной фигуры зная то, что всего 4 ступеньки и 5 подъемов: 4 · 2000 + 5 · 1200 = 14000.
Аналоги к заданию № 518403: 518431 518451 518475 Все
Задание 13 № 518475
Пять ступеней лестницы покрасили в тёмный цвет, как показано на рисунке (штриховкой). Найдите площадь окрашенной поверхности, если глубина каждой ступеньки равна 35 см, высота — 15 см, а ширина — 80 см. Ответ дайте в квадратных сантиметрах.
Площадь одной ступеньки равна 35 · 80 = 2800, а площадь подъема равна 15 · 80 = 1200. Найдем площадь закрашенной фигуры зная то, что всего 4 ступеньки и 5 подъемов: 4 · 2800 + 5 · 1200 = 17 200.
—>
Задание 13 № 518451
Площадь одной ступеньки равна 30 90 2700, а площадь подъема равна 15 90 1350.
Mathb-ege. sdamgia. ru
18.04.2018 0:19:46
2018-04-18 00:19:46
Источники:
Https://mathb-ege. sdamgia. ru/test? likes=518403
Лестница соединяет точки и
, расстояние между которыми равно
м. Высота каждой ступени равна
см, а длина —
см. Найдите высоту
(в метрах), на которую поднимается лестница.

Решение задачи
Данный урок демонстрирует решение задачи с применением теоремы Пифагора. По условию задачи лестница соединяет точки и
, расстояние между которыми — величина известная. Требуется узнать высоту лестницы при заданной высоте и длине ступени. Для этого прежде всего необходимо определить количество ступеней, при этом каждая ступень рассматривается в виде геометрической фигуры — прямоугольного треугольника. Далее применяется формула
, где
,
— катеты,
— гипотенуза. Подставляя в данную формулу известные по условию величины, рассчитывается величина отрезка, которую занимает каждая ступень на отрезке
. Данная величина и позволяет определить количество ступеней путем деления расстояния между заданными точками
и
на величину занимаемого ступенькой отрезка. Искомая высота определяется путем умножению высоты одной ступени на общее количество ступеней.
Решение данной задачи типа ОГЭ 17 позволяет с успехом подготовиться к ОГЭ по математике.
Прикладная геометрия
В задании №8 ЕГЭ по математике нас ждут задания из области прикладной геометрии. Задачи простые на знания основных понятий, адаптированные под реальные жизненные ситуации. Перейдем к разбору и решению типовых заданий №8.
Разбор типовых вариантов заданий №8 ЕГЭ по математике базового уровня
Вариант 8МБ1
[su_note note_color=”#defae6″]
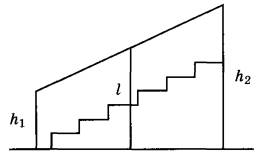
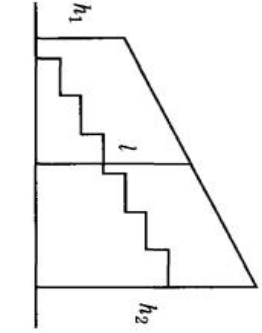
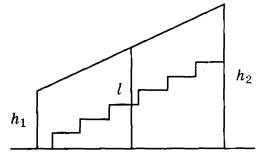
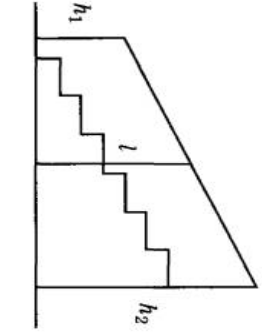
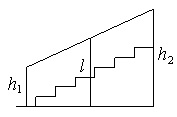
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах.
[/su_note]
Алгоритм выполнения
- Определить, что за фигура на рисунке.
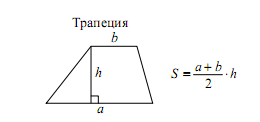
- Вспомнить определение средней линии трапеции.
- Записать формулу для нахождения средней линии трапеции.
- Подставить данные.
- Вычислить среднюю линию трапеции.
Решение:
Определим, что за фигура на рисунке. Для этого вспомним определение трапеции.
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.
Стороны h1 и h2 параллельны, остальные две стороны не параллельны. Значит перед нами трапеция. Стороны h1 и h2 называются основаниями трапеции.
Если перевернуть рисунок, то получим трапецию в более привычном виде.
Вспомним определение средней линии трапеции.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям.
По условию столб l закреплен посередине, следовательно, l – средняя линия трапеции.
Запишем формулу для нахождения средней линии трапеции.
Формулу нахождения средней линии трапеции можно найти в справочных материалах (полусумма оснований).
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.
То есть l = ( h1 + h2 )/2
Подставим данные и вычислим.
l = (1,25 м + 2,25 м)/2 = (3,5 м)/2 = 1,75 м
Примечание: Десятичные дроби складывают столбиком, записав запятую под запятой.
Ответ: 1,75.
Решение в общем виде:
Столб длиной l представляет собой среднюю линию трапеции с основаниями h1 и h2, поэтому длину этого столба можно вычислить по формуле средней линии трапеции как
Выполняем деление 3,5 на 2, имеем:
Ответ: 1,75.
Вариант 8МБ2
[su_note note_color=”#defae6″]
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 2,1 м, а наибольшая высота h2 равна 3,1 м. Ответ дайте в метрах.
[/su_note]
Алгоритм выполнения
- Определить, что за фигура на рисунке.
- Вспомнить определение средней линии трапеции.
- Записать формулу для нахождения средней линии трапеции.
- Подставить данные.
- Вычислить среднюю линию трапеции.
Решение:
Определим, что за фигура на рисунке. Для этого вспомним определение трапеции.
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.
Стороны h1 и h2 параллельны, остальные две стороны не параллельны. Значит перед нами трапеция. Стороны h1 и h2 называются основаниями трапеции.
Если перевернуть рисунок, то получим трапецию в более привычном виде.
Вспомним определение средней линии трапеции.
Средняя линия трапеции – отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям.
По условию столб l закреплен посередине, следовательно, l – средняя линия трапеции.
Запишем формулу для нахождения средней линии трапеции.
Формулу нахождения средней линии трапеции можно найти в справочных материалах.
Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.
То есть l = ( h1 + h2 )/2
Подставим данные и вычислим.
l = (2,1 м + 3,1 м)/2 = (5,2 м)/2 = 2,6 м
Примечание: Десятичные дроби складывают столбиком, записав запятую под запятой. В данном случае удобно устно сложить целые части и дробные.
Ответ: 2,6.
Решение в общем виде:
Столб представляет собой среднюю линию трапеции с основаниями h1 и h2, поэтому длину столба l можно найти по формуле средней линии трапеции:
Ответ: 2,6.
Вариант 8МБ3
[su_note note_color=”#defae6″]
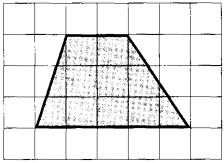
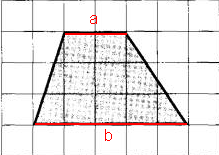
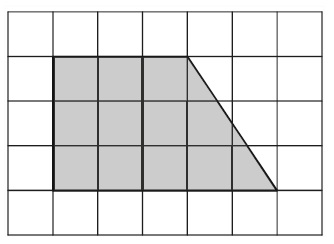
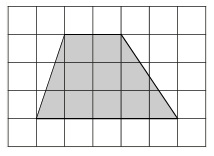
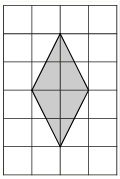
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- Определить что за фигура на рисунке.
- Записать формулу нахождения площади данной фигуры.
- Определить по чертежу все необходимые данные.
- Вычислить площадь участка.
Решение:
Определим, что за фигура на рисунке.
Видно, что у данного четырехугольника две противоположные стороны параллельны.
Четырёхугольник, у которого две противоположные стороны параллельны, а другие две не параллельны, называется трапецией.
Следовательно, перед нами трапеция.
Записываем формулу нахождения площади данной фигуры.
Площадь трапеции равна произведению полусуммы оснований на высоту.
Определяем по чертежу все необходимые данные.
Основания трапеции – параллельные стороны.
На рисунке красным выделены основания. Обозначим их a и b.
a = 2 м( длина 2 клеточек, каждая из которых по условию 1 м х 1 м)
b = 5 м(длина 5 клеточек, каждая из которых по условию 1 м х 1 м)
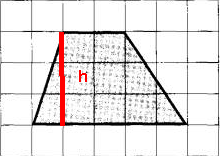
Высота трапеции -отрезок, соединяющий основания и при этом перпендикулярный им. Обозначим высоту трапеции h.
h = 3 м (длина 3 клеточек, каждая из которых по условию 1 м х 1 м)
Вычислим площадь участка.
Найдем площадь трапеции с основаниями a = 2, b = 5 и высотой h = 3:
Ответ: 10,5.
Вариант 8МБ4
[su_note note_color=”#defae6″]
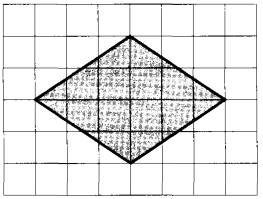
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- Определить что за фигура на рисунке.
- Записать формулу нахождения площади данной фигуры.
- Определить по чертежу все необходимые данные.
- Вычислить площадь участка.
Решение:
Определим, что за фигура на рисунке.
Видно, что у данного четырехугольника все стороны равны, проверяем это с помощью линейки.
Ромб — это параллелограмм, у которого все стороны равны.
Следовательно, перед нами ромб.
Запишем формулу нахождения площади данной фигуры.
Площадь ромба равна половине произведения диагоналей.
Определим по чертежу все необходимые данные.
Диагонали ромба – это прямые, соединяющие противоположные вершины.
На рисунке красным выделены диагонали. Обозначим их d1 и d2.
d1 = 4 м(длина 4 клеточек, каждая из которых по условию 1 м х 1 м)
d2 = 6 м(длина 5 клеточек, каждая из которых по условию 1 м х 1 м)
Вычислим площадь участка.
Нужно найти площадь ромба с диагоналями 6 и 4, получим:
Ответ: 12.
Вариант восьмого задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
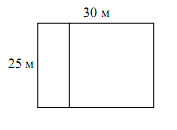
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
[/su_note]
Алгоритм выполнения
- Вычислить периметр прямоугольника.
- Прибавить длину разделяющей части.
Решение:
Вычислим периметр прямоугольника.
Периметр – сумма длин всех сторон.
В прямоугольнике противоположные стороны равны.
P = 30 м + 30 м + 25 м + 25 м = 110 м.
110 м – длина забора без перегородки.
Прибавим длину разделяющей части.
По рисунку видно, что длина разделяющей части 25 м.
110 м + 25 м = 135 м.
Ответ: 135.
Вариант 8МБ5
[su_note note_color=”#defae6″]
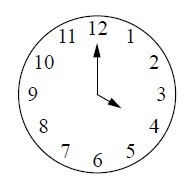
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
[/su_note]
Алгоритм выполнения
- Сначала мы найдем, сколько в градусах занимает один час.
- Затем найдем угол, который образуют стрелки в 16:00
Решение:
Так как вся окружность – 360°, а часов 12, то один час:
360° : 12 = 30°
Значит в четыре часа угол будет равен:
30° • 4 = 120°
Ответ: 120°
Вариант 8МБ6
[su_note note_color=”#defae6″]
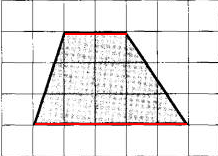
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- Так как перед нами изображена трапеция, то вспомним площадь трапеции: полусумма оснований умноженная на высоту.
- В нашем примере большее основание равно пяти, меньшее – трем, высота равна трем, следовательно площадь участка:
Решение:
(5 + 3) : 2 • 3 = 12
Ответ: 12
Вариант 8МБ7
[su_note note_color=”#defae6″]
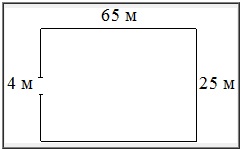
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Алгоритм выполнения
- Находим периметр данного прямоугольного участка по ф-ле Р=2(a+b), где a – его длина, b – ширина.
- Вычитаем из полученного числа 4 (в метрах), т.е. ширину, выделенную для проезда.
Решение:
2 · (25 + 65) = 2 · 90 = 180 (м) – периметр прямоугольного участка
180 – 4 = 176 (м) – длина забора
Ответ: 176
Вариант 8МБ8
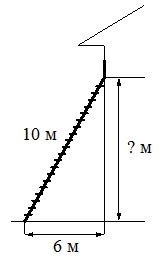
[su_note note_color=”#defae6″]
Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.
[/su_note]
Алгоритм выполнения
Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора.
Решение:
По теореме Пифагора с2=a2+b2, где с – гипотенуза, a и b – катеты. Примем, что а – расстояние между нижним концом лестницы и основанием дома. Тогда b – расстояние от основания дома до верхнего конца лестницы.
В данном случае с=10, а=6. Отсюда получаем: 100-36=64, квадратный корень из 64 – 8.
Ответ: 8
Вариант 8МБ9
[su_note note_color=”#defae6″]
Какой наименьший угол (в градусах) образуем минутная и часовая стрелки часов в 11:00?
[/su_note]
Алгоритм выполнения
В момент времени 11:00 минутная стрелка стоит на 12, а часовая – на 11, т.е. они находятся на соседних числах циферблата. Определяем, какую часть (долю) от полного круга составляет угол между парой соседних чисел на циферблате, а затем находим, сколько эта доля составляет в градусах.
Решение:
На циферблате 12 чисел-делений. Соответственно, угол между соседними числами составляет 1/12 долю от полного круга. Поскольку полный круг равен 3600, то 1/12 его часть равна:
3600:12=300.
Ответ: 30
Вариант 8МБ10
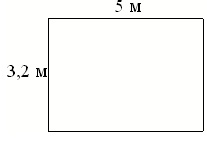
[su_note note_color=”#defae6″]
На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
[/su_note]
Алгоритм выполнения
- Находим площадь комнаты, используя параметры, полученные в результате точных измерений. Используем для этого формулу для вычисления площади прямоугольника S=ab, где a – его длина, b – ширина.
- Находим разницу между полученным числом и величиной площади, указанной на плане (от большего числа отняв меньшее).
Решение:
3,2 · 5 = 16 (кв.м) – площадь комнаты, определенная на основании точных измерений
16 – 15,7 = 0,3 (кв.м) – отличие найденного значения площади от того, которое указано на плане
Ответ: 0,3
Вариант 8МБ11
[su_note note_color=”#defae6″]
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- Условно разбиваем план на 3 части: 1) прямоугольник из полностью окрашенных квадратов площадью 2×3 (посередине); 2) прямоугольник из частично окрашенных квадратов площадью 1×3 (слева); 3) прямоугольник из частично окрашенных квадратов площадью 2×3 (справа).
- Площади участков вычисляем по ф-ле для прямоугольника. При этом учитываем, что участки слева и справы окрашены ровно наполовину. Это можно утверждать на основании того, что границы окрашивания являются диагоналями рассматриваемых прямоугольных участков.
- Находим суммарную площадь.
Решение:
Площадь участка посередине (полностью окрашенного, размером 2×3 клетки) равна: 2 ·3 = 6 (кв.м).
Площадь участка слева (частично окрашенного, размером 1×3 клетки) составляет: (1 · 3) / 2 = 1,5 (кв.м).
Площадь участка справа (частично окрашенного, размером 2×3 клетки) равна: (2 · 3) / 2 = 3 (кв.м).
Общая площадь местности: 6 + 1,5 + 3 = 7,5 (кв.м).
Ответ: 7,5
Вариант 8МБ12
[su_note note_color=”#defae6″]
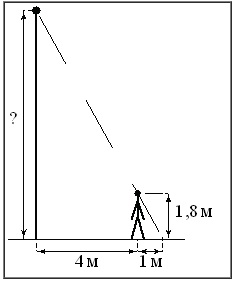
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
[/su_note]
Алгоритм выполнения
- Рассматриваем 2 подобных треугольника: 1) образуемый человеком и длиной его тени; 2) формируемый линией фонаря, а также расстоянием между его основанием и человеком + линией отбрасываемой им тени.
- Поскольку у подобных треугольников длины соответствующих сторон пропорциональны, то формируем пропорцию, включающую искомую величину.
- Вычисляем высоту фонаря.
Решение:
Обозначим через х искомую высоту фонаря.
Имеем 2 подобных прямоуг.треугольника. Первый (больший) имеет катеты 4+1=5 м и х. Второй (меньший) – 1,8 м (рост человека) и 1 м. Поскольку треугольники подобны, то можем записать: х : 5 = 1,8 : 1.
Решим полученную пропорцию: х · 1 = 5 · 1,8 → х = 9 (м) – высота фонаря.
Ответ: 9
Вариант 8МБ13
[su_note note_color=”#defae6″]
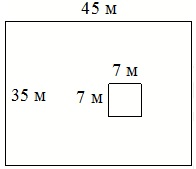
Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- Находим площадь прямоугольного участка.
- Находим площадь квадратного дома.
- Находим разность этих площадей, отняв от большего числа меньшее.
Решение:
35 · 45 = 1575 (кв.м) – площадь всего участка
7 · 7 = 49 (кв.м) – площадь дома
1575 – 49 = 1526 (кв.м) – площадь оставшейся части участка
Ответ: 1526
Вариант 8МБ14
[su_note note_color=”#defae6″]
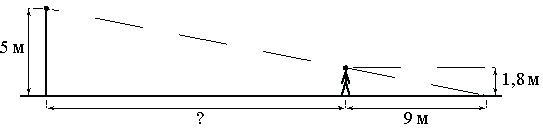
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
[/su_note]
Алгоритм выполнения
- Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени.
- Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию.
- Из полученной пропорции выражаем искомую величину. Вычисляем ее.
Решение:
Обозначим искомое расстояние через х.
Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и (х+9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников:
5 : 1,8 = (х + 9) : 9.
Из пропорции получим:
5 · 9 = 1,8 · (х + 9)
1,8х + 16,2 = 45
1,8х = 28,8
х = 16 (м)
Ответ: 16
Вариант 8МБ15
[su_note note_color=”#defae6″]
Перила лестницы дачного дома для надежности укреплены посередине вертикальным способом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 0,7 м, а наибольшая h2 равна 1,5 м. Ответ дайте в метрах.
[/su_note]
Алгоритм выполнения
- Из рисунка можно (и нужно) заметить, что фигура, построенная на горизонтальном основании, на сторонах h1 и h2 и на линии перил, представляет собой лежащую на боковой стороне прямоугольную трапецию. Тогда h1 и h2 – основания этой трапеции.
- Поскольку линия l тоже направлена вертикально, то это значит, что она параллельна h1 и h2. А т.к. она равноудалена от h1 и h2, то означает, что l является средней линией трапеции. Ср.линию трапеции найдем как ср.арифметическое ее оснований.
Решение:
L = (h1 + h2) / 2
L = (0,7+1,5) / 2 = 2,2 / 2 = 1,1 (м)
Ответ: 1,1
Вариант 8МБ16
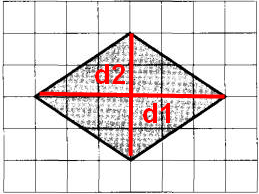
[su_note note_color=”#defae6″]
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
[/su_note]
Алгоритм выполнения
- На плане изображен ромб. Условно разбиваем его на 4 части диагоналями, т.е. парой отрезков, соединяющих вертикальные вершины ромба и горизонтальные. Эти части равны в соответствии со свойствами ромба. Тогда общую площадь на плане будем вычислять как сумму 4 одинаковых частей плана, охватываемых прямоугольниками 1×3 клетки.
- Каждая из 4 частей представляет собой половину площади прямоугольника 1×3 клетки. Это именно так, поскольку ее граница на плане (сторона ромба) является диагональю прямоугольника, в котором она размещается.
Решение:
Обозначим общую площадь на плане через S, каждую из 4-х одинаковых частей, на которые эта площадь разделена, – через S1. Тогда S = 4S1.
Т.к. каждая часть охватывает половину участка 1×3 клетки, то S1 = (1 · 3) / 2 =1,5 (кв.м). поэтому S = 4 · 1,5 = 6 (кв.м).
Ответ: 6
Даниил Романович | Просмотров: 11.1k
-
ЕГЭ по математике (база) 2023
- /
-
Задание 10
- /
- Задача 22
- /
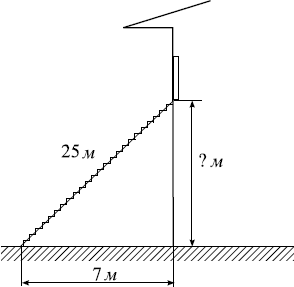
Пожарную лестницу длиной 25 м приставили к окну дома. Нижний конец лестницы отс…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 1 мин. 15 сек.
ЕГЭ по математике (база) 2023 задание 10: номер 22 | 13fzh | Пожарную лестницу длиной 25 м…
25
Пожарную лестницу длиной 25 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 7 м. На какой высоте расположено окно? Ответ дайте в метрах.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м $×$1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
От столба высотой 15 м к дому натянут провод, который крепится на высоте 3 м от земли. Расстояние от дома до столба 5 м. Найдите длину провода. Ответ дайте в метрах.
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образуют две соседние спицы.
Масштаб карты такой, что в одном сантиметре 3 км. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 15 см?
Слайд 1
Разбор типовых заданий ЕГЭ по математике базового уровня Геометрия
Слайд 2
Прикладная геометрия 1. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах. ! Алгоритм выполнения Определить, что за фигура на рисунке. Вспомнить определение средней линии трапеции. Записать формулу для нахождения средней линии трапеции. Подставить данные. Вычислить среднюю линию трапеции.
Слайд 3
2. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Определить что за фигура на рисунке. Записать формулу нахождения площади данной фигуры. Определить по чертежу все необходимые данные. Вычислить площадь участка.
Слайд 4
3. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Определить что за фигура на рисунке. Записать формулу нахождения площади данной фигуры. Определить по чертежу все необходимые данные. Вычислить площадь участка.
Слайд 5
4. Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах . ! Алгоритм выполнения Вычислить периметр прямоугольника. Прибавить длину разделяющей части. P = 30 м + 30 м + 25 м + 25 м = 110 м. 110 м – длина забора без перегородки. Прибавим длину разделяющей части. По рисунку видно, что длина разделяющей части 25 м. 110 м + 25 м = 135 м.
Слайд 6
5. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00? ! Алгоритм выполнения Сначала мы найдем, сколько в градусах занимает один час. Затем найдем угол, который образуют стрелки в 16:00 Так как вся окружность — 360°, а часов 12, то один час: 360° : 12 = 30° Значит, в четыре часа угол будет равен: 30° • 4 = 120°
Слайд 7
6. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах. ! Алгоритм выполнения Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора.
Слайд 8
7. Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах. ! Алгоритм выполнения Находим площадь прямоугольного участка. Находим площадь квадратного дома. Находим разность этих площадей, отняв от большего числа меньшее. 35 · 45 = 1575 ( кв.м ) – площадь всего участка 7 · 7 = 49 ( кв.м ) – площадь дома 1575 – 49 = 1526 ( кв.м ) – площадь оставшейся части участка
Слайд 9
8. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м? ! Алгоритм выполнения Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени. Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию. Из полученной пропорции выражаем искомую величину. Вычисляем ее. Обозначим искомое расстояние через х . Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и ( х +9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников: 5 : 1,8 = ( х + 9) : 9. Из пропорции получим: 5 · 9 = 1,8 · ( х + 9) 1,8 х + 16,2 = 45 1,8 х = 28,8 х = 16 (м)
Слайд 10
Наглядная стереометрия 9. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах. ! Алгоритм выполнения: Записать формулу объема цилиндра. Подставить значения для цилиндра с жидкостью в первом и во втором случае. Объем жидкости не изменялся, следовательно, можно приравнять объемы. Полученное уравнение решить относительно второй высоты h 2 . Подставить данные и вычислить искомую величину. V 1 = π r 1 2 h 1 V 2 = π r 2 2 h 2 Объем жидкости не изменялся, следовательно, можно приравнять объемы. V 1 = V 2 π r 1 2 h 1 = π r 2 2 h 2 h 2 =( π r 1 2 h 1 )/ π r 2 2 По условию площадь основания стала в 4 раза больше, то есть r 2 = 4 r 1 . Подставим r 2 = 4 r 1 в выражение для h 1. Получим: h 2 =( π r 1 2 h 1 )/ π (4 r 1 ) 2 Полученную дробь сократим на π, получим h 2 =( r 1 2 h 1 )/ 16 r 1 2 Полученную дробь сократим на r 1 , получим h 2 = h 1 / 16. Подставим известные данные: h 2 = 80/ 16 = 5 см. Ответ: 5.
Слайд 11
10. Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй? ! Алгоритм выполнения: Записать формулу, для вычисления объема правильной четырехугольной призмы. Записать в общем виде формулу для нахождения объема в первом и втором случае. Найти отношение объемов. Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы. Сократить получившуюся дробь. V 1 = a 1 · b 1 · c 1 V 2 = a 2 · b 2 · c 2 Найдем отношение объемов. V 1 / V 2 = (a 1 · b 1 · c 1 )/ ( a 2 · b 2 · c 2 ) По условию c 1 = 4,5 c 2 (первая коробка в четыре с половиной раза выше второй), b 2 = 3 b 1 (вторая коробка втрое шире первой). Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a 2 = 3 a 1 Подставим эти выражения в формулу отношения объемов: V 1 / V 2 = (a 1 · b 1 · c 1 )/ ( a 2 · b 2 · c 2 ) = (a 1 · b 1 · 4,5c 2 )/ ( 3a 1 · 3b 1 · c 2 ) = (a 1 · b 1 · 4,5c 2 )/ ( 9a 1 · b 1 · c 2 ) Сократим получившуюся дробь на a 1 · b 1 · c 2 . Получим: V 1 / V 2 = (a 1 · b 1 · 4,5c 2 )/ ( 9a 1 · b 1 · c 2 ) = 4,5/9 = ½. Объем первой коробочки в 2 раза меньше объема второй. Ответ: 2.
Слайд 12
11. От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)? ! Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней. Ответ: 14. Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Слайд 13
12. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого? ! Алгоритм выполнения Записываем ф- лу для вычисления объема цилиндра. Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра. Формируем формулы для объема 1-го и 2-го цилиндров. Вычисляем отношение объемов. V 1 =πR 1 2 H 1 , V 2 =πR 2 2 H 2 .
Слайд 14
13. В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров. ! Алгоритм выполнения Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V 1 и V 2 . Фиксируем значение для V 1 . Выражаем V 2 через V 1 . Находим значение V 2 . Переводим результат, полученный в литрах, в куб.см . Объем бака до погружения V 1 =5 (л). Т.к. после погружения детали объем стал равным V 2 . Согласно условию, увеличение составило 1,4 раза, поэтому V 2 =1,4 V 1 . Отсюда получаем: V 2 =1,4·5=7 (л). Т.о ., разница объемов, которая и составляет объем детали, равна: V 2 –V 1 =7–5=2 (л). 2 л=2·1000=2000 ( куб.см ).
Слайд 15
14. В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах. ! Алгоритм выполнения Доказываем, что данные в условии конусы подобны. Определяем коэффициент подобия. Используя свойство для объемов подобных тел, находим объем жидкости. Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны. По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½. Применяем св -во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V 1 , малого – V 2 . Получим: Поскольку по условию V 1 =1600 мл, то V 2 =1600/8=200 мл.
Слайд 16
15. Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего? ! Алгоритм выполнения Записываем формулу для вычисления объема шара. Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2. Записываем отношение объемов, вычисляем его, подставив числовые данные из условия. Вывод: объем большего шара в 64 раза больше.
Слайд 17
16. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго? ! Алгоритм выполнения Записываем формулу для определения площади бок.поверхности цилиндра. Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров. Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия. Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Слайд 18
17. Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала? ! Алгоритм выполнения Записываем формулу для определения массы большего шаров через плотность и объем. Объем в этой формуле расписываем через ф- лу объема шара (через его радиус). Записываем ф- лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2). Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф- ле для массы меньшего шара. Вычисляем искомую массу. m 1 = ρ V 1 . V 1 = (4/3)π R 1 3 . Отсюда получаем: m 1 =(4/3)πρ R 1 3 . m 2 =ρ V 2 V 2 =(4/3)π R 2 3
Слайд 19
Планиметрия. №15 18 . В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(см. рисунок). Найдите длину отрезка AH . ! Алгоритм выполнения: Вспомнить определение косинуса угла. Записать выражение для нахождения косинуса угла. Выразить неизвестную величину. Вычислить. cos A = АН/АС. АН = АС · cos A АН = АС · cos A = 4 · 0,8 = 3,2 Ответ: 3,2.
Слайд 20
19. Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах. ! Алгоритм выполнения: Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается. Вычислить градусную меру угла, на который опирается дуга. Вычислить вписанный угол. Весь круг составляет 360°, а 5/18 от его длины это Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен 100°:2 = 50°. Ответ: 50.
Слайд 21
20.В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ ! Алгоритм выполнения Определяем вид треугольника. Доказываем, что медиана ВМ является и высотой. Из прямоугольного треугольника АМВ по т. Пифагора находим медиану ВМ. Если АВ=ВС, то ∆АВС – равнобедренный. Т.к. АМ медиана, то AM=АС:2=24:2=12.
Слайд 22
21. На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD. ! Алгоритм выполнения Находим ЕС. Определяем значение СD. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD. Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12. Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12. ЕС=ВС–ВЕ=17–12=5. ∆ЕСD прямоугольный. Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 .
Слайд 23
22. В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B. ! Алгоритм выполнения По т.Пифагора находим величину катета ВС. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе. Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .
Слайд 24
23. В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС. ! Алгоритм выполнения Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB. Из ∆ADB находим катет ВD, используя sin A. Находим АD из ∆ADB по т.Пифагора . Далее определяем АС как 2AD. Находим площадь ∆АВС по формуле S= ah /2 . В ∆ ADB sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15. Из ∆ ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 АС=2АD=2·20=40.
Слайд 25
24. В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ. ! Алгоритм выполнения Определяем величину угла АВМ. Доказываем, что ∆АМВ прямоугольный. Находим АВ, используя формулу-определение для косинуса. По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет 120 0 :2=60 0 . Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.
Слайд 26
25. В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон. ! Алгоритм выполнения Доказываем, что ∆АКВ прямоугольный. Из ∆АКВ по т.Пифагора находим АК. Находим АС как 2АК. Находим МN как среднюю линию. Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Поскольку ВК медиана, то АС=2АК=2·24=48. Значит, MN=AC:2=48:2=24.
Слайд 27
26. В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН. ! Алгоритм выполнения Находим длину отрезков АМ и МС как половину от АС. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС. 3. Находим АН как сумму АМ и МН. Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28. МН=НС=МС/2=28/2=14. АН=АМ+МН=28+14=42.
Слайд 28
Стереометрия (№16) 27. Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения. ! Алгоритм выполнения: Определить тип фигуры, образующей сечение. Записать формулу для нахождения площади фигуры, образующей сечение. Вычислить недостающие данные. Вычислить искомую площадь сечения. Сечение является прямоугольником, одна из сторон которого образующая цилиндра. Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху :
Слайд 29
Ширина прямоугольника – CD. По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12. СD = СВ + ВD. СВ = ВD Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В данном случае СА 2 = СВ 2 + АВ 2 СВ 2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое. СВ 2 = СА 2 — АВ 2 СВ = √(СА 2 — АВ 2 ) СВ = √(13 2 — 12 2 ) = √(169 — 144) = √25 = 5 Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10 Вычислим искомую площадь сечения. 10 · 18 = 180 Ответ: 180.
Слайд 30
29. Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды. ! Алгоритм выполнения: Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи. Найти площади треугольников. Найти площадь боковой поверхности пирамиды. В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность. Найдем площади треугольников. Так как треугольник равнобедренный, AH=AC:2=24:2=12. Р/м треугольник АВН. АВ 2 = ВН 2 + АН 2 . ВН 2 = АВ 2 — АН 2 Боковая поверхность пирамиды состоит из трех треугольников
Слайд 31
30. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17. Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты . После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту: V = 1/3 • 16 •3 = 16
Слайд 32
31. Сторона основания правильной треугольной призмы АВСА 1 В 1 С 1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА 1 В 1 С 1 . ! Алгоритм выполнения Находим площадь основы призмы через формулу для площади правильного треугольника. Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину. Объем призмы: V= Sh
Слайд 33
32. Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса. ! Алгоритм выполнения Записываем формулу для объема конуса. Из нее выражаем площадь основания. Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса. Из этих двух формул выражаем искомую величину. Вычисляем ее. S осн =3 V / h . S = π R 2 Поскольку в данном случае S осн = S , то π R 2 =3 V / h
Слайд 34
33. Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда. ! Алгоритм выполнения Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра. Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение. Объем прямоугольного параллелепипеда равен: V= abc , где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно. Тогда: с=V / ( ab ). с=280 /(8·5)=7. Площадь поверхности прямоугольного параллелепипеда вычисляется так: S =2( ab+bc+ac ). Отсюда имеем: S=2(8·5+5·7+8·7)=2(40+35+56)=2·131=262.
Слайд 35
34. Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса. ! Алгоритм выполнения Записываем формулу для объема конуса. Из нее выражаем высоту. Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь. Подставляем числовые данные в формулу для объема, вычисляем искомую величину. Площадь основания (как площадь круга) равна: S осн =π R 2 . Вычисляем площадь: Sосн =π·2 2 =4π.